Appendix B
Groups
The group is the basic algebraic structure with one operation. Groups appear in many contexts in this book. For example, all the signal domains introduced in Chapters 2–5 have the structure of an additive commutative group. Also, sets of transformations of domains and signals have the structure of a noncommutative group. This is used extensively in Chapter 12. This appendix provides basic definitions and properties of groups, but any standard text on abstract algebra should be consulted for a more detailed treatment, e.g, part I of Dummit and Foote (2004) or chapter 1 of Miller (1972).
- 1. A binary operation
 in a set
in a set 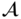 is a function from
is a function from  into
into  . We write
. We write 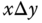 for
for  .
.
For example, addition
 is a binary operation on the set
is a binary operation on the set 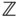 of integers.
of integers. - 2. A binary operation
 on a set
on a set  is associative if
is associative if  for all
for all 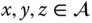 .
.
For an associative operation, the parentheses are not required, and we can write simply
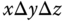 . Addition on
. Addition on  is associative.
is associative. - 3. A binary operation
 on a set
on a set  is commutative if
is commutative if 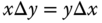 for all
for all  .
.
Addition on
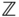 is also commutative.
is also commutative. - 4. A semigroup is a set
 with one associative binary operation
with one associative binary operation  , and is denoted
, and is denoted  . A semigroup is commutative if its binary operation is commutative.
. A semigroup is commutative if its binary operation is commutative.
The set of strictly positive integers
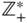 is a commutative semigroup.
is a commutative semigroup. - 5. Let
 be a binary operation on a set
be a binary operation on a set  . An element
. An element  is a neutral element if
is a neutral element if  for all
for all  . If a neutral element exists, it is unique.
. If a neutral element exists, it is unique.
The set of strictly positive integers
 under addition has no neutral element while the set of non‐negative integers
under addition has no neutral element while the set of non‐negative integers  has the neutral element 0.
has the neutral element 0. - 6. Let
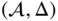 be a semigroup with a neutral element
be a semigroup with a neutral element  . An element
. An element  is invertible if there exists
is invertible if there exists  such that
such that 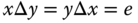 . Such an element
. Such an element 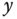 is called the inverse of
is called the inverse of  , and it is unique if it exists. The inverse is denoted
, and it is unique if it exists. The inverse is denoted  in general, or
in general, or  when the operation is addition.
when the operation is addition. - 7. A group is a semigroup
 with a neutral element such that every element of
with a neutral element such that every element of 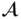 is invertible. The group
is invertible. The group  is called Abelian (or cummutative) if the operation
is called Abelian (or cummutative) if the operation  is commutative. We will generally write that
is commutative. We will generally write that  is a group under the operation
is a group under the operation  or simply
or simply 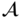 when the operation is clear from context.
when the operation is clear from context.
All of the domains studied in Chapters 2–5 are examples of additive Abelian groups.
- 8. Let
 be a group. The nonempty subset
be a group. The nonempty subset  of
of  is a subgroup of
is a subgroup of 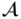 if
if 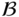 is closed under the group operation and under inverses. If
is closed under the group operation and under inverses. If  , then
, then  and
and 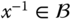 . If
. If 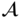 is a finite group, then the number of elements in any subgroup divides the number of elements in the group (Lagrange's Theorem).
is a finite group, then the number of elements in any subgroup divides the number of elements in the group (Lagrange's Theorem).
The set
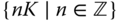 for any
for any  is a subgroup of the additive Abelian group
is a subgroup of the additive Abelian group 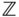 . We denote this subgroup
. We denote this subgroup  .
. - 9. Let
 be a subgroup of
be a subgroup of 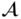 . For any
. For any  , let
(B.1)
, let
(B.1)
These are called respectively a left coset of
 and a right coset of
and a right coset of  . If
. If 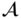 is an Abelian group, the left and right cosets are the same and we write
is an Abelian group, the left and right cosets are the same and we write 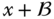 for a coset of
for a coset of 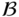 in
in 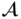 .
.The set
 is a coset of
is a coset of 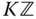 in
in  for any
for any  .
. - 10. Let
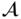 be an Abelian group and let
be an Abelian group and let  be a subgroup. For any
be a subgroup. For any 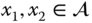 , we say that
, we say that  if
if 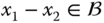 . Then
. Then 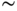 is an equivalence relation, and the equivalence classes are the cosets of
is an equivalence relation, and the equivalence classes are the cosets of  in
in  . Any element of a coset can be used as a coset representative. The cosets of
. Any element of a coset can be used as a coset representative. The cosets of  in
in  form a partition of
form a partition of  .
.
There are
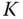 cosets of
cosets of  in
in  . We can use the elements
. We can use the elements 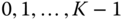 as coset representatives.
as coset representatives. - 11. Let
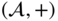 be an Abelian group and
be an Abelian group and  a subgroup. Let
a subgroup. Let 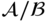 denote the set of cosets of
denote the set of cosets of  in
in 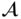 . We define a binary operation
. We define a binary operation  on
on  to be
to be 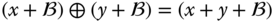 . This operation is well defined and
. This operation is well defined and  is an Abelian group called the quotient group.
is an Abelian group called the quotient group.
Note that these last two concepts can be defined on nonAbelian groups as well, but we do not use them explicitly in this book.
