CHAPTER 9: The Priority Queue ADT
© Ake13bk/Shutterstock
Chapter 4 focused on the queue, a first-in, first-out (FIFO) structure. In this short chapter we look at a related structure, the priority queue. Rather than dequeuing the element that has been in the queue for the longest time, with a priority queue we dequeue the element with the highest priority. Here we define priority queues, how they are used, and how they are implemented. In particular, we look at a clever implementation approach called the “heap,” which features fast insertion and removal of elements.
9.1 The Priority Queue Interface
A priority queue is an abstract data type with an interesting accessing protocol. Only the highest-priority element can be accessed. “Highest priority” can mean different things, depending on the application. Consider, for example:
A small company with one IT specialist. When several employees need IT support at the same time, which request gets handled first? The requests are processed in order of the employee’s importance in the company; the specialist handles the president’s request before starting on the vice president’s, and so on. The priority of each request relates to the level of the employee who initiated it.
An ice cream vendor serves customers in the order that they arrive; that is, the highest-priority customer is the one who has been waiting the longest. The FIFO queue studied in Chapter 4 can be considered a priority queue whose highest-priority element is the one that has been queued the longest time.
Sometimes a printer shared by a number of computers is configured to always print the smallest job in its queue first. This way, someone who is printing only a few pages does not have to wait for large jobs to finish. For such printers, the priority of the jobs relates to the size of the job: shortest job first.
Using Priority Queues
Priority queues are useful for any application that involves processing elements by priority.
In discussing FIFO queue applications in Chapter 4, we said that an operating system often maintains a queue of processes that are ready to execute. It is common, however, for such processes to have different priority levels, so that rather than using a standard queue, an operating system may use a priority queue to manage process execution.
In Section 4.8, “Application: Average Waiting Time,” we used queues to help us model a customer service system. This was a relatively simple model that generated all the information about the customers first, and then simulated servicing them. For more complex models it is possible to generate customer information during processing—consider, for example, that a man arrives at the service counter only to discover he incorrectly filled out a form; he needs to redo the form and get back in the queue. His reentry to the queue is a dynamic event that could not have been predicted ahead of time. Modeling this type of system is termed discrete event simulation and is an interesting area of study. A common approach with discrete event models is to maintain a priority queue of events. As events are generated they are enqueued, with a priority level equal to the time at which the event is to take place. Earlier events have higher priority. The event-driven simulation proceeds by dequeuing the highest-priority event (the earliest event available) and then modeling that event, which may generate subsequent events to be enqueued.
Priority queues are also useful for sorting data. Given a set of elements to sort, the elements can be enqueued into a priority queue, and then dequeued in sorted order (from largest to smallest). We look at how priority queues and their implementations can be used in sorting in Chapter 11.
The Interface
The operations defined for the Priority Queue ADT include enqueuing elements and dequeuing elements, as well as testing for an empty or full-priority queue and determining the queue’s size. These operations are very similar to those specified for the FIFO queue discussed in Chapter 4. In fact, except for the information in the comments and the name and package of the interface, the queue interface and the priority queue interface are indistinguishable. Functionally, the difference between the two types of queues is due to how the dequeue operation is implemented. The Priority Queue ADT does not follow the “FIFO” approach; instead, it always returns the highest-priority element from the current set of enqueued elements, no matter when the element was enqueued. For our purposes we define highest priority as the “largest” element based on the indicated ordering of elements. Here is the interface:
//--------------------------------------------------------------------------- // PriQueueInterface.java by Dale/Joyce/Weems Chapter 9 // // Interface for a class that implements a priority queue of T. // The largest element as determined by the indicated comparison has the // highest priority. // // Null elements are not allowed. Duplicate elements are allowed. //--------------------------------------------------------------------------- package ch09.priorityQueues; public interface PriQueueInterface<T> { void enqueue(T element); // Throws PriQOverflowException if this priority queue is full; // otherwise, adds element to this priority queue. T dequeue(); // Throws PriQUnderflowException if this priority queue is empty; // otherwise, removes element with highest priority from this // priority queue and returns it. boolean isEmpty(); // Returns true if this priority queue is empty; otherwise, returns false. boolean isFull(); // Returns true if this priority queue is full; otherwise, returns false. int size(); // Returns the number of elements in this priority queue. }
The exception objects mentioned in the comments are defined as part of the ch09. priorityQueues package. They are unchecked exceptions.
As with all of the ADTs we have studied, variations of the Priority Queue ADT exist. In particular, it is common to include operations that allow an application to reach into a priority queue to examine, manipulate, or remove elements. For some applications such operations are necessary. Consider the previously discussed use of priority queues for discrete event simulation. With some discrete event models the result of handling an event may affect other scheduled events, delaying or canceling them. The additional priority queue functionality allows them to be used for such models. Here though, we focus solely on the basic Priority Queue operations as listed in PriQueueInterface.
9.2 Priority Queue Implementations
There are many ways to implement a priority queue. In any implementation, we want to be able to access the element with the highest priority quickly and easily.
Let us briefly consider some possible approaches.
Unsorted Array
Enqueuing an element would be very easy with an unsorted array—simply insert it in the next available array slot, an O(1) operation. Dequeuing, however, would require searching through the entire array to find the largest element, an O(N) operation.
Sorted Array
Dequeuing is very easy with this array-based approach: Simply return the last array element (which is the largest) and reduce the size of the queue; dequeue is a O(1) operation. Enqueuing, however, would be more expensive, because we have to find the place to insert the element. This is an O(log2N) step if we use a binary search. Shifting the elements of the array to make room for the new element is an O(N) step, so overall the enqueue operation is O(N).
The SortedABPriQ class implements the PriQueueInterface using the approach outlined earlier. It provides two constructors, one of which allows the client to pass a Comparator argument to be used to determine priority, and the other which has no parameters, indicating that the natural order of the elements should be used. This is an unbounded array-based implementation. To enable easy testing it includes a toString method. The reader is invited to study the code found in the ch09.priorityQueues package. Here is a short program that demonstrates use of the SortedABPriQ class, followed by its output.
//--------------------------------------------------------------------------- // UseSortedABPriQ.java by Dale/Joyce/Weems Chapter 9 // // Example use of the SortedABPriQ //--------------------------------------------------------------------------- package ch09.apps; import ch09.priorityQueues.*; public class UseSortedABPriQ { public static void main(String[] args) { PriQueueInterface<String> pq = new SortedABPriQ<String>(); pq.enqueue("C"); pq.enqueue("O"); pq.enqueue("M"); pq.enqueue("P"); pq.enqueue("U"); pq.enqueue("T"); pq.enqueue("E"); pq.enqueue("R"); System.out.println(pq); System.out.println(pq.dequeue()); System.out.println(pq.dequeue()); System.out.println(pq); } } The output is: Priority Queue: C E M O P R T U U T Priority Queue: C E M O P R
Sorted Linked List
Assume the linked list is kept sorted from largest to smallest. Dequeuing with this reference-based approach simply requires removing and returning the first list element, an operation that takes only a few steps. But enqueuing again is an O(N) operation, because we must search the list one element at a time to find the insertion location.
Binary Search Tree
For this approach, the enqueue operation is implemented as a standard binary search tree insert operation. We know that operation requires O(log2N) steps on average. Assuming access to the underlying implementation structure of the tree, we can implement the dequeue operation by returning the largest element, which is the rightmost tree element. We follow the right subtree references down, maintaining a trailing reference, until reaching a node with an empty right subtree. The trailing reference allows us to “unlink” the node from the tree. We then return the element contained in the node. This is also a O(log2N) operation, on average.
The binary search tree approach is the best so far—it requires, on average, only O(log2N) steps for both enqueue and dequeue. If the tree is skewed, however, the performance degenerates to O(N) steps for each operation. The time efficiency benefits depend on the tree remaining balanced. Unless a self-balancing tree is used it is likely the tree will become skewed—after all, elements will continually be removed from the far right of the tree only, which will result in a tree that is heavier on its left side. We can do better.
The next section presents a very clever approach, called the heap, that guarantees O(log2N) steps, even in the worst case.
9.3 The Heap
A heap is an implementation of a priority queue that uses a binary tree that satisfies two properties, one concerning its shape and the other concerning the order of its elements. Before discussing these properties we need to expand our tree-related terminology.1
A full binary tree is a binary tree in which all of the leaves are on the same level and every nonleaf node has two children. The basic shape of a full binary tree is triangular:

A complete binary tree is a binary tree that is either full or full through the next-to-last level, with the leaves on the last level as far to the left as possible. The shape of a complete binary tree is either triangular (if the tree is full) or something like the following:

Figure 9.1 shows some examples of different types of binary trees.
Now we are ready to define a heap. As previously stated, a heap is an implementation of a priority queue that uses a binary tree that satisfies two properties: one concerning its shape and the other concerning the order of its elements. The shape property is simply stated: The underlying tree must be a complete binary tree. The order property says that, for every node in the tree, the value stored in that node is greater than or equal to the value in each of its children.
It might be more accurate to call this structure a “maximum heap,” because the root node contains the maximum value in the structure. It is also possible to create a “minimum heap,” each of whose elements contains a value that is less than or equal to the value of each of its children.
The term heap is used for both the abstract concept, that is, a binary tree that maintains the shape and order properties, and the underlying structure, usually an efficient array-based tree implementation. This section concentrates on the properties of heaps and how a heap is used to implement a priority queue. The next section describes the standard implementation of the heap itself, using an array.

Figure 9.1 Examples of different types of binary trees

Figure 9.2 Two heaps containing the letters A through J
Figure 9.2 shows two trees containing the letters A through J that fulfill both the shape and order properties. The placement of the values differs in the two trees, but the shape is the same: a complete binary tree of 10 elements. The two trees have the same root node. A group of values can be stored in a binary tree in many ways and still satisfy the order property of heaps. Because of the shape property, we know that all heap trees with a given number of elements have the same shape. We also know, because of the order property, that the root node always contains the largest value in the tree. This helps us implement an efficient dequeue operation, supporting the Priority Queue ADT.
Let us say we want to dequeue an element from the heap in Figure 9.2a—in other words, we want to remove and return the element with the largest value from the tree, the J. The largest element is in the root node, and since we know exactly where to find it we can easily remove it, as illustrated in Figure 9.3a. Of course, this leaves a hole in the root position (Figure 9.3b). Because the heap’s tree must be complete, we decide to fill the hole with the bottom rightmost element from the tree; now the structure satisfies the shape property (Figure 9.3c). The replacement value, however, came from the bottom of the tree, where the smaller values are; as a consequence, the tree no longer satisfies the order property of heaps.
This situation suggests one of the standard heap-support operations: Given a binary tree that satisfies the heap properties, except that the root position is empty, insert an element into the structure so that it again becomes a heap. This operation, called reheapDown, involves starting at the root position and moving the new element down, while moving child elements up, until we find a legal position for the newelement (see Figure 9.3d and e). We swap the element with one of its children—its largest child, in fact, so that the order property will be restored.

Figure 9.3 The dequeue operation
To dequeue an element from the heap, we remove and return the root element, remove the bottom rightmost element, and then pass the bottom rightmost element to reheapDown to restore the heap (Figure 9.3f).
Now suppose we want to enqueue an element to the heap—where do we put it? Let us enqueue the element ‘I’ into the heap represented in Figure 9.3f. Yes, it is true that ‘I’ is already in the heap, but heaps (and priority queues) are allowed to contain duplicate elements. The shape property tells us that the tree must be complete, so we put the new element in the next bottom rightmost place in the tree, as illustrated in Figure 9.4a. Now the shape property is satisfied, but the order property may be violated. This situation illustrates the need for another heap-support operation: Given a binary tree that satisfies the heap properties, except that the last position is empty, insert a given element into the structure so that it again becomes a heap. After inserting the element in the next bottom rightmost position in the tree, we float the element up the tree, while moving tree elements down, until the element is in a position that satisfies the order property (see Figure 9.4b and c) resulting once again in a legal heap (Figure 9.4d). This operation is called reheapUp—it adds an element to the heap, assuming the last index position of the array-based tree implementation is empty.
To review how our heap supports a priority queue we show the results of a sequence of enqueues and dequeues in Figure 9.5. Initially the priority queue is empty. The sequence of operations that correspond to the changes depicted in the figure are listed in the text box embedded in the figure. At each stage we show only the final result of the reheap up or reheap down operation, allowing you to fill in the details of how the heap elements are adjusted to maintain the heap properties.

Figure 9.4 The reheapUp operation

Figure 9.5 A sequence of priority queue operations performed by a heap
Note that because a heap is always a complete tree, the height of a heap is always at most ⌊log2N⌋, where N represents the number of elements in the heap. The reheap up and reheap down operations involve moving an element up the tree or down the tree through these ⌊log2N⌋ levels. Assuming we can implement the primitive statements involved in these operations in constant time, we can support both enqueue and dequeue priority queue methods with O(log2N) efficiency. In the next section we learn how to do this.
9.4 The Heap Implementation
Although we have graphically depicted heaps as binary trees with nodes and links, it would be very impractical to implement the heap operations using the linked binary tree representation presented in Chapter 7. For example, our binary search tree implementation does not efficiently support “moving” elements up a tree. Due to the shape property of heaps an alternate representation is possible, one that supports constant time implementation of all of the operations we need to manage our heaps. We first explore this tree implementation approach and then see how it can be used to implement a heap (and therefore a priority queue).
A Nonlinked Representation of Binary Trees
The implementation of binary trees we studied in Chapter 7 used a scheme in which the links from parent to children are explicit in the implementation structure. In other words, instance variables were declared in each node for the reference to the left child and the reference to the right child.
A binary tree can be stored in an array in such a way that the relationships in the tree are not directly represented by references, but rather are implicit in the positions used within the array to hold the elements.
Let us take a binary tree and store it in an array in such a way that the parent–child relationships are not lost. We store the tree elements in the array, level by level, from left to right. We call the array elements and store the index of the last tree element in a variable lastIndex, as illustrated in Figure 9.6. The tree elements are stored with the root in elements[0] and the last node in elements[lastIndex].
To implement the algorithms that manipulate the tree, we must be able to find the left and right children of a node in the tree. Comparing the tree and the array in Figure 9.6, we make the following observations:
elements[0]’s children are inelements[1]andelements[2].
elements[1]’s children are inelements[3]andelements[4].
elements[2]’s children are inelements[5]andelements[6].
Do you see the pattern? For any node elements[index], its left child is in elements[index * 2 + 1] and its right child is in elements[(index * 2) + 2] (provided that these child nodes exist). Notice that nodes from elements[(tree. lastIndex + 1) / 2] to elements[tree.lastindex] are leaf nodes.

Figure 9.6 An abstract binary tree and its concrete array-based representation
Not only can we easily calculate the location of a node’s children, but we can also determine the location of its parent node, a required operation for reheapUp. This task is not an easy one in a binary tree linked together with references from parent to child nodes, but it is very simple in our implicit link implementation: elements[index]’s parent is in elements[(index - 1) / 2].
Because integer division truncates any remainder, (index - 1) / 2 is the correct parent index for either a left or right child. Thus, this implementation of a binary tree is linked in both directions: from parent to child, and from child to parent.
The array-based representation is simple to implement for trees that are full or complete, because the elements occupy contiguous array slots. If a tree is not full or complete, however, we must account for the gaps where nodes are missing. To use the array representation, we must store a dummy value in those positions in the array to maintain the proper parent–child relationship. The choice of a dummy value depends on the information that is stored in the tree. For instance, if the elements in the tree are nonnegative integers, a negative value can be stored in the dummy nodes; if the elements are objects, we can use a null value.
Figure 9.7 illustrates an incomplete tree and its corresponding array. Some of the array slots do not contain actual tree elements, but rather dummy values. The algorithms to manipulate the tree must reflect this situation. For example, to determine that the node in elements[index] has a left child, we must verify that (index * 2) + 1 <= lastIndex, and that the value in elements[(index * 2) + 1] is not the dummy value.

Figure 9.7 An abstract binary tree and its concrete array-based representation using dummy values
Implementing a Heap
Although when there are many “holes” in the tree, the array-based binary tree implementation can waste a lot of space, in the case of the heap it is a perfect representation. The shape property of heaps tells us that the binary tree is complete, so we know that it is never unbalanced. Thus, we can easily store the tree in an array with implicit links without wasting any space. Figure 9.8 shows how the values in a heap would be stored in the array-based representation.
If a heap with N elements is implemented this way, the shape property says that the heap elements are stored in N consecutive slots in the array, with the root element in the first slot (index 0) and the last leaf node in the slot with index lastIndex = N – 1. Therefore, when implementing this approach there is no need for dummy values—there are never gaps in the tree.
Recall that when we use this representation of a binary tree, the following relationships hold for an element at position index:
If the element is not the root, its parent is at position
(index - 1) / 2.If the element has a left child, the child is at position
(index * 2) + 1.If the element has a right child, the child is at position
(index * 2) + 2.
These relationships allow us to efficiently calculate the parent, left child, or right child of any node. Also, because the tree is complete, no space is wasted using the array representation. Time efficiency and space efficiency! We make use of these features in our heap implementation.

Figure 9.8 An abstract heap and its concrete array-based representation
Rather than directly use an array to implement our heaps we use the Java library’s ArrayList class. This allows us to create a generic heap without needing to deal with the troublesome issues surrounding the use of generics and arrays in Java. An ArrayList is essentially just a wrapper around an array—therefore, the use of an ArrayList does not cost much, if anything, in terms of efficiency. This is especially true since we design our heap-based priority queue to be of a fixed capacity, and therefore prevent the use of the automatic, time-inefficient copying of the underlying array that occurs when an ArrayList object needs to be resized. Furthermore, the code only ever adds or removes elements at the “end” of the ArrayList—adding or removing anywhere else would require costly element shifting.
Here is the beginning of our HeapPriQ class. As you can see, it implements PriQueueInterface. Because it implements a priority queue, we placed it in the ch09. priorityQueues package. Also, note that both constructors require an integer argument, used to set the size of the underlying ArrayList. As with several of our ADTs, one constructor accepts a Comparator argument and the other creates a Comparator based on the “natural order” of T. The isEmpty, isFull, and size operations are trivial.
//--------------------------------------------------------------------------- // Heap.java by Dale/Joyce/Weems Chapter 9 // Priority Queue using Heap (implemented with an ArrayList) // // Two constructors are provided: one that use the natural order of the // elements as defined by their compareTo method and one that uses an // ordering based on a comparator argument. //--------------------------------------------------------------------------- package ch09.priorityQueues; import java.util.*; // ArrayList, Comparator public class HeapPriQ<T> implements PriQueueInterface<T> { protected ArrayList<T> elements; // priority queue elements protected int lastIndex; // index of last element in priority queue protected int maxIndex; // index of last position in ArrayList protected Comparator<T> comp; public HeapPriQ(int maxSize) // Precondition: T implements Comparable { elements = new ArrayList<T>(maxSize); lastIndex = -1; maxIndex = maxSize - 1; comp = new Comparator<T>() { public int compare(T element1, T element2) { return ((Comparable)element1).compareTo(element2); } }; } public HeapPriQ(int maxSize, Comparator<T> comp) // Precondition: T implements Comparable { elements = new ArrayList<T>(maxSize); lastIndex = -1; maxIndex = maxSize - 1; this.comp = comp; } public boolean isEmpty() // Returns true if this priority queue is empty; otherwise, returns false. { return (lastIndex == -1); } public boolean isFull() // Returns true if this priority queue is full; otherwise, returns false. { return (lastIndex == maxIndex); } public int size() // Returns the number of elements on this priority queue. { return lastIndex + 1; }
The enqueue Method
We next look at the enqueue method, which is the simpler of the two transformer methods. Assuming the existence of a reheapUp helper method, as specified previously, the enqueue method is
public void enqueue(T element) throws PriQOverflowException // Throws PriQOverflowException if this priority queue is full; // otherwise, adds element to this priority queue. { if (lastIndex == maxIndex) throw new PriQOverflowException("Priority queue is full"); else { lastIndex++; elements.add(lastIndex,element); reheapUp(element); } }
If the heap is already full, the appropriate exception is thrown. Otherwise, we increase the lastIndex value, add the element to the heap at that location, and call the reheapUp method. Of course, the reheapUp method is doing all of the interesting work. Let us look at it more closely.
The reheapUp algorithm starts with a tree whose last node is empty; we call this empty node the “hole.” We swap the hole up the tree until it reaches a spot where the element argument can be placed into the hole without violating the order property of the heap. While the hole moves up the tree, the elements it is replacing move down the tree, filling in the previous location of the hole. This situation is illustrated in Figure 9.9.

Figure 9.9 The reheapUp operation in action
The sequence of nodes between a leaf and the root of a heap can be viewed as a sorted linked list. This is guaranteed by the heap’s order property. The reheapUp algorithm is essentially inserting an element into this sorted linked list. As we progress from the leaf to the root along this path, we compare the value of element with the value in the hole’s parent node. If the parent’s value is smaller, we cannot place element into the current hole, because the order property would be violated, so we move the hole up. Moving the hole up really means copying the value of the hole’s parent into the hole’s location. Now the parent’s location is available, and it becomes the new hole. We repeat this process until (1) the hole is the root of the heap or (2) element’s value is less than or equal to the value in the hole’s parent node. In either case, we can now safely copy element into the hole’s position.
This approach requires us to be able to find a given node’s parent quickly. This task appears difficult, based on our experiences with references that can be traversed in only one direction. But, as we saw earlier, it is very simple with our implicit link implementation:
If the element is not the root, its parent is at position
(index - 1) / 2.
Here is the code for the reheapUp method:
private void reheapUp(T element) // Current lastIndex position is empty. // Inserts element into the tree and ensures shape and order properties. { int hole = lastIndex; while ((hole > 0) // hole is not root and element > hole's parent && (comp.compare(element, elements.get((hole - 1) / 2)) > 0)) { // move hole's parent down and then move hole up elements.set(hole,elements.get((hole - 1) / 2)); hole = (hole - 1) / 2; } elements.set(hole, element); // place element into final hole }
This method takes advantage of the short-circuit nature of Java’s && operator. If the current hole is the root of the heap, then the first half of the while loop control expression
(hole > 0)
is false, and the second half
(element.compareTo(elements.get((hole - 1) / 2)) > 0))
is not evaluated. If it was evaluated in that case, it would cause an IndexOutOfBoundsException to be thrown.
The dequeue Method
Finally, we look at the dequeue method. As for enqueue, assuming the existence of the helper method, in this case the reheapDown method, the dequeue method is relatively simple:
public T dequeue() throws PriQUnderflowException // Throws PriQUnderflowException if this priority queue is empty; // otherwise, removes element with highest priority from this // priority queue and returns it. { T hold; // element to be dequeued and returned T toMove; // element to move down heap if (lastIndex == -1) throw new PriQUnderflowException("Priority queue is empty"); else { hold = elements.get(0); // remember element to be returned toMove = elements.remove(lastIndex); // element to reheap down lastIndex--; // decrease priority queue size if (lastIndex != -1) // if priority queue is not empty reheapDown(toMove); // restore heap properties return hold; // return largest element } }
If the heap is empty, the appropriate exception is thrown. Otherwise, we first store a reference to the root element (the maximum element in the tree), so that it can be returned to the client program when finished. We also store a reference to the element in the “last” position and remove it from the ArrayList. Recall that this is the element used to move into the hole vacated by the root element, so we call it the toMove element. We decrement the lastIndex variable to reflect the new bounds of the heap and, assuming the heap is not now empty, pass the toMove element to the reheapDown method. The only thing remaining to do is to return the saved value of the previous root element, the hold variable, to the client.
Look at the reheapDown algorithm more closely. In many ways, it is similar to the reheapUp algorithm. In both cases, we have a “hole” in the tree and an element to be placed into the tree so that the tree remains a heap. In both cases, we move the hole through the tree (actually moving tree elements into the hole) until it reaches a location where it can legally hold the element. The reheapDown operation, however, is a more complex operation because it is moving the hole down the tree instead of up the tree. When we are moving down, there are more decisions to make.
When reheapDown is first called, the root of the tree can be considered a hole; that position in the tree is available, because the dequeue method has already saved the contents in its hold variable. The job of reheapDown is to “move” the hole down the tree until it reaches a spot where element can replace it. See Figure 9.10.
Before we can move the hole, we need to know where to move it. It should move either to its left child or to its right child, or it should stay where it is. Assume the existence of another helper method, called newHole, that provides us this information. The newHole method accepts arguments representing the index of the hole (hole), and the element to be inserted (element). The specification for newHole is
private int newHole(int hole, T element) // If either child of hole is larger than element, return the index // of the larger child; otherwise, return the index of hole.
Given the index of the hole, newHole returns the index of the next location for the hole. If newHole returns the same index that is passed to it, we know the hole is at its final location. The reheapDown algorithm repeatedly calls newHole to find the next index for the hole, and then moves the hole down to that location. It does this until newHole returns the same index that is passed to it. The existence of newHole simplifies reheapDown so that we can now create its code:

Figure 9.10 The reheapDown operation in action
private void reheapDown(T element) // Current root position is "empty"; // Inserts element into the tree and ensures shape and order properties. { int hole = 0; // current index of hole int next; // next index where hole should move to next = newHole(hole, element); // find next hole while (next != hole) { elements.set(hole,elements.get(next)); // move element up hole = next; // move hole down next = newHole(hole, element); // find next hole } elements.set(hole, element); // fill in the final hole }
Now the only thing left to do is create the newHole method. This method does quite a lot of work for us. Consider Figure 9.10 again. Given the initial configuration, newHole should return the index of the node containing J, the right child of the hole node; J is larger than either the element (E) or the left child of the hole node (H). Thus, newHole must compare three values (the values in element, the left child of the hole node, and the right child of the hole node) and return the index of the greatest value. Think about that. It does not seem very hard, but it does require quite a few steps:
Other approaches to this algorithm are possible, but they all require about the same number of comparisons. One benefit of the preceding algorithm is that if element is tied for being the largest of the three arguments, its index is returned. This choice increases the efficiency of our program because in this situation we want the hole to stop moving (reheapDown breaks out of its loop when the value of hole is returned). Trace the algorithm with various combinations of arguments to convince yourself that it works.
Our algorithm applies only to the case when the hole node has two children. Of course, the newHole method must also handle the cases where the hole node is a leaf and where the hole node has only one child. How can we tell if a node is a leaf or if it has only one child? Easily, based on the fact that our tree is complete. First, we calculate the expected position of the left child; if this position is greater than lastIndex, then the tree has no node at this position and the hole node is a leaf. (Remember, if it does not have a left child, it cannot have a right child because the tree is complete.) In this case newHole just returns the index of its hole parameter, because the hole cannot move anymore. If the expected position of the left child is equal to lastIndex, then the node has only one child, and newHole returns the index of that child if the child’s value is larger than the value of element.
Here is the code for newHole. As you can see, it is a sequence of if-else statements that capture the approaches described in the preceding paragraphs.
private int newHole(int hole, T element) // If either child of hole is larger than element, return the index // of the larger child; otherwise, return the index of hole. { int left = (hole * 2) + 1; int right = (hole * 2) + 2; if (left > lastIndex) // hole has no children return hole; else if (left == lastIndex) // hole has left child only if (comp.compare(element, elements.get(left)) < 0) // element < left child return left; else // element >= left child return hole; else // hole has two children if (comp.compare(elements.get(left), elements.get(right)) < 0) // left child < right child if (comp.compare(elements.get(right), element) <= 0) // right child <= element return hole; else // element < right child return right; else // left child >= right child if (comp.compare(elements.get(left), element) <= 0) // left child <= element return hole; else // element < left child return left; }
A Sample Use
To allow us to test our heap we include the following toString method within its implementation:
@Override
public String toString()
// Returns a string of all the heap elements.
{
String theHeap = new String("the heap is:
");
for (int index = 0; index <= lastIndex; index++)
theHeap = theHeap + index + ". " + elements.get(index) + "
";
return theHeap;
}
This toString method simply returns a string indicating each index used in the heap, along with the corresponding element contained at that index. It allows us to devise test programs that create and manipulate heaps, and then displays their structure.
Suppose you enqueue the strings “J”, “A”, “M”, “B”, “L”, and “E” into a new heap. How would you draw our abstract view of the ensuing heap? Which values would be in which ArrayList slots? Suppose you dequeue an element and print it? Which element would be printed, and how would the realigned heap appear?
To demonstrate how you might declare and use a heap in an application we provide a short example of a program that performs those operations, and we show the output from the program. Were your predictions correct?
//--------------------------------------------------------------------------- // UseHeap.java by Dale/Joyce/Weems Chapter 9 // // Example of a simple use of the HeapPriQ. //--------------------------------------------------------------------------- package ch09.apps; import ch09.priorityQueues.*; public class UseHeap { public static void main(String[] args) { PriQueueInterface<String> h = new HeapPriQ<String>(10); h.enqueue("J"); h.enqueue("A"); h.enqueue("M"); h.enqueue("B"); h.enqueue("L"); h.enqueue("E"); System.out.println(h); System.out.println(h.dequeue() + " "); System.out.println(h); } }
Here is the output from the program, with our abstract view of the heap, both before and after dequeuing the largest element, drawn to the right:

Heaps Versus Other Representations of Priority Queues
How efficient is the heap implementation of a priority queue? The constructors, isEmpty, isFull, and size methods are trivial, so we examine only the operations to add and remove elements. The enqueue and dequeue methods both consist of a few basic operations plus a call to a helper method. The reheapUp method creates a slot for a new element by moving a hole up the tree, level by level; because a complete tree is of minimum height, there are at most ⌊log2N⌋ levels above the leaf level (N = number of elements). Thus, enqueue is an O(log2N) operation. The reheapDown method is invoked to fill the hole in the root created by the dequeue method. This operation moves the hole down in the tree, level by level. Again, there are at most ⌊log2N⌋ levels below the root, so dequeue is also an O(log2N) operation.
How does this implementation compare to the others we mentioned in Section 9.2, “Priority Queue Implementations”? As discussed there, the only approach with comparable efficiency is the binary search tree approach; however, in that case the efficiency of the operations depends on the shape of the tree. When the tree is bushy, both dequeue and enqueue are O(log2N) operations. In the worst case, if the tree degenerates to a linked list, both enqueue and dequeue have O(N) efficiency.
Overall, the binary search tree looks good if it is balanced. It can, however, become skewed, which reduces the efficiency of the operations. The heap, by contrast, is always a tree of minimum height. It is not a good structure for accessing a randomly selected element, but that is not one of the operations defined for priority queues. The accessing protocol of a priority queue specifies that only the largest (or highest-priority) element can be accessed. For the operations specified for priority queues; therefore, the heap is an excellent choice.
Summary
In this chapter, we discussed the Priority Queue ADT—what it is, how it is used, and how to implement it. In particular, we studied an elegant implementation called a heap. A heap is based on a binary tree with special shape and order properties, constructed from an array rather than with links as is typical for a tree representation. The properties of heaps make them particularly well suited to implementing the priority queue. Although the algorithms for maintaining the heap in the correct shape and order are relatively complex, they allow us to create O(log2N) enqueue and dequeue operations, all while using a space-efficient array-based structure. The heap can also be used to provide a very time- and space-efficient sorting algorithm, the Heap Sort, which is presented in Chapter 11.
Exercises
9.1 The Priority Queue Interface
-
Give an example from everyday life that involves a priority queue.
-
If a priority queue is used to implement a busy queue it is conceivable that some elements may spend a very long time in the queue, waiting to be serviced. We say such elements “starve.”
Describe two examples where this type of “starvation” might be an issue.
For each of your examples, describe an approach to prevent the starvation from occurring.
-
What is the output of the following code (remember, the “largest” string lexicographically, i.e., lexicographically last, has the highest priority)—
SortedABPriQis an implementation of thePriQInterfacethat is developed in Section 9.2, “Priority Queue Implementations.”PriQInterface<String> question; question = new SortedABPriQ<String>(); System.out.println(question.isEmpty()); System.out.println(question.size()); question.enqueue("map"); question.enqueue("ant"); question.enqueue("sit"); question.enqueue("dog"); System.out.println(question.isEmpty()); System.out.println(question.size()); System.out.println(question.dequeue()); System.out.println(question.dequeue()); System.out.println(question.size());
9.2 Priority Queue Implementations
-
In this section we discussed several approaches to implementing a priority queue using previously studied data structures (Unsorted Array, Sorted Array, Sorted Linked List, and Binary Search Tree). Discuss, in a similar fashion, using
an Unsorted Linked List.
a Hash Table.
-
Bill announces that he has found a clever approach to implementing a Priority Queue with an Unsorted Array that supports an O(1) dequeue operation. He states “It is simple actually, I just create an
intinstance variablehighestthat holds the index of the largest element enqueued so far. That is easy to check and update whenever an element is enqueued, and when it is time to dequeue I return the element at indexhighest— constant time dequeue!” What do you tell Bill, or maybe, what do you ask Bill? -
Describe the ramifications of each of the following changes to
SortedABPriQ(code is in thech09.priorityQueuespackage):In the first constructor the statement
return ((Comparable)element1).compareTo(element2);
is changed to
return ((Comparable)element2).compareTo(element1);
In the boolean expression for the while loop of the
enqueuemethod the first>is changed to>=.In the boolean expression for the while loop of the
enqueuemethod the second>is changed to>=.
-
Suppose a priority queue is implemented as a binary search tree of integers. Draw the tree resulting from
enqueuing, in this order, the following integers: 15, 10, 27, 8, 18, 56, 4, 9.
continuing from part a, three dequeues are invoked.
Discuss the results.
-
 Implement the Priority Queue ADT using
Implement the Priority Queue ADT usingan Unsorted Array.
an Unsorted Linked List.
a Sorted Linked List (sort in decreasing order).
our Binary Search Tree (wrap the tree inside your priority queue implementation).
-
 Use the
Use the SortedABPriQclass to help solve the following problem. Create an applicationRandom10Kthat generates 100 numbers between 1 and 10,000, stores them in a priority queue (you can wrap them in anIntegerobject), and then prints them out in columns 10 integers wide indecreasing order.
increasing order.
ordered increasingly by the sum of the digits in the number.
9.3 The Heap
-
Consider the following trees.
Classify each as either full, complete, both full and complete, or neither full nor complete.
Which of the trees can be considered a heap? If they are not, why not?

-
Consider a tree with the following number of levels: 1 (contains only the root), 2, 3, 5, 10, N.
If full, how many nodes does it contain?
If complete, what is the minimum number of nodes it contains?
If complete, what is the maximum number of nodes it contains?
-
Draw three separate heaps containing the nodes 1, 2, 3, and 4.
-
Starting with the priority queue represented by the heap shown below (start over again with this heap for each part of the question) draw the heap that results from
one dequeue.
two dequeues.
three dequeues.
enqueue 1.
enqueue 47.
enqueue 56.
the following sequence: dequeue, enqueue 50.
the following sequence: dequeue, dequeue, enqueue 46, enqueue 50.

-
Starting with an empty priority queue, represented as a heap, draw the heap that results from:
enqueue 25, enqueue 13, enqueue 30, enqueue 10, enqueue 39, enqueue 27, dequeue
enqueue 1, enqueue 2, enqueue 3, enqueue 4, enqueue 5, enqueue 6, enqueue 7, dequeue
enqueue 7, enqueue 6, enqueue 5, enqueue 4, enqueue 3, enqueue 2, enqueue 1, dequeue
enqueue 4, enqueue 2, enqueue 6, enqueue 1, enqueue 3, enqueue 5, enqueue 7, dequeue
9.4 The Heap Implementation
-
The elements in a binary tree are to be stored in an array, as described in this section. Each element is a nonnegative
intvalue.Which value can you use as the dummy value, if the binary tree is not complete?
Draw the array that would represent the following tree:

-
The elements in a complete binary tree are to be stored in an array, as described in this section. Each element is a nonnegative
intvalue. Show the contents of the array, given the following tree: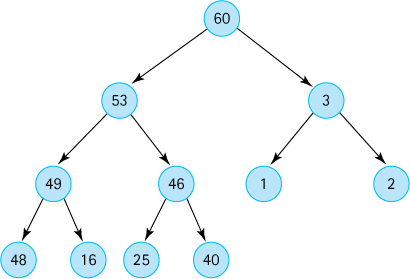
-
Given the array pictured below, draw the binary tree that can be created from its elements. (The elements are arranged in the array to represent a tree as discussed in this section.)

-
A complete binary tree is stored in an array called
treeNodes, which is indexed from 0 to 99, as described in this section. The tree contains 85 elements. Mark each of the following statements as true or false, and explain your answers.treeNodes[42]is a leaf node.treeNodes[41]has only one child.The right child of
treeNodes[12]istreeNodes[25].The subtree rooted at
treeNodes[7]is a full binary tree with four levels.The tree has seven levels that are full, and one additional level that contains some elements.
-
The
enqueuemethod listed in this section uses theArrayList addmethod to add the argument to the internal array list. But theArrayList addmethod will add the argument in the next available slot, in other words to the “right” of all the other current elements. This might not be the correct location. Explain how this is resolved.Questions 20, 21, and 22 use the following heap:

-
Show the array that stores the above heap.
-
Given the array that stores the above heap indicate the sequence of indices of the array which would be occupied by the hole during the
reheapDownmethod execution of ourHeapPriQclassif
dequeue()is invoked.if
dequeue()is invoked a second time.
-
Given the array that stores the above heap, indicate the sequence of indices of the array which would be occupied by the hole during the
reheapUpmethod execution ofHeapPriQclassif
enqueue(48)is invoked.if
enqueue(60)is then invoked.
-
Show the expected output of the following program:
package ch09.apps; import ch09.priorityQueues.*; public class UseHeap { public static void main(String[] args) { PriQueueInterface<String> h = new HeapPriQ<String>(10); h.enqueue("C"); h.enqueue("O"); h.enqueue("M"); h.enqueue("P"); h.enqueue("U"); h.enqueue("T"); h.enqueue("E"); h.enqueue("R"); System.out.println(h); System.out.println(h.dequeue() + " "); System.out.println(h); } }
