5    Seeing with the Mind's Eye

The Platonist Alternative

 
The most vexing question about mathematical knowledge is rather simple: How do we get it? We cannot learn about numbers the way we learn about apples, by looking at them. We cannot see them indirectly either, the way we see electrons by looking at streaks in a cloud chamber. To say it's a mystery would be an understatement. Nevertheless, Platonism has an answer. In fact, it can offer several different types of answer to explain how we acquire mathematical knowledge. I will describe some of the more unusual in this chapter.

In Chapter 2 I briefly sketched some of the main features of Platonism. I will do it again but in more detail this time. That will come later. First, an unusual example that will play a role in much that follows. It should also be interesting in its own right.

THE CONTINUUM HYPOTHESIS

I'll begin with an example that is remarkable for two reasons. It's a refutation of the continuum hypothesis (CH). This makes it mathematically remarkable. But is it really a refutation? That's debatable, but the argument, discovered by Christopher Freiling (1986), is plausible enough to make it worth considering. The second thing that makes it remarkable is the epistemic issue it raises: How do we come to know the result? It is certainly not in the way we normally come to know mathematical truths; so, how does it work?

First of all, some background. The cardinality of the set of natural numbers is the first infinite or transfinite cardinal number. If N = {0, 1, 2, . . . }, then the cardinality of N is |N| = ₀. The infinite cardinal numbers increase without bound: ₀, ₁, ₃,. . . It, is known that the cardinality of the real numbers is greater than that of the natural numbers, . The interesting question is which one of the cardinal numbers this is. Does |R| equal ₀ or ₂₇ or which other? The CH is the conjecture that |R|= ₁. Is it true? It has been shown that CH is independent of the rest of set theory, which means it cannot be proven or refuted in the normal sense of proof (i.e., by a logical derivation of CH or of ~CH from the standard axioms).

The second thing to mention is that we shall take ZFC for granted. ZF is Zermelo-Frankel set theory, which is standard and widely used. The C refers to the axiom of choice, which we also assume. An important consequence of ZFC is the so-called well-ordering principle. It says that any set can be well ordered, that is, can be ordered in such a way that every subset has a first element. The usual ordering, <, on the natural numbers is also a well ordering of the natural numbers. Pick any subset, say, {63972, 14, 6, 82}, it has a first element in the well ordering, namely, the number 6. But unlike the natural numbers, the usual ordering on the real numbers is not a well ordering. The subset (0, 1) = {x : 0 < x < 1}, for instance, does not have a first element. Nevertheless, ZFC guarantees that the real numbers can be well ordered by some relation, , even though no one has yet found such a well ordering. One might think the same must be true of the rational numbers Q, since the subset (0, 1) = {q : 0 < q < 1} also fails to have a first element. It is actually quite easy to construct a well ordering for Q. Think of the way we would prove that |Q| = |N|. A two-dimensional array that contains all the rationals is set up. We work through them in a zigzag manner, pairing each rational number with a natural number. The standard order is lost, so that comes before , for instance. But with this new ordering, , each subset of Q will have a first element. There is a well ordering of R, just as there is of Q, though no one has an inkling of what it might be like. Now we can turn to CH.

Imagine throwing darts at the real line, specifically at the interval [0,1]. Two darts are thrown and they are independent of one another. The point is to select two random numbers. We assume ZFC and further assume that CH is true.

The points on the line can be well ordered, so that for each q [0, 1], the set {p [0, 1]: p q} is countable. (Note that is the well-ordering relation, not the usual less than, <.) The well ordering, as earlier noted, is guaranteed by ZFC; the fact that the set is countable stems from the nature of an ordering of any set that has cardinality ₁ To get a feel for this, imagine the set of natural numbers. It is infinite, but if you pick a number in the ordering, there will be only finitely many numbers earlier (and infinitely many numbers later). Similarly, pick a number in an ordered set that is ₁ in size and you will get a set of earlier members that is at most ₀ in size and possibly even finite. (Sets of size ₀ or smaller are called “countable.”) The specific reason is that cardinal numbers are defined as the least equivalent ordinal. In the finite case this is trivial: the cardinal 27 is equal to the ordinal 27. In the infinite case, different ordinals, say ω, ω+1, ω2, can all be put in one-one correspondence; hence have the same cardinal number, ₀. It is identified with the smallest, which is ω. Anything smaller than this would have to be finite. Similarly, anything smaller than ₁ would have to be ₀ or less.

Figure 5.1 Darts picking out real numbers.

We shall call the set of elements that are earlier than the point p in the well ordering S_p. Suppose the first throw hits point p and the second hits q. Either p q, or vice versa; we'll assume the first. Thus, p S_q.. Note that S_q is a countable subset of points on the line. Since the two throws were independent, we can say the throw landing on q defines the set S_q “before” or “independently from” the throw that picks out p The measure of any countable set is 0. So the probability of landing on a point in S_q is 0. (It is not important to understand the notion of measure, only the consequence for probability theory.) While logically possible, this sort of thing is almost never the case. Yet it will happen every time there is a pair of darts thrown at the real line. Consequently, we should abandon the initial assumption, CH, since it leads to this absurdity. Thus, CH is refuted and so the number of points on the line is greater than ₁.

If the cardinality of the continuum is ₂ or greater, the argument, as set out here so far, would not work, since the set of points S_q earlier in the well ordering need not be countable, and so would not automatically lead to a zero probability of hitting a point in it. However, it is easy to extend the argument. Three darts will refute the hypothesis that the continuum is ₂, four darts will refute ₃, and so on. Continuing the thought experiment in the same way means that the continuum must be greater than _a for any finite α.

There are some aspects of this example on which I should elaborate. The darts give us a pair of real numbers picked at random. These are “real random variables,” says Mumford (2000), whose version of the thought experiment I have (with some alterations) followed. The concept of random variable at work here is not the mathematical concept found in measure theory (a defined concept inside set theory that could not yield ~CH). Moreover, the two real numbers are picked independently; either could be considered as chosen “first.” This means that the example cannot be dismissed in the way we might dismiss someone who said of a licence plate number, say, 1895372, on a passing car: “Wow, there was only a one in a million chance of that happening.” We're rightly impressed of something important, only if the number is fixed in advance. The independence and randomness of the darts guarantees the symmetry of the throws. Consequently, either dart could be considered the first throw that fixes the set of real numbers that are earlier in the well ordering.

The argument refuting CH is due to Christopher Freiling (1986). He calls his argument “philosophical,” since he does not provide a proof or a counterexample in the normal mathematical way, that is, the refutation of CH is not derived by means of logic from the axioms of the theory. That, of course, is no surprise, since CH is independent of the rest of set theory.

Freiling's refutation of CH has not been widely accepted; in fact, it has largely been ignored. Of course, Freiling's refutation of CH could have been largely ignored because it is plainly and simply wrong. But I suspect the real reason is because his approach is so unusual and far removed from mainstream thinking. One mathematician who has taken up Freiling's work, David Mumford (2000), comes at it from an interest in stochastic processes. He has called Freiling's work as important as Gödel's. Mumford (a Field's Medal winner for work in analysis) has become interested in the foundations of stochastic physics, and he hopes to reform mathematics in order to improve its use in applications. In particular, he would like to see the concept of a random variable be a primitive, not defined as it currently is, in terms of set theory.

Freiling's argument, as I indicated at the outset, raises a wonderfully interesting philosophical question: If we know ~CH, but not because we have a standard proof, then how do we know it? Let's put this question on hold for now and return to it later. But in the meantime it should be kept in the back of the mind while we consider other matters.

PERCEPTION

The principal objection to Platonism is epistemic. We have seen this repeatedly. More than any other feature of Platonism, naturalists find Platonic intuitions incredible. Many, of course, object to the supposed existence of abstract entities, since they are outside of space and time. But the real sticking point concerns our ability to perceive them. Platonists say we can see them; naturalists insist we can't. The debate, it seems safe to say, is on hold and has been at a standstill for several years. However, the question at issue has suffered, I suspect, from a lack of development of Platonistic epistemology. Naturalists typically (though not always) borrow from the well-developed epistemology of the natural sciences. To perceive something, they point out, a mediating agent, such as photons, is needed. And, of course, there is nothing like this connecting us to the entities in Plato's heaven. There are no little “platons” emitted by perfect circles that enter the mind's eye. Contemporary Platonists have almost nothing to offer in the way of a detailed epistemology of abstract entities. The original Platonist, namely, Plato himself, conjectured a wholly implausible epistemology involving immortal souls that previously existed in this abstract realm. These souls came to know mathematical objects directly, but forgot what they knew in the act of being born, and now in an embodied form are recollecting bits and pieces of what they forgot. We must do better than this.

Contemporary Platonists cling to the idea of perception. They talk of “grasping,” or “intuiting,” or “seeing” abstract entities “with the mind's eye.” It's metaphorical, to be sure, but the idea is that we can have some sort of perception of the objects of our mathematical knowledge. One of the more picturesque versions of this is in an oft-quoted passage from G.H. Hardy.

I have myself always thought of a mathematician as in the first instance an observer, a man who gazes at a distant range of mountains and notes down his observations. His object is simply to distinguish clearly and notify to others as many different peaks as he can. There are some peaks which he can distinguish easily, while others are less clear. He sees A sharply, while of B he can obtain only transitory glimpses. At last he makes out a ridge which leads from A, and following it to its end he discovers that it culminates in B. B is now fixed in his vision, and from this point he can proceed to further discoveries. In other cases perhaps he can distinguish a ridge which vanishes in the distance, and conjectures that it leads to a peak in the clouds or below the horizon. But when he sees a peak he believes that it is there simply because he sees it. If he wishes someone else to see it, he points to it, either directly or through the chain of summits which led him to recognize it himself. (1929, 18)

Naturalists react to views such as this with impatience, or amusement, or both. I don't. I take Hardy's account seriously. But there is one thing wrong. Hardy sees all mathematical evidence as ultimately some sort of perception. Eventually, with enough training and guidance, we can directly see that any given theorem is true; we simply perceive the objects in question. This is surely wrong. But Platonism needn't go this far. We need only commit ourselves to the perception of some mathematical objects and some mathematical facts. And these perceptions are evidential grounds for other mathematical propositions. The situation is similar to natural science. We don't see elementary particles and we never will, but we do see white streaks in cloud chambers. What we do see can be turned into evidence for theories about what we don't see. This brings us back to Gödel's brand of Platonism, which I mentioned earlier.

Kurt Gödel likened the epistemology of mathematics to the epistemology of the natural sciences in two important respects. This does not make one a naturalist—far from it. First, we have intuitions or mathematical perceptions that are the counterpart of sense perceptions of the physical world. Second, we evaluate (some) mathematical axioms on the basis of their consequences, especially the consequences that we can intuit, just as we evaluate theories in physics or biology on the basis of their empirical consequences. No one can see subatomic particles, but we do see line spectra and streaks in a cloud chamber. No one can see evolution, but we can see fossils and the geographical distribution of species with differing characteristics. What we can see is evidence for theories about things we can't see. Similarly, says Gödel, intuitions are evidence for conjectured axioms in mathematics.

On Gödel's view, mathematics is fallible for a number of reasons. We can have faulty intuitions, just as we can make mistakes in our sense perceptions. Moreover, false premisses can have true consequences, so the testing of axioms is not foolproof either, even when our intuitions are correct. Many people dislike the idea of giving up certainty in mathematics; perhaps they expect axioms to be “self-evident” truths. Naturalists typically will not object to this test-the-axioms-by-their-consequences feature of Gödel's view. This, after all, is how much of natural science works. But physicalist-cum nominalist-cum empiricist-minded naturalists will utterly oppose the idea of intuitions, fallible or not.

In what are perhaps the three most famous and most often quoted passages in all of Gödel's works (I have already quoted them earlier), he asserts the key ingredients of Platonism: the ontology of realism and the epistemology of intuitions.

Classes and concepts may, however, also be conceived as real objects . . . existing independently of our definitions and constructions. It seems to me that the assumption of such objects is quite as legitimate as the assumption of physical bodies and there is quite as much reason to believe in their existence. They are in the same sense necessary to obtain a satisfactory system of mathematics as physical bodies are necessary for a satisfactory theory of our sense perceptions. (1944, 456–456)

[D]espite their remoteness from sense experience, we do have something like a perception also of the objects of set theory, as is seen from the fact that the axioms force themselves upon us as being true. I don't see any reason why we should have any less confidence in this kind of perception, i.e., in mathematical intuition, than in sense perception, which induces us to build up physical theories and to expect that future sense perceptions will agree with them and, moreover, to believe that a question not decidable now has meaning and may be decided in the future. The set-theoretical paradoxes are hardly more troublesome for mathematics than deceptions of the senses are for physics . . . [N]ew mathematical intuitions leading to a decision of such problems as Cantor's continuum hypothesis are perfectly possible. (1947/1964, 484)

[E]ven disregarding the intrinsic necessity of some new axiom, and even in case it has no intrinsic necessity at all, a probable decision about its truth is possible also in another way, namely, inductively by studying its “success.” Success here means fruitfulness in consequences, in particular in “verifiable” consequences, i.e., consequences demonstrable without the new axiom, whose proofs with the help of the new axiom, however, are considerably simpler and easier to discover, and make it possible to contract into one proof many different proofs. . . . There might exist axioms so abundant in their verifiable consequences, shedding so much light upon a whole field, and yielding such powerful methods for solving problems . . . that, no matter whether or not they are intrinsically necessary, they would have to be accepted at least in the same sense as any well-established physical theory. (1947/1964, 477)

I take these passages to assert a number of important things, including: mathematical objects exist independently from us; we can perceive or intuit them; our perceptions or intuitions are fallible (similar to our fallible sense perception of physical objects); we conjecture mathematical theories or adopt axioms on the basis of suggestive intuitions (as physical theories are conjectured on the basis of suggestive sense perceptions); these theories typically go well beyond the intuitions themselves, but are tested by them (just as physical theories go beyond empirical observations but are tested by them); and in the future we might have striking new intuitions that could lead to new axioms that would settle some of today's outstanding questions. Gödel would have endorsed Freiling's approach to CH, if not in detail, at least in principle.

Though sketchy, these are the main ingredients of modern mathematical Platonism. I'll list them again in fuller detail momentarily. The only one I want to focus on in this chapter is perception, intuition, seeing with the mind's eye.

Gödel, as I just mentioned, took intuitions to be the counterparts of ordinary sense perception. Just as we can see some physical objects (trees, dogs, rocks, the moon), we can intuit some mathematical entities. And just as we can see that grass is green and the moon is full, we can intuit that particular mathematical propositions are true. Mathematical perceptions can presumably be “theory-laden,” too. Whether we see the sun moving through the sky or we see the Earth turning, will depend on our background beliefs and expectations. Similarly, some looking at a particular mathematical structure will see a commutative ring while others will not. Years of training may be required in many of the most interesting cases.

These perceptual facts will play a big role in deciding which propositions to accept or to reject when they cannot be directly evaluated perceptually. Since Gödel invokes the analogy with the empirical sciences, it is natural to look there for details about the relation between our mathematical theories and intuitions. Gödel himself offered little in the way of specifics. But first, a bit more detail about Platonism itself.

PLATONISM

I take the following ingredients to be more or less central to Platonism. They were presented in Chapter 2; here I will just sketch them as a reminder. Recall that some of these are standard while others are not but should be. This is especially true of the last point.

1. Mathematical objects and mathematical facts exist independently of us.

2. Mathematical objects are outside of space and time; they are not part of the natural, physical world.

3. The term “abstract” has come to have two distinct meanings. The older sense pertains to universals and particulars, which might be appropriate for structures such as groups. Numbers, by contrast, are not abstract in this sense, since each of the integers is a unique individual, a particular, not a universal.¹ In current usage “abstract” means outside space and time, not physical. In this sense all mathematical objects are abstract.

4. We can intuit mathematical objects and mathematical truths.

5. Mathematics is a priori, not empirical.

6. Mathematics is fallible. Even though it is a priori, it need not be certain.

7. Mathematical truths are necessary.

8. Many methods are possible in mathematics. There is no limit to what might count as evidence, just as there is no limit in principle to how physics must be done.

For my purposes here it is probably not necessary to be too specific about the various details of Platonism, since I am really only concerned with one aspect, intuition. But it may from time to time be useful to keep the other aspects in mind when considering the details of mathematical perception.

THE CONCEPT OF OBSERVATION

It's surprising how much counts as perception within the natural sciences. Physicists, for example, regularly talk about “seeing the interior of the sun.” How do they manage this while standing well back? The sun produces neutrinos which normally pass through regular matter. Because of this, neutrinos produced in the deep interior of the sun pass with ease to the outside, some in the direction of the Earth. In deep, abandoned mine shafts² large tanks filled with dry cleaning fluid detect the odd neutrino on those very rare occasions when one is absorbed by a proton which subsequently decays. Out of this whole process a number of conclusions about the interior of the sun are drawn.

Is this really seeing the interior of the sun? Or is this such a stretch that it amounts to an outright abuse of the concept of observation? It seems plausible to insist that all we really see are a few streaks in a photo, which are thought to be caused by the products of the decaying proton. The rest is inference, based on some rather sophisticated theory. But this reaction may be unjustified. We are happy to claim we can see things with a magnifying glass or microscope that we couldn't otherwise see with the unaided eye. This goes for high-powered electron microscopes as well as for low-powered optical microscopes. It's hard to draw a line between the naked eye and a powerful instrument. Perhaps the apparatus for neutrino detection should also be taken as an instrument for seeing the interior of the sun. The literature on this is extensive, and I can't begin to do it justice.³ But a plausible case for seeing with neutrinos can be made.

There is quite a different sort of thing that we also happily call observable. Consider the sort of thing we often see in an article or textbook on high-energy physics, namely, a picture of some subatomic decay process. These pictures are often given to us twice over. One of them is a photo of an event, say, in a spark chamber. The second (usually placed beside the first) is an artist's drawing of the same event. The difference is that all the messiness of the first is tidied up in the second. There are just a few bare lines in the artist's version, everything else in the photo is eliminated as irrelevant, perhaps stemming from processes having nothing to do with the one we're interested in, perhaps mere scratches produced in the process of photographing, and so on. There is certainly a difference between these two pictures, yet it seems fair to call both a representation of something observable.

There is a useful terminology for this. The original photo is of a datum, while the artist's drawing is of a phenomenon (Bogen and Woodward 1988, Brown 1993). Interestingly, scientific theories usually try to explain phenomena, not data. Phenomena are doubtless constructed (in some sense) from data and occupy a middle ground between data and theory. One of the most interesting and important aspects of phenomena is that they seem to legitimize inductive inference from a single example. They are not alone in doing this. So-called natural kind inference has this pattern. If any sample of water is discovered to have the chemical structure H₂O, then all water has this structure. True, for safety's sake a few samples would typically be considered, just to make sure the test was done properly. By contrast, for many other properties we would insist on a very large sample before cautiously drawing any conclusions. Not so in a natural kind inference where a single instance is in principle sufficient.

Chicken sexing provides us with yet another unusual sense of seeing. Expert chicken sexers are remarkable people. They can classify day-old chicks into male and female with 98 percent accuracy, and they can do this at a rate of about one thousand per hour. The vast majority of us get it right about 50 percent of the time, which is to say we're utterly hopeless. The skill is considered economically important, if you want to feed those chicks who will eventually become egg-layers, but not the others. (In a book on the epistemology of mathematics, it is perhaps inappropriate to reflect on the fate of the males.)

How do chicken sexers do it? No one could do it at all until the Japanese discovered a perceptual method of discrimination in the 1920s. This method was passed on to North Americans in the 1930s. The initial practitioners have recently retired. Heimer Carlson of Petaluma, California, for instance, spent fifty years classifying a total of fifty-five million day-old chicks. His expertise has been the subject of psychological study (Biederman and Shiffrar 1987).

The ability to classify correctly is so difficult that it takes years of training, which consists largely of repeated trials, in order to achieve the rare expert level. The difference between good sexers and poor ones consists for the most part in where they look and what distinctive features they look for, especially contrastive features. It seems that expert chicken sexers were not aware of the fact that they had learned the contrasting features, nor were they aware of the exact location of the distinguishing information. By telling novices where the relevant information was precisely located, the novices became experts themselves at a much quicker rate.

For our purposes the crucial thing to note is that the experts had some sort of tacit understanding of where to look and what to look for. It may seem that chicken sexing is similar to riding a bicycle. We all know how to do it, but we can't say what it is that we know. These two different types of knowing are usually called “knowing how” and “knowing that.” Is chicken sexing just a case of knowing how, rather than knowing that? There are certainly similarities, but there is one important difference between classifying chicks and riding a bicycle. Knowing how to ride a bicycle is a non-propositional skill; it results in actually riding. Knowing how to classify chicks is also a non-propositional skill; but it results in propositional knowledge, namely, being able to say truly “This is a male.” (One might think that knowing how to ride a bicycle also results in propositional knowledge: “I am riding.” Not so. This piece of propositional knowledge does not come from knowing how, but rather from a different empirical observation: I see myself riding.)

Of course, there are lots of every-day examples, such as seeing a cup on a table just in front of us. This is certainly a legitimate case of perception. I mention the other unusual cases mainly to help prepare the case for mathematical perception. What we eventually arrive at may seem a deviation from the ordinary sense of seeing. Indeed it is, but so are a lot of other things and it is not so great a deviation as to be dismissed as being not genuine perception. Even though chicken sexing was something of a mystery, it was clear that somehow chicken sexers could observe something. It may be a mystery how mathematical perception works, but it is clear from the spectacular achievements of mathematics that somehow some mathematicians are pulling it off.

There is one thing I have not included, but would be insisted upon by most naturalists. Observation is a process that must be accounted for in purely natural terms. There must be some sort of causal connection, naturalists usually claim, between the perceiver and the perceived. This claim is often developed into an argument against any form of Platonism, since it is thought no such causal connection could exist between us (inside space and time) and abstract entities (outside of space and time). I'll take up this serious and very influential challenge soon. But before that, I'll present a case where it is very hard to deny that some sort of intellectual perception is occurring.

PICTURE PROOFS AND INTUITIONS

Consider the following theorem and the picture that attempts to prove it. It may take a few moments to see for yourself how the picture works, but it is certainly worth the effort.

Theorem: 1 + 2 + 3 + . . . + n = n²/2 + n/2

Proof:

Figure 5.2 Picture proof.

The proof works like this: Start at the top and work down, letting the little squares represent numbers, 1 + 2 + 3 + 4 + 5. The total number of squares in the picture is equal to this sum. Notice also that the numbers of squares is equal to a large square with sides of length 5 that is cut in half along the diagonal, i.e., 5²/2, plus the shaded bits that were cut off by the diagonal cut, i.e., 5/2.

I wish to claim that the diagram is a perfectly good proof of the theorem. One can “see” complete generality in the picture. Even though it only illustrates the theorem for n = 5, somehow we can see that it works for every number, all infinitely many of them. The diagram does not implicitly suggest a “rigorous” verbal or symbolic proof. The regular proof of this theorem is by mathematical induction, but the diagram does not correspond to an inductive proof at all, since the key element in an inductive proof is the passage from n to n + 1. The simple moral I want to draw from this example is just this: We can in special cases correctly infer theories from pictures, that is, from visualizable situations. There is an intuition and from this intuition we can grasp the truth of the theorem.

What is an intuition? A standard definition of intuitive knowledge runs as follows.

A knows p intuitively if and only if:

1. A knows that p

2. A's knowledge that p is immediate

3. A's knowledge is not an instance of the operation of any of the five senses. (Dancy 1992, 222)

This is good for a start, but there are problems with this definition. For one thing, “immediate” should also be qualified. It does not mean temporally immediate, though typically the process of coming to know is fairly quick. Moreover, background knowledge and significant reflection may be involved. The crucial thing in calling it immediate is that p is not derived from other propositions as the conclusion of an argument. Other propositions in the form of background beliefs may play a role, but they do not entail p.

Following Gödel, Platonists think of mathematical intuition as similar to the sense perception of physical objects. Indeed, we could imagine an analogous definition of sensory knowledge. It would be exactly the same as the definition of intuitive knowledge except for the final clause which would assert, rather than deny, that some of the five senses are involved (and nothing else).

If we return to the picture proof presented earlier, it seems a perfect candidate for intuitive knowledge. There is one objection that might be raised. It might be claimed that pictures give us sensory information and that is sufficient for the proof. After all, I could come to know that Alice has red hair just by looking at a colour photo of Alice. It is very doubtful, however, that something similar is happening in the number theory example. The most that one can acquire from the diagram by means of sense impressions is a limited version of the proof, namely, a proof that works in the special case of n = 5. Clearly, the picture provides a proof of very much more than that. It proves the theorem for every natural number, all infinitely many of them. One sees empirically in the case for n = 5, but one intuits or sees non-empirically for all the infinitely many others.

We might try, as Jon Barwise and some of his associates have tried, to take the picture to be not isomorphic but rather homomorphic to the structure described in the theorem. Barwise and Etchemendy remark that “a good diagram is isomorphic, or at least homomorphic, to the situation it represents” (1991, 22). The problem with this proposal is: First, that the picture is obviously not isomorphic to the whole natural number structure, since there are infinitely many numbers but only 1 + 2 + 3 + 4 + 5 objects here, and second, that there are too many homomorphisms; the picture does not tell us which is the right one. And yet, we seem to “grasp” it nonetheless. So, I conclude that the diagram is not a representation or a picture as these notions are normally understood, but rather something like a telescope that helps us to “see” into the Platonic realm. In short, it's a device for facilitating a mathematical intuition.⁴

OBJECTIONS TO INTUITIONS

The argument that so many naturalists like to level against Platonism turns on considerations such as the so-called causal theory of knowledge. The argument was first forcefully made by Benacerraf (1973). It has since evolved, so I will take up the original form (which is still popular) and then the more recent versions.

Benacerraf raised his problem when causal theories of everything were in high fashion. The causal theory of reference, the causal theory of perception, and the causal theory of knowledge were all triumphant in the 1970s. This is no longer true, though a strong influence lingers, especially among naturalists. Benacerraf worried that Platonism requires an epistemology that is utterly at odds with how we normally come to know something, namely, by being causally connected to it. We can express the principle and the consequence for Platonism as follows:

To know anything at all, there must be some sort of causal connection between the object known and the knower. Abstract entities, being outside of space and time, are causally inert; so, we, who are inside space and time, cannot possibly interact with them. Consequently, even if they exist, we could not know them. Since Platonism is committed to our knowing abstract entities, it is hopelessly wrong.

The basic idea is plausible. When we consider how we come to know various every-day things, we invariably find some sort of causal chain between the objects of knowledge and ourselves. If I know a cup is on the table, it is because I am in causal contact: Photons from the cup enter my eyes, and so on. Even my knowledge of the past and future is causally grounded. I know, for example, that it will snow tomorrow, since the cloud formation I see now will cause snow tomorrow. In this indirect way, I am causally connected to tomorrow's event. In routine cases—past, present, or future—we seem able to pick out a causal chain between ourselves and the object or event that we know about. What's more, if this or some other causal connection did not exist, it seems safe to say that we simply would not have the knowledge in question.

These simple considerations make the causal theory of knowledge appear quite plausible. And when applied to abstract objects, it would seem that any causal connection is completely lacking; so, according to this naturalistic account, we cannot actually know anything about abstract entities after all, even if they do exist. Our mathematical knowledge cannot be about abstract objects, but must be understood in some quite different, non-Platonistic, way.

This argument has been used repeatedly in recent years in favour of some sort of naturalism.⁵ However, there is no need for Platonists to retreat, reflect, and be wretched, since the argument is seriously flawed. The best way to show that the causal theory of knowledge is wrong is to show that there is a case within the natural realm itself where it fails miserably. If we can show that we have knowledge of some physical event, but that we cannot be in causal contact with that event, then we will have shown that a causal connection is not necessary for knowledge.

The counterexample comes, not surprisingly, from quantum mechanics. In an EPR-type setup (from the thought experiment of Einstein, Podolsky, and Rosen) a decay process gives rise to two photons moving in opposite directions toward detectors at either end of a room (see Figure 5.3). The detectors include Polaroid filters which can determine whether the incoming photons have the so-called property spin-up or spin-down (often represented by a simple + or–). Both theory and experience tell us that the two outcomes are always correlated: One photon is up and the other down. But we can never determine in advance which will arrive at either side; it's a case of complete randomness.

The interesting part is the perfect correlation: one up, the other down. Why does it occur? One possibility is that the measurement on one wing of the measuring apparatus causes the outcome at the other. However, we can rule this out by assuming with special relativity that no causal influences travel faster than light. The two measurements (made simultaneously) are outside of each other's light cones; so neither measurement causally affects the other. The second possibility is to assume that there must be something at the origin (at the time of the creation of the pair of photons) that is responsible for their correlated properties. This was the EPR conclusion; in this case such a common cause would be a hidden variable. Unfortunately, this common cause turns out to be impossible, too. The so-called Bell results show that such a common cause (a so-called local hidden variable), predicts a different measurement outcome than either quantum mechanics predicts or experience determines.⁶

Figure 5.3 EPR setup.

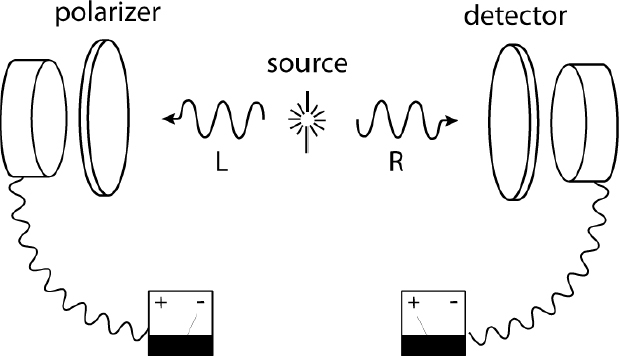
The implications for the causal theory of knowledge are straightforward—it's false. Suppose I am at one wing of the measuring apparatus and get the result: spin-up. Then I can immediately infer that you at the other wing have the result: spin-down. I know the distant outcome without being causally connected to the remote wing. A direct causal connection would have to be faster than light, something ruled out by special relativity, and a common cause in the past grounding my knowledge would amount to a local hidden variable, something ruled out by the Bell results.

The causal theory is simply refuted by this example. We can have knowledge without a causal connection. Of course, arguments like this are likely to be controversial. It relies on significant assumptions about the physical world. Perhaps special relativity is false; maybe some signals do go faster than light. This would make a direct causal connection possible after all. Perhaps the complex analysis of the situation involved in ruling out local hidden variables is flawed, making a common cause possible after all. These are indeed possibilities, but the assumptions that go into the physics of this situation are at least as plausible, or even more plausible, than the assumptions involved in the causal theory of knowledge. The sensible thing is to dump the latter.⁷

Once the causal theory is rejected, there is no objection to our knowing about abstract entities without being causally related to them. Before continuing, there is one possibility worth exploring, though I won't do it here. Perhaps we could accept the causal theory of knowledge but add formal to the list of scientifically acceptable causes. Champions of the current causal theory (including liberal variants) take efficient causation to be the only kind. When discussing abstract entities, however, formal causation and formal explanation seem much more appropriate. I would have no qualms invoking them to account for our knowledge of mathematics and perhaps to explain the EPR correlations, as well.

Many naturalists, however, have moved away from strict causal theories of perception and knowledge to something more liberal, known as reliablism. It is currently a very popular account of epistemic justification. Roughly, it says that a belief is justified if and only if it is produced by a reliable method. The method does not have to be infallible, only that it typically works. For instance, beliefs that are formed on the basis of “hearing the voice of God” are not reliable. Nor is mere guessing or reading tea leaves. On the other hand, looking in the box is a very reliable way of forming a justified belief about whether any pizza remains, and putting litmus paper in a solution, then checking its colour, is a reliable way of determining whether the substance is an acid.

So far, this looks harmless. Platonists could merely maintain that intuitions are reliable and expect no more grumbling from naturalists. However, this won't do. Reliablism is a naturalistic doctrine because it demands an account of any allegedly reliable process. (See, for instance, Goldman 1986.) It insists that we who form beliefs have various psychological, social, and biological properties, and it wants the details of our interactions with the objects of our knowledge in order to evaluate the reliability of the process. This is the basis of Hartry Field's objection to Platonism. Field does not endorse the strict causal theory of knowledge, so the original Benacerraf problem is set aside, but he does claim that a related problem is suggested by it.

The way to understand Benacerraf's challenge, I think, is not to our ability to justify our mathematical beliefs, but as a challenge to our ability to explain the reliability of those beliefs. . . . Benacerraf's challenge . . . is to provide an account of the mechanisms that explain how our beliefs about these remote entities can so well reflect the facts about them. The idea is that if it appears in principle impossible to explain this, then that tends to undermine the belief in mathematical entities, despite, whatever reason we might have for believing in them. (Field 1989, 25–26; his italics)

The idea, in a nutshell is simple: Even if the process that we call Platonic intuition can reliably generate mathematical truths, we cannot in principle explain how this could be done. So our belief that we do have mathematical intuitions is seriously undermined.

There are two replies to be made to this. First, Field has no reason for saying we cannot explain the process of intuition in principle. True, we are stunningly ignorant of how it works now, but perhaps we will understand it in the future. And perhaps that understanding will be in terms of formal causes.

Second, the requirement of being able to give an account of the mechanism is a double-edged sword with which Field may not want to play. Consider ordinary perception and an instance of it, such as looking in the pizza box to see if any is left. Can we account for why beliefs formed this way are reliable? What do we actually know about it? We have a wonderful theory involving several ingredients: photons coming from the pizza and entering the eye where they interact with the rods and cones, resulting in a signal being sent down the optic nerve into the visual cortex. This is wonderfully well understood. But this account of the mechanism of belief formation stops short of the crucial thing—belief. How is the belief formed? No one knows and no one has any idea. It is, in fact, the mind–body problem and it is not solved. We can hope that it will be solved some day, but there is the possibility that it will never be solved. Colin McGinn (1999), for instance, holds the view that it will never be solved. Our minds, he thinks, are too complicated for us ever to be able to understand how they work. If McGinn is right, then even every-day beliefs about pizza are impossible in principle to account for in the way that Field demands. The reliabilist challenge to Platonism is no more plausible than the challenge coming from the causal theory of knowledge. This is not to challenge reliablism; it may well be right. It is only to reject the ill-founded claim that Platonism is in trouble, if reliablism is true.

THE CONTINUUM HYPOTHESIS AGAIN

It is now time to come back to the example that I began with, Freiling's refutation of the CH. His argument is possibly wrong and certainly contentious. But the mere possibility of its correctness (for all we know), is enough to make it an extremely interesting example and one that is useful for my purposes. Any realistic example is likely to be contentious and I suspect that the majority of set theorists don't accept this refutation of CH. Some do accept it, including David Mumford, who would like to reformulate set theory, in consequence. I will take up his interesting proposal in connection with Maddy's naturalism in later chapters.

I'm going to present the example again, but this time I will give Freiling's version, which is different in some respects from Mumford's. Freiling assumes the following four “self-evident philosophical principles":

1. Choosing reals at random is a physical reality, or at least an intuition mathematics should embrace to the extent possible.

2. A fixed Lebesgue measure zero set predictably will not be hit by a random dart.

3. If an accurate Yes–No prediction can always be made after a preliminary event takes place (e.g., the first dart is thrown) and, no matter what the outcome of that event, the prediction is always the same, then the prediction is also in some sense accurate before the preliminary event.

4. The real number line cannot tell the order of the darts. (Freiling 1986, 199)

To these I would add one more: The line consists of pre-existing points. Aristotle, by contrast, thought that points could be constructed, say, by throwing darts, but those points do not already exist on the line. If Aristotle is right, then Freiling's argument would certainly not work; so the assumption of pre-existing points is crucial.

Freiling's argument runs as follows: We throw two darts, one after the other, at the real line [0,1]. Let be a function that assigns a countable set of real numbers to each real. The number hit by the second dart will (with probability one) not be in the countable set assigned to the number hit by the first dart. The situation is symmetrical; the order of throwing is irrelevant. Thus, we can say that the number hit by the first dart will not be in the set assigned to the second. This leads to the following intuitive principle that I'll call Freiling's Symmetry Axiom:

Theorem (of ZFC): FSA ↔ ~CH

Proof: (→): Assume FSA and let < be a well ordering of R. The existence of a well ordering follows from the axiom of choice which we have assumed as part of ZFC. We will further assume CH, which implies that the length of the well ordering is ₁ Now let f (x) = {y: y ≤ x}. Thus, . The way cardinal numbers are defined implies that we are always bumped down a cardinality when picking a set of earlier points in a well ordering. Moreover, a well ordering is total, so if some particular , then x > y. Consequently, by FSA, , which is a contradiction. Therefore, ~CH.

(←): Assume that CH is false, i.e., . Let x ₁, x ₂, x ₃, . . . , x _n be an ₁-sequence of distinct real numbers and let . Now consider the set , which is the ₁-union of countable sets. Thus, the cardinality of A is ₁ Since . Thus, . Since f (y) is countable, we have . Therefore, y f (x_α) & x _α f (y).

For our purposes we are really only interested in the first half of this proof, i.e., FSA → ~CH, but I've included the other half for those who might be interested to see the full equivalence. Freiling's overall argument can be broken into three separate stages. I'll now work through these.

The first stage is the dart-throwing thought experiment. This picks out a pair of real numbers. The crucial thing about these real numbers is that they are independent random variables. Freiling says that picking them out is a “physical reality,” and in his discussion of Freiling's work, Davis Mumford calls them “real random variables.” This isn't quite true. One can't actually pick out real numbers with actual darts. It's highly idealized and can be done only in a thought experiment. The crucial thing that each is implicitly alluding to is that the concept of random variable at work here is not an existing mathematical concept and cannot be defined in terms of other existing mathematical concepts.

Standard mathematical definitions of random variables go something like this: A random variable is a measurable function from a probability space into a measurable space (often called a state space). Could the concept acquired in the thought experiment turn out to be a disguised version of the measure theory concept? No. Here's my argument: There is a chain of reasoning leading from the dart-throwing concept of random variable (plus ZFC) to ~CH. There cannot be such a chain of reasoning using the measure theory concept of random variable, since that concept and all the mathematical facts about it are part of standard mathematics (i.e., part of ZFC) which is provably independent of CH. The dart-generated concept of random variable is something new. It is not an empirical concept, but one generated in a highly intellectualized thought experiment. I am quite happy to call it a mathematical concept, but it is not an existing mathematical concept, nor is it definable in terms of existing mathematical concepts.

The second stage of Freiling's argument involves a process of intellectual reflection. We have a new concept of random variable—what can we know about it? Often we can discover new facts just by reflecting on the concept. To take a simple example, consider the concept of a set. We think of a set as having members and the set is the very set it is in virtue of those members. This concept of set leads rather obviously to the axiom of extensionality: Sets A and B are identical if and only if the members of A are exactly the same as the members of B. This is a very simple example, but many of the axioms of set theory are justified in this sort of way. (See Maddy 1997, 36–62, for a nice discussion.) Freiling has done much the same. He has taken the concept of random variable generated in the dart-throwing thought experiment and generated a new principle which I have called Freiling's symmetry axiom, FSA. This process is a lot more complex and sophisticated than the axiom of extensionality example, but it's the same sort of thing going on in each case.

The third stage is fairly straightforward. Freiling uses his symmetry axiom to derive ~CH. This part is simply an uncontentious derivation and not philosophically interesting or unusual in any way. The burden of his thought experiment or “philosophical argument,” as he calls it, concerns the initial generation of the new concept of random variable and the subsequent generation of the symmetry principle based on that concept. These, needless to say, remain contentious.

Thought experiments, like real experiments, do not have clear boundaries. Published reports of experimental findings often include photos or diagrams of what was actually seen, calculations, bits of applied theory, and so on. The Freiling thought experiment construed broadly includes everything starting from throwing the darts and finishing with a derivation that refutes CH. If we construe it quite narrowly, then the thought experiment consists in the dart throwing which generates the new concept of random variable and in which the independence and symmetry of the two throws is evident. Which is “the” thought experiment? I doubt it matters where we draw the line. In the Freiling thought experiment we generated a concept and from that a new mathematical principle. There was no empirical input. In the chain of reasoning there is at least one step along the way that could only be called an a priori perception, an intuition.

Seeing with the mind's eye is fallible, just as regular sense perception is. Freiling's thought experiment may be deeply flawed. Perhaps time will tell. Galileo saw mountains on the surface of the moon. Others objected. In the long run, the objectors were proven wrong. Many saw canals on the surface of Mars. Again, others objected. This time the objectors were proven right. There is a great deal to learn about the wondrous thing Platonists call intuition: Why does the mind's eye work at all? Under what conditions might it be reliable or unreliable? We have little or no idea at the moment. But this is not a reason to discard Platonic intuition. For a very long time we had no idea how microscopes or telescopes worked, but it would have been foolish to deny they were revealing something real. The trick will be to get intuitions to work reliably for us.

The last point in my list of the ingredients of modern Platonism was that it, unlike other philosophies of mathematics, places no bars on mathematical methods. Many of the brilliant achievements of natural science consist in new ways to learn about the world: telescopes, cloud chambers, spectrometers, Monte Carlo statistical techniques, and so on. Modern Platonism envisages the same for mathematics. Proofs are wonderful, but there is no good reason to limit research and rational belief to that. Implicitly, we already believe something like this. Mathematicians work on this problem with that strategy rather than some other. Supervisors give PhD students plausible problems for a dissertation. They have some kind of knowledge that is quite different from a proof. Platonism makes ready sense of this, while other accounts can only flounder. It is analogous to what goes on in the natural sciences. Just as there is an independent physical reality that we have some glimpse of, so there is an independent mathematical reality that we perceive, however dimly, and it guides us in our research efforts.