1    Mathematical Explanation

THE PRIME OF LIFE

If cicadas courted with verse, as any subtle suitor should, we might expect something like this from these patient insects:

Since we have world enough, and time,
This coyness, Lady, is no crime
We shall sit down and think which way
To walk and pass our long love's day.¹

It takes seventeen long years before cicadas hear “Time's wingèd chariot hurrying near” and so get down to the business of biology. Why the delayed gratification? According to some biologists and philosophers, the fact that seventeen is a prime number has much to do with it. In short, they say, mathematics explains this remarkable biological phenomenon. It is not the whole explanation; biological ingredients are needed, too. But facts about prime numbers play an essential role, and there would be no proper explanation at all without those mathematical facts. At least, that is the claim made by a number of philosophers of mathematics, starting with Alan Baker (Baker 2005, Colyvan 2001, 2003).

Can this be right? The cicada example certainly grabs the imagination, but can mathematics actually explain anything at all in nature? The question is both strikingly simple and deceptively difficult. It seems elementary, yet the question contains an important ambiguity. In one sense of “explain” a theory accounts for some phenomenon; for instance, General Relativity explains the shift in the perihelion of Mercury. In another sense, someone makes an idea comprehensible by explaining it, as in “Alice explained General Relativity to me.” With this distinction in mind, I would answer the question of whether mathematics has the ability to explain with a clear: No and Yes.

Mathematics, I will argue, cannot explain in the sense that a scientific theory can. There is nothing in mathematics that can explain phenomena in the natural realm the way scientific theories explain those sorts of things. On the other hand, mathematics can explain in the sense of making something comprehensible or intelligible. And in some cases, mathematics provides the only explanation, in this second sense, that we have or could have.

Before proceeding, a bit of background. For quite some time, arguments over the status of mathematics have turned on its being (or not being) essential to science. The cicadas example is used in favour of mathematics being indispensable, thus supporting the so-called indispensability argument for mathematical realism. Briefly, older versions of the argument, especially those by Quine (1970) and Putnam (1971), run as follows: The first ingredient simply says that mathematics is essential to science; physics, for instance, could not be done without the resources of mathematics. The second component of the argument is Quine's epistemic holism: Evaluation is not a piecemeal thing; theories, auxiliary assumptions, initial conditions, and the mathematics used, are all evaluated together; any part could take the blame for failure and all share the credit when empirical predictions turn out to be correct. The third component is Quine's doctrine of onto-logical commitment: To accept as true a statement of the form “There is an x, such that x is F” is to accept the real existence of things that have the property F. If I believe there are quark components to a proton, then intellectual honesty demands that I also believe that there are quarks—it is not a merely useful calculating device.

Given these three premisses, one seems committed to mathematical objects and facts about them. If the statement “There are prime numbers” plays an essential role in the theory of cicada reproductive cycles, and we believe that theory to be true, then we must accept the literal reality of numbers. Any attempt to wriggle out by saying that cicadas are real but numbers are not, or are “real” in a different sense, is simply dishonest, according to Quine.

After Quine, Putnam (1971) argued in a similar fashion, claiming that no one could formulate Newton's theory of gravity without mathematics. Hartry Field (1980) attempted exactly that, but got a mixed reception—many thought he succeeded, others not. That debate is stalled but has given rise to another.

Newer versions of the indispensability argument (sometimes called “the enhanced indispensability argument”) do not draw on epistemic holism, a doctrine that is now largely out of favour. Instead, the focus has been on specific cases, such as the cicadas example, which seem to provide direct mathematical explanations for a specific natural phenomenon. And in such cases inference to the best explanation is the favoured form of argument. The mathematical facts of primality, it is claimed, offer the best explanation for the cicada life cycle, so we should accept that explanation as true. And from this, mathematical realism follows on naturally.

The old argument has been roundly rejected by nominalists such as Hartry Field (1980), who would no doubt reject the more recent versions as well. Realists, not surprisingly, like indispensability arguments, especially realists who are sympathetic to naturalism. The argument gives them the ontology they like (realism), but it does not require the full Platonistic epistemology of intuitions, as well. Mathematical beliefs are justified the same way all scientific beliefs are—empirically. And there is no need to appeal to mysterious intuitions. But even those who happily embrace Platonistic epistemology might still embrace the claims of indispensability. After all, it does not explicitly deny mathematical intuition, and it makes mathematics even more important than previously thought.

There is already a sizable literature on the newer versions of the indispensability argument. I won't try to do justice to it, but only mention some of the contributions, several of which are quite important. The list would include: Baker, Bangu, Batterman, Bueno, Colyvan, Leng, Lyon, Mancosu, Melia, Pincock, Steiner, and several others (see Bibliography for details).

Next, a word about terms. The following chapter is devoted to explaining Platonism and naturalism. Indeed, it might be thought I should have started this book with that chapter. I thought it best to jump into a current debate, so that there would be a clear motivation for the characterization of Platonism and naturalism that are to come. However, a brief, preliminary account of these terms will be useful. Naturalism is the doctrine that the natural sciences are or should be our model for all inquiry. This usually means that sense-experience is the only source of information and that material objects in space and time are the only things that exist. Anything we claim to know, such as ethics or mathematics, must be somehow reconciled with this. Platonism is the very different view that numbers, functions, and other abstract entities exist in their own right, and that there are many ways of learning about them, including intuition, a kind of perception with the mind's eye. Occasionally, naturalists, such as Quine, will reluctantly embrace abstract entities, but none will allow anything that smacks of intuition or a priori knowledge.

The epistemic issue, empiricism versus rational intuition, is at the heart of the debate. The reason naturalists like indispensability arguments is that they yield objective mathematical knowledge without abandoning empiricism. With this rough distinction in mind, let's return to the argument.

I share the realist conclusion, but find the indispensability argument unpersuasive. At least this is so, given the way indispensability is currently understood as essential for explaining some phenomena. When it comes to concept formation, however, there may be a good argument for realism, indeed for full-fledged Platonism, based on a kind of indispensability, but of a different sort. In any case, I should lay my cards on the table and warn readers that we're headed in a Platonistic direction. The key ingredient will be the assumption of two realms, one is the physical realm of material entities and processes, the other is the realm of the abstract and mathematical, or, in other words, Plato's heaven.² I shall argue that the latter realm does not explain happenings in the former, but it can provide the tools needed for concept formation, by means of models and analogies. Understanding of this sort will often be the only form of understanding that we could possibly obtain for some parts of nature. In this second sense, mathematics is very likely indispensable for science.

ACCOUNTING FOR PHENOMENA

I'll begin with the first sense of “explain,” that is, the sense in which we explain phenomena, as in “Copernicus's theory explained stellar parallax,” “Newton's theory explained the tides,” and “Darwin's theory explained the characteristics of different species.” Beyond providing a few examples, I will be vague when it comes to specifying the nature of explanation in any detail. There are deep, long-standing debates about this, but we all tend to agree that particular examples of explanation (such as the ones just cited), are indeed explanations. This will allow us to avoid debates between Hempelians and non-Hempelians, top-downers and bottom-uppers, unifiers and their detractors, and so on.

There is a second issue to get out of the way. Many take explanation to mean causal explanation. Often this is right. But it is then implicitly assumed that cause just means efficient cause, and it is then pointed out that mathematics is causally inert, so it couldn't explain anything. We should be able to answer the question: “Can mathematics explain?” in a way that is independent of specific views on the nature of causation; in particular, I would be happy to allow the idea of “formal cause” and “formal explanation” to enter the scene. The problem of mathematical explanation lies elsewhere, and won't turn on debatable features of causation.

We use mathematics in science and in daily life, but that doesn't mean it explains anything. After all, Newton used Latin to explain the tides, but Latin itself did no explaining. That might seem like cheating on my part. A better, yet still simple every-day example will illustrate what I mean by a non-explanation. Suppose a balance scale has three apples in one pan and five in the other (and these apples are qualitatively the same). The side with five apples drops and the side with two rises. Why? Someone might offer this explanation: “The scale tipped as it did because 5 > 3.”

Are you impressed? I suspect not. The side with five apples dropped because it is heavier, not because 5 > 3. It is gravitating mass that is responsible for the phenomenon, not numbers, even though numbers provide a good means of keeping track of massive objects. I hope there is consensus on this example. As a purported instance of mathematical explanation, this example is easy to dismiss, but others are a challenge. The cases that have impressed people are, I think, merely complex instances of the same sort of thing and should be similarly rejected.

Perhaps the most intriguing instance of a purported mathematical explanation involves the life cycle of the cicada, which is seventeen years (Baker 2005). Cicadas live underground, consuming the juice from tree roots, over much of eastern North America. (A variant in the southern US has a life cycle of thirteen years.) Within a few weeks of one another, the mature nymphs emerge, mate, lay eggs, and die. Seventeen years later it will happen again. There are three different species of cicada that follow the same seventeen-year cycle and mature at the same time. That is, in a given geographic area, the cicadas mature together every seventeen years, with none maturing in the intervening years.

Why such a long life cycle and why are they synchronized? The answer seems to lie in overwhelming any predator. According to Stephen Jay Gould,

Natural history, to a large extent, is a tale of different adaptations to avoid predation. Some individuals hide, others taste bad, others grow spines or thick shells, still others evolve to look conspicuously like a noxious relative; the list is nearly endless, a stunning tribute to nature's variety. Bamboo seeds and cicadas follow an uncommon strategy: they are eminently and conspicuously available, but so rarely and in such great numbers that predators cannot possibly consume the entire bounty. Among evolutionary biologists, this defense goes by the name of “predator satiation.” (1977, 101)

There are, according to Gould, two key features.

An effective strategy of predator satiation involved two adaptations. First, the synchrony of emergence or reproduction must be very precise, thus assuring that the market is truly flooded, and only for a short time. Secondly, this flooding cannot occur very often, lest predators simply adjust their own life cycle to predictable times of superfluidity. (Ibid.)

Cicadas exemplify both features.

The synchrony of three species among cicadas is particularly impressive—especially since years of emergence vary from place to place, while all three species invariably emerge together in any one area. But I am most impressed by the timing of the cycles themselves. Why do we have 13 and 17 year cicadas, but no cycles of 12, 14, 15, 16, 18? (Ibid., 102)

The answer seems to be genuinely mathematical.

[Thirteen] and 17 share a common property. They are large enough to exceed the life cycle of any predator, but they are also prime numbers (divisible by no integer smaller than themselves). Many potential predators have 2–5-year life cycles. Such cycles are not set by the availability of periodical cicadas (for they peak too often in years of nonemergence), but cicadas might be easily harvested when the cycles coincide. Consider a predator with a cycle of five years: if cicadas emerged every 15 years, each bloom would be hit by the predator. By cycling at a large prime number, cicadas minimize the number of coincidences (every 5 × 17, or 85 years, in this case). Thirteen-and 17–year cycles cannot be tracked by any smaller number. (Ibid.)

On the face of it, this is a wonderful explanation. Not surprisingly, it is widely accepted by biologists, though not by everyone. Its detractors suggest, for instance, that it is not falsifiable, or that it may be due merely to chance, since there are other species of cicada that do not have long, prime-based life cycles. Or they ask, why, if it is such a good explanation, do we fail to see similar evolutionary strategies in other species more often? I am happy to ignore the critics and accept that the prime number account offered by Gould and others is correct, that is, correct in some sense relevant to biology. Baker, however, claims much more for the explanation.

The explanation makes use of specific ecological facts, general biological laws, and number theoretic results. My claim is that the purely mathematical component is both essential to the overall explanation and genuinely explanatory in its own right. In particular it explains why prime periods are evolutionary advantageous in this case. (2005, 233)

This is what I will resist. It is not an explanation, as I will try to argue in the following. There are several issues involved: First, is mathematics essential and indispensable to science? Second, even if mathematics is indispensable, is that a sign of the truth of mathematics? Third, does mathematics function as a premiss in a derivation of a prediction or explanation? A response to the third question is necessary in order to answer the first and second. My answer will be no, it is not a premiss like the others. In trying to make this clear, I need to say something about how I see mathematics applying to the natural world.

APPLIED MATHEMATICS

I'll begin by painting a picture of applied mathematics that is fairly common to those who work in measurement theory. Such a view can be found in the classic text of Krantz et al. (1971–1990). There are two realms in this view, one is mathematical and the other is the natural realm or whatever real or fictional thing we wish to mathematize. Note that we can count fairies, toothaches, and social faux pas, as well as rocks and electrons, but I will stick to physical examples here. The mathematical realm represents the natural one. We pick out some aspect of the physical world, and then find an appropriate structure in the mathematical realm to represent it.

Here is a simple example. Weight can be represented on a numerical scale. The main physical relations among objects with weight are that some have more weight than others and that when the objects are combined their joint weight is greater than either of their individual weights. These features could be operationalized using a balance beam. Weight can then be represented by any mathematical structure, such as the positive real numbers, in which there is an equal or greater than relation matching the physical equal or greater than relation and a combination relation matching the physical addition relation. Let us formalize this idea and try to make it more precise.

A mathematical representation of a non-mathematical realm occurs when there is a homomorphism between a relational system P and a mathematical system M. The system P consists of a domain D and relations R₁, R₂,. . . , R_n defined on that domain; M similarly consists of a domain D* and relations R*₁ R*₂,. . . , R*_n on its domain. A homomorphism is a mapping from D to D* that preserves the structure in an appropriate way.

More detail should help make this clear. Let D be a set of bodies, a, b, c,. . . with weight and let D* = R⁺, the set of non-negative real numbers. Next, let ≤ and ⊕ be the relations of physically weighs the same or less than and physical combination, where these can be understood in terms of how things behave on a balance. The mathematical relations ≤ and + are just the familiar relations on real numbers of equal or less than and addition. We also specify one of the bodies, u, to serve as a standard unit. Consequently, the two systems are P = 〈D, ≤, ⊕, u〉 and M = 〈R⁺, ≤, +, 1〉. In this way, numbers are associated with the bodies a, b, c, . . .  in D by the homomorphism φ: D → R⁺ which satisfies the three conditions:

We can put this simple example into plain English. Equation (1) says that if body a weighs the same or less than body b, then the real number associated with a is equal to or less than the number associated with b. Equation (2) says that the number associated with the weight of the body a ⊕ b (the combined weight of bodies a and b) is equal to the sum of the numbers associated with the separate bodies. Equation (3) says the special body that serves as a standard unit is assigned the number 1.³

In brief, this view of the nature of applied mathematics says that physical relations that hold among physical bodies are encoded into the mathematical realm where they are represented by relations among mathematical entities. The crucial thing to keep in mind is that there are clearly two realms, P and M, one representing the other.⁴

The preceding account, as I mentioned earlier, is drawn from so-called measurement theory. Recent discussions of applied mathematics are sometimes in danger of reinventing the wheel, so a word on the history of this topic seems in order. Much important work on how mathematics hooks on to the world has been done already by philosophers and psychologists under the heading “measurement theory.” They were not concerned with the issues of realism or explanation, but they did clarify a great deal, some of which should be of use in the current debate. Helmholtz, Russell, Campbell, and Nagel, for instance, all made major contributions. The three- volume work by Krantz et al. (1971–1990) is encyclopaedic and contains in full detail the view I outlined earlier, a view that seems to have recently been rediscovered in the current debate under the name “the mapping view.” The view, I think, is correct as far as it goes, but it might be useful to see more developed forms of it.⁵

Measurement theory often classifies different types of scale; ordinal measurements are the simplest. The Mohs scale of hardness, for example, uses the numbers 1 to 10 in ranking the physical relation of “scratches”: talc is 1 and diamond is 10. Addition plays no role in this scale; the only property of the numbers used is their order, which, by the way, is a strict order; nothing scratches itself. Addition is crucial in extensive measurements, such as the measurement of weight or speed. In the case of speed, the physical combination of the speeds of two bodies, say, the combined speed of a ball tossed inside an aeroplane is represented by the addition of two real numbers. But the embedding homomorphism isn't always simple. The relativistic addition of two speeds is constrained by an upper limit on their joint speed. An interval measurement uses the greater than relation between real numbers, but does not employ addition. Temperature and (perhaps) subjective probability are examples. Two bodies at 50°C each do not combine to make one body at 100°C. This is but the briefest sketch of a rich field, a mere taste of some developments.

The characterization of mathematics that is implicit in measurement theory favours Platonism, since we are implicitly endorsing the existence of a distinct mathematical realm with which we represent the natural world. Nominalists might respond that we represent with numerals, not numbers, so the point does not conclusively favour Platonism. Still, the naturalness of Platonism in applied mathematics, just as in pure, is manifestly obvious. This is not a strong argument for Platonism, but it is worth mentioning. (And as I said at the outset, Platonism is assumed in this chapter, since my aim is to show that even when Platonism is true, mathematics still does not explain what happens in the physical realm.) The main point in this two-realm account of applied mathematics in making the case for no mathematical explanations of the physical realm concerns the representational character of applied mathematics: Mathematics hooks on to the world by providing representations in the form of structurally similar models. The fact that it works this way means that it cannot explain physical facts, except in some derivative sense that is far removed from the doctrines of explanation employed in indispensability arguments.

In passing, I should add that there are interesting issues that arise in applied mathematics involving idealizations and fictions that I am going to skirt. One might map the actual world into the mathematical realm, resulting in the fictitious half child of the average family. Or one might idealize first, as is done in seismology, where we take the Earth to be continuous, and then map it into the real numbers, which allows us to use continuum mechanics to model it. There is much of interest to investigate here concerning fictions in general, but it is not essential to the present debate. For more on idealizations and applied mathematics, see Batterman (forthcoming) and Brown and Slawinsky (forthcoming).

INDISPENSABILITY, REALISM, AND EXPLANATION

The background to the philosophical discussions of cicada life cycles is the indispensability argument I sketched at the outset. It was first proposed by Quine (1970) and Putnam (1971), who were arguing for mathematical realism. Colyvan (2001) is the most thorough presentation and defence. Crudely, we might restate the argument this way: Theories offer explanations and they make predictions. In the latter case, we could take the theory as a set of premisses and deduce observation statements which might be otherwise unexpected. When those predictions turn out to be true, we credit the theory with being on the right track, that is, with being true or at least approximately so. But the premisses in such derivations include auxiliary theories, some of which are mathematical. They, too, deserve some of the credit for making true predictions, so they should be considered true, as well. Newton's theory of universal gravitation is supported by various true predictions derived from the theory, such as the observed motion of the moons of Jupiter. These same true predictions also confirm the algebra, geometry, trigonometry, and calculus used in making the predictions.

However, as soon as one considers the nature of applied mathematics, one sees that mathematics cannot be just another premiss in an argument, on a par with the physical theory, the auxiliary assumptions, or the initial conditions. As we saw in the earlier account of measurement theory, mathematics works in a different way. Auxiliary theories and initial conditions are further (purported) descriptions of nature. Mathematics is not descriptive in that way at all. Instead, it provides models in the form of analogies of how things might be. To theorize in the sciences is to pick out some particular mathematical structure and claim that the world is similar to that, where the similarity is spelled out by some isomorphism or homomorphism, as was indicated schematically earlier.

John Stuart Mill gave an account of mathematics where it would act as a premiss in an explanation, not unlike a physical theory (I will say more about Mill in the next chapter). He claimed that mathematical facts are very general facts about the natural world, not facts about entities in Plato's heaven. The reason that 5 + 7 = 12 is because five and seven instances of anything whatsoever can be combined into twelve instances. This, according to Mill and empiricists who followed him, is not a fact about objects in Plato's heaven; it is a very general fact about the natural world. Consequently, if it were to be used successfully in an explanation or prediction, Mill and his followers would say that the statement 5 + 7 = 12 has received some degree of empirical confirmation.

Few today would be tempted in the least to follow Mill. No doubt more sophisticated alternatives are possible (e.g., Kitcher 1983), but I won't try to anticipate and criticize them here. Mill and Kitcher are discussed in Chapters 2 and 3. Instead, let me simply give a quick analogy to illustrate my view. Suppose Bob is acting strange and somewhat indecisive following his father's unexpected death and his mother's speedy remarriage to his uncle. We might say, “Bob is Hamlet.” Those who accept this might then go on to make some predictions, for example, that Bob is in danger of rejecting his longtime girlfriend, or of challenging someone to a fight, or even of killing his mother and stepfather. Let us suppose that these predictions all turn out to be correct. Does anyone think Shakespeare's play actually describes or explains Bob's actions? Certainly not. Instead, the play tracks Bob's actions. To look for an explanation, we would examine Bob's psychological state and the social situation in which Bob finds himself. These would explain his initial indecisiveness and his subsequent violent behaviour.

The Bob–Hamlet case is the same as the apples example I mentioned at the outset. The motion of the apples on the balance scale is explained by their mass and by gravity, not by the mathematical fact that 5 > 3. The mathematical facts are remarkably useful for tracking what happens to the apples, and Shakespeare's play is similarly remarkable in tracking Bob's actions. But neither contributes a thing to the explanation of what happens. The apples–numbers example and the Bob–Hamlet example should both be clear. The cicada–prime number example, however, is more complicated and in need of unpacking. Let's turn to that now.

Reproductive cycles are of some temporal duration, measured, let us say for the sake of simplicity, in whole years. Let's use “—” to represent a year. Some species reproduce in a short cycle: —, others in longer cycles of length — —, or — — —, and so on. Cicadas reproduce in a rather long cycle: — — — — — — — — — — — —. Let us introduce a notion of “cycle factorizability” to mean that a long cycle can be broken into repeated shorter cycles of equal duration without leaving any years out. Thus, a cycle — — — — — — can be factored or broken into — — and — — and — —. Or it could be factored into — — — —and — — — — —. Trial and error in the case of the cicada cycle shows that it cannot be physically factored in this way. This means that a predator's reproductive cycle could not coincide with the cicada's cycle.

You may have been tempted to use your arithmetic knowledge in making sense of the preceding, but it was not necessary. I borrowed the term “factorizable,” but that in itself is harmless. No genuine mathematical notions were introduced. But we will introduce them now. We let a year, —, the shortest reproductive cycle, be associated with the number 1, —— with 2, and so on. The notion of a species's reproductive cycle is then associated with some whole number, which in the case of cicadas is 17. The physical notions of cycle factorizability and non-factorizability are linked to the mathematical notions of composite and prime numbers, respectively. It then turns out that a reproductive cycle is not cycle factorizable if and only if it is associated with a prime number.

Species with shorter reproductive cycles than cicadas will not (after one or a small number of generations) coincide with the cicada cycle. It is the different durations of the respective reproductive cycles that explain this, and so explain how cicadas avoid predator onslaught. Arithmetic and the notions of prime and composite numbers track this wonderfully well. They stand as a model, a mirror to what is happening. But numbers do not explain what happens.

It is probably unnecessary, but for the sake of thoroughness we can illustrate this in the formal terms used to characterize applied mathematics, as outlined earlier. Suppose, a = — — and b = — — —, then φ(a) = 2 and φ(b) =3. Given this, condition (1) a ≤ b → φ(a) ≤ φ(b) is obviously satisfied. That is, if duration a is shorter than duration b, then the number representing a is less than the number representing b. Similarly, if we combine two durations, then the number representing the combined duration equals the sum of the individual representing numbers. Thus, condition (2) φ(a ⊕ b) = φ(a) + φ(b) is satisfied as well. Condition (3), which concerns the unit duration, is simply: φ(—) = 1.

In passing, I should stress that I have not merely introduced a new (and clumsy) notation for the natural numbers, similar perhaps to |, | |, | | |, etc. It is nothing of the sort. The dashes represent years, temporal durations, not numbers. Of course, they can be mapped onto numbers, just as apples in a basket can. This is something we do almost instinctively and is hard to resist. But neither apples nor temporal durations are themselves a system of numerals any more than they are themselves numbers.

There is another point worth a brief mention. The homomorphism φ maps a set of physical objects to a set of abstract objects. Does this mean that the abstract realm of mathematical entities somehow reaches into the physical realm, after all? I don't know. But if that is any sort of problem, there is a ready alternative. The association of the two realms could be viewed as a primitive similarity, not a homomorphism. Thus, the two realms would be quite distinct, with the relation between them neither physical nor mathematical. But the primitive similarity itself could be modelled by the mathematical homomorphism φ, which fits perfectly and naturally with all that we have said so far.

ABSTRACT VERSUS CONCRETE

There is a standard argument often used by empiricists, nominalists, and naturalists against Platonism. There are distinct epistemic and ontological versions of this argument. The latter go something like this: Numbers and other mathematical entities are outside of space and time, so they can't causally interact with us. Unlike gravity, which makes things fall, and germs, which make us sick, numbers cannot make things happen. Since they cannot make things happen, they cannot explain them. The epistemic version says that some sort of interaction with the thing known is required for knowledge of that thing. For instance, I know there is a cup on the table; photons from the cup enter my eye, and so on, which causes me to be aware of its presence. But we cannot interact with numbers, so we could not get to know about them, even if they did exist. And yet, the argument concludes, we do know something about numbers, so they cannot be Platonic entities.

I reject both of these arguments for the same simple reason. They assume that “making things happen” or that “interacting with” are to be understood in terms of efficient causation. I agree that if efficient causation is the only sort, then Platonism is probably hopeless. But it is not the only kind of causation. Aristotle famously claimed there are four types of cause and four corresponding types of explanation: material, efficient, formal, and final. The one I would like to resurrect is formal causation. Indeed, I think it is already with us, though not recognized as such. The account of laws of nature advocated by Armstrong, Dretske, and Tooley postulates properties or universals, conceived as real abstract entities, and laws of nature are taken to be relations among these properties. Events in nature, and the regularities that may hold, are caused by these abstract entities. Clearly, this is something like formal, not efficient, causation. The widespread use of symmetry in physics, to cite another example, is often an appeal to a formal principle, not to some underlying efficient cause that leads to a symmetry. The symmetries of the “eightfold way,” for instance, are irreducible. The explanation is a formal explanation, and the cause is a formal cause.

I have no idea how the mind is able to “grasp” or “perceive” mathematical objects and mathematical facts. It certainly is not by means of some efficient cause—little platons emitted from Plato's heaven, entering the mind's eye. I suspect the answer is in terms of formal causation. Much work, obviously, remains to be done on this issue. The rejection of the view that all causation is efficient and that formal causation is also at work should be seen as a research programme that is just getting off the ground. It will be opposed by naturalism, the dominant contemporary philosophical outlook. But naturalism is far from fulfilling its promise and remains a long shot at best in its attempts to account for mathematics, morals, meaning, and several other important topics. It is at best a promising research programme, but no more than that.

Those who typically endorse mathematical explanations of the natural world also use it to defend mathematical realism or Platonism. Though I reject the argument, I gladly accept their conclusion. Not only are there mathematical entities, but I would happily embrace many more abstract objects into Plato's heaven. I mentioned symmetries, properties, and laws of nature, but I would add propositions and moral facts, as well. Some of these cause events in the world; for instance, laws cause regularities. And these formal causes are explanations.

Mathematics, however, is not the formal cause of what happens in the natural world, any more than it is the efficient cause. But if one embraces abstract entities and allows that they can cause/explain things (albeit formally, not efficiently), then why would one balk at mathematical explanations? Unlike Hartry Field (1970), who is nominalist-minded, my objection to indispensability arguments for mathematical realism is not based on a distaste for abstract entities, but rather on how I see mathematics as applying to the natural world. To repeat: It models or tracks the natural world, it does not describe in the way that a normal scientific theory does, except perhaps derivatively. That is why it is not an explanation.

Consider one more factor in support of the account given of applied mathematics, an historical argument. The various natural sciences interact by refuting one another from time to time. For instance, discoveries in optics have changed theories in biology or astronomy, since the latter were based on what we now believe are false theories of how microscopes and telescopes work. The rise of quantum mechanics led to the overthrow of significant amounts of chemistry and cosmology. We could go on producing examples ad nauseam. Mathematics, however, has not interacted with the natural sciences in this way. Though fallible and subject to change, mathematics has its own internal history and has never been refuted by discoveries in the natural world. It is autonomous. The account of applied mathematics here defended respects this history. The same cannot be said for the view incorporated in the indispensability argument. Any account that sees mathematics as offering explanations of the natural world must be prepared to see the occasional refutation. If this never happens, then there is an obligation to say why, that is, to explain the remarkable historical fact that science never challenges mathematics. Developments such as non-Euclidean geometry are not counterexamples. The discovery of consistent alternatives to Euclid opened up new modelling possibilities for physics, which were famously exploited by Einstein in General Relativity. This mathematical discovery did not, however, refute Newtonian physics.

WHY THIS MATTERS

Tachyons are hypothetical entities that go faster than the speed of light. They arise from a simple symmetry argument. Ordinary matter (tardyons) cannot be accelerated to c, the speed of light, since it would require an infinite amount of energy to do so. But this does not imply that no entity could go faster than light. What about entities that always go faster than c and require an infinite amount of energy to slow down to c? There might be logical room for such entities.

There were a couple of arguments against tachyons. In some situations, they go backwards in time. This meant one could set up a device, say, a tachyon emitter and receiver that is attached to a bomb. A tachyon is emitted; it reflects at some distant mirror and returns to the source where it sets off the bomb preventing the emission. It is, of course, the same problem as the grandfather paradox in the time travel literature. I won't concern myself with this problem.

The second object to tachyons is that they have imaginary mass, that is, mass that is not a real number but an imaginary number. The argument for imaginary mass is quite simple. Consider the energy equation:

Notice that when v > c, the denominator will be imaginary, that is, the square root of a negative number. In order to keep the energy a real number, we must make the numerator an imaginary number, as well. This means that m is imaginary. Imaginary mass is taken to be absurd, so tachyons are ruled out.

While I have no particular sympathy for tachyons, this argument strikes me as flawed. If one reflects on the nature of applied mathematics, one can see the mistake. To start with, mass is not a real number, it is represented by a real number. If mass is indeed a real number then the argument is cogent, but when it is merely represented by a real number, the argument loses its force.

The application of mathematics involves two things in a situation such as this. We link mass to the real numbers and we provide some sort of operation for the precise assignment in a specific case. For instance, we assign a number to an object based on how far it stretches a spring. Normally, we can move in either direction: Given an object, we can find a number; given a number we can find (or make) an appropriate object. This is what breaks down in the tachyon case.

The surprise is that given how we have set up the link between mass and real numbers, there is a logical consequence that tachyons have imaginary mass. That is, the mass of a tachyon is mapped to an imaginary number, just as the mass of a rock is mapped to a real number. To repeat, this is not to say that the mass is an imaginary number, just that it is represented by an imaginary number. We do not face an absurdity. Instead, we face the practical problem of finding a technique for measuring, something like stretching a spring. Now the problem is a different one: We are entertaining a property, tachyon mass, that we have no idea how to measure. The verificationist-minded will take this to be a serious objection, and maybe it is. But it is a very different sort of problem—if it is a problem at all—than the earlier alleged problem of outright absurdity. There is no reason to think the problem is insurmountable. Perhaps we simply haven't been imaginative enough. Just keep in mind the history of negative numbers and how we now represent all sorts of physical things with them.

The philosophical conclusion I want to draw from this example is simply this: Some problems in physics are sensitive to how we see the nature of applied mathematics. That's putting it weakly. The stronger version would add: And we see those physics problems, such as tachyon mass, in a clearer light when we take mathematics to represent, not describe, the physical realm.

EXPLANATION AND UNDERSTANDING

At the outset I mentioned that there are different senses of explanation. So far I've been dealing with explanations of phenomena, perhaps the primary sense of explanation, the one involved in all the debate about indispensability. The other sense of explanation might be just as important in science and our daily lives. Our demands for explanation are usually demands for understanding or justification. Some examples: “I don't understand string theory. Could someone explain it to me?” “Mary explained general covariance better than Einstein.” “The teacher explained how Newton's theory explains the tides” (this example involves both senses of explanation).

As well as asking for explanations of whole theories (General Relativity, quantum mechanics, Darwinian evolution, Psychoanalysis), we also request explanations of particular concepts (metric tensor, spin, natural selection, superego). Explanations of whole theories or of particular concepts within a theory often take the form of models or analogies that are already familiar to us. We use billiard balls to explain what a gas is and we say that pressure is due to the collision of the balls (or molecules of the gas) against the walls of the container. It is easy to see that the pressure would increase if the balls (molecules) moved faster or if there were more of them moving at the same speed.

The two senses of explanation often work in different directions. In the first sense, we commonly use things we do not understand (theoretical entities) to explain things we do understand. Thus, quantum mechanics explains the solidity of the table, a case of the bizarre explaining the commonplace. The second sense of explanation works in the opposite direction. We use things we do understand to explain things we do not. Thus, billiard balls are used to explain the role of molecules in the kinetic theory of matter and heat. I take this to be almost a banality. Some might insist on qualifications, but we needn't trouble ourselves with subtleties here, since they are not relevant to the main point of the second part of this chapter, which is this: There are concepts such as spin in quantum mechanics that can be understood in terms of a mathematical model or analogy, but cannot be understood in any other way. Mathematics provides the only explanation of spin, that is, the only explanation in the sense of providing us with some sort of understanding. My inclination, as we saw earlier, is to reject the indispensability argument as commonly conceived, namely, as an explanation of phenomena. But in this second sense of explanation, where concept formation is at issue, there are cases where only mathematics can provide us with understanding. In this regard, mathematics is indeed both explanatory and indispensable for science.⁶

To make the case, let us turn now to the example of spin in quantum mechanics. Spin, by the way, has sometimes been called the first truly quantum mechanical concept. We'll soon see why.

SPIN

In quantum mechanics, the state of a physical system, such as an electron, is represented by a vector ψ in a Hilbert space, which is a special type of vector space. The state is said to contain all the information about the system. Properties of a system, such as position, momentum, energy, etc. (misleadingly called “observables”), are represented by linear operators. Operators are functions defined on the Hilbert space; they map vectors to vectors. A given operator, say, the momentum operator, will be associated with a set of special vectors known as eigenvectors. When an operator working on the state vector is equal to that state vector multiplied by a number, then the state is an eigenstate of the system, and the special number is an eigenvalue. These, according to the theory, are the only magnitudes that a property can actually have when measured. There are lots of potential magnitudes for the momentum of an electron in a bound state, but there are lots of other values that it cannot have. The theory tells us how to calculate the probabilities of finding specific eigenvalues, given a measurement. In all of this, quantum mechanics is a magnificent success, no matter how bizarre it may seem.

If we wanted to explain the properties of an electron (in the sense of understanding them), we would do well to start with their classical counterparts. That is, an electron's position and momentum are similar to a rock's position or momentum. But that's only a beginning. There are lots of surprises: quantum theory, for instance, does not predict the same position and momentum for an electron in a given situation as classical physics would predict. Bizarrely, it also tells us that the position and momentum do not exist simultaneously (or at least cannot be known simultaneously— this is a controversial issue). We learn outlandish new ways to calculate the momentum of an electron, but someone could plausibly claim that the idea of momentum in quantum mechanics is sufficiently similar to the classical concept, that we can claim to have a reasonable grasp of it.

Since an electron in, say, a hydrogen atom, has an energy level, it would seem that orbital angular momentum (defined in terms of position and momentum, as in classical physics), would be comprehensible in a similar way. In analogy with the earth going around the sun, we can make rough sense of its position, its momentum, and its orbital angular momentum. It would also seem natural to think that the electron spins on its own axis, just as the earth does. However, there were good reasons at the time quantum mechanical spin was introduced (in the mid-1920s), for thinking an electron is a point particle, so actual spinning would make no sense. On the other hand, there were phenomena in desperate need of explanation (in the first sense of explanation). These included features of line spectra (the anomalous Zeeman effect) and the electron's magnetic moment, including various phenomena associated with it, such as the results of the Stern-Gerlach experiment. Spin or something like it was needed.

In this context, Uhlenbeck and Goudsmit made their now famous proposal.⁷ When introduced, it was first thought that the electron's spinning motion could explain some of the unexpected properties of the hydrogen spectrum and would be the obvious source of the electron's magnetic moment, since magnetic phenomena are known to arise from accelerating electric charges. Of course, spin would be subject to the usual quantum conditions, just as position and momentum are, but something akin to rotation must be happening. And, if so, we should be able to understand it, at least to the same extent that we understand the other quantum properties that seem to have counterparts in classical physics.

However, this was not to be the case. In no sense whatsoever can the electron be thought of as actually rotating on its own axis. There is no coordinate frame in which the electron's spin can be eliminated. To see how unimaginably bizarre this is, just consider: If I stand at the centre of a merry-go-round, I rotate at some angular velocity relative to the ground, but I am stationary in the merry-go-round frame. I move in one frame and am stationary in the other. There is, however, no merry-go-round frame for an electron. In any frame whatsoever, it maintains its spin. This is why spin is called “intrinsic,” and why it is sometimes said to be a genuine quantum mechanical property, unlike the others, meaning it has no classical counterpart.

Looking back in his Nobel acceptance speech awarded for the exclusion principle, Wolfgang Pauli described the situation in the 1920s.

With the exception of experts on the classification of spectral terms, the physicists found it difficult to understand the exclusion principle, since no meaning in terms of a model was given to the fourth degree of freedom of the electron. The gap was filled by Uhlenbeck and Goudsmit's idea of electron spin, which made it possible to understand the anomalous Zeeman effect simply by assuming that the spin quantum number of one electron is equal to and that the quotient of the magnetic moment to the mechanical angular moment has for the spin a value twice as large as for the ordinary orbit of the electron. Since that time, the exclusion principle has been closely connected with the idea of spin. Although at first I strongly doubted the correctness of this idea because of its classical mechanical character, I was finally converted to it by Thomas’ calculations on the magnitude of doublet splitting. On the other hand, my earlier doubts as well as the cautious expression “classically non-describable two-valuedness” experienced a certain verification during later developments, since Bohr was able to show on the basis of wave mechanics that the electron spin cannot be measured by classically describable experiments (as, for instance, deflection of molecular beams in external electromagnetic fields) and must therefore be considered as an essentially quantum mechanical property of the electron. (1994, 169; my italics)

We're faced with the following conundrum: If the electron's spin is not like a spinning top or the earth's spin on its axis, then what is it? As I mentioned earlier, we can make rough sense of the electron's orbital angular momentum on analogy with the earth's orbit around the sun. But spin is wholly different. It cannot be comprehended at all by means of metaphors or analogies associated with physical things we do understand.

Not even Maxwell, who was fond of mechanical models and brilliant at constructing them, could come to the rescue. Maxwell constructed a mechanical model of the aether. In his day, an aether theorist might reject Maxwell's particular model without changing her beliefs about the mechanical nature of the aether itself. That is, one might believe that a mechanical model is possible, perhaps even necessary. Kelvin famously remarked that he didn't understand a thing until he had a mechanical model of it. But a similar hope is utterly out of the question when it comes to the electron's spin. There cannot be a mechanical model of it. If there were, it would have to behave differently than it does.

In what, then, does our understanding of electron spin consist? The answer is at once simple and unsettling. It consists in understanding the mathematical representation of spin—and in nothing else. Notice that I said “mathematical representation” and not “mathematical description.” In doing so, of course, I am appealing to the account of applied mathematics given earlier.

The details of spin are as follows. We begin with what are known as the Pauli spin matrices.

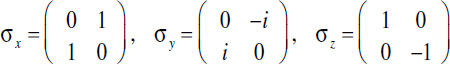
The linear operators that represent spin (in the x-direction, the y-direction, and the z-direction, respectively), are defined as follows:

The eigenvalue equation allows us to find the eigenvectors and eigenvalues. There are two eigenvectors for each operator:

The corresponding eigenvalues are, ; and -, associated with each pair of eigenvectors. The term is why it is called spin-half. In any given direction, the spin can have the value ; or -; . No other value is possible. (For convenience, the two eigenvalues are sometimes called 1 and 0, or + and -, or ↑ and ↓, or simply up and down.)

Using this formalism, we can make predictions about how electrons behave, say, in a Stern-Gerlach apparatus. If a beam of electrons passes through this device, then, generally, two beams will come out, corresponding to the two eigenvalues, and - . We can call the two beams the upper and the lower, respectively (spin up and spin down). A single electron will have a one-half chance of coming out in either beam. When we know the initial state, we can make specific predictions. For instance, if the electrons in the beam are all in state ψ = α_z, and we decide to measure the spin in the z-direction, then we will certainly find each electron to have eigenvalue , i.e., each will be in the upper beam. How do we know this? We apply the operator S_z = σ_z to the state ψ = α_z. The calculation is:

The result of the operator acting on the vector is to multiply that vector by a number, namely, , so that number is the eigenvalue.

If we wanted to measure the spin component in, say, the x- or y -direction, or more generally, along any angle θ, then we would use the S_θ operator. If the Stern-Gerlach apparatus is oriented at angle θ in the z-x plane, then the operator S_θ is defined:

The eigenvalues of this operator are exactly the same as the others, and –. This matrix will also allow us to calculate the probabilities of getting one or the other of these eigenvalues.

Of course, there is nothing new in what I am saying. Since the birth of quantum mechanics, it has been generally conceded that the quantum world cannot be visualized. I am not going much beyond that rather profound claim in saying spin cannot be understood in any normal sense whatsoever. We have some mathematical rules that we can apply and the empirical results are spectacularly successful. But there is no intuitive grip we can get on the concept of spin beyond that.

Spin is a dramatic example, but not unique. Newton's universal gravity was, in his day, often called “unintelligible,” since it involved action-at-a-distance. No mechanism was provided to explain how one body of mass m₁ would move toward another m₂. All that was given was an equation, F(m₁ m₂) = Gm₁m₂/d², from which one could calculate the motions of the two bodies. As with spin, the only understanding of Newtonian gravitational attraction that we had was thanks to the mathematics involved. Newton's action-at-a-distance gravity is not as dramatic as spin, because we can at least visualize two bodies moving toward one another in otherwise empty space.

For emphasis, let me return to spin and repeat an all-important point. There is a property P of an electron that explains (in the first sense of explains) various observable phenomena. But, mathematics aside, no explanation of P (in the second sense of explains) is possible. That is, there is nothing in the natural world that we can intellectually grasp that could serve as an analogy. However, P has a structure that is similar to a particular mathematical structure, namely, the Pauli spin matrices. These mathematical structures are, I claim (with all due Platonic hubris), utterly transparent to the mind, as are mathematical objects generally. In so far as we understand the mathematical analogy, we understand the concept of electron spin, and we understand it to that extent, neither more nor less. In this sense of explanation, mathematics can explain physics. In the case of spin, in particular, mathematics is indispensable.

FIELDS AND POTENTIALS: AN EXTENDED EXAMPLE

It is often very difficult to tell which parts of a physical theory are the physics and which are the mathematics. Sorting it out is sometimes part of the process of doing science, one that frequently leads to surprises. There are lots of simple cases where we're not fooled. When it is said that the average family has two and a half children, no one is likely to think there are such physical beings as half children. Children are real things and we associate them with numbers. Families are real things and we associate then, too, with numbers. We then divide the former number by the latter to arrive at the average family. While the number 2 is a perfectly real Platonic entity, it does not correspond to anything in the physical human realm. Other cases are not always so clear.

When Faraday and Maxwell were creating what we now call classical electrodynamics they faced a problem. Both believed in the reality of charged bodies—even unseen ones. But they were also faced with the onto-logical status of an entirely new entity: the electromagnetic field. Was it to be a real thing, like a charged body, or just an extremely useful mathematical device? There were two considerations that favoured a realistic view of fields: the conservation of energy and the finite propagation in time of electromagnetic interactions. Maxwell addressed both issues. First, he complained about action-at-a-distance theories:

we are unable to conceive of propagation in time, except as the flight of a material substance through space, or as the propagation of a condition of motion or stress in a medium already existing in space. . .  . But in all of these [action-at-a-distance] theories the question naturally occurs: If something is transmitted from one particle to another at a distance, what is its condition after it has left the one particle and before it has reached the other? (1891, 866)

Maxwell answered his own question in another place:

In speaking of the energy of the field, however, I wish to be understood literally. All energy is the same as mechanical energy, whether it exists in the form of motion, or in that of elasticity, or in any other form. The energy in electro-magnetic phenomena is mechanical energy. The only question is, Where does it reside? On the old theories it resides in the electrified bodies, conducting circuits, and magnets, in the form of an unknown quality called potential energy, or the power of producing certain effects at a distance. On our theory it resides in the electromagnetic field, in the space surrounding the electrified and magnetic bodies, as well as in those bodies themselves, and is in two different forms, which may be described without hypothesis as magnetic polarization, or, according to a very probable hypothesis, as the motion and the strain of one and the same medium. (1890, 563)

Maxwell's remarks taken together suggest an explicit argument for the physical reality of the electromagnetic field. Consider a system of two isolated electrified bodies at some distance from one another. One body is jiggled and after a delay the other wiggles in response.

1. Energy is conserved and localized (i.e., its magnitude remains constant and it is located in some entity or other).
2. Electromagnetic interaction is propagated with a finite velocity.
3. The total energy of the system will be located in the electrified bodies at the start and at the end of an interaction; but not at intermediate times.
4. The energy at intermediate times must be located in the electromagnetic field.
5. The electromagnetic field is physically real (and not just a useful fiction or some sort of mathematical device).

Faraday and Maxwell were persuaded by this type of consideration, and both were realists about electromagnetic fields from the start. Our contemporaries hold similar views. Richard Feynman, for example, writes: “The fact that the electro-magnetic field can possess momentum and energy makes that field very real” (1963, vol. I, ch. 10, 9). But we can better appreciate the argument by seeing that it does not work in the case of Newtonian gravitation, even though that theory can also be formulated as a field theory. The reason for the ineffectiveness of the parallel argument is simple: Gravitational interactions are instantaneous; so the total energy will always be located in some body or other. Consequently, in the case of Newtonian (but not relativistic) gravitation, it would still be reasonable to hold the view that the gravitational field is nothing more than a mathematical fiction, similar to the half child.

Anti-realists are likely to be unimpressed with all of this. The argument for the reality of the electromagnetic field is for the benefit of those who are happy with theoretical entities, in principle, and who simply want to know which terms correspond to something real (“children” and “electromagnetic fields”) and which terms don't (“average families” and “Newtonian gravitational fields”).

In debates over the reality of fields, it is evident that people are searching for the right explanation of electromagnetic phenomena. Is it the sources and some sort of action-at-a-distance? Or is it the fields acting locally? Clearly, mathematics itself is not one of the candidates offering an explanation, or this debate would not take place. The mathematics of vector fields will be the same whether or not the fields are real, which shows that mathematics is not at issue. What matters is the correspondence between the mathematical entities and the physical world. The mathematics of vector fields is good for tracking the physical world whether it corresponds, as in the electrodynamics case, or does not correspond, as in the Newtonian gravitational case.

Now let's move to a much richer example. Earlier I said we pick out some part of the world and associate it with some part of Plato's heaven. That's how it starts, but it quickly becomes much more complicated. We might discover something in the mathematics that then makes us look for a counterpart in the physical realm, something we missed earlier. In short, it becomes a two-way street. This is the case with the vector potential.

Maxwell's theory of electromagnetic fields is embodied in his famous equations.

The first of these is Gauss's law, which relates the divergence of the electric field through a surface to the charge contained inside (ρ is the charge density and ε has to do with the medium; in our case we are only concerned with free space, hence ε₀). The second is Faraday's law of magnetic induction, which relates the strength of an electric field to a changing magnetic field. The third equation says, in effect, that there are no magnetic monopoles. Unlike electrons and protons, which have either a negative or a positive charge, magnetic bodies always have a north and a south pole, so their field lines are always closed loops. The final equation is a generalization of Ampere's law, which, like Faraday's law, relates the electric to the magnetic field; in particular, it says that the properties of the magnetic field are due to electric currents or to changing electric fields, or both (j is the current and c is a constant of proportionality which turns out to be the same as the velocity of light).

According to the argument given earlier, the E field and the B field are real. They denote real physical things and they are not mere mathematical artefacts. Notice, however, that the terms “E” and “B” are ambiguous, denoting both the mathematical entities (vector fields) and real physical fields that exist in space and time. No doubt this ambiguity contributes to the confusion about the relation between the physical and mathematical realms.

Except for principled anti-realists, almost everyone is willing to accept the physical reality of electric and magnetic fields. But what about some of the other exotic entities in electrodynamics? In particular, what about the vector potential? Is it just a mathematical entity, like the average family, or is there a physically real field corresponding to it as well? First, we must explain what it is. Initially, the vector potential arises as a purely mathematical result, a theorem: When the divergence of a vector field B is zero, there exists another vector field A such that B = × A. When combined with the third of Maxwell's equations, it implies the existence of the A field, known as the vector potential. The theorem behind this is: • ( × A) = 0.

Recall the two senses of “explanation” we distinguished. The second sense, making things intelligible, is at work here. The concept of magnetic field might arise because of various things we can do and observe, such as making patterns with iron filings on a sheet of paper by holding a magnet below. But the concept of vector potential, like quantum mechanical spin, could only be grasped by means of mathematics. The only way to understand a real, physical A field, if such a thing exists at all, is to say it is the physical counterpart of the A field in vector field theory. Once we have grasped it mathematically, we can then ask about the existence of a physical counterpart.

The way the A field is conjured into existence suggests that it is merely a mathematical artefact, just as lacking in flesh and blood as the half child of the average family. From the first days of electrodynamics, this was the common attitude. Hendrik Lorentz called the vector potential an “auxiliary function” (1915/1952, 19) which he introduced to make calculations easier. Feynman remarked, “for a long time it was believed that A was not a ’real’ field” (1963, vol. II, 15, 8) And Leslie Ballentine declared, “the vector and scalar potentials were introduced as convenient mathematical aids for calculating the electric and magnetic fields. Only the fields and not the potentials, were regarded as having physical significance” (1990, 220).

Why would anyone think otherwise? That is, why think of A as physically real? The change in attitude toward the vector potential came from considering its role in a simple quantum mechanical case that has come to be known as the Aharonov-Bohm effect. The received wisdom now is that the A field is just as physically real as the E and B fields. Let's turn to the details of the Aharonov-Bohm effect to see why the change in attitude.

From a purely classical point of view, the vector potential plays no physically significant role at all. The Lorentz force law is F = q (E + v × B), which means that the force on a charged particle depends only on the E and B fields (as well as on the charge q and velocity v). So even if the A field should have a non-zero value at some point occupied by the charged particle, it would have no physical effect. In a solenoid (Figure 1.1), the value of the B field outside the solenoid is zero, but the A field is non-zero.⁸

In spite of this non-zero value, a classically charged particle in the vicinity of such a solenoid wouldn't feel a thing; it would pass by as if the solenoid wasn't there, indifferent to the intensity of the A field. However, in a quantum mechanical setting this is no longer true. Consider a splitscreen device, the kind commonly used in quantum mechanics to illustrate interference effects. We set things up in the usual way, except that behind the two-slit barrier there is a solenoid (coming out of the page, Figure 1.2). When the current is off, the interference pattern on the back screen is the usual one. But when the current is turned on the interference pattern is shifted. The B field is everywhere zero except inside the solenoid, but the A field has a non-zero value outside the solenoid; the more intense it is, the greater the shift in the interference pattern. This is the Aharonov-Bohm effect. (For those with a taste for such things, I include a derivation in the endnotes.⁹)

There is no question about the argument from a theoretical point of view: The combined formalisms of classical field theory and of quantum mechanics certainly lead to this predicted outcome. Moreover, experiments of remarkable sensitivity have detected the effect.¹⁰ So the problem now is entirely one of interpretation: How are we to understand the A field? Is it a mathematical artefact? A real field? Or something else? The overwhelming opinion seems to be this: The A field is not just a mathematical entity; it is a physically real field, just as real as the E and B fields. In the words of those who initiated this very plausible argument:

Figure 1.1

in quantum theory, an electron (for example) can be influenced by the potentials even if all the field regions are excluded from it. In other words, in a field-free multiply-connected region of space, the physical properties of the system still depend on the potentials. . . . the potentials must, in certain cases, be considered as physically effective, even when there are no fields acting n the charged particles. (Aharonov and Bohm 1959, 490)

To head off possible confusion, I should note that Aharonov and Bohm use “field” to mean only B or E while A is called a “potential,” whereas I'm following the common practice of calling A a field. This terminological point is irrelevant to the main issue, namely, the physical reality of A.

Interpreting the vector potential as physically real is one way to deal with the Aharonov-Bohm effect. Another way is often mentioned, only to be dismissed. This alternative is to take the magnetic field as causally responsible for the effect, but to allow that it is acting at a distance. Of course, it seems almost self-contradictory to say that a field is acting at a distance, but there is no logical problem with this. The B field is confined within the solenoid, but it might (like a massive body in Newtonian gravitation theory) act where it is not. Thus, on this view, it is the physically real B field, not the physically unreal A field, that causes the phase shift in the interference pattern—but it does so at a distance.

Figure 1.2

Such an interpretation is dismissed out of hand as a gross violation of the proper spirit of modern physics:

according to current relativistic notions, all fields must interact only locally. And since the electrons cannot reach the regions where the fields are, we cannot interpret such effects as due to the fields [i.e., E or B] themselves. (Aharonov and Bohm 1959, 490)

In our sense then, the A field is “real.” You might say: “But there was a magnetic field.” There was, but remember our original idea—that a field is “real” if it is what must be specified at the position of the particle in order to get the motion. The B field [in the solenoid] acts at a distance. If we want to describe its influence not as action-at-a-distance, we must use the vector potential. (Feynman 1963, vol. II, 15, 12)

So our options in accounting for the Aharonov-Bohm effect appear to be these: First, there is a non-local effect of the magnetic field, B. This has the advantage of evoking something to which we already ascribe physical reality, but it has the disadvantage of involving action-at-a-distance. It is universally rejected, and rightly so. Second, there is a local effect of the vector potential, A. This account of the Aharonov-Bohm effect is nearly universally favoured, since it is in the spirit of field theory. Once we're over our initial shock, we are happy to give up the idea that the vector potential is merely a mathematical entity and we cheerfully ascribe physical reality to it as well.

The story of the vector potential is, I think, far from finished, but I will pursue it no further. Not everyone is happy acknowledging the A field as being physically real, as the E and B fields are. Though I myself am one of the discontents, there is no need to develop things further, since we have seen enough to draw the relevant morals about the role of mathematics. In brief, the morals to be drawn from the example of the vector potential are:

1. Vector field theory (which is mathematics) was usefully applied to electrodynamical phenomena, but the status of the mathematical entities, E and B, was initially unknown. Did they have physical counterparts?
2. Arguments for the physical reality of these fields (based on finite action and conservation of energy) were persuasive, so that the dominant view is now that the E and B fields are indeed physically real.
3. It is the physically real fields E and B that explain various electrodynamic phenomena. The mathematical vector fields E and B model or track, but do not explain those phenomena.
4. The concept of the vector potential A could only arise and be intelligible to us in the mathematical theory of vector fields. Mathematics is essential for the explanation of this concept, in the sense of understanding it, and, of course, for our knowledge of its existence in the mathematical realm.
5. The existence of a physically real A field rests on various theoretical and experimental considerations (i.e., the Aharonov-Bohm effect), which are currently thought to favour its physical reality.
6. The chief argument for the reality of each of the three fields, E, B, and A, is that they need to be physically real in order to explain various phenomena.
7. This argument in turn strongly suggests that it is the physically real A field that is to be used to explain various phenomena, not the mathematical A field.
8. The mathematical entity A is indispensable in forming the concept of the physically real A field (the vector potential), but the mathematical entity A does not explain the observable phase shift (the Aharonov-Bohm effect).
9. General moral: There is no principled philosophical way of settling all questions concerning the status of mathematical entities and their counterparts. Each case (half children, vector potential) must be decided on its own merits. Whether some part of a mathematical structure corresponds to a counterpart in the world is itself part of the (fallible) physical theory.

The mathematical theory of vector fields, while excellent at tracking phenomena, does nothing to explain them. From Maxwell to Aharonov-Bohm, a physical argument establishing the physical reality of X was needed to show that X was actually the cause and the explanation of the experimental phenomenon. Otherwise, X might be terrific for calculating, but it explained nothing. Furthermore, for some X, we have no hope of even grasping the concept, except through mathematics. The vector potential illustrates both of these points.

Before getting to the concluding remarks, there is one more consideration to address. Earlier I mentioned that the view of applied mathematics I sketched, which was drawn from measurement theory, has been independently proposed in the current debate by Pincock and been called “the mapping view.” Bueno and Colyvan endorse the view to a limited extent. They object, however, to what they see as a major shortcoming. The mapping view, according to them, cannot tell us which parts of the mathematical model correspond to the world and which do not. They cite the example of a quadratic equation for projectile motion and note that only one of its two solutions corresponds to the physical situation. “At the very least, the mapping account is incomplete as a philosophical account of applied mathematics” (Bueno and Colyvan 2011). Their quadratic equation example, the half child, and the vector potential are instances of the same thing, so their objection applies to me, too. They would say that my account of how mathematics is applied fails to settle whether the vector potential is physically real or not, and that is a major shortcoming of my account.

In response, I would say they demand far too much. It should surely be left to the physicists to decide whether there are fields at all, and if so, whether there are any in addition to the electric and magnetic. Having the right account of applied mathematics would not have helped them to decide on the physical reality of the vector potential. Much as I like a priori science, not even I would go that far. The way I think we should look at this is somewhat different. We represent the physical world by associating it with a mathematical structure—which structure is a fallible conjecture. We fill in the details as we come to them (i.e., we specify that there are no half children, that only the positive solution of the quadratic has a physical counterpart, and so on). These can be trivial or they can be subtle issues, as indicated by the vector potential example. Dirac and his equation provide another. It gave two solutions; most scientists examining it initially thought only one was physically meaningful, but Dirac claimed that the other solution represented holes in a negative sea of energy, later interpreted as anti-particles. This audacious move is now seen as brilliant.

Specifying the details of how the mathematics connects to the world is part of a physical theory, not a philosophical theory about the nature of applied mathematics. As we learn more about nature and we learn more about the mathematical structure itself, we alter our claims about the details of the mapping. This is what happened in the case of the vector potential. We should not look for a principled solution that applies smoothly everywhere; each case should be decided on its own and those (fallible) decisions can be overturned.

Bueno and Colyvan acknowledge that something like the specification of details does go on by scientists as they develop their theory. But they want to know how that is possible, and the mapping account, they say, does not provide it. At this point I am not sure how to respond, except to say that generally we are not dealing with an isomorphism, but a homomorphism 9, which is an into function that need not be one-one. This allows a lot of flexibility. It is clear, however, what really worries them about this view of applied mathematics: They want an account of applied mathematics that will underwrite mathematical explanations. “The problem is simply that it is hard to see how a mere representational system can provide explanations” (MS 6). Exactly. Their modus tollens is my modus ponens.

CONCLUDING REMARKS

Does mathematics explain anything in the natural realm? The answer, as I said at the outset, is no and yes. It does not explain phenomena, in the sense of telling us why things happen, even though it often tracks these things brilliantly. But it does explain concepts, in the sense of helping us to understand them. I'm inclined to say that not only is this the right answer, but it is also the answer any mathematical realist should give. Though in full agreement with the conclusions of my fellow mathematical realists, from Quine and Putnam to Baker, Colyvan, and many others, I nevertheless see mathematics hooking on to the physical world much differently than they do.

What is mainly at issue here is the nature of applied mathematics. Much of the difference between Platonists, such as myself, and the more naturalist-minded realists, turns on rival views of how mathematics connects to the world. That is the question that needs to be answered first. It would, of course, be too much to say that once that question is settled, everything else will automatically fall into place, since there will still be plenty of room to disagree over various other questions. But a remarkable amount of what is at issue will be seriously affected by adopting the view that mathematics models and tracks the natural world rather than by the view that it somehow directly describes and explains it.

Where do we go from here? The main moral to be drawn from the foregoing is that the physical realm and the mathematical realm are distinct. Mathematics has an autonomous existence. How, then, do we come to possess mathematical knowledge? This is the battleground in the struggle between Platonism and naturalism. The case for Platonism is strong. But naturalists are not without considerable resources. Before getting into them, the next step is to say just what naturalism might be.