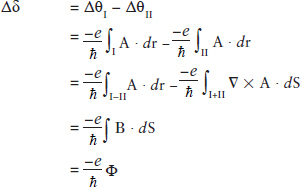Notes
NOTES TO CHAPTER 1
1. Apologies to Andrew Marvell, author of “To His Coy Mistress.”
2. Strictly, this is only a first approximation. The real distinction I want to uphold is between the mathematical and the non-mathematical. The latter might be a combination of material entities and abstract ones, such as an electron and the state of an electron. A quantum state is an abstract entity, not a physical one. But it is not a mathematical entity, though it is represented by one, namely, by a vector ψ in a Hilbert space.
3. Usually this body will be singled out with an eye to practical considerations. Thus, the standard metre in Paris is a convenient length and an easily obtained litre of water will serve as the standard kilogram. Modern units, of course, are typically based on much more sophisticated considerations, but the basic idea of a standard sample is the same.
4. The relation can work the other way, too, which is why material objects and diagrams can tell us important things about the mathematical realm (see Brown 1999/2008).
5. A brief account of measurement theory can be found in Brown (1999/2008, ch. 4) and a much more detailed history in Mitchell (1999).
6. I will assume that science is in the business of providing understanding, among other things. If not, then my claim might be short-circuited. Duhem, for instance, asserted that the aim of science is empirical adequacy, nothing more. He mocked the English for wanting mechanical models of everything, such as the aether. It is enough that the theory predicts the things we can see, he claimed, and we needn't understand the theory beyond being able to use it for deriving empirical consequences. Most people reject this, and I do, too. But even if this view were adopted, we would still have no way of dealing with some theoretical entities to see what they imply for empirical observation, except by means of the mathematics that is associated with them.
7. Goudsmit's informal account of the events can be found at http://www.lorentz.leidenuniv.nl/history/spin/goudsmit.html. Standard histories of quantum theory will also present an account, e.g., Jammer (1966).
8. In cylindrical coordinates (r, φ, z), the components of the B field are as follows:
Inside the solenoid: Br = Bφ = 0, Bz = B (where B = |B|).
Outside the solenoid: Br = Bφ = Bz = 0.
The components of the vector potential, however, are:
Inside: Ar = Az = 0, Aφ = Br/2.
Outside: Ar = Az = 0, Aφ = BR2/2r (where R = radius of the solenoid).
9. The phase difference of the electrons (with wave length λ) arriving from the two slits is δ = 2ϖxd/Lλ (see Figure 1.2). Let the flux through the solenoid be Φ. The state of a free electron is ψ = exp[il p r]. As a result of moving through the A field there is a change of phase
ψ → ψ’ = exp[il p r - iel A r].
Over the entire trajectory the phase change is
![]()
The change in the phase difference δ d can now be calculated.
The interference pattern then shifts by the amount
![]()
10. The first of these was by Chambers (1960); more recent experimental results are reported in Tonomura (1986), Tonomura et al. (1986), van Loosdrecht et al. (1988).
NOTES TO CHAPTER 2
1. As well as the passages to follow, more in the same vein can be found in the major survey articles by Papineau (2007) and Paseau (2008), both of which are available online from the Stanford Encyclopaedia of Philosophy, a very reliable source of philosophical information.
2. For a large sample of naturalist writings (both pro and anti), see the anthologies edited by Kornblith (1994); Wagner and Warner (1993); French, Uehling, and Wettstein (1994); and De Caro and Macarthur (2004).
3. This issue spills over into the philosophy of mathematics, since Brouwer claims that we prove theorems by making mental constructions; but each of us can only grasp our own mental constructions; others have to do it themselves. Brouwer is unquestionably an anti-naturalist, as well as being an anti-Platonist.
4. I'm inclined to hold both of these true, that is, in current science laws of nature are relations among abstract entities and in some thought experiments we can “perceive” laws of nature. See my (1991/2010) for details.
5. Structuralists such as Resnik and Shapiro have considerable sympathy with Platonism, but would reject the claim that all mathematical objects are outside space and time. In some cases mathematical structures and their objects are physical entities.
6. There are, however, echoes of the earlier notion in some definitions of number. Russell, for example, defined the number 2 as the set of all sets having two members. This suggests a universal.
NOTES TO CHAPTER 3
1. A special case of this famous conjecture was proven in 1993 by Andrew Wiles; it was the key element in his proof of Fermat's last theorem. Recently, the whole conjecture was proven by Conrad, Taylor, and Diamond.
2. I said “crudely” because anthropologists will often distinguish between beliefs that they take to reasonable in the circumstances, even if they think those beliefs false, and beliefs that they take to be unreasonable. In the latter case they will often look to unusual social factors to explain them. Even so, it is still common to take a hands-off attitude and not try to “correct” the false beliefs. The attitude is not stable. I have yet to meet an anthropologist who is happy either “correcting” or “not correcting” a significant belief thought to be false. Though never put this way, ambivalence on this point is really an ambivalence about naturalism.
3. I realize I may not be speaking for all at this point. Some (e.g., Bloor) may have no more than a sociological interest in our mathematics, or at least he may think that normative questions are irrelevant.
4. In the first chapter I distinguished between so-called formal and efficient causes. The type assumed here is efficient. I would have no objection to anyone who posits a formal cause between us and the Platonic realm.
5. Note that I say “independent,” not “prior.” It may well be that it takes playing around with a few apples to grasp the relevant number relations. But the sense perception of the apples should be seen as stimulating something else, namely, the apprehension of the relevant relations in Plato's heaven, which then allows us to do the counting.
6. Seeing the mathematical practice or the linguistic behaviour might “trigger” the knowledge in the observer, but that knowledge is independent of the observation. For Chomsky, grammar will be innate. A mathematical Platonist needn't say this, but (as I stressed in the previous footnote) only that the mind is somehow directed to the abstract realm by this sensory experience. The point in common with Chomsky is not innateness, but the independence of the mathematical or linguistic knowledge from our sensory experiences.
7. For a brief account, see Brown (1999/2008, ch. 5).
8. Of course, besides being crudely expressed, this is a controversial claim. But at the very least it makes a kind of sense that Kitcher's mathematical naturalism can't hope to emulate.
NOTES TO CHAPTER 4
1. This chapter stems from a joint article with Glenn Parsons. I am very grateful to him for allowing me to use it here.
2. See Lakoff and Johnson (1980, 1999).
3. For instance, Bonnie Gold in her Review in MAA Online remarks that “this book is a significant contribution to our understanding of mathematics’ relations to people.” The Mathematical Association of America is one of the two leading mathematical organizations in the US, and produces one of the most influential and widely read journals.
4. For presentation of many of the standard philosophical views on metaphor, see the papers in Johnson (1984).
5. Note that transfer requires that “the entailments of such a mapping must be consistent with the properties of innate arithmetic and its basic extensions” (2000, 59).
6. Lakoff and Núñez also discuss ‘redefinitional metaphors’ that ‘impose a technical understanding replacing ordinary concepts’ (2000, 150). As an example they give ‘Cantor's metaphor,’ in which the concept ‘Have the Same Number’ is understood metaphorically as the concept ‘Are One to One Pairable’ (2000, 142–144). Since these metaphors do not involve seeing one mathematical entity as another, but rather seeing one sort of property as another sort, they cannot be employed straightforwardly in the anti-realist argument we are discussing. The Cantor example will be discussed later.
7. See Suppes (1957, ch. 8) for a thorough discussion of the standard account of definition, and Brown (1999/2008) for a discussion of alternatives.
8. Related morals can be drawn when it comes to understanding applied mathematics in esoteric realms. We will not belabour the point, but only assert it. The concepts of, say, high-energy physics are hopelessly inaccessible from the point of view of every-day experience. We cannot understand things like “isospin” or “principle connection on a fibre bundle” in terms of metaphors drawn from life. It goes the other way. We first understand mathematics. We then understand the esoteric concepts of physics in terms of our prior understanding of the relevant mathematics. The abstract horse comes before the physical cart.
9. Sets provide for further examples. Spatial regions containing physical objects have physical properties such as diameter and area. Sets have none of these properties.
10. Lakoff and Núñez tend to run these concepts together (see, e.g., 2000, 363).
11. Given their account of truth, Lakoff and Núñez might accept the view that mathematics cannot be false in the sense that we employ. If so, however, then it is clearly disingenuous of them to berate Platonism for failing to allow mathematics to be false in that sense.
12. For further discussion of the politics of the science wars, see Brown (2001).
NOTES TO CHAPTER 5
1. There are, however, some echoes of the earlier notion in some definitions of number. Russell, for example, defined two as the set of all sets having two members. This suggests a universal.
2. In Sudbury, Ontario, where, in pre-university days, I spent some time drilling, blasting, and mucking for a living.
3. For a taste, see G. Maxwell (1962) and Shapere (1982).
4. For more on this example and further fleshing out of the argument, see my (1999/2008, ch. 3).
5. This sort of argument goes back at least to Sextus Empiricus; current versions stem from Benacerraf (1973); others include Kitcher (1983), Field (1980), and Maddy (1990), just to name a few.
6. For an elementary exposition of EPR and the Bell results, see Albert (1992).
7. This example is developed in a bit more detail in my (1990) and (1991/2010).
NOTES TO CHAPTER 6
1. For those inclined to read Quine as a nominalist, consider: “A more accountable misapprehension is that I am a nominalist. I must correct it . . . In all my books and most papers I have appealed to classes and recognized them as abstract entities. I have indeed inveighed against making and imputing Platonistic assumptions gratuitously, but equally against obscuring them” (1960, 243n).
2. This objection may not be fair since Maddy distinguishes perceptual from inferential knowledge. She writes, “I base my case that the belief that there are three eggs is non-inferential on empirical studies that suggest we don't count, don't infer, for such small numbers” (private communication). I am not as confident as she is that we have a sharp distinction, but I will not pursue the issue here. I am grateful to her for this and other clarifications.
3. In a private communication Bernie Linsky wrote: “Ed Zalta had the basic account of mathematical theories as like stories and mathematical entities as like characters in stories, all within his formal object theory, back in his Abstract Objects (Dordrecht: Reidel, 1983). That's including the two interpretations of his theory as Platonist and as Meinongian, depending on how the quantifiers are read, as ‘there are’ or ‘there exists,’ and the predicate E! as ‘exists’ or ‘is concrete.’ Ed definitely has priority for the idea of a rich ontology of mathematical objects, except the official interpretation of the formal theory was Meinongian. I think I suggested the thought that a plentitude of objects would solve the epistemological and referential problems of Benacerraf. In fact I think I mentioned this to you around 1993. It certainly is true, however, that Ed and I had the idea of applying his object theory to math in this way before we saw Balaguer's manuscript. Then Zalta and I worked on our paper in 1994 and read it around in 1995, when it was published. Balaguer heard us give the talk at Irvine, but he had already been in correspondence with Ed, sending him the manuscript of his first paper on the topic, in Synthese, which came out that year, too. Balaguer must have done his thesis on this, before we wrote our paper, but we didn't know about it. Except that I got the idea that a plentitude of objects would solve the Benacerraf problems from reading Lewis's On the Plurality of Worlds, and so it was an idea floating around.”
4. The view called “if-thenism” says any mathematical statement, say, 5 + 7 = 12, is really short for a logical claim of the form: “If the Peano Axioms are true, then so is 5 + 7 = 12.” It is generally considered an unsatisfactory account, though it has its defenders.
5. The cumulative hierarchy starts with the empty set, ø, then applies all possible operations, such as forming the power set, to get the next level. Successive levels are built from those below in the same way.
6. I won't pursue the issue here, but for a discussion, see Brown (1999/2008).
7. For an excellent account of second-order logic, both formal and philosophical aspects, see Shapiro (1994).
8. Of course, other accounts are possible. We might, for example, be hardwired to count this way. Needless to say, this wouldn't help Balaguer.
NOTES TO CHAPTER 7
1. Neil Tennant makes some similar objections to Maddy on this point and others. See his essay review, Tennant (2000).
2. I would be sympathetic to the claim that idealization is essential to science. The part I would resist, as argued in Chapter 1, is that mathematics is essential (in the sense used here) for science, whether that science is idealized or not.
3. This is standard notation, but those unfamiliar with it may find it confusing. It should not be read as saying (ZFC + V) = L, but rather as asserting the usual axioms of ZFC and the additional axiom, V = L.
4. The precise definition of inaccessible cardinal can be found in most advanced set theory texts, e.g., Drake (1974).
5. To say the mathematical realm is as full as it could be is only to say that nothing more could be added without falling into inconsistency. So-called “plenitudinous Platonism” wants even more, as we saw in Chapter 6; it allows pair-wise inconsistent theories both to be true. I reject this latter view.
NOTES TO THE AFTERWORD
1. Richard Rorty raises the problem in his autobiographical essay “Trotsky and Wild Orchids” (1999). The conflict, as he saw it as a teenager, was between his personal interests (a love of wild orchids) and his sense of social duty (as a follower of Trotsky). Didn't the latter preclude the former? He came to think that a good life could (and perhaps should) include both.