Engineers, scientists, and data analysts who perform large-scale or long duration numeric work crave ever faster and more cores, memory, bandwidth, and storage. By their nature, numerical models can always be improved with higher resolution, finer discretizations, and an abundance of everything—degrees of freedom, time steps, frequency intervals, neurons, layers, iterations, pixels, rays, cases.
A large subset of MATLAB users falls in this power-hungry group. The MathWorks invests considerable effort to make MATLAB as performant as possible for this core segment of its customer base. Accordingly, performance will interest many MATLAB users investigating Python.
- 1.
Profile the program to learn where time is being spent.
- 2.
Eliminate redundant I/O and batch I/O operations where possible.
- 3.
Study the complexity of algorithms in the expensive sections of code. Are there, for example, O(N2) steps that could be replaced by O(N log N ) algorithms?
- 4.
Enable compiler or interpreter optimization features.
- 5.
Organize the data into contiguous memory blocks.
- 6.
Implement vector-capable portions of the algorithm as vector operations.
- 7.
Call functions in optimized libraries (likely written in compiled languages).
- 8.
Distribute work across cores on the same machine.
- 9.
Use hardware with more cores (specifically GPUs).
- 10.
Distribute the work across multiple machines.
A fundamental challenge in HPC is that steps 3–10 often conflict and their relative benefits vary with problem type, size, and available computer hardware. An O(N2) algorithm running on a GPU may run faster than an O(N log(N)) algorithm on a conventional CPU, and a communication-intensive parallel program running on a single multicore computer can be faster than the same program running on many such computers tied by a slow network.
Finding a suitable balance in the performance tradespace comes down to deciding how much effort you’re willing to expend to achieve a satisfactory speed boost.
14.1 Paths to Faster Python Code
- 1.
Improve single CPU performance with Python-specific tools such as Cython, Numba, and Pythran.
- 2.
Parallelize code over multiple cores with multiprocessing, Pythran, Numba, or Dask.
- 3.
Rewrite critical segments in C, C++, or Fortran and create Python interface modules to them.
- 4.
Parallelize code over multiple computers with Dask.
As we’ll see in the recipes at the end of this chapter (Sections 14.12 and 14.14), MATLAB programs may also run much faster by calling accelerated Python code.
14.2 Reference Problems
Two programs will be used to demonstrate HPC techniques in Python. The first, computing terms of the Mandelbrot set, appears straightforward but has load balancing aspects that complicate vectorization. The second, a finite element solver, more closely resembles a real-world problem. It involves loading data from tens of megabytes of text data, assembling sparse mass and stiffness matrices with a million degrees of freedom, and solving the generalized eigenvalue problem with them. Code is spread across multiple files and classes.
The reference programs are also implemented in MATLAB to allow performance comparison with the Python versions.
A final remark about these problems is that their absolute performance numbers are not especially interesting. The reference problems are presented as proxies for computationally intensive work you want to do. The goal is to show the detailed steps to find slow sections of code, options to speed it up, and compare the techniques and their effectiveness.
14.2.1 The Mandelbrot Set
“The Mandelbrot set
is the set of complex numbers c having magnitude ≤ 2 for which the function fc(z) = z2 + c does not diverge when iterated from z = 0, i.e., for which the sequence fc(0), fc(fc(0)), etc., remains bounded in absolute value.”1 In other words, if we pick a random complex number c with magnitude ≤ 2 and initialize the complex number z to zero, at what iteration i will the recurrence  exceed magnitude 2? The set is often visualized as a contour plot of iteration count, i, as a function of the real and imaginary components of z.
exceed magnitude 2? The set is often visualized as a contour plot of iteration count, i, as a function of the real and imaginary components of z.
While a “toy” problem, several aspects make computing terms of the Mandelbrot set useful in illustrating HPC problems: the algorithm is easy to describe, can be implemented with little code, can be vectorized and readily implemented in parallel yet has nontrivial load balancing aspects, and can be made arbitrarily large. The fascinating images that arise are a nice side benefit.
MATLAB: | Python: |
|---|---|
% file: code/hpc/MB_main.m main() function [i]=nIter(c, imax) z = complex(0,0); for i = 0:imax-1 z = z*z + c; if abs(z) > 2 break end end end function [img]=MB(Re,Im,imax) nR = size(Im,2); nC = size(Re,2); img = zeros(nR, nC, ... 'uint8'); for i = 1:nR for j = 1:nC c = complex(Re(j),Im(i)); img(i,j) = nIter(c,imax); end end end | #!/usr/bin/env python3 # file: code/hpc/MB.py import numpy as np import time def nIter(c, imax): z = complex(0, 0) for i in range(imax): z = z*z + c if abs(z) > 2: break return np.uint8(i) def MB(Re, Im, imax): nR = len(Im) nC = len(Re) img = np.zeros((nR, nC), dtype=np.uint8) for i in range(nR): for j in range(nC): c = complex(Re[j],Im[i]) img[i,j] = nIter(c,imax) return img |
function [] = main() imax = 255; for N = [500 1000 2000 5000] tic nR = N; nC = N; Re = linspace(-0.7440,... -0.7433, nC); Im = linspace( 0.1315,... 0.1322, nR); img = MB(Re, Im, imax); fprintf('%5d %.3f ',N,toc); end end | def main(): imax = 255 for N in [500,1000,2000,5000]: T_s = time.time() nR, nC = N, N Re = np.linspace(-0.7440, -0.7433, nC) Im = np.linspace( 0.1315, 0.1322, nR) img = MB(Re, Im, imax) print(N, time.time() - T_s) if __name__ == '__main__': main() |
14.2.2 A 2D Finite Element Solver
Many excellent finite element (FE) packages are available for Python. Industrial-strength applications include deal.II2, FEniCS3, SfePy4, and Code-Aster.5 These are substantial projects with hundreds of thousands of lines of source code developed by many domain experts.
- 1.
Reads text files of triangular element and 2D nodal coordinate data created by the triangle [4] program
- 2.
Creates rod elements from the triangle edges
- 3.
Computes stiffness and mass matrices for each rod element, then inserts these into sparse global stiffness and mass matrices, K and M
- 4.
Computes modes of vibration of the unconstrained model by solving the generalized eigenvalue problem Kx = λMx
The K produced in step 3 is exceptionally sparse; a typical mesh of rod elements derived from triangle’s output leaves on average of just 14 non-zero terms per row or column. M is a diagonal matrix. As a result, a million degree of freedom models can be processed quite easily with 8 GB of memory. The names of the Python and MATLAB finite element source files appear in Appendix C; the source files themselves are available on the book's Github repository.6
The mesh from beam.2.ele and beam.2.node, for example, looks like this:

The last pair of files, beam.5.ele and beam.5.node, are 32 MB and 28 MB and define a mesh with more than a million degrees of freedom.
14.3 Reference Hardware and OS
2015 Dell XPS13 laptop
4 cores of i5-5200U CPU @ 2.2 GHz
8 GB memory
Ubuntu 20.04
MATLAB 2020b
Anaconda Python 2020.07
While the Python code can easily run on faster cloud-hosted hardware, the MATLAB code, being license-locked to this machine, cannot.
14.4 Baseline Performance
Performance for the reference programs shown in Section 14.5.2 and Appendix C appears in the following for a variety of problem sizes.
14.4.1 Mandelbrot Set Performance
MATLAB does well on this problem as it runs three times faster than the Python version. Table 14-1 shows elapsed times for a variety of N × N image sizes.
The larger values of N may seem excessive, but their inclusion will be apparent once we begin applying optimization techniques.
14.4.2 FE Solver Performance
Execution time in seconds for original Mandelbrot programs
N | MATLAB | Python |
|---|---|---|
500 | 1.3 | 4.2 |
1000 | 4.4 | 17.1 |
2000 | 17.7 | 67.4 |
5000 | 112.5 | 420.0 |
The third stage combines floating-point computations for element matrix generation and sparse matrix creation. The final stage, computing the smallest six eigenvalues and corresponding eigenvectors of the sparse matrices, is dominated by floating-point computation.
CPU time and memory use for baseline finite element solver
Model | Degrees of Freedom | Stage | MATLAB | Python | ||
|---|---|---|---|---|---|---|
Seconds | Peak GB | Seconds | Peak GB | |||
beam.4 | 99,324 | Read files | 5.0 | 0.4 | ||
Triangle → rod | 8.2 | 2.1 | ||||
Assemble K, M | 6.8 | 6.5 | ||||
Eigensolution | 2.9 | 2.5 | ||||
Total | 22.9 | 1.0 | 11.9 | 0.5 | ||
beam.5 | 1,025,250 | Read files | 48.4 | 4.1 | ||
Triangle → rod | 84.6 | 26.5 | ||||
Assemble K, M | 70.0 | 68.9 | ||||
Eigensolution | 43.9 | 55.4 | ||||
Total | 240.2 | 7.1 | 157.1 | 5.4 | ||
Python code outperforms MATLAB on the first three stages—and the total solution time—but MATLAB’s eigensolution is notably faster. Reading model data from text files in particular is ten times faster in Python than MATLAB. Python also uses considerably less memory than MATLAB.
14.5 Profiling Python Code
The first step to any performance boosting attempt is measuring where code is slow. Sometimes, such spots are obvious and one can wrap simple timing statements, as done for the preceding FE solver, at strategic locations to assess the effectiveness of subsequent code refinements. For fine-grained results though, we need additional profiling tools.
- 1.
Results are coarse; resolution is at the level of functions. This obscures individual performance-killing lines.
- 2.
The text table can be difficult to interpret for large programs.
- 3.
Only CPU use is profiled; there are no options to profile memory use.
Python IDEs such as Spyder and PyCharm, like MATLAB’s IDE, have integrated profiling features, but the Python versions are based on cProfile and thus only give function-level resolution. MATLAB’s IDE can show profiling results for individual lines. Per-line results are indispensable for performance tuning, so we turn to tools that do not come with Anaconda and must be installed separately.
14.5.1 Scalene
Scalene [1] is a low overhead sampling profiler that additionally reports GPU use (if a GPU is detected), memory copy metrics, and memory consumption—all at a per-line level.
Scalene is unique among Python code profilers for several reasons. Its primary killer feature is stratifying CPU results on each line to time spent in pure Python, time spent in underlying compiled libraries (referred to as “native” time), and system time (for I/O and operations not related to the code). This separation helps answer the implied question of what to do about a slow line of code. If the bulk of time is in pure Python, there might be a way to rewrite the code to call a faster library function. On the other hand, if most of the time is taken by an underlying library or the system, there may be less opportunity for improvement. Scalene also works with multiple threads and processes.
Lines 8 and 9 are shown to be the hot spots, consuming nearly 90% of the solution time. The memory results on the other hand are counterintuitive because peak use is shown to happen on a line that simply multiplies and adds complex scalars.
The portion of profile.html showing the single most expensive line of code—12% overall CPU time spent returning an element stiffness matrix—looks like this in a browser:

Interestingly, the scalene results suggest the time was spent copying memory rather than performing computations.
14.5.2 Austin and FlameGraph
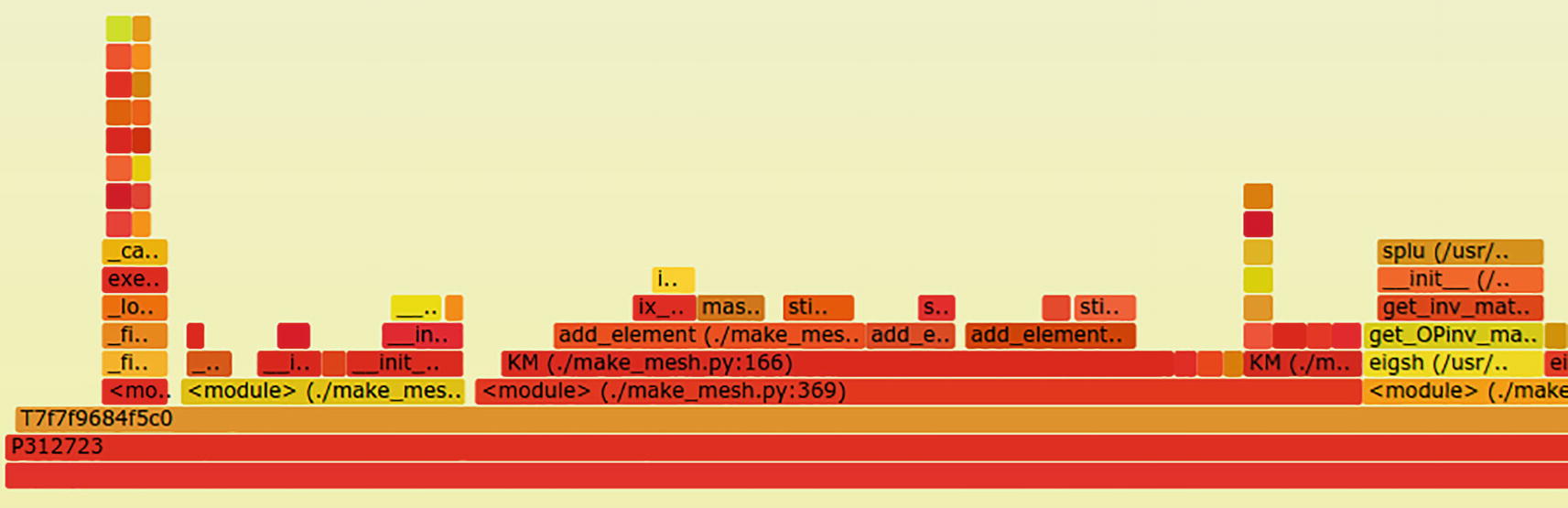
Austin 8 is another sampling profiler. Like scalene, it adds little overhead, requires no change to the code being profiled, and can send results to other metrics tools such as FlameGraph9 for graphical display. (MATLAB’s profiler also displays timing results as FlameGraphs, although with a slate gray color scheme instead of red/orange/yellow.)
FlameGraphs represent the call stack vertically, with the main program at the bottom. The width of each bar represents the amount of time spent at a particular function in MATLAB or line of code with austin; hot spots in the code appear as the widest bars. The left-to-right arrangement of bars is arbitrary and does not indicate chronological execution sequence. Bar colors also are arbitrary. Vertical arrangement is significant: code represented by a bar calls the code in the bars immediately above it. The lowest bar is, naturally, the widest as it represents the program’s main function entry point. Recognizable function names generally appear at the third or fourth bars from the bottom.
The --minwidth 10 switch to FlameGraph excludes entries that would leave a bar fewer than 10 pixels wide. Without it, the graph would be cluttered with entries having inconsequential contributions that make it harder to interpret. Raise or lower this pixel width value to produce the level of resolution that interests you. FlameGraph’s output is an SVG file which can be viewed with a web browser. The image

shows the bulk of compute time is spent in function nIter() at lines 8 and 9. Recall from Section 14.2.1 that nIter()’s implementation is
The computational effort at lines 8 and 9 happens with the statements z = z*z + c and if abs(z) > 2.
The same profiling command run against the finite element solver for the beam.4 case produces a more complex plot.
14.6 Multicore Computation with multiprocessing
Python has a threading module which leads one to believe it can fork work off to multiple threads. It can, but is only effective for I/O events waiting to proceed. Generic computations submitted this way are blocked so that only one thread runs at a time, which renders it pointless for non-I/O tasks. To run arbitrary code simultaneously on a computer’s multiple cores, you’ll need to use another of Python’s standard modules, multiprocessing .
The most common way to use multiprocessing is to set up a pool of workers—generally the number of cores you want to run on—then submit functions that are to run in parallel to the pool.
The following code shows one way to run the Mandelbrot computations on three cores with multiprocessing. Work is subdivided across cores by stepping through rows of the Im array in strides equal to the number of cores we’ll employ. In our case, we’ll set n_workers = 3 so process 0 gets rows 0, 3, 6, …; process 1 gets 1, 4, 7, …; and so on; this is done with the line Im_subset = Im[i::n_workers].
The highlighted code shows the code modifications applied to use the multiprocessing module :
The loop at lines 35–38 finishes quickly because the functions are submitted to the worker pool asynchronously. Computations don’t begin on the multiple cores until the .get() method is invoked for each submitted function on line 40.
Execution time in seconds for scalar vs. vector Mandelbrot implementations
N | MATLAB 1 Core | Python 1 Core | Python multiprocessing + 3 Cores |
|---|---|---|---|
500 | 1.6 | 4.2 | 3.0 |
1000 | 5.8 | 17.1 | 11.4 |
2000 | 23.2 | 67.4 | 41.6 |
5000 | 145.1 | 420.0 | 250.0 |
Better options lie ahead, so for the sake of space I’ll omit multiprocessing results from future benchmark results.
14.7 Vectorization
A well-known optimization technique for both MATLAB and NumPy is to write vectorized code—code that performs operations on entire matrices rather than on indexed terms within them. When all terms in the matrices require the same set of operations, vectorization can often yield a performance boost ranging between 10x and 60x over scalar code using explicit loops.
An interesting characteristic of the Mandelbrot set is the amount of computation varies widely across the solution domain. It isn’t clear that vectorization will help performance because the slowest-converging terms govern the speed for the entire region. The only way to know for sure is to implement the solution in vector form and then compare performance.
MATLAB: | Python: |
|---|---|
% file: code/hpc/MB_vectorized.m main() function [img]=nIter(c, imax) [nR,nC]= size(c); z = complex(zeros(nR,nC), ... zeros(nR,nC)); img = zeros(nR,nC,'uint8'); Idx = ones(nR,nC,'logical'); for i = 0:imax-1 z(Idx) = z(Idx).*z(Idx)+ ... + c(Idx); New = (real(z).^2+ ... imag(z).^2 <= 4); if ~any(New,'all') break end img(New) = i; Idx = Idx & New; end end function [] = main() imax = 255; for N = [500 1000 2000 5000] tic nR = N; nC = N; Re = linspace(-0.7440,... -0.7433, nC); Im = linspace( 0.1315,... 0.1322, nR); [zR, zI] = meshgrid(Re,Im); z_init = complex(zR,zI); img = nIter(z_init, imax); fprintf('%5d %.3f ',N,toc); end end | #!/usr/bin/env python3 # file: code/hpc/MB_vectorized.py import numpy as np import time def nIter(c, imax): nR,nC = c.shape z = np.zeros_like(c) img = np.zeros(z.shape, dtype=np.uint8) Idx = np.ones(z.shape, dtype=np.bool ) for i in range(imax): z[Idx] = z[Idx]*z[Idx] + c[Idx] New = (z.real**2 + z.imag**2 <= 4) .reshape(nR,nC) if not np.any(New): break img[New] = i Idx *= New return img def main(): imax = 255 for N in [500,1000,2000,5000]: T_s = time.time() nR, nC = N, N Re = np.linspace(-0.7440, -0.7433, nC) Im = np.linspace( 0.1315, 0.1322, nR) zR,zI = np.meshgrid(Re,Im) z_init = zR + zI*(1j) img = nIter(z_init, imax) print(N, time.time() - T_s) if __name__ == '__main__': main() |
Execution time in seconds for scalar vs. vector Mandelbrot implementations
N | MATLAB Scalar | MATLAB Vector | Python Scalar | Python Vector |
|---|---|---|---|---|
500 | 1.6 | 1.7 | 4.2 | 1.3 |
1000 | 5.8 | 5.7 | 17.1 | 4.7 |
2000 | 23.2 | 24.6 | 67.4 | 19.3 |
5000 | 145.1 | crashes | 420.0 | 184.4 |
14.8 Cython
Cython10 is a Python-to-C compiler. Although it doesn’t implement the complete Python language, features which are not implemented are interpreted conventionally, just not compiled.
Translates portions of your Python to C and then compiles the C into an optimized shared object that can be loaded as a Python module
Provides an interface layer that makes it straightforward to call native C and C++ libraries
14.8.1 Python Compiled with Cython
- 1.
Copy functions from existing Python source files you wish to compile to new files that end with .pyx instead of .py. The file containing main() is not compiled and must remain in a .py file.
- 2.
Add C language type annotations to Python variables in the .pyx files where speed improvements are desired. If your code uses NumPy, also add a cimport line that mirrors the NumPy import.
- 3.
Create a setup file—a small Python program—that tells Cython which .pyx files to compile and optionally identify the compiler and compile and link flags to use.
- 4.
Run the setup file to compile your code.
Python, Baseline: | Python, with Cython Annotations: |
|---|---|
1 #!/usr/bin/env python3 2 # cython/mb/MB_orig.py 3 4 import numpy as np 5 import time 6 def nIter(c, imax): 7 8 9 10 z = complex(0, 0) 11 for i in range(imax): 12 z = z*z + c 13 if abs(z) > 2: 14 break 15 return i 16 17 def MB(Re, Im, imax): 18 19 20 21 nR = len(Im) 22 nC = len(Re) 23 img = np.zeros((nR, nC)) 24 for i,I in enumerate(Im): 25 for j,R in enumerate(Re): 26 c = complex(R, I) 27 img[i, j] = nIter(c, imax) 28 return img | 1 # cython/mb/MB_cython.pyx 2 cimport numpy as np 3 import numpy as np 4 import time 5 def nIter(double complex c, 6 long imax): 7 cdef int i 8 cdef double complex z 9 z = complex(0, 0) 10 for i in range(imax): 11 z = z*z + c 12 if z.real*z.real + z.imag*z.imag > 4: 13 break 14 return i 15 16 def MB(Re, Im, imax): 17 cdef int i,j 18 cdef double I, R 19 cdef double complex c 20 nR = len(Im) 21 nC = len(Re) 22 img = np.zeros((nR, nC), dtype=np.uint8) 23 for i,I in enumerate(Im): 24 for j,R in enumerate(Re): 25 c = complex(R, I) 26 img[i, j] = nIter(c, imax) 27 return img |
A setup file that works for the third step looks like this:
A typical invocation produces warnings, then new C source files, and, hopefully, a shared object named after the .pyx file. On my Linux machine, the shared object is MB_cython.cpython-38-x86_64-linux-gnu.so. Despite the long name, it is imported into Python with import MB_cython.
What have we gained for our efforts? A small driver program loads the compiled module and runs the cases:
For N = 1000, runtime drops from 17.1 seconds to just 1.85 seconds. The original Python code is 3x slower than MATLAB, but Cython enhancements have made Python 3x faster.
Python: | Python: |
|---|---|
13 if abs(z) > 2: | 13 if z.real**2 + z.imag**2 > 4: |
This single line refinement cuts the N = 1000 Python+Cython time from 1.85 to 1.01 seconds, and the MATLAB time, with an equivalent change, from 5.8 to 4.4 seconds.
14.8.2 Parallel for Loops with Cython
The core MATLAB product does not include the parfor parallel for loop command—that can only be found in MATLAB Coder or the Parallel Computing Toolbox. MATLAB implementations in this book are therefore limited to sequential for loops.
Cython has a prange() function that allows one to write parallel for loops. Under the hood, this prange() function is implemented via OpenMP and therefore inherits OpenMP restrictions. The Cython documentation shows trivial parallel for loop examples,11 but in practice, nontrivial loops require an inordinate amount of code tweaks to overcome compile error such as “Indexing Python object not allowed without gil,” “Constructing Python tuple not allowed without gil,” and “Coercion from Python not allowed without the GIL.”
Unless your code sections have elementary for loops, you will either need to spend a lot of time with the Cython documentation or avoid its prange(). The Pythran and Numba options for parallel for loops, described in Sections 14.9 and 14.10.1, are much easier to use.
14.8.3 Cython Performance
Execution time in seconds for Mandelbrot programs
N | MATLAB | Python Baseline | Python+ Cython |
|---|---|---|---|
500 | 1.3 | 4.2 | 0.25 |
1000 | 4.4 | 17.1 | 1.01 |
2000 | 17.7 | 67.4 | 4.03 |
5000 | 112.5 | 420.0 | 25.18 |
14.9 Pythran
Pythran [3] resembles Cython in that it creates a compiled binary module from a file of lightly annotated Python functions. Its primary advantage over Cython is that the required code modifications are implemented entirely as source code comments. This means Pythran-enhanced code is pure Python; the code will run identically, albeit slower, on a system that lacks the Pythran compiler. Another advantage is that for loop parallelization with OpenMP is implemented easily.
Pythran has disadvantages compared to Cython: Pythran supports a smaller subset of Python and then Cython. Some statements like with are not supported at all, and others, like f-strings, have limited support. Another drawback (as of late 2021) is the project’s documentation website12 lacks sufficient examples. To get a comprehensive sense of the different forms the #pythran directives can take, the best option is to download the project’s source code and then study the many examples in pythran/tests/cases.
14.9.1 Examples of Signature Comments
Pythran function signature types
Scalar Type or Data Container | Pythran Type Designation |
|---|---|
String | str |
Boolean | bool |
Unsigned 8-bit integer | uint8 |
Unsigned 16-bit integer | uint16 |
Unsigned 32-bit integer | uint32 |
Unsigned 64-bit integer | uint64 |
32- or 64-bit integer | int |
String or integer | str or int |
8-bit integer | int8 |
16-bit integer | int16 |
32-bit integer | int32 |
64-bit integer | int64 |
32- or 64-bit float | float |
32-bit float | float32 |
64- or 128-bit complex | complex |
128-bit complex | complex128 |
List of integers | int list |
List of lists of integers | int list list |
List of floats | float list |
1D array integers | int[] or int[:] |
1D array floats | float[] or float[:] |
2D array integers | int[][] or int[:,:] |
2D array floats | float[][] or float[:,:] |
Dict of strings to integers | str : int dict |
Tuple of two integers | (int, int) |
The comment line preceding the definition of a function Fn() which takes a string, a list of integers, and a 2D array of 32-bit floats would therefore be
14.9.2 Python Compiled with Pythran; Parallel for Loops
As with Cython, the Mandelbrot functions nIter() and MB() are separated to their own file for compilation. Only three comment lines are needed to enable Pythran to compile our code:
The first two comments define signatures (excluding return type, which Pythran figures out on its own) of the functions on the following lines, and the third comment designates the for i,I loop to be parallel.
Among other things, Pythran needs the C header file to the basic linear algebra subroutines (BLAS). If your compile command shows
and does not create a shared object file, you’ll need to download and install development headers for BLAS suitable to your OS. On Ubuntu, for example, this is resolved with apt install libopenblas-dev. Even after installing the headers, you may still see the “fatal error” even though the shared object file is created successfully.
To suppress OpenMP parallelism of the for loop, either remove the #omp parallel for comment from the source or remove the -fopenmp switch from the compile command.
The pythran command produces a compiled shared object file named after the input source file (MB_pythran.cpython-38-x86_64-linux-gnu.so on my computer). The driver program to run the Pythran-compiled module is identical to the driver used for the Cython-compiled module. The only difference is the name of the module being loaded—import MB_pythran instead of import MB_cython:
14.9.3 Pythran Performance
Execution time in seconds for Mandelbrot programs
N | MATLAB 1 Core | Python Baseline 1 Core | Python+ Cython 1 Core | Python+ Pythran 1 Core | Python+ Pythran 4 Cores |
|---|---|---|---|---|---|
500 | 1.3 | 4.2 | 0.25 | 0.10 | 0.05 |
1000 | 4.4 | 17.1 | 1.01 | 0.40 | 0.15 |
2000 | 17.7 | 67.4 | 4.03 | 1.59 | 0.62 |
5000 | 112.5 | 420.0 | 25.18 | 9.93 | 3.88 |
14.10 Numba
Numba13 is a just-in-time (JIT) compiler for Python with emphasis on accelerating numeric calculations. Like Cython and Pythran, Numba also allows one to write parallel for loops.
Also like Cython and Pythran, code modifications needed to use Numba mostly deal with type definitions. These changes are pure Python. Moreover, there are no externally generated source files, languages, or compilers to deal with. Another benefit is that the functions to be accelerated may coexist with unaltered functions—including the main program—they need not be sequestered to a separate file. For these reasons, Numba-enhanced code is more convenient to use and deploy than Cython- or Pythran-enhanced code.
- 1.
Include an import to the numba module, pulling in the jit decorator, numeric data types to be used, and optionally the prange function to write parallel for loops.
- 2.
Apply the @jit() decorator to each function that is to be sped up. The arguments to this decorator are the function’s signature, that is, its return type, and the types of each input argument. The decorator also takes additional keyword arguments such as nopython and fastmath.
- 3.
Optionally, rewrite for loops using the Numba parallel range function prange().
The Mandelbrot program enhanced with Numba looks like this:
The @jit() decorators to nIter() and MB() may look daunting, but their components are straightforward. nIter() returns a scalar uint8. Inputs are a double-precision complex scalar—a complex128—and a conventional Python integer scalar, an int64. Thus, nIter()’s signature is uint8(complex128, int64). The keyword arguments nopython and fastmath are explained in Section 14.10.2.
The MB() function returns a 2D array of uint8 which is expressed in Numba as uint8[:,:]. Inputs are a pair of 1D double-precision floating-point arrays and an integer scalar. Therefore, MB()’s signature is uint8[:,:](float64[:],float64[:], int64). MB()’s decorator has an additional keyword argument, parallel=True, to denote the use of the parallel range function prange().
14.10.1 Parallel for Loops with Numba
Numba’s prange() function resembles Cython’s. Writing a parallel for loop amounts to replacing the existing for i in ... construct with for i in prange(N) where N is an integer scalar. The requirement that the loop iterate over a range of integers may mean the loop needs small modifications if the existing loop iterates over other objects.
Python, Baseline: | Python, Numba Parallel for: |
|---|---|
for i,I in enumerate(Im): | for i in prange(len(Im)): I=Im[i] |
Numba handles the distribution of work in the body of the loop to different cores as well as aggregation of results for variables shared between simultaneous computations.
14.10.2 Numba Keyword Arguments nopython, fastmath
The @jit() keyword argument nopython, most often seen set to True, instructs the JIT compiler to skip the Python interpreter completely and use only compiled code. This is the recommended setting and even has its dedicated decorator: @njit() is the same as @jit(...,nopython=True). This keyword should only be set to False if the compilation fails.
The keyword argument fastmath enables unsafe operations14 such as assuming inputs are never NaNs or Infs and allows the compiler to reorder floating-point instructions. Naturally, compare output of your code with and without fastmath=True to ensure your results are not compromised.
14.10.3 Numba Performance
Performance of the Numba-enhanced Mandelbrot program, shown in Table 14-8, is nothing less than astonishing. With Numba, pure Python code exceeds the speed of Cython- and Pythran-compiled modules.
14.10.4 Numba Limitations
Execution time in seconds for Mandelbrot programs
N | MATLAB 1 Core | Python Baseline 1 Core | Python+ Cython 1 Core | Python+ Pythran 1 Core | Python+ Pythran 4 Cores | Python+ Numba 1 Core | Python+ Numba 4 Cores |
|---|---|---|---|---|---|---|---|
500 | 1.3 | 4.2 | 0.25 | 0.10 | 0.05 | 0.09 | 0.04 |
1000 | 4.4 | 17.1 | 1.01 | 0.40 | 0.15 | 0.36 | 0.15 |
2000 | 17.7 | 67.4 | 4.03 | 1.59 | 0.62 | 1.44 | 0.62 |
5000 | 112.5 | 420.0 | 25.18 | 9.93 | 3.88 | 8.95 | 3.71 |
Unless one employs Numba’s Wrapper Address Protocol,15 functions decorated by @jit may call only a subset of NumPy and standard library functions.
and a call to XYZ() exists in a function decorated by @jit, it means Numba cannot compile this function. In this case, your options are to simplify the function until it can be compiled, revert to the multiprocessing module (Section 14.6), or use dask, to be covered in Section 14.13.
14.11 f2py
f2py is a command-line utility that comes with NumPy. It allows one to create compiled Python modules from specially annotated Fortran code far more easily than with any other binary interface tool. f2py brings two important benefits: it can create Python interface modules to legacy Fortran code, and it can give a substantial computational boost to Python functions that are rewritten in Fortran.
The following Fortran code implements the nIter() and MB() functions seen early in the Mandelbrot implementations. The five cf2py lines defining the input and output arguments are all f2py needs to create the Python interface, including documentation.
generates Python/Fortran interface code, compiles it and mb.f listed earlier with the system’s Fortran compiler, then links these into a compiled Python module, MB_fortran (the full name of this module is MB_fortran.cpython-38-x86_64-linux-gnu.so on my computer).
In addition to writing the interface code, f2py also generates documentation for each function:
This driver program loads the Fortran-compiled module and then runs our benchmark cases:
Execution time in seconds for Mandelbrot programs
N | MATLAB 1 Core | Python Baseline 1 Core | Python+ Cython 1 Core | Python+ Pythran 1 Core | Python+ Numba 1 Core | Python+ f2py 1 Core |
|---|---|---|---|---|---|---|
500 | 1.3 | 4.2 | 0.25 | 0.10 | 0.09 | 0.10 |
1000 | 4.4 | 17.1 | 1.01 | 0.40 | 0.36 | 0.40 |
2000 | 17.7 | 67.4 | 4.03 | 1.59 | 1.44 | 1.60 |
5000 | 112.5 | 420.0 | 25.18 | 9.93 | 8.95 | 10.05 |
14.12 Recipe 14-1: Accelerating MATLAB with Python on a Single Computer
Use parallel for loops (needs the Parallel Computing Toolbox or the MATLAB Coder).
Write MB() and nIter() in C, C++, or Fortran, add headers and call mex API functions, then create a compiled MATLAB extension with the mex command.
Call performance-enhanced Python modules.
Here, we’ll explore the last option by calling the Python-based Cython, Pythran, Numba, and f2py accelerated solutions from MATLAB. In all cases, the solution includes the overhead of converting MATLAB inputs to Python variables and converting the Python return value to a MATLAB variable. Timing results, shown in Table 14-10, do not include Python module load times within MATLAB when the MATLAB programs start.
14.12.1 Compile Python Modules in a MATLAB-Friendly Virtual Environment
Three of the next four sections, Sections 14.12.2, 14.12.3, and 14.12.5, use your computer’s C, C++, or Fortran compiler to build binary Python modules. On macOS, this means the Xcode development library must be installed. On all operating systems, it is important to work in a conda environment like matpy (Section 2.5.1) whose shared libraries are consistent with MATLAB’s. The compiled modules won’t load in MATLAB otherwise.
14.12.2 MATLAB + Cython
This driver loads the MB_cython module compiled in Section 14.11.
14.12.3 MATLAB + Pythran
This driver loads the MB_pythran module compiled in Section 14.9.
14.12.4 MATLAB + Numba
This driver loads the parallel for loop MB_numba_prange module of Section 14.10.
14.12.5 MATLAB + f2py
This driver loads the MB_fortran module compiled in Section 14.11.
14.12.6 MATLAB + Python Performance Results
Execution time in seconds for MATLAB-based Mandelbrot programs enhanced by Python
N | MATLAB 1 Core | MATLAB+ Cython 1 Core | MATLAB+ Pythran 4 Cores | MATLAB+ Numba 4 Cores | MATLAB+ f2py 1 Core |
|---|---|---|---|---|---|
500 | 1.3 | 0.29 | 0.05 | 0.05 | 0.11 |
1000 | 4.4 | 1.02 | 0.21 | 0.19 | 0.41 |
2000 | 17.7 | 4.21 | 0.69 | 0.58 | 1.59 |
5000 | 112.5 | 26.02 | 4.10 | 3.93 | 10.13 |
While the single-core f2py performance is modest compared to multicore Numba performance, f2py offers a secondary benefit the other accelerants lack: with f2py you can create a Fortran interface to MATLAB much more easily than you can with MATLAB’s own mex utility.
14.13 Distributed Memory Parallel Processing with Dask
Previous sections showed that distributing work across a computer’s multiple cores can give significant performance increases. We can do even better—much better—by distributing work across multiple computers. Several Python modules, among them Ray,16 dispy,17 and dask,18 make it easy to run a Python program that farms work out to many computers.
Dask has advantages over the other modules because it also provides an out-of-core data container, the dask array, which enables computation with arrays too large to fit in a computer’s memory, similar to MATLAB’s “tall arrays.” Additionally, dask is backed by Coiled19 which offers commercial support and cloud computing for dask jobs. Coiled offers 1000 hours of free CPU hours on up to 100 cores each month for dask jobs, an attractive proposition for individuals who lack access to high-end compute clusters.
Dask will be used to demonstrate distributed memory parallel processing in the following sections. The main dask concepts are covered in Section 14.13.2, but they likely won’t mean much without a detailed example. Such an example follows in Section 14.13.3 where we tackle an embarrassingly parallel and computationally intensive problem—summing prime factors of many numbers. For starters, we’ll just use multiple cores of a single computer.
The real fun doesn’t begin until we use multiple computers. Before we can run dask on multiple computers, we have to launch background scheduler and worker jobs on those computers; the details of that are explained in Section 14.13.4. Once the background machinery is in place, in Section 14.13.5 we’ll rerun the prime factor summation problem on a collection of computers and see some nice speed-ups.
Memory-intensive jobs introduce additional complications. In Section 14.13.6, we’ll generate a gigapixel image of the Mandelbrot set we computed earlier in Section 14.2 using a collection of computers with only 1 GB of memory. Needless to say, we have to take precautions to avoid crashes.
Finally, in Section 14.13.7, we’ll combine our accumulated experience with dask to solve a problem closely resembling a real-world application. We’ll solve a transient dynamic finite element problem with a half million degree of freedom model using a frequency domain solution spanning thousands of frequencies. Such problems can take days on individual computers, but we’ll get solutions—from either Python or MATLAB—in less than 15 minutes using Coiled’s cloud.
14.13.1 Parallel MATLAB
Like Python, MATLAB can run on distributed memory clusters and on clusters in the cloud. The most direct way to do so is to use the Parallel Computing Toolbox. Other options include using MATLAB Coder or the MATLAB Compiler to create a stand-alone executable that can be sent to remote computers.
The MathWorks also offers MATLAB Online, and through it, MATLAB in the Cloud, but its capabilities are limited to those enabled in your MATLAB license. In other words, if you don’t have a license for the Parallel Computing Toolbox or for cloud use, you won’t be able to run your m-files on multiple computers in the cloud.
As mentioned earlier (Section 1.3), this book’s scope is limited to the core MATLAB product which precludes comparisons of pure MATLAB cloud solutions to their Python equivalents. Nonetheless, we’ll see in Section 14.14 that hybrid MATLAB/Python code runs quite effectively on private clusters as well as Coiled’s cloud.
14.13.2 Dask Execution Paradigm and Performance Expectations
A cluster is a collection of computers the job owner can access. The computers in the cluster must have a consistent Python installation with the dask and distributed modules. The cluster can actually be as small as just the single computer you are currently working on, in which case dask jobs are distributed across the computer’s cores, or it can be a large HPC compute cluster, optionally with its own job scheduler like LSF, Slurm, or PBS. In the latter case, the user must have the same account on all computers, be able to ssh between computers without a password, or be able to submit jobs to the computers through a separate job scheduler.
dask-scheduler and dask-worker are background jobs that run on the computers of the cluster. An instance of the scheduler runs on one of the computers, while a worker instance runs on each computer. These processes have to be started manually with the dask-ssh command or will be started and managed by a job scheduler–specific configuration file.
A client is a Python variable created by connecting to the dask scheduler process.
A delayed task is a Python function plus its calling arguments that is not evaluated immediately but instead added to a list of tasks that will be executed later.
A dask-enabled Python program populates a list with delayed tasks and then passes this list to dask.compute(). This function hands tasks off to the dask scheduler which in turn sends each task to the next idle worker (likely running on a different computer). After a worker receives a task, the worker calls the user-provided function defined for the task with the user’s arguments, then sends its return values back to the scheduler. dask.compute() gets the task return values from the scheduler and appends these to its list of results.
Our program sets up the function calls to be made in parallel, and dask handles everything else—assigning these calls to processors, serializing and then sending input arguments over the network, invoking the calls on remote computers, and finally serializing and sending the return arguments back to the computer which launched the jobs.
Load balancing strategy
Volume of data passed to or received from remotely executed functions
Network speed
Uniformity of computer resources
Most importantly, dask decides how and when to transmit data. Code developers are generally happy to offload this burden even if the interleaving of compute/transmit steps isn’t ideal, yet may be disappointed by the ensuing parallel efficiency. The adage “your mileage may vary” is ever true in parallel processing.
This all sounds complicated (and under the hood, it is!). How exactly do we set up and run a distributed memory parallel program? What can be done to make the code run faster? The only way to make sense of this is to work through examples.
14.13.3 Example 1: Sum of Prime Factors on One Computer
MATLAB: | Python: |
|---|---|
% code/dask/prime_seq.m A = 2; B = 10000000; incr = 1; [S, dT] = my_fn(A, B, incr); fprintf('A=%d B=%d, %.3f sec ',... A, B, dT); fprintf('S=%ld ', S); function [S, dT]=my_fn(A, B, incr) tic; S = 0; for i = A:incr:B-1 S = S + sum(unique(factor(i))); end dT = toc; end | #!/usr/bin/env python3 # code/dask/prime_seq.py from sympy import primefactors import time def my_fn(a, b, incr): Ts = time.time() s = 0 for x in range(a,b,incr): s += sum(primefactors(x)) return s, time.time() - Ts def main(): A = 2 B = 10_000_000 incr = 1 S, dT = my_fn(A, B, incr) print(f'A={A} B={B}, ' f'{dT:.4f} sec') print(f'S={S}') if __name__ == "__main__": main() |
MATLAB: | Python: |
|---|---|
>> prime_seq A=2 B=10000000, 682.681 sec S=5495501355056 | > ./prime_seq.py A=1 B=10000000, 519.531 sec S=5495501355056 |
Calls to the compute-intensive function my_fn() are independent and can be called in any order, or even simultaneously. We’ll do exactly that with dask, using three cores of the local machine. To spread the load evenly, we merely need to offset the starting counter by the job number and let the call to range(a,b,incr) in my fn() scatter the numbers to factor across processors. For example, if we compute prime factors for numbers between 2 and 20 and want to spread the work evenly over three jobs, the assignments will be
or equivalently in MATLAB
The dask-enabled version of the prime factor summation program on the local computer, splitting up the work to three tasks that are to run simultaneously, looks like this:
When the program runs, the call to Client(’127.0.0.1:8786’) at line 16 attempts to connect to a dask scheduler running on the localhost and listening on port 8786. (Line 17, currently commented out, will be discussed in Section 14.13.5.) If such a scheduler isn’t running, the program fails after 30 seconds with
Line 21 defines n_jobs, our counter for the number of tasks to create. At a minimum, to take full advantage of your hardware, this should equal or exceed the number of cores available in your cluster. If tasks vary in duration and you have many of them, setting n_jobs to a value much greater than the number of cores will help balance the load across cores more equitably.
Lines 24–26 add delayed tasks to the list tasks which was initialized at line 18. Each task is a call to my_fn() with arguments A+i, B, incr.
The computations are performed at line 27 when dask hands the list of delayed tasks to the scheduler to farm out to workers. Return values from each call appear in the list results which will have n_jobs entries.
Finally, lines 29–32 aggregate the partial sums of primes into a total value.
then passing this file name as an argument to the dask-ssh command:
This starts a worker process on each computer defined in the file, plus a scheduler process on the computer defined on the first line. Of course, in this case, all these background processes run on the local computer.
With the scheduler and workers running in the background, we can now run the dask-enabled prime factor summation program prime_dask.py. It runs faster than the sequential version, but not by much:
Performance disappoints for two reasons. First, the workload is clearly imbalanced since one job took around 200 seconds, while the other two took more than 320. Evidently, terms of the sequence 3, 6, 9 … can be factored much more rapidly than terms in 2, 5, 8 … and 4, 7, 10 …—who knew? The second reason is less obvious. It is that the sum of individual core times, 328.0 + 206.2 + 327.7 = 861.9 seconds, is 66% higher than the single-core time of 519.5 seconds. Dask seems to impose a severe overhead.
Three experiments shed light on the source of dask’s overhead. First, we’ll repeat the single-core runtime using the dask infrastructure with only one worker process, meaning only one CPU core will receive work. A scheduler is always needed so that must also run in the background. Performance in this case is reasonable since dask added less than 7% overhead (555.0 seconds vs. 519.5 seconds):
Next, we’ll spin up two more dask worker processes, but still only submit one job:
This time, overhead doubled to 13% even though the additional two workers are merely standing by, waiting for work that never comes.
Finally, we’ll again use just one worker but give it three tasks where the ranges are separated by strides of three, just as when these ranges are given to three workers.
The cause of the overhead must be related to how the work is split up. While there’s no obvious remedy to improve this situation, dask does have nice performance monitoring and reporting tools to help diagnose performance issues. One of these tools is the web-based real-time cluster statistics seen on the scheduler host’s port 8787, http://127.0.0.1:8787 in our case. Another is a report generator that can be invoked directly from our program. We merely need to import the performance_report function from dask.distributed and then wrap the dask-specific code in a context manager that calls performance_report to get a rich HTML file graphically showing many different aspects of the parallel job.
While the reporting tool is easy to use, comprehending the output is less so.
14.13.4 Setting Up a Dask Cluster on Multiple Computers
Running dask on a single computer is a useful first step during code development and initial troubleshooting. It fails to satisfy on the performance front, however. To really benefit from dask’s power, we’ll need to run it on many computers.
Compatible (preferably identical) Python installations
The same path to the Python executable
The same account name for the user setting up and using the cluster
Uniform bidirectional, key-based ssh access across all computers for the user account
Same ssh port
Firewall rules open to allow ssh and the dask scheduler and metrics ports (8786 and 8787 by default)
Setting up a distributed dask cluster with dask-ssh is extremely insecure! Any user who knows the scheduler’s IP address and port can connect to your cluster and run arbitrary Python code under the account—namely, yours—that launched the workers.
The correct way to set up a secure, multi-user dask cluster is to configure a dask gateway21 which implements an authentication layer.
14.13.5 Example 2: Sum of Prime Factors on Multiple Computers
Once the computers in the dask cluster are running a scheduler and workers, we can begin to enjoy significant performance increases. This section uses a collection of 18 virtual machines running on DigitalOcean’s22 cloud infrastructure. Each VM runs their lowest tier “droplet” which has 1 GB of memory, 1 CPU core @ 2.5 GHz, and 25 GB of storage. The VMs run Ubuntu 20.04.3 LTS, have Anaconda 2021.05 installed, and use the matpy conda environment (Section 2.5.1).
where DigitalOcean_VMs.txt has the IP addresses of all 18 computers. The only change needed to prime_dask.py (code listing in Section 14.13.3) is replacing the call to Client(127.0.0.1:8786) with the IP address of the VM running the scheduler, in other words, the first entry in DigitalOcean_VMs.txt. Line 17 shows what this might look like.
The sequential version of the program takes 718.057 seconds on a single VM, so the 18 cores gave a 16.5 × speed-up.
14.13.6 Example 3: A Gigapixel Mandelbrot Image
In Section 14.10.3, we used Numba to reduce the time needed to compute a 5000 x 5000 Mandelbrot image from 420 seconds to about 9 seconds on one core. Let’s up the stakes and use our dask cluster of 18 single-core VMs to compute an image with 35,000 x 35,000—1.2 billion—pixels. Each pixel will be represented by a single byte which is the number of iterations needed for the z equation to converge. Both MATLAB and Python running on a computer with at least 8 GB of memory can easily store such an image; MATLAB can even display it with imshow() (matplotlib’s imshow() crashes with an image this size).
Our gigapixel image will be 72, or about 50x larger than our 5k image so a single Numba-powered core should take about 440 seconds to generate it. Then, again, our dask cluster has 18 computers, so if we can load balance the jobs well, that time will come down by a lot. Let’s give it a shot.
One strategy for load balancing the Mandelbrot set is to assign rows or columns to workers in a round-robin fashion. Here’s what the dask + Numba solution looks like with that strategy:
In other words, the workers crashed because they ran out of memory. While the computer submitting the job has 8 GB of memory, the workers only have 1 GB, some of which is taken by the operating system and the dask worker processes.
Rather than have each remote computer accumulate all results for the jobs it was assigned, we’ll need to harvest results from the remote computers as the run progresses. One way to do that is to split the jobs into groups and then call the .compute() method after each group is submitted. The revised version of the following Mandelbrot program does just that. An additional modification is implemented to improve parallel efficiency: instead of sending the real and imaginary arrays to the remote workers, we’ll just send the starting and ending values and let the workers figure out the array terms on their own. Finally, to simplify reassembly of the final image, we’ll have each worker tell us the row indices it worked on in addition to its image slices.
Launched on Home Computer: | Launched on DigitalOcean Computer: |
|---|---|
chunk 0 took 7.500 sec chunk 1 took 5.564 sec chunk 2 took 4.944 sec chunk 3 took 4.873 sec chunk 4 took 4.978 sec chunk 5 took 5.834 sec chunk 6 took 5.280 sec chunk 7 took 4.559 sec chunk 8 took 4.531 sec chunk 9 took 5.989 sec chunk 10 took 4.997 sec chunk 11 took 4.574 sec chunk 12 took 4.459 sec chunk 13 took 4.799 sec chunk 14 took 5.020 sec chunk 15 took 4.785 sec 83.715 35000 | chunk 0 took 7.929 sec chunk 1 took 2.427 sec chunk 2 took 1.955 sec chunk 3 took 1.851 sec chunk 4 took 1.808 sec chunk 5 took 1.806 sec chunk 6 took 1.812 sec chunk 7 took 1.817 sec chunk 8 took 1.805 sec chunk 9 took 3.032 sec chunk 10 took 3.456 sec chunk 11 took 2.697 sec chunk 12 took 2.612 sec chunk 13 took 2.114 sec chunk 14 took 1.842 sec chunk 15 took 1.777 sec 40.819 35000 |
My original estimate for solving the Numba-accelerated Mandelbrot set of this size on a single core of my home computer was 440 seconds, so the 83 seconds using 18 cloud-based computers represents a speed-up of 5.3. Disappointing, perhaps, but a clear demonstration that performance for problems involving substantial data transfers depends heavily on the network.
14.13.7 Example 4: Finite Element Frequency Domain Response
As in the multicore sections earlier, I’ll use a finite element model subject to a dynamic load to represent a more real-world distributed memory computing problem. Toy problems for summing prime numbers and computing the Mandelbrot set are instructional but don’t deal with complications that arise with large input sets.

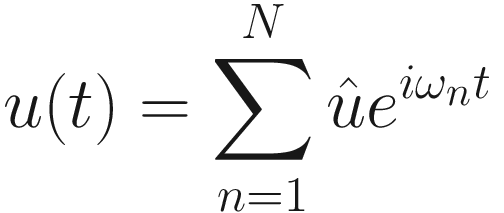

![$$ left[K+i{omega}_nC-{omega}_n^2M
ight]{hat{u}}_n=Pleft({omega}_n
ight) $$](https://imgdetail.ebookreading.net/2023/10/9781484272237/9781484272237__9781484272237__files__images__516169_1_En_14_Chapter__516169_1_En_14_Chapter_TeX_Equd.png)
where P(ω) is the Fourier transform of the load time history P(t). Our time domain second-order differential equation now becomes a collection of linear equations which are independent at each of the N frequencies ωn. The frequency band must be sufficiently wide to capture the full spectral content of the applied load, and the frequency interval small enough that all motion has been dampened to a quiescent state in the equivalent time domain.
In theory, if we had N processors, we could give each processor one frequency and get our solution  in the amount of time it takes to solve the system of equations just once. The time domain solution u(t) can then be recovered with an inverse Fourier transform of
in the amount of time it takes to solve the system of equations just once. The time domain solution u(t) can then be recovered with an inverse Fourier transform of 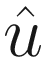 [2]. In reality, thousands of frequencies are needed for accurate solutions, and a few of us have access to that many processors. Also, the data volumes are substantial; the overhead of transmitting matrices to a processor so it can solve a system of linear equations just once is unlikely to be worthwhile.
[2]. In reality, thousands of frequencies are needed for accurate solutions, and a few of us have access to that many processors. Also, the data volumes are substantial; the overhead of transmitting matrices to a processor so it can solve a system of linear equations just once is unlikely to be worthwhile.
For our final example, we’ll use dask to solve a direct frequency response problem. This example is more representative of real workloads because, unlike the earlier problems, this one requires large amounts of input data to be sent to the workers.
14.13.7.1 A Notional Satellite Model
As a sample problem, we’ll model a satellite whose solar panel extension mechanism is to be released by an explosive bolt. The satellite has a delicate sensor in the middle. Our objective is to measure the deformation of the sensor’s mount as a result of the detonation.
After the last command, we’ll have a pair of files satellite.7.ele and satellite.7.node, that define a model with about 600,000 degrees of freedom that we’ll use for the analysis. The model will be fully constrained at the base of the adapter ring (the lowest horizontal edge) and loaded (meaning the location of the explosive bolt) at the elbow joint on the left. We’ll only save deformation at the few nodes that represent the sensor’s mount which is the small stem supporting the central cutout. The following figure is of the second refinement of the model, satellite.2, which has about 7600 degrees of freedom (roughly 1% of our 600k DOF model).

Time and frequency domain plots of the explosive bolt’s load history look like this:

14.13.7.2 An Outline of the Problem
Which part should be done sequentially on the parent (also referred to as the client, or driver) program and which should be sent to the remote workers? A couple of strategies come to mind: (1) send the model data and force history files to the remote computers and have them solve the entire problem from beginning to end but only portions of the frequency loop, or (2) do everything before the frequency loop on the client, then send the matrices and load history to the remote computers to run their portions of the frequency loop.
Both approaches are feasible, especially since the steps before the frequency loop can be done relatively quickly on a single computer.
Say you’re tackling this problem in MATLAB where you already have the entire solution coded in m-files, but it runs too slowly on your computer. You can use Python and dask to distribute the work to a cluster, but the remote computing part has to be written in Python. Now the decision boils down to (1) translate the entire application to Python or (2) write a linear equation wrapper in Python. While I like Python, I like to avoid extra work even more. In this situation, I’d definitely leave the majority of the direct frequency response program in MATLAB and only do the linear algebra part in Python.
14.13.7.3 Sending Large Inputs to Remote Computers
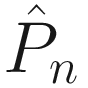 ; and the list of degrees of freedom at which we want the response. Unlike the examples for prime number summation and Mandelbrot set, for this problem we have to send huge arrays totalling hundreds of megabytes or more to each worker. (A .mat file of K, C, M, and b for satellite.7 is 224 MB.) Fortunately, dask has a data distribution mechanism—a client’s .scatter() method followed by a client _submit()—to handle this situation. The following code fragments show the conventional method to send data to remote workers on the left and the data distribution method on the right:
; and the list of degrees of freedom at which we want the response. Unlike the examples for prime number summation and Mandelbrot set, for this problem we have to send huge arrays totalling hundreds of megabytes or more to each worker. (A .mat file of K, C, M, and b for satellite.7 is 224 MB.) Fortunately, dask has a data distribution mechanism—a client’s .scatter() method followed by a client _submit()—to handle this situation. The following code fragments show the conventional method to send data to remote workers on the left and the data distribution method on the right:Python; Dask Without Scatter: | Python; Dask with Scatter: |
|---|---|
client = Client(cluster) for i in range(n_jobs): job = dask.delayed(solve)( K, C, M, b, omega_subset[i]) tasks.append(job) results = dask.compute(*tasks) | client = Client(cluster) client.wait_for_workers(n_jobs) KCMb_dist = client.scatter( [K, C, M, b], broadcast=True) for i in range(n_jobs): job = client.submit(solve2, KCMb_dist, omega_subset[i]) tasks.append(job) results = client.gather(tasks) |
Python: | Python, Using Prescattered Data: |
|---|---|
def solve(K, C, M, b, omega): | def solve2(KCMb, omega): K, C, M, b = KCMb |
14.13.7.4 Subdividing Work to Minimize Data Movement
We’ve taken care to predistribute our matrices to each remote computer. The last thing we want is to have the dask scheduler make more calls to the solver, and therefore possibly transfer more data, than are strictly necessary. To achieve this goal, we’ll submit exactly one dask job for each computer in our cluster and have that job run a subset of the frequencies.
MATLAB: | Python: |
|---|---|
Hz_subset = Hertz(i:n_jobs:end); | Hz_subset = Hertz[i::n_jobs] |
14.13.7.5 Subsetting Results from the Remote Computers
Finite element direct frequency response solutions can be enormous, even for modestly sized models. The complex double-precision frequency domain displacement vector 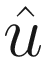 takes Ndof x Nfreq x 16 bytes. Our 600k degree of freedom model at 4092 frequencies would take 40 GB.
takes Ndof x Nfreq x 16 bytes. Our 600k degree of freedom model at 4092 frequencies would take 40 GB.
Both dask and MATLAB can store and work with arrays larger than memory, but there’s rarely a need to store everything in a direct frequency response analysis. There the goal is to measure displacement (and from it, derived quantities like velocity, acceleration, strain) over time at critical locations rather than at every node. In our case, we just want the response at the sensor mount. We’ll therefore subset our solution 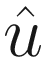 after computing results to just a critical list of user-provided degrees of freedom. This will be done by passing the solver routine an extra list of indices, keep_dof, which identify the rows of
after computing results to just a critical list of user-provided degrees of freedom. This will be done by passing the solver routine an extra list of indices, keep_dof, which identify the rows of  to return.
to return.
The center of the stem holding the sensor in our finite element model is at (23.5, 10.5). We can get the degree of freedom list by first getting the indices of nodes around that point, say within ±0.5 units, then inflating the node list to a degree of freedom list with the simple rule that horizontal DOF IDs are twice the node ID and vertical DOF are twice the node ID plus 1. The DOFs found this way correspond to the unconstrained model. The solution DOF set is smaller because the constrained DOF, those belonging to the base of the adapter ring, have been removed. The dictionary u_to_c maps unconstrained DOF to constrained DOF, so we can use that to get the correct DOF in our solution set:
MATLAB: | Python, Subsetted Ax=b: |
|---|---|
KCM = K+1j*omega*C-omega**2*M; xfull = KCM(b*P); x = xfull(keep_dof); | from scikits import umfpack KCM = K+1j*omega*C-omega**2*M LU = umfpack.splu(KCM) x = LU.solve(b*P)[keep_dof] |
Regarding the solver: I picked UMFPACK’s linear equation solver over than the one from SciPy since the UMFPACK solver is faster with complex matrices. It can be found in the scikit-umfpack package.
14.13.7.6 A Parallel Solver Module
The pseudocode of Section 14.13.7.2presents a simple algorithm: loop over a collection of frequencies and at each one sum matrices together and then solve the resulting sparse complex system of equations.
remote_solve() takes the user’s top-level inputs (matrices K, C, M, load vector b, frequency-dependent load magnitude P, the list of frequencies at which to solve, and the degrees of freedom at which to report results), configures a dask cluster for n_jobs workers, waits until all workers are ready, distributes the large inputs to those workers, then calls submit_solve_jobs(). One instance of remote_solve() runs on the computer submitting the job.
Submit_solve_jobs() subdivides the frequency domain into n_jobs pieces, then submits a dask job to run solve_subset() on each piece. It waits for all workers to produce their solutions and then returns them to remote_solve(). One instance of submit_solve_jobs() runs on the computer submitting the job.
Solve_subset() implements the for loop described in the pseudocode. It solves the system of equations on its given frequencies and returns the subsetted solution. When invoked from submit_solve_jobs(), one instance runs on each of n_jobs remote workers. Solve_subset() can also be invoked directly from a conventional, non-dask sequential program in which case only one instance runs.
Here’s the code:
Organizing the code this way lets us use the same module for both sequential processing, where solve_subset() is called directly, and parallel processing—including parallel processing invoked from MATLAB, as we’ll see in Section 14.14.
The compound if statement on lines 31–42 is part of a “walk before you run” strategy. Sending an untested parallel program to 1000 processors is seldom a good idea. Success comes incrementally: first, get the sequential algorithm working, then verify a parallel run on two or three cores of your local machine, then on a small cluster, and finally pull the trigger on a massive run after the smaller runs check out. The variable solve_with lets me choose the target dask cluster for the run I have in mind—a shake-out of new features or bug fixes on the local machine, an initial performance test on my DigitalOcean virtual machine cluster, or a production run on Coiled’s cloud.
The Python driver which loads the satellite.7 node and element data, assembles the finite element model, applies constraints, then calls pycode.remote_solve() can be found in code/dask/run_fr_dask.py.
14.13.7.7 Running on Coiled’s Cloud
Coiled, the company behind dask, offers a cloud service specifically for dask jobs. This is ideal for individuals or companies that lack access to a private cluster and want to avoid the complications of creating a dask-capable cluster on commercial clouds such as Amazon’s AWS, Microsoft Azure, or Google Cloud. Better still, as of late 2021, Coiled offers its users 1000 CPU hours per month at no cost.
Using Coiled’s cloud requires initial setup. First, create an account at their website.23 Next, install the coiled Python module following instructions you’ll receive by email on all the computers from which you plan to launch dask jobs.
The last setup step involves creating a custom software configuration that includes Python modules you need but are not included in Coiled’s default configuration. The default includes NumPy, SciPy, Pandas, and many others but lacks Numba and UMFPACK. The commented lines 37–41 of the pysolve.py module listing show how I created my own custom environment, called and-fe-env, with extra modules. (An earlier experiment used the requests module but that didn’t pan out.) The custom environment is created on Coiled’s cloud the first time these lines run. This is a one-time step so the call to coiled.create_software_environment() can be commented out or deleted in later runs; your custom setup will be remembered and used in future runs when referenced by name with the software = keyword to coiled.Cluster(). Perhaps it goes without saying, but when you submit your initial setup run, there’s no need to use more than one or two workers.
14.13.7.8 Performance and Cost on Coiled’s Cloud
followed by a delay, possibly a long one. What’s going on?
Your job runs after two conditions are met: (1) your job’s container is created, and (2) the number of workers you requested is available. Upon receiving your job, Coiled creates a Docker image containing Python, your extra modules, and the code you submitted. This can take up to five minutes. Next, your job has to wait until the requested number of workers is available. If you’re running during prime time hours in the United States or requesting a huge number of workers, this delay could be substantial. If the delay exceeds 20 minutes, the dask job times out, and you’ll need to resubmit.
The state of your job can be found by logging in to your Coiled account and visiting the Dashboard page. The “Num Workers” column shows the number of workers running your job. Additional details appear in log files which can be seen by hitting the “Logs” button on the right side of the job.
Another source of delay is the data distribution step. In our case, the call
in pysolve.remote_solve() takes about 200 seconds to send our 600k matrices to 100 workers, which works out to about 1 MB per second per 100 workers.
With this much overhead—creating a Docker image, waiting for workers, distributing large datasets—it is pretty clear there’s no point in using Coiled’s cloud for small problems.
Elapsed time and cost for direct frequency response on Coiled’s cloud
Number of Workers | Number of Frequencies | Time [Seconds] | Cost [US$] |
|---|---|---|---|
2 | 2 | 388.6 | 0.01 |
3 | 16 | 413.1 | 0.02 |
16 | 16 | 348.9 | 0.08 |
32 | 32 | 388.4 | 0.19 |
64 | 64 | 445.6 | 0.31 |
100 | 100 | 523.7 | 0.58 |
100 | 1024 | 740.1 | 1.21 |
100 | 2048 | 918.3 | 1.55 |
The “price of admission” to run just a single frequency on 32 workers or less on the Coiled cloud is around 400 seconds.
The time to solve the 600k system of equations on my Linux laptop is about 12 seconds per frequency using UMFPACK in Python and 15 seconds using MATLAB’s sparse solver. 2048 frequencies would take about 7 hours on a single computer in Python and 8.5 hours in MATLAB. The 100 Coiled workers give us a speed-up of 26× over sequential Python and 33× over sequential MATLAB.
Elapsed time to solve 2048 frequencies with 100 workers is only 1.75 greater than solving 100 frequencies. The baseline overhead still amounts to one-third of the overall time.
Bottom line: The Coiled cloud excels at solving large computational problems. Keep small problems on your local computer.
14.14 Recipe 14-2: Accelerating MATLAB with Python on Multiple Computers
MATLAB can send work to a dask cluster—and gain the same performance increases—as easily as Python can. The “work” sent by MATLAB must be implemented in Python though. In this recipe, we’ll write MATLAB programs that submit the Python functions from the three example problems of Section 14.13 (sum prime factors, create a gigapixel Mandelbrot image, and solve a direct frequency response problem) to a dask cluster, then collect the solutions as MATLAB variables.
The first two examples, prime sums and the Mandelbrot set, will use this small bridge module from MATLAB to submit the jobs to dask and then to start the computations:
The third example, direct frequency response, requires a different strategy and does not use the bridge module.
14.14.1 Parallel Prime Sums with MATLAB
The following MATLAB program uploads the file my_fn.py to the dask cluster and then calls the same-named function within it, my_fn.my_fn(), to sum prime factors in the given interval.
14.14.2 Parallel Gigapixel Mandelbrot with MATLAB
Here’s a MATLAB program that sends the Numba-enhanced MB() function in MB_numba_dask2.py shown in Section 14.13.6 to a dask cluster:
Recall the 5k x 5k performance time of 112 seconds for MATLAB from Table 14-1. Here, with the help of Python and an 18-node cluster, MATLAB can solve a problem 49x larger in the same amount of time. Much of the performance boost comes from Numba running the MB() function much faster, while the rest from the number of computer themselves.
One advantage MATLAB has over Python for this problem is that MATLAB is able to render the gigapixel image. matplotlib in Python fails with an obscure error.

14.14.3 Parallel Direct Frequency Response with MATLAB
The previous two MATLAB-with-dask examples imported the Python dask module directly into MATLAB and from there submitted jobs to, and collected results from, the dask cluster.
That does not work with the much more substantial direct frequency response problem. For unknown reasons, the Python-based workers for this problem lose connection with the MATLAB-based dask cluster variable, and the job fails. The only way I can get MATLAB to run this large problem is by keeping all dask objects and activity—cluster creation, data distribution, job submittal—in Python. MATLAB then has to access the dask-based solver indirectly through a Python wrapper. This actually the main reason for organizing the direct frequency response solver code of pysolve.py shown in Section 14.13.7.6 into the three functions. The remote_solve() function in pysolve.py is the wrapper MATLAB needs.
Here is the MATLAB code that solves the direct frequency response problem by using the Python-based dask solver. Rather than recreating the finite element model from scratch, we’ll load matrices from .mat files created with the Python program code/dask/save_KCMb.py.
Performance and cost resemble the values in Table 14-11. The load on Coiled’s cloud causes time and cost variations that are beyond our control.
Elapsed time and cost for MATLAB-based direct frequency response on Coiled’s cloud
Number of Workers | Number of Frequencies | Time [Seconds] | Cost [US$] |
|---|---|---|---|
3 | 16 | 402.1 | 0.02 |
64 | 64 | 472.1 | 0.50 |
100 | 100 | 628.0 | 0.88 |
100 | 1024 | 743.0 | 0.95 |
100 | 2048 | 940.2 | 1.60 |
14.15 References
- [1]
Emery D. Berger. Scalene: Scripting-Language Aware Profiling for Python. 2020. arXiv: 2006 . 03879 [cs.PL]. URL: https://github.com/plasma-umass/scalene
- [2]
James F. Doyle. Wave Propagation in Structures. Springer-Verlag, 1989.
- [3]
Serge Guelton et al. “Pythran: Enabling static optimization of scientific python programs.” In: Computational Science & Discovery 8.1 (2015), p. 014001.
- [4]
Jonathan Richard Shewchuk. “Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator.” In: Applied Computational Geometry: Towards Geometric Engineering. Ed. by Ming C. Lin and Dinesh Manocha. Vol. 1148. Lecture Notes in Computer Science. From the First ACM Workshop on Applied Computational Geometry. Springer-Verlag, May 1996, pp. 203–222. URL: www.cs.cmu.edu/˜quake/triangle.html
