Appendix A. Working with Numbers: Binary and Hexadecimal
Understanding how the binary and hexadecimal number systems work is not critical to programming better applications in C++, but it helps you to better understand what happens under the hood.
Decimal Numeral System
Numbers that we use on a daily basis are in the range of 0 through 9. This set of numbers is called the decimal numeral system. Because this system is composed of 10 unique digits, it’s a system with a base of 10.
Hence, as the base is 10, the zero-based position of each digit denotes the power of 10 that the digit is multiplied with. For example, in the number 957, the zero-based position of 7 is 0, that of 5 is 1, and that of 9 is 2. These position indexes become powers of the base 10, as shown in the following example:
957 = 9 × 102 + 5 × 101 + 7 × 100 = 9 × 100 + 5 × 10 + 7
Remember that any number to the power 0 is 1 (so, 100 is the same as 10000 as both evaluate to 1).
Note
In the decimal system, powers of 10 are important. Digits in a number are multiplied by 10, 100, 1000, and so on to determine the magnitude of the number.
Binary Numeral System
A system with a base of 2 is called a binary system. The binary numeral system allows only two states and is represented by the numbers 0 and 1. These numbers in C++ typically evaluate to false and true (true being nonzero).
Just as numbers in the decimal system are evaluated to powers of base 10, those in binary are evaluated to powers of their base 2:
101 (binary) = 1 × 22 + 0 × 21 + 1 × 20 = 4 + 0 + 1 = 5 (decimal)
So, the decimal equivalent of binary 101 is 5.
Note
Digits in a binary number are multiplied by powers of 2—such as 4, 8, 16, 32, and so on—to determine the magnitude of the number. The power is decided by the zero-based place of the digit in question.
To understand the binary numeral system better, examine Table A.1, which lists the various powers of 2.
Table A.1 Powers of 2

Why Do Computers Use Binary?
The binary system has been in widespread use for a comparatively short period of time. Its use has been accelerated by the development of electronics and computers. The evolution of electronics and electronic components resulted in a system that detected states of a component as being ON (that is, under a significant potential difference or voltage) or OFF (that is, no or low potential difference).
These ON and OFF states were conveniently interpreted as 1 and 0, completely representing the binary number set and making it the method of choice for performing arithmetic calculations. Logical operations, such as NOT, AND, OR, and XOR, as covered in Lesson 5, “Working with Expressions, Statements, and Operators” (in Tables 5.2 through 5.5), were easily supported by the development of electronic gates, resulting in the binary system being wholeheartedly adopted as conditional processing became easy.
What Are Bits and Bytes?
A bit is a basic unit in a computational system that contains a binary state. Thus, a bit is said to be “set” if it contains state 1 or “reset” if it contains state 0. A collection of bits is a byte. The number of bits in a byte is theoretically not fixed and is a hardware-dependent number. However, most computational systems assume 8 bits in a byte—for the simple, convenient reason that 8 is a power of 2. Assuming 8 bits in a byte also allows the transmission of up to 28 different values, allowing for 255 distinct values. These 255 distinct values are enough for the display or transaction of all characters in the ASCII character set—and more.
How Many Bytes Make a Kilobyte?
1024 bytes (210 bytes) make a kilobyte. Similarly, 1024 kilobytes make a megabyte. 1024 megabytes make a gigabyte. 1024 gigabytes make a terabyte.
Hexadecimal Numeral System
The hexadecimal numeral system has a base of 16. A digit in the hexadecimal system can be in the range 0 through 9 and A through F. For example, 10 in decimal is equivalent to A in hexadecimal, and 15 in decimal is equivalent to F in hexadecimal. Table A.2 shows how the hexadecimal digits translate to decimal.
Table A.2 Decimal and Hexadecimal Equivalents
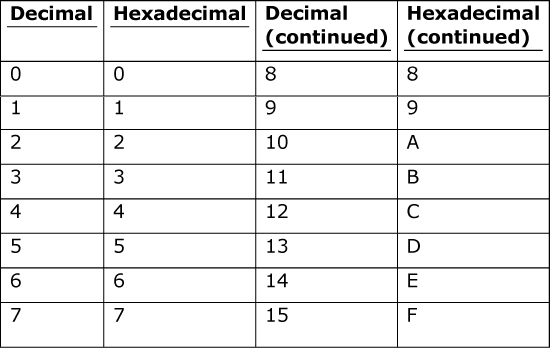
Just as numbers in a decimal system are evaluated to powers of base 10 and numbers in binary are evaluated to powers of their base 2, those in hexadecimal are evaluated to powers of base 16. Consider this example:
0x31F = 3 × 162 + 1 × 161 + F × 160 = 3 × 256 + 16 + 15 (in decimal) = 799
Note
By convention, hexadecimal numbers are represented with the prefix 0x.
Why Do We Need Hexadecimal?
Computers use the binary numeral system, and the state of each unit of memory in a computer is a 0 or a 1. However, if we humans were to interact with computer- or programming-specific information using 0s and 1s, we would need a lot of space to record even small pieces of information. A hexadecimal representation can very efficiently represent the state of 4 bits in a digit by using a maximum of two hexadecimal digits to represent the state of a byte. For example, instead of writing 1111 in binary, you are a lot more efficient writing F in hexadecimal.
Note
A less-used number system is the octal numeral system. This is a system with base 8, comprising the numbers 0 through 7.
Converting to a Different Base
When dealing with numbers, you might sometimes need to view a number in a different base. For instance, you might need to know the value of a binary number in decimal or the value of a decimal number in hexadecimal.
Earlier in this appendix, you saw how numbers can be converted from binary or hexadecimal into decimal. The following section gives you a look at converting binary and hexadecimal numbers into decimal.
The Generic Conversion Process
When converting a number in one system to another system, you successively divide with the base, starting with the number being converted. Each remainder fills places in the destination numeral system, starting with the lowest place. The next division uses the quotient of the previous division operation with the base as the divisor.
This continues until the remainder is within the destination numeral system and the quotient is 0.
This process is also called the breakdown method.
Converting Decimal to Binary
To convert decimal 33 into binary, you subtract the highest power of 2 possible (that is, 32):
Place 1: 33 / 2 = quotient 16, remainder 1
Place 2: 16 / 2 = quotient 8, remainder 0
Place 3: 8 / 2 = quotient 4, remainder 0
Place 4: 4 / 2 = quotient 2, remainder 0
Place 5: 2 / 2 = quotient 1, remainder 0
Place 6: 1 / 2 = quotient 0, remainder 1
Therefore, the binary equivalent of 33 (reading places) is 100001.
Similarly, the binary equivalent of 156 is
Place 1: 156 / 2 = quotient 78, remainder 0
Place 2: 78 / 2 = quotient 39, remainder 0
Place 3: 39 / 2 = quotient 19, remainder 1
Place 4: 19 / 2 = quotient 9, remainder 1
Place 5: 9 / 2 = quotient 4, remainder 1
Place 6: 4 / 2 = quotient 2, remainder 0
Place 7: 2 / 2 = quotient 1, remainder 0
Place 9: 1 / 0 = quotient 0, remainder 1
Therefore, the binary equivalent of 156 is 10011100.
Converting Decimal to Hexadecimal
The process of converting decimal to hexadecimal is the same as for converting decimal to binary—but you divide by base 16 instead of 2.
So, to convert decimal 5211 to hex:
Place 1: 5211 / 16 = quotient 325, remainder B16 (1110 is B16)
Place 2: 325 / 16 = quotient 20, remainder 5
Place 3: 20 / 16 = quotient 1, remainder 4
Place 4: 1 / 16 = quotient 0, remainder 1
Therefore, 521110 = 145B16.
Tip
To better understand how different number systems work, you can write a simple C++ program similar to Listing 27.1 in Lesson 27, “Using Streams for Input and Output.” It uses std::cout with manipulators for displaying an integer in hex, decimal, and octal notations.
To display an integer in binary, you can use std::bitset, as explained in Lesson 25, “Working with Bit Flags Using the STL,” deriving inspiration from Listing 25.1.
