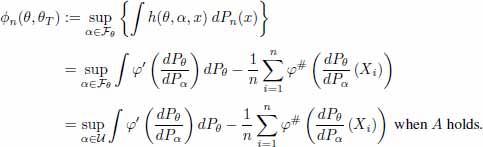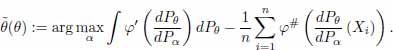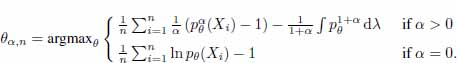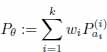8.1. Introduction

This paper aims to present the main features of Csiszár-type divergences in relation with statistical inference. We first introduce some notations and definitions, and then embed the present setup in the context of decomposable measures of discrepancy between probability measures. A variational representation of Csiszár divergences is the basic ingredient for this embedding. The specificity of the classes of decomposable measures of discrepancy allows us to select such a class for specific inference purposes.

Minimizing a discrepancy between a given distribution P and a class of measures M occurs in a certain number of problems. On the one hand, when the distribution P is known, then the resulting problem is of analytic nature and bears no statistical aspect. On the other hand, the measure P might only be known through a sampling of observations X₁, .., X_n, whose empirical distribution

converges to P in some sense. The class M is then called a model, which may be parametric, therefore indexed by some θ in a subset Θ of a finite dimensional space; the model M might be semi-parametric, for example described by moment or L-moment conditions; or non-parametric, for example when described by shape conditions, such as unimodality. Inference in those cases aims at answering basic questions:

Does P belong to M?

If yes, and when the model is of parametric or semi-parametric nature, what is the “true” value θ_T of the parameter for which P = P_θT, a question which should obviously be made more precise according to the context; for example, in semi-parametric models, the class M is usually described as

[8.1]

where M_θ represents a whole submodel sharing a common feature θ, and the inference estimation step aims at identifying θ_T such that P belongs to M_θT. The case when each of the M_θ is defined by specific moment conditions extends the classical empirical likelihood context and will be described in section 8.2. Other fields of application of a minimum divergence approach cover robust inference in parametric models, considering minimum divergence estimation between the distribution of the data and some tubular neighborhoods of the model. Model selection criteria such as AIC or BIC can be considered as minimum divergence estimators. Broadly speaking, divergence-based methods extend the likelihood paradigm in a natural way, paving the way to trade-off between efficiency and robustness requirements. In this chapter, we will show the way in which some non-regular problems can be solved accordingly, in the realm of mixture models.

We now turn to some definitions and notations.

8.1.1. Csiszár divergences, variational form

8.1.1.1. Parametric framework

Let P := {P_θ,θ ∈ Θ} be an identifiable parametric model on ℝ^d, where Θ is a subset of ℝ^s. All measures in P will be assumed to be measure equivalent, therefore sharing the same support. The parameter space Θ does not need to be an open set in the present setting. It may even happen that the model includes measures which would not be probability distributions; cases of interest cover models including mixtures of probability distributions; this will be developed in section 8.3. Let ϕ be a proper closed convex function from ] – ∞, +∞[ to [0, +∞] with ϕ(1) = 0 and such that its domain domϕ := {x ∈ ℝ such that ϕ(x) < ∞} is an interval with endpoints a_ϕ < 1 < b_ϕ(which may be finite or infinite). For two measures P_α and P_θ in P, the ϕ-divergence between P_α and P_θ is defined by

In a broader context, the ϕ-divergences were introduced by Csiszár (1964) as “f-divergences”, defined between two probability measures Q and P, with Q absolutely continuous (a.c.) with respect to (w.r.t.) P by

where f satisfies the same requirements as ϕ above. The basic property of ϕ-divergences states that when ϕ is strictly convex on a neighborhood of x = 1, then

We refer to (Liese and Vajda 1987, Chapter 1) for a complete study of those properties. Let us simply quote that in general φ(α, θ) and φ(θ, α) are not equal. Hence, ϕ-divergences usually are not distances, but they merely quantify some difference between two measures. A main feature of divergences between distributions of random variables X and Y is the invariance property with respect to a common smooth change of variables.

8.1.1.1.1. Examples of ϕ-divergences

The Kullback-Leibler (KL), modified Kullback-Leibler (KL_m), χ², modified χ², Hellinger (H) and L₁ divergences are, respectively, associated with the convex functions ϕ(x) = x log x – x + 1, ϕ(x) = –log x + x –1, and ϕ(x) = |x – 1|. All of these divergences, except the L₁, belong to the class of the so-called “power divergences” introduced in Read and Cressie (1988) (see also Liese and Vajda 1987, Chapter 2), a class that takes its origin from Rényi et al. (1961). They are defined through the class of convex functions

[8.2]

if γ ∈ ℝ {0,1}, ϕ₀(x) := – log x + x – 1 and ϕ₁(x) := x log x – x + 1. So, the KL-divergence is associated with ϕ₁, the KL_m to ϕ₀, the χ² to ϕ₂, the to ϕ _–1 and the Hellinger distance to ϕ1/2.

It may be convenient to extend the definition of the power divergences in such a way that φ(α, θ) may be defined (possibly infinite) even when P_α or P_θ is not a probability measure. This is achieved setting

[8.3]

when domϕ = ℝ⁺/{0}. Note that, for the χ²-divergence, the corresponding ϕ function is defined and convex on whole R.

We will only consider divergences defined through differentiable functions ϕ, which we assume to satisfy the following condition:

RC	There exists a positive δ such that, for all c in [1 – δ, 1 + δ], we can find numbers c1, c2, c3 such that ϕ(cx) ≤ c1 ϕ(x) + c2 |x| + c3, for all real x

Condition (RC) holds for all power divergences including KL and KL_m divergences.

8.1.2. Dual form of the divergence and dual estimators in parametric models

Let θ and θ_T be any parameters in Θ. We intend to provide a new expression for φ(θ,θ_T).

As will be considered in statistical applications pertaining to non-regular models, it may be of interest, at times, to consider enhanced statistical models indexed by the parameter θ, and those models may include signed measures, although, obviously, no dataset would be generated by those. In any case, P_θT clearly will designate a probability measure, under which the data are supposed to be generated. In those cases, the domain of ϕ will be assumed to contain all possible real values for (dP_θ/dP_θT) (x), henceforth a (possibly infinite) interval in ℝ; the χ² divergence function

is the prototype for those cases.

By strict convexity, for all a and b the domain of ϕ it holds

[8.4]

with equality if and only if a = b.

Let us denote ϕ^# (x) := xϕ’(x) – ϕ(x). For any α in Θ, define and also define Inserting these values in [8.4] and integrating with respect to P_θT yields

Assume at present that this entails

[8.5]

for suitable α’s in some set F_θ included in Θ.

When α = θ_T, the inequality in [8.5] turns to equality, which yields

[8.6]

Denote

[8.7]

from which

[8.8]

Furthermore, by [8.5], for all α in F_θ

and the function x → h(θ, θ_T, x) = – h(θ, α, x) is non-negative due to [8.4]. It follows that φ(θ, θ_T) – ∫ h(θ, α,x)dP_θT is zero if and only if (iff) h(θ,α,x) = h(θ, θ_T, x) – P_θT a.e. Therefore, φ(θ, θ_T) – ∫ h(θ, α, x)dP_θT = 0 iff for any x in the support of P_θT,

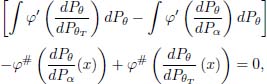
which cannot hold when the functions , and 1 are linearly independent, unless α = θ_T. We have proved that θ_T is the unique optimizer in [8.6].

We have skipped some sufficient conditions that ensure that [8.5] holds.

Assume that for all α in F_θ

[8.9]

Assume further that φ(θ, θ_T) is finite. Since

we obtain

which entails [8.5]. When , then clearly, under [8.9]

We have proved that [8.6] holds when α satisfies [8.9].

Sufficient and simple conditions encompassing [8.9] can be assessed under standard requirements for nearly all divergences. We state the following result (see Liese and Vajda 1987; Broniatowski and Keziou 2006, lemma 3.2).

LEMMA 8.1.– Assume that RC holds and φ(θ, α) is finite. Then [8.9] holds.

Summing up, we can state the following result.

THEOREM 8.1.– Let θ belong to Θ and let φ(θ, θ_T) be finite. Assume that RC holds. Let F_θ be the subset of all α’s in Θ such that φ(θ, α) is finite. Then

[8.10]

Furthermore, the supremum is attained for θ_T and uniqueness holds true.

For the Cressie-Read family of divergences with γ ≠ 0,1, this representation writes

The set F_θ may depend on the choice of the parameter θ. Such is the case for the χ² divergence, i.e. ϕ(x) = (x – 1)²/2, when p_θ(x) = θ exp(–θ_x)1_[0,∞)(x). In most cases, the difficulty of dealing with a specific set F_θ depending on θ can be encompassed when

there exists a neighbourhood U of θ_T for which [A]

which, for example, holds in the above case for any θ_T. This simplification deserves to be stated in the next result.

THEOREM 8.2.– When φ(θ, θ_T) is finite and RC holds, then, under condition [A],

Furthermore, the supremum is attained for θ_T and uniqueness holds true.

REMARK 8.1.– Identifying F_θ might be cumbersome. This difficulty also appears in the classical MLE case, a special case of the above statement with divergence function ϕ₀, for which it is assumed that

is finite for θ in a neighborhood of θ_T.

Under the above notation and hypotheses, define

[8.11]

It then holds that T_θ (P_θT) = θ_T for all θ_T in Θ. Also let

[8.12]

which also satisfies S(P_θT) = θ_T for all θ_T in Θ. We thus can state the following result.

THEOREM 8.3.– When φ(θ, θ_T) is finite for all θ in Θ and RC holds, both functionals T_θ and S are Fisher consistent for all θ_T in Θ.

8.1.2.1. Plug in estimators

From [8.8], simple estimators for θ_T can be defined, plugging any convergent empirical measure in place of P_θT and taking the infimum w.r.t. θ in the resulting estimator of φ(θ, θ_T).

In the context of simple i.i.d. sampling, introducing the empirical measure

where the X_i ’s are i.i.d. r.v’s with common unknown distribution P_θT in P, the natural estimator of φ(θ, θ_T) is

[8.13]

Denote by θ any given value in Θ and call it an escort parameter. Note that for any such θ, the supremum w.r.t. α in [8.10] is achieved at θ_T. A first M-estimator of θ_T with escort parameter θ can then be defined through

[8.14]

Those estimators coincide with the MLE for ϕ(x) = – log x + x = – 1 and they can be tuned through the choice of the escort parameter θ. Under condition A, since

the resulting estimator of φ(θ_T, θ_T) is

[8.15]

Also the estimator of θ_T is obtained as

[8.16]

In the case when ϕ = ϕ_γ defined by [8.2], it holds true

for γ ≠ 0,1. When γ = 0 the above expression [8.16] boils down to the classical expression

where μ is some dominating measure P. When γ = 1, then

The resulting minimum dual divergence estimators [8.15] and [8.16] do not require any smoothing or grouping, in contrast with the classical approach that involves quantization. The paper by Broniatowski and Keziou (2009) provides a complete study of those estimates and subsequent inference tools for the usual i.i.d. sample scheme. For all divergences considered here, these estimators are asymptotically efficient in the sense that they achieve the Cramer-Rao bound asymptotically in regular models. The case when ϕ = ϕ₀ leads to θ_ML defined as the celebrated maximum likelihood estimator (MLE), in the context of the simple sampling.

8.1.2.2. Dual form of the divergence and dual estimators in a general framework

The above derivation clearly leads to a similar description of

whenever Q is an a.c. measure w.r.t. P and φ (Q, P) = +∞ otherwise. Here, Q might be a signed measure and P is a probability measure; therefore, the domain of the convex function ϕ may at time overlap with the negative axis. The same development as above clearly yields for finite φ(Q, P)

[8.17]

where F designates any class of function that contains the function x → (dQ/dP)(x), since indeed the supremum in the RHS of the above display holds when f = (dQ/dP) (x) – Pa.e. Integrability condition for this representation to hold can be written

for all f in F, in accordance with [8.9].

Formula [8.17] is of relevance when Q belongs to some class of distributions for which (dQ/dP) (x) has a known functional form; such is the case in many semi-parametric settings, for example for models M defined through moment conditions, or in odd ratio models (see Broniatowski and Keziou 2012; Keziou and Leoni-Aubin 2008) for which the functional form of the likelihood ratio between the true unknown distribution P and the measures in the model is indeed a specification of the model; the resulting plug in estimator of the φ-projection Q^* of P on M can be obtained through a similar procedure as in the parametric case

where X₁, .., X_n are sampled under P.

8.1.3. Decomposable discrepancies

We now explore the relation between Csiszár discrepancies and statistical criteria; see Broniatowski and Vajda (2012) for additional insights. Turning back to the parametric setting, the φ-divergences can be embedded in the broader class of pseudodistances D, which are defined by the condition that

An additional restriction imposed on pseudodistances D(P,Q) will be the decomposability property. In the sequel Q would designate a probability measure, which may be an atomic one (typically Q is the empirical measure P_n). Here, P designates the class of probability measures on some measurable set X.

A pseudodistance D is a decomposable pseudodistance if there exist functional D⁰ : P ↦ ℝ, D¹ :P ↦ ℝ and measurable mappings

such that for all θ ∈ Θ and Q ∈ P the expectations ∫ ρ_θdQ exist and

We say that a functional T_D : Q ↦ Θ defines a minimum pseudodistance estimator (briefly, min D-estimator) if D(P_θ,Q) is a decomposable pseudodistance and the parameters T_D(Q) ∈ Θ minimize D⁰(P_θ) + ∫ ρ_θdQ on Θ, in symbols

In particular, for Q = P_n

Every min D-estimator θ_D,n is Fisher consistent in the sense that

Clearly, minimal φ-divergence estimators with escort θ, as defined in [8.14], are min D-estimators for the decomposable pseudodistance

and the maximum subdivergence estimator

with the divergence ϕ and escort parameter θ ∈ Θ is the min D-estimator for the decomposable pseudodistance.

8.1.3.1. Power pseudodistance estimators

A special class of pseudodistances D_ψ (P_θ, Q) is defined on P ⊗ P by the integral

where ψ(s,t) are reflexive in the sense that they are non-negative functions of arguments s,t > 0 with ψ(s,t) = 0 iff s = t. If a function ψ is reflexive and also decomposable in the sense

[8.18]

for some ψ⁰,ψ¹,ρ : (0, ∞) → ℝ, then the corresponding ψ-pseudodistance D_ψ(P_θ,Q) is a decomposable pseudodistance satisfying

for

8.1.3.1.1. ϕ-divergences D_ϕ(P_θ,Q)

The ϕ-divergences D_ϕ,(P_θ, Q) are special ψ-pseudodistances for the functions

[8.19]

since they are non-negative and reflexive, and [8.19] implies D_ψ(P_θ,Q) = D_ϕ(P_θ,Q) for all P ∈ P,Q ∈ P when ϕ and ψ are related by [8.19]. However, the functions [8.19] in general do not satisfy the decomposability condition [8.18] so that the ϕ-divergences are not in general decomposable pseudodistances. An exception is the logarithmic function ϕ = ϕ₀ = – log x + x – 1 for which the min D_ϕ0 -estimator is the MLE.

8.1.3.1.2. L₂-estimator

The quadratic function ψ(s,t) = (s – t)² is reflexive and also decomposable. Thus, it defines the decomposable pseudodistance

on P ⊗ P. It is easy to verify that

The corresponding min D_ψ-estimator is in this case the L₂ -estimator

which is known to be robust but not efficient (see for example Hampel et al. 1988).

To build a smooth bridge between the robustness and efficiency, one needs to replace the reflexive and decomposable functions ψ by families {ψ_α : α ≥ 0} of reflexive functions decomposable in the sense

where the two functions and are defined at α = 0 through the limits

for some constant x all s > 0. Then for all α ≥ 0 and (P_θ,Q) ∈ P ⊗ P, the family of ψ_α-pseudodistances

satisfies the decomposability condition

for

8.1.3.2. D_α estimators

The pseudodistances D_α(P_θ,Q) are decomposable and define the family of min D_α-estimators

This family contains as a special case for α = 0 the efficient but non-robust MLE

while for α > 0 the θ_α,n’s are expected to be less efficient but more robust than θ_0,n.

Decomposable pseudodistances D_α(P_θ, Q) defined by the functions

of variables s, t > 0 where ϕ_1+α and ϕ_α are the power functions defined through

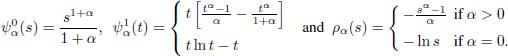
Moreover, this family is continuous in the parameter α ↓ 0 and leads to MLE as its limit.

8.1.3.3. Relation with other estimation criteria

Let us call the pseudodistances D_α(P,Q) simply power distances of orders α ≥ 0.

8.1.3.3.1. L₂-estimator revisited

The min D_α-estimator of order α = 1 is defined by

so that it is nothing but the L₂-estimator θ_n. The family of estimators θ_n,α smoothly connects this robust estimator with the efficient MLE θ_n,0 when the parameter α decreases from 1 to 0.

The special class of the min D_α-estimators θ_α,n given above was proposed by Basu et al. (1998) who confirmed their efficiency for α ≈ 0 and their intuitively expected robustness for α > 0. These authors called θ_α,n minimum density power divergence estimators without actual clarification of the relation of the “density power divergences” D_α(P,Q) to the standard power divergences D_α(P, Q) studied in Liese and Vajda (1987) and Read and Cressie (1988).

[8.20]

This subclass of general min D_α-estimators [8.20] was included in a wider family of generalized MLE’s introduced and studied previously in Vajda (1984 and 1986).

8.1.3.4. Invariance

If the observations x ∈ χ are replaced by y = T(x), where T : (χ, A) ↦ (y,B) is a measurable statistic with the inverse T^–1 then the densities

in the transformed model w.r.t. the σ-finite dominating measure

where J_T(y) is the determinant

The min D_α -estimators are in general not equivariant w.r.t. invertible transformations of observations T, unless α = 0.

However, the min D_α-estimates in the above-considered transformed model coincide with the original min D_α-estimates θ_α,n if the Jacobian J_T of transformation is a non-zero constant on the transformed observation space y. Thus, if X,Y are Euclidean spaces, then the min D_α-estimators are equivariant under linear statistics Tx = ax + b.

8.2. Models and selection of statistical criteria

We now turn back to the Csiszár class of divergences and illustrate the role of this class in statistical inference.

Semi-parametric models defined by moment conditions provide a simple case where the question of the selection of statistical criterion appears in a natural way. Such models M satisfy [8.1] where the submodel M_θ is defined as the collection of all distributions Q such that, for some function (x, θ) → g(x, θ) ∈ ℝ^d, the moment condition

[8.21]

holds. The parameter of interest is θ and an extensive literature is devoted to inference about it in many contexts. The Csiszár divergence approach to it consists of finding the ϕ-projection of P_n on M_θ

[8.22]

and then to estimate θ_T through

[8.23]

The optimization in [8.22] is easy; indeed, M_θ can be divided into the class of all distributions with support included in the support of P_n (hence supported by the sample points), denoted M_θ(P_n), and its complementary set. On M_θ(P_n), the divergence ϕ(Q,P_n) is finite, and this divergence is infinite on the complementary set. Therefore, the ϕ-projection of P_n on M_θ is a point in the simplex of ℝⁿ. The optimization step in [8.22] is a finite dimensional problem. This is the core argument underlying the empirical likelihood approach and its generalizations, and this gives a sound motivation for the Csiszár divergence approach in this setting. However, in some cases we may be interested in introducing some additional assumptions in the model, specifying some smoothness property for the distributions in M_θ, typically pertaining to their density with respect to the Lebesgue measure. The approach through Csiszár divergences does not allow for such a requirement since definition [8.22] cannot include any additional information on but the moment condition [8.21]. On the contrary, the density power divergences introduced in Basu et al. (1998), which are not of Csiszár type, allow us to handle those cases, at the cost of some enhanced optimization approaches in appropriate function spaces (see Broniatowski and Moutsouka 2020). Similar approaches can be handled for models defined by constraints pertaining to expectations of L-statistics (linear functions of order statistics); see Broniatowski and Decurninge (2016) for inference in models defined by conditions on L-moments.

8.3. Non-regular cases: the interplay between the model and the criterion

This section illustrates the flexibility of the Csiszár divergence approach to handle inference in non-regular models in a simple and commonly met situation. We consider the test of the number of components in a mixture. For the sake of clearness, the model at hand consists of a mixture of two components with given densities; therefore, the test consists of assessing whether the mixing coefficient θ is 0. There exists a large literature devoted to such questions either when the components of the mixture are known or when their own parameters are unknown; a classical result quoted in Titterington et al. (1985) provides the limit distribution of the likelihood ratio statistics under the null hypothesis, which includes a Dirac measure; such results have been extended to mixtures with more than two compnents; however, the asymptotic distribution is quite complex and the problem is therefore still quite open. In the present context, we will embed the mixture model in the space of the signed measures, allowing the mixing coefficient to take negative values; the coefficient θ is then an interior point of the parameter set, and we make use of divergences whose domain extends on ℝ^–. The extended model is regular and the divergence between the empirical measure and the model can be analyzed under the null hypothesis, leading to a classical χ² distribution, as expected.

Let us thus consider a set of signed measures defined by

[8.24]

where p₀ and p₁ are two known densities (belonging, or not, to the same parametric family).

We observe a random sample X₁,..., X_n of distribution p_T. We are willing to test:

[8.25]

which can be reduced to

[8.26]

whenever p₀ ≠ p₁ is met. The latter condition ensures the identifiability of the model and enables us to consider different parametric families for p₀ and p₁. Conversely, Chen et al. (2001), for instance, assume that 0 < θ < 1, and tests the equality of the parameters of p₀ and p₁ inside a unique family F.

In the following, we thus assume that p₀ ≠ p₁. The result proposed in Titterington et al. (1985) adapts the Wilks statistics (likelihood ratio test) for this situation; however, the limit distribution is not standard, even in this simple case, since it is a mixture of a Dirac distribution at 0 and a χ² distribution with 1df; this procedure seems untractable in cases with more than two components, adding the difficulty due to the estimation of the parameters of the components; note that in the present derivation we assumed that the parameters of the components are known, which is clearly not the case in practice. So any global inference on the number of components adds an extra derivation of the test statistics taking into account the distribution of the estimators of the parameters of the components; this does not play in favor of methods that would involve non-classical limit laws for the Wilks statistics. This explains the amount of efforts toward a classical solution for this non-regular problem, still quite commonly met.

8.3.1. Test statistics

For adequate divergence ϕ, the estimate of ϕ(0, θ_T) provides a test statistic for the test defined by [8.25]; indeed, it quantifies the discrepancy between the actual distribution p_θT and p₀. Let ϕ be any Csiszár divergence with 0 an interior point in the domain of ϕ. Then the statistic 2nϕ_n(0,θ_T) can be used as a test statistic for [8.25] and

[8.27]

This result also holds when testing whether the true distribution is a k₀-component mixture or a k-component mixture, which can be stated as follows. Consider a k-component parametric mixture model P_θ (k ≥ 2) defined by

[8.28]

where are k-parametric models and A₁,...,A_k are k sets in ℝ^d_l,...,ℝ^d_k with d₁,...,d_k ∈ ℕ^* and 0 ≤ w_i ≤ 1, ∑ w_i = 1. Note that we consider a non-standard framework in which the weights are allowed to be equal to 0. Note Θ the parameter space

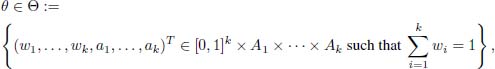
and assume that the model is identifiable. Let k₀ ∈ {1, . . . , k – 1}.

We are willing to test if (k – k₀) components in [8.28] have null coefficients. We assume that their labels are k₀ + 1,..., k. Denote Θ₀ the subset of Θ defined by

In this case, the test statistic 2nϕ_n (Θ₀, θ_T):= 2n inf_θ∈Θ0 ϕ_n (θ, θ_T) converges to a distribution when H₀ holds.

While many divergences meet the former properties, we restrict ourselves to two generators in the following.

8.3.1.1. Chi-square divergence

The first divergence that we consider is the χ² -divergence. The corresponding ϕ function is defined and convex on whole R; an example when P may contain signed finite measures and not be restricted to probability measures is considered in Broniatowski and Keziou (2006) in relation with a two-component mixture model defined in [8.24] and where θ is allowed to assume values in an open neighborhood Θ of 0, in order to provide a test for [8.26], with θ an interior point of Θ.

8.3.1.2. Modified Kullback-Leibler divergence

The second divergence that we retain is generated by a function described below, namely

[8.29]

[8.30]

which has been derived within the recent general framework of Broniatowski and Stummer (2019). It is straightforward to see that φ_c is strictly convex and satisfies . For the special choice c = 0, [8.29] reduces to the omnipresent Kullback-Leibler divergence generator

According to [8.29], in the case of c > 0 the domain ]1 – e^c, ∞[ of ϕ_c also covers negative numbers (see Broniatowski and Stummer (2019) for insights on divergence-generators with general real-valued domain); thus, the same facts hold for the new generator as for the χ² and this opens the gate to considerable comfort in testing mixture-type hypotheses against corresponding marginal-type alternatives, as we derive in the following. We denote KL_c the corresponding divergence functional for which KL_c(Q, P) is well defined, whenever P is a probability measure and Q is a signed measure.

It can be noted that, depending on the type of model considered, the validity of the test can be subject to constraints over the parameters of the densities. Indeed, the convergence of is not always guaranteed. This kind of consideration may guide the choice of the test statistic. For instance, in some cases, including scaling models, conditions that are required for the χ² -divergence, do not apply to the KL_c-divergence. For instance, consider a Gaussian mixture model with different variances

The convergence of I with the χ² requires either . On the other hand, the convergence is always ensured with the KL_c-divergence.

The same observations can be made for the lognormal, exponential and Weibull densities. This fact enlightens the necessary interplay between the model and the statistical criterion, which should impose as little restriction as possible on the unknown part of the inference process. We refer to Broniatowski et al. (2019) for extensions to models with estimated parameters and numerical results.

8.4. References

Basu, A., Harris, I.R., Hjort, N.L., and Jones, M. (1998). Robust and efficient estimation by minimising a density power divergence. Biometrika, 85(3), 549–549.

Broniatowski, M., and Moutsouka, J. (2020). Smooth min-divergence inference in semi parametric models. [Online]. Available at: https://hal.archives-ouvertes.fr/hal-02586204.

Broniatowski, M., and Decurninge, A. (2016). Estimation for models defined by conditions on their L-moments. IEEE Transactions on Information Theory, 62(9), 5181–5181.

Broniatowski, M., and Keziou, A. (2006). Minimization of (ϕ-divergences on sets of signed measures. Studia Scientiarum Mathematicarum Hungarica, 43(4), 403–403.

Broniatowski, M., and Keziou, A. (2009). Parametric estimation and tests through divergences and the duality technique. Journal of Multivariate Analysis, 100(1), 16–16.

Broniatowski, M., and Keziou, A. (2012). Divergences and duality for estimation and test under moment condition models. Journal of Statistical Planning and Inference, 142(9), 2554–2554.

Broniatowski, M., Miranda, E., and Stummer, W. (2019). Testing the number and the nature of the components in a mixture distribution. Lecture Notes in Computer Science 11712. Geometric Science of Information - 4th International Conference. Springer, Cham.

Broniatowski, M., and Stummer, W. (2019). Some universal insights on divergences for statistics, machine learning and articial intelligence. In Nielsen, F. (ed.). Geometric Structures of Information. Springer, Cham.

Broniatowski, M., and Vajda, I. (2012). Several applications of divergence criteria in continuous families. Kybernetika, 48(4), 600 – 636.

Chen, H., Chen, J., and Kalbfleisch, J.D. (2001). A modified likelihood ratio test for homogeneity in finite mixture models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 63(1), 19–29.

Csiszár, I. (1964). Eine informationstheoretische Ungleichung und ihre Anwendung auf Beweis der Ergodizitaet von markoffschen Ketten. Magyer Tud. Akad. Mat. Kutato Int. Koezl., 8, 85 – 108.

Hampel, F.R., Ronchetti, E.M., Rousseeuw, P.J., Stahel, W.A. (1986). Robust statistics. The approach based on influence functions. John Wiley & Sons, Inc., New York.

Keziou, A., and Leoni-Aubin, S. (2008). On empirical likelihood for semiparametric two-sample density ratio models. Journal of Statistical Planning and Inference, 138(4), 915–928.

Liese, F., and Vajda, I. (1987). Convex Statistical Distances. BSB B.G. Teubner Verlagsgesellschaft, Leipzig.

Read, T.R.C., Cressie, N.A.C. (1988). Goodness-of-Fit Statistics for Discrete Multivariate Data. Springer-Verlag, New York.

Rényi, A. (1961). On measures of entropy and information. Proc. 4th Berkeley Sympos. Math. Statist. and Prob. University of California Press, Berkeley.

Titterington, D.M., Smith, A.F.M., and Makov, U.E. (1985). Statistical Analysis of Finite Mixture Distributions. John Wiley & Sons Ltd., Chichester.

Vajda, I. (1984). Minimum divergence principle in statistical estimation. Statistics and Decisions, 1, 239 – 261.

Vajda, I. (1986). Efficiency and robustness control via distorted maximum likelihood estimation. Kybernetika, 22(1), 47 – 67.

Chapter written by Michel BRONIATOWSKI.