In this chapter, we look at several predefined and standard packages, which provide types and operators for use in VHDL models. While we could define all of the data types and operations we need for a given model, we can greatly increase our productivity by reusing the standard packages. Moreover, simulation and synthesis tools often have optimized, built-in implementations of the operations from these packages.
In previous chapters, we have introduced numerous predefined types and operators. We can use them in our VHDL models without having to write type declarations or subprogram definitions for them. These predefined items all come from a special package called standard, located in a special design library called std. A full listing of the standard package is included for reference in Appendix A.
Because nearly every model we write needs to make use of the contents of this library and package, as well as the library work, VHDL includes an implicit context clause of the form
library std, work; use std.standard.all;
at the beginning of each design unit. Hence we can refer to the simple names of the predefined items without having to resort to their selected names. In the occasional case where we need to distinguish a reference to a predefined operator from an overloaded version, we can use a selected name, for example:
result := std.standard."<" ( a, b );
Example 9.1. A comparison operator for signed binary-coded integers
A package that provides signed arithmetic operations on integers represented as bit vectors might include a relational operator, defined as follows:
function "<" ( a, b : bit_vector ) return boolean is variable tmp1 : bit_vector(a'range) := a; variable tmp2 : bit_vector(b'range) := b; begin tmp1(tmp1'left) := not tmp1(tmp1'left); tmp2(tmp2'left) := not tmp2(tmp2'left); return std.standard."<" ( tmp1, tmp2 ); end function "<";
The function negates the sign bit of each operand, then compares the resultant bit vectors using the predefined relational operator from the package standard. The full selected name for the predefined operator is necessary to distinguish it from the function being defined. If the return expression were written as “tmp1 < tmp2”, it would refer to the function in which it occurs, creating a circular definition.
VHDL-87, -93, and -2002
A number of new operations were added to VHDL in the 2008 revision. They are not available in earlier versions of the language. In summary, the changes are
The types
boolean_vector,integer_vector,real_vector, andtime_vectorare predefined (see Section 4.2.1). The predefined operations onboolean_vectorare the same as those defined forbit_vector. The predefined operations oninteger_vectorinclude the relational operators (“=”, “/=”, “<”, “>”, “<=”, and “>=”) and the concatenation operator (“&”). The predefined operations onreal_vectorandtime_vectorinclude the equality and inequality operators (“=” and “/=”) and the concatenation operator (“&”).The array/scalar logic operations and logical reduction operations are predefined for
bit_vectorandboolean_vector, since they are arrays withbitandbooleanelements, respectively.The matching relational operators “
?=”, “?/=”, “?>”, “?>=”, “?<”, and “?<=” are predefined forbit. Further, the operators “?=” and “?/=” are predefined forbit_vector.The condition operator “
??” is predefined forbit.The operators
modandremare predefined fortime, since it is a physical type.The
maximumandminimumoperations are predefined for all of the predefined types.The functions
rising_edgeandfalling_edgeare predefined forbitandboolean. Prior to VHDL-2008, thebitversions of these functions were declared in the packagenumeric_bit(see Section 9.2.3). However, that was mainly to provide consistency with thestd_ulogicversions defined in thestd_logic_1164package. They rightly belong with the definition of the type on which they operate; hence, VHDL-2008 includes them in the packagestandard. The VHDL-2008 revision of thenumeric_bitpackage redefines the operations there as aliases for the predefined versions. (We discuss aliases in Chapter 11.)The
to_stringoperations are predefined for all scalar types and forbit_vector. Further, theto_bstring,to_ostring, andto_hstringoperations and associated aliases are predefined forbit_vector.
VHDL also provided a second special package, called env, in the std library. The env package includes operations for accessing the simulation environment provided by a simulator. First, there are procedures for controlling the progress of a simulation:
procedure stop (status: integer); procedure stop; procedure finish (status: integer); procedure finish;
When the procedure stop is called, the simulator stops and accepts further input from the user interface (if interactive) or command file (if running in batch mode). When the procedure finish is called, the simulator terminates; simulation cannot continue. The versions of the procedures that have the status parameter use the parameter value in an implementation-defined way. They might, for example, provide the value to a control script so that the script can determine what action to take next.
The env package also defines a function to access the resolution limit for the simulation:
function resolution_limit return delay_length;
We described the resolution limit in Section 2.2.4 when we introduced the predefined type time. One way in which we might use the resolution_limit function is to wait for simulation time to advance by one time step, as follows:
wait for env.resolution_limit;Since the resolution limit, and hence the minimum time by which simulation advances, can vary from one simulation run to another, we cannot write a literal time value in such a wait statement. The use of the resolution_limit function allows us to write models that adapt to the resolution limit used in each simulation. We need to take care in using this function, however. It might be tempting to compare the return value with a given time unit, for example:
if env.resolution_limit > ns then -- potentially illegal! ... -- do coarse-resolution actions else ... -- do fine-resolution actions end if;
The problem is that we are not allowed to write a time unit smaller than the resolution limit used in a simulation. If this code were simulated with a resolution limit greater than ns, the use of the unit name ns would cause an error; so the code can only succeed if the resolution limit is less than or equal to ns. We can avoid this problem by rewriting the example as:
if env.resolution_limit > 1.0E–9 sec then ... -- do coarse-resolution actions else ... -- do fine-resolution actions end if;
For resolution limits less than or equal to ns, the test returns false, so the “else” alternative is taken. For resolution limits greater than ns, the time literal 1.0E-9 sec is truncated to zero, and so the test returns true. Thus, even though the calculation is not quite what appears, it produces the result we want.
When we design models, we can define types and operations using the built-in facilities of VHDL. However, the IEEE has published standards for packages that define commonly used data types and operations. Using these standards can save us development time. Furthermore, many tool vendors provide optimized implementations of the standard packages, so using them makes our simulations run faster. In this section, we outline the types and operations defined in a number of the IEEE standard packages. Complete details of the package declarations are included in Appendix A. Each of these packages is included in a library called ieee. Hence, to use one of the packages in a design, we name the library ieee in a library clause, and name the required package in a use clause. We have seen examples of how to do this for the IEEE standard package std_logic_1164; the same applies for the other IEEE standard packages.
The IEEE standard packages math_real and math_complex define constants and mathematical functions on real and complex numbers, respectively.
The constants defined in math_real are listed in Table 9.1. The functions, their operand types and meanings are listed in Table 9.2. In the figure, the parameters x and y are of type real, and the parameter n is of type integer.
Table 9.1. Constants defined in the package math_real
Value | Constant | Value | |
|---|---|---|---|
| e |
| ln2 |
| 1/e |
| ln10 |
| π |
| log2 e |
| 2π |
| log10 e |
| 1/π |
|
|
| π/2 |
|
|
| π/3 |
|
|
| π/4 |
| 2π/360 |
| 3π/2 |
| 360/2π |
Table 9.2. Functions defined in the package math_real
Function | Meaning | Function | Meaning |
|---|---|---|---|
| Ceiling of x (least integer ≥ x)Floor of x (greatest integer ≤ x)x rounded to nearest integer value (ties rounded away from 0.0)x truncated toward 0.0 |
| Sign of x (-1.0, 0.0 or +1.0)Floating-point modulus of x/yGreater of x and yLesser of x and y |
|
|
| lnxlog2xlog10xlogyx |
| sin x (x in radians)cos x (x in radians)tan x (x in radians) |
| arcsin xarccos xarctan xarctan of point (x, y) |
sinh xcosh xtanh x |
| arcsinh xarccosh xarctanh x |
In addition to the functions listed in Table 9.2, the math_real package defines the procedure uniform as follows:
procedure uniform ( variable seed1, seed2 : inout positive; variable × : out real);
This procedure generates successive values between 0.0 and 1.0 (exclusive) in a pseudo-random number sequence. The variables seed1 and seed2 store the state of the generator and are modified by each call to the procedure. Seed1 must be initialized to a value between 1 and 2,147,483,562, and seed2 to a value between 1 and 2,147,483,398, before the first call to uniform.
Example 9.2. A random-stimulus test bench for an ALU
Suppose we need to test a structural implementation of an ALU, whose entity is declared as follows:
use ieee.numeric_bit.all; subtype ALU_func is unsigned(3 downto 0); subtype data_word is unsigned(15 downto 0); ... entity ALU is port ( a, b : in data_word; func : in ALU_func; result : out data_word; carry : out bit ); end entity ALU;
We can devise a test bench that stimulates an instance of the ALU with randomly generated data and function-code inputs:
architecture random_test of test_ALU is use ieee.numeric_bit.all; use ieee.math_real.uniform; signal a, b, result : data_word; signal func : ALU_func; signal carry : bit; begin dut : entity work.ALU(structural) port map ( a, b, func, result, carry ); stimulus : process is variable seed1, seed2 : positive := 1; variable a_real, b_real, func_real : real; begin wait for 100 ns; uniform ( seed1, seed2, a_real ); uniform ( seed1, seed2, b_real ); uniform ( seed1, seed2, func_real ); a <= to_unsigned( natural(a_real * real(2**integer'(data_word'length)) - 0.5), data_word'length ); b <= to_unsigned( natural(b_real * real(2**integer'(data_word'length)) - 0.5), data_word'length ); func <= to_unsigned( natural(func_real * real(2**integer'(ALU_func'length)) - 0.5), ALU_func'length ); end process stimulus; ... --verification process to check result and carry end architecture random_test;
The stimulus process generates new random stimuli for the ALU input signals every 100 ns. The process generates three random numbers in the range (0.0, 1.0) in the variables a_real, b_real and func_real. It then scales these values to get numbers in the range (–0.5, 65,635.5) for the data values and (–0.5, 15.5) for the function code value. These are rounded and converted to unsigned bit vectors for assignment to the ALU input signals.
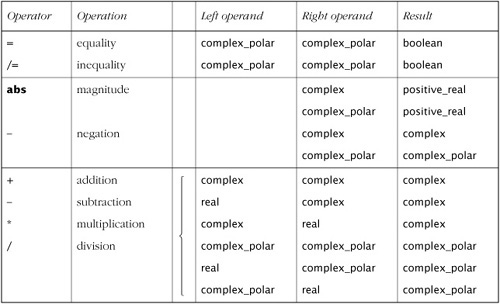
The math_complex package deals with complex numbers represented in Cartesian and polar form. The package defines types for these representations, as follows:
type complex is record re : real; -- Real part im : real; -- Imaginary part end record; subtype positive_real is real range 0.0 to real'high; subtype principal_value is real range -math_pi to math_pi; type complex_polar is record mag : positive_real; -- Magnitude arg : principal_value; -- Angle in radians; -math_pi is illegal end record;
The constants defined in math_complex are
math_cbase_11.0 + j0.0math_cbase_j0.0 + j1.0math_czero0.0 + j0.0
The package defines a number of overloaded operators, listed in Table 9.3. The curly braces indicate that for each operator to the left of the brace, there are overloaded versions for all combinations of types to the right of the brace. Thus, there are six overloaded versions of each of the “+”, “–”, “*” and “/” operators.
Overloaded versions of “=” and “/=” are necessary for numbers in polar form, since two complex numbers are equal if their magnitudes are both 0.0, even if their arguments are different. The predefined equality and inequality operators do not have this behavior. No overloaded versions of these operators are required for Cartesian form, since the predefined operators behave correctly.
In addition to the operators, the math_complex package defines a number of mathematical functions, listed in Table 9.4. In the table, the parameters x and y are real, the parameter c is complex, the parameter p is complex_polar, and the parameter z is either complex or complex_polar.
Table 9.4. Functions defined in the package math_complex
Function | Result type | Meaning |
|---|---|---|
|
| x + jyx + 2πk for some k,such that -π < result ≤ πc in polar formp in Cartesian form |
|
| arg(z) in radianscomplex conjugate of z |
| same as |
|
| same as | lnzlog2zlog10zlogyz |
| same as | sinzcoszsinhzcoshz |
The IEEE standard package std_logic_1164 defines types and operations for models that need to deal with strong, weak and high-impedance strengths, and with unknown values. We have already described most of the types and operations in previous chapters and seen their use in examples. For completeness, we draw the information together in this section.
The types declared in std_logic_1164 are
| The basic multivalued enumeration type (see page 48) |
| Array of std_ulogicelements (see page 108) |
| Resolved multivalued enumeration subtype (see Section 8.1.3 on page 278) |
| Subtype of std_ulogic_vector with resolved elements (see Section 8.1.3 on page 278) |
In addition, the package declares the subtypes X01, X01Z, UX01 and UX01Z for cases where we do not need to distinguish between strong and weak driving strengths. Each of these subtypes includes just the values listed in the subtype name.
Since the type std_ulogic and the subtype std_logic are scalar enumeration types, all of the predefined operations for such types are available. This includes the relational operators, maximum, minimum, and to_string. In addition, the matching relational operators “?=”, “?/=”, “?>”, “?>=”, “?<”, and “?<=” are predefined for std_ulogic and std_logic. For the array type std_ulogic_vector and the subtype std_logic_vector, the predefined operations on one-dimensional arrays of discrete-type elements are available. This includes “&” and the relational operators. In addition, the matching equality (“?=”) and inequality (“?/=”) operators are defined for these types.
The operations provided by the std_logic_1164 package include overloaded versions of the logical operators and, nand, or, nor, xor, xnor and not, operating on values of each of the scalar and vector types and subtypes listed above. It also includes overloaded versions of the shift operators sll, srl, rol and ror operating on the vector types. It does not overload the sla and sra operators on the premise that they assume a numeric interpretation of vectors. Instead, those operators are overloaded in separate packages, numeric_std and numeric_std_unsigned, that provide arithmetic operations assuming a numeric interpretation (see Section 9.2.3). The std_logic_1164 package provides an overloaded version of the “??” operator, allowing std_ulogic and std_logic value to be used in conditions with implicit conversion.
In Section 4.3.5 we described the to_ostring and to_hstring operations for converting bit_vector operands to strings in octal and hexadecimal form. The std_logic_1164 package provides overloaded versions of these operations for std_ulogic_vector and std_logic_vector operands. The operations group elements into threes (octal) or fours (hexadecimal) for conversion into digits. However, if the vector needs to be extended on the left to make a multiple of three or four, the assumed value for the extra elements depends on the leftmost actual element. If the leftmost element is ‘Z’, then ‘Z’ elements are assumed; if it is ‘X’, then ‘X’ elements are assumed; otherwise, ‘0’ elements are assumed.
Having grouped elements, they are converted to digits. If all of the elements in a group are ‘0’, ‘L’, ‘1’, or ‘H’, the group is converted to a normal digit character, with ‘0’ and ‘L’ elements treated as ‘0’, and ‘1’ and ‘H’ elements treated as ‘1’. If all of the elements in a group are ‘Z’, then ‘Z’ is used as the digit character for the group. In all other cases, where a group contains one or more non-‘0’, -‘L’, -‘1’, -‘H’ or -‘Z’ elements, ‘X’ is used as the digit character for the group. Some examples are
to_ostring(B"01L_1H1") = "27" to_ostring(B"011_ZZZ") = "3Z" to_ostring(B"01U_UZZ") = "XX" to_ostring(B"HH_000") = to_ostring(B"0HH_000") = "30" to_ostring(B"ZZ_ZZZ") = to_ostring(B"ZZZ_ZZZ") = "ZZ" to_ostring(B"X1_000") = to_ostring(B"XX1_000") = "X0" to_ostring(B"1X_000") = to_ostring(B"01X_000") = "X0"
As well as providing the overloaded to_ostring and to_hstring operations, the std_logic_1164 package provides all of the alternative names: to_bstring, to_binary_string, to_octal_string, and to_hex_string. Further, the package provides overloaded versions of the file read and write operations for text-based input/output. We describe files and input/output in Chapter 16.
In addition to the overloaded operations, the package declares a number of functions for conversion between values of different types. In the following lists, the parameter b represents a bit value or bit vector, the parameter s represents a standard logic value or standard logic vector, and the parameter x represents a value of any of these types.
| Convert a standard logic value to a bit value |
| |
| |
| Convert a standard logic vector to a bit vector |
In these functions, the parameter xmap is a bit value that is used in the result when a bit to be converted is other than ‘0’, ‘1’, ‘L’ or ‘H’. There are multiple alternative names for the second function, allowing us to choose based on consideration of coding style.
| Convert a bit value to a standard logic value |
| |
| |
| Convert to a |
| |
| |
| Convert to a |
Note that the To_StdLogicVector and To_StdULogicVector function perform essentially the same operation. The fact that std_logic_vector has resolved elements is not relevant to the conversion. The two forms are provided for backward compatibility with previous versions of VHDL, where the distinction was relevant.
| Strip strength |
| Strip strength |
| Strip strength |
| Strip strength |
These strength-stripping functions remove the driving strength information from the parameter value. To_01 convert ‘L’ and ‘H’ digits in a vector to ‘0’ and ‘1’ digits. The optional second parameter specifies the result value to produce if any digit in the first parameter is other than ‘0’, ‘1’, ‘L’ or ‘H’. In that case, all digits of the result are set to the value specified in the second parameter. The default value of the second parameter is ‘0’. Some examples are
to_01( "LLHH01" ) = "001101" to_01( "00X11U" ) = "000110" to_01( "100LLL", 'X' ) = "100000" to_01( "00W000", 'X' ) = "XXXXXX"
To_X01 converts ‘U’, ‘X’, ‘Z’, ‘W’ and ‘–’ elements to ‘X’. To_X01Z is similar, but leaves ‘Z’ elements intact. To_UX01 is similar to To_X01, but leaves ‘U’ elements intact.
Finally, the std_logic_1164 package contains the following utility functions:
| True when there is a rising edge on s, false otherwise |
| True when there is a falling edge on s, false otherwise |
| True if scontains an unknown value, false otherwise |
The edge-detection functions detect changes between low and high values on a scalar signal, irrespective of the driving strengths of the values. The functions are true only during the simulation cycles on which such events occur. They serve the same purpose as the predefined functions of the same name operating on bit and boolean signals. The unknown-detection function determines whether there is a ‘U’, ‘X’, ‘Z’ or ‘W’ value in the scalar or vector value s.
VHDL-87, -93, and -2002
In the version of std_logic_1164 for these versions of VHDL, std_ulogic_vector and std_logic_vector were declared as distinct array types, rather than one being a subtype of the other. This led to considerable inconvenience when both types were used in a design. The std_logic_1164 package provided separate overloaded declarations for operations on each of the two types, and additional conversion functions between them were required.
Since VHDL-2008 adds numerous new predefined operations, the VHDL-2008 version of the package provides overloaded versions of them. They are not provided in the version of the package for earlier versions of VHDL.
The IEEE standard packages numeric_bit and numeric_std define arithmetic operations on integers represented using vectors of bit and std_ulogic elements respectively. Most synthesis tools accept models that use these types and operations for numeric computations. We discuss the topic of synthesis of VHDL models in more detail in Chapter 21. In this section, we outline the types and operations provided by the IEEE standard integer numeric packages. Full listings of the package declarations are included in Appendix A.
Each of the packages defines two types, unsigned and signed, to represent unsigned and signed integer values, respectively. In the case of the numeric_bit package, the types are unconstrained arrays of bit elements:
type unsigned is array ( natural range <> ) of bit; type signed is array ( natural range <> ) of bit;
In the case of the numeric_std package, the types are defined similarly, but with resolved std_ulogic as the element type. This package also defines the types unresolved_unsigned and unresolved_signed (and the shorter aliases u_unsigned and u_signed) as arrays of unresolved std_ulogic elements. The declarations are
type unresolved_unsigned is array (natural range <>) of std_ulogic; type unresolved_signed is array (natural range <>) of std_ulogic; alias u_unsigned is unresolved_unsigned; alias u_signed is unresolved_signed; subtype unsigned is (resolved) unresolved_unsigned; subtype signed is (resolved) unresolved_signed;
Whichever package and type we use, the leftmost element is the most-significant digit, and the rightmost element is the least-significant digit. Signed numbers are represented using two’s-complement encoding.
We declare objects of these types either directly or using a subtype to define the index range. For example:
signal head_position : signed ( 0 to 15 ); subtype address is unsigned ( 31 downto 0 ); signal next_PC : address; constant PC_increment : unsigned := X"4";
The operations defined for unsigned and signed numbers are listed in Table 9.5. The curly braces indicate that for each operator to the left of the brace, there are overloaded versions for all combinations of types to the right of the brace. For example, there are six overloaded versions of each of the “+”, “–”, “*”, “/”, rem and mod operators. The notation “element type” refers to the element type (bit or std_ulogic) of the vector operand or operands.
The operands of arithmetic and relational operators need not be of the same length. The relational operators determine the result based on the numeric values represented by the operands, rather than using left-to-right lexicographic comparison. For those operators that produce a vector result, the length of the result depends on the length of the operands, as follows.
absand “–”: the length of the operandAddition and subtraction of two vectors: the larger of the two operand lengths
Addition and subtraction of a vector and an integer, natural number or scalar element: the length of the vector operand
Multiplication of two vectors: the sum of the operand lengths
Multiplication of a vector and an integer or natural number: twice the length of the vector operand
Remainder and modulo of two vectors: the length of the right operand
Division, remainder and modulo of a vector and an integer or natural number: the length of the vector operand. If the result value is too large to fit in the result vector, the value is truncated and a warning issued during simulation.
Shift and rotate operators: the length of the vector operand
not: the length of the operandBinary logical operators: the length of the operands, whose lengths must be the same
Example 9.3. Addition with carry
The addition operator that has two vector operands can be used to produce both the sum vector and a carry bit by extending the operands. For example, if we declare unsigned operand signals and a carry signal as
signal a, b, sum : unsigned(15 downto 0); signal c_out : std_ulogic;
we can write an assignment that produces both the sum and the carry value:
(c_out, sum) <= ('0' & a) + ('0' & b);The concatenations extend the operands by one bit, so the addition produces a 17-bit result. This is assigned to the aggregate of the carry signal (the leftmost bit of the result) and the sum signal (the rightmost 16 bits of the result).
The addition and subtraction operators that have an operand of the scalar element type allow us to describe an addition with carry in or a subtraction with borrow in. For example:
signal a, b : unsigned(15 downto 0); signal sum : unsigned(16 downto 0); signal c_in; ... sum <= ('0' & a) + ('0' & b) + c_in;
This can be synthesized as a single 16-bit adder with a carry input and a 17-bit result.
Example 9.4. A conditional incrementer
We can use the “+” operator to treat a scalar control signal as an operand in a conditional incrementer. If the control signal is ‘0’, an unsigned operand value is not incremented; if the control signal is ‘1’’, the value is incremented. The declarations and process are:
signal inc_en : std_ulogic; signal inc_reg : unsigned(7 downto 0); ... inc_reg_proc : process (clk) is begin if rising_edge(clk) then inc_reg <= inc_reg + inc_en; end if; end process inc_reg_proc;
If we had written the if statement as follows:
if inc_en = '1' then inc_reg <= inc_reg + 1; end if;
a synthesis tool might have generated an adder with the vector “00000001”as an input, connected to a regsiter with clock enable. By using the control signal as an operand, we more clearly imply an incrementer and a simple register without clock enable. We discuss coding styles for synthesis in more detail in Chapter 21.
For the division, remainder and modulo operators, if the right operand is zero, an assertion violation with severity level error is issued during simulation.
The logical shift operators sll and srl fill the vacated elements with ‘0’. Their behavior is the same as that of the predefined operators for bit_vector values. The behavior of the sla and sra operators, on the other hand, is different from the predefined versions, in that they assume a binary-coded numeric interpretation for a vector. The type of the left operand determines the kind of shift performed. If the operand is unsigned, a logical shift is performed, whereas if the parameter is signed, an arithmetic shift is performed. An arithmetic shift right (sra with a positive right operand or sla with a negative right operand) replicates the sign bit, giving the effect of division by a power of 2. An arithmetic shift left (sra with a negative right operand or sla with a positive right operand) fills the vacated bits on the right with ‘0’, giving the effect of multiplication by a power of 2.
In addition to the overloaded operators, the numeric_bit and numeric_std packages define a number of functions, listed in Table 9.6. As in Table 9.5, the curly braces indicate that for each function to the left of the brace, there are overloaded versions for all combinations of types to the right of the brace.
The maximum and minimum functions are overloaded to compare their operands based on a numeric interpretation in the same way as the relational operators. For the versions that take two vector operands, the operands do not need to be of the same length.
The shift, rotate and to_01 functions all produce a result that has the same length as the vector parameter. The shift and rotate functions perform similar operations to the overloaded shift and rotate operators. However, their second parameter is constrained to be a non-negative integer. Hence each of these functions can only shift or rotate elements in one direction. These functions were included in the package for earlier versions of VHDL that did not include the shift operators. They are maintained in the package for backward compatibility.
The find_leftmost function returns the index of the leftmost occurrence of the right-operand value in the left-operand vector. Similarly, the find_rightmost function returns the index of the rightmost occurrence of the right-operand value in the left-operand vector. If there is no such occurrence, the functions return –1. Since the index bound of an unsigned or signed vector are natural numbers, –1 is a clear indication that the value was not found. In both functions, search for the element value is performed using a matching equality test. We can use find_leftmost to gauge the magnitude of a number, since the leftmost occurrence of a 1 bit in an unsigned number is approximately log2 of the number. For a signed number, the leftmost bit that differs from the sign bit is likewise approximately log2 of the number.
The resize functions produce a result whose length is specified by the second parameter. For a second parameter of type natural, the parameter value specifies the number of bits in the result directly. For a second parameter of type unsigned or signed, the result has the same number of bits as the parameter value. Increasing the size of an unsigned number zero-extends to the left, whereas increasing the size of a signed number replicates the sign bit to the left. Truncating an unsigned number to length L keeps the rightmost L bits. Truncating a signed number to length L keeps the sign bit and the rightmost L – 1 bits.
The to_integer functions convert unsigned or signed values to natural or integer values, respectively. The to_unsigned and to_signed functions convert their first parameter to a vector whose length is given by the second parameter, either as a natural number directly, or as a vector whose length is used.
The edge-detection functions rising_edge and falling_edge are provided as aliases for the predefined edge-detection functions on type bit. They are included here for backward compatibility with earlier versions of VHDL, in which the edge-detection functions were not predefined. The std_match functions perform the same operations as the “?=” operator. Again, they are included for backward compatibility with earlier versions of VHDL that did not provide that operator.
The strength-stripping functions to_01, to_X01, to_X01Z, and to_UX01 are overloaded for unsigned and signed operands, and perform the same operation as the corresponding functions for vectors in the std_logic_1164 package.
Finally, the packages provide the string conversion operations. The to_string operation is actually predefined for unsigned and signed, since they are one-dimensional arrays of character elements in both packages. The to_ostring and to_hstring operations work in the same way as the corresponding operations in the std_logic_1164 package. The only difference is that, when extending a signed value to form a complete group of three (for octal) or four (for hexadecimal) bits, the sign bit is replicated rather than ‘0’ bits being added. The same aliases for all of the operations are also defined. Further, the packages provide overloaded versions of the file read and write operations for text-based input/ output. We describe files and input/output in Chapter 16.
VHDL-87, -93, and -2002
Since VHDL-2008 adds numerous new predefined operations, the VHDL-2008 version of the package provides overloaded versions of them. They are not provided in the version of the package for earlier versions of VHDL.
VHDL-87
Since VHDL-87 does not include the shift, rotate and xnor operators, they should be commented out of the standard synthesis packages when used with VHDL-87 tools. The shift and rotate functions can be used in VHDL-87 models. The xnor operator can be expressed as the negation (not) of the xor operator in VHDL-87.
Since the standard numeric packages are widely used in many models, VHDL defines two standard context declarations (see Section 5.4.2) within the standard library ieee:
context ieee_bit_context is library ieee; use ieee.numeric_bit.all; end context ieee_bit_context; context ieee_std_context is library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; end context ieee_std_context;
A design based on bit values might refer to the first of these context declarations, either in the context clause of a design unit or nested within a project context declaration. Similarly, a design based on std_ulogic values might refer to the second of these context declarations.
VHDL-87, -93, and -2002
Since context declarations are not provided in these versions of VHDL, the standard context declaration cannot be used. If a tool does not support VHDL-2008, it would not include the context declarations in its version of the ieee library.
As we have mentioned, the numeric_bit and numeric_std packages define new array types, unsigned and signed, to represent numbers in binary-coded form. Many designers, however, prefer to use the bit_vector and std_ulogic_vector types for numeric data. This approach is particularly useful in designs that include components, such as multiplexers, registers, and so on, that do not rely on numeric properties of data; they just store or manipulate arrays of bits. When such designs also include arithmetic elements, having to convert between the types for numeric interpretation and the plain vector type is a distraction. Historically, designers have adopted non-standard packages that provide arithmetic operations on bit_vector or std_ulogic_vector operands.
In the 2008 revision of VHDL, two new packages were added to library ieee for this purpose: numeric_bit_unsigned and numeric_std_unsigned. They are largely compatible with numeric_bit and numeric_std, respectively, and provide the corresponding unsigned operations. In summary, the similarities and differences among the packages are
Numeric_bit_unsignedandnumeric_std_unsignedprovide the following operations corresponding to operations on unsigned innumeric_bitandnumeric_std: arithmetic operators, shift operators, and relational operators;maximum,minimum,shift_left,shift_right,find_leftmost,find_rightmost,resize, andto_integerfunctions.Numeric_bit_unsignedprovides ato_bitvectorfunction (plus aliasesto_bit_vectorandto_bv) instead ofto_unsigned.Numeric_std_unsignedprovidesto_stdulogicvectorandto_stdlogicvectorfunctions (plus aliasesto_std_ulogic_vector,to_sulv,to_std_logic_vector, andto_slv) instead ofto_unsigned.Numeric_bit_unsignedandnumeric_std_unsigneddo not provided other operations, since the normalbit_vectorandstd_ulogic_vectorversions can be used. This includes overloaded logical operators;rising_edge,falling_edge,std_matchand strength-stripping functions;to_ostringandto_hstringfunctions and the corresponding aliases; and read and write operations.
Many digital-signal processing applications involve mathematical operations on non-integral data. While we could use floating-point representation and hardware, that would be excessively resource intensive in many cases. Instead, we can use a fixed-point representation, in which the radix point (analogous to the base-10 decimal point) is assumed to have a fixed position. VHDL defines a number of packages for fixed-point math that we introduce in this section. Since the packages provide a large number of overloaded operations and functions, we will not describe them in full detail here. We will simply provide an overview of the data types provided and some basic information on their usage. More details are provided in Appendix A and on the author’s companion website for this book. In addition, Section 9.2.6 summarizes the operations provided by these packages and the other standard numeric packages.
For simple cases, fixed-point math amounts to integer math with scaling by a power of 2. More generally, we need to take account of rounding and overflow. The main VHDL fixed-point package, fixed_generic_pkg, is written in such a way that we can choose the rounding and overflow behaviors that are most appropriate for our application. The package uses formal generic constants, a topic that we will cover in detail in Chapter 12. For now, suffice it to say that the package defines four constants as follows:
fixed_round_style : fixed_round_style_typeThis constant determines the rounding behavior for operations in the package. The type
fixed_round_style_typeis an enumeration type defined in the packagefixed_float_types, also in libraryieee. The values arefixed_round, if results are to be rounded to the nearest representable value; andfixed_truncate, if results are to be truncated toward zero to the next smallest representable value. The default isfixed_round.fixed_overflow_style : fixed_overflow_style_typeThis constant determines the behavior on overflow. The type
fixed_overlow_style_typeis defined in the packagefixed_float_types. The values arefixed_saturate, if an overflowing result is to remain at the largest representable value; andfixed_wrap, if modulo-based behavior is required. The default isfixed_saturate.fixed_guard_bits : naturalThis constant specifies the number of extra bits of precision to use for division operations. The default is 3.
no_warning : booleanThis constant allows suppression of warning messages on conditions such as non-matching operand lengths and occurrence of metalogical values (values other than ‘0’, ‘L’, ‘1’ and ‘H’). The default is
false.
If the default values are acceptable for our application, we can use a version of the package named fixed_pkg, located in the ieee library. For other cases, the main package must be instantiated, as described in Chapter 12, to supply alternative values for the constants.
The package fixed_generic_pkg (and any instance of it, such as fixed_pkg) defines types for unsigned and signed fixed-point representation in the form of vectors of std_ulogic elements. The base type for unsigned representation is unresolved_ufixed, declared as
type unresolved_ufixed is array (integer range <>) of std_ulogic;
The name u_ufixed is defined, for convenience, as an alias to unresolved_ufixed. The package also defines a subtype ufixed with resolved elements. The declarations are
alias u_ufixed is unresolved_ufixed; subtype ufixed is (resolved) unresolved_ufixed;
When declaring signals, we should choose between the base type or the subtype with resolved elements, depending on whether the signal has only one source or multiple sources, respectively.
Objects of these types must have descending (downto) index ranges. The whole-number part of the value is on the left of the vector, down to index 0, and the fractional part is on the right, starting at index –1. For example, given the following declaration of a fixed-point signal A:
signal A : ufixed(3 downto -3) := "0110100";
the whole-number part is A(3 downto 0), and the fractional part is A(–1 downto –3). The range of values represented is 0 to just less than 16 in steps of 0.125 (one-eighth). The value represented by the default initial value is 0110.1002 = 6.510.
This example shows a number with both whole-number and fractional parts. In general, we can declare number with just a whole-number part (the right index being 0) or just a fraction part (the left index being –1). Indeed, we can declare numbers in which the radix point is completely outside the index range of the vector. For example, in the following:
variable X : ufixed(9 downto 2); variable Y : ufixed(-5 downto -14);
X is an 8-bit vector representing values in the range 0 to 1020 in steps of 4, and Y is a 10-bit vector representing values in the range 0 to just less than 0.0625 (one-sixteenth) in steps of 2–14.
The base type defined in the package for signed representation is unresolved_sfixed, declared as:
type unresolved_sfixed is array (integer range <>) of std_ulogic;
As for the unsigned representation, there is an alias, u_sfixed, and a subtype with resolved elements, sfixed:
alias u_sfixed is unresolved_sfixed; subtype sfixed is (resolved) unresolved_sfixed;
Likewise, the index range for a signed value must be descending (downto), with the radix point being assumed between index 0 and index –1. The difference is that the signed type and subtypes use 2s-complement binary representation, with the leftmost bit being the sign bit. Thus, for example, the signal:
signal S : sfixed(3 downto -3);
represents values from –8 to just less than 8 in steps of 0.125.
The fixed-point math packages perform operations with full precision. This is illustrated in the following example:
signal A4_2 : ufixed(3 downto -2); signal B3_3 : ufixed(2 downto -3); signal Y5_3 : ufixed(4 downto -3); ... Y5_3 <= A4_2 + B3_3;
The whole-number part of the addition result is one bit larger than the larger of the two operand whole-number parts. In this example, the operand whole-number parts are 4 bits and 3 bits, respectively, so the result’s whole-number part is 5 bits. The fractional part of the result is the larger fractional part of the operands. In this example, the operands’ fractional parts are 2 bits and 3 bits, respectively, so the result has a 3-bit fractional part.
If we want to assign a fixed-point value to an object, one way is to use a string literal, for example:
signal A4 : ufixed(3 downto -3); ... A4 <= "0110100"; -- string literal for 6.5
Alternatively, we can apply a conversion function, to_ufixed or to_sfixed, to an integer or real value. In this case, we need to specify the index range for the conversion result. There are two forms of conversion function. For the first form, we specify the left and right indices for the result, for example:
A4 <= to_ufixed(6.5, 3, -3); -- pass indicesFor the second form, we provide an object whose index range is used:
A4 <= to_ufixed(6.5, A4); -- sized by A4In this example, the only use of A4 by the to_ufixed function is to read its left and right indices to determine the index range of the result.
The use of a string literal in an arithmetic expression is problematic, since the index range of such a literal is ascending (to) and starts with integer’low. Fixed-point numbers must have descending index ranges. Instead we can use integer literals, real literals, and qualified string literals, as shown in the following examples:
subtype ufixed4_3 is ufixed(3 downto -3); signal A4, B4 : ufixed4_3; signal Y5 : ufixed (4 downto -3); ... Y5 <= A4 + "0110100"; -- illegal Y5 <= A4 + ufixed4_3'("0110100"); Y5 <= A4 + 6.5; -- overloading with real Y5 <= A4 + 6; -- overloading with integer
In the assignment marked “illegal,” the index range of the string literal would be integer‘low to integer‘low + 6. The type qualification in the next assignment avoids this problem and results in a bit-string value with index bounds taken from the subtype ufixed4_3. We can safely apply the addition operator to this value and the operand A4, giving a result with index range 4 down to –3.
If we need to change the size of an expression result, we can use a resize function. As for the conversion functions, there are two forms, one in which we specify the left and right index values and the other in which we provide an object whose index range is used. For example, in the following accumulator assignment, since the addition result is one bit larger than the accumulator, we need to resize the result:
signal A4_3 : ufixed(3 downto -3); signal Y7_3 : ufixed(6 downto -3); ... Y7_3 <= Y7_3 + A4_3; -- illegal, result too big Y7_3 <= resize(arg => Y7_3 + A4_3, size_res => Y7_3, overflow_style => fixed_wrap, round_style => fixed_truncate);
The overflow_style and round_style parameters allow us to control the way the value is processed if it cannot be represented exactly. The default values for these parameters are taken from the package constants described on page 314. If those values are satisfactory, we can omit them in the resize call. This is shown in the following example, which uses the form of the function specifying left and right index values for the result:
Y7_3 <= resize (arg => Y7_3 + A4_3,
left_index => 7,
right_index => -3);Full-precision arithmetic can lead to some unexpected results in expressions involving multiple operators. Consider, as an example, the following declarations and assignment:
signal A4, B4, C4, D4 : ufixed(3 downto 0); signal Y6 : ufixed(5 downto 0); signal Y7A, Y7B : ufixed(6 downto 0); ... Y6 <= (A4 + B4) + (C4 + D4);
The expression in the assignment is built as a balanced tree. Each of the additions A4 + B4 and C4 + D4 yields a 5-bit result, so the final result size is 6 bits. However, if we build the expression in a cascaded fashion, the result size is 7 bits. We can see this most clearly by explicitly parenthesizing the expression:
Y7A <= ((A4 + B4) + C4) + D4;
The addition A4 + B4 yields a 5-bit result. This added to C4 yields a 6-bit result, and the 6-bit result added to D4 yields a 7-bit result. Since addition is associative, the following unparenthesized expression yields the same 7-bit result:
Y7B <= A4 + B4 + C4 + D4;
Included in the set of operations provided by the fixed-point packages are overloaded versions of the string conversion operations and file read and write operations for text-based input/output. Since the ufixed and sfixed types are one-dimensional arrays of character elements, to_string is predefined for both types. However, the packages overload the operation with a version that includes a radix point (a ‘.’ character) at the appropriate position. For example, given the following declaration:
constant x : ufixed(3 downto -8) := "010000110101";
to_string(x) returns the string “0100.00110101”.
The packages also define overloaded versions of to_ostring and to_hstring that behave similarly to the versions for the integer numeric packages (see Section 9.2.3). Elements are grouped into threes (for octal) or fours (for hexadecimal) starting either side of the radix point. Extension on the left to make up a complete group is performed in the same way as for unsigned and signed numeric values. If extension is required on the right, ‘0’ bits are added. For values in which the radix-point position lies outside the index range, to_ostring and to_hstring extend the value to include the radix point in the result. For example, a to_hstring operation for the value “10100”with index range 7 down to 3 would result in the string “A0.0”, corresponding to the binary number 10100000.0. Similarly, a to_hstring operation for the value “10100”with index range –3 down to –7 would result in “0.28” (0.0010100 in binary).
The fixed-point math packages described in the previous section allow us to represent non-integral values with constant absolute precision over a given range. In some applications, however, we would prefer to use a floating-point representation, in which we can represent a greater dynamic range with a given number of bits, and have constant relative precision over the range. VHDL provides abstract floating-point types, including the type real, built into the language. However, they are defined to use IEEE 64-bit double-precision representation. That may not be the best choice for all applications. VHDL provides a set of packages for binary-coded floating-point representation and operations in which we can control the range and precision and many aspects of the way arithmetic operations are performed. Floating-point values are represented using the same principles as IEEE-standard floating-point, specified in IEEE Std 754 [9] and IEEE Std 854 [10], with a sign bit, an exponent field, and a fraction field. However, we can choose the field widths that are appropriate for our application.
Since these packages, like the fixed-point packages, provide a large number of overloaded operations and functions, we will not describe them in full detail here. Again, we will simply provide an overview of the data types provided and some basic information on their usage. More details are provided in Appendix A and on the author’s companion website; and Section 9.2.6 summarizes the operations provided.
Like the main fixed-point package, the main VHDL fixed-point package, float_generic_pkg, is written using formal generic constants so that we can choose the behaviors that are most appropriate for our application. The package defines seven constants as follows:
float_exponent_width : naturalThis constant determines the default width of the exponent field resulting from the
to_floatconversion functions in the package. The default is 8, corresponding to IEEE single-precision representation.float_fraction_width : naturalThis constant determines the default width of the fraction field resulting from the
to_floatconversion functions in the package. The default is 23, corresponding to IEEE single-precision representation.float_round_style : round_typeThis constant determines the rounding behavior for operations in the package. The type
round_typeis an enumeration type defined in the packagefixed_float_types, also in libraryieee. The values are:round_nearest,round_zero(truncation),round_inf(round up toward infinity) andround_neginf(round down toward negative infinity). The default isround_nearest.float_denormalize : booleanDenormalized numbers are a form of floating-point numbers that represent very small values near zero. If the constant
float_denormalizedis true, operations in the package deal with denormalized values; otherwise, all numbers are treated as normalized. The default istrue.float_check_error : booleanThis constant controls detection of invalid numbers and overflow. The default is
true.float_guard_bits : naturalThis constant specifies the number of extra bits of precision to use within operations prior to rounding the result. The default is 3.
no_warning : booleanThis constant allows suppression of warning messages. The default is
false.
The main package also makes use of the fixed-point package, both for conversions between fixed-point and floating-point values and for internal implementation of floating-point operations. Since we can choose the way the fixed-point package behaves by varying the values of its constants, we need to provide the floating-point package with a reference the appropriate version of the fixed-point package for our application. We can do this, if we need to, using the mechanism of formal generic packages, described in Chapter 12. If the default values for the constants are acceptable for our application, we can use a version of the package named float_pkg, located in the ieee library. For other cases, the main package must be instantiated, as described in Chapter 12, to supply alternative values for the constants.
The package float_generic_pkg (and each instance of it, such as float_pkg) defines the base type for floating-point numbers, unresolved_float, declared as:
type unresolved_float is array (integer range <>) of std_ulogic;
The alias u_float is defined as a convenient shorthand for this type. There is also a subtype, float, which has resolved elements. The declarations are:
alias u_float is unresolved_float; subtype float is (resolved) unresolved_float;
When declaring signals, we should choose between the base type or the subtype with resolved elements, depending on whether the signal has only one source or multiple sources, respectively.
Objects of these types must have descending (downto) index ranges; for example:
signal A : float(8 downto -23) := "01000000110100000000000000000000";
The sign bit is at index A‘left (bit 8 in this example), the exponent is indexed from A‘left – 1 down to 0 (7 down to 0 in the example), and the fraction is indexed from –1 down to A‘right (–1 down to –23 in the example). Unlike fixed-point numbers, floating-point numbers must have the sign, exponent, and fraction all present. The smallest floating-point representation supported by the package has a range of 3 down to –3. In practice, we would expect representations to be 16 bits or more, with at least 6 bits for the exponent and at least 10 bits for the fraction. For the sign bit, 0 is positive, and 1 is negative. The exponent field is an unsigned binary value representing the actual exponent biased by 2e – 1 – 1 (where e is the width of the exponent field). Thus, for the signal A declared above, the bias is 127. The actual fraction is normalized to the range of 1.0 to just less than 2.0. Since the bit to the left of the radix point would always be 1, it is not explicitly represented. Instead, the fraction field of a floating-point number just contains the bits to the right of the radix point, with a 1 bit implied to the left of the radix point.
We can use these properties of the representation to analyze the bit string used as the default initial value for the signal A above. The leftmost bit is 0, so the number is positive. The next 8 bits, A(7 downto 0), are 10000001. As an unsigned number, this is 129. We subtract the bias, 127, to give an actual exponent of 2. The fraction field is 101000000000000000000000. We include the implied 1 bit to give an actual fraction of 1.101. Thus, the value represented is +1.1012 × 22 = 1.625 × 4 = 6.5.
The packages declare a number of subtypes and aliases for IEEE standard floating-point representations. The unresolved subtypes are
subtype unresolved_float32 is unresolved_float(8 downto -23); subtype unresolved_float64 is unresolved_float(11 downto -52); subtype unresolved_float128 is unresolved_float (15 downto -112);
The unresolved_float32 subtype correponds to IEEE Std 754 single-precision representation. There are a shorthand alias u_float32 and a subtype with resolved elements, float32. Similarly, unresolved_float64 corresponds to IEEE Std 754 double-precision representation (like double float in C, float*8 in Fortran, and real in VHDL), with an alias u_float64 and a subtype with resolve elements, float64; and unresolved_float128 corresponds to IEEE Std 854 extended-precision representation (like long double in C and float*16 in Fortran), with an alias u_float128 and a subtype with resolve elements, float128.
The IEEE floating-point number standards reserve a number of representations for special purposes. In particular, numbers with all 0 or all 1 bits in the exponent field have the following meanings:
Positive zero: 0 00000000 00000000000000000000000
Negative zero: 1 00000000 00000000000000000000000
Positive infinity: 0 11111111 00000000000000000000000
Negative infinity: 1 11111111 00000000000000000000000
Note that there are two representations of 0, one positive and the other negative. Operations on floating-point values generally treat them as equivalent. In addition to these representations, a number with all 1 bits in the exponent field and at least one 1 bit in the fraction field (such as 1 11111111 00000000000000000000001) is called Not-a-Number, or NaN. Such values can result from otherwise illegal operations, such as division of zero by zero, or square root of –1.
Here are some further examples of floating-point numbers. First, the following is a large float32 value (though not the largest, as that is just less than 2**128).
0 11111110 00000000000000000000000
= +1 × 2254–127 × (1.0 + 0.0)
= 2127 = 1.70141 × 1038
Next, the following is the smallest float32 value, without using denormals:
0 00000001 00000000000000000000000
= +1 × 21–127 × (1.0 + 0.0)
= 2–126 = 1.17549 × 10–38
Finally, the following is a small float32 value using denormals (though not the smallest):
0 00000000 10000000000000000000000
= +1 × 21–127 × (0.0 + 0.5)
= +1 × 2–126 × 0.5
= 2–127 = 5.87747 × 10–39
For floating-point math operations, the result always has the largest of the exponent sizes and fraction sizes of the operands. Most often, the numbers are all of the same size, as in the following example:
signal A32, B32, Y32 : float(8 downto -23); ... Y32 <= A32 + B32;
Further details of overloaded operations and result sizes are provided in the tables in Section 9.2.6.
If we want to assign a value to a floating-point object, we can either use a string literal or we can apply a to_float conversion function to an integer or real number. This is similar to the way in which we assign values to fixed-point objects (see Section 9.2.4). In the case of conversion functions, we can specify the result size either by specifying the exponent and fraction size, or by providing an object whose index range is used. These approaches are shown in the following example:
signal A_fp32 : float32; ... A_fp32 <= "01000000110100000000000000000000"; A_fp32 <= to_float(6.5, 8, -32); -- pass sizes A_fp32 <= to_float(6.5, A_fp32); -- size using A_fp32
As with fixed-point math, use of string literals in an expression is problematic, since their index ranges are ascending (to) and start with integer‘low. The solution is the same, namely, using type-qualified string literals or using overloaded operations that accept integer or real operands. These are shown in the following example:
signal A, Y : float32; ... Y <= A + "01000000110100000000000000000000"; -- illegal Y <= A + float32'("01000000110100000000000000000000"); Y <= A + 6.5; -- overloading with real Y <= A + 6; -- overloading with integer
The floating-point packages also include overloaded versions of the string conversion operations and file read and write operations for text-based input/output. The overload to_string operation includes colon characters to separate the sign, exponent, and fraction fields. For example, given the following declaration:
constant x : float(6 downto -11) := "011101100010001110";
to_string(x) returns the string “0:111011:00010001110”.
The floating-point packages also define overloaded versions of to_ostring and to_hstring that behave similarly to the versions for standard logic vectors (see Section 9.2.2). They do not attempt to include the radix point in the way that the fixed-point versions do, since the radix point is not at a fixed position.
In this section, we summarize the operations defined in the standard packages: std_logic_1164, numeric_std, numeric_bit, numeric_std_unsigned, and numeric_bit_unsigned, fixed_generic_pkg, and float_generic_pkg.
Table 9.7summarizes the operand and result types for overloaded operations defined in the standard packages. The table does not include the predefined operations on the various types.
Table 9.7. Operand and result types
Operators | Left | Right | Result |
|---|---|---|---|
Binary |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
| ||
Unary reduction |
|
| |
=, /=, <, <=, >, >= |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
?=, ?/=, ?<, ?<=, ?>, ?>= |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
|
|
Binary +, -, *, /, |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
Binary +, - |
|
|
|
|
|
| |
Unary -, |
|
| |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
Where overloaded operations are defined, the predefined operations are hidden. In the table, the notation use is as follows:
LogicArrayType: arrays of
std_ulogicelementsNumericArrayType:
signed,unsigned,ufixed,sfixed,float,bit_vectorwith operations innumeric_bit_unsignedvisible, orstd_ulogic_vectorwith operations innumeric_std_unsignedvisibleRealArrayType:
ufixed,sfixed, orfloatArrayElementType: the element type of the operand array or arrays
Table 9.8 summarizes the result size and/or index range for operations with array results. For arrays representing unsigned or signed integer values, only the size is relevant, as the leftmost bit is the most-significant bit and the rightmost bit is the least-significant bit. For fixed-point and floating-point values, the specific index bounds are relevant, as described in Sections 9.2.4 and 9.2.5. The notation for types is the same as that used in Table 9.7. In addition, L represents the left operand, R represents the right operand, A represents the array operand in the case where the other operand is scalar, and Result represents the result of the operation.
Table 9.8. Result sizes and index ranges
Result type | Result size and/or range | |
|---|---|---|
Array/array | ArrayOfBits | Result‘length = L‘length = R‘lengthFixed, Float: Result‘range = L‘range |
Array/scalar | ArrayOfBits | Result‘length = A‘lengthFixed, Float: Result‘range = A‘range |
| ArrayOfBits | Result‘length = R‘lengthFixed, Float: Result‘range = R‘range |
| ArrayOfBits | Result‘length = A‘lengthFixed, Float: Result‘range = A‘range |
+, -, *, /, | float | maximum(L’left, R’left) down to minimum(L‘right, R‘right) |
Binary +, - |
| maximum(L‘length, R‘length) - 1 down to 0 |
| maximum(L’left, R’left) + 1 down to minimum(L‘right, R‘right) | |
* |
| L‘length + R‘length - 1 down to 0 |
| L’left + R’left + 1 down to L‘right + R‘right | |
/ |
| L‘length - 1 down to 0 |
ufixed | L’left - R‘right down to L‘right - R’left - 1 | |
sfixed | L’left - R‘right + 1 down to L‘right - R’left | |
|
| R‘length - 1 down to 0 |
| minimum(L’left, R’left) down to minimum(L‘right, R‘right) | |
|
| R‘length - 1 down to 0 |
| minimum(L’left, R’left) down to minimum(L‘right, R‘right) | |
| R’left down to minimum(L‘right, R‘right) | |
Unary -, |
| R‘length - 1 down to 0 |
sfixed | R’left + 1 down to R‘right | |
| DiscreteArrayType | Result‘length = A‘length Fixed, Float: Result‘range = A‘range |
| maximum(L‘length, R‘length) - 1 down to 0 | |
| minimum(L’left, R’left) down to minimum(L‘right, R‘right) |
Next, we summarize the conversion functions defined in the standard packages. In order to present the information in more compact form, we have used some abbreviations for types and the packages in which the functions are defined: “bv” for bit_vector, “slv” for std_logic_vector, “sulv” for std_ulogic_vector, “1164” for std_logic_1164, “nbu” for numeric_bit_unsigned, “nsu” for numeric_std_unsigned, and “ns/b” for numeric_std and numeric_bit, “fixed” for fixed_generic_pkg, and “float” for float_generic_pkg.
Table 9.9 shows the functions that convert between bit and std_ulogic scalar types, and between vectors of these types. We use the shorthand aliases for the functions here for brevity. The first parameter is the value to be converted. The to_bit and to_bv functions have a second parameter, xmap, as described in Section 9.2.2, to specify how metalogical values should be mapped. Those functions that convert from an abstract numeric value to a vector representation have a second parameter, either a natural value, size, specifying the size of the result or a value of the result type, size_res, whose size is used for the result.
Table 9.9. Conversions between bit and standard-logic types
Function | Result type | Parameter 1 type | Parameter 2 | Package |
|---|---|---|---|---|
|
|
|
| 1164 |
|
|
| 1164 | |
|
| sulv |
| 1164 |
|
| nbu | ||
|
| nbu | ||
| sulv | bv | 1164 | |
slv | 1164 | |||
|
| nsu | ||
|
| nsu | ||
|
| |||
| fixed | |||
| float | |||
| slv | bv | 1164 | |
sulv | 1164 | |||
|
| nsu | ||
|
| nsu | ||
| fixed | |||
| fixed | |||
| float |
Table 9.10 shows the functions that convert from the various numeric types to the unsigned and signed types defined in numeric_std and numeric_bit. The first parameter is the value to be converted, and the second parameter is either a natural value, size, specifying the size of the result or a value of the result type, size_res, whose size is used for the result.
Table 9.10. Conversion functions yielding unsigned and signed values
Function | Result type | Param 1 type | Param 2 | Param 3 | Param 4 | Package |
|---|---|---|---|---|---|---|
|
|
|
| ns/b | ||
| ||||||
|
| overflow | round | fixed | ||
| overflow | round | ||||
|
| round | chk_err | float | ||
| round | chk_err | ||||
|
|
|
| ns/b | ||
| ||||||
|
| overflow | round | fixed | ||
| overflow | round | ||||
|
| round | chk_err | float | ||
| round | chk_err |
The conversions from fixed-point representation have a third parameter, overflow_style (abbreviated to “overflow” in the table), of type fixed_overflow_style_type. The default value is the value of the generic fixed_overflow_style. The fourth parameter, round_style (abbreviated to “round”), is of type fixed_round_style_type and defaults to the value of the generic fixed_round_style.
The conversions from float have a third parameter, round_style (abbreviated to “round”), of type round_type, with the default being the value of the package generic float_round_style. The fourth parameter is check_error (abbreviated to “chk_err”), of type boolean, for controlling error checking during the conversion. The default is the value of the package generic float_check_error.
Table 9.11 shows the functions that convert from numeric types to the ufixed and sfixed types defined in the fixed-point packages. In the case of conversion functions defined in the floating-point packages, the definitions of ufixed and sfixed come from the fixed-point package referenced as a generic package, as outlined in Section 9.2.5. The first parameter of each function is the value to be converted. Following this are either two parameters, left_index and right_index (abbreviated to “L_index” and “R_index” in the table), to specify the index bounds of the result, or a single parameter of the result type, size_res, whose index range is used for the result. For the conversions from natural or unsigned to ufixed, and for the conversions to integer or signed to sfixed, the default for right_index is 0. Additional parameters specify overflow and rounding modes (overflow_style and round_style), the number of guard bits to use (guard_bits), whether error checking is required (check_error), and whether operands of type float use denormalized representation (denormalize). The default values for the overflow_style, round_style, and guard_bits parameters come from the various generic constants of the packages. Note that there are also versions of to_ufixed and to_sfixed with no parameters beyond the first unsigned or signed parameter. (This is not an error in the table layout!) These versions simply return the value of the parameter as a fixed-point value with no fractional part (that is, indexed from one less than the length down to 0).
Table 9.11. Conversion functions yielding ufixed and sfixed values
Result type | Param 1 type | Param 2 | Param 3 | Param 4 | Param 5 | Param 6 | Param 7 | Package | |
|---|---|---|---|---|---|---|---|---|---|
|
|
| L_index | R_index | fixed | ||||
size_res | |||||||||
unsigned | |||||||||
L_index | R_index | overflow | round | ||||||
size_res | overflow | round | |||||||
| L_index | R_index | overflow | round | |||||
| overflow | round | |||||||
| L_index | R_index | overflow | round | guard | ||||
| overflow | round | guard | ||||||
float | L_index | R_index | overflow | round | chk_err | denorm | float | ||
| overflow | round | chk_err | denorm | |||||
|
|
| fixed | ||||||
sulv | L_index | R_index | |||||||
| |||||||||
signed | |||||||||
L_index | R_index | overflow | round | ||||||
| overflow | round | |||||||
| L_index | R_index | overflow | round | |||||
| overflow | round | |||||||
| L_index | R_index | overflow | round | guard | ||||
| overflow | round | guard | ||||||
| L_index | R_index | overflow | round | chk_err | denorm | float | ||
| overflow | round | chk_err | denorm |
Table 9.12 shows the functions that convert from numeric types to the float type defined in the floating-point packages. Again, the definitions of ufixed and sfixed come from the fixed-point package referenced as a generic package. The first parameter of each function is the value to be converted. Following this are either two parameters, exponent_width and fraction_width (abbreviated to “exponent” and “fraction” in the table), to specify the sizes of the corresponding fields in the result, or a single parameter of the result type, size_res, whose index range is used for the result. Additional parameters specify the rounding mode (round_style) and whether denormalized representation is used (denormalize). The default values for the field size, round_style and denormalize parameters come from the generic constants of the package.
Table 9.12. Conversion functions yielding float values
Function | Result type | Param 1 type | Param 2 | Param 3 | Param 4 | Param 5 | Package |
|---|---|---|---|---|---|---|---|
|
| sulv | exponent | fraction | float | ||
| |||||||
| |||||||
exponent | fraction | round | |||||
| round | ||||||
| exponent | fraction | round | ||||
| round | ||||||
| exponent | fraction | round | denorm | |||
| round | denorm | |||||
sfixed | exponent | fraction | round | denorm | |||
| round | denorm | |||||
| exponent | fraction | round | ||||
| round | ||||||
| exponent | fraction | round | denorm | |||
| round | denorm |
The final group of conversion functions is shown in Table 9.13. These functions convert from binary-coded vectors to abstract integer or real types. As in the preceding tables, the first parameter is the value to be converted, and subsequent parameters specify overflow and rounding modes (overflow_style and round_style), whether error checking is required (check_error), and whether operands of type float use denormalized representation (denormalize). The default values for these subsequent parameters come from the generic constants of the packages.
Table 9.13. Conversion functions yielding integer and real values
Function | Result type | Param 1 type | Param 2 | Param 3 | Param 4 | Package |
|---|---|---|---|---|---|---|
| natural | bv | nbu | |||
natural | sulv | nsu | ||||
natural | unsigned | ns/b | ||||
integer | signed | |||||
natural | ufixed | overflow | round | fixed | ||
integer | sfixed | overflow | round | |||
integer | float | round | chk_err | float | ||
to_real | real | ufixed | fixed | |||
sfixed | ||||||
float | round | chk_err | denorm | float |
As we have mentioned, the packages provide aliases for the conversion functions for convenience and enhanced readability: for conversion to bit_vector, the names we can use are to_bv, to_bitvector and to_bit_vector; for conversion to std_ulogic_vector, the names are to_sulv, to_stdulogicvector and to_std_ulogic_vector; and for conversion to std_logic_vector, the names are to_slv, to_stdlogicvector and to_std_logic_vector.
For each binary-coded numeric type, there is a resize function, shown in Table 9.14. The versions yielding bit_vector, std_ulogic_vector, unsigned, and signed results The functions have a parameter new_size to specify the result size, or a parameter size_res for an object whose index range is used for that of the result. The versions that yield fixed-point results have either two parameters (left_index and right_index) to specify the index bounds of the result, or one parameter (size_res) for an object whose index range is used for that of the result. They also have parameters to specify overflow and rounding modes (overflow_style and round_style), with default values coming from the package generics. Similarly, the versions that yield floating-point results have either two parameters to specify the field sizes for the result (exponent_width and fraction_width), or one parameter (size_res) for an object whose index range is used for that of the result. Subsequent parameters specify rounding modes (round_style), whether error checking is required (check_error), and whether the operand and result use denormalized representation (denormalize_in and denormalize_out, respectively). The default values for these subsequent parameters come from the generic constants of the package.
Table 9.14. Resizing functions
Result type | Param 1 type | Param 2 | Param 3 | Param 4 | Param 5 | Param 6 | Param 7 | Package | |
|---|---|---|---|---|---|---|---|---|---|
| bv | bv |
| nbu | |||||
| |||||||||
sulv | sulv |
| nsu | ||||||
| |||||||||
|
| new_size | ns/b | ||||||
| |||||||||
|
| new_size | |||||||
size_res | |||||||||
|
| L_index | R_index | overflow | round | fixed | |||
| overflow | round | |||||||
sfixed | sfixed | L_index | R_index | overflow | round | ||||
| overflow | round | |||||||
float | float | exponent | fraction | round | chk_err | den_in | den_out | float | |
| round | chk_err | den_in | den_out |
Resizing an unsigned vector of type bit_vector, std_ulogic_vector or unsigned to produce a larger vector involves filling leftmost bits with ‘0’. Resizing these types to produce a smaller vector involves truncating the leftmost bits. For type signed, producing a larger vector involves filling the leftmost bits with copies of the operand’s sign bit, and producing a smaller vector involves truncating the leftmost bits while retaining the sign bit.
Resizing a fixed-point value is similar. A ufixed vector is extended on the left or right by filling bits with ‘0’. An sfixed vector is extended on the left by replicating the sign bit and extended on the right by filling bits with ‘0’. Reducing the size of a fixed-point vector is more complicated, and depends on the overflow and rounding modes. If the vector is to be truncated on the right, a rounding mode of fixed_truncate causes the truncated bits to be discarded and the rightmost result bit to be unchanged, whereas a rounding mode of fixed_round causes the result to be rounded based on the values of the discarded bits and the rightmost result bit. If the vector is to be truncated to the left and the operand value is out of the representable range for the result, the value returned depends on the overflow style. For fixed_saturate, the largest representable value (for ufixed or for positive sfixed values) or the most negative representable value (for negative sfixed values) is returned. For fixed_wrap, the leftmost bits are simply truncated, which, in the case of sfixed values, may result in a change of sign.
Resizing a floating-point value is much more involved than resizing integral and fixed-point values. It involves determining the class of value represented by the operand (normal, denormal, zero, infinity, or NaN), resizing the exponent and fractional parts, rounding according to the round_style parameter, renormalizing or representing as a denormal if required, checking for errors, and transforming overflow to infinity.
The strength reduction functions are defined for the entire family of types based on std_ulogic. Functions of the following form are defined:
function to_01 (s : Type; xmap : std_ulogic := '0') return Type; function to_X01 (s : Type) return Type; function to_X01Z (s : Type) return Type; function to_UX01 (s : Type) return Type;
The type Type includes std_ulogic, std_ulogic_vector, unresolved_unsigned, unresolved_signed, unresolved_ufixed, unresolved_sfixed, unresolved_float, and the subtypes of the vector types with resolved elements. The value returned by each function for each operand element value is shown in Table 9.15. The functions to_X01, to_X01Z, and to_UX01, when applied to vector operands, convert each operand element according to the table to yield the corresponding result element. The to_01 function, however, behaves differently. Provided all of the elements are ‘0’, ‘1’, ‘L’, or ‘H’, they are converted according to the table. However, if any element is a metalogical value (a value other than ‘0’, ‘1’, ‘L’, or ‘H’), all elements of the result are set to the value of the xmap parameter. Thus, we can test any element of the result to determine whether there were any metalogical elements in the operand.
Table 9.15. Strength reduction mappings
Function | ‘U’ | ‘X’ | ‘0’ | ‘1’ | ‘Z’ | ‘W’ | ‘L’ | ‘H’ | ‘-’ |
|---|---|---|---|---|---|---|---|---|---|
to_01 | xmap | xmap | ‘0’ | ‘1’ | xmap | xmap | ‘0’ | ‘1’ | xmap |
to_X01 | ‘X’ | ‘X’ | ‘0’ | ‘1’ | ‘X’ | ‘X’ | ‘0’ | ‘1’ | ‘X’ |
to_X01Z | ‘X’ | ‘X’ | ‘0’ | ‘1’ | ‘Z’ | ‘X’ | ‘0’ | ‘1’ | ‘X’ |
to_UX01 | ‘U’ | ‘X’ | ‘0’ | ‘1’ | ‘X’ | ‘X’ | ‘0’ | ‘1’ | ‘X’ |
The ‘X’ detection function is also defined for the entire family of types based on std_ulogic. The function definitions are of the form:
function is_X (S : Type) return boolean;The version for std_ulogic returns true if the operand is a metalogical value, or false otherwise. The versions for vector types return true if any element of the operand is a metalogical value, or false otherwise.
Example 9.5. Unknown detection for a state-machine input
We can use the to_X01 function in behavioral models of ASIC and FPGA input cells to promote a resistive strength to a driving level as follows:
ncs_x01 <= to_X01(ncs);
We can use the is_X function to detect ‘X’ values in behavioral models and RTL code, for example, in the input to a state machine:
assert not is_X(ncs) report "ncs is X" severity error;