Descriptive statistics allow you to present large amounts of data in quantitative summaries that are simple to understand. When you sum data, count data, and average data, you are producing descriptive statistics. It is important to note that descriptive statistics are used only to profile a dataset and enable comparisons that can be used in other analyses. This is different from inferential statistics, where you infer conclusions that extend beyond the scope of the data. To help solidify the difference between descriptive and inferential statistics, consider a customer survey. Descriptive statistics summarize the survey results for all customers and describe the data in understandable metrics, while inferential statistics infer conclusions such as customer loyalty based on the observed differences between groups of customers.
When it comes to inferential statistics, Excel is better suited to handle these types of analyses than Access. Why? First, Excel comes with a plethora of built-in functions and tools that make it easy to perform inferential statistics; tools that Access simply does not have. Secondarily, inferential statistics are usually performed on small subsets of data that can flexibly be analyzed and presented by Excel. Running descriptive statistics, on the other hand, is quite practical in Access. In fact, running descriptive statistics in Access versus Excel is often the smartest option due to the structure and volume of the dataset.
Tip
The examples shown in this chapter can be found in the sample database for this book. The sample database for this book can be found on Wrox.com.
This section discusses some of the basic tasks you can perform by using descriptive statistics, including:
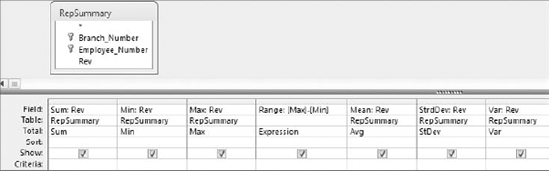
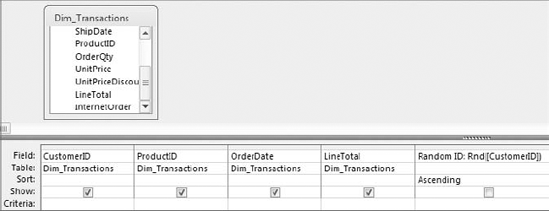
At this point in the book, you have run many Access queries, some of which have been aggregate queries. Little did you know that when you ran those aggregate queries, you were actually creating descriptive statistics. It's true. The simplest descriptive statistics can be generated using an aggregate query. To demonstrate this point, build the query shown in Figure 8-1.
Similar to the descriptive statistics functionality found in Excel, the result of this query, shown in Figure 8-2, provides key statistical metrics for the entire dataset.
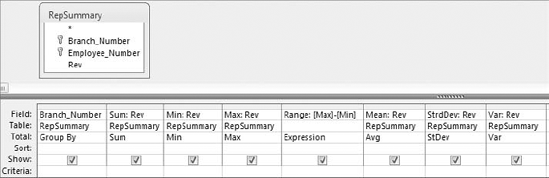
You can easily add layers to your descriptive statistics. In Figure 8-3, you are adding the Branch_Number field to your query. This gives you key statistical metrics for each branch.
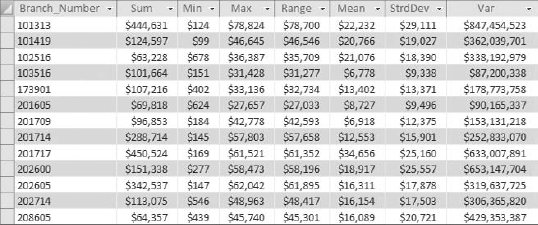
As you can see in Figure 8-4, you can now compare the descriptive statistics across branches to measure how they perform against each other.
Ranking the records in your dataset, getting the mode of a dataset, and getting the median of a dataset are all tasks that data analysts need to perform from time to time. Unfortunately, Access does not provide built-in functionality to perform these tasks easily. This means you have to come up with a way to carry out these descriptive statistics. In this section, you learn some of the techniques you can use to determine rank, mode, and median.
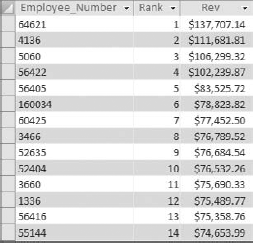
You will undoubtedly encounter scenarios where you have to rank the records in your dataset based on a specific metric such as revenue. A record's rank is not only useful in presenting data; it is also a key variable when calculating advanced descriptive statistics such as median, percentile, and quartile.
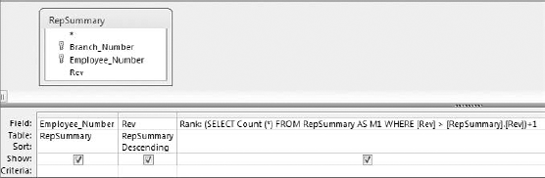
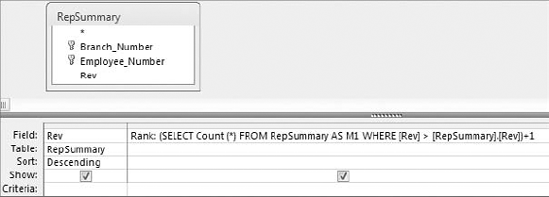
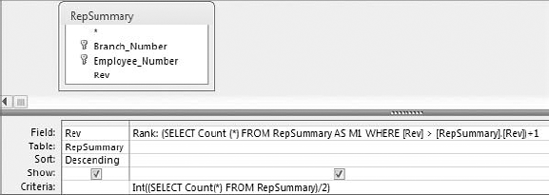
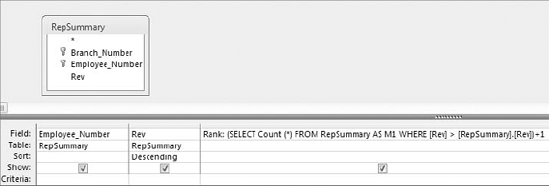
The easiest way to determine a record's ranking within a dataset is by using a correlated subquery. The query shown in Figure 8-5 demonstrates how a rank is created using a subquery.
Take a moment to examine the subquery that generates the rank.
(SELECT Count(*)FROM RepSummary AS M1 WHERE [Rev]>[RepSummary].[Rev])+1
This correlated subquery returns the total count of records from the M1 table (this is the RepSummary table with an alias of M1), where the Rev field in the M1 table is greater than the Rev field in the RepSummary table. The value returned by the subquery is then increased by one. Why increase the value by one? If you don't, the record with the highest value will return 0 because zero records are greater than the record with the highest value. The result would be that your ranking starts with 0 instead of 1. Adding one effectively ensures that your ranking starts with 1.
Note
Because this is a correlated subquery, this subquery is evaluated for every record in your dataset, giving you a different rank value for each record. Correlated subqueries are covered in detail in Chapter 8. In Appendix B, you'll find a primer on using SQL syntax.
Figure 8-6 shows the result.
Tip
This technique is also useful when you want to create an autonumber field within a query.
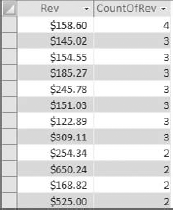
The mode of a dataset is the number that appears the most often in a set of numbers. For instance, the mode for 4, 5, 5, 6, 7, 5, 3, 4 is 5.
Unlike Excel, Access does not have a built-in Mode function, so you must create your own method of determining the mode of a dataset. Although there are various ways to get the mode of a dataset, one of the easiest is to use a query to count the occurrences of a certain data item, and then filter for the highest count. To demonstrate this method, build the query shown in Figure 8-7.
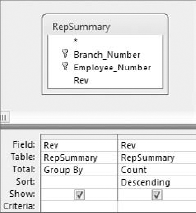
Figure 8.7. This query groups by the Rev field and then counts the occurrences of each number in Rev field. The query is sorted in descending order by Rev.
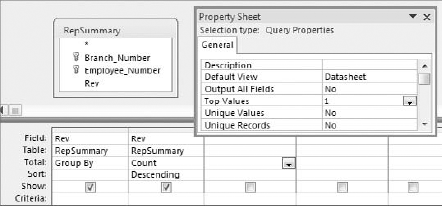
The results, shown in Figure 8-8, do not seem very helpful, but if you turn this into a top values query, returning only the top one record, you will effectively get the mode.
Change the Top Values property to 1, as shown in Figure 8-9, and you will get one record with the highest count.
As you can see in Figure 8-10, you now have only one Rev figure: the one that occurs most often. This is your mode.
Note
Keep in mind that in the event of a tie, a top values query shows all records. This effectively gives you more than one mode. You must make a manual determination which mode to use.
The median of a dataset is the middle number in the dataset. In other words, half of the numbers have values greater than the median, and half have values less than the median. For instance, the median number in 3, 4, 5, 6, 7, 8, 9 is 6 because 6 is the middle number of the dataset.
Tip
Why can't you just calculate an average and be done with it? Sometimes, calculating an average on a dataset that contains outliers can dramatically skew your analysis. For example, if you were to calculate an average on the numbers, 32, 34, 35, 37, and 89, you would get an answer of 45.4. The problem is that 45.4 does not accurately represent the central tendency of this sampling of numbers. Using median on this sample makes more sense. The median in this case would be 35, which is more representative of what's going on in this data.
Access does not have a built-in Median function, so you have to create your own method of determining the median of a dataset. An easy way to get the median is to build a query in two steps. The first step is to create a query that sorts and ranks your records. The query shown in Figure 8-11 sorts and ranks the records in the RepSummary table.
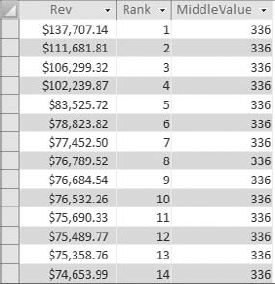
The next step is to identify the middle-most record in your dataset by counting the total number of records in the dataset and then dividing that number by two. This gives you a middle value. The idea is that because the records are now sorted and ranked, the record that has the same rank as the middle value is the median. Figure 8-12 shows the subquery that returns a middle value for the dataset. Note that the value is wrapped in an Int function to strip out the fractional portion of the number.
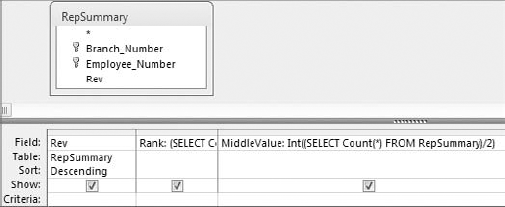
Figure 8.12. The Middle Value subquery counts all the records in the dataset and then divides that number by 2.
As you can see in Figure 8-13, the middle value is 336. You can go down to record 336 to see the median.
If you want to return only the median value, simply use the subquery as a criterion for the Rank field, as shown in Figure 8-14.
Although the creation of a random sample of data does not necessarily fall into the category of descriptive statistics, a random sampling is often the basis for statistical analysis.
There are many ways to create a random sampling of data in Access, but one of the easiest is to use the Rnd function within a top values query. The Rnd function returns a random number based on an initial value. The idea is to build an expression that applies the Rnd function to a field that contains numbers, and then limit the records returned by setting the Top Values property of the query.
To demonstrate this method, follow these steps:
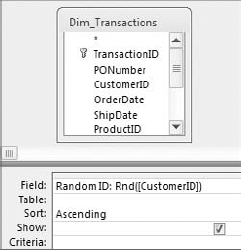
Start a query in Design view on the TransactionMaster table.
Create a Random ID field, as shown in Figure 8-15, and then sort the field (either ascending or descending will work).
Note
The
Rndfunction does not work with fields that contain text or Null values. Strangely enough, though, theRndfunction works with fields that contain all numerical values even if the field is formatted as a Text type field.If your table is made up of fields that only contain text, you can add an Autonumber field to use with the
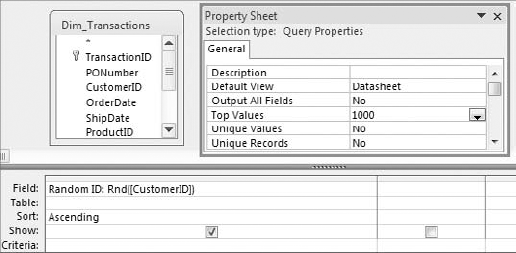
Rndfunction. Another option is to pass the field containing text through theLenfunction, and then use that expression in yourRndfunction. For example:Rnd(Len([Mytext])).Change the Top Values property of the query to the number of random records you want returned. The scenario shown in Figure 8-16 limits this dataset to 1,000 records.
Set the Show row for the Random ID field to false and add the fields you want to see in your dataset.
Run the query and you will have a completely random sampling of data.
Warning
Re-running the query, switching the view state, or sorting the dataset, results in a different set of random records. If you want to perform extensive analysis on an established set of random records that does not change, you must run this query as a Make-Table query in order to create a hard table.
When working with descriptive statistics, a little knowledge goes a long way. Indeed, basic statistical analyses often lead to more advanced statistical analyses. In this section, you build on the fundamentals you have just learned to create advanced descriptive statistics.
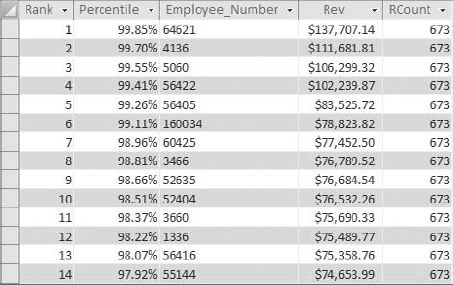
A percentile rank indicates the standing of a particular score relative to the normal group standard. Percentiles are most notably used in determining performance on standardized tests. If a child scores in the 90th percentile on a standardized test, this means that his score is higher than 90 percent of the other children taking the test. Another way to look at it is to say that his score is in the top 10 percent of all the children taking the test. Percentiles are often used in data analysis as a method of measuring a subject's performance in relation to the group as a whole—for instance, determining the percentile ranking for each employee based on annual revenue.
Calculating a percentile ranking for a dataset is simply a mathematical operation. The formula for a percentile rank is (Record Count–Rank)/Record Count. The trick is to getting all the variables needed for this mathematical operation.
To start, follow these steps:
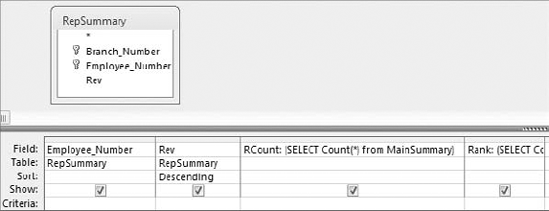
Build the query you see in Figure 8-18. This query will start by ranking each employee by annual revenue. Be sure to give you new field an alias of "Rank."
Add a field that counts all the records in your dataset. As you can see in Figure 8-19, you are using a subquery to do this. Be sure to give your new field an alias of "RCount."
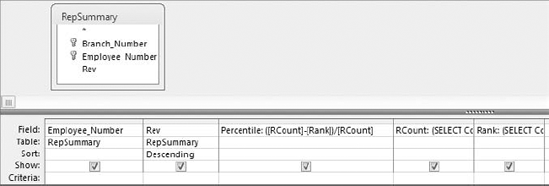
Create a calculated field with the expression
(RCount–Rank)/RCount. At this point, your query should look like the one shown in Figure 8-20.Running the query give you the results shown in Figure 8-21.
Again, the resulting dataset enables you to measure each employee's performance in relation to the group as a whole. For example, the employee ranked sixth in the dataset is in the 99th percentile, meaning this employee earned more revenue than 99 percent of other employees.
A quartile is a statistical division of a dataset into four equal groups, with each group making up 25 percent of the dataset. The top 25 percent of a collection is considered to be the first quartile, whereas the bottom 25 percent is considered the fourth quartile. Quartile standings typically are used for the purposes of separating data into logical groupings that can be compared and analyzed individually. For example, if you want to establish a minimum performance standard around monthly revenue, you could set the minimum to equal the average revenue for employees in the second quartile. This ensures you have a minimum performance standard that at least 50 percent of your employees have historically achieved or exceeded.
Establishing the quartile for each record in a dataset does not involve a mathematical operation; rather, it is a question of comparison. The idea is to compare each record's rank value to the quartile benchmarks for the dataset. What are quartile benchmarks? Imagine that your dataset contains 100 records. Dividing 100 by 4 would give you the first quartile benchmark (25). This means that any record with a rank of 25 or less is in the first quartile. To get the second quartile benchmark, you would calculate 100/4*2. To get the third, you would calculate 100/4*3 and so on.
Given that information, you know right away that you need to rank the records in your dataset and count the records in your dataset. Follow these steps:
Start by building the query shown in Figure 8-22. Build the Rank field the same way you did in Figure 8-18.
Build the RCount field the same way you did in Figure 8-19.
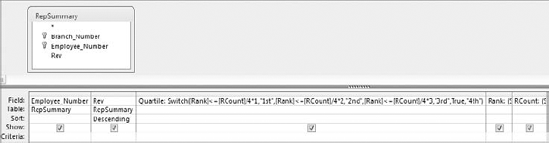
Once you create the Rank and RCount fields in your query, you can use these fields in a
Switchfunction that tag each record with the appropriate quartile standing. Take a moment and look at theSwitchfunction you will be using.
Switch([Rank]<=[RCount]/4*1,"1st",[Rank]<=[RCount]/4*2,"2nd", [Rank]<= [RCount]/4*3,"3rd",True,"4th")
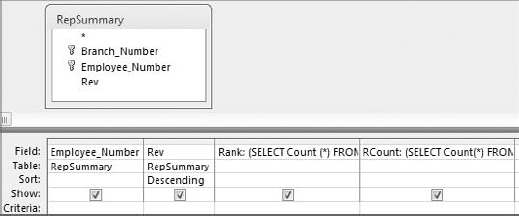
Figure 8.22. Start by creating a field named Rank that ranks each employee by revenue and a field named RCount that counts the total records in the dataset.
This Switch function is going through four conditions, comparing each record's rank value to the quartile benchmarks for the dataset.
Note
For more information on the Switch function, see Chapter 6.
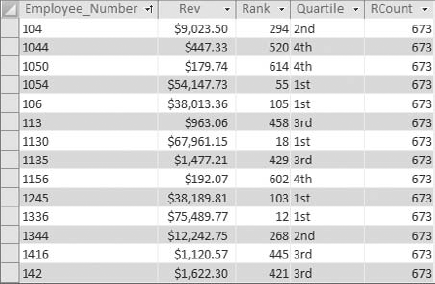
Figure 8-23 demonstrates how this Switch function fits into the query. Note that you are using an alias of Quartile here.
As you can see in Figure 8-24, you can sort the resulting dataset on any field without compromising your quartile standing tags.
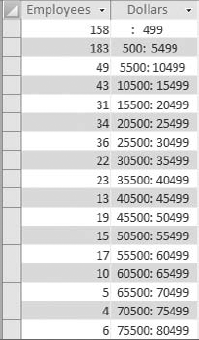
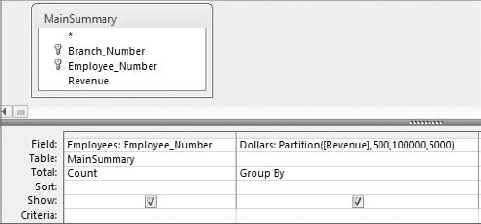
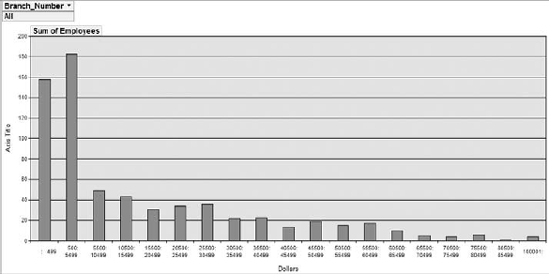
A frequency distribution is a special kind of analysis that categorizes data based on the count of occurrences where a variable assumes a specified value attribute. Figure 8-25 illustrates a frequency distribution created by using the Partition function.
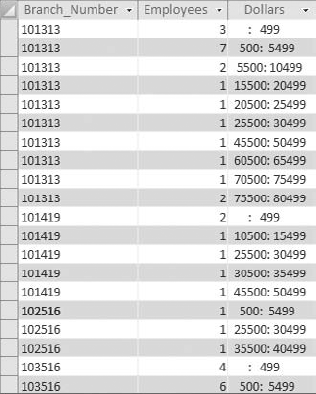
With this frequency distribution, you are clustering employees by the range of revenue dollars they fall in. For instance, 183 employees fall into the 500: 5999 grouping, meaning that 183 employees earn between 500 and 5,999 revenue dollars per employee. Although there are several ways to get the results you see here, the easiest way to build a frequency distribution is to use the Partition function.
To create the frequency distribution you saw in Figure 8-25, build the query shown in Figure 8-26. As you can see in this query, you are using a Partition function to specify that you want to evaluate the Revenue field, start the series range at 500, end the series range at 100,000, and set the range intervals to 5,000.
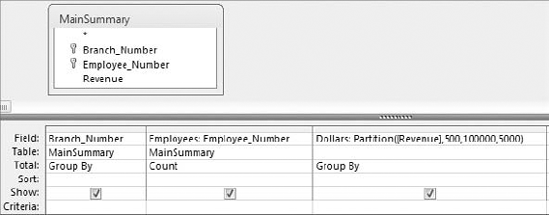
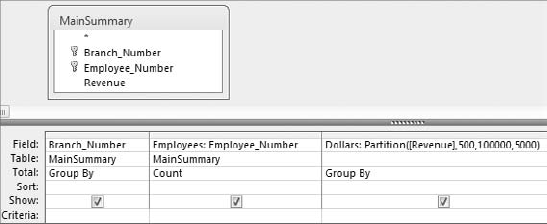
You can also create a frequency distribution by group by adding a Group By field to your query. Figure 8-27 demonstrates this by adding the Branch_Number field.
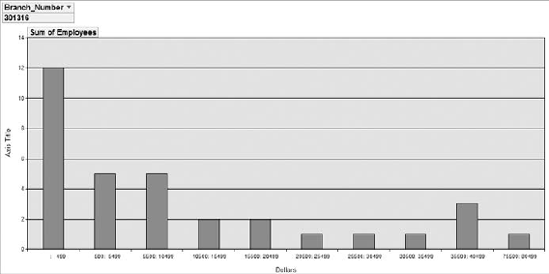
The result is a dataset (see Figure 8-28) that contains a separate frequency distribution for each branch, detailing the count of employees in each revenue distribution range.
Descriptive statistics allow you to profile a dataset and enable comparisons that you can use in other analyses. With descriptive statistics, you can present large amounts of data in quantitative summaries that are meaningful, yet simple to understand. Although many users turn to Excel to perform statistical operations, running descriptive statistics in Access is often the smartest option due to the structure and volume of the data that is to be analyzed.
The simplest descriptive statistics can be generated using aggregate queries (sum, average, min, max, etc.), while more advanced descriptive analyses can be performed by leveraging the power of subqueries and domain aggregate functions. Indeed, using the tools and techniques you have learned thus far, you can create a wide array of descriptive analyses; from determining rank, mode, and median, to creating a frequency distribution.