Conformal geometry 137
r
r
d
(r /r ) d
1
2 1
2
2
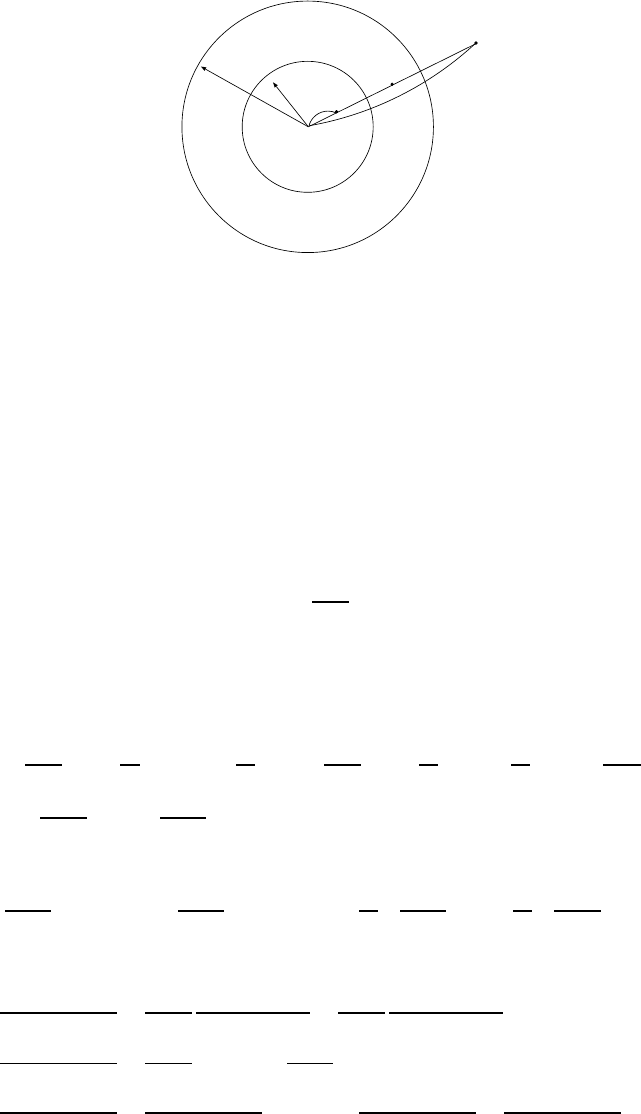
FIGURE 8.10 Consecutive reflections with respect to spheres of radii r
1
and r
2
result in a dilation
by (r
2
/r
1
)
2
.
8.6.4 Dilator
Just a s consecutive reflections with respect to parallel planes give a translation by twice the
distance between them and consecutive reflections with resp e c t to intersecting planes give
a rotation by twice the angle between them, consecutive inversions give a dilation. In fact,
for the sphere σ
1
= e
0
−r
2
1
e
∞
/2 of radius r
1
centered at the origin e
0
, a p oint at distance d
from e
0
is inverted to the point at dis tance r
2
1
/d, and if this point is inverted by the sphere
σ
2
= e
0
−r
2
2
e
∞
/2 of radius r
2
also centered at e
0
, it moves to a point at distance r
2
2
/(r
2
1
/d)
= (r
2
/r
1
)
2
d (Fig. 8 .10). This is a dilation by the square of the ratio of the radii of the two
spheres. The versor
D =
1
r
1
r
2
σ
2
σ
1
(8.100)
that describes this operation is called the dilator, where the coefficient 1/(r
1
r
2
), which
does not affect the versor o peration, is introduced merely for simplifying the subsequent
expressions. However, we need some tricks to obtain a useful form of the dilator. First, we
note that
D =
1
r
1
r
2
e
0
−
r
2
2
2
e
∞
e
0
−
r
2
1
2
e
∞
=
1
r
1
r
2
e
2
0
−
r
2
1
2
e
0
e
∞
−
r
2
2
2
e
∞
e
0
+
r
2
1
r
2
2
4
e
2
∞
= −
r
1
/r
2
2
e
0
e
∞
−
r
2
/r
1
2
e
∞
e
0
, (8.101 )
which is rewritten as follows:
D = −
r
1
/r
2
2
(−2−e
∞
e
0
)−
r
2
/r
1
2
(−2−e
0
e
∞
) =
r
1
r
2
+
r
1
/r
2
2
e
∞
e
0
+
r
2
r
1
+
r
2
/r
1
2
e
0
e
∞
. (8.102)
Adding Eqs. (8.101) and (8.102) and dividing the sum by 2, we obtain
D =
r
1
/r
2
+ r
2
/r
1
2
+
r
1
/r
2
2
e
∞
e
0
− e
0
e
∞
2
+
r
2
/r
1
2
e
0
e
∞
− e
∞
e
0
2
=
r
1
/r
2
+ r
2
/r
1
2
+
r
1
/r
2
2
e
∞
∧ e
0
+
r
2
/r
1
2
e
0
∧ e
∞
=
r
2
/r
1
+ r
1
/r
2
2
+
r
2
/r
1
− r
1
/r
2
2
e
0
∧e
∞
=
r
2
/r
1
+ r
1
/r
2
2
+
r
2
/r
1
− r
1
/r
2
2
O, (8.103 )
where we put
O = e
0
∧e
∞
. (8.104)

138 Conformal Space and Conformal Geometry: Geometric Algebra
This is the origin e
0
viewed as a flat point, i.e., a pair with the infinity e
∞
, rather than a n
isolated point. If we use, instead of the ratio (r
2
/r
1
)
2
, its logarithm
γ = log (
r
2
r
1
)
2
(8.105)
for the parameter of dilation, we can write
r
2
r
1
= e
γ/2
, (8.106)
so Eq. (8.103) is written in the form
D =
e
γ/2
+ e
−γ/2
2
+
e
γ/2
− e
−γ/2
2
O = co sh
γ
2
+ Osinh
γ
2
= exp
γ
2
O, (8 .107)
where the exponential function “exp” is defined via Taylor expansion of Eq. (8.73). In fact,
if we note that
O
2
= 1 (8.108)
(֒→ Exercise 8 .1(6)), we see that
exp
γ
2
O = 1 +
γ
2
O +
1
2!
(
γ
2
O)
2
+
1
3!
(
γ
2
O)
3
+ ···
=
1 +
1
2!
(
γ
2
)
2
+
1
4!
(
γ
2
)
4
+ ···
+
γ
2
+
1
3!
(
γ
2
)
3
+ ···
O = co sh
γ
2
+ Osinh
γ
2
.
(8.109)
The inverse of Eq. (8.107) is given by
D
−1
= cosh
γ
2
− O sinh
γ
2
= exp(−
γ
2
O). (8.110)
This is obvious from Eq. (8.105) if we note that the reciprocal of the magnification ratio
(r
2
/r
1
)
2
corresponds to the sign reversal of γ, but this can be confirmed as follows:
cosh
γ
2
− Osinh
γ
2
cosh
γ
2
+ Osinh
γ
2
= cosh
2
γ
2
+ Ocosh
γ
2
sinh
γ
2
− O c osh
γ
2
sinh
γ
2
− O
2
sinh
2
γ
2
= cosh
2
γ
2
− sinh
2
γ
2
= 1.
(8.111)
To see how a given point is dilated, it is sufficient to know how the origin e
0
, a vector
a, and the infinity e
∞
are dilated. From the identities
Oe
0
= −e
0
= −e
0
O, Oe
∞
= e
∞
= −e
∞
O (8.112)
(֒→ Exercise 8 .6(2)), we see that
De
0
=
cosh
γ
2
+ O sinh
γ
2
e
0
= e
0
cosh
γ
2
− Osinh
γ
2
= e
0
D
−1
, (8.113)
De
∞
=
cosh
γ
2
+ O sinh
γ
2
e
∞
= e
∞
cosh
γ
2
− Osinh
γ
2
= e
∞
D
−1
. (8.114)
Using these and noting that D has grade 2 so that D
†
= D
−1
, we obtain the following:

Conformal geometry 139
TABLE 8.2 Versors in the conformal space.
name grade expression
reflector 1 π = n + he
∞
invertor 1 σ = c − r
2
e
∞
/2
translator 2 T
t
= 1 − te
∞
/2 = exp(−te
∞
/2)
consecutive reflections for parallel planes
rotor 2 R = cos Ω/2 − I sin Ω/2 = exp(−IΩ/2)
consecutive reflections for intersecting planes
dilator 2 D = cosh γ/2 + O sin γ/2 = exp Oγ/2
consecutive inversions for concentric spheres
motor 4 M = T
t
R
composition of rotation and tr ansl ation
origin e
0
The origin e
0
is dilated to
De
0
D
†
= D
2
e
0
=
exp
γ
2
O
2
e
0
= exp γOe
0
= (co sh γ + Osinh γ)e
0
= e
0
cosh γ −e
0
sinh γ = e
−γ
e
0
. (8.115)
Since the space is homogeneous, this still represents the origin.
vector a Since the basis elements e
i
, i = 1, 2, 3, are anticommutative with e
0
and e
∞
,
they are commutative with O = (e
0
e
∞
−e
∞
e
0
)/2. Hence, they are also commuta tive
with D and D
−1
, so we see that
DaD
†
= DD
−1
a = a, (8.116)
i.e., vectors are invariant to dilation.
infinity e
∞
The infinity e
∞
is dilated to
De
∞
D
†
= D
2
e
∞
=
exp
γ
2
O
2
e
0
= exp γOe
∞
= (co sh γ + Osinh γ)e
∞
= e
∞
cosh γ + e
∞
sinh γ = e
γ
e
∞
. (8.117)
Due to the homogeneity of the space, this still represents infinity.
From these results, dilation of point p = e
0
+ x + kxk
2
e
∞
/2 is computed by applying
the dilator term by term as follows:
DpD
†
= De
0
D
†
+ DxD
†
+
1
2
kxk
2
De
∞
D
†
= e
−γ
e
0
+ x +
1
2
kxk
2
e
γ
e
∞
= e
−γ
e
0
+ e
γ
x +
1
2
ke
γ
xk
2
e
∞
. (8.118)
Since the s pace is homogeneous, this represe nts the same position as e
0
+e
γ
x+ke
γ
xk
2
e
∞
/2,
i.e., the position x is dilated to the position e
γ
x.
8.6.5 Versors and conformal transformations
The versors introduced so far are summar ize d in Table 8.2. The important property of
versors is that the geometric product is preserved up to sign. What we mean by this is that
140 Conformal Space and Conformal Geometry: Geometric Algebra
if elements x and y are transfor med by a versor V of grade k, their geometric product after
the transforma tion is given by
(VxV
†
)(VyV
†
) = Vx(V
†
V)yV
†
= (−1)
k
VxyV
†
, (8.119)
where we note from the definition of Eq. (8.8 1) that
V
†
V = VV
†
= (−1)
k
. (8.120)
Since the outer product x ∧ y is defined by antisymmetrization (xy − yx)/2 of the
geometric product, we obtain the following (֒→ Sec . 6.8 in Chapter 6):
Proposition 8.1 (Versors and outer product) After a versor of grade k is applied, the
outer product of elements x and y is preserved up to sign:
(VxV
†
) ∧ (VyV
†
) = (−1)
k
V(x ∧ y)V
†
. (8.121)
From this, we observe that
Proposition 8.2 (Versors and spheres) A versor V maps a sphere p
1
∧p
2
∧p
3
∧p
4
that
passes through four points p
i
, i = 1, 2, 3, 4, to the sphere p
′
1
∧ p
′
2
∧ p
′
3
∧ p
′
4
that passes
through the transformed points p
′
i
= Vp
i
V
†
.
In fact, if a point p satisfies the equation of the sphere p
1
∧ p
2
∧p
3
∧ p
4
, i.e.,
p ∧ (p
1
∧ p
2
∧p
3
∧ p
4
) = 0, (8.122)
and if p is transformed to p
′
= VpV
†
, applicatio n of the versor V to the above equation
yields
0 = V(p ∧ p
1
∧ p
2
∧ p
3
∧p
4
)V
†
= (VpV
†
) ∧ (Vp
1
V
†
) ∧ (Vp
2
V
†
) ∧ (Vp
3
V
†
) ∧ (Vp
4
V
†
)
= p
′
∧ (p
′
1
∧ p
′
2
∧ p
′
3
∧ p
′
4
). (8 .123)
Hence, p
′
satisfies the eq uation of the sphere p
′
1
∧p
′
2
∧p
′
3
∧p
′
4
. Note that here the sign (−1)
k
arises fo ur times, so it has no effect (in general, it is irrelevant for expressions that are 0).
Thus, we conclude that versors map a sphere to a sphere.
We can e asily co nfirm that angle is preserved by reflection, translation, rotation, and
inversion. It is known that confor mal mappings that map a sphere to sphere and preserve
angle are generated by composing the reflector, the translator, the rotor, and the invertor.
Since the inner product hx, yi is defined by symmetrization (xy + yx)/2 of the geometric
product and since the inner product is a scalar, we see from Eq. (8.120) that
hVxV
†
, VyV
†
i = (−1)
k
Vhx, yiV
†
= (−1)
k
hx, yiVV
†
= hx, yi. (8.124)
Thus, we observe
Proposition 8.3 (Versors and inner product) The inner product of elements x and y
is preserved by transformation by a versor V:
hVxV
†
, VyV
†
i = hx, yi. (8.125)

Supplemental note 141
We should note that invariance of the inner product do e s not necessarily mean invariance
of the distance between two points. In fact, Eq. (8.11) holds only when the expression is
normalized so that e
0
has coefficient 1 as Eq. (8.8). In the conformal space, the e xpression
˜p = αe
0
+ αx +
α
2
kxk
2
e
∞
(8.126)
multiplied by a nonzero scala r α also represents the same position as p . In this case, we see
from he
0
, e
∞
i = −1 that
h˜p, e
∞
i = αhe
0
, e
∞
i = −α. (8.127)
Thus, we have α = −h˜p, e
∞
i. Hence, for normalizing ˜p so that e
0
has coefficient 1, we nee d to
write −˜p/h˜p, e
∞
i, which corresponds to the form of Eq. (8.8). Hence, extension of Eq. (8.11)
to the case of a non-unit coefficient of e
0
is given by
kx − yk
2
=
−2hp, qi
hp, e
∞
ihq, e
∞
i
. (8.128)
Using this, we can compute the distance between two the positions x
′
and y
′
after trans-
formation by a versor V as follows:
kx
′
− y
′
k
2
=
−2hVpV
†
, VqV
†
i
hVpV
†
, e
∞
ihVqV
†
, e
∞
i
=
−2hp, qi
hVpV
†
, V(V
†
e
∞
V)V
†
ihVqV
†
, V(V
†
e
∞
V)V
†
i
=
−2hp, qi
hp, V
†
e
∞
Vihq, V
†
e
∞
Vi
. (8.129)
This equals kx − yk
2
if V
†
e
∞
V = e
∞
, which is rewritten by multiplication of V from the
left and V
†
from the right into the form e
∞
= Ve
∞
V
†
. Hence, we observe that
Proposition 8.4 (Versors and iso metry) The conformal transformation defined by ver-
sor V is an isometry if and only if
Ve
∞
V
†
= e
∞
. (8.130)
From Eqs. (8.6 8), (8.77), and (8.87), we see that Eq. (8.130) holds for the translator T
t
,
the rotor R, and the reflec tor π. As seen from Eqs. (8.98) and (8.117), however, Eq. (8.130)
does not hold for the invertor σ and the dilator D. Hence, we conclude that
Proposition 8.5 (Isometric conformal transformations) A conformal transformation
is an isometry only when it is generated by translations, rotations, and reflections.
8.7 SUPPLEMENTAL NOTE
Conformal mappings are mappings that preserve angles b e tween tangents. In 2D, they are
given by an analytical (or regular or holomorphic) function over a do main of the complex
plane. Among them, those defined over all the complex plane including the point at infinity
that map to circles have the form
z
′
=
αz + β
γz + δ
, αδ − βγ 6= 0. (
8.131)
This linear fractional transfor mation is called the M¨obius transformation and is generated
by compositions of translation z
′
= z+α, rotation/reflection/dilation z
′
= αz, and inversion
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
