Chapter Five

Tokuyama’s Theorem

Let z = diag(z₁, · · · , z_r+1) be an element of the group (), which is the diagonal subgroup of GL_r+1(). In the application to the Casselman-Shalika formula we will take the z_i to be the Langlands parameters. (In terms of the s_i the z_i are determined by the conditions that Π z_i = 1 and z_i/z_i+1 = .)

Let us write the Weyl character formula in the form

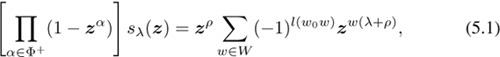
where we recall that s_λ(z) = s_λ(z₁, · · · , z_r+1) is the Schur polynomial. The sum over the Weyl group on the right-hand side is the numerator in the Weyl formula and the product on the left is essentially the Weyl denominator. The Weyl vector ρ, we recall, is ρ = (r, r − 1 , · · · , 2, 1, 0).

We have seen in (4.4) and (4.2) that p-part of the Whittaker coefficient of the Eisenstein series is

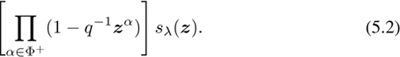
The similarity of this expression to (5.1) indicates that the p-parts of Whittaker coefficients of Eisenstein series can be profitably regarded as a deformation of the numerator in the Weyl character formula.

Thus we are led to deformations of the Weyl character formula. Tokuyama [70] gave such a deformation. It is an expression of s_λ(z) as a ratio of a numerator to a denominator. The denominator is a deformation of the Weyl denominator, and the numerator is a sum over Gelfand-Tsetlin patterns with top row λ + ρ. It can be rewritten as a sum over _λ+ρ.

Tokuyama’s formula has a parameter t, which can be specialized in various ways. If t = 1, it is the Weyl character formula. If t = 0, it is equivalent to the combinatorial definition of the Schur polynomial as a sum over semistandard Young tableaux, that is, over _λ. If t is specialized to −q⁻¹ then the denominator in Tokuyama’s formula matches the product in (5.2). In this specialization, the numerator in Tokuyama’s formula agrees with the p-parts of the Weyl group multiple Dirichlet series in the special case n = 1.

We will state and prove Tokuyama’s formula, then translate it into the language of crystals.

If is a Gelfand-Tsetlin pattern in the notation (1.5) let s() be the number of entries a_ij with i > 0 such that a_i−1,j−1 < a_ij < a_i−1,j. Let l() be the number of entries a_ij with i > 0 such that a_ij = a_i−1,j−1. Thus l() is the number of boxed elements in Γ(), and s() is the number of entries that are neither boxed nor circled. For 0 ≤ i ≤ r let d_i = d_i() = be the i-th row sum of .

We recall that the Schur polynomial s_λ is symmetric, and if z_i are the eigenvalues of g ∈ GL_r+1() then s_λ(z₁, · · · , z_r+1) = χ_λ(g), where χ_λ the character of the irreducible representation with highest weight λ. In this chapter there will be an induction on r, so we will sometimes write ρ = ρ_r = (r, r − 1, · · · , 0). Let GT(λ) = GT_r(λ) be the set of Gelfand-Tsetlin patterns with r + 1 rows having top row λ.

THEOREM 5.1 (Tokuyama [70]) We have

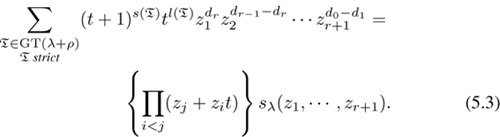
For comparison with the original paper, we note that we have reversed the order of the z_i, which does not affect the Schur polynomial since it is symmetric. The following proof is essentially Tokuyama’s original one.

Proof. Let Λ^(r) be the ring of symmetric polynomials in z₁, · · · , z_r. There is a homomorphism Λ^(r+1) Λ^(r) in which one sets z_r+1 1. The homomorphism is not injective, but its restriction to the homogeneous part of Λ of fixed degree r is injective. We note that as polynomials in the z_i both sides of (5.3) are homogeneous of degree d₀ = |λ| + r(r + 1). (If λ is a partition then |λ| = Σ_i λ_i. See Macdonald [64] for background on partitions and symmetric functions.) Two homogeneous polynomials of the same degree are equal if they are equal when z_r+1 = 1, so it is sufficient to show that (5.3) is true when z_r+1 = 1, and for this we may assume inductively that the formula is true for r − 1.

The branching rule from GL_r+1() to GL_r(), already mentioned in connection with (2.4), may be expressed as

See for example Bump [19], Chapter 44.

Also on setting z_r+1 = 1,

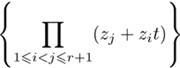
becomes

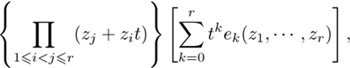
where e_k is the k-th elementary symmetric polynomial, that is, the sum of all squarefree monomials of degree k.

Now we recall Pieri’s formula in the form

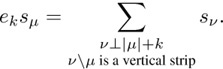
See for example Bump [19], Chapter 42. The notation v⊥|μ| + k means that v is a partition of |μ| + k. The condition that vμ is a vertical strip means that the Young diagram of v contains the Young diagram of μ, and that the skew-diagram vμ has no two entries in the same row. Thus vμ is a vertical strip if and only if each v_i = μ_i or μ_i + 1, and since v⊥|μ| + k, it follows that v_i = μ_i + 1 exactly k times. Thus when z_r+1 = 1 the right-hand side of (5.3) becomes

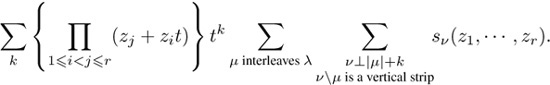
Now by induction

where are the row sums of ′. We substitute this and interchange the order of summation and make the summation over μ the innermost sum. The condition that vμ is a vertical strip means that μ_i ≤ v_i ≤ μ_i + 1. Combining this with the fact that μ interleaves λ we have

and therefore v + ρ_r−1 interleaves λ + ρ_r. Since k = |v| − |μ|, the right-hand side of (5.3), with z_r+1 specialized to 1, equals

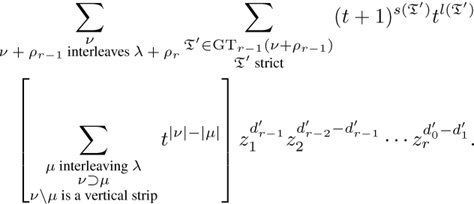
Now we assemble λ + ρ_r and the Gelfand-Tsetlin pattern ′ into a big Gelfand-Tsetlin parterns . The row sums of and ′ are the same except the top row, so d_i = for 1 ≤ i ≤ r. We may just as well sum over , in which case ′ is the pattern obtained by discarding the top row of . We get

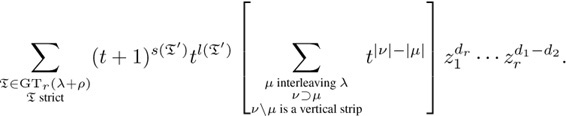
We evaluate the term in brackets. It is

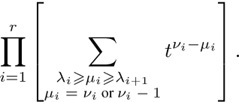
We now show that this equals (t + 1)^s()−s(′)t^l()−l(′). By (5.5), if v_i = λ_i + 1 then v_i = μ_i + 1 and so The number of such terms is l() − l(′) and so we have a contribution of t^l()−l(′). If v_i = λ_i+1, then (5.5) implies that v_i = μ_i and these factors equal 1. Hence they may be discarded from the product. In the remaining cases we have λ_i + 1 > v_i > λ_i+1 both t and 1 can occur. The number of such terms is s() − s(′), and so we have a contribution of (t + 1)^s()−s(′). Hence the term in brackets equals where l_top() is number of boxed entries in the top row of Γ() and s_top() is the number of entries in the top row of Γ() that are neither boxed nor circled. Clearly l() = l(′) + l_top() and s() = s(′) + s_top() so we obtain the left-hand side of (5.3), with z_r+1 = 1. This completes the induction.

We will give a version of Tokuyama’s formula for crystals. We will take n = 1 in (1.15). In this case the Gauss sums may be evaluated explicitly and

g(a) = q^ag^b,     h(a) = q^ah^b

where

g^b = g^b(a) = −q⁻¹,     h^b = h^b(a) = (q − 1)q⁻¹

are independent of a.

LEMMA 5.2 If υ ∈ _λ+ρ then

Proof. If _υ is non-strict then some a_i,j = a_i,j+1. This means that

a_i,j = a_i+1,j+1 = a_i,j+1

and so the entry Γ_i+1,j+1 is both boxed and circled in Γ(_υ), which implies that . On the other hand if _υ is strict then

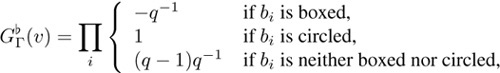
which clearly equals and the statement is proved.

THEOREM 5.3 If λ is a dominant weight, and if z₁, · · · , z_r+1 are the eigenvalues of q ∈ GL_r+1(), then

Proof. We will prove this in the form

This is equivalent since

By Theorem 5.1 with t = −q⁻¹, the right-hand side of (5.6) equals

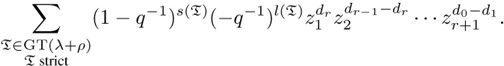
Turning to the left-hand side of (5.6), let υ ∈ _λ+ρ. By (2.17) we have z^wt(υ) = . Combining this with Lemma 5.2, we obtain (5.6).