Chapter Eleven
Types
We now divide the prototypes into much smaller units that we call types. We fix a top and bottom row, and therefore a cartoon. For each episode ε of the cartoon, we fix an integer kε. Then the set ![]() of all short Gelfand-Tsetlin patterns (6.2) with the given top and bottom rows such that for each ε
of all short Gelfand-Tsetlin patterns (6.2) with the given top and bottom rows such that for each ε
![]()
is called a type. Thus two patterns are in the same type if and only if they have the same top and bottom rows (and hence the same cartoon), and if the sum of the first (middle) row elements in each episode is the same for both patterns.
Let us choose Γ and Δ′ indexings as in Proposition 9.1. With notations as in that Proposition, and ε a fixed episode of the corresponding cartoon, there exist k and l such that ![]() (i) ∈ ε and
(i) ∈ ε and ![]() (i) ∈ ε precisely when k ≤ i ≤ l. let
(i) ∈ ε precisely when k ≤ i ≤ l. let

Then Proposition 9.1 implies that
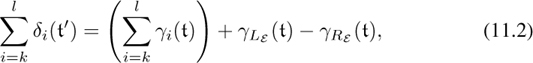
for all elements of the type. We recall that our convention was that γ0 = γ2d+2 = 0. We take Lε = 0 for the first (leftmost) cartoon and Rε = 2d+2 for the last episode.
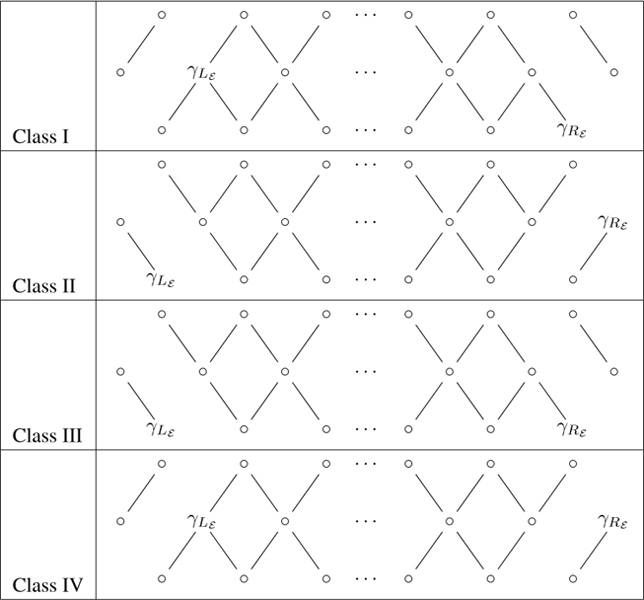
We may classify the possible episodes into four classes generalizing the classification in Table 9.1, and indicate in each case the locations of γLε and γRε in the Γ preaccordions, which may be checked by comparison with Table 9.1. Indeed, it must be remembered that in that proof, every panel of type R is replaced by one of type T or type B. Whichever choice is made, Table 9.1 gives the same location for Lε and Rε. The classification of the episode into one of four types is given in Table 11.1.
The location of ![]() and
and ![]() in the Δ preaccordion of
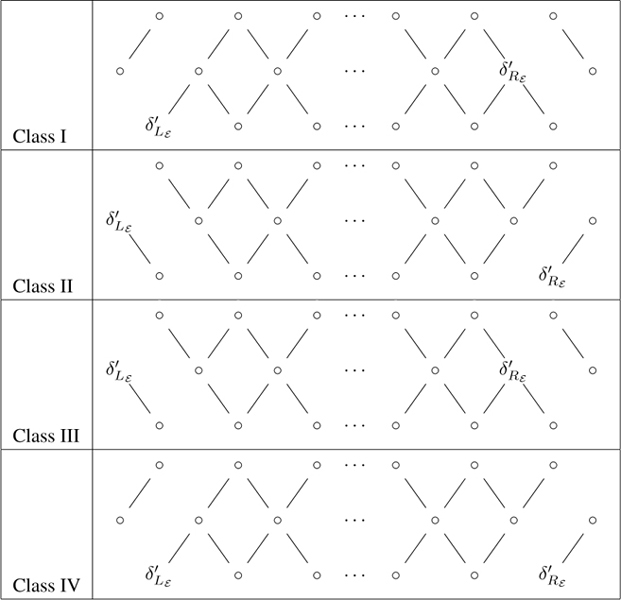
in the Δ preaccordion of ![]() may also be read off from Table 9.1. The classification of the episode into one of four classes is given in Table 11.2.
may also be read off from Table 9.1. The classification of the episode into one of four classes is given in Table 11.2.
PROPOSITION 11.1 If ![]() is the episode that consecutively follows ε, then Rε = L
is the episode that consecutively follows ε, then Rε = L![]() . The values γLε(
. The values γLε(![]() ) and γRε(
) and γRε(![]() ) are constant on each type. Moreover GΓ(
) are constant on each type. Moreover GΓ(![]() ) = GΔ(
) = GΔ(![]() ) = 0 for all patterns
) = 0 for all patterns ![]() in the type unless the γLε are divisible by n. In the Γ and Δ′ preaccordions, γLε and
in the type unless the γLε are divisible by n. In the Γ and Δ′ preaccordions, γLε and ![]() may be circled or not, but never boxed.
may be circled or not, but never boxed.
Table 11.1 The four classes of episodes in Γ![]() .
.
Proof. From Tables 11.1 and 11.2, it is clear that Rε = L![]() for consecutive episodes.
for consecutive episodes.
If ε is of Class I or Class IV, then we see that
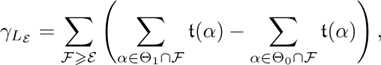
where the notation means that we sum over all episodes to the right of ε (including ε itself). If ε is of Class II or III, we have
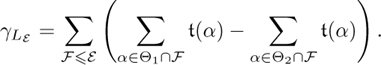
In either case, these formulas imply that γLε is constant on the patterns of the type.
Given their described locations, the fact that ![]() is never boxed in either the Γ or Δ′ preaccordions may be seen from the definitions.
is never boxed in either the Γ or Δ′ preaccordions may be seen from the definitions.
We now show that GΓ(![]() ) = GΔ(
) = GΔ(![]() ) = 0 unless n|γLε. Indeed, it follows from an examination of the locations of γLε in the Γ preaccordions and in the Δ′ preaccordions (where the same value appears as
) = 0 unless n|γLε. Indeed, it follows from an examination of the locations of γLε in the Γ preaccordions and in the Δ′ preaccordions (where the same value appears as ![]() ) that this entry is unboxed in both Γ and Δ′. If it is uncircled in the Γ preaccordion, then GΓ(
) that this entry is unboxed in both Γ and Δ′. If it is uncircled in the Γ preaccordion, then GΓ(![]() ) is divisible by h(γLε), hence vanishes unless n|γLε. If it is circled, then we apply the Circling Lemma (Lemma 9.6) to conclude that the same value appears somewhere else uncircled and unboxed, unless γLε = 0 (which is divisible by n) which again forces GΓ(
) is divisible by h(γLε), hence vanishes unless n|γLε. If it is circled, then we apply the Circling Lemma (Lemma 9.6) to conclude that the same value appears somewhere else uncircled and unboxed, unless γLε = 0 (which is divisible by n) which again forces GΓ(![]() ) = 0 if n
) = 0 if n ![]() γLε; and similarly for GΓ(
γLε; and similarly for GΓ(![]() ) = 0.
) = 0.
Table 11.2 The four classes of episodes in Δ![]() .
.
![]()
- Due to this result, we may impose the assumption that n|γLε for every episode. This assumption is in force for the rest of the book.
Now let ε1, · · · , εN be the episodes of the cartoon arranged from left to right, and let ki = k(εi). By a local pattern on εi subordinate to ![]() we mean an integer-valued function on εi that can occur as the restriction of an element of
we mean an integer-valued function on εi that can occur as the restriction of an element of ![]() to εi. Its top and bottom rows are thus the restrictions of the given top rows, and it follows from the definition of the episode that if (0, t) and (2, t − 1) are both in εi then
to εi. Its top and bottom rows are thus the restrictions of the given top rows, and it follows from the definition of the episode that if (0, t) and (2, t − 1) are both in εi then ![]() (0, t) =
(0, t) = ![]() (2, t − 1); that is, if both an element of the top row and the element of the bottom row that is directly below it are in the same episode, then
(2, t − 1); that is, if both an element of the top row and the element of the bottom row that is directly below it are in the same episode, then ![]() has the same value on both, and patterns in the type are resonant at t. The local pattern is subject to the same inequalities as a short pattern, and by (11.2) the sum of its first (middle) row elements must be ki. Let
has the same value on both, and patterns in the type are resonant at t. The local pattern is subject to the same inequalities as a short pattern, and by (11.2) the sum of its first (middle) row elements must be ki. Let ![]() i be the set of local patterns subordinate to
i be the set of local patterns subordinate to ![]() . We call
. We call ![]() i a local type.
i a local type.
LEMMA 11.2 A pattern is in ![]() if and only if its restriction to εi is in
if and only if its restriction to εi is in ![]() i for each i and so we have a bijection
i for each i and so we have a bijection
![]()
Proof. This is obvious from the definitions, since the inequalities (11.1) for the various episodes are independent of each other.
![]()
Now if ![]() is a short pattern let us define for each episode ε
is a short pattern let us define for each episode ε

provided ![]() is locally strict at ε, by which we mean that if α, β ∈ ε ∩ Θ1 and α is to the left of β then
is locally strict at ε, by which we mean that if α, β ∈ ε ∩ Θ1 and α is to the left of β then ![]() (α) >
(α) > ![]() (β). If
(β). If ![]() is not locally strict, then we define
is not locally strict, then we define ![]() .
.
PROPOSITION 11.3 Suppose that n|γLε for every episode. Assume also that for each ![]() i we have
i we have
![]()
Then
![]()
This proposition is the bridge between types and local types. Two observations are implicit in the statement of (11.4).
- Since by its definition
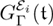 (
(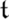 ) depends only on the restriction
) depends only on the restriction 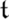 i of
i of 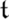 to
to 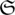 i, we may write
i, we may write 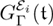 (
(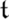 i) instead of
i) instead of 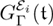 , and this is well-defined.
, and this is well-defined. - The statement uses the fact that γLε(
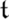 ) and γRε(
) and γRε(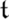 ) are constant on the type, since otherwise
) are constant on the type, since otherwise 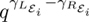 would be inside the summation.
would be inside the summation.
Proof. If ![]() i ∈
i ∈ ![]() i is the restriction of
i is the restriction of ![]() ∈
∈ ![]() , we have
, we have
![]()
By Proposition 11.1 we have Rεi = Lεi+1. Since our convention is that γ0 = γ2d+2 = 0, it follows that the factors ![]() cancel. Thus
cancel. Thus
![]()
![]()
In the rest of the chapter we will fix an episode ε = εi, and denote L = Lε and R = Rε to simplify the notation. The four remaining Propositions give relations between the Γ and Δ′ preaccordions within the episode ε.
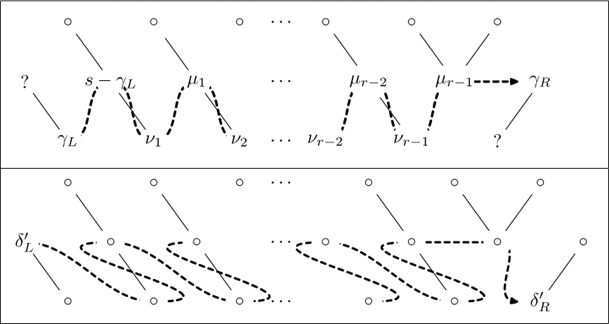
PROPOSITION 11.4 Let ![]() be a short pattern whose cartoon contains the following Class II resonant episode ε of order d:
be a short pattern whose cartoon contains the following Class II resonant episode ε of order d:
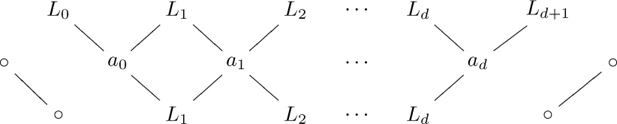
Then there exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the Γ and Δ′ preaccordions are given in the following table.

The values s, γL and γR are constant on the type containing the pattern.
Note: If the episode ε occurs at the left edge of the cartoon, then our convention is that γL = γ0 = 0, and if ε occurs at the right edge of the cartoon, then γR = γ2d+2 = 0. We would modify the picture by omitting γL or γR in these cases, but the proof below is unchanged.
Proof. Let γL = γLε and γR = γRε in the notation of the previous chapter, and let s, μi, νi be defined by their locations in the Γ preaccordion. Let s = ![]() + γR + γL,
+ γR + γL, ![]() and
and ![]() . It is immediate from the definitions that
. It is immediate from the definitions that

From this it we see that μi + νi = s and ![]() .
.
In order to check the correctness of the Δ′ diagram, we observe that the resonance contains d panels of type R, each of which may be specialized to a panel of type T or B. We specialize these to panels of type T. We obtain the following canonical snakes, representing the Γ and Δ′ preaccordions.
Looking at the even-numbered locations in these indexings, starting with γL = ![]() , Proposition 9.1 asserts that the values ν1, · · · , νd are as advertised in the Δ′ labeling. It also asserts that the value at the first odd-numbered location, which is the first spot in the bottom row of the episode, is (s − γL) + γL − ν1 = μ1; the second odd-numbered location gets the value μ1 + ν1 − ν2 = μ2, and so forth.
, Proposition 9.1 asserts that the values ν1, · · · , νd are as advertised in the Δ′ labeling. It also asserts that the value at the first odd-numbered location, which is the first spot in the bottom row of the episode, is (s − γL) + γL − ν1 = μ1; the second odd-numbered location gets the value μ1 + ν1 − ν2 = μ2, and so forth.
![]()
PROPOSITION 11.5 Let ![]() be a short pattern whose cartoon contains a Class I resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of in Γ and Δ′ preaccordions in ε are given in the following table.
be a short pattern whose cartoon contains a Class I resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of in Γ and Δ′ preaccordions in ε are given in the following table.
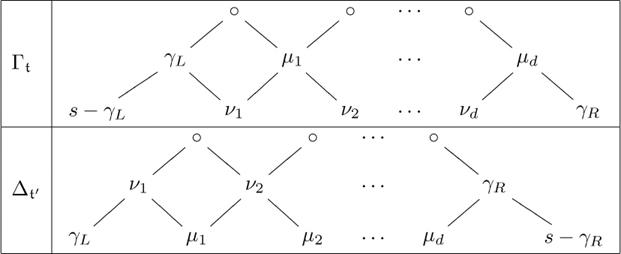
The values s, γL, and γR are constant on the type containing the pattern.
Proof. We define s, μi and νi to be the quantities that make the Γ preaccordion correct. The correctness of the second diagram may be proved using snakes as in Proposition 11.4. The proof that μi + νi = s is also similar to Proposition 11.4.
![]()
PROPOSITION 11.6 Let ![]() be a short pattern whose cartoon contains a Class III resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of the Γ and Δ′ preaccordions in ε are given in the following table.
be a short pattern whose cartoon contains a Class III resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of the Γ and Δ′ preaccordions in ε are given in the following table.

The values s, γL, γR and ξ are constant on the type containing the pattern.
Proof. This is similar and left to the reader.
![]()
PROPOSITION 11.7 Let ![]() be a short pattern whose cartoon contains a Class IV resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of the Γ and Δ′ preaccordions in ε are given in the following table.
be a short pattern whose cartoon contains a Class IV resonant episode ε of order d. There exist integers s, μ1, ν1, μ2, ν2, · · · , μd, νd such that μi + νi = s (i = 1, · · · , d), and the portions of the Γ and Δ′ preaccordions in ε are given in the following table.
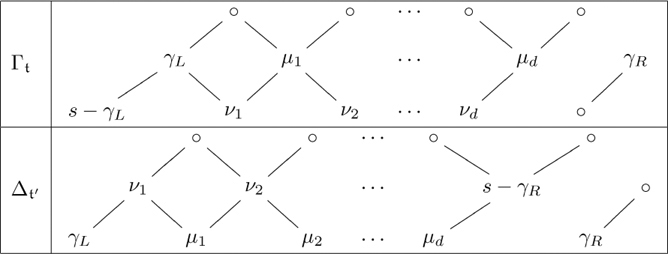
The values s, γL, γR and ξ are constant on the type containing the pattern.
Proof. This is similar and left to the reader.
![]()