 Don't forget the milk, honey!
Don't forget the milk, honey!
Lists are everywhere, starting from the laundry list and grocery list to the checklist on your smartphone's task manager. There are two types of lists. Simple lists, which just store some items disregarding the order allowing duplicates; and other types which don't allow duplicates. These second types of lists which don't allow duplicates are called sets in mathematics. The other broad category of list is associative list, where each element in some list gets mapped to another element in another list.
In this chapter, we shall learn about these generic containers and related methods. We shall learn when to use which list-based container depending on the situation.
Reading this chapter and following the exercises you will learn the following:
Why bother learning about generic lists?
Types of generic lists and how to use them
Give proper rationale for choosing a generic list such as one container over the other
How to create custom generic list-based containers
So let's get on with it...
Let us see why generic lists are important:
It ensures compile-time type checking. So type-unsafe code becomes a thing of the past.
It saves us a lot of typing, because compiler can generate type-safe code for generic types at runtime. So the same code works for different data types.
It is faster in many cases than its non-generic cousins, because it removes the need to box and unbox (also known as type-casting) from the code.
It makes source code much cleaner than its older, non-generic, unsafe cousins.
In this chapter, you shall find examples of how generic list-based containers make these possible. Happy listing!
There are mainly three types of lists you can imagine or would ever need:
A simple list is just a collection of items. Say a laundry list, a grocery list, a task list, a list of courses. The elements in a simple container don't associate them with any other element. There are several generic container classes to represent simple lists. They are
Stack<T>, Queue<T>
, List<T>
, LinkedList<T>
, and SortedSet<T>. These are generic implementations of classic data structures. So Stack<T> is a Last In First Out (LIFO) list, Queue<T> is a First In First Out (FIFO) list, List<T> is a simple unordered list, and so is LinkedList<T>. But List<T> supports random integer indexing natively, while the others don't.
Sets are simple lists that don't allow duplicates. All sets implement the interface ISet<T>. There are two set implementations HashSet<T> and SortedSet<T>. HashSet<T> doesn't maintain the order of elements, while SortedSet<T> keeps the elements sorted, if it knows how to sort the type. For custom types, you can pass a custom IComparer<T> instance to delegate the task of comparing. For HashSet<T>, you can pass IEqualityComparer<T> for custom equality comparison.
An associative list, as the name suggests, brings in an association between two different entities and represents them in a single list for example, marks obtained by a student in a different semester of a course, share values for a company over the years, and so on. To represent these type of lists, there is an interface IDictionary<TKey,TValue> and SortedList<TKey,TValue> is a derived class that implements this interface. So we can use SortedList<TKey,TValue> to represent any associative list in .NET Generics. SortedList<TKey,TValue> is also a list. This is implemented using an array. So unlike other IDictionary<TKey,TValue> implementations, SortedList<TKey,TValue> supports indexing over keys and values. So the order of insertion in a SortedList determines the order of elements; unlike other IDictionary<TKey,TValue> implementations, as we shall see in the next chapter.
If you were wondering what the heck are TKey
and
TValue, they are short and quite traditional ways of representing the type of key and type of value respectively. As generic lists can support any type, they are represented in this way. So at runtime the compiler generates appropriate code for the specified data type. This greatly helps to reduce code duplication and type mismatch issues.
In a nutshell:
|
This is a generic Stack implementation. This is first in last out. | |
|
This is a generic Queue implementation. This is a first in first out list. | |
|
This is a generic implementation of a simple list. This offers native random zero based integer indexing like an array. | |
|
This is a generic implementation of a classic double-linked list. No native random indexing is offered. | |
|
This is a generic Set implementation. The elements are not sorted. For custom equality comparison, you can pass the | |
|
This is a generic Set implementation. The value type elements remain sorted, by default. For reference types, we have to pass custom-comparer objects for custom element sorting; you can use the | |
|
Sometimes you want an associative container, but you still want to be able to access each key-value pair, like you do in a plain old array using the index. Then all you need is a |
Now that we have some basic idea about these generic list based containers, we shall see how these can be used to solve some real-world problems. Let's get started with a fun app!
A generic collection can contain objects of value and reference types. This means you can create nested types.
For example, if you want a list of stacks, you can get that by declaring List<Stack<T>>.
If you want a SortedList of integer keys and associate a list of string values with each such integer key, you can write SortedList<int,List<string>>.
All the following sequences share a common attribute. They all read the same both ways, save for the punctuations
"Madam I'm Adam"
"A Man, A Plan, A Canal, Panama!!"
12321
Detroit-Chicago-Detroit (This reads same word by word backwards, unlike others that read the same character by character.)
A Toyota
These types of sequences are called palindromes. A sequence is palindromic too, if the contents read the same both ways, for example, A-B-A. In this example, we shall see how a generic stack (that is, a Stack<T> instance) can be used to implement this, so that we can detect whether a given sequence is a palindrome or not for any given type that knows how to compare itself (that is, implements the IComparable interface).
So the task at hand is to build a generic palindrome checker that can check whether any sequence is a palindrome or not. All we have to do is let it know the type of the sequence at runtime.
The algorithm to find whether a sequence is a palindrome or not is really simple. If we arrange the tasks to be done in order to check whether the given sequence is a palindrome or not, it will be like:

The sequence can be of any type; char, string, integer, float, and so on to name a few. Also, note that the algorithm is not different for all these different types. However, we shall have to write several methods for supporting several data types.
However, if we use Generics we can avoid this code duplication for each type. We can write a single method (also known as
Generic Method) that can write the data type-specific code at runtime depending on what type of data type we want. The tradition is to use the letter T (which is short for Type) to create the generic method. When we consume this method, we pass concrete Types that conform to the standard expectations from the Type; like in this case, we expect the Type to implement IComparable.
The heart of the solution is to reverse the elements of the input sequence. This can be done by a stack. Since we want to make the method generic, we need a generic stack.
Follow the given steps:
Create a console application project. Call it
Palindrome Checker.Create a method called
IsPalindromic()with the following signature:public static bool IsPalindromic<T>(IEnumerable<T> inputSequence) where T:IComparable { Stack<T> buffer = new Stack<T>(); return true; }Add the following code in the
Main()method:static void Main(string[] args) { bool status = IsPalindromic<char>(new int[] { 1, 2, 2, 1 }); }Try to compile the program.
You will see a compiler error as shown in the following screenshot:

Let's see why that compile-time error occurred. Before that, let's learn a little more about generic stacks.
Creating a generic stack is very easy. Here is how:
Stack<T> myGenericStack = new Stack<T>();
So if you want a generic stack to be used to store a stack of string, then you change T with string as follows:
Stack<string> myCDs = new Stack<string>();
If you want a stack of integers, you just say:
Stack<int> opCodes = new Stack<int>();
If you are dealing with reference types, then you can declare a stack of base types and put derived types in that. Say if D is a class that implements an ID interface, then if you create a stack of ID objects, you can put ID objects in the Stack as follows:
Stack<ID> somethings = new Stack<ID>(); Somethings.Push(new ID());
However, the method needs to know how to compare the elements in the buffer. So now the obvious question you might have is, if we write the code using a generic place holder (T in this case) which gets replaced by the original data type at runtime, how will the method know at compile time how to compare variables of such data type?
Well, that's a very good question and the answer lies in the very first line of the method. Let's take a close look at it:
public static bool IsPalindromic<T>(IEnumerable<T> inputSequence) where T:IComparable
The keyword where is used to constrain the types that can be used as a valid argument in the generic method IsPalindromic<T>()
, we just created. where T:IComparable means T has to be a type that implements the IComparable interface. This syntax is known as Constraints in Generics
.
Now, let's get back to the compilation error part. Generics ensure compile-time type checking as follows:
bool status = IsPalindromic<char>(new int[] { 1, 2, 2, 1 });In this code, IsPalindromic<char> promises that everything that follows in the argument to this method will be of type character. However, we have an integer array as the input sequence. This is causing a type mismatch and thus is caught at compile time.
We are passing an array as the parameter, where the method expects something of type IEnumerable<T>. This is possible because IEnumerable<T> inherits from IEnumerable and good old arrays implement IEnumerable too. Thus, IEnumerable serves as a bridge between pre-generic collections and generic collections.
Follow the given steps:
Add the following code after the initialization of the buffer in the source, as carried out previously in step 2:
foreach (T element in inputSequence) { buffer.Push(element); }Count()andElementAt()are extension methods and are available atSystem.Linqnamespace in .NET Framework 3.5 and above. You can get it with Visual Studio 2008 and above. So please include that namespace:for (int i = 0; i < inputSequence.Count(); i++) { if(buffer.Pop().CompareTo(inputSequence.ElementAt(i))==0) continue; else return false; }Make sure you retain the last
return true;statement.Replace the content of the
Main()method with the following:static void Main(string[] args) { //Checking if a string (Which is basically a sequence of //characters) bool status1 = IsPalindromic<char>("LIRIL"); //Checking if an array of string is palindromic bool status2 = IsPalindromic<string>(new string[]{"mango","apple","mango"}); //Checking if an array of int is palindromic bool status3 = IsPalindromic<int>(new int[] { 1,2,3,4,5,6,0,6,5,4,3,2,1 }); //Checking if an array of float is palindromic bool status4 = IsPalindromic<float>(new float[] { 1.34F,2.34F,43.1F}); Console.WriteLine(status1 + " " + status2 + " " + status3 + " " + status4); }Run the program.
The program shall print the following to the console:
The following looping construct:
foreach (T element in inputSequence)
{
buffer.Push(element);
}pushes all the elements in the input sequence to a stack. The stack is a last in first out list. It keeps the elements in reverse order. So if you want to add an element to the top of the stack, you should use the push method.
So when the method is called by bool status1 = IsPalindromic<char>("GENERICS"); it stores the characters of the input sequence in the internal generic stack buffer as follows:

buffer.Pop() returns the top-most element from the stack and removes that from the stack. The ElementAt() method returns the ith element from the input sequence. As long as these two are equal, the sequence might be a palindrome. So, we must continue going through the input sequence. However, if they mismatch at any point, it becomes evident immediately that the input sequence is not a palindrome. Thus, we can return False. However, if we can get to the end of the input sequence without encountering a mismatch, the input sequence is a palindrome and thus we have to return True.
Let's now try to decode the output. Among four input sequences in the Main() method, the first three are palindromes. However, the last one doesn't read the same both ways and surely isn't a palindrome. Output matches that. We get True for the first three input sequences and False for the last one.
Any type that implements IComparable would work. Other types will fail.
Generics are not limited to lists and you can even mix parameterized types with specialized types as well. For instance, what if you want to store the frequency of occurrence of a string, number, or a symbol. While the type of what you keep the frequency of is unknown or undecided, however you see that the frequency itself is always a number. Let's take a look at how we can implement that using anagrams as an example.
Anagrams are as fascinating as palindromes. Two sequences are said to be anagrams of each another, when they share the same number of elements in the same frequency.
For example, two strings "The eyes" and "They see" both have the same number of characters, and the frequency of each character in these two strings is the same. Both of them have a single "T", a couple of "e"s, and so on. Thus, they are anagrams of each other.
http://www.anagrammy.com/ organizes a competition for the best anagrams each month. Assume your friend wants to participate and is now seeking your help to develop a program that can find anagrams of a given word. Let's get into action and help your buddy.
A strategy to check whether two sequences are anagrams of each other or not is really simple. We need a container that would let us store each unique element of the sequence and their frequency of appearance in the sequence.
For example, the string "The eyes" will be stored in such a container as follows:
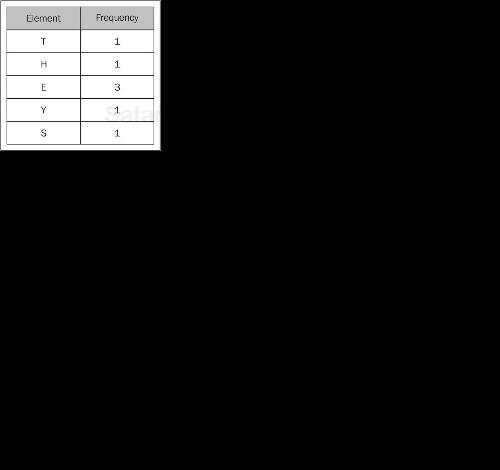
If another string stored in the same way shares the same frequency of characters, then that will be an anagram of "The eyes". So, if we deduct 1 from the frequency as soon as we get the same character in the second string; we shall have all zeros in the frequency column of the preceding table at the end of scanning the second string; in this case, we are dealing with two anagrams.
This algorithm is applicable to any type of anagram sequence, not only for strings. So, we can write a generic method to check whether two sequences are anagrams of each other or not, for any type.
Follow the given steps:
Create a console application called
Ganagram(short form for generic anagram). This is a showcase ofSortedList<TKey,TValue>, solving a real problem.Add the following method in the
Program.csfile:public static bool IsAnagram<T>(IEnumerable<T> first, IEnumerable<T> second) { SortedList<T, int> val = new SortedList<<T, int>(); foreach (T element in first) { if (!val.ContainsKey(element)) val.Add(element, 1); else val[element]++; } foreach (T element in second) { if (val.ContainsKey(element)) val[element]--; else return false; } foreach (T element in val.Keys) { if (val[element] != 0) return false; } return true; }Call this method from the
Main()method of the console application as follows:static void Main(string[] args) { bool status = IsAnagram<char>("dream", "armed"); bool status2 = IsAnagram<string>("yesterday today tomorrow".Split(' '), "tomorrow today yesterday".Split (' ')); bool status3 = IsAnagram<int>(new int[]{1,2,3}, new int[]{ 3,4,1}); Console.WriteLine(status + " " + status2 + " " + status3); }Compile and execute the program.
As you execute the program, you will see the following output:
"dream" and "armed" are anagrams of each other so the first one returned True. So are the sentences where the words "Yesterday", "Today", and "Tomorrow" appear in different locations. However, the last sequence of integers are not anagrams of each other because the second one has a four and the first one doesn't. That's why the generic method returns False for that one.
Ok. So the method works well. Let's see how it works.
SortedList<T, int> means a sorted list where the data type of the key is T and that of the value is an integer, there is no duplicate entry, and the entries in the SortedList<T,int> are sorted.
SortedList can be used to store key-value pairs as long as the keys are unique. This is the condition imposed by IDictionary and thus has to be followed by all IDictionary implementations. A sequence can be expressed as a list of key-value pairs as shown earlier. Keys are the individual elements of the sequence and the value for each key is the frequency of that particular element in the sequence.
At runtime, when we pass two strings, the compiler generates code for SortedList<char, int>.
In the next loop, we are adding all the elements from the first sequence to this SortedList. The ContainsKey() method returns true if the key is present in the sorted list. Otherwise it returns false.
Note
Warning!
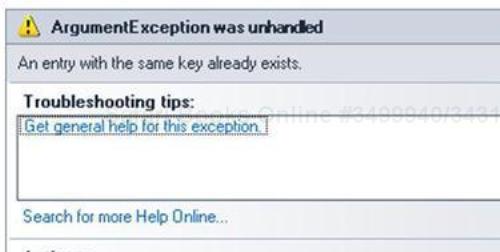
As the SortedList can only store key-value pairs with unique keys, it is good practice to check for the existence of the key before trying to add it. If the key is already present, it will throw the following exception:
The following screenshot shows the exception that occurs when we want to add a duplicate key:
val.Add(element, 1); adds the element for the first time, when it is not present in the SortedList. However, from the second time onwards the frequency of the element is increased by the code snippet val[element]++;.
The SortedList class implements the IDictionary<TKey,TValue> interface. So there is a concrete implementation for SortedList of the interface indexer:
TValue this[TKey key] { get; set; }This is why the corresponding value can be obtained by passing the key in square brackets. So in the statement val[element]++; val[element] refers to the corresponding frequency of the key, whose value is stored in the element. Thus, val[element]++ means increasing the corresponding element by unity.
In the third loop, we are iterating over the second sequence. If the sequence contains an element not present in the SortedList already, we don't need to look any further. They can't be anagrams. However, if the current element of the second sequence is present in the SortedList as a key, then we must decrease the frequency by unity; and continue to do so as long as we don't hit the end of the second sequence or encounter an element that is not present as a key in the SortedList already.
The last loop checks whether all the values of the SortedList are zero or not. If they are, both the sequences are anagrams to each other, otherwise they aren't. We return the status accordingly.
Now that we have the method that can find whether two given sequences are palindromes to each other or not, can you write a program that uses this method and finds all the anagrams of the given word? You can use any dictionary you want. You can verify your program by several word anagram duos listed at http://sudipta.posterous.com/found-these-word-beauties-on-the-taxi-ride-ho.
As gadget addicts, there are so many gadgets we desire to buy, but often our budget is limiting. So, let's keep a prioritized list of gadgets we hope to buy.
Priority queues come to our help here.
Let's see how we can create our own implementation of the generic priority queue. .NET doesn't offer a built-in generic priority queue.
As there can be more than one gadget that you want with the same zest, so the shopping list can have more than one element with the same priority. We shall represent the priority queue as a SortedList<TKey,TValue>, where the priority will be represented by any type that can be compared for equality and the values will be represented by a list of values of type TValue.
Create a console application.
Add a class called
PriorityQueueto the project. Change the signature of the class header as follows:public class PriorityQueue<Tkey, TValue> where Tkey : IComparable
The heart of this
PriorityQueueis aSortedList. I want to call itinnerDS, add this private variable as follows:private SortedList<Tkey, List<TValue>> innerDS; public PriorityQueue() { innerDS = new SortedList<Tkey, List<TValue>>(); }Go to the
Main()method of the console app and add the following code:PriorityQueue<int, string> gadgets = new PriorityQueue<int, string>();
Try to compile. You will see that it compiles. It will run too. But don't expect any visible output yet.
When you run the console application, you will see nothing happens. But in the background the compiler created a type-safe copy of the generic priority queue, where the priorities are of type integer and the values are of type string.
Now, go and change the priority queue declaration as follows:
PriorityQueue<TimeZone, string> set = new PriorityQueue<TimeZone, string>();
and try to compile. You will get the following compile-time error:
There is no implicit reference conversion from 'System.TimeZone' to 'System.IComparable'.
This will happen because the TimeZone class doesn't implement the Compare() method of the IComparable interface.
Add the following code, in the same
PriorityQueueclass:/// <summary> /// Adds a new entry to the priority queue /// </summary> /// <param name="key">priority of the item.</param> /// <param name="value">the item itself.</param> public void Enque(Tkey key, TValue value) { if (!innerDS.ContainsKey(key))//O(log n) { List<TValue > vals = new List<TValue>(); vals.Add(value); innerDS.Add(key, vals); } else if (!innerDS[key].Contains(value)) innerDS[key].Add(value); }Add this method in the
PriorityQueueclass as follows:/// <summary> /// Gets elements of given priority /// </summary> /// <param name="priority">Given priority</param> /// <returns>A list of elements that has this priority</returns> public IEnumerable< TValue > GetElemenets(Tkey priority) { try { return innerDS[priority]; } catch (KeyNotFoundException ex) { //return empty list. So the caller wouldn't crash. return new List<TValue>(); } }Go to the
Main()method and replace the existing content with the following:PriorityQueue<int, string> gadgetShoppingList = new PriorityQueue<int, string>(); gadgetShoppingList.Enque(1, "iPhone"); gadgetShoppingList.Enque(2, "iPad"); gadgetShoppingList.Enque(1, "MacBook"); gadgetShoppingList.Enque(3, "Amazon Kindle"); var gadgetsIWantMost = gadgetShoppingList.GetElemenets(1); foreach (string gadgetName in gadgetsIWantMost) Console.WriteLine(gadgetName); Console.ReadLine();
This will print the following output. Can you explain why?

Now, let's see what caused this. The first line in the Main() method: PriorityQueue<int, string> gadgetShoppingList = new PriorityQueue<int, string>(); creates a specific copy of a generic priority queue, where the priorities are of type integer, and data types of objects to be stored as values are set to string. I wanted to assign integer priorities to the gadgets I want to buy. This call internally replaces the TKey with int and TValue with string at runtime, in the generic implementation of the PriorityQueue<TKey,TValue> defined previously.
Note that the internal data structure is a sorted list, where each key of the list maps to a list of values depicted by List<TValue>. So, with the four calls to the Enque() method, the internal SortedList will look as follows:

In the Enque() method, the elements are entered, if the priority attached to the element is not already present in the innerDS.Keys. However, users might get over-enthusiastic and add the same element twice or more. That will result in duplicate entries in the prioritized list. In order to avoid that innerDS[key].Contains(value) is used to check whether this gadget is already there or not.
Now that we know how the elements made their way to the inner list, let's see what happens when we try to retrieve the elements for a given priority.
As described earlier, the value for a corresponding key from a SortedList is found by indexing over the key. So in the method GetElements() innerDS[priority]; shall return all the gadgets that were added with the given priority. However, if no element exists with that priority, it will throw a KeyNotFoundException. In such a case, we shall return a blank list of TValue to match the method signature. In order to validate this point, do a little experiment.
Add the following code in the Main() method:
Console.WriteLine(gadgetShoppingList.GetElemenets(4).Count());
This will print "0" to the console as there is no element in the ShoppingList with priority 4.
Note
Tips!
If we get an exception of type KeyNotFoundException and the caller method is expecting a list of items, it is best practice to return an empty list so that the caller method doesn't have to do anything special with the return value.
Now suppose you have enough money to buy a few of the top gadgets you wanted, it's time to strike them off the ShoppingList. Let's see how.
Add the following method in the
PriorityQueueclass:/// <summary> /// Removes the first element with top priority /// </summary> public void Deque()() { if (innerDS.Count > 0) { int i; for (i = 0; i < innerDS.Count; i++) if (innerDS[innerDS.Keys[i]].Count > 0) break; try { innerDS[innerDS.Keys[i]].RemoveAt(0); } catch (KeyNotFoundException ex) { return; } } }Add the following property in the
PriorityQueueclass:/// <summary> /// This is a port between other functionalities that are omitted. /// This returns a Queue implementation of the Prioritized Queue. /// </summary> public Queue<TValue> OriginalQueue { get { Queue<TValue> actual = new Queue<TValue>(); foreach (Tkey key in innerDS.Keys) { foreach (TValue value in innerDS[key]) { actual.Enqueue(value); } } return actual; } }This
OriginalQueue, read-only property, flattens theSortedList<TKey,TValue>instance and arranges all the elements in thePriorityQueuemaintaining the order using aQueue<TValue>instance.Add the following property in the
PriorityQueueclass:/// <summary> /// The first element with top priority /// </summary> public TValue First { get { try { int i; for (i = 0; i < innerDS.Count; i++) if (innerDS[innerDS.Keys[i]].Count > 0) break; return innerDS[innerDS.Keys[i]][0]; } catch (Exception ex) { return default(TValue); } } }Add the following code in the
Main()method:static void Main(string[] args) { PriorityQueue<int, string> gadgetShoppingList = new PriorityQueue<int, string>(); gadgetShoppingList.Enque(1, "iPhone"); gadgetShoppingList.Enque(2, "iPad"); gadgetShoppingList.Enque(1, "MacBook"); gadgetShoppingList.Enque(3, "Amazon Kindle"); //Returning the first element from the prioritized Shopping List string gadgetIWantTheMost = gadgetShoppingList.First; Console.WriteLine("Buying {0}",gadgetIWantTheMost ); Console.WriteLine("Bought " + gadgetIWantTheMost); //Bought the first gadget. Let's strike it off the list. gadgetShoppingList.Deque(); //Let's see what else I can buy if I get some more dollars ;) Console.WriteLine("Need more cash to buy "); Queue<string> gadgets = gadgetShoppingList.OriginalQueue; foreach (string gadgetName in gadgets) Console.WriteLine(gadgetName); }
This will print the following output to the console:

Let's see how we got there.
The property First returns the value of the first element of the PriorityQueue or in this case the gadget I want most.
innerDS[innerDS.Keys[i]].count returns the list of gadgets, where the priority is the ith key of the inner SortedList. So first in the list of gadgets that has at least one element are the gadgets of top-most priority. The first item (which is located at index zero of such a list) is the item with top-most priority and entered in the ShoppingList first. So, technically that's the first element with top-most priority. This is referenced by innerDS[innerDS.Keys[i]][0].
The method Deque() just removes this first element from the priority queue. The property OriginalQueue returns a queue of gadgets in order of their priority.
Using this generic PriorityQueue, we can deal with other priorities of our life too. Say we want to schedule our meetings and appointments. This is how we can do it.
Add the following code to the
Main()method://Creating a priority queue to store the appointments. PriorityQueue<DateTime, string> myAppointments = new PriorityQueue<DateTime, string>(); //Adding appointments myAppointments.Enque(DateTime.Today.AddDays(1), "Dental checkup @ Doctor Smiley :)"); myAppointments.Enque(DateTime.Today.AddDays(3), "Weekly grocery shopping"); myAppointments.Enque(DateTime.Today.AddDays(1), "Trip to Art Gallery."); myAppointments.Enque(DateTime.Today.AddDays(2), "Son's football tournament at school"); //Listing all appointments as per they are scheduled foreach (string task in myAppointments.OriginalQueue) Console.WriteLine(task);
Imagine you work for an online bidding company such as eBay. Your company deals in several product lines. On the company website, live bidding prices for all the products have to be displayed. In this example, we shall see how LinkedList<T> can be used to offer such functionalities.
There are a lot of hits on the server per second, so sorting the data at regular intervals is not an option. You have to come up with a structure such that the bidding prices get inserted in a list in the sorted order as the user submits them from the site console. This is what I like to call live sorting. Moreover, as two or more people can quote the same bid amount, so the list where you store the bidding values must allow duplicates. Your boss is interested to know the following:
What are the actual bid amounts submitted for any product?
What is the range of bid amounts (minimum and maximum) for any product?
What is/are the common bidding amounts across different product lines?
Besides this, your boss would be happy to see whether you can design a system to capture the demographics of the bidders. This will help your company distribute targeted advertisements. For example, which newspaper is mostly read by people who bid for smartphones and MP3 players?
Thankfully, .NET can help and we can build a couple of generic structures to solve this problem. First, we shall build a structure that will help us solve the live sorting challenge. Later, we shall use this and some other generic .NET classes to solve the remaining demographics issues.
Create a class library project. Call it
LiveSortedListAPI.Change the name of the class from
Class1.cstoLiveSortedList.cs.Change the header of the class as follows:
public class LiveSortedList<T> where T:IComparable
Add the following private variables and properties:
LinkedList<T> innerDS; LinkedList<T> innerDSDesc; LinkedList<T> actualValues; public List<T> LiveSortedValues { get { return new List<T>(innerDS); } } public List<T> LiveSortedValuesDesc { get { return new List<T>(innerDSDesc); } } public List<T> ActualValues { get { return new List<T>(actualValues); } }Add the constructor as follows:
public LiveSortedList() { innerDS = new LinkedList<T>(); innerDSDesc = new LinkedList<T>(); actualValues = new LinkedList<T>(); } /// Add the following method to add elements in the Live Sorted /// List /// <summary> /// Adds a new element in the LiveSortedList /// </summary> /// <param name="val">The value to be added.</param> public void Add(T val) { //Adding to the actual list actualValues.AddLast(val); //If there is no item in the list, //This is the first item in the list if (innerDS.Count == 0) { //Adding the first item to the ascending values list innerDS.AddFirst(val); //Adding the first item to the descending values list innerDSDesc.AddFirst(val); } else { //If the current value is less than first value //in the ascending list if (innerDS.First.Value.CompareTo(val) >= 0) { //Add this as the first item in the ascending values list innerDS.AddFirst(val); //Add this as the last item in the descending values list innerDSDesc.AddLast(val); //return the control return; } //If the current value is more than the last value //in the ascending list if (innerDS.Last.Value.CompareTo(val) <= 0) { //Add this as the last item in the ascending values list innerDS.AddLast(val); //Add this as the first item in the descending values list innerDSDesc.AddFirst(val); //return the control return; } //For all other range of values of the current value else { T temp = default(T); //Iterate over the current ascending collection to //find the proper place of insertion. foreach (T t in innerDS) { if (t.CompareTo(val) > 0) { //Temp is the value Just greater than the current value temp = t; break; } } //Add this value before temp in the ascending list innerDS.AddBefore(innerDS.Find(temp), val); //Add this value after temp in the descendng list innerDSDesc.AddAfter(innerDSDesc.Find(temp), val); } } }Add a console application project to this solution, where you created the class library.
In the
Main()method of the console application, add the following code:LiveSortedList<double> bids = new LiveSortedList<double>(); //Say, Adding bidding amount for a iPod bids.Add(12.50); bids.Add(11.50); bids.Add(11.32); bids.Add(13.35); bids.Add(11.50); bids.Add(12.60); bids.Add(18.40); bids.Add(19.50); bids.Add(11.65); foreach (double bidAmount in bids.LiveSortedValues) Console.WriteLine(bidAmount.ToString("$00.00"));Compile and run the program. Don't forget to set the console application as the start-up project.
As you execute the program, you will see the following output:
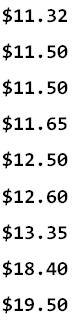
LinkedList<T> is a generic linked list that stores elements of type T in LinkedListNode<T>. A linked list offers several methods to insert nodes in several parts of the list. The names of these methods are very straightforward. AddFirst() lets you add an element at the start of the linked list. AddLast() lets you add an element at the end of the linked list. AddBefore() lets you add an element before a particular node in the linked list, whereas AddAfter() lets you add an element after a particular node in the linked list.
The properties First and Last represent the first and the last node of a linked list. First.Value returns the value of the first node. Last.Value returns the value of the last node. These nodes are of type LinkedListNode<T>.
The Add() method of LiveSortedList<T> class works very simply. If the element to be added is less than the first value, then we have to add it as the first element. If, however, the element to be added is more than the last value, then we have to add it as the last element. However, if the element's value is somewhere in between, we need to find the LinkedListNode<T> whose value is just greater than the element's value.
The Find() method of the LinkedList<T> class returns the LinkedListNode<T> that has the value passed as an argument of Find(). So in the call innerDS.AddBefore(innerDS.Find(temp), val); innerDS.Find(temp) returns the LinkedListNode<T> whose value is temp. So this call will insert val before temp in the LinkedList<T> innerDS.
For now, assume that your company deals with bidding on iPad, iPhone, MacBook, and iPod. So you shall have to keep an eye on the bidding prices of these products. This means we would need a way of associating product name/ID to the live sorted bid amount values. SortedList<TKey,TValue> as discussed earlier, fits the bill perfectly. Let's see how.
Stay in the class library project, where we defined
LiveSortedList<T>. Add a different class. Call itMultiLiveSortedList.cs.Change the class header as follows:
public class MultiLiveSortedList<TKey,TValue> where TKey:IComparable where TValue:IComparableAdd the following variable and the constructor:
SortedList<TKey, LiveSortedList<TValue>> innerDS; public MultiLiveSortedList() { innerDS = new SortedList<TKey, LiveSortedList<TValue>>(); }Add the following method to the class to add elements in the list:
public void Add(TKey key, IEnumerable<TValue> values) { if (!innerDS.ContainsKey(key)) { innerDS.Add(key, new LiveSortedList<TValue>()); foreach (TValue val in values) innerDS[key].Add(val); } else { foreach (TValue val in values) innerDS[key].Add(val); } }Add the following method to return bid values for a particular product:
public List<TValue> BidAmountsFor(TKey key) { try { return innerDS[key].LiveSortedValues; } catch { throw new KeyNotFoundException("No such product exist"); } }Create a console app and attach the reference of this class library to that. Add the following code in the
Main()method:MultiLiveSortedList<string, double> categorizedBidValues =new MultiLiveSortedList<string, double>(); //Adding live sorted bid amounts for each product categorizedBidValues.Add("iPod", new List<double>(){12.50,11.50,11.32,13.35,11.50}); categorizedBidValues.Add("iPad", new List<double>() { 212.50, 211.50, 211.32, 213.35, 213.50 }); categorizedBidValues.Add("MacBook", new List<double>() { 212.50, 211.50, 300, 223, 320 }); categorizedBidValues.Add("iPhone", new List<double>() { 333, 242, 302, 301.40, 310 }); //Finding Bid Amounts for the product "iPad" List<double> BidsForIPad = categorizedBidValues.BidAmountsFor("iPad"); //Maximum Bid Amount for "iPad" double MaxBidForIPad = BidsForIPad[BidsForIPad.Count - 1]; //Minimum Bid Amount for "iPad" double MinBidForIPad = BidsForIPad[0]; Console.WriteLine("iPad bid amounts are between " + MinBidForIPad.ToString ("$.00") + " and " + MaxBidForIPad.ToString ("$.00"));Compile and run the program.
As you execute the program, the following output will be printed to the console:
The new class created is basically a SortedList<TKey,TValue> in disguise where the TValue will be a LiveSortedList<TValue>. So, you saw how two different generic collections are used together to solve a problem. LiveSortedList ensures that the bid amount values being added are always in a sorted order and the SortedList class ensures that these LiveSortedLists are kept indexed by the product name.
innerDS[key], in this case, returns the LiveSortedList<TValue> for the given key.
innerDS[key].LiveSortedValues, as shown earlier, returns a list of sorted TValue values.
Now is the time to take a look at the other questions your boss had. How to find common bidding amounts. That's conceptually different. That's actually a set theory problem. We have a list of values representing the bidding amount for several products. Now we need to find common values among these lists. This can be solved using an intersection of these two lists of values. .NET makes breathing easy with the introduction of the SortedSet<T> class in the System.Collections.Generics namespace. Let's see how we can use this.
Stay in the
MultiLiveSortedListclass. Add the following methods:public SortedSet<TValue> CommonAcross { get { SortedSet<TValue> com; com = new SortedSet<TValue>(innerDS.Values[0].LiveSortedValues); for (int i = 1; i < innerDS.Count; i++) com.IntersectWith (new SortedSet<TValue>(innerDS.Values[i].LiveSortedValues)); return com; } } public SortedSet<TValue> CommonAmong(TKey key1, TKey key2) { SortedSet<TValue> com; com = new SortedSet<TValue>(innerDS[key1].LiveSortedValues); com.IntersectWith(new SortedSet<TValue>(innerDS[key2].LiveSortedValues)); return com; }Go to the console app previously created. Add the following snippet after the previous code in the
Main()method. Then compile and run the program:SortedSet<double> mostCommonBiddingAmounts = categorizedBidValues.CommonAcross; SortedSet<double> commonBidAmountForIPadAndMacBook = categorizedBidValues.CommonAmong("iPad","MacBook"); Console.WriteLine("Common Bid amounts for iPad and MacBook are "); foreach (double commonBidAmount in commonBidAmountForIPadAndMacBook) Console.WriteLine(commonBidAmount.ToString("$.00"));
As you execute the program, you will see the following output:

SortedSet<T> has several methods. The IntersectWith() method accepts another SortedSet<T> as an argument and modifies the caller SortedSet<T> object content with the intersection result. So this is an in-place operation.
SortedSet<T> has an overloaded constructor that can take an IEnumerable<T> instance and create a sorted set out of it. It removes the duplicates as a set can't have duplicates. In the method CommonAmong(),innerDS[key1] returns a LiveSortedList<T> instance. Thus, innerDS[key1].LiveSortedValues is a List<T> instance that implements IEnumerable<T>. So, this is a valid argument to the SortedSet<T> constructor.
I was playing the following word-making game with one of my friends. I lost a couple of times:
http://www.eastoftheweb.com/games/index.php?p=games/multieight/1
So, I decided to write a program that will help me find all the words from the characters of a given word. This task is not very easy. But with Generics, this becomes lightweight.
In this example, we shall create a console app, where the computer finds all the possible words from the T9 dictionary that uses a subset of the alphabet used in the given word. The following is a sample run:

Create a console application and add the following method in the program:
/// <summary> /// Finds the histogram of the characters of the word. /// </summary> /// <param name="word">The word for which the histogram of /// characters has to be found.</param> /// <returns>Histogram of charactres</returns> private static SortedList<char, int> GetWordHistogram(string word) { SortedList<char, int> wordHistogram = new SortedList<char, int>(); foreach (char c in word.ToArray()) { if (!wordHistogram.ContainsKey(c)) wordHistogram.Add(c, 1); else wordHistogram[c]++; } return wordHistogram; }
Add the following method in the
Program.csfile:/// <summary> /// A word can be formed using a set of characters, if one of /// their histogram is a /// subset of the other in terms that they share some of the /// characters and /// occurrence of characters is not more than in the other one. /// </summary> /// <param name="firstOne">The first character histogram</param> /// <param name="secondOne">The second histogram</param> /// <returns></returns> private static bool CanIFormAWord(SortedList<char, int> firstOne, SortedList<char, int> secondOne) { int count = 0; bool status = false; foreach (char c in firstOne.Keys) { //In order to be a subset all the characters //in this first SortedList has to be there //in the second one. if (secondOne.ContainsKey(c)) { //The frequency of these characters should not be exceeding //that of the other one. if (secondOne[c] >= firstOne[c]) { status = true; continue; } else { status = false; break; } } else { status = false; break; } } return status; }
Add the following code snippet in the
Main()method:static void Main(string[] args) { //Save the T9.txt file in the applications bin/debug directory. StreamReader sr = new StreamReader("T9.txt"); Console.WriteLine("Enter the word or phrase"); string word = Console.ReadLine(); //Stores the histogram of the current given word SortedList<char, int> soughtWordHistogram = GetWordHistogram(word); //Stores histogram of all words in the SortedList SortedList<string, SortedList<char, int>> allWordHistogram = new SortedList<string, SortedList<char, int>>(); string line = string.Empty; while ((line = sr.ReadLine()) != null) { foreach (string w in line.Split(' ')) { string x = w.Trim(); if(x.Length > 0) if(!allWordHistogram.ContainsKey(x)) allWordHistogram.Add(x, GetWordHistogram(w)); } } sr.Close(); foreach (string w in allWordHistogram.Keys) { //Checks If the current word can be formed using the letters //of the given word if (CanIFormAWord(allWordHistogram[w], soughtWordHistogram)) { //If yes, print that Console.WriteLine(count.ToString() + ". " + w); count++; //print 20 words or less per page if (count % 20 == 0) { Console.WriteLine(); Console.WriteLine("---More--"); Console.WriteLine("---Hit <Enter> to proceed --"); Console.ReadLine(); } } } //Wait for a final keystroke Console.ReadLine(); }
Can you explain how the program works? Everything used in this example is discussed earlier in another example app in the chapter. You can download the T9 dictionary from the book's website.
Also, as an extension, can you use whatever you learned in this chapter to create a system that offers predictive text suggestions as the user types.
The last time I went to see a doctor, I wished I could have seen a specialist the same day. We can build a system that can answer very important questions (such as the ones shown in the following list) that patients might have:
When is doctor A available?
When are both doctor A and doctor B there?
Does doctor A work on all the days that doctor B does and vice versa?
Which are the days when either of the doctors is available?
When either of these two doctors available, but not both?
Which doctor is available over the weekends?
Whether doctor A is available on the given date?
Who is more available, doctor A or doctor B?
Create a console application. Add the following variables:
HashSet<DateTime> AvailabilityOfDoctorA = new HashSet<DateTime>() { DateTime.Today, DateTime.Today.AddDays(-1), DateTime.Today.AddDays(1) }; HashSet<DateTime> AvailabilityOfDoctorB = new HashSet<DateTime>() { DateTime.Today.AddDays(-3), DateTime.Today.AddDays(1),DateTime.Today.AddDays(1) };Add the following code in the
Main()method:Console.WriteLine("Doctor A is avilable on these days "); Console.WriteLine(); foreach (DateTime d in AvailabilityOfDoctorA) Console.WriteLine(d.ToLongDateString());Execute the program.
You will see a similar output:

We are looping through all the dates in the HashTable that holds the dates Doctor A is available. That's not very interesting. But let's see how we can do a lot more with sets.
You see here in this list Sunday appeared before Saturday. If you want to keep your entries sorted, then please resort to a sorted set implementation such as SortedSet<T>.
Go back to the
Main()method and change its content as follows:Console.WriteLine("Doctor A and Doctor B both shall be available on "); Console.WriteLine(); HashSet<DateTime> commonDates = AvailabilityOfDoctorA; commonDates.IntersectWith(AvailabilityOfDoctorB); foreach (DateTime d in commonDates) Console.WriteLine(d.ToLongDateString());Execute this new program.
You will see the following output:

Before we dig deep to see what caused the output, please note that every time you run this snippet, you shall see different results because the example uses DateTime.Today that will change every second if you are right on the 11th hour of a day.
The IntersectWith() method returns the set representing the intersection of two sets. Or in other words, sets with common elements in two sets.
IntersectWith()
is a method that modifies the caller instance of the ISet<T> implementation; in place. So, after the call to IntersectWith(); commonDates will contain only this: Tuesday, May 10, 2011 entry. So, if you don't want to modify the HashSet in place, try copying that to a temporary variable as I did in this case, in the commonDates HashSet<T> instance.
All the methods of ISet<T> that end with a With are in place. So be careful while calling them. If you want to use a method that returns a new set without modifying the caller set instance; you have to use the extension method Intersect<T> available on the System.Linq namespace.

We shall learn more about extension methods in Chapter 4, LINQ to Objects. For now it would be enough to know that native ISet<T> implementations are in place, while the extension methods are not.
What will be the content of
Set Aafter the following calls:HashSet<string> A = new HashSet<string>() { "a", "b", "c", "d" }; HashSet<string> B = new HashSet<string>() { "d","e" }; A.IntersectWith(B);What will be the content of
Set Bafter the following calls:HashSet<string> A = new HashSet<string>() { "a", "b", "c", "d" }; HashSet<string> B = new HashSet<string>() { "d","e" }; B.UnionWith(A);
We solved the anagram problem earlier, so let's take a second look. An anagram duo results in the same sorted collection. For example, consider the following two strings:
"The Eyes"
"They See"
When sorted and any special character (including whitespace) is removed; these two strings result in the following string:
"eeehsty"
or in other words that can be written as follows:
"e3h1s1t1y1"
where the digits next to each character represents the frequency of that character in the phrase.
Create a class library project. Call it
GenEx.Add the following class there:
/// <summary> /// A Set that allows multiple copies of the same element. /// It keeps a count of how many elements are present. /// </summary> /// <typeparam name="T"></typeparam> public class MultiSet<T> { private SortedList<T, int> innerDS; /// <summary> /// Creating a multiset instance from an IEnumerable of T /// </summary> /// <param name="input"> /// create the multiset instance.</param> public MultiSet(IEnumerable<T> input) { innerDS = new SortedList<T, int>(); foreach (T item in input) { if (!innerDS.ContainsKey(item)) { innerDS.Add(item, 1); } else innerDS[item]++; } } /// <summary> /// The flattend value combining all the elements. /// </summary> public IEnumerable<T> Value { get { List<T> vals = new List<T>(); foreach (T item in innerDS.Keys) { for (int i = 0; i < innerDS[item]; i++) vals.Add(item); } return vals; } } }Add a console application to this project. Name it
GenExTest. Add a reference of the class library project to this one.Add the following to the
Main()method:static void Main(string[] args) { MultiSet<char> firstPhrase = new MultiSet<char>("theeyes".ToCharArray()); MultiSet<char> secondPhrase = new MultiSet<char>("theysee".ToCharArray()); bool isAnagram = firstPhrase.Value.SequenceEquals(secondPhrase.Value); Display("The Eyes", "They See", isAnagram); MultiSet<string> firstSentence = new MultiSet<string> ("nay nada nay".Split(' ')); MultiSet<string> secondSentence = new MultiSet<string> ("nada nay nay".Split(' ')); isAnagram = false; isAnagram = firstSentence.Value.SequenceEquals(secondSentence.Value); Display("nay nada nay", "nada nay nay", isAnagram); Console.ReadKey(); }Add the following
Display()method:private static void Display(string a, string b, bool isAnagram) { Console.WriteLine(""{0}" and "{1}" are {2}", a, b, isAnagram == true ? "Anagrams" : "Not Anagrams"); }Compile and run the program.
As you execute the program, you will see the following output:

Now, let's see how we got here. The constructor of the MultiSet class creates an element histogram.
The public read-only property Value flattens the histogram by returning an enumerable of type T.
For example, the entry "the eyes" histogram will look like this:
|
Element |
Frequency |
|---|---|
|
e |
3 |
|
h |
1 |
|
s |
1 |
|
t |
1 |
|
y |
1 |
And the Value property will be eeehsty.
So, we get these sorted versions of the input from two sources in the Value property and then compare those using the SequenceEquals() extension method.
Note
Warning!
The extension method SequenceEquals() and the native method SetEquals() expects inputs to be in order, otherwise they return false. It is kind of misleading for SetEquals(), because ideally SetEquals() should check whether two sets contain the same elements or not, disregarding the order of elements.
If you are familiar with multiset in C++, then you shall be able to co-relate with this structure we have just built.
So far in this chapter, we have learnt about many generic containers. This is the perfect time to know how they fit in to the entire ecosystem of .NET Generics. Different list-based implementations implement different interfaces. These relationships are shown as follows:
|
Generic collection |
Interfaces it implements |
What's the significance? |
|---|---|---|
|
|
| |
|
|
From compiler's standpoint | |
|
|
It is a list. So | |
|
|
This is a generic implementation of a classic | |
|
|
This is a Hash-based set implementation. The fastest of its kind. As with mathematical sets, no duplicates are allowed. Elements are not sorted. | |
|
|
This is a tree-based set implementation. Entries remain sorted for value types, for reference the default comparer implementation is used. | |
|
|
This is a list as well as a dictionary that offers indexing over its contents and values can be obtained by key indexing. |
We learned a lot in this chapter about .NET Generics' list-based containers. We have learnt which generic container to use depending on the task at hand. The main idea of this chapter was not to be yet another API reference; but to learn how to use these generic list-based containers to solve real-world problems.
Although some of the applications built in the chapter might look trivial, they share the same pattern of several other problems in other domains.
Some concepts such as constraints and extension methods are used, but not explained here. Constraints shall be discussed in the appendix and extension methods in Chapter 4, LINQ to Objects.
In this chapter, we have learnt about a list-based associative container SortedList. However, that's not much use for performance issues. In the next chapter, we shall discuss tree-based IDictionary implementations that are much faster than SortedList.

