 If all you have is a hammer, every problem would seem like a nail. Know thy tools.
If all you have is a hammer, every problem would seem like a nail. Know thy tools.
We have come a long way. Starting at why Generics is important, we have learnt the basics of this API by building several applications. This chapter, however, will be different from the previous chapters. It will be a reference of best practices while dealing with Generics. The content of this chapter has been broken down into the following sections:
Generic container patterns: There are several patterns that are used more than the others in code bases that use Generics. Here, we shall walk through some of these very popular generic structures.
Best practices: Here we shall walk through a list of best practices with succinct causes to back them.
Performances: Here we shall walk through a list of benchmarking including techniques and results.
There are several generic containers such as List<T>, Dictionary<Tkey,Tvalue>, and so on, which you have learnt about in the previous chapters. Now, let's take a look at some of the patterns involving these generic containers that show up more often in code.
Each pattern discussed in this chapter has a few sections. First is the title. This is written against the pattern sequence number. For example, the title for Pattern 1 is One-to-one mapping. The Pattern interface section denotes the interface implementation of the pattern. So anything that conforms to that interface is a concrete implementation of that pattern. For example, Dictionary<TKey,TValue> is a concrete implementation of IDictionary<TKey,TValue>. The Example usages section shows some implementations where TKey and TValue are replaced with real data types such as string or int. The last section, as the name suggests, showcases some ideas where this pattern can be used.
One-to-one mapping maps one element to another.
Some concrete implementations of this pattern are as follows:
Dictionary<TKey,TValue>SortedDictionary<TKey,TValue>SortedList<TKey,TValue>
The following are examples where TKey and TValue are replaced with real data types such as string or int:
Dictionary<string,int>SortedDictionary<int,string>SortedList<string,string>Dictionary<string,IClass>
One-to-one mapping can be used in the following situations:
Mapping some class objects with a string ID
Converting an
enumto a stringGeneral conversion between types
Find and replace algorithms where the
findandreplacestrings become key and value pairsImplementing a state machine where each state has a description, which becomes the key, and the concrete implementation of the
IStateinterface becomes the value of a structure such asDictionary<string,IState>
One-to-many unique value mapping maps one element to a set of unique values.
Some concrete implementations of this pattern are as follows:
Dictionary<TKey,HashSet<TValue>>SortedDictionary<TKey,HashSet<TValue>>SortedList<TKey,SortedSet<TValue>>Dictionary<TKey,SortedSet<TValue>>
One-to-many value mapping maps an element to a list of values. This might contain duplicates.
The following are the interface implementations of this pattern:
IDictionary<TKey,ICollection<Tvalue>>IDictionary<TKey,Ilist<TValue>>
Some concrete implementations of this pattern are as follows:
Dictionary<TKey,List<TValue>>SortedDictionary<TKey,Queue<TValue>>SortedList<TKey,Stack<TValue>>Dictionary<TKey,LinkedList<TValue>>
The following are examples where TKey and TValue are replaced with real data types such as string or int:
One-to-many value mapping can be used in the following situations:
Mapping all the grades obtained by a student. The ID of the student can be the key and the grades obtained in each subject (which may be duplicate) can be stored as the values in a list.
Tracking all the followers of a Twitter account. The user ID for the account will be the key and all follower IDs can be stored as values in a list.
Scheduling all the appointments for a patient whose user ID will serve as the key.
Many-to-many mapping maps many elements of a group to many elements in other groups. Both can have duplicate entries.
The following are the interface implementations of this pattern:
IEnumerable<Tuple<T1,T2,..,ISet<Tresult>>IEnumerable<Tuple<T1,T2,..,ICollection<Tresult>>>
The following are examples where TKey and TValue are replaced with real data types such as string or int:
List<Tuple<string,int,int,int>>List<Tuple<string,int,int,int,HashSet<float>>
Many-to-many mapping can be used in the following situations:
If many independent values can be mapped to a set of values, then these patterns should be used.
ISet<T>implementations don't allow duplicates whileICollection<T>implementations, such asIList<T>, do.Imagine a company wants to give a pay hike to its employees based on certain conditions. In this situation, the parameters for conditions can be the independent variable of the Tuples, and IDs of employees eligible for the hike can be stored in an
ISet<T>implementation.
For concurrency support, replace non-concurrent implementations with their concurrent cousins. For example, replace Dictionary<TKey,TValue> with ConcurrentDictionary<TKey,TValue>. For a complete list of mappings refer to Appendix B, Migration Cheat Sheet.
Since Tuple is a new inclusion in the .NET 4.0 Framework and can prove to be handy in a lot of situations, I thought it would be a great place to showcase an unusual use of this beautiful data representation technique.
Let's say we have situations involving four integers. This is generally represented using nested if-else blocks, as shown in the following code. However, we can use a Tuple to refactor this code, as we shall see in a while:
Create a console app and add these four variables:
static int x = 11; static int y = 9; static int z = 20; static int w = 30;
Now, add these nested if-else blocks in the
Main()method:if (x > 9) { if (y > x) { if (z > y) { if (w > 10) { Console.WriteLine(" y > x and z > y and w > 10 "); } else { Console.WriteLine(" y > x and z > y and w <= 10 "); } } else { if (w > 10) { Console.WriteLine(" y > x and z <= y and w > 10 "); } else { Console.WriteLine(" y > x and z <= y and w <= 10 "); } } } else { if (z > y) { if (w > 10) { Console.WriteLine(" y <= x and z > y and w > 10 "); } else { Console.WriteLine(" y <= x and z > y and w <= 10 "); } } else { if (w > 10) { Console.WriteLine(" y <= x and z <= y and w > 10 "); } else { Console.WriteLine(" y <= x and z <= y and w <= 10 "); } } } }If you run this, you shall see the following output:
y <= x and z > y and w > 10
Although this code performs the job, it has the following problems:
We must acknowledge that by using a maximum of four variables there can be 16 different branchings. Of these only eight are shown here. This type of code can be remodeled using the following structure. Now, delete everything in the
Main()method and copy the following code://Creating rules list List<Tuple<bool, bool, bool, bool, Func<int,int,int,int,string>>> rules = new List<Tuple<bool, bool, bool, bool, Func<int,int,int,int,string>>>(); //adding rules.The benefit is that entire nested if-else is //flatend. rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y > x, z > y, w > 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y > x, z > y, w <= 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y > x, z <= y, w > 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y > x, z <= y, w <= 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y <= x, z > y, w > 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y <= x, z > y, w <= 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y <= x, z <= y, w > 10, DoThis)); rules.Add(new Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> (x > 9, y <= x, z <= y, w <= 10, DoThis)); Console.WriteLine ("Printing using tuple"); //Finding the first rule that matches these conditions. Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>> matchingRule = rules.First ( rule => rule.Item1 == GetExpression(x, 9)//represents x > 9 && rule.Item2 == GetExpression(y, x)//represents y > x && rule.Item3 == GetExpression(z, y)//represents z > y && rule.Item4 == GetExpression(w, 10)//represents w > 10 ); //Find the Matching function. Func<int, int, int, int, string> function = matchingRule.Item5; //Invoke the function. Console.WriteLine(function.Invoke(x,y,z,w));
This will not compile yet because the
DoThis()andGetExpression()methods are not defined. So add these methods as follows:private static string DoThis(int x, int y, int z, int w) { string partOne = y > x ? " y > x " : " y <= x "; string partTwo = z > y ? " z > y " : " z <= y "; string partThree = w > 10 ? " w > 10 " : " w <= 10 "; return partOne + "and" + partTwo + "and" + partThree; } private static bool GetExpression(int x, int y) { return x > y; }
Now if you run the program, you shall see the same output as before:
y <= x and z > y and w > 10
So you saw how the if-else blocks were removed while the rules are still intact. Moreover, the code is more readable now.
Let's see how this worked. Notice carefully that the last parameter of the Tuples used in the rules is Func<int,int,int,string>. This means, we can place any function that takes four integer parameters and returns a string. The DoThis()
method matches this requirement and so we place it in the list:
Tuple<bool, bool, bool, bool, Func<int, int, int, int, string>>
The previous list represents a relationship between four Boolean expressions and a function. These Boolean expressions are independent and the associated function is found using the following concern:
Func<int, int, int, int, string> function = matchingRule.Item5;
Invoke() is a method to call the function.
The following are the best practices to be followed while using Generics:
Don't use Generics when you know the situation won't always be generic.
Use
Stack<T>for a Last In First Out (LIFO) list implementation.Use
Queue<T>for a First In First Out (FIFO) implementation.Use
List<T>for random access lists with zero-based indexing.Use
LinkedList<T>to implement a deque because it offers faster insertion and deletion at both ends as opposed to other collections.If you have to frequently insert random locations in the list, prefer
LinkedList<T>overList<T>becauseLinkedList<T>is a constant time operation to insert one item in between two elements in a linked list.If the random list does not have a duplicate, use
HashSet<T>instead. It is the fastest. Check out the performance analysis in Appendix A, Performance Cheat Sheet.Don't use a
forloop over aIDictionary<TKey,TValue>implementation. It can give incorrect results. Use aforeachloop over the keys collection instead.Avoid using
ElementAt()or, its cousin, theElementAtOrDefault()method on generic collections that natively don't support zero-based integer indexing, (for example,Stack<T>orDictionary<TKey,TValue>); since dictionary elements are not guaranteed to be available on an index where they were added.Don't use a Tuple with more than seven parameters. Create a class with those parameters and then create a list of that class' objects. Using a Tuple with more than four parameters makes the code look messy and it's not efficient.
Use
SortedDictionary<TKey,TValue>just to get the entries sorted. Don't use it to store simple associative "one-to-one" and "one-to-many" relationships as keeping the keys sorted isn't absolutely necessary. It is very slow compared to a normal dictionary.Use
HashSet<T>to create a generic set. It's the fastest set implementation available in the .NET Framework. Check out the Performance analysis later in the chapter.Use
SortedSet<T>only to create a sorted generic set. Don't use it when you don't want the set to be sorted because it is slower thanHashSet<T>.Don't expect indexing to work on an array or a list as it would on sets or dictionaries, because sets and dictionaries use hashing or tree-based internal data structures to place elements in the collection.
Use the available bare minimum implementation for your customized need or resort to creating your own
custom collectionclass from the interfaces. This is a design guideline. Try to make sure your code is as lightweight as possible. If you want a queue, use aQueue<T>instead of aList<T>.Use
LinkedList<T>when you need to insert elements at arbitrary positions but you don't need to access them randomly via integer indexing.Use
KeyValuePair<TKey,TValue>to store a key value pair. Avoid usingTuple<T1,T2>for this purpose becauseKeyValuePair<TKey,TValue>is more efficient.Prefer
Dictionary<TKey,List<TValue>>overList<KeyValuePair<TKey,TValue>>whenever possible for representing a one-to-many relationship between two entities. Lookup speed will be much faster and client code will be less clumsy.Prefer
List<Tuple<..>>to represent a many-to-one relationship between two entities overDictionary<List<TKey>,TValue>if there is a duplicate.If no more entries need to be added to a collection, call
TrimExcess()to free up the extra memory.Prefer LINQ Standard Query Operator
Where()overContains(),Exists(),orFind()methods to check whether a value is present in aList<T>instance.If you implement
IEnumerable<T>in your custom collection, don't forget to implement IEnumerable also. This is to ensure backward compatibility and the Liskov substitution principle.Use
SortedList<TKey,TValue>if you want a concrete implementation ofIDictionary<TKey,TValue>that supports native indexing. However, it is slower thanDictionary<TKey,TValue>. AvoidSortedList<TKey,TValue>when you don't want indexing.Don't use the
ElementAt()or theElementAtOrDefault()method onIDictionary<TKey,TValue>implementations exceptSortedList<TKey,TValue>, because dictionary elements are not guaranteed to be in the index where they are added.Avoid conversions between data structure formats (for example, array to list, or vice versa using LINQ operators) as far as possible. Use other language constructs. For example, consider using a
foreachloop than converting anIEnumerable<T>instance to a list using theToList()method before performing some operations on each item in the list.Use the
OrderBy()or theOrderByDescending()method to sort anyIEnumerable<T>.
Not all generic containers are geared to do each job well, as we already know it. Here is a table that will let you pick a generic container that supports some features listed in the left-hand column.
|
How to pick a list? |
Stack<T> |
Queue<T> |
List<T> |
LinkedList<T> |
HashSet<T> |
SortedSet<T> |
|---|---|---|---|---|---|---|
|
Allows duplicates |
Yes |
Yes |
Yes |
Yes |
No |
No |
|
Native integer indexing |
No |
No |
Yes |
No |
No |
No |
|
Keeps entries sorted |
No |
No |
No |
No |
No |
Yes |
|
Native sorting capability |
No |
No |
Yes |
No |
No |
Yes |
|
How to pick a dictionary? |
Dictionary<TKey,TValue> |
SortedDictionary<TKey,TValue> |
SortedList<TKey,TValue> |
|---|---|---|---|
|
Native sorting support |
No |
Yes |
Yes |
|
Zero-based indexing |
No |
No |
Yes |
|
Keeps entries sorted |
No |
Yes |
Yes |
You can download the GenGuru app from the book's website. It's a kind of wizard that will recommend the generic containers available in .NET Generics that you should use. It will ask you few questions and recommend a collection. You can see it in action at http://sudipta.posterous.com/private/niixaeFlmk.
The following are the best practices while creating custom generic collections:
Try to use built-in generic classes for maintaining internal data structures.
Try to use interfaces as return type and method arguments for publicly exposed methods for your collection. For example, consider using
IEnumerable<T>overList<T>.Try to keep the names aligned as much as possible towards the names available in frameworks. For example, if you are creating a concrete implementation of
IDictionary<TKey,TValue>then try to use the suffix Dictionary in the name of the class, such asMultiDictionary<TKey,TValue>.Try to provide overloaded constructors to offer flexibility such that the class can be created from many diverse data sources.
Use Generics constraints judiciously. Remember that these constraints are like boomerangs. You should know what exactly you can allow as an input parameter for a constrained generic type. Otherwise, these can backfire and hurt you and the users of your collection.
Make sure to always implement the
IEnumerable<T>,IEnumerable,ICollection,IDisposable, andIClonableinterfaces.Make sure that your collection confirms to the Liskov substitution principle. Divide into subclasses only when it makes sense, otherwise use composition.
Offer a constructor overload to create a thread-safe instance of your collection.
Make sure it supports LINQ, which will be obvious if you implement
IEnumearble<T>properly. LINQ is changing the way we see and solve problems. So if you miss LINQ, your collection will probably fail to impress a large section of the target audience.Thrive for performance. Make sure that performance is as best as it could be. Refer to the Performance Analysis section later in the chapter and Appendix A, Performance Cheat Sheet.
Make sure your collection is as lightweight as possible. If a
Queue<T>can do what you want done internally in your collection, use it. Don't consider using a more versatile list implementation such asList<T>.Don't write raw events by yourself to monitor the collection; rather expose
ObservableCollection<T>to offer this functionality.Don't provide functionalities that can be achieved by a simple combination of exposed functions. For example, take a look at the Date Time API from the .NET Framework. There is a method called
AddDays()that can take a positive or negative integer such that you can go to a past or a future date. However, the framework doesn't provide a method or a public property to computeTomorrow()orYesterday()as they can be easily calculated using theAddDays()method. While exposing public functions for your generic collection, remember to expose only those methods that can be used as building blocks for several reasons.However, you have to strike a balance. The framework also has the
AddYears()method because it will be cumbersome, although technically achievable, to duplicateAddYears()using theAddDays()method.
Remember these points while coming up with your own generic collection.
Let's accept that we are impatient. Rather, we are becoming more and more impatient with each year. Part of this is due to the availability of processors that are a zillion times faster than the previous ones and come in pairs in almost every computer. Buying a single core machine these days is almost impossible. Computer hardware is faster than ever. Software developers have to put in extra effort to put these new powers to good use.
"Algorithms + Data Structures = Programs" said Niklaus Wirth. He was absolutely right in the title. If you add the word 'faster' to all the words in the equation mentioned earlier, it would result in "Faster Algorithms + Faster Data Structures = Faster Programs".
For a moment, forget whatever you know about data structures and think like a mathematician rather than a programmer. You should see that there are basically only a few types of data structures possible. They are Lists, Associative Containers, Sets, and sorted versions of each of these. It doesn't matter to a client code developer whether you use "Red-black tree" or "HashTable" internally to implement your dictionary as long as they both expose the same functionality. Take an ATM machine, for example. As long as the machine functions in a way people are familiar with, no one complains. But users complain if the machine requires some extra input or the interface changes.
In this chapter, we shall try to see which generic container outperforms its peers in practice even if their theoretical worst-case time complexity limit is identical. For example, HashSet<T> in System.Collections.Generics namespace and HashSet<T> in C5 collections, both are documented to offer constant time lookup activity. But in practice, as you will find in a little while, HashSet<T> in System.Collections.Generics is way faster than HashSet<T> in C5 collections.
We will investigate the following important situations for each kind of data structures:
The following are the important situations for lists:
How much time does it take to check whether an element is present in a list-based collection?
How much time does it take to find the index of the first occurrence of an item in a list-based collection?
How much time does it take to find the last index of an item in a list-based collection?
How much time does it take to insert a single element in a random location in a list-based collection?
The following are the important situations for dictionaries/associative containers:
The following are the important situations for sets:
How quickly can we find the union of two or more sets?
How quickly can we find the intersection of two or more sets?
How quickly can we check whether a set is a subset of another set or not?
This is a special case of superset find. Changing the caller and called objects in a subset find call would suffice. For example, the statements
set1.IsSubsetOf(set2)andset2.IsSuperSetOf(set1)are identical.
We shall put all data structures under a lot of stress! We shall perform the same operations over and over again starting at 100,000 times to 2,000,000 times with a step size of 100,000 operations at a time. I have put the results in spreadsheets and have generated graphs and tables for your future reference. All source code used in these benchmarking experiements are also available for download from the book's website. Benchmarking results are recorded in tables. In this chapter, we shall use fewer rows of these tables to save some space. If you want the entire table, you can always get that from the spreadsheet.
Codes used to benchmark these data structures are given right next to the benchmarking result. Actual results (measurement figures) that you would get from running these code snippets on your system could be very different in absolute terms; however, they will surely share the same relative resemblance.
In the following tables, the figures that represent the time taken for the operation are measured in milliseconds. Create a console application and put the code and assemblies required (for example, C5.dll when you are using generic collections from this namespace) and the benchmarking code in the Main() method. You should be good to go. Further, you can download the Excel file from the book's website if you want to add some more values and see it in reference with others. Excel also enables you to add trend lines. So you can experiment with that too. The advice is don't trust documentation. Don't trust me. Do the profiling yourself. You as the developer of a program know what your requirement is better than anyone else. Use the strategies discussed in this chapter to find out the collection that works best for you. Good Luck!
How much time does it take to check whether an element is present in a list-based collection?
In order to determine whether a given item is in a collection or not, we have to call the Contains() method on linear containers.
The following are the steps to create the benchmarking code that I have used. You shall have to change the Contain()
method accordingly, to alter it for the next benchmarking on another equivalent container:
Create a console app.
In the
Main()method, add the following code:static void Main(string[] args) { HashSet<char> codes = new HashSet<char>(); string alphabets = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"; foreach (char c in alphabets) codes.Add(c); Dictionary<int, double> perfMap = new Dictionary<int, double>(); int N = 100000; for (; N <= 2000000; N += 100000) { DateTime start = DateTime.Now; for (int k = 0; k < N; k++) { codes.Contains('D'), } DateTime end = DateTime.Now; perfMap.Add(N, end.Subtract(start).TotalMilliseconds); } foreach (int k in perfMap.Keys) Console.WriteLine(k + " " + perfMap[k]); Console.ReadLine(); }As you run this app, you shall get a similar output. Exact figures shall vary depending on how much free memory is available on the computer you are running this code on and how busy the processors are. I recommend you close all other apps and run this. This way, the figures that you will get will convey more meaningful data about the performance of the generic container;
HashSet<T>in this case.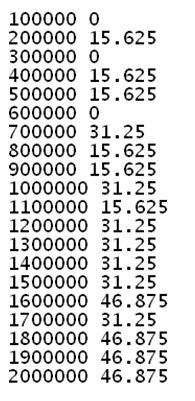
The numbers at the beginning of each line of the output denote the number of times the code snippet is executed. The second decimal number denotes total time in milliseconds taken for those many iterations of the given code execution. Looking at the figures, I can tell
HashSet<T>is very fast. With further investigation we shall see that it is in fact the fastest of its kind in the .NET API eco-system.
What we just did, can hardly be termed as benchmarking. We have to compare the results obtained for HashSet<T> with other equivalent containers such as SortedSet<T>, C5.HashSet<T>, and so on. In order to do that, we have to run the previous program after changing it to use the container we want. For example, if we want to benchmark C5.HashSet<T> next, we'll have to perform the following steps:
Add a reference of
C5.dllin the project.Add the following
usingdirective:using C5;
As soon as you perform step 2, the compiler will return an error that
HashSet<T>is ambiguous because there are twoHashSet<T>now available; one fromSystem.Collections.Genericand the other from C5. As we want to benchmark theHashSet<T>from the C5 Collection, explicitly mention that by replacing the following line of code:HashSet<char> codes = new HashSet<char>();
with
C5.HashSet<char> codes = new C5.HashSet<char>();
We are now ready to run the application again. This time the figures will represent the performance of
C5.HashSet<T>.
This is the way I got the performance figures of all linear lists such as containers by slightly changing the given benchmarking code. Once I got these numbers, I kept saving them on an Excel sheet.
Towards the end, I got something similar to the following screenshot:
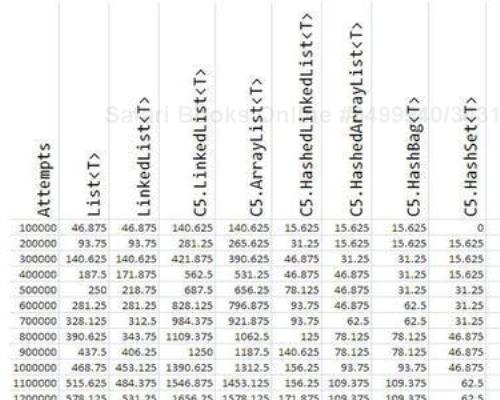
From these data, I generated the following graph:
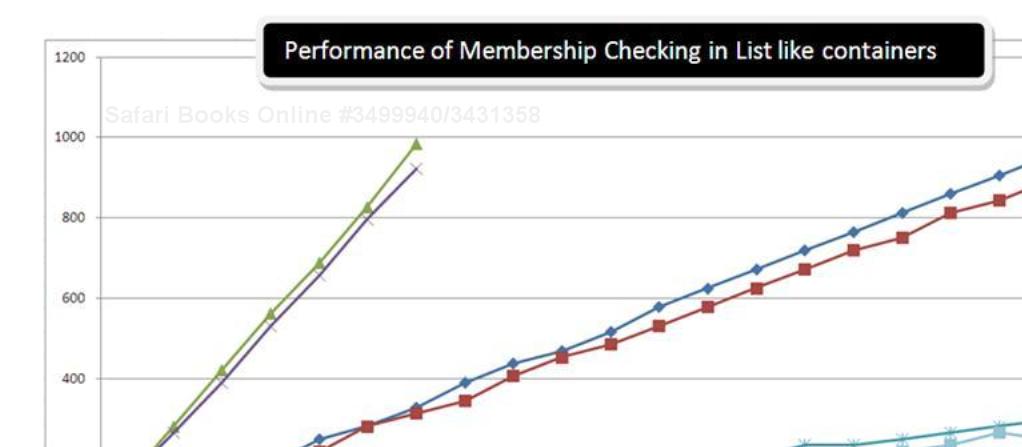
I was trying to check whether a given element is there in the list or not. This is also known as checking for membership in a given container. Thus the title of the graph is "Performance of Membership Checking".
You can download the Excel sheet with all these figures from the book's website.
It will be a great idea to create a tag cloud as a performance poster. From this data, I created the following tag cloud using Wordle (www.wordle.net):

I am quite happy with the end result of my benchmarking. This will stick longer in my brain than the actual figures and the graph. This means HashSet<T> is the fastest of all containers when it comes to membership checking. As a rule of thumb, anything that you can't read without a magnifying glass (such as LinkedList shown above the letter e in
HashSet) should be among your last choices for this functionality.
If you are interested to know how I created this tag cloud with container names, please refer to the article at http://sudipta.posterous.com/private/kzccCdJaDg.
You can download benchmarking code for all these containers for membership checking from http://sudipta.posterous.com/private/HmrocplDxg.
I shall use the same pattern for all other benchmarking experiments in this chapter. I reckoned that it might be difficult to follow for some of you, so I created a screencast of the first experiment from start to finish. You can download this screencast (PerformanceAnalysis_Screencast.MP4) from the book's website.
How much time does it take to find the index of the first occurrence of an item in a list such as collection?
When dealing with a list such as containers, it is very common to face a situation where we need to know the index of a given element in the collection. Here, we shall compare the following containers to see how efficient they are in this situation:
List<T> C5.LinkedList<T> C5.ArrayList<T> C5.HashedArrayList<T> C5.HashedLinkedList<T> C5.TreeSet<T>
The approach remains the same as the previous task. The benchmarking code is as follows:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
List<char> codes = new List<char>();
string alphabets = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
foreach (char c in alphabets)
codes.Add(c);
Dictionary<int, double> perfMap =
new Dictionary<int, double>();
int N = 100000;
int index = 0;
for (; N <= 2000000; N += 100000)
{
DateTime start = DateTime.Now;
for (int k = 0; k < N; k++)
{
index = codes.IndexOf('Z'),
}
DateTime end = DateTime.Now;
perfMap.Add(N, end.Subtract(start).TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadLine();
}
}
}As you run the code, you shall get an output similar to the following screenshot:

And using the previous approach and running the program for all other containers mentioned, we get the following output in an Excel sheet:
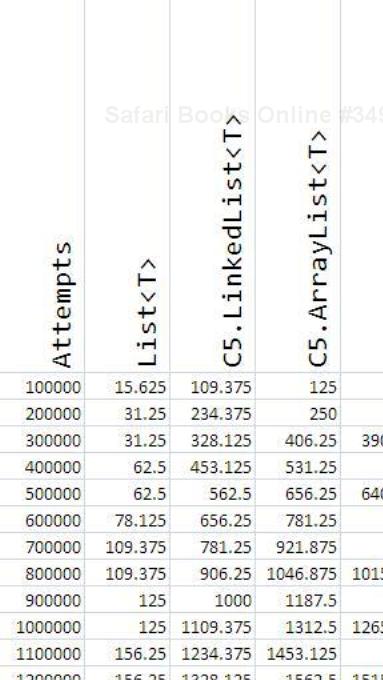
After plotting the entire data, I got the following graph:

From this graph, it is evident that C5.HashedArrayList<T> is the fastest when it comes to finding the first index of occurrence of a given element in the container.
Following the previous approach, I got the following tag cloud:

Also, from the previous graph, it is evident that C5.HashedArrayList<T> is the fastest and C5.HashedLinkedList<T> is prohibitively slow. So, think twice before you call IndexOf() on a linked implementation.
To modify the benchmarking code for all other containers, just change the following line with the appropriate instantiation call:
List<char> codes = new List<char>();
For example, if you want to benchmark C5.HashedArrayList<T>, then follow the given steps:
Include
C5.dllreference in the project.Add the following
usingdirective:using C5;
Replace the following line:
List<char> codes = new List<char>();
with
C5.HashedArrayist<char> codes = new C5.HashedArrayList<char>();
How much time does it take to find the last index of an item in a list-based collection?
If you go by your intuition, it might seem obvious that the container that offers the lowest time for first index lookup of a given element will do so for the last index of occurrence too. However, soon you shall find that's not the case. Here, we shall benchmark the same containers as in the previous one.
The benchmarking code will be exactly the same. Except, instead of the IndexOf() method, you have to call the LastIndexOf() method on the containers.
The following is the result for all these containers:
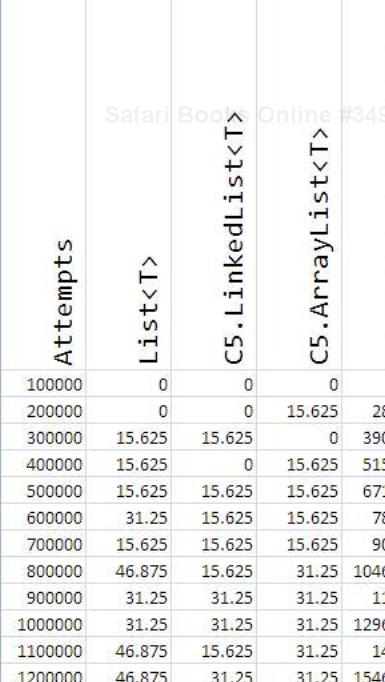
The graph depicting the relative performance of all these containers for this operation is as follows:

And the following is what I got putting the data to Wordle, as I did earlier:

From the previous graph, it is pretty much evident that C5.LinkedList<T>, C5.ArrayList<T>, and List<T> offer equivalent performance. Anything beyond these collections would be an underperformer for this task.
How much time it takes to insert a single element in a random location in a list-based collection?
Sometimes we need to insert an element at a random location. Think about sorting, for example. Not all collections are geared to make this efficient. However, I shall benchmark the containers that support this operation:
List<T> LinkedList<T> C5.HashedLinkedList<T> C5.HashedArrayList<T> C5.LinkedList<T> C5.ArrayList<T>
Apart from LinkedList<T> in the System.Collections.Generic namespace, all other containers listed previously have a method called insert() to insert an element at the mentioned index:
using System; using SCG = System.Collections.Generic; using System.Linq; using System.Text; using C5; namespace PerformanceMap { class Program { static void Main(string[] args) { SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>(); int N = 1000; //Change the container here and you should be done. //C5.HashedArrayList<int> nums = new C5.HashedArrayList<int>(); C5.HashedLinkedList<int> nums = new C5.HashedLinkedList<int>(); Enumerable.Range(1, 100).Reverse().ToList().ForEach(n => nums.Add(n)); for (; N <= 20000; N += 1000) { DateTime start = DateTime.Now; for (int i = 0; i < N; i++) { nums.Remove(100); nums.Insert(new Random().Next(0,99),100); } DateTime end = DateTime.Now; perfMap.Add(N, end.Subtract(start).TotalMilliseconds ); } foreach (int k in perfMap.Keys) Console.WriteLine(k + " " + perfMap[k]); Console.ReadKey(); } } }
C5.HashedArrayList<T> and C5.HashedLinkedList<T> don't allow duplicate entries. So before inserting 100, we have to remove it. But since these are hash-based collections, removing items from these is a constant time operation. Thus, removing them doesn't have much impact on the overall performance.
The previous code will work for all except LinkedList<T> in the System.Collections.Generic namespace, as it doesn't offer any insert() method to directly insert elements. For LinkedList<T>, we have to use a different code for benchmarking:
using System;
using SCG = System.Collections.Generic;
using System.Linq;
using System.Text;
using C5;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>();
int N = 1000;
SCG.LinkedList<int> nums = new SCG.LinkedList<int>();
Enumerable.Range(1, 100).Reverse().ToList().ForEach(n => nums.AddLast(n));
for (; N <= 20000; N += 1000)
{
DateTime start = DateTime.Now;
for (int i = 0; i < N; i++)
{
SCG.LinkedListNode<int> node = nums.Find(new Random().Next(0, 101));
if (node == null)
{
nums.AddFirst(100);
}
else
{
nums.AddBefore(node, 100);
}
}
DateTime end = DateTime.Now;
perfMap.Add(N, end.Subtract(start).TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadKey();
}
}
}As you run these programs for several containers and collect the data and put them on an Excel sheet, you will get an output similar to the following screenshot:
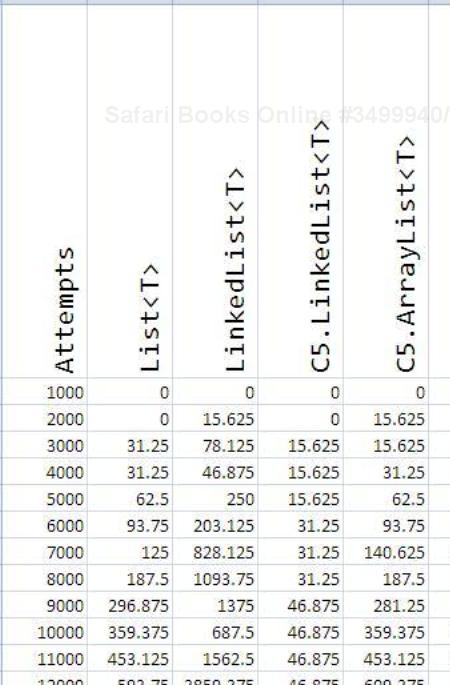
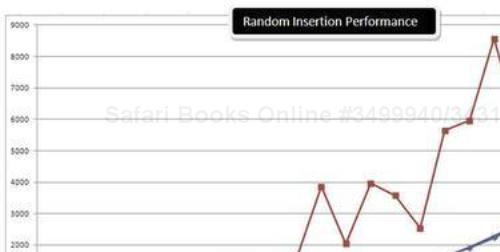
After plotting the data, I got the following graph:
And the following shows how Wordle looks for the previous benchmarking test:

So, if your code demands a lot of insertions at random locations in the container, consider using C5.HashedLinkedList<T>, as that's the fastest you can get.
We can also tell from this tag cloud that List<T> offers one of the worst performances for random insertion. This finding is rather intuitive because containers that implement IList<T> generally use array as the internal data structure to offer native zero-based integer indexing. Therefore, inserting in a IList<T> implementation is actually inserting at a random location in an array. So, all elements after the location where the insertion happens have to be updated. Thus, inserting at a random index in an
IList<T> implantation that uses array as the internal data structure is a O(n) operation in the worst case.
How much time does it take to delete a single element in a random location in a list-based collection?
Being able to delete at random locations is also a very important functionality sought by developers. Although it doesn't make much sense in IDictionary implementations and is advisable to avoid; it is almost taken for granted for an IList<T> implantation such as List<T>.
In this experiment, we shall try random deletions from List<T>, LinkedList<T>, C5.LinkedList<T>, C5.ArrayList<T>, C5.HashedLinkedList<T>, and C5.HashedArrayList<T> and see which one wins.
The following is the benchmarking code that will work for LinkedList<T> in System.Collections.Generic:
using System;
using SCG = System.Collections.Generic;
using System.Linq;
using System.Text;
using C5;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
SCG.Dictionary<int, double> perfMap
= new SCG.Dictionary<int, double>();
int N = 1000;
SCG.LinkedList<int> nums = new SCG.LinkedList<int>();
Enumerable.Range(1, 100).Reverse().ToList()
.ForEach(n => nums.AddLast(n));
for (; N <= 20000; N += 1000)
{
DateTime start = DateTime.Now;
int x;
for (int i = 0; i < N; i++)
{
nums.Remove(new Random().Next(0, 100));
}
DateTime end = DateTime.Now;
perfMap.Add(N, end.Subtract(start)
.TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadLine();
}
}
}For all other types, just change the highlighted part of the following line:
Enumerable.Range(1, 100).Reverse().ToList() .ForEach(n => nums.AddLast(n));
to
Enumerable.Range(1, 100).Reverse().ToList() .ForEach(n => nums.Add(n));
After running all the code snippets and collecting the data in the Excel sheet, you shall get a data trend similar to the following:
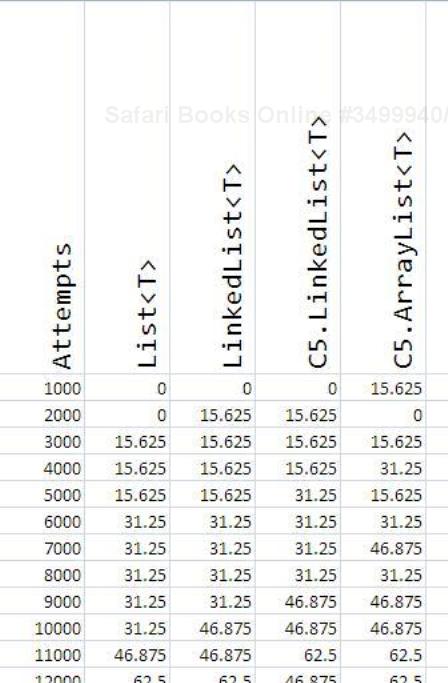
Using this data, I created the following plot:
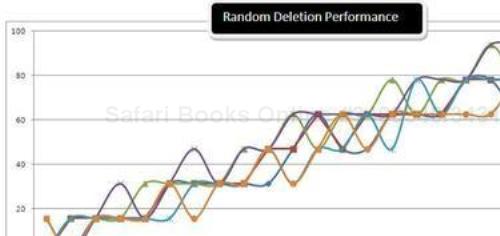
I think this is the fanciest looking graph so far! This means that all of these containers offer similar performance when it comes to random deletion. This statement is quite supported in the Wordle art too.

However, array-based collections such as C5.ArrayList<T> and List<T> in System.Collections.Generic are trailing in this functionality too because of the same reason that in case of deletion, in an array worst case performance in O(n) there are n elements in the array.
How fast can we look up an element (or the unique key) in an associative collection?
IDictionary implementations are around for one good reason. They offer very good performance for unique key lookup. In this experiment, we shall see which of the IDictionary implementations is the best when it comes to key lookup. In this experiment, we shall limit our test with the following dictionaries:
Dictionary<TKey,TValue SortedDictionary<TKey,TValue> C5.HashDictionary<TKey,TValue> C5.TreeDictionary<TKey,TValue>
The following benchmarking code is to be used for C5.HashDictionary<TKey,TValue> and C5.TreeDictionary<TKey,TValue>:
using System;
using SCG = System.Collections.Generic;
using System.Linq;
using System.Text;
using C5;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
string alphabets = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
SCG.Dictionary<int, double> perfMap =
new SCG.Dictionary<int, double>();
int N = 100000;
C5.HashDictionary<string, int> dic
= new C5.HashDictionary<string, int>();
alphabets.ToList()
.ForEach(a => dic.Add(a.ToString(),
alphabets.IndexOf(a)));
for (; N <= 2000000; N += 100000)
{
DateTime start = DateTime.Now;
for (int k = 0; k < N; k++)
{
dic.Contains("Z");
}
DateTime end = DateTime.Now;
perfMap.Add(N,
end.Subtract(start).TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadLine();
}
}
}For Dictionary<TKey,TValue> and SortedDictionary<TKey,TValue> in System.Collections.Generic change the following line:
dic.Contains("Z");to
dic.ContainsKey("Z");since the method to look up an item in these two IDictionary implementations is ContainsKey().
After executing all the code snippets and entering the data in our Performance Excel Sheet, I got the following output:
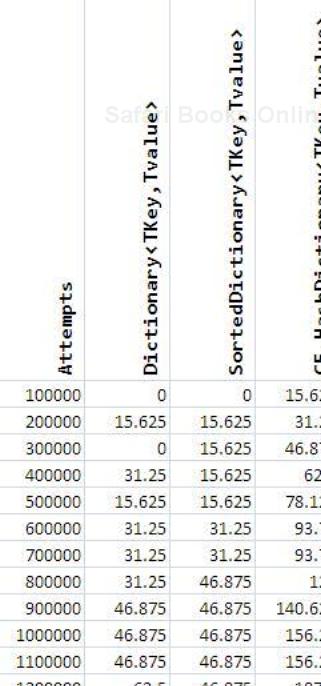
Plotting the previous data, I got the following graph:

From the graph, it is evident that C5.TreeDictionary<TKey,TValue> is prohibitively slow and we have to limit our choice between Dictionary<TKey,TValue> and SortedDictionary<TKey,TValue>.
The following screenshot shows how Wordle looks:

There is something about the previous random word. As you can see, Dictionary not only has the highest font size, but it is also the first in the list. The second is SortedDictionary and the last is C5.HashDictionary. C5.TreeDictionary is so slow on key lookup that it almost didn't show up at all. So, the lesson learnt is if you just need a way to associate one type with another and no sorting, use Dictionary else use SortedDictionary.
How fast can we find the union of two or more sets?
Being able to find unions of large sets in a short time is what makes a 21st century algorithm click. We are living in a very interesting time and there is lot of data around us. Our applications have to deal with loads of data every day. But a seemingly simple task of keeping duplicate items at bay is a stupendously difficult task in practice.
To avoid this, we need quick set implementations. The .NET Framework and C5 offer a couple of set implementations. We shall put these containers under a lot of stress and find out how they perform.
The benchmarking code for HashSet<T> and SortedSet<T> available in System.Collections.Generic is as follows:
using System; using SCG = System.Collections.Generic; using System.Linq; using System.Text; using C5; namespace PerformanceMap { class Program { static void Main(string[] args) { SCG.HashSet<string> set1 = new SCG.HashSet<string>() { "A", "B", "C", "D", "E" }; SCG.HashSet<string> set2 = new SCG.HashSet<string>() { "A", "D", "F", "C", "G" }; SCG.HashSet<string> copyOfSet1 = new SCG.HashSet<string>() { "A", "B", "C", "D", "E" }; SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>(); int N = 100000; for (; N <= 2000000; N += 100000) { DateTime start = DateTime.Now; for (int k = 0; k < N; k++) { set1.UnionWith(set2); set1 = copyOfSet1; } DateTime end = DateTime.Now; perfMap.Add(N, end.Subtract(start).TotalMilliseconds); } foreach (int k in perfMap.Keys) Console.WriteLine(k + " " + perfMap[k]); Console.ReadLine(); } } }
The following is the benchmarking code for C5 set implementations. You can replace C5.TreeSet<T> with C5.HashSet<T> in the following code:
using System;
using SCG = System.Collections.Generic;
using System.Linq;
using System.Text;
using C5;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
C5.TreeSet<string> set1 = new C5.TreeSet<string>()
{ "A", "B", "C", "D", "E" };
C5.TreeSet<string> set2 = new C5.TreeSet<string>()
{ "A", "D", "F", "C", "G" };
C5.TreeSet<string> copyOfSet1 = new C5.TreeSet<string>()
{ "A", "B", "C", "D", "E" };
SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>();
int N = 100000;
for (; N <= 2000000; N += 100000)
{
DateTime start = DateTime.Now;
for (int k = 0; k < N; k++)
{
set1.AddAll(set2);
set1 = copyOfSet1;
}
DateTime end = DateTime.Now;
perfMap.Add(N,
end.Subtract(start).TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadLine();
}
}
}The following table has all the data collected from the previous benchmarking:

From the previous data, I got the following plot:
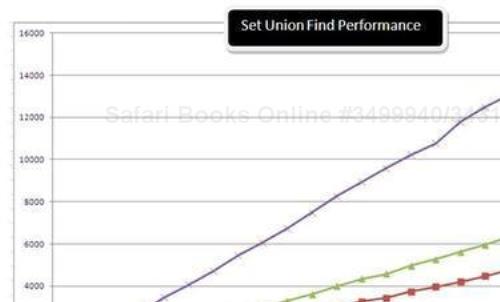
The result of this experiment is supportive of the result of experiment 1. In order to find the union of two sets, it is required to find whether a given element is present in either one or not. So, the container that offers the highest lookup speed for checking whether an element is present or not would intuitively offer the best performance for union also. That's exactly what the result of this experiment shows. HashSet<T> offers the highest lookup speed and also the best union find time.
My Wordle experiment with the data is as follows:

How fast can we find the intersection of two or more sets?
The result of this experiment is exactly the same as that of experiment 7 because intuitively finding a union is similar to finding an intersection. So, in this case, the order of performance is as follows:
HashSet<T> offers the best performance followed by SortedSet<T>, C5.HashSet<T>, and C5.TreeSet.<T>.
The following benchmarking code can be used with C5.HashSet<T> and C5.TreeSet<T>:
using System; using SCG = System.Collections.Generic; using System.Linq; using System.Text; using C5; namespace PerformanceMap { class Program { static void Main(string[] args) { C5.TreeSet<string> set1 = new C5.TreeSet<string>() { "A", "B", "C", "D", "E" }; C5.TreeSet<string> set2 = new C5.TreeSet<string>() { "A", "D", "F", "C", "G" }; C5.TreeSet<string> copyOfSet1 = new C5.TreeSet<string>() { "A", "B", "C", "D", "E" }; SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>(); int N = 100000; for (; N <= 2000000; N += 100000) { DateTime start = DateTime.Now; for (int k = 0; k < N; k++) { set1.RetainAll(set2); //to make sure that we start //with the new set implementation //every time set1 = copyOfSet1; } DateTime end = DateTime.Now; perfMap.Add(N, end.Subtract(start).TotalMilliseconds); } foreach (int k in perfMap.Keys) Console.WriteLine(k + " " + perfMap[k]); Console.ReadLine(); } } }
For HashSet<T> and SortedSet<T> in System.Collections.Generic just change the following line:
set1.RetainAll(set2);
to
set1.IntersectWith(set2);
As the results show a trend similar to the previous experiment, I didn't include the table values and the Wordle for this experiment.
How fast can we check whether a set is a subset of another set or not?
We shall benchmark the same four set implementations here.
The following code is to be used for HashSet<T> and SortedSet<T>:
using System;
using SCG = System.Collections.Generic;
using System.Linq;
using System.Text;
using C5;
namespace PerformanceMap
{
class Program
{
static void Main(string[] args)
{
SCG.HashSet<string> set1 = new SCG.HashSet<string>()
{ "A", "B", "C", "D", "E" };
SCG.HashSet<string> set2 = new SCG.HashSet<string>()
{ "A", "D", "F", "C", "G" };
SCG.HashSet<string> copyOfSet1 = new SCG.HashSet<string>()
{ "A", "B", "C", "D", "E" };
SCG.Dictionary<int, double> perfMap = new SCG.Dictionary<int, double>();
int N = 100000;
for (; N <= 2000000; N += 100000)
{
DateTime start = DateTime.Now;
for (int k = 0; k < N; k++)
set1.IsSubsetOf(set2);
DateTime end = DateTime.Now;
perfMap.Add(N, end.Subtract(start).TotalMilliseconds);
}
foreach (int k in perfMap.Keys)
Console.WriteLine(k + " " + perfMap[k]);
Console.ReadLine();
}
}
}For C5.HashSet<T> and C5.TreeSet<T> the benchmarking code has to be modified by changing the following line:
to
set1.ContainsAll(set2);
When the details are copied to our performance spreadsheet, we get data similar to the following screenshot:

Plotting the previous data, I got the following graph:

And the Wordle for this benchmarking looks similar to the following screenshot:

We have come to an end with our experiments for this chapter. I hope you got an idea how to benchmark your collections for several needs. It is very interesting that while C5.TreeSet<T> is almost unusable for a union or an intersection, it outperforms other set implementations when it comes to the finding subset functionality.
So, the lesson learnt is one size doesn't fit all. Learn what works best for the job at hand by benchmarking it against several options.
We have come a long way and now know with confidence which container is better in a given situation than another, even though theoretical time complexity for the mentioned operation in question is the same.
I hope the guidelines mentioned in this chapter will help you steer clear of pitfalls that can appear easily while dealing with code involving Generics.
You can download an Excel Workbook with all these benchmarking details from the book's website.
