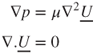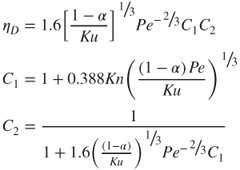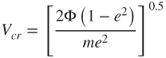Chapter 5

Filtration Mechanisms

Sarah Dunnett

Department of Aeronautical and Automotive Engineering, Loughborough University, UK

5.1 Introduction

Filtration may be defined as a process of separating particles from a gas (usually air) flow by means of a porous medium. The needs for such a process are many; for example, in many working environments people are exposed to harmful particles, and so protection must be provided. This might be in the form of a large-scale industrial filter or of personal protective equipment such as respirator filters. Some industries, including parts of the pharmaceutical and electronic sectors, rely on clean air of exceptional quality, which is provided through filtration. This is also true of the medical sector, where the control of infection is crucial. Filtration can also improve the quality of air in homes, workplaces, schools and transport.

There are two principal types of filtration: surface filtration and depth filtration. In surface filtration, particles are collected on a permeable surface; as the deposit builds, it forms a cake on the filter, which increases the resistance to flow. Depth filtration removes particles both from the surface and throughout the depth of the medium. One of the most important types of depth filter is one made up of fibres. Such filters consist of pads of fibres in an open three-dimensional network. Porosity is high, generally from 70 to 99%. An example of such a filter is shown in Figure 5.1. Because of their high porosity, fibrous filters generally offer a low resistance to flow. Gas flows through the open structure of the filter and particles suspended in it are captured on the fibres. Due to the distances between the fibres, any captured particle is unlikely to come in contact with more than one fibre, and hence the modelling of filter performance is often undertaken using single-fibre theory.

In addition to fibrous filters there are other particulate filters, such as granular filters, fabric filters and membrane filters. Granular filters are composed of packed beds of particles and are used extensively in the water and sewage industries. These are covered in detail in Tien and Ramarao (2007). Fabric filters are made from textile fibres, which are processed into a relatively compacted form. Most of the dust does not penetrate into the material but is captured on the surface. Membrane filters are made of perforated material or highly compacted fibrous material, resulting in a lower porosity than that in fibrous filters. They tend to act principally by surface filtration.

Fibrous filters are the most important type of filter for aerosol sampling, due to their ability to obtain high separation efficiencies with a relatively low pressure drop. Use is sometimes made of electrostatic interactions between particles and fibres, which enhance filter performance. Filters that are made of permanently charged fibres have become known as ‘electrets’. In this work, a summary is made of the main factors affecting the performance of fibrous filters and significant work in the area is reviewed.

There are two main parameters used to assess the performance of a filter: collection efficiency, E, and penetration, P. The first is employed when filters are used for the recovery of particulates or when particulate is collected for analysis. It refers to the fraction of particles entering the filter that are retained:

5.1

where N_in and N_out are the number of particles entering and leaving the filter, respectively.

Penetration is important when air quality is being considered. It refers to the fraction of particles entering the filter that exit again:

5.2

The penetration of monodisperse aerosol through homogeneous filters of depth X can be given by (Hinds, 1999), where γ is the layer efficiency. This layer efficiency is related to the single-fibre efficiency, η, which is the ratio of the number of actual particles removed by the fibre to the number that would be removed by a 100% efficient fibre, by (Hinds, 1999):

5.3

where α is the filter packing fraction, which is the fraction of the perceived volume of the filter that is actually occupied by fibres, and d_f is the fibre diameter. Hence the efficiency of a fibrous filter of thickness X is related to the single-fibre efficiency by:

5.4

The difficulty in applying Equation 5.4 is how to determine the value of the single-fibre efficiency, η. This has been the subject of many previous studies and is discussed in Sections 5.2.2–5.2.6. This efficiency is dependent upon the mechanism by which the particles deposit upon the fibre.

5.2 Deposition Mechanisms

The objective of filtration is to remove harmful aerosols from a gas, so the effectiveness of the mechanisms of aerosol deposition to the surfaces contained in a filter is fundamental to its use. Table 5.1 gives a fairly complete set of possible mechanisms, including the conditions under which they are effective and the filter types in which they are employed. The alternatives to the filters included in Table 5.1, whose use for particle removal is generally limited to large-scale operations, are centrifuges, used in vacuum cleaners, and electrostatic precipitators, used in large industrial plants. A comprehensive theoretical analysis of most of the mechanisms is given in Williams and Loyalka (1991). The last four mechanisms listed in the table are not generally practical for filtration. In the case of thermophoresis, the creation of a large temperature gradient is required, as aerosol particles will move to lower temperatures due to more energetic collisions with molecules on their high-temperature sides, leading to deposition. This is not practical in filters. Diffusiophoresis and vapour condensation and particle growth also require a temperature gradient to the filter surface in order to produce condensation. In the case of bubbling through liquids, splitting up of a gas flow into small bubbles passing through a liquid would have the advantage of simple removal of aerosol particles deposited by various mechanisms into bubble walls during their passage. A problem could arise, however, from aerosol created by the bursting of bubbles on their emergence from the liquid.

Table 5.1 Deposition mechanisms and filter use

Mechanism or process	Conditions for which mechanism is effective	Filter type
Diffusion	Small or very small particles	Fibrous filters Ceramic filters at high T
Interception	Intermediate-size particles	Fibrous filters
Inertial impaction	Large-size particles, or smaller ones in high-velocity accelerated flows	Fibrous filters Centrifuges
Gravitational settling	Very large, or heavy, particles	Not effective in practice
Electrostatic attraction	Determined by charge; most effective for small or intermediate-size particles	Electret filters Electrostatic precipitators
Thermophoresis	Temperature gradient to surface needed	Not used in practice
Diffusiophoresis	Vapour condensation on surface needed	Not used in practice
Vapour condensation and particle growth	Particle size increased for easier removal	Used for particle observation but not in filtration
Bubbling through liquids	Depends on secondary mechanism to reach bubble walls	Can be effective with small bubbles

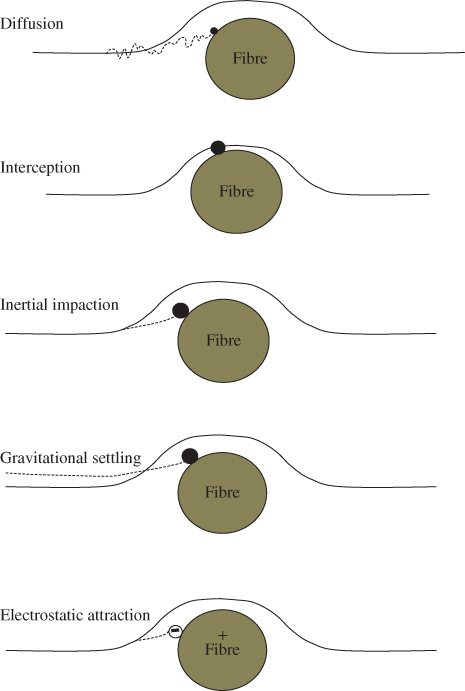
Due to these limitations, the main mechanisms by which filters remove aerosol particles from the fluid stream are the first five listed in the table: (i) diffusion, (ii) interception, (iii) inertial impaction, (iv) gravitational settling and (v) electrostatic attraction. This review will concentrate on these mechanisms and their application in fibrous filters.

The first four are mechanical capture mechanisms that work without the influence of attractive forces between the particles and the fibres. Diffusional deposition is important for small particles whose Brownian motion causes them to deviate from the flow streamlines and come into contact with the filter. Interception and inertial impaction are important for larger particles. Interception occurs when particles follow the streamlines of the flow and pass close to a filter fibre. Inertial impaction occurs when particles deviate from the flow streamlines due to their inertia and impact upon a fibre. Gravitational settling is only significant for those particles whose settling velocity is larger than the convective velocity of the flow through the filter and hence is limited to very large or heavy particles. In filters constructed from charged fibres there is an additional mechanism of deposition: electrostatic attraction. These five mechanisms are shown schematically in Figure 5.2.

In order to understand the performance of filters for the different particle-deposition mechanisms, it is important to obtain a good understanding of the flow through them. Section 5.2.1 reviews the flow models developed to describe the flow field and their comparison with experimental measurements. Following sections consider the different deposition mechanisms in turn.

5.2.1 Flow Models

In theory it is possible to calculate the rate at which particles deposit directly on the surfaces of the fibres by solving the appropriate equations of motion. However, as the flow within the filter is complex, this is not possible without simplifications. The fluid flowing through a filter can be treated as continuous so long as the obstacles in its path are large compared with the mean free path of the fluid molecules. This condition is fulfilled if the Knudsen number, Kn, is negligible:

5.5

where λ is the mean free path of the fluid molecules.

In the majority of filters, Kn 1, and hence the fluid can be assumed to be continuous. For example, under normal conditions in air, λ is 0.065 µm, and hence the condition is satisfied for fibrous filters as long as the fibres are not submicron size.

Another important parameter when studying the fluid flow through filters is the Reynolds number, Re:

5.6

where ρ and μ are the density and viscosity of the fluid and U₀ is its mean velocity. This parameter is the ratio of the inertia and viscous forces of the fluid and in filtration theory it is generally small. For example, for air passing through a fibrous filter with fibres of diameter 10 µm at a velocity of 0.1 m/s, the value of Re is approximately 0.065. This shows that the flow is dominated by the fluid's viscosity. Hence in filtration theory, an assumption of negligible Re is usually made. The equations of motion describing the fluid flow are then given by:

5.7

where p is the fluid pressure. In order to solve these equations, the majority of the analytical and numerical studies in filtration theory have been based on cell models for the fluid flow (Brown, 1993). In these models, the 3D filter structure in which fibres are randomly distributed is approximated by a 2D regularly staggered array of fibres, as shown in Figure 5.3. In two dimensions, Equation 5.7 can be written in terms of the stream function, ψ, as:

5.8

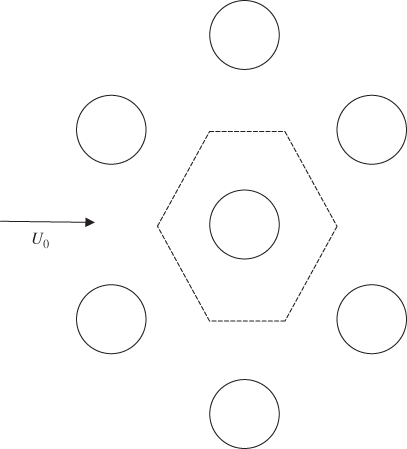
The hexagonal cell shown in Figure 5.3 is approximated by a circular cell. Solutions to Equation 5.8 of the form:

5.9

in the cell were obtained by Kuwabara (1959) and Happel (1959), where the A_i's are constants dependent upon α, the difference between the two models lies in the boundary condition applied on the cell boundary. Experiments performed by Kirsch and Fuchs (1967) found that these models gave an accurate description of the flow field near a fibre, with Kuwabara's model being the most accurate. This cell model approach has been adopted extensively in filtration theory; see, for example, Asgharian and Cheng (2002), Kirsh (2005), Raynor (2008), Dunnett and Clement (2009) and Chernyakov, Kirsh and Kirsh (2011). However, due to the assumptions made, such approaches do have their limitations; for example, the full filter space cannot be covered by circular cells and hence the description of the flow away from the fibres is poor. Therefore, other models have been developed; see for example Kirsh (2006) and Hellou, Martinez and El Yazidi (2004), who included higher-order terms in the solution to Equation 5.8 than those taken in Equation 5.9. In recent years, with the increasing power of computers, computational fluid dynamics (CFD) models have become more widespread. This technique allows, in principal, any filter structure to be modelled, as a mesh can be set up throughout the filter and the equations of fluid motion approximated at discrete mesh points. Generally, however, due to the computational demands of the technique, simple lattice structures are studied. For example, when Li and Marshall (2007) modelled the flow through a 2D array of cylindrical fibres, the use of CFD allowed flows with Re up to O(1) to be considered. Wang and Pui (2009) used CFD to model a staggered array of elliptical fibres. In a study by Qian, Zhang and Huang (2009), the flow field of a filter with a staggered array of fibres and varying solid volume fraction was modelled using CFD. In work by Wang et al. (2006), a virtual 3D fibrous filter structure was generated based on information obtained from analysis of microscopic images of filter media and the flow field obtained inside the filter using CFD. Experimental results for the filter efficiency were also obtained and were found to lie between those obtained by the CFD model and those using the Kuwabara cell model. In Maze et al. (2007), a similar approach was adopted in order to study the performance of filters composed of nanofibres operating at reduced pressures. The disturbance to the flow field caused by the fibres was neglected. In a study by Jaganathan, Tafreshi and Pourdeyhimi (2008), CFD simulations were performed on the microstructure of a real fibrous media. Digital volumetric imagining was used to obtain a 3D image of the filter. In a recent study by Hosseini and Tafreshi (2010), 2D random fibrous geometries were generated numerically and their efficiencies determined using CFD. These were compared with the 3D results obtained in the studies of Wang et al. (2006). Although computing power has increased considerably over recent years, that required by 3D simulations is still excessive, which may well prohibit extensive studies.

An efficient alternative approach introduced in order to determine the flow in filters by Filippova and Hanel (1997) is the lattice-Boltzmann method, which is a discrete computational method based upon an approximation of the Boltzmann equation. The technique is shown to simulate in an effective way the low-Re flow around complex geometries. It has been adopted by Przekop, Moskal and Gradon (2003) to describe the structure of deposited particulate matter in filters and by Przekop and Gradon (2008) to consider the filtration of nanoparticles.

Once the flow through a filter is understood, the behaviour of the particles within that flow can be studied. As mentioned earlier, there are five main particle-deposition mechanisms that are important for filtration. These will now be considered in turn for a clean filter. The different mechanisms are generally considered separately for ease of study, but in reality some of the mechanisms will act simultaneously. However, depending upon the situation, it is likely that one of the mechanisms will be dominant. Single-fibre efficiency, η, has been studied in detail for all of the deposition mechanisms. The simplest way of estimating η when more than one mechanism is important is to assume that the contributions from the different mechanisms are additive (Ramarao, Tien and Mohan, 1994):

5.10

where η_D, η_R, η_I, η_G and η_EL are the single-fibre efficiencies due to diffusion, interception, inertial impaction, gravity and electrostatic deposition, respectively. An alternative and more accurate approach is to assume that the aerosol penetration, 1—η, is the product of the penetration due to the different mechanisms:

5.11

It is possible when considering the problem numerically to include all the mechanisms in the model and hence determine η directly (Ramarao, Tien and Mohan, 1994; Oh et al., 2002). Results obtained this way have shown that for intermediate-sized particles there is a coupling between Brownian diffusion and inertial impaction (Ramarao, Tien and Mohan, 1994).

5.2.2 Diffusional Deposition

As stated in Table 5.1, this mechanism is important for small particles, which due to Brownian motion do not follow the streamlines of the flow and may diffuse from the flow to the fibres and deposit. The intensity of the Brownian motion increases for smaller particles and as a consequence so does the efficiency of removal. In this case, the nondimensional particle concentration, n, is determined by the nondimensional Fokker–Planck equation (Fuchs, 1964):

5.12

where Pe is the Peclet number, which is a measure of the relative magnitude of the diffusional motion of the particles and of the convective motion of the air past the fibre:

5.13

where D is the coefficient of diffusion of the particles.

In this case, the single-fibre efficiency is given by:

5.14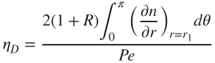

where R is the interception parameter, R = d_p/d_f and r₁ = 1 + R.

An exact solution of Equation 5.12 has not been found but by assuming the Kuwabara flow field given by Equation 5.9 and taking the diffusion layer around the fibre to be small, Lee and Liu (1982) found η_D to be given by:

5.15

where Ku is the hydrodynamic factor of Kuwabara flow:

5.16

and A is a constant, which was 2.6 in Lee and Lui's study and has been found to be 2.9 in others (Brown, 1993). This expression has been verified experimentally. The semiempirical Equation 5.15 applies to a continuum flow regime when Kn, given by Equation 5.5, is negligible. When the fibre diameter, d_f, is of the same magnitude as the mean free path of the fluid molecules, λ, the effect of the slip flow must be taken into account when estimating η_D. In this case, an expression for η_D is given by Payet et al. (1992) (Equation 5.17), which agrees well with experimental results for particles of size 80–400 nm and fibre diameter 1 µm:

5.17

There have been a number of recent studies on the performance of filters with submicron particles, including one by Qian, Zhang and Huang (2009), who numerically determined the filter efficiency for different operating conditions and found Brownian diffusion played a significant role for particles with particle diameter, d_p, <0.2 µm. The diffusional deposition of polydisperse aerosol has been considered analytically by Kwon, Kim and Lee (2002), who obtained expressions for the filters efficiency. In the CFD study by Hosseini and Tafreshi (2010), η_D was determined for a 2D model with randomly distributed fibres and the situations in which slip flow was and was not important were considered. As noncircular fibres may perform better than circular ones, due to their increased surface area, a numerical simulation was undertaken by Wang and Pui (2009) to investigate the single-fibre efficiency of elliptical fibres. They found that long and slim fibres performed better for particles dominated by the diffusion effect. A numerical study has also been undertaken by Kirsh (2007, 2011); the 2007 paper modelled the deposition of submicron particles in a model filter with fibres covered with porous shells and the 2011 paper looked at a 3D filter.

In recent years, the filtration of nanoparticles (d_p <100 nm) has become an important issue, as they are becoming produced more widely, for example in combustion emissions. As their size decreases, particles will begin to behave more like molecules and rebound from fibres may become significant. The preceding single-fibre theory has assumed that particles adhere to a fibre on impact and the lower bounds of particle size for which this theory holds are thus important. Works by Heim et al. (2005), Japuntich et al. (2007), Kim, Harrington and Pui (2007) and Wang, Chen and Pui (2007) have found that the single-fibre efficiency theory predicts filter efficiency well down to particles as small as 2.5 nm. The effect upon the filtration of nanoparticles of polydisperse filters was considered by Podgorski (2009), Podgorski, Maisser and Wladyslaw (2011) and Yamada, Takafumi and Yoshio (2011), who found that the classical theory significantly underestimates penetration in this case. A study was made of the effect of particle shape upon efficiency for particles in the size range 50–300 nm by Boskovic et al. (2008), who found it to be important at low filter-face velocity but less so as the velocity increased.

As the size of the particle increases relative to the thickness of the diffusion layer around the fibre, the effects of particle interception with the fibre will increase. It has been found (Stechkina and Fuchs, 1966; Dunnett and Clement, 2009) that this can be characterised by the parameter s = R/δ, where δ represents the nondimensional thickness of the diffusion layer around the fibre. Diffusion dominates for s <1 and interception for s >1.

5.2.3 Deposition by Interception

Deposition by interception occurs as a result of the finite size of the particles. As stated in Table 5.1, it holds for intermediate-sized particles, which have negligible inertia, gravitational settling and Brownian motion and hence follow the flow streamlines. Deposition occurs when a streamline, called the ‘limiting streamline’, comes within one particle radius of the fibre. If y_C is the distance from the centreline at which the limiting streamline enters the solution domain then the single-fibre efficiency due to interception can be obtained from:

5.18

Using the Kuwabara flow field, Kuwabara (1959) and Lee and Liu (1982) obtained an expression for η_R of the form:

5.19

where Ku is the hydrodynamic factor of Kuwabara flow, defined in Equation 5.16.

The Kuwabara flow field used to determine Equation 5.19 assumes that the fibres in the filter are staggered such that they are separated from each other by the same horizontal and vertical distances. Liu and Wang (1997) modified Equation 5.19 to include the effects of fibre arrangement. The performance of elliptical fibres for particles in the interception regime was investigated by Raynor (2008), who found η_R to depend upon the fibre aspect ratio and the orientation of the fibre axis to the flow, as well as on R and α. The capture of fibrous aerosol by interception was investigated by Asgharian and Cheng (2002), who found interception to be the sole loss mechanism for St_m <0.2, where the modified Stokes number, St_m, is given by . The Stokes number, St, is the ratio of the particle stopping distance to the fibre diameter and is given by:

5.20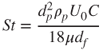

where C is the Cunningham correction factor, which is necessary because of aerodynamic slip at the particle surface:

5.21

For larger values of St_m, it has been found that interception cannot be treated separately from impaction.

5.2.4 Deposition due to Inertial Impaction

For particles for which Brownian diffusion is negligible, the general nondimensional equation of motion for a spherical aerosol particle is given by Equation 5.22:

5.22

where U_p is the particle velocity, St and N_g are nondimensional parameters related to the importance of inertia and gravity upon particle transport, respectively, and i₃ is the unit vector in the direction in which gravity is acting.

The gravitational parameter N_g is the ratio of the particle settling velocity, V_s, to the mean filter velocity, U₀:

5.23

where g is the acceleration due to gravity.

If St and N_g are both negligible then Equation 5.22 gives U = U_p; that is, the particles follow the fluid streamlines and hence interception is the mechanism of deposition (see Section 5.2.3). The ratio of St and N_g is the Froude number, Fr:

5.24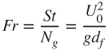

If Fr1 then gravity effects are negligible relative to inertia and Equation 5.22 reduces to:

5.25

This equation does not have a general solution, due to the complexity of U, and hence no general analytical expression for the single-fibre efficiency resulting from inertial impaction, η_I, has been determined. Expressions have however been obtained for the limiting cases of small and large values of St (Brown, 1993):

5.26

5.27

where for 0.01 <R <0.4 and 0.0035 <α <0.111 and k₁ is a constant that depends on the flow field; it is 0.805 for the Kuwabara flow field, with α = 0.05.

For moderate values of St, empirical formulae have been obtained with fitted coefficients (Brown, 1993):

5.28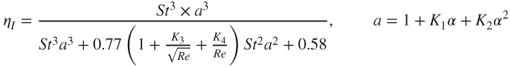

Parameters K₁–K₄ have been fitted by least squares to experimental data and given as (Nguyen and Beeckmans, 1975):

Wang and Pui (2009) obtained numerical results for large St and compared them with Equation 5.27, finding agreement to be good for St >3. More recently, an analytical expression for η_I has been derived for the situation of R 1, Stα^1/2 1 by Zhu, Lin and Cheung (2000):

5.29

Wang and Pui (2009) considered numerically the efficiency of filtration by elliptical fibres for the combined effects of interception and inertial deposition and found that blunt and near-circular fibres performed best for particles in this regime.

5.2.5 Gravitational Deposition

The effect of gravity on filtration efficiency depends on the direction of the airflow and can work to either increase or decrease deposition. In general, the settling velocity of a particle under the influence of gravity, V_s, will tend to increase deposition, whereas the mean convective velocity of the fluid through the filter, U₀, will tend to carry the particles past the fibre. The relative size of these two velocities, N_g, is generally equal to the single-fibre efficiency due to gravitational deposition, η_G (Brown, 1993):

5.30

In general, this mechanism is small compared with the others, except when particles are large or heavy and U₀ is low. When U₀ is greater than about 0.1 m/s, impaction is generally more important than settling.

Kirsh (2005) found that it is important to take into account the effects of gravity when determining the radius of the most penetrating particle while considering the diffusional deposition of heavy submicron particles.

5.2.6 Electrostatic Deposition

The deposition mechanisms considered in Sections 5.2.2–5.2.5 do not involve any attractive forces between the particles and the fibres. One technique applied to augment these mechanisms is the use of electrostatic forces. This is particularly useful for intermediate-sized particles, where the main mechanical deposition mechanism is interception. The filtration efficiency has a minimum in this region, due to the weakness of the particle Brownian motion and the particle inertia. With the addition of electrostatic forces, a filter can achieve a certain efficiency at a lower packing fraction, and hence a lower resistance to the air flow in the filter. Filters that are composed of permanently charged fibres have become known as ‘electret filters’ and are commonly used for air-cleaning applications that require high efficiency and a low pressure drop (Romay, Liu and Chae, 1998).

When a filter's fibres are charged, in addition to the deposition mechanisms discussed in Sections 5.2.2–5.2.5, particle deposition occurs because of polarisation forces. The electric field of the fibre induces a dipole in the particle, the strength of which depends upon the particle volume and the dielectric constant of its constituent material. As the electric field decreases with distance from the fibre, the attractive force on the negative part of the induced dipole exceeds the repulsive force on the positive part, causing the particle to be attracted by the fibre. For oppositely charged particles, this mechanism is increased by coulomb forces. The efficiency of the deposition mechanism depends on the ratio of the drift velocity, V_d, which moves the particle to the fibre, to the convective velocity of the flow, which tends to move the particle past the fibre. Hence all electrostatic filters are more efficient at low filtration velocities. The drift velocity of a particle is a product of the electrostatic force acting on it and of its mechanical mobility and is given by:

5.31

where q is the net charge on the particle and E is the electric field due to the charge on the fibre. In early work on electrostatic deposition, the assumption was usually made that the fibres were uniformly charged, but details of the techniques used to charge filters suggest that this is not the case. More complicated configurations of charge have thus been considered, such as bipolarly charged fibres (Podgorski and Balazy, 2008). Reviews of work on the performance of clean filters are given by Brown (1993) and Wang (2001).

A dimensionless parameter, N_sub, which is the ratio of the drift velocity at the fibre surface to the freestream velocity, U₀, is used to describe the capture efficiency. The subscript sub is related to the charge on the fibre and the particles. In the following expressions for N_sub, the Cunningham correction factor is assumed to be unity.

5.2.6.1 Uniformly Charged Fibres

Assuming that a filter fibre has a uniform charge, Q, per unit length, then:

5.32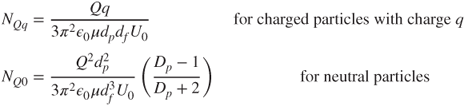

where ε₀ is the permittivity of free space, 10⁻⁹/36π Farads per metre (F/m), and D_p is the dielectric constant of the particle material (Brown, 1993).

The single-fibre efficiency due to electrostatic deposition for these two cases has been shown to be:

5.33

An empirical expression for η_Q0 has been obtained for 0.03 <N_Q0 <0.91 using Kuwabara's flow field with α = 0.03 (Brown, 1993):

5.34

5.2.6.2 Fibres with Nonuniform Charge

In real filters, the charge on a fibre is generally nonuniform. Although the calculation of electric fields due to the complex real-world configurations of charge are complicated, some simplified situations have been modelled. For example, if a fibre carries a line dipole charge with surface charge distribution σcosθ then:

5.35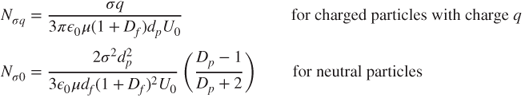

where D_f is the dielectric constant of the fibre material. The corresponding expressions for the single-fibre efficiency are given by (Brown, 1993):

5.36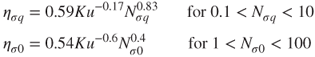

Experimental results by Romay, Liu and Chae (1998) obtained on three commercially available fibrous electret filters for single-fibre efficiencies were fitted to power-law functions of N_σq; it was found that for charged particles the exponent of N_σq was between 0.69 and 0.9 and for uncharged particles the exponent of N_σ0 varied from 0.38 to 0.48, agreeing well with the predictions of Brown (1993).

The expression for neutral particles was later extended to values of N_σ0 less than unity for Kuwabara flow (see Kim et al., 2005):

5.37

More recently, Podgorski and Balazy (2008) simulated numerically the case for neutral particles and fitted their data to obtain two expressions for η_σ0:

5.38

The first equation is believed to be more accurate for nanoparticles filtered in weakly charged electret media and the second equation for an intermediate strength of electrostatic interactions and particles larger than 0.3 µm.

5.2.6.3 Neutral Fibre, Charged Particles

In this case, the dimensionless parameter describing particle capture is given by:

5.39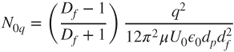

and the single -fibre efficiency by:

5.40

An experimental study by Huang et al. (2006) investigated the capture of four different kinds of aerosol particle under different kinds of charging condition.

5.2.6.4 External Electric Fields

Single-fibre efficiency can be enhanced by placing the fibre in an external electric field, E. In this case, the fibre is polarised and any particles passing it will be affected by both the external electric field and the polarisation field. Expressions for N and η for both charged and neutral particles are given in Brown (1993) and reproduced here:

5.41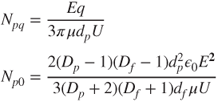

where E is the size of the electric field.

5.42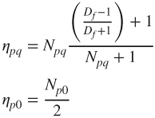

An experimental investigation of the use of external electric fields with textile fibre filters for the capture of micrometre-size particles was undertaken by Thorpe and Brown (2003).

5.2.6.5 Combinations of Electrostatic and Mechanical Effects

The efficiency of an electret filter with rectangular fibres was studied experimentally by Kanaoka et al. (1987) for cases in which electrostatic and Brownian diffusion mechanisms were important. Empirical expressions were obtained for the single-fibre efficiency for charged and uncharged particles:

5.43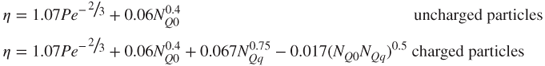

There is some uncertainty about the coefficients in these equations (Brown, 1993) due to the assumptions made. However, the exponents are consistent with the theory.

Numerical simulations, including mechanical and electrostatic effects, have been undertaken by Oh et al. (2002), Cao, Cheung and Yan (2004) and Cheung, Cao and Yan (2005). In the work by Oh et al. (2002), Kuwabara's flow field was assumed and the fibres were uniformly charged, while Cao, Cheung and Yan (2004) and Cheung, Cao and Yan (2005) considered rectangular bipolarly charged fibres.

5.3 Factors Affecting Efficiency

5.3.1 Particle Rebound

The expressions given for single-fibre efficiency in this chapter have assumed that particles adhere to fibres on contact, but in some situations particles will rebound from the fibre surface and hence remain uncaptured. Taking into account rebound, single-fibre efficiency, η_Re, is a product of the collision efficiency, η (the efficiency assuming all particles that impact adhere), and an adhesion efficiency or probability, h:

5.44

where η is the single-fibre efficiency discussed in Sections 5.2.2–5.2.6; that is, the assumption is made that . This assumption is only valid for particles between about 10 nm and a few micrometres in diameter, where diffusion and interception are the main deposition mechanisms (Wang and Kasper, 1991). For larger particles, rebound following impaction decreases efficiency, and for the smaller nanosized particles, bounce occurs as a result of the thermal impact velocity. This process of rebound is different from re-entrainment, where deposited particles are removed from the fibre due to drag forces acting on them or as a result of bombardment by airborne particles.

In the case of rebound, the adhesion efficiency is dependent upon the particle impact velocity, V_i. A particle will rebound from the surface if V_i is greater than a critical value given by:

5.45

Equation 5.45 is valid when the adhesion energy of the approaching particle is the same as that of the rebounding particle. If the adhesion energy of the rebounding particle is much greater than that of approach, the 1 − e² in the numerator is replaced by e² (Brown, 1993).

In Equation 5.45, Φ is the energy of adhesion, m is the particle mass and e is the coefficient of restitution. Due to the number of unknown quantities present in the description of h, such as e and Φ, most expressions in the literature are of an empirical nature. The one most commonly adopted comes from Ptak and Jaroszcyk (1990) and is valid for 0.4 <Re <5.75:

5.46

In an experimental study on a single fibre for 0.4 <St <4.82 (Rembor, Maus and Umhauer, 1999), it was found that Equation 5.46 overestimated h by a factor of up to 6. Later experimental work (Kasper et al., 2009), for single fibres of size 8, 20 and 30 µm and 0.4 <St <9 obtained:

5.47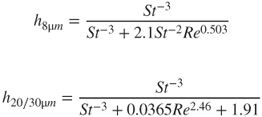

The efficiency of a nonwoven metal filter was considered by Klouda et al. (2011) for U₀ = 10 m/s and compared with expressions obtained using Equation 5.46. For the smaller particles, d_p <0.7 µm, agreement was reasonable, but for d_p >0.7 µm, agreement deteriorated.

For small particles, V_i is characterised by its thermal velocity and the mean thermal impact velocity is given by:

5.48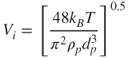

where k_B is Boltzmann's constant and T is temperature (Wang and Kasper, 1991). The theoretical model developed by Wang and Kasper suggests that the thermal impact velocity of a particle will exceed the critical sticking velocity in the size range between 1 and 10 nm, depending on elastic and surface adhesion parameters. Experimental evidence for the effect of thermal rebound upon filtration is however scarce. For example, Kim, Harrington and Pui (2007) measured the penetration of particles of size 3–20 nm through a wide range of filter media and found no significant evidence of rebound. Heim et al. (2005) examined the filtration of charged and uncharged particles in the range 2.5–20.0 nm on grounded metal fibres and meshes and also detected no thermal rebound effects. However, Kim et al. (2006) measured the filtration efficiency through glass fibrous filters for nanoparticles down to 1 nm and detected rebound effects for particles below 2 nm. An experimental study was performed at temperatures up to 500 K by Shin et al. (2008) for particles in the range 3–20 nm and no thermal rebound was detected.

Recently, Mouret et al. (2011) extended the theoretical model of Wang and Kasper and concluded that thermal rebound effects should only be observable in the subnanometre particle range.

5.3.2 Particle Loading

As particles are collected in a filter, they alter its structure and affect both the pressure drop and the collection efficiency. Hence an understanding of the mechanisms of deposit and the effects upon filter performance is important. However, this is a very complex process and is still an area of active research.

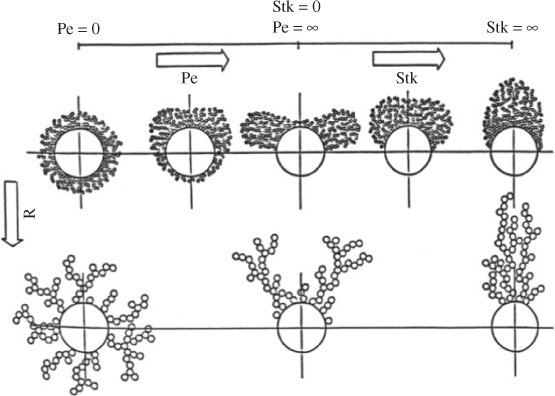
If a fibre is taken from a loaded filter and examined, it will be seen that dendrites are formed on its surface. Dendrites are essentially branchlike structures made up of deposited particles (see Figure 5.4). The formation of dendrites on a fibre is dependent upon the dominant deposition mechanism. In the case of diffusional deposition, dendrites are formed over the entire fibre surface, and for interception they are captured on the leading surface of the fibre. In the case of inertial impaction, particles will be mainly deposited close to the front stagnation point of the fibre. Electrostatic forces tend to cause deposition at any point on the fibre surface, similar to diffusional deposition (Oh et al., 2002). Electric forces also encourage the collapse of dendrites as they tend to attract both captured and airborne particles. External electric fields cause particles to form long dendrites with relatively few branches (Brown, 1993). Considering only mechanical deposition mechanisms, Figure 5.5 shows the relationship between deposit structure and filtration operating conditions. As can be seen in the figure, for small Pe and small R, when diffusional deposition is the dominant mechanism, the particles will be evenly distributed around the fibre with a relatively open pore structure. As interception becomes more important, the basic distribution of the deposit will remain the same but the structure will be more open. For large St, when inertial impaction is dominant, the deposition will purely be on the front of the fibre, with the majority close to the stagnation point. As stated by Kasper, Schollmeier and Meyer (2010), this figure does not reflect the entire reality, especially when particle bounce is significant.

Numerical simulations of dendrite formation on fibres have been performed for many years; for a review of much of this work, see Brown (1993). Such simulations concern the early stages of deposition for the various mechanisms and are computationally very expensive. More recent work in this area has been done by Li and Marshall (2007), who included rebound effects for particles in the inertial impaction regime. A dimensionless adhesion parameter was found to have a dominant effect on the predicted particle deposition rate. The lattice-Boltzmann approach was adopted by Przekop, Moskal and Gradon (2003) to describe the structure of deposits on a cylindrical collector for particles in the diffusional regime. One of the reasons that the study of particle loading is computationally expensive is the need to recalculate the flow field when deposition occurs; Karadimos and Ocone (2003) investigated this and found that the single-fibre efficiency is overestimated when recalculation is not performed. CFD simulations by Lehmann and Kasper (2002) demonstrate the importance of particle rebound upon deposit structure in the inertial regime and show that simulations must be three-dimensional in order to be accurate. Lehmann and Kasper (2002) also used the simulations to determine the packing density of the deposits formed. The deposition of particles on an electret fibre was simulated by Kanaoka, Hiragi and Tanthapanichakoon (2001). Despite the increasing power of computers, numerical models of particle loading are still limited in what they can achieve.

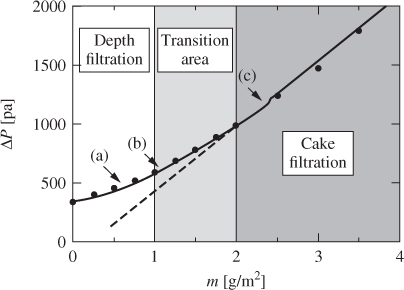
Experimental work on the performance of loaded filters has shown that the rise in the pressure drop across the filter as load increases can be described in two main steps: during the first stage, the evolution is slow, but in the second, the increase becomes markedly rapid and linear (Thomas et al., 1999), as shown in Figure 5.6. Thomas et al. (1999) developed a model to describe the filter performance during loading, which was found to agree well with experimental data (Thomas et al., 2001). In an experimental study by Song, Park and Lee (2006), an empirical expression was obtained for the pressure drop as a function of particle diameter and Cunningham correction factor. Using the experimental results of Walsh and Stenhouse (1997) on the performance of an electret filter under dust loading conditions for charged and uncharged particles (Sae-lim, Tanthapanichakoon and Kanaoka, 2006), a semiempirical expression was obtained for η as a sum of the electrical and mechanical contributions.

Recently, detailed experimental work was undertaken to gain a greater understanding of the performance of single fibres (Kasper et al., 2009; Kasper, Schollmeier and Meyer, 2010). The single-fibre efficiency was found to be described by a power law of the type:

5.49

where b and c are empirical fit coefficients and M is the accumulated mass per unit filter volume. The experimental process undertaken by Kasper's group generated much useful structural information about the deposit, including qualitative information about deposit morphology as a function of particle size, flow velocity and fibre diameter for particles in which inertia, interception and bounce are important. It was found that the transition from compact deposits to the more dendritic structures shown in Figure 5.5 is driven not by interception but by particle bounce.

5.4 Filter Randomness

Practically all the theoretical results given here have been obtained for a single fibre, or a regular array of fibres, arranged perpendicular to the gas flow. A realistic fibrous filter, such as that in Figure 5.1, shows a random array of fibres not exactly at right angles to the flow. There has been relatively little research on the effect of this randomness, but a pioneering study by Schweers and Löffler (1994) showed that it is essential to take account of it in calculating the efficiency of a filter. Their numerical model considered transmission through a random array of cells containing fibres specified by random geometry (angle to the flow) and local packing fraction. The problem has also been approached by a direct statistical model treating transmission through a series of cells of random variable efficiencies (Clement and Dunnett, 2000), which shows that randomness always reduces the overall filtration efficiency compared to that obtained from mean values of the variables that specify the cells. Much more experimental information on the randomness of filters, such as that for packing density distributions investigated by Lehmann, Hardy and Kasper (2003), needs to be obtained in order to further this research.

5.5 Applications

Fibrous filters are efficient devices for capturing particles and hence have many applications. This section touches upon just a few of these, and references will be provided that give more detail.

People are exposed to harmful particulates in the workplace and at home. A wide range of control systems have been designed to reduce exposure, from small personal devices to large-scale industrial installations. Small-scale respirator filters are commonly used to protect individuals against harmful biological and nonbiological aerosol. Work on the performance of respirators against nonbiological particles has been done by Wake and Brown (1988), Ortiz, Soderholm and Valdez (1988), Brown, Wake and Gray (1988) and Eshbaugh et al. (2009). The recent increase in the production of engineered nanoparticles in workplaces has led to studies on the performance of respirators for these small particles, many of which are reviewed in Mostofi et al. (2010). Another area of increasing importance is the filtration of bioaerosols: particles of biological origin, including viruses, bacteria, fungi and pollen. Interest has increased in this area since the severe acute respiratory syndrome (SARS) outbreak in 2003 and the global H1N1 viral infection in 2009 and with the increasing threat of bioterrorism. A review of some of the work on the performance of respirators in filtering bioaerosols can be found in Rengasamy, Zhuang and BerryAnn (2004) and Xu et al. (2011).

For people who suffer from allergic respiratory disease, air filtration is often recommended as part of a group of measures designed to reduce exposure to indoor allergens. In such situations, air filtration can be provided by whole-house filtration via the home-heating, ventilation or air-conditioning system, by portable room air cleaners, or through a combination of these methods. A review of studies on the various types of filtration is given in Sublett (2011).

High-efficiency particulate air (HEPA)-type filters, which remove airborne particles sized 0.3 mm and above with 99.97% efficiency, are used in many hospital environments (such as operating theatres) to reduce infection rates (Dharan and Pittet, 2002). As HEPA filtration is relatively inexpensive and studies have shown that it can significantly reduce airborne levels and/or infection rates for several aerolised pathogens, Curtis (2008) states that it should probably be used in all hospital rooms. The use of portable HEPA filters has also been found to significantly reduce airborne levels of some viruses (Curtis, 2008).

Diesel exhaust is a major contributor to ultrafine particles in places with high traffic intensity. Studies suggest that commuters travelling in their vehicles may experience a high exposure to ultrafine particles (Zhu et al., 2007). In order to reduce this exposure, many automobiles are now equipped with a cabin air filter. Some work on the efficiency of these filters is given in Rudell et al. (1999) and Qi et al. (2008). Another increasingly popular mode of transport that carries the risk of exposing passengers to particulates is air travel. Confined space, limited ventilation, prolonged exposure times and recirculating air are risk factors for the transmission of respiratory tract infections. Use of recirculated air means that filtration is required (Leder and Newman, 2005). The majority of large, modern, commercial aircraft use HEPA filters, which have been found to be effective at removing airborne contamination from the recirculated air in such vehicles (Bull, 2008).

5.6 Conclusions

In this work, an attempt has been made to summarise the main factors affecting the performance of fibrous filters and to discuss their application. The main significant findings from past studies have been mentioned. Although filters and the process of filtration have been studied for many years, especially since the 1960s and the development of computer systems and experimental facilities (Spurny, 1997), this is still an active area of research. For example, the current interest in nanotechnology, despite offering great technological promise, also carries potential health risks and raises the question of how effective filters are at protecting people. The need to protect against global threats such as an influenza epidemic or bioterrorism requires further understanding of the filtration of microorganisms. In addition to new paths of research opening as a result of changing human needs, there are still fundamental areas of filtration performance that are not fully understood. For example, although there are formulae, validated by experimental work, that describe the performance of a clean filter well, our understanding of the performance of filters that contain deposit is less complete and still requires further research.

In conclusion, although we have advanced considerably in our understanding of fibrous filters, there are still many questions to be answered before this understanding is complete.

Nomenclature

C	Cunningham correction factor
D	Diffusion coefficient
Df	Dielectric constant of the fibre material
Dp	Dielectric constant of the particle material
df	Filter fibre diameter
dp	Particle diameter
E	Electric field
E	Collection efficiency
e	Coefficient of restitution
Fr	Froude number
h	Adhesion probability or efficiency
Kn	Knudsen number
Ku	Kuwabara factor (= −0.5ln(α) − 0.75 + α − 0.25α2)
kB	Boltzmann constant
M	Mass of deposited material per unit volume of filter material
m	Particle mass
Ng	Gravitational parameter
Nin	Number of particles entering the filter
Nout	Number of particles leaving the filter
NQq	Dimensionless parameter describing capture of charged particles by a charged fibre
NQ0	Dimensionless parameter describing capture of neutral particles by a charged fibre
Nσq	Dimensionless parameter describing capture of charged particles by a line dipole charged fibre
Nσ0	Dimensionless parameter describing capture of neutral particles by a line dipole charged fibre
Npq	Dimensionless parameter describing capture of charged particles by a polarised fibre
Np0	Dimensionless parameter describing capture of neutral particles by a polarised fibre
N0q	Dimensionless parameter describing capture of charged particles by a neutral fibre
N	Nondimensional particle concentration
P	Penetration
p	Fluid pressure
Pe	Peclet number
q	Charge held by a particle
Q	Charge per unit length of fibre
R	Interception parameter, ratio of particle and fibre diameters
Re	Reynolds number of the flow
r	Polar coordinate
s	Deposit mechanism parameter (= R/δ)
St	Stokes number
Stm	Modified Stokes number (= St/(2Ku))
T	Temperature
U0	Freestream velocity
U	Fluid velocity
Up	Particle velocity
Vd	Particle drift velocity
Vi	Particle impact velocity
VS	Particle settling velocity
x,y	Cartesian components
α	Filter packing fraction
δ	Nondimensional thickness of the diffusion layer
ε0	Permittivity of free space
Φ	Adhesion energy
γ	Layer efficiency
η	Single-fibre efficiency
ηD	Single-fibre efficiency by diffusional deposition
ηG	Single-fibre efficiency by gravitational deposition
ηI	Single-fibre efficiency by inertial deposition
ηR	Single-fibre efficiency by interception
ηEL	General expression for single-fibre efficiency by electrostatic deposition
ηRe	General expression for single-fibre efficiency, taking into account particle rebound
ηQq	Single-fibre efficiency by charged fibre with charged particles
ηQ0	Single-fibre efficiency by charged fibre with neutral particles
ησq	Single-fibre efficiency by line dipole fibre with charged particles
ησ0	Single-fibre efficiency by line dipole fibre with neutral particles
ηpq	Single-fibre efficiency by polarised fibre with charged particles
ηp0	Single-fibre efficiency by polarised fibre with neutral particles
η0q	Single-fibre efficiency by neutral fibre with charged particles
λ	Mean free path of fluid molecules
μ	Fluid viscosity
θ	Polar coordinate
ρ	Fluid density
ρp	Particle density
σ	Surface charge density of fibre
ψ	Stream function

References

Asgharian, B. and Cheng, Y.S. (2002) The filtration of fibrous aerosol. Aerosol Science and Technology, 36, 10–17.

Boskovic, L., Agranovski, I.E., Altman, I.S. and Braddock, R.D. (2008) Filter efficiency as a function of nanoparticle velocity and shape. Journal of Aerosol Science, 39, 635–644.

Brown, R.C. (1993) Air Filtration. An Integrated Approach to the Theory and Application of Fibrous Filters, Pergamon Press, Oxford.

Brown, R.C., Wake, D., Gray, R. et al. (1988) Effect of industrial aerosols on the performance of electrically charged filter material. Annals of Occupational Hygiene, 32, 271–294.

Bull, K. (2008) Cabin air filtration: helping to protect occupants from infectious diseases. Travel Medicine and Infectious Disease, 6, 142–144.

Cao, Y.H., Cheung, C.S. and Yan, Z.D. (2004) Numerical study of an electrets filter composed of an array of staggered parallel rectangular split-type fibres. Aerosol Science and Technology, 38, 603–618.

Chernyakov, A.L., Kirsh, A.A. and Kirsh, V.A. (2011) Efficiency of inertial deposition of aerosol particles in fibrous filters with regard to particle rebounds from fibers. Colloid Journal, 73(3), 389–393.

Cheung, C.S., Cao, Y.H. and Yan, Z.D. (2005) Numerical model for particle deposition and loading in electrets filter with rectangular split-type fibers. Computational Mechanics, 35, 449–458.

Clement, C.F. and Dunnett, S.J. (2000) The use of random variables in fibrous filtration theory, European Aerosol Conference 2000. Journal of Aerosol Science, 31, S200–201.

Curtis, L.T. (2008) Prevention of hospital-acquired infections: review of non-pharmacological interventions. Journal of Hospital Infection, 69, 204–219.

Dharan, S. and Pittet, D. (2002) Environmental controls in operating theatres. Journal of Hospital Infection, 51, 79–84.

Dunnett, S.J. and Clement, C.F. (2009) A numerical model of fibrous filters containing deposit. Engineering Analysis with Boundary Elements, 33(5), 601–610.

Eshbaugh, J.P., Gardner, P.D., Richardson, A.W. and Hofacre, K.C. (2009) N95 and P100 respirator filter efficiency under high constant and cyclic flow. Journal of Occupational and Environmental Hygiene, 6(1), 52–61.

Filippova, O. and Hanel, D. (1997) Lattice-Boltzmann simulation of gas-particle flow in filters. Computers and Fluids, 26(7), 697–712.

Fuchs, N.A. (1964) The Mechanics of Aerosols, Dover Publication, New York.

Happel, J. (1959) Viscous flow relative to arrays of cylinders. AIChE Journal, 5(2), 174–177.

Heim, M., Mullins, B.J., Wild, M. et al. (2005) Filtration efficiency of aerosol particles below 20 nanometers. Aerosol Science and Technology, 39, 782–789.

Hellou, M., Martinez, J. and El Yazidi, M. (2004) Stokes flow through microstructural model of fibrous media. Mechanics Research Communications, 31, 97–103.

Hinds, W.C. (1999) Aerosol Technology: Properties, Behaviour, and Measurement of Airborne Particles, John Wiley & Sons, Inc., New York.

Hosseini, S.A. and Tafreshi, H.V. (2010) Modeling particle filtration in disordered 2-D domains: a comparison with cell models. Separation and Purification Technology, 74, 160–169.

Huang, B., Yao, Q., Li, S.Q. et al. (2006) Experimental investigation on the particle capture by a single fibre using microscopic image technique. Powder Technology, 163, 125–133.

Jaganathan, S., Tafreshi, H.V. and Pourdeyhimi, B. (2008) A realistic approach for modelling permeability of fibrous media: 3-D imaging coupled with CFD simulation. Chemical Engineering and Technology, 63, 244–252.

Japuntich, D.A., Franklin, L.M., Pui, D.Y. et al. (2007) A comparison of two nano–sized particle air filtration tests in the diameter range of 10 to 400 nanometres. Journal of Nanoparticle Research, 9, 93–107.

Kanaoka, C., Emi, H., Hiragi, S. and Myojo, T. (1986) Morphology of particulate agglomerates on a cylindrical fiber and collection efficiency of a dustloaded fiber. Aerosols—Formation and Reactivity. Proceedings 2nd International Aerosol Conference, Berlin 1986, Pergamon Journals Ltd, Oxford, pp. 674–677.

Kanaoka, C., Emi, H., Otani, Y. and Iiyama, T. (1987) Effect of charging state of particles on electret filtration. Aerosol Science and Technology, 7(1), 1–13.

Kanaoka, C., Hiragi, S. and Tanthapanichakoon, W. (2001) Stochastic simulation of the agglomerative deposition process of aerosol particles on an electret fiber. Powder Technology, 118, 97–106.

Karadimos, A. and Ocone, R. (2003) The effect of the flow field recalculation on fibrous filter loading: a numerical simulation. Powder Technology, 137, 109–119.

Kasper, G., Schollmeier, S. and Meyer, J. (2010) Structure and density of deposits formed on filter fibers by inertial particle deposition and bounce. Journal of Aerosol Science, 41, 1167–1182.

Kasper, G., Schollmeier, S., Meyer, J. and Hoferer, J. (2009) The collection efficiency of a particle-loaded single filter fiber. Journal of Aerosol Science, 40, 993–1009.

Kim, C.S., Bao, L., Okuyama, K. et al. (2006) Filtration efficiency of a fibrous filter for nanoparticles. Journal of Nanoparticle Research, 8, 215–221.

Kim, S.C., Harrington, M.S. and Pui, D.Y.H. (2007) Experimental study of nanoparticles penetration through commercial filter media. Journal of Nanoparticle Research, 9, 117–125.

Kim, J.C., Otani, Y., Noto, D. et al. (2005) Initial collection performance of resin wool filters and estimation of charge density. Aerosol Science and Technology, 39, 501–508.

Kirsch, A.A. and Fuchs, N.A. (1967) The fluid flow in a system of parallel cylinders perpendicular to the flow direction at small Reynolds number. Journal of the Physical Society of Japan, 22(5), 1251–1255.

Kirsh, V.A. (2005) Diffusional deposition of heavy submicron aerosol particles on fibrous filters. Colloid Journal, 67(3), 313–317.

Kirsh, V.A. (2006) Stokes flow in periodic systems of parallel cylinders with porous permeable shells. Colloid Journal, 68(2), 173–181.

Kirsh, V.A. (2007) Deposition of aerosol nanoparticles in filters composed of fibres with porous shells. Colloid Journal, 69(5), 655–660.

Kirsh, V.A. (2011) Diffusional deposition of nanoparticles in 3D model fibre filter. Russian Journal of Physical Chemistry A, 85(11), 2089–2093.

Klouda, G.A., Fletcher, R.A., Gillen, J.G. and Verkouteren, R. (2011) Aerosol collection efficiency of a graded metal-fibre filter at high airflow velocity (10 m/s). Aerosol Science and Technology, 45(3), 336–342.

Kuwabara, S. (1959) The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. Journal of the Physical Society of Japan, 14(4), 527–532.

Kwon, S.B., Kim, H.T. and Lee, K.W. (2002) Analytical solutions to diffusional deposition of polydisperse aerosols in fibrous filters. Aerosol Science and Technology, 36(6), 742–747.

Leder, K. and Newman, D. (2005) Respiratory infections during air travel. Internal Medicine Journal, 35, 50–55.

Lee, K.W. and Liu, B.Y.H. (1982) Theoretical study of aerosol filtration by fibrous filters. Aerosol Science and Technology, 1, 147–161.

Lehmann, M.J., Hardy, E.H. and Kasper, G. (2003) Local packing density distribution within a fibrous filter—determination by MRI. Abstracts of the European Aerosol Conference, 513–514.

Lehmann, M.J. and Kasper, G. (2002) CFD simulations of single fibre loading, in (eds M.J. Lehmann and G. Kasper), Particle Loading and Kinetics of Filtration in Fibrous Filters, pp. 91–98, Institutfur Mechanische Verfahrenstechnik und Mechanik Universitat Karlsruhe, ISBN: 3-9805-220-2-4.

Li, S.Q. and Marshall, J.S. (2007) Discrete element simulation of micro-particle deposition on a cylindrical fiber in an array. Journal of Aerosol Science, 38, 1031–1046.

Liu, G.Z. and Wang, P.K. (1997) Pressure drop and interception efficiency of multifibre filters. Aerosol Science and Technology, 26(4), 313–325.

Maze, B., Tafreshi, H.V., Wang, Q. and Pourdeyhimi, B. (2007) A simulation of unsteady-state filtration via nanofiber media at reduced operating pressures. Journal of Aerosol Science, 38, 550–571.

Mostofi, R., Wang, B., Haghighat, F. et al. (2010) Performance of mechanical filters and respirators for capturing nanoparticles—limitations and future direction. Industrial Health, 48, 296–304.

Mouret, G., Chazelet, S., Thomas, D. and Berner, D. (2011) Discussion about the thermal rebound of nanoparticles. Separation and Purification Technology, 78, 125–131.

Nguyen, X. and Beeckmans, J.M. (1975) Single fibre capture efficiencies of aerosol particles in real and model filters in the inertial-interceptive domain. Journal of Aerosol Science, 6, 205–212.

Oh, Y.W., Jeon, K.J., Jung, A.I. and Jung, Y.W. (2002) A simulation study on the collection of submicron particles in a unipolar charged fibre. Aerosol Science and Technology, 36, 573–582.

Ortiz, L.W., Soderholm, S.C. and Valdez, F.O. (1988) Penetration of respirator filters by an asbestos aerosol. American Industrial Hygiene Association Journal, 49(9), 451–460.

Payet, S., Bouland, D., Madelaine, G. and Renoux, A. (1992) Penetration and pressure drop of a HEPA filter during loading with submicron liquid particles. Journal of Aerosol Science, 23(7), 723–735.

Podgorski, A. (2009) Estimation of the upper limit of aerosol nanoparticles penetration through inhomogeneous fibrous filters. Journal of Nanoparticle Research, 11, 197–207.

Podgorski, A. and Balazy, A. (2008) Novel formulae for deposition efficiency of electrically neutral, submicron aerosol particles in bipolarly charged fibrous filters derived using Brownian dynamics approach. Aerosol Science and Technology, 42(2), 123–133.

Podgorski, A., Maisser, A. and Wladyslaw, S.W. (2011) Penetration of monodisperse, singly charged nanoparticles through polydisperse filters. Aerosol Science and Technology, 45(2), 215–233.

Przekop, R. and Gradon, L. (2008) Deposition and filtration of nanoparticles in the composites of nano and microsized fibers. Aerosol Science and Technology, 42, 483–493.

Przekop, R., Moskal, A. and Gradon, L. (2003) Lattice-Boltzmann approach for description of the structure of deposited particulate matter in fibrous filters. Journal of Aerosol Science, 34, 133–147.

Ptak, T. and Jaroszcyk, T. (1990) Theoretical-experimental aerosol filtration model for fibrous filters at intermediate Reynolds numbers. Proceedings 5th World Filtration Congress, Nice.

Qi, C., Stanley, N., Pui, D.Y.H. and Kuehn, T.H. (2008) Laboratory and on-road evaluations of cabin air filters using number and surface area concentration monitors. Environmental Science and Technology, 42, 4128–4132.

Qian, F., Zhang, J. and Huang, Z. (2009) Effects of the operating conditions and geometry parameter on the filtration performance of a fibrous filter. Chemical Engineering and Technology, 32(5), 789–797.

Ramarao, B.V., Tien, C. and Mohan, S. (1994) Calculation of single fibre efficiencies for interception and impaction with superposed Brownian motion. Journal of Aerosol Science, 25(2), 295–313.

Raynor, P.C. (2008) Single-fiber interception efficiency for elliptical fibers. Aerosol Science and Technology, 42(5), 347–368.

Rembor, H.J., Maus, R. and Umhauer, H. (1999) Measurements of single fibre efficiencies at critical values of the Stokes number. Particle and Particle Systems Characterization, 16, 54–59.

Rengasamy, A., Zhuang, Z.P. and BerryAnn, M.S. (2004) Respiratory protection against bioaerosols: literature review and research needs. American Journal of Infection Control, 32(6), 345–354.

Romay, F.J., Liu, B.Y.H. and Chae, S.J. (1998) Experimental study of electrostatic capture mechanisms in commercial electret filters. Aerosol Science and Technology, 28(3), 224–234.

Rudell, B., Wass, U., Hörstedt, P. et al. (1999) Efficiency of automotive cabin air filters to reduce acute health effects of diesel exhaust in human subjects. Occupational and Environmental Medicine, 56, 222–231.

Sae-lim, W., Tanthapanichakoon, W. and Kanaoka, C. (2006) Correlation for the efficiency enhancement factor of a single electret fibre. Journal of Aerosol Science, 37, 228–240.

Schweers, E. and Löffler, F. (1994) Realistic modeling of the behaviour of fibrous filters through consideration of filter structure. Powder Technology, 80, 191–206.

Shin, W.G., Mulholland, G.W., Kim, S.C. and Pui, D.Y.H. (2008) Experimental study of filtration efficiency of nanoparticles below 20 nm at elevated temperatures. Journal of Aerosol Science, 39, 488–499.

Song, C.B., Park, H.S. and Lee, K.W. (2006) Experimental study of filter clogging with monodisperse PSL particles. Powder Technology, 163, 152–159.

Spurny, K.R. (1997) Advances in Aerosol Filtration, Lewis Publisher, London.

Stechkina, I.B. and Fuchs, N.A. (1966) Studies in fibrous aerosol filters—I. Calculation of diffusional deposition of aerosols in fibrous filters. Annals of Occupational Hygiene, 9, 59–64.

Sublett, J.L. (2011) Effectiveness of air filters and air cleaners in allergic respiratory diseases: a review of the recent literature. Current Allergy and Asthma Reports, 11, 395–402.

Thomas, D., Contal, P., Renaudin, V. et al. (1999) Modelling pressure drop in HEPA filters during dynamic filtration. Journal of Aerosol Science, 30, 235–246.

Thomas, D., Penicot, P., Contal, P. et al. (2001) Clogging of fibrous filters by solid aerosol particles experimental and modelling study. Chemical Engineering Science, 56, 3549–3561.

Thorpe, A. and Brown, R.C. (2003) Performance of electrically augmented fibrous filters, measured with monodisperse aerosols. Aerosol Science and Technology, 37(3), 231–245.

Tien, C.V. and Ramarao, B.V. (2007) Granular Filtration of Aerosols and Hydrosols, Elsevier, New York.

Wake, D. and Brown, R.C. (1988) Measurements of the filtration efficiency of nuisance dust respirators against respirable and non-respirable aerosols. Annals of Occupational Hygiene, 32(3), 295–315.

Walsh, D.C. and Stenhouse, J.I.T. (1997) The effect of particle size, charge and composition on the loading characteristics of an electrically active fibrous filter material. Journal of Aerosol Science, 28, 307–321.

Wang, C.S. (2001) Electrostatic forces in fibrous filters—a review. Powder Technology, 118, 166–170.

Wang, J., Chen, D.R. and Pui, D.Y.H. (2007) Modelling of filtration efficiency of nanoparticles in standard filter media. Journal of Nanoparticle Research, 9, 109–115.

Wang, H.C. and Kasper, G. (1991) Filtration efficiency of nanometre-size aerosol particles. Journal of Aerosol Science, 22(1), 31–41.

Wang, Q., Maze, B., Tafreshi, H.V. and Pourdeyhimi, B. (2006) A case study of simulating submicron aerosol filtration via lightweight spun-bonded filter media. Chemical Engineering Science, 61, 4871–4883.

Wang, J. and Pui, D.Y.H. (2009) Filtration of aerosol particles by elliptical fibers: a numerical study. Journal of Nanoparticle Research, 11, 185–196.

Williams, M.M.R. and Loyalka, S.K. (1991) Particle deposition and resuspension. Aerosol Science: Theory and Practice, Chapter 7, Pergamon, Oxford, pp. 326–374.

Xu, Z., Wu, Y., Shen, F. et al. (2011) Bioaerosol science, technology, and engineering: past, present, and future. Aerosol Science and Technology, 45(11), 1337–1349.

Yamada, S., Takafumi, S. and Yoshio, O. (2011) Influence of filter inhomogeneity on air filtration of nanoparticles. Aerosol and Air Quality Research, 11, 155–160.

Zhu, Y., Eiguren-Fernandez, A., Hinds, W.C. and Miguel, A.H. (2007) In-cabin commuter exposure to ultrafine particles on Los Angeles freeways. Environmental Science and Technology, 41, 2138–2145.

Zhu, C., Lin, C.H. and Cheung, C.S. (2000) Inertial impaction-dominated fibrous filtration with rectangular or cylindrical fibers. Powder Technology, 112, 149–162.