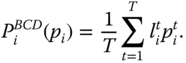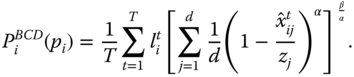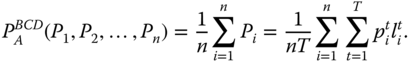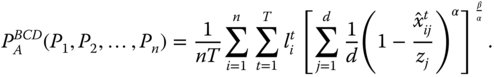Chapter 5
Poverty and Time: A Multidimensional Appraisal
5.1 Introduction
Our investigations on multidimensional poverty in Chapters 3 and 4 employ individual multidimensional achievements as inputs in a single period only. As a result, these atemporal studies do not convey us any information on the time span of poverty at the individual or society level. However, there are reasons not to regard poverty as a timeless concept, but to interpret it as a notion that undergoes evolution over time. It has a particular trajectory – a path with a past and a future. There are no reasons to expect that evolvement of income and nonincome dimensions of life will be the same over time (see Bourguignon and Morrison, 2002, and Decancq et al., 2006). If we restrict attention on each period of the trajectory independently of the past and future poverty experiences, then the assessment of the actual time path is ignored. In consequence, it becomes necessary to have knowledge on the durations and extents of poverty across persons. It has been stressed in the literature that continued periods of poverty are worse than scattered poverty occurrences over time (see Rodgers and Rodgers, 2003 and Jenkins, 2000). Prolonged poverty can be endemic if it arises because of political institutions and structure of the economy (Green and Hulme, 2005). A person, stricken by a long duration of poverty, may suffer from depression on finding that he is deprived even from “minimally acceptable levels” of one or more dimensions of human well-being necessary for leading a decent standard of living (Sen, 1992, p. 139). This feeling of depression may be accompanied by ruination of health and ailment. It is highly unlikely that such a socially excluded person will remain loyal to the society norms (Walker, 1995). This in turn may give rise to social turmoil. Consequently, from long-term policy perspectives, it becomes essential to look at the dynamics of individual and overall poverty.
A dynamic analysis of poverty should make a clear distinction between chronically poor and transiently poor. For effective implementation of antipoverty policy in the current context, it is necessary to pinpoint the chronically poor among the poor (Lybbert et al., 2004; Carter and Barrett, 2006). According to Hulme and Shepherd (2003), chronically poor persons may be characterized as those “people who remain poor for much of their life course, and who may ‘pass on’ their poverty to subsequent generations” (p. 405). Two criteria that have been suggested in the literature for developing quantifiers of chronic poverty that aggregate an individual's poverty positions over time are the spells or duration approach and the permanent income approach (see Yaqub, 2000a,b; Mckay and Lawson, 2003; Hoy et al., 2012). The former relies on the fraction of time a person is perceived to be in poverty.1
Foster (2009) employed the duration approach to suggest a family of income-based chronic poverty indices using an axiomatic framework. This class of indices, which is the chronic variant of the Foster et al. (1984) family of poverty indices, invokes an aggregation first across time and then over individuals. Chakravarty (2009) considered the entire one-dimensional subgroup-decomposable chronic poverty indices within this framework and investigated their properties.
The permanent income approach, also known as the components approach (Yaqub, 2000b), to the identification of the chronically poor persons, relies on the comparison between the resources that he has over time with the poverty line. Jalan and Ravallion (1998) defined a person as chronically poor if his resources, averaged over time, fall below an appropriate poverty line.2
As Foster and Santos (2014) noted, these two different desiderata to the identification of chronically poor persons can be clearly separated depending on the nature of substitutability between periods. While by concentrating simply on periodwise resources, the duration approach does not allow the transfer of resources across periods, the permanent income approach makes use of the average value of resources and hence implicitly allows perfect substitutability across periods. An expansion of the permanent income approach by incorporating savings and borrowings of an individual was suggested by Rodgers and Rodgers (2003). Foster and Santos (2014) put forward a new methodology for assessing chronic poverty that adopts the permanent income approach but incorporates explicitly imperfect degree of substitutability between periods. Porter and Quinn (2008) also replaced the perfect substitution assumption by an alternative supposition of increasing elasticity of substitution using a linear combination of constant elasticity of substitution functions. The family of indices advocated by Porter and Quinn (2014) takes into account the view that the lower the income of a poor person, the higher will be the negative effect of variations in well-being.
A person who is irregularly or occasionally poor over time can be treated as transiently poor. Such a person is poor in some of the periods but not in other periods, and he is not also poor for a minimum number of periods so that he may not be regarded as chronically poor. A person, stricken by this notion of poverty, transiently falls below the poverty line. Transient poverty can be defined as the difference between average of the static periodwise poverty levels and the chronic poverty value (see Ravallion, 1988; Rodgers and Rodgers, 2003; Kurosaki, 2006; Foster, 2009). Time here becomes a characteristic for differentiating among the poor: chronic poverty is different from temporary poverty. The major source of transient poverty is income fluctuation over the periods. A transient poverty index represents a composite picture of fluctuations of income over time that force individuals to be in poverty transiently. In case there are no variations in income over time due to uncertainty, total poverty is determined by value of a poverty index using incomes observed with certainty across periods. It has been argued that transient poverty is equally significant as chronic poverty, and its relative significance varies across social groups and regions (Ravallion, 1988; Ravallion et al., 1995; Jalan and Ravallion, 1998; Baluch and Hoddinott, 2000; Kurosaki, 2006). Foster (2009) and Foster and Santos (2014) suggested transient poverty indices using, respectively, the duration and permanent income approaches to poverty measurement with shorter durations. Duclos et al. (2010) suggested aggregate chronic and transient poverty indices, and there is no identification yardstick for the chronically poor.
There is also a related literature on poverty dynamics that does not deal with chronic poverty but instead concentrates on lifetime or intertemporal poverty. In a recent contribution, Bossert et al. (2012) argued that a metric of individual intertemporal poverty should explicitly incorporate persistence in a state of poverty. The notion of persistence takes into account the durations of poverty spells along with the requisite that the states of affairs where poverty exists in consecutive periods should be regarded as more severe than comparatively the situations in which poverty occurs in separated periods. Thus, while chronic poverty is characterized by frequent occurrence of poverty states, persistence in poverty stipulates that in addition to frequency, consecutiveness of poverty appearance is also vital. To understand the difference between the duration and the persistence approaches in greater detail, let us refer to a cluster of ![]() consecutive poverty (respectively, nonpoverty) spells as a poverty (respectively, nonpoverty) block of size
consecutive poverty (respectively, nonpoverty) spells as a poverty (respectively, nonpoverty) block of size ![]() , where
, where ![]() is an integer. Now, suppose that, given income data for six consecutive periods, a person will be identified as chronically poor if he spends at least three periods in poverty. However, a person is found to be poor only in the first and second periods and out of poverty in all the other periods. While the duration approach does not regard him as chronically poor, the Bossert–Chakravarty–D'Ambrosio approach, which we refer to as the block approach (Zheng, 2012), treats him as intertemporally poor because in this approach, poverty blocks of any length are taken into account. Further, his total poverty is more here than in the situation if he would have experienced the same poverty extents in the first and third periods, that is, when an interchange of poverty values between the second and third periods takes place. In other words, a two-period poverty block is regarded as more damaging than two one-period poverty blocks that are separated by one or more nonzero poverty blocks. More precisely, severity of individual intertemporal poverty is an increasing function of the size of poverty blocks. This indicates that the negative effects of poverty are cumulative.
is an integer. Now, suppose that, given income data for six consecutive periods, a person will be identified as chronically poor if he spends at least three periods in poverty. However, a person is found to be poor only in the first and second periods and out of poverty in all the other periods. While the duration approach does not regard him as chronically poor, the Bossert–Chakravarty–D'Ambrosio approach, which we refer to as the block approach (Zheng, 2012), treats him as intertemporally poor because in this approach, poverty blocks of any length are taken into account. Further, his total poverty is more here than in the situation if he would have experienced the same poverty extents in the first and third periods, that is, when an interchange of poverty values between the second and third periods takes place. In other words, a two-period poverty block is regarded as more damaging than two one-period poverty blocks that are separated by one or more nonzero poverty blocks. More precisely, severity of individual intertemporal poverty is an increasing function of the size of poverty blocks. This indicates that the negative effects of poverty are cumulative.
There are empirical evidences that support negative consequences of cumulative poverty. For instance, individuals characterized by persistent poverty are affected by capability deprivations with respect to education, health, and social capital (Chronic Poverty Research Center, 2004). Arranz and Cantó (2012) used Spanish longitudinal data to demonstrate that poverty exit rates are negatively affected by accumulation of poverty spells and length of past spells. It has been argued in the literature that when individuals are affected by poverty spells of long size, getting away from poverty becomes quite difficult (see Bane and Ellwood, 1986; Walker, 1995; Cappellari and Jenkins, 2004). Bossert et al. (2012) axiomatically characterized an individual's intertemporal poverty index given by the weighted sum of periodwise poverty levels, where the weights are the sizes of poverty blocks. In consequence, it reflects the views adopted in the block approach. In Lillard and Willis (1978) and Duncan and Rodgers (1991), proportion of persons with incomes below the permanent income has been taken as an index of persistent poverty, where permanent income has been estimated as a person's intercept in fixed-effects earnings model, and the transitory component was represented by the error term. Bossert et al. (2012) also axiomatically characterized an intertemporal poverty index for the society as a whole using the individual intertemporal indices. In Dutta et al. (2013), a variant of the Bossert–Chakravarty–D'Ambrosio approach was developed by discounting the effect of a period in poverty using the number of periods out of poverty that precede it.
The persistence issue has also been considered by Calvo and Dercon (2009), but their suggested index considers the poverty of the immediately preceding period only without taking into account the entire history of the individuals. Calvo and Dercon (2009) made a thorough presentation of several issues on lifetime poverty for an individual. The three critical features that were addressed in their study are as follows: aiding poverty spells by nonpoverty spells, treating consecutive poverty spells as more harmful than separated spells, and discounting instead of valuing all spells equally. They suggested several indices that provide different answers to these issues.
Hoy and Zheng (2011) attempted to provide an axiomatic framework to investigate the notion of lifetime poverty for an individual as well as for a society. A major difference between the duration approach and the Hoy–Zheng approach is that the latter does not directly identify the chronically poor; instead, it concentrates on closeness of poverty spells. The impact of closeness is maximized when all the spells constitute a block, and it is minimized if the spells are separated evenly over the entire period. For any situation in between these two extremes, the impact changes continuously. They also invoked an axiom that stresses that poverty in earlier phases of life not only produces an effect on incomes in later periods but also intensifies lifetime poverty. Their approach, which attaches importance on closeness of poverty spells, may be referred to as a closeness approach (Zheng, 2012). Similarly to the Bossert–Chakravarty–D'Ambrosio index, the Hoy and Zheng (2011) individual index of lifetime poverty is a weighted average of snapshot poverty levels with the weights being a decreasing and strictly concave function of the time period. For the society lifetime index, Hoy and Zheng (2011) demanded that aggregation first across individuals and then across time is equivalent to aggregation in the reverse order, that is, for each individual, intertemporal aggregation is done first, which is then followed by aggregation across individuals. This gives rise to the concept of “path independence.”
Mendola and Busetta (2012) proposed a persistent individual poverty index that is based on a path dependence axiom. According to this axiom, different weight is assigned to each pair of years of poverty, irrespective of whether they are consecutive or not. It assigns a higher degree of (longitudinal) poverty to people who suffer from poverty in blocks, rather than in separated periods, for whom the gaps from the poverty line are larger through time and when the worst years are in blocks and/or recent. They also introduced an aggregate index of persistence in poverty with the objective of measuring the distribution of the persistence of poverty in the society. Gradin et al. (2012) made a methodological proposal to measure intertemporal poverty by suggesting a new family of poverty indices that attempts to harmonize the ways poverty is quantified in a static and a dynamic framework. Their index explicitly indicates social preference for equality in the distribution of poverty across periods through income transfer from one period to another.
Hojman and Kast (2009) developed an intertemporal index that relies on trade-off between levels of poverty and changes in poverty (gains and losses). The individual index characterized by Hojman and Kast (2009) turns out to be an increasing function of periodwise absolute poverty levels and changes in poverty. Bossert et al. (2014) suggested an index of individual intertemporal material deprivation as the sum of average material deprivation suffered by the individual over time and the average of weighted changes in material deprivation met by the person overt time, where weights can behave in a similar way as loss aversion. However, while the Hojman–Kast analysis is concerned with a single dimension of well-being, the Bossert et al. approach looks at material deprivations in different possible dimensions. In Bossert et al. (2014), it has also been explored how the Foster (2009) and block approaches can be utilized to ascertain material deprivation.
A generalization of the Chakravarty and D'Ambrosio (2006) counting approach to the measurement of social exclusion was considered by Nicholas and Ray (2011) for measuring multidimensional deprivation, building on the proposals of Bossert et al. (2012) and Gradin et al. (2012) for evaluating intertemporal poverty.
The objective of this chapter is to analyze alternative approaches that propose or develop specific indices of lifetime poverty in a multidimensional framework. All such indices may be regarded as indices of intertemporal capability deprivation. Now, when time and multidimensionality are simultaneously subsumed into the analysis of poverty measurement, the picture becomes quite complex. The principal reason behind this is that the identification of a poor in a multidimensional intertemporal setup itself is complicated. For instance, it becomes necessary to investigate whether we aggregate multidimensional poverty levels of an individual at different time periods to arrive at an overall measure, or periodwise dimensional deprivations of the persons are aggregated to get a comprehensive picture of his intertemporal poverty. Consequently, it becomes imperative to examine what matter in defining and conceptualizing the notion of multidimensional intertemporal poverty and how to record these features accurately.
Section 5.2 of the chapter reports the preliminaries and background materials. The concern of Section 5.3 is to extend the one-dimensional block approach advocated by Bossert et al. (2012) to a multidimensional framework. A comparative analysis with some one-dimensional variants of this approach, when it is adapted to the unidimensional case, is also presented in a subsection of the section. Two multidimensional counting approaches to the determination of intertemporal deprivation are examined in Section 5.4. Section 5.5 presents a deliberation on a generalization of Foster's (2009) chronic income poverty measurement proposal to a multidimensional situation, suggested by Alkire et al. (2017). A short subsection of Section 5.5 deals with one-dimensional chronic poverty measurement. The functional form of the multidimensional chronic poverty index we propose relies on the Bourguignon and Chakravarty (2003) approach to multidimensional poverty measurement. Its transient counterpart is also explored rigorously. One characteristic of this specific choice is that it can accommodate a scrutiny of relationship between any two dimensions of well-being in terms of substitutability and complementarity. A detailed investigation of the axioms considered for each case is made in the respective section. The objective of Section 5.6 is to study intertemporal poverty orderings explored by Bresson and Duclos (2015). Finally, Section 5.7 concludes the discussion.
5.2 Preliminaries
Assume availability of observations on d dimensions of well-being for n individuals at T consecutive time periods, where ![]() , with N being the set of natural numbers. We denote the set of all dimensions
, with N being the set of natural numbers. We denote the set of all dimensions ![]() by
by ![]() . For any
. For any ![]() , we say that
, we say that ![]() is a period profile of length T. The set
is a period profile of length T. The set ![]() denotes the set of periods in the profile
denotes the set of periods in the profile ![]() of length T. Person i's achievement in dimension j in the tth period is denoted by
of length T. Person i's achievement in dimension j in the tth period is denoted by ![]() , where
, where ![]() ,
, ![]() and
and ![]() are arbitrary. These numbers constitute the basic ingredients of our analysis. Unless specified, it will be assumed that
are arbitrary. These numbers constitute the basic ingredients of our analysis. Unless specified, it will be assumed that ![]() . Given that we are concerned here with intertemporal analysis, it is likely that
. Given that we are concerned here with intertemporal analysis, it is likely that ![]() . For
. For ![]() , we go back to the atemporal situation considered in Chapter 3. Assume also that no ambiguity arises with respect to the definition of a period, for instance, it can be a year or three-quarters of a year and so on. Each period is assumed to be sufficiently long for achievements to be observed and measured.
, we go back to the atemporal situation considered in Chapter 3. Assume also that no ambiguity arises with respect to the definition of a period, for instance, it can be a year or three-quarters of a year and so on. Each period is assumed to be sufficiently long for achievements to be observed and measured.
Let ![]() stand for the
stand for the ![]() dimensional matrix whose ith row is
dimensional matrix whose ith row is ![]() , which is a listing of the quantities in d dimensions that person i possesses in period t. More formally, for
, which is a listing of the quantities in d dimensions that person i possesses in period t. More formally, for ![]() ,
, ![]() , this
, this ![]() matrix represents person i's achievements in different dimensions in the tth period. The number of dimensions d is assumed to be fixed. We refer to the
matrix represents person i's achievements in different dimensions in the tth period. The number of dimensions d is assumed to be fixed. We refer to the ![]() matrix Xt as the achievement or distributional matrix in period t. Often, we will refer to
matrix Xt as the achievement or distributional matrix in period t. Often, we will refer to ![]() as the social distribution or social matrix in the tth period. The distribution of achievements in dimension j in period t is depicted by the column vector
as the social distribution or social matrix in the tth period. The distribution of achievements in dimension j in period t is depicted by the column vector ![]() . We write
. We write ![]() for the set of all
for the set of all ![]() achievement matrices in period t.
achievement matrices in period t.
We assume at the outset that the dimensional achievements have been suitably tailored to take into consideration variations across time periods, for instance, by discounting. Consequently, for each dimension, a common threshold limit can be used. Let ![]() be the d dimensional vector (i.e.,
be the d dimensional vector (i.e., ![]() matrix) of time invariant threshold limits, where
matrix) of time invariant threshold limits, where ![]() for all
for all ![]() . The vector
. The vector ![]() is assumed to be an element of the set
is assumed to be an element of the set ![]() , strictly positive part of the d dimensional Euclidean space. Person i is regarded as deprived (respectively, nondeprived) with respect to dimension j in period
, strictly positive part of the d dimensional Euclidean space. Person i is regarded as deprived (respectively, nondeprived) with respect to dimension j in period ![]() if
if ![]() (respectively,
(respectively, ![]() ). Equivalently, we say that dimension j is meager (respectively, nonmeager) for person i in period
). Equivalently, we say that dimension j is meager (respectively, nonmeager) for person i in period ![]() . For any period
. For any period ![]() and each pair
and each pair ![]() , let
, let ![]() be the censored amount of achievement in dimension
be the censored amount of achievement in dimension ![]() possessed by person
possessed by person ![]() in period
in period ![]() . Then the deprivation indicator of person
. Then the deprivation indicator of person ![]() in the dimension–period pair
in the dimension–period pair ![]() is given by
is given by ![]() . Thus, if individual
. Thus, if individual ![]() is deprived in dimension
is deprived in dimension ![]() at period
at period ![]() , then he experiences a positive deprivation; otherwise, his deprivation is zero.
, then he experiences a positive deprivation; otherwise, his deprivation is zero.
Let ![]() be the
be the ![]() intertemporal achievement matrix of the
intertemporal achievement matrix of the ![]() individuals for all the periods, whose typical entry is
individuals for all the periods, whose typical entry is ![]() , person i's achievement in dimension
, person i's achievement in dimension ![]() in period
in period ![]() . The first
. The first ![]() rows of
rows of ![]() indicate the achievements of
indicate the achievements of ![]() individuals in different dimensions in period 1, the second
individuals in different dimensions in period 1, the second ![]() rows, starting from the
rows, starting from the ![]() row to the
row to the ![]() row, specify similar figures in period 2, and so on. Unless mentioned explicitly, it will be assumed that
row, specify similar figures in period 2, and so on. Unless mentioned explicitly, it will be assumed that ![]() , the number of periods over which observations are made, is given. It is also assumed that the choice of the vector of threshold limits
, the number of periods over which observations are made, is given. It is also assumed that the choice of the vector of threshold limits ![]() is arbitrary. The population size
is arbitrary. The population size ![]() is allowed to vary over the set of natural numbers
is allowed to vary over the set of natural numbers ![]() . Let
. Let ![]() stand for the set of all
stand for the set of all ![]() intertemporal achievement matrices. The set of intertemporal achievement matrices for all population sizes are given by
intertemporal achievement matrices. The set of intertemporal achievement matrices for all population sizes are given by ![]() , that is,
, that is, ![]() . We denote the n coordinated vector of ones by
. We denote the n coordinated vector of ones by ![]() . For any
. For any ![]() ,
, ![]() ,
, ![]() represents an intertemporal achievement profile for person
represents an intertemporal achievement profile for person ![]() , where
, where ![]() is
is ![]() row of
row of ![]() , with
, with ![]() ,
, ![]() ,
, ![]() being arbitrary.
being arbitrary.
We assume the union method of identifying the poor in each period in this multidimensional framework. In consequence, if a person is deprived in at least one dimension in a period, then he is regarded as poor in that period. Evidently, a person deprived in a dimension in a period may or may not be deprived in the same dimension next period.
5.3 The Block Approach
For expositional ease, we will subdivide our discussion in this section into several subsections.
5.3.1 Individual Multidimensional Intertemporal Poverty Index
The objective of this subsection is to develop an analytical formulation of the block approach to the quantification of intertemporal poverty for any arbitrary individual ![]() . Essentials to the approach are the individual poverty profiles across periods. It is assumed that individual poverty indicators are observed in each of the periods under consideration. For each person
. Essentials to the approach are the individual poverty profiles across periods. It is assumed that individual poverty indicators are observed in each of the periods under consideration. For each person ![]() , the per-period poverty profile is a vector
, the per-period poverty profile is a vector ![]() , the nonnegative part of the T-dimensional Euclidean space. We can as well say that
, the nonnegative part of the T-dimensional Euclidean space. We can as well say that ![]() is person i's intertemporal poverty profile of length
is person i's intertemporal poverty profile of length ![]() . For any given period
. For any given period ![]() ,
, ![]() represents person i's overall deprivation in the period, as determined by a nonconstant subgroup-decomposable multidimensional poverty index
represents person i's overall deprivation in the period, as determined by a nonconstant subgroup-decomposable multidimensional poverty index ![]() . More precisely, for any
. More precisely, for any ![]() ,
, ![]() . That is, for any
. That is, for any ![]() and
and ![]() ,
, ![]() gives the extent of poverty corresponding to
gives the extent of poverty corresponding to ![]() and the threshold vector
and the threshold vector ![]() . It takes on the minimal value 0 if person
. It takes on the minimal value 0 if person ![]() is nondeprived in all the dimensions. We assume subgroup decomposability at the outset because of its appealing policy applications.
is nondeprived in all the dimensions. We assume subgroup decomposability at the outset because of its appealing policy applications.
By assumption,
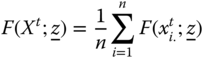
The index ![]() is ratio-scale invariant, strongly (hence weakly) focused, symmetric, population replication invariant, monotonic, monotonically sensitive, dimensionally monotonic, increasing under a Pigou–Dalton bundle of regressive transfers between two poor persons, increasing (respectively, decreasing) under a correlation-increasing switch if the underlying dimensions are substitutes (respectively, complements) and bounded. It varies continuously with respect to changes in achievement levels of the individual in the period provided that the person's poverty status remains unchanged in the period (period-restricted continuity). (See Chapter 3, for details.)
is ratio-scale invariant, strongly (hence weakly) focused, symmetric, population replication invariant, monotonic, monotonically sensitive, dimensionally monotonic, increasing under a Pigou–Dalton bundle of regressive transfers between two poor persons, increasing (respectively, decreasing) under a correlation-increasing switch if the underlying dimensions are substitutes (respectively, complements) and bounded. It varies continuously with respect to changes in achievement levels of the individual in the period provided that the person's poverty status remains unchanged in the period (period-restricted continuity). (See Chapter 3, for details.)
The individual poverty function considered next turns out to be satisfactory from these perspectives. It corresponds to a member of the Bourguignon–Chakravarty family and is formally defined as

where ![]() and
and ![]() are parameters. Some restrictions on inequality between
are parameters. Some restrictions on inequality between ![]() and
and ![]() have to be imposed for sensitivity under a correlation-increasing switch (see Chapter 3). For all
have to be imposed for sensitivity under a correlation-increasing switch (see Chapter 3). For all ![]() ,
, ![]() means that individual
means that individual ![]() is nonpoor in period
is nonpoor in period ![]() , whereas a positive value of
, whereas a positive value of ![]() indicates that he is in poverty in this period.
indicates that he is in poverty in this period.
It may often be necessary to compare intertemporal poverty profiles of different lengths. This type of comparison can be made if we assume that the individual intertemporal poverty index entertains time replication invariance, that is, it remains invariant under replication of the poverty profile with respect to time (see Shorrocks, 2009a). Fulfillment of this property also makes comparisons of individual intertemporal poverty meaningful when possibilities of profiles with different lengths, coming from populations with different sizes, are allowed. To state this principle, formally, we need to define an individual intertemporal index rigorously.
Let ![]() , where
, where ![]() is the set of natural numbers. Here
is the set of natural numbers. Here ![]() represents the set of person
represents the set of person ![]() intertemporal poverty profiles of all possible lengths.
intertemporal poverty profiles of all possible lengths.
For any ![]() ,
, ![]() ,
, ![]() determines the extent of intertemporal poverty suffered by person
determines the extent of intertemporal poverty suffered by person ![]() over the time profile
over the time profile ![]() . By defining
. By defining ![]() over the set all poverty profiles of different lengths, we consider the possibility of allowing comparisons of intertemporal poverty profiles with different lengths using the metric
over the set all poverty profiles of different lengths, we consider the possibility of allowing comparisons of intertemporal poverty profiles with different lengths using the metric ![]() .
.
The time replication principle may now be formally stated as follows:
- Time Replication Principle: The intertemporal poverty index
 is said to be time replication invariant if for all
is said to be time replication invariant if for all  ,
, 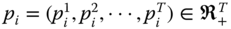 ,
, 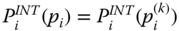 ,where
,where 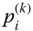 is the
is the 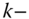 fold replication of
fold replication of 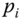 , and
, and 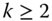 is any integer.
is any integer.
In the replicated poverty profile ![]() , each entry
, each entry ![]() of
of ![]() is repeated
is repeated ![]() times so that
times so that ![]() has a length of
has a length of ![]() . In consequence,
. In consequence, ![]() . Satisfaction of the time replication principle by an individual intertemporal poverty index means that intertemporal poverty is an average concept.
. Satisfaction of the time replication principle by an individual intertemporal poverty index means that intertemporal poverty is an average concept.
We now suggest two basic postulates for an individual intertemporal poverty index. The first property, monotonicity, involves a curtailment in a deprived dimension's achievement of the person in a period in which he is poor.
In Definition 5.2, person ![]() is poor in period
is poor in period ![]() because of his positive deprivation in dimension
because of his positive deprivation in dimension ![]() in the profile
in the profile ![]() in period
in period ![]() , and his deprivation in the dimension in the same period is higher in the profile
, and his deprivation in the dimension in the same period is higher in the profile ![]() . (Recall that we follow the union method of identification of the poor.) His achievements in all other dimensions in
. (Recall that we follow the union method of identification of the poor.) His achievements in all other dimensions in ![]() and also in all the dimensions in all other periods across the profiles remain unchanged. In consequence,
and also in all the dimensions in all other periods across the profiles remain unchanged. In consequence, ![]() should indicate a higher level of intertemporal poverty than
should indicate a higher level of intertemporal poverty than ![]() . This postulate, which may be treated as a multidimensional translation of the axiom “monotonicity in outcomes,” suggested by Calvo and Dercon (2009), can now be formally stated as follows.
. This postulate, which may be treated as a multidimensional translation of the axiom “monotonicity in outcomes,” suggested by Calvo and Dercon (2009), can now be formally stated as follows.
- Period-Restricted Monotonicity: For all
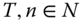 , and
, and 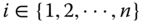 ,
, 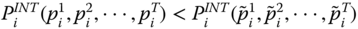 , given that for all
, given that for all  ,
, 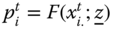 and
and 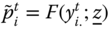 , where
, where 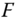 is an individual poverty function, and
is an individual poverty function, and 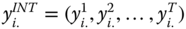 is obtained from
is obtained from 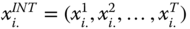 by a simple reduction in the achievement in a deprived dimension of person
by a simple reduction in the achievement in a deprived dimension of person  .
.
This axiom demands that a cutback in a deprived dimension's achievement of a person in any period leads to an augmentation in intertemporal poverty level of the person. To understand the axiom in greater detail, let ![]() and
and ![]() . The three dimensions of well-being are daily energy consumption in calories by an adult male, per capita income, and life expectancy. The vector of respective thresholds limits is
. The three dimensions of well-being are daily energy consumption in calories by an adult male, per capita income, and life expectancy. The vector of respective thresholds limits is ![]() . The achievement profiles of person
. The achievement profiles of person ![]() in the 3 periods are, respectively,
in the 3 periods are, respectively, ![]() ,
, ![]() , and
, and ![]() . In periods 1 and 2, the person is deprived in life expectancy and income. In period 3, he is deprived only in calorie consumption. In period 1, if life expectancy of the person goes down to 59, then the profile
. In periods 1 and 2, the person is deprived in life expectancy and income. In period 3, he is deprived only in calorie consumption. In period 1, if life expectancy of the person goes down to 59, then the profile ![]() is obtained from the profile
is obtained from the profile ![]() by a simple reduction in person i's life expectancy, a deprived dimension of the person, in period 1. The state-restricted monotonicity axiom demands that the former profile should be more intertemporally poverty stricken than the latter.
by a simple reduction in person i's life expectancy, a deprived dimension of the person, in period 1. The state-restricted monotonicity axiom demands that the former profile should be more intertemporally poverty stricken than the latter.
For ![]() and
and ![]() considered in Definition 5.2, assume that
considered in Definition 5.2, assume that ![]() is such
is such ![]() and
and ![]() . Define
. Define ![]() as follows: (i)
as follows: (i) ![]() , (ii)
, (ii) ![]() for all
for all ![]() , and (iii)
, and (iii) ![]() for all
for all ![]() . Then the shortfall of achievement in dimension
. Then the shortfall of achievement in dimension ![]() between the profiles
between the profiles ![]() and
and ![]() in period
in period ![]() is identical to that between
is identical to that between ![]() and
and ![]() . But in
. But in ![]() , person
, person ![]() achievement in the dimension is lower than that in the original profile
achievement in the dimension is lower than that in the original profile ![]() . One may argue that intertemporal poverty should hit a person harder if achievement loss takes at a lower level. To state this formally in terms of an axiom, for all
. One may argue that intertemporal poverty should hit a person harder if achievement loss takes at a lower level. To state this formally in terms of an axiom, for all ![]() , let
, let ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() is an individual poverty function. Then the following postulate, which may be treated as a multidimensional twin of Calvo and Dercon's (2009) “increasing cost of hardship” axiom in the one-dimensional case, may be stated as follows:
is an individual poverty function. Then the following postulate, which may be treated as a multidimensional twin of Calvo and Dercon's (2009) “increasing cost of hardship” axiom in the one-dimensional case, may be stated as follows:
- Period-Restricted Monotonicity Sensitivity: For all
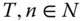 , and
, and 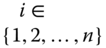 ,
, 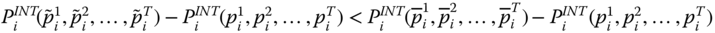 .
.
In the aforementioned example, suppose that person i's life expectancy in period 1 reduces further from 59 to 58.5. Then the period-restricted monotonicity sensitivity axiom appeals that the escalation in the person's intertemporal poverty when the intertemporal achievement profile modifies from ![]() to
to ![]() is lower than that when it shifts from
is lower than that when it shifts from ![]() to
to ![]() .
.
In the block approach, aggregation of the components of the individual per-period poverty profile into an individual intertemporal poverty index assumes, under ceteris paribus conditions, that longer breaks between poverty blocks will decrease intertemporal poverty. To understand this requirement, consider the per-period poverty profiles ![]() and
and ![]() . There are two breaks in each profile, but the first break in the second profile has higher length. This suggests that the second profile should have lower intertemporal poverty. More precisely, both the profiles are portrayed by a two-period block with poverty levels
. There are two breaks in each profile, but the first break in the second profile has higher length. This suggests that the second profile should have lower intertemporal poverty. More precisely, both the profiles are portrayed by a two-period block with poverty levels ![]() and
and ![]() , respectively, one one-period block with a poverty value of
, respectively, one one-period block with a poverty value of ![]() , and also one one-period block having a poverty value of
, and also one one-period block having a poverty value of ![]() . But while in the former profile, there is one zero-poverty block between the sequences
. But while in the former profile, there is one zero-poverty block between the sequences ![]() and
and ![]() , in the latter profile, the same sequences are separated by a zero-poverty block of size 2. In order to make the presence of zero-poverty block significant in a situation of this type, from antipoverty perspective, it is desirable that the former profile should indicate higher individual intertemporal poverty than the latter, under ceteris paribus conditions. We refer to this property as sensitivity to the length in poverty break.
, in the latter profile, the same sequences are separated by a zero-poverty block of size 2. In order to make the presence of zero-poverty block significant in a situation of this type, from antipoverty perspective, it is desirable that the former profile should indicate higher individual intertemporal poverty than the latter, under ceteris paribus conditions. We refer to this property as sensitivity to the length in poverty break.
The second feature of the aggregation is that intertemporal poverty increases as the longer length of a poverty block increases at the expense of shorter length of a poverty block. To illustrate this, consider the profiles ![]() and
and ![]() . In both the profiles, the positive poverty values
. In both the profiles, the positive poverty values ![]() ,
, ![]() , and
, and ![]() appear respectively twice, once, and once. In the first profile, the length of the first poverty block is 3 and that of the second poverty block is 1. Now, in the second profile, the length of the first poverty block increases to 4 and that of the second poverty block reduces to 0. Then the former profile should have less intertemporal poverty than the latter under ceteris paribus conditions. This property reflects sensitivity to the length of poverty blocks.
appear respectively twice, once, and once. In the first profile, the length of the first poverty block is 3 and that of the second poverty block is 1. Now, in the second profile, the length of the first poverty block increases to 4 and that of the second poverty block reduces to 0. Then the former profile should have less intertemporal poverty than the latter under ceteris paribus conditions. This property reflects sensitivity to the length of poverty blocks.
In sum, we have argued that evaluation of poverty over time from a multidimensional perspective is highly positively correlated with the lengths of individual poverty spells and negatively correlated with the lengths of breaks between two poverty spells.
Now, for any ![]() such that
such that ![]() , let
, let ![]() be the maximal number of consecutive periods including
be the maximal number of consecutive periods including ![]() with positive (respectively, zero) per-period poverty values. For instance, let
with positive (respectively, zero) per-period poverty values. For instance, let ![]() . Since the individual is in poverty in the first two periods,
. Since the individual is in poverty in the first two periods, ![]() . This is followed by a zero-poverty block of length 1 and hence,
. This is followed by a zero-poverty block of length 1 and hence, ![]() . The individual is again in poverty in the next period and out of poverty then, which in turn implies that
. The individual is again in poverty in the next period and out of poverty then, which in turn implies that ![]() . The final period in which the person is in poverty is a single period after the fifth block with a zero poverty. This implies that
. The final period in which the person is in poverty is a single period after the fifth block with a zero poverty. This implies that ![]() .
.
The Bossert et al. (2012) multidimensional intertemporal poverty index for person ![]() can now be defined as
can now be defined as
Note that nonnegativity of ![]() ensures that
ensures that ![]() , where the lower bound 0 is achieved if nobody is deprived in any period (
, where the lower bound 0 is achieved if nobody is deprived in any period (![]() for all triplets
for all triplets ![]() ). This time replication individual intertemporal index unambiguously reduces when profiles have longer breaks between poverty blocks and increases when the length of a poverty block increases. Now, each component
). This time replication individual intertemporal index unambiguously reduces when profiles have longer breaks between poverty blocks and increases when the length of a poverty block increases. Now, each component ![]() of
of ![]() is the individual function, evaluated using person i's achievements, associated with a subgroup-decomposable multidimensional poverty index
is the individual function, evaluated using person i's achievements, associated with a subgroup-decomposable multidimensional poverty index ![]() . Given that
. Given that ![]() are positive, all postulates of
are positive, all postulates of ![]() are periodwise satisfied by
are periodwise satisfied by ![]() . In the discussion on sensitivity to length in poverty break, the two profiles, we have considered, are of lengths 5 and 7, respectively. The time replication invariance postulate empowers us to compare them with respect to intertemporal poverty.
. In the discussion on sensitivity to length in poverty break, the two profiles, we have considered, are of lengths 5 and 7, respectively. The time replication invariance postulate empowers us to compare them with respect to intertemporal poverty.
To illustrate the formula in (5.3), we now calculate its values for the examples considered earlier. The values of person i's intertemporal poverty, as determined by ![]() , for these profiles are given as follows:
, for these profiles are given as follows:

The first two calculations clearly indicate that individual intertemporal poverty decreases as the breaks between poverty blocks become longer, and the other two calculations show that it increases whenever the lengths of poverty blocks increase.
In the property that reflects sensitivity of ![]() to the length of a poverty block, we assumed an arbitrary number of poverty periods. We will now state a related property of a general individual intertemporal poverty index involving the lengths of poverty blocks in profiles with only two poverty periods. This postulate will be stated as a necessary and sufficient requirement. To illustrate the idea, consider the profile
to the length of a poverty block, we assumed an arbitrary number of poverty periods. We will now state a related property of a general individual intertemporal poverty index involving the lengths of poverty blocks in profiles with only two poverty periods. This postulate will be stated as a necessary and sufficient requirement. To illustrate the idea, consider the profile ![]() . The common length of each of the two poverty blocks in this profile is 1, and they are separated by a nonpoverty block of length 2. Now, if we swap the poverty experiences of periods 3 and 5 in this profile, the resulting profile turns out to be
. The common length of each of the two poverty blocks in this profile is 1, and they are separated by a nonpoverty block of length 2. Now, if we swap the poverty experiences of periods 3 and 5 in this profile, the resulting profile turns out to be ![]() . The value of the index
. The value of the index ![]() for this postswitch intertemporal profile is
for this postswitch intertemporal profile is ![]() . But
. But ![]() . This means that contiguous locations of poverty occurrence increase intertemporal poverty. In other words, contiguous poverty periods in an intertemporal poverty profile generate higher impact on
. This means that contiguous locations of poverty occurrence increase intertemporal poverty. In other words, contiguous poverty periods in an intertemporal poverty profile generate higher impact on ![]() . Conversely, we can derive the profile
. Conversely, we can derive the profile ![]() from the profile
from the profile ![]() by moving two contiguous periods of poverty further apart. This movement decreases the value of
by moving two contiguous periods of poverty further apart. This movement decreases the value of ![]() . Loosely speaking, this example shows that, in this particular case, switch of atemporal poverty locations in an intertemporal profile increases intertemporal poverty if and only if their postswitch positions are contiguous. We can state this property of
. Loosely speaking, this example shows that, in this particular case, switch of atemporal poverty locations in an intertemporal profile increases intertemporal poverty if and only if their postswitch positions are contiguous. We can state this property of ![]() for a general intertemporal poverty index
for a general intertemporal poverty index ![]() as follows:
as follows:
- Block Monotonicity: Suppose that there are only two distinct and nonadjacent poverty periods
 in the intertemporal poverty profile
in the intertemporal poverty profile 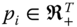 , where
, where 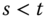 and
and 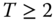 . Now, if
. Now, if  is obtained from
is obtained from 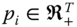 by trading temporal positions of these two poverty incidents to
by trading temporal positions of these two poverty incidents to 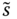 and
and 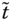 , where
, where 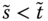 , then
, then 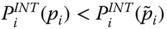 holds if and only if
holds if and only if 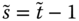 .
.
Since contiguous sites of poverty experiences increase the length of a poverty block, which in turn intensifies intertemporal poverty, we refer to this axiom as block monotonicity axiom. Hoy and Zheng (2015) defined intertemporal poverty on the space of lifetime income distributions and called it strong chronic poverty axiom.
Of the four properties we introduce next, for a general index ![]() , the first three were suggested by Bossert et al. (2012), and the fourth one is by Calvo and Dercon (2009). The first postulate claims that if there is only one period, then one-period poverty is the same as individual intertemporal poverty. Formally,
, the first three were suggested by Bossert et al. (2012), and the fourth one is by Calvo and Dercon (2009). The first postulate claims that if there is only one period, then one-period poverty is the same as individual intertemporal poverty. Formally,
- One-Period Equivalence: For all
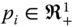 ,
5.4
,
5.4
The next property says that when the individual is in poverty for all the periods, then for any subperiod ![]() ,
, ![]() , intertemporal poverty can be calculated as the sum of the intertemporal poverties of the profiles
, intertemporal poverty can be calculated as the sum of the intertemporal poverties of the profiles ![]() and
and ![]() . More precisely,
. More precisely,
- Single-Block Additive Decomposability: For all
 , all
, all 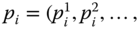
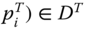 and all
and all  ,
5.5
,
5.5
where
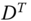 is the strictly positive part of the
is the strictly positive part of the 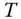 dimensional Euclidean space.
dimensional Euclidean space.
Repeated application of this postulate shows that
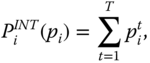
given that ![]() for all
for all ![]() . That is, an individual's intertemporal poverty is simply the sum of periodwise poverty levels. This decomposition becomes quite useful from antipoverty policy perspective; it enables us to identify those periods that are more poverty stricken. In consequence, if
. That is, an individual's intertemporal poverty is simply the sum of periodwise poverty levels. This decomposition becomes quite useful from antipoverty policy perspective; it enables us to identify those periods that are more poverty stricken. In consequence, if ![]() , we can partition the set of periods
, we can partition the set of periods ![]() into nonoverlapping subsets, say,
into nonoverlapping subsets, say, ![]() and
and ![]() , and intertemporal poverty
, and intertemporal poverty ![]() equals
equals ![]() .
.
According to the third property, for all nonnegative poverty profiles, if two subgroups of periods are separated by at least one zero-poverty period, then the total intertemporal poverty can be expressed as the weighted average of subgroup intertemporal poverty values, where the weights are the proportional lengths of the subgroups. Analytically,
- Across-Blocks Average Decomposability: For all
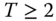 , all
, all 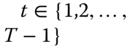 , all
, all  if
if  or
or 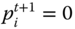 , then
5.7
, then
5.7
This axiom shows significance of the lengths of poverty blocks and lengths of blocks out of poverty. The length of a block becomes an important characteristic for evaluation of intertemporal poverty. Accordingly, if ![]() , then
, then ![]() equals
equals ![]() .
.
However, across-blocks average decomposability does not apply to any arbitrary poverty profile, rather to some restricted profiles. A stronger decomposability condition, presented by Calvo and Dercon (2009), applies to any arbitrary profile of poverty. This stronger form, the subperiod decomposability postulate, does not require the separating spell ![]() or
or ![]() to be a zero-poverty spell, where
to be a zero-poverty spell, where ![]() is arbitrary. More concretely,
is arbitrary. More concretely,
- Subperiod Decomposability: For all
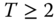 , all
, all 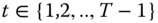 , all
, all  ,
5.8
,
5.8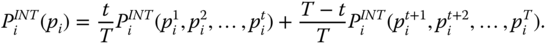
This is a direct counterpart of the population subgroup decomposability axiom considered in the poverty measurement literature. Repeated application of the postulate shows that 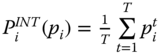 (see also Hoy and Zheng, 2015).
(see also Hoy and Zheng, 2015).
The following axiom also specifies a reasonable requirement.
- Intertemporal Continuity: For all
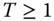 ,
, 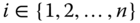 ,
, 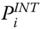 is a continuous function of each period's poverty level provided that the person's poverty status remains unchanged in all periods.
is a continuous function of each period's poverty level provided that the person's poverty status remains unchanged in all periods.
The poverty statistic ![]() is a violator of subperiod decomposability. However, it fulfills the other three postulates of the set of the aforementioned four postulates. In the example taken earlier,
is a violator of subperiod decomposability. However, it fulfills the other three postulates of the set of the aforementioned four postulates. In the example taken earlier, ![]() ,
, ![]() , and
, and ![]() . Then the percentage contribution made by the subgroup
. Then the percentage contribution made by the subgroup ![]() of the periods to total intertemporal poverty of the person is
of the periods to total intertemporal poverty of the person is 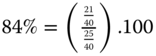 . Hence from antiperiod policy perspective, the subgroup
. Hence from antiperiod policy perspective, the subgroup ![]() of periods requires more attention. This illustration demonstrates an appropriate policy relevance of the axiom across-blocks average decomposability.
of periods requires more attention. This illustration demonstrates an appropriate policy relevance of the axiom across-blocks average decomposability.
We now employ the periodwise Bourguignon–Chakravarty poverty function for individual ![]() in (5.3). The resulting individual intertemporal poverty index becomes a positive weighted function of individual temporal poverty levels
in (5.3). The resulting individual intertemporal poverty index becomes a positive weighted function of individual temporal poverty levels ![]() , where
, where ![]() , person
, person ![]() poverty in period
poverty in period ![]() , is evaluated using his achievements in the period by the individual function
, is evaluated using his achievements in the period by the individual function ![]() associated with
associated with ![]() .
.
If ![]() for at least one
for at least one ![]() , then for a given value of
, then for a given value of ![]() , an increase in the value of
, an increase in the value of ![]() increases the intertemporal continuous poverty index
increases the intertemporal continuous poverty index ![]() in (5.9). Since for any
in (5.9). Since for any ![]() ,
, ![]() is positive, this index unambiguously verifies the period-restricted monotonicity axioms for any
is positive, this index unambiguously verifies the period-restricted monotonicity axioms for any ![]() and
and ![]() .
.
Another desirable postulate is formulated in terms of a transfer of a bundle of achievements from one period to another, where the dimensions that are affected by the transfer are more deprived in the former than in the latter. To state this property formally, let ![]() be the identical set of dimensions in which person
be the identical set of dimensions in which person ![]() is deprived in periods
is deprived in periods ![]() and
and ![]() in
in ![]() , where
, where ![]() are arbitrary and
are arbitrary and ![]() . Formally,
. Formally, ![]() . Assume further that the person's deprivations in different dimensions in period
. Assume further that the person's deprivations in different dimensions in period ![]() are lower than his corresponding deprivations in period
are lower than his corresponding deprivations in period ![]() . More precisely, for all
. More precisely, for all ![]() ,
, ![]() .
.
Since ![]() can at most be
can at most be ![]() , it is ensured that for any
, it is ensured that for any ![]() ,
, ![]() . The inequality
. The inequality ![]() guarantees that the regressive transfer in any dimension from the bequest period
guarantees that the regressive transfer in any dimension from the bequest period ![]() to the beneficiary period
to the beneficiary period ![]() does not permit the person to be nondeprived in the dimension in the beneficiary period.
does not permit the person to be nondeprived in the dimension in the beneficiary period.
In the example we have taken earlier to illustrate the monotonicity axioms, let ![]() and
and ![]() . Then
. Then ![]() . Choose
. Choose ![]() . As a result,
. As a result, ![]() and
and 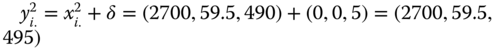 . Then we say that the intertemporal profile
. Then we say that the intertemporal profile 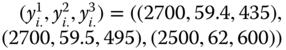 is obtained from the profile
is obtained from the profile ![]() by an across-periods Pigou–Dalton bundle of regressive transfers. (Strictly speaking, since income is the only affected dimension, it is one-dimensional regressive transfer considered by Bourguignon and Chakravarty (2003).)
by an across-periods Pigou–Dalton bundle of regressive transfers. (Strictly speaking, since income is the only affected dimension, it is one-dimensional regressive transfer considered by Bourguignon and Chakravarty (2003).)
The following axiom, which can be viewed as a multidimensional companion of the one-dimensional intertemporal regressive transfer axiom advocated by Gradin et al. (2012), can now be stated:
- Across-Periods Transfer: For all
 ,
,  , given that for all
, given that for all  ,
, 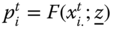 and
and 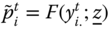 , where
, where 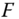 is an individual poverty function and
is an individual poverty function and 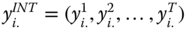 is obtained from
is obtained from  by an across-periods Pigou–Dalton bundle of regressive transfers.
by an across-periods Pigou–Dalton bundle of regressive transfers.
The across-periods transfer axiom requires that individual intertemporal poverty should rise under an across-periods Pigou–Dalton bundle of regressive transfers. Similarly, intertemporal poverty should decrease if a bundle of progressive transfers takes place. The two time locations ![]() and
and ![]() we have chosen in the period profile are arbitrary. Therefore, one sufficient condition that ensures satisfaction of the transfer axiom is that all poverty spells in (5.9) are assigned the same weight in the aggregation. For unequally weighted spells, some restrictions may be required for fulfillment of the axiom. Given
we have chosen in the period profile are arbitrary. Therefore, one sufficient condition that ensures satisfaction of the transfer axiom is that all poverty spells in (5.9) are assigned the same weight in the aggregation. For unequally weighted spells, some restrictions may be required for fulfillment of the axiom. Given ![]() and
and ![]() , a sufficient condition that ensures its verification of the axiom of across-periods Pigou–Dalton bundle of regressive transfers by
, a sufficient condition that ensures its verification of the axiom of across-periods Pigou–Dalton bundle of regressive transfers by ![]() in (5.9) is that
in (5.9) is that ![]() . An intertemporal poverty index will be called transfer sensitive if it fulfills the across-periods transfer postulate.
. An intertemporal poverty index will be called transfer sensitive if it fulfills the across-periods transfer postulate.
5.3.2 Aggregate Multidimensional Intertemporal Poverty Index
We assume that the society intertemporal poverty index ![]() is a nonnegative real-valued function of individual intertemporal poverty components. Since under this assumption, the index relies only on individualistic intertemporal poverty features, we name it as independence of irrelevant information.
is a nonnegative real-valued function of individual intertemporal poverty components. Since under this assumption, the index relies only on individualistic intertemporal poverty features, we name it as independence of irrelevant information.
For the reason that a typical element of the set ![]() of all intertemporal poverty profiles of an
of all intertemporal poverty profiles of an ![]() person society is
person society is ![]() , the set of all possible intertemporal poverty profiles at the society level is
, the set of all possible intertemporal poverty profiles at the society level is ![]() . Following Bossert et al. (2012), we define the average intertemporal poverty index for the society as
. Following Bossert et al. (2012), we define the average intertemporal poverty index for the society as ![]() , where for all
, where for all ![]() ,
, ![]() ,
,
For any ![]() ,
, ![]() gives the level of overall intertemporal poverty associated with the intertemporal poverty profile
gives the level of overall intertemporal poverty associated with the intertemporal poverty profile ![]() across persons. That is, the overall intertemporal poverty level is the simple arithmetic average of individual intertemporal poverty values. We allow variability of the population size to broaden the framework sufficiently so that across-populations collation of overall intertemporal poverty becomes possible.
across persons. That is, the overall intertemporal poverty level is the simple arithmetic average of individual intertemporal poverty values. We allow variability of the population size to broaden the framework sufficiently so that across-populations collation of overall intertemporal poverty becomes possible.
For ![]() of the form given by (5.9), the resulting index turns out to be
of the form given by (5.9), the resulting index turns out to be
This population replication invariant overall intertemporal poverty index enables us to perform cross-population comparisons of intertemporal poverty allowing variability of the sampling period. It can as well be employed to compare intertemporal poverty extents of the same population for different sampling periods. The population replication invariance principle views global intertemporal poverty as a per-capita concept. Its subgroup decomposability property facilitates us to button down those persons in the society who are beset more by intertemporal poverty and hence to design antipoverty policy. This policy is about lifetime elude or lack of elude from poverty. It is definitely about a future situation, not just involving one future period distress.
The per-capita notion of global poverty is also reflected by the average critical levels postulate, which necessitates that if a person with average poverty level migrates to the society, then global poverty remains unchanged (see Blackorby et al., 2005). This property is captured by the index ![]() .
.
- Average Critical Levels: For all
 , for all
, for all 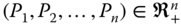 ,
, 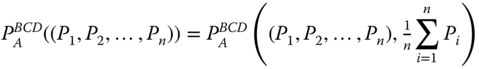 .
.
Observe that the average of intertemporal poverty levels across persons takes into account all information on periodwise poverty thresholds. In consequence, the choice of the average intertemporal poverty as the critical level does not lead to any loss of information.
If any two individuals trade their positions in (5.10), then this exchange has no effect on ![]() because of its anonymity property. It also gladdens an impartiality principle with respect to an increment or a decrement in individual poverty. If a single person's intertemporal poverty changes by a certain amount, then it is immaterial whose poverty changes. For the postulate to be well defined, it is necessary to assume that the change in poverty is the same across persons. In order to state this postulate rigorously, let
because of its anonymity property. It also gladdens an impartiality principle with respect to an increment or a decrement in individual poverty. If a single person's intertemporal poverty changes by a certain amount, then it is immaterial whose poverty changes. For the postulate to be well defined, it is necessary to assume that the change in poverty is the same across persons. In order to state this postulate rigorously, let ![]() , where
, where ![]() for all
for all ![]() and
and ![]() .
.
- Incremental Equity: For all
 ,
,  , for all
, for all 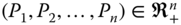 , for all
, for all 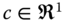 and for all
and for all 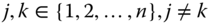 , such that
, such that 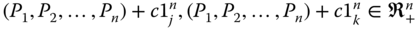 ,
, 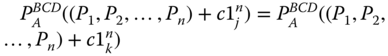 .
.
Thus, incremental equity needs that the impact on global poverty of a change in any person j's poverty has the effect of a similar change in a different person k's poverty. Consequently, the persons ![]() and
and ![]() are treated anonymously from this perspective.
are treated anonymously from this perspective.
The index takes on the value 0 if ![]() for all
for all ![]() . More generally, if
. More generally, if ![]() for all
for all ![]() , then
, then ![]() . For any
. For any ![]() ,
, ![]() is bounded between the minimal and maximal values of individualwise intertemporal poverty levels. More precisely,
is bounded between the minimal and maximal values of individualwise intertemporal poverty levels. More precisely, ![]() .
.
If for some pair (j, t), there is an increase in 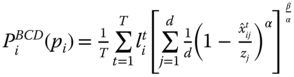 , say, following a reduction in
, say, following a reduction in ![]() , then
, then ![]() increases unambiguously. Formally,
increases unambiguously. Formally,
- Strong Monotonicity: For all
 , and for all
, and for all 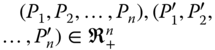 ,
, 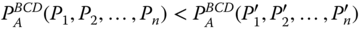 ,where
,where 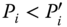 for some
for some 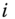 and
and 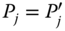 for all
for all 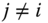 .
.
This strong monotonicity property of ![]() demands that society's intertemporal poverty increases under an upsurge of any individual's intertemporal poverty. It implies its weak sister, which says that overall intertemporal increases when all the individuals' intertemporal poverty levels get augmented. More precisely,
demands that society's intertemporal poverty increases under an upsurge of any individual's intertemporal poverty. It implies its weak sister, which says that overall intertemporal increases when all the individuals' intertemporal poverty levels get augmented. More precisely,
- Weak Monotonicity: For all
 , and for all
, and for all  ,
, 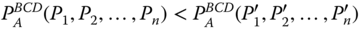 , where
, where 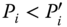 for all
for all 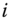 .
.
Among the other notions of monotonicity that are captured by ![]() are (i) ratio-scale improvement, (ii) translation-scale improvement, and (iii) minimal increasingness. According to the ratio-scale improvement postulate, an equiproportionate contraction in individualwise intertemporal poverty values leads to a shrinkage of global intertemporal poverty (Shorrocks, 1983). More concretely,
are (i) ratio-scale improvement, (ii) translation-scale improvement, and (iii) minimal increasingness. According to the ratio-scale improvement postulate, an equiproportionate contraction in individualwise intertemporal poverty values leads to a shrinkage of global intertemporal poverty (Shorrocks, 1983). More concretely,
- Ratio-Scale Improvement: For all
 , for all
, for all 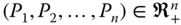 ,where
,where 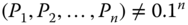 , and for all scalars
, and for all scalars 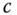 ,
,  ,
, 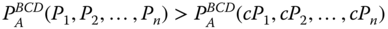 .
.
The translation-scale improvement condition claims that an equal absolute diminution of amounts of all persons' intertermporal poverties generates a lessening of society's intertemporal poverty value (Shorrocks, 1983).
- Translation-Scale Improvement: For all
 , for all
, for all  ,
, 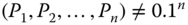 , and for all scalars
, and for all scalars 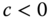 such that
such that 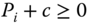 for all
for all  ,
,  .
.
Finally, minimal increasingness appeals that if intertemporal poverty is equal across individuals, then lower poverty is preferred to higher poverty (Blackorby and Donaldson, 1984). More explicitly,
- Minimal Increasingness: For all
 ,and for all
,and for all  , where a > b,
, where a > b,  .
.
This axiom, formulated in terms of an equal intertemporal poverty across persons, is very weak and appealing.
5.3.3 A Review of Some Related One-Dimensional Proposals
The literature contains several recommendations for measuring individual intertemporal poverty in the univariate case. A comparative analysis of the proposals that bear similarity with our block-approach-based endorsement explored earlier, when it is adapted to the single-variable situation, will be a useful exercise. This is the objective of this subsection.
We denote individual i's income in period ![]() by
by ![]() ,
, ![]() , and
, and ![]() . Denote the time-invariant income poverty line by
. Denote the time-invariant income poverty line by ![]() . The censored income level associated with
. The censored income level associated with ![]() is symbolized by
is symbolized by ![]() , that is,
, that is, ![]() . We write
. We write ![]() for the income deprivation indicator for the person in period
for the income deprivation indicator for the person in period ![]() .
.
The three steps that were employed in the Calvo–Dercon formulation for developing lifetime individual statistic of poverty are as follows: focus (truncation of above-threshold incomes in different periods), transformation (all atemporal deprivations are transformed by some increasing and strictly convex function so that unidimensional monotonicity and monotonicity sensitivity axioms are fulfilled), and aggregation of transformed deprivations into an overall index of individual lifetime poverty. We denote these three steps by F, T, and A, respectively. The six possible orderings of the steps are FTA, FAT, TFA, TAF, AFT, and ATF. Since the orderings FTA and AFT draw out all the insights in TFA and ATF, respectively, the latter two can be ignored.
Under the sequence FTA, after focus, identical increasing and strictly convex transformation is imposed on the atemporal deprivations to preserve the monotonicity axioms, before aggregation. The resulting indices resemble “the well-known Chakravarty and Foster–Greer–Thorbecke measures of aggregate poverty” (Calvo and Dercon, 2009, p. 40). Formally, they are given respectively by
where ![]() ,
, ![]() , and
, and
where ![]() and
and ![]() . The common parameter
. The common parameter ![]() in the aforementioned two indices is a discounting parameter. Consequently,
in the aforementioned two indices is a discounting parameter. Consequently, ![]() ascertains the rate of time discounting. It gives us the weights assigned to transformed deprivations in different periods over the profile
ascertains the rate of time discounting. It gives us the weights assigned to transformed deprivations in different periods over the profile ![]() . If the weights are chosen in decreasing order of time, then distant future-period spells are paid lower attention in the aggregation. A necessary condition that guarantees this is that
. If the weights are chosen in decreasing order of time, then distant future-period spells are paid lower attention in the aggregation. A necessary condition that guarantees this is that ![]() . Thus, while in
. Thus, while in ![]() , equal weight is assigned to the spells in a block, and as the size of the block increases, the constant weight across the spells in the block increases, for the Calvo–Dercon indices, the weight unambiguously decreases as the period becomes more distant. If
, equal weight is assigned to the spells in a block, and as the size of the block increases, the constant weight across the spells in the block increases, for the Calvo–Dercon indices, the weight unambiguously decreases as the period becomes more distant. If ![]() , each spell is allotted the same weight (=1), and this happens irrespective of its location in the profile
, each spell is allotted the same weight (=1), and this happens irrespective of its location in the profile ![]() . In other words, these indices remain invariant under any rearrangement of the periods in the profile
. In other words, these indices remain invariant under any rearrangement of the periods in the profile ![]() . As a result, there is no discounting of the periods. In this case, a progressive transfer of income from a less deprived period to a more deprived one decreases individual intertemporal poverty. In other words, of two deprived periods, the higher one can be subsidized by the lower one.
. As a result, there is no discounting of the periods. In this case, a progressive transfer of income from a less deprived period to a more deprived one decreases individual intertemporal poverty. In other words, of two deprived periods, the higher one can be subsidized by the lower one.
The two subperiod decomposable Calvo–Dercon indices comply with the one-dimensional versions of the monotonicity and monotonicity sensitivity axioms. For ![]() and
and ![]() ,
, ![]() becomes the number of periods in which the person stays below the poverty line. This is the individual intertemporal period count index for income poverty.
becomes the number of periods in which the person stays below the poverty line. This is the individual intertemporal period count index for income poverty.
When the sequences AFT and TAF are adopted, the variants of the pair of indices ((5.11) (5.12)) are given respectively by the pairs
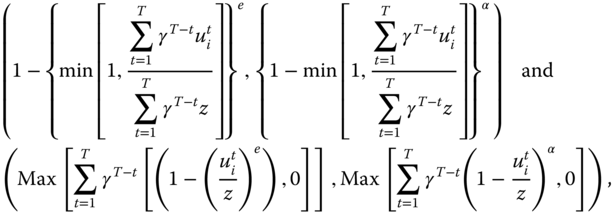
where the parameters ![]() , and
, and ![]() obey the same restrictions as in (5.12) and (5.13). Each component of the two pairs is a violator of subperiod decomposability. While each constituent of the first pair fails to meet monotonicity sensitivity, monotonicity is risked for any constituent of the second pair. The set of violators of subperiod decomposability and monotonicity sensitivity also include indices derived under the sequence FAT. In view of these problems identified with the indices underlying these three sequences, we do not analyze them further.
obey the same restrictions as in (5.12) and (5.13). Each component of the two pairs is a violator of subperiod decomposability. While each constituent of the first pair fails to meet monotonicity sensitivity, monotonicity is risked for any constituent of the second pair. The set of violators of subperiod decomposability and monotonicity sensitivity also include indices derived under the sequence FAT. In view of these problems identified with the indices underlying these three sequences, we do not analyze them further.
Dutta et al. (2013) proposed a deviant of the Bossert–Chakravarty–D'Ambrosio quantifier of individual intertemporal poverty. They noted that in the Bossert–Chakravarty–D'Ambrosio formulation, the distribution of nonpoverty spells does not play any role in the determination of individual intertemporal poverty. Their alternative approach relies on the assumption that the longer nonpoverty spells experienced by an individual prior to becoming poor make him more capable of dealing with poverty. However, preceding poverty periods cannot be made milder by nonpoverty spells. In other words, affluence cannot weaken a previous poverty spell but can help one to be better equipped to fight poverty in future. They also characterized a family of individual intertemporal poverty indices.
The explicit form of their alternative recommendation is given by
where ![]() is income deprivation indicator in period
is income deprivation indicator in period ![]() ,
, ![]() is the number of consecutive poverty periods prior to period
is the number of consecutive poverty periods prior to period ![]() ,
, ![]() is the number of nonpoverty periods immediately prior to period
is the number of nonpoverty periods immediately prior to period ![]() , and
, and ![]() ,
, ![]() , are positive parameters. The parameter
, are positive parameters. The parameter ![]() represents sensitivity of period-by-period deprivation indicators to intertemporal poverty in the sense that given
represents sensitivity of period-by-period deprivation indicators to intertemporal poverty in the sense that given ![]() values, how a change in
values, how a change in ![]() changes
changes ![]() , and
, and ![]() and
and ![]() determine, respectively, sensitivity of the poverty block size prior to period
determine, respectively, sensitivity of the poverty block size prior to period ![]() and the number of nonpoverty periods just prior to period
and the number of nonpoverty periods just prior to period ![]() . Evidently, under ceteris paribus assumptions,
. Evidently, under ceteris paribus assumptions, ![]() increases as
increases as ![]() increases (i.e., as poverty periods cluster) and
increases (i.e., as poverty periods cluster) and ![]() decreases as
decreases as ![]() increases (i.e., as nonpoverty periods cluster just before a poverty period). The approach has a clear merit – in the aggregation, it incorporates the characteristic of appeasing in terms of preceding nonpoverty spells and increasing impact of bunching of poverty spells. This nonnegative individual intertemporal index that upholds the block monotonicity and one-period equivalence axioms is a normalized index in the sense that it takes on the value 0 if
increases (i.e., as nonpoverty periods cluster just before a poverty period). The approach has a clear merit – in the aggregation, it incorporates the characteristic of appeasing in terms of preceding nonpoverty spells and increasing impact of bunching of poverty spells. This nonnegative individual intertemporal index that upholds the block monotonicity and one-period equivalence axioms is a normalized index in the sense that it takes on the value 0 if ![]() for all
for all ![]() . Dutta et al. (2013) suggested a modification of (5.14) by replacing
. Dutta et al. (2013) suggested a modification of (5.14) by replacing ![]() by
by ![]() and
and ![]() , if income is above certain threshold limit
, if income is above certain threshold limit ![]() , and 1 otherwise. Under this modification, the index verifies a weak poverty mitigation axiom, which claims that there is some particular level of income,
, and 1 otherwise. Under this modification, the index verifies a weak poverty mitigation axiom, which claims that there is some particular level of income, ![]() , exceeding the poverty line, such that income in a nonpoverty period can lighten the effect of poverty episodes in other periods but only up to the specified limit
, exceeding the poverty line, such that income in a nonpoverty period can lighten the effect of poverty episodes in other periods but only up to the specified limit ![]() . To understand this, let
. To understand this, let ![]() and
and ![]() be two lifetime income profiles, the poverty line
be two lifetime income profiles, the poverty line ![]() and
and ![]() . Then
. Then ![]() should have less lifetime poverty than
should have less lifetime poverty than ![]() because mitigation effect happens to exist up to the limit
because mitigation effect happens to exist up to the limit ![]() . Further, the profile
. Further, the profile ![]() has the same intertemporal poverty as
has the same intertemporal poverty as ![]() , although period 1 income in
, although period 1 income in ![]() is lower than that in
is lower than that in ![]() . The reason behind this is that an increase in income beyond
. The reason behind this is that an increase in income beyond ![]() has no further mitigation effect. However, it fails to verify the strong poverty mitigation axiom, which requires continuity of the mitigation operation and impact to be increasing with income (see Hoy and Zheng, 2015).
has no further mitigation effect. However, it fails to verify the strong poverty mitigation axiom, which requires continuity of the mitigation operation and impact to be increasing with income (see Hoy and Zheng, 2015).
Another one-dimensional variant of the Bossert–Chakravarty–D'Ambrosio proposal was suggested by Gradin et al. (2012). According to these authors, a regressive transfer of income from one period to another, where the size of the poverty block to which the bequest period belongs is at least as high as that of the poverty block to which the beneficiary period is attached, should increase individual intertemporal poverty under ceteris paribus assumptions. (See the across-periods transfer axiom presented in the Section 5.3.1.) To perceive this in greater detail, let ![]() be person i's intertemporal income profile and
be person i's intertemporal income profile and ![]() be the income poverty line. The person is poor in periods 2,3,4,6, and 7. Now, consider a regressive income transfer of size 1 from period 3 to period 6 generating the profile
be the income poverty line. The person is poor in periods 2,3,4,6, and 7. Now, consider a regressive income transfer of size 1 from period 3 to period 6 generating the profile ![]() . The size of the block to which the bequest period pertains is 3 (with poverty periods being 2, 3, and 4). In contrast, the size of the block to which the beneficiary period is attached is 2 (with poverty periods being 6 and 7). Hence, this regressive transfer should increase person i's intertemporal poverty.
. The size of the block to which the bequest period pertains is 3 (with poverty periods being 2, 3, and 4). In contrast, the size of the block to which the beneficiary period is attached is 2 (with poverty periods being 6 and 7). Hence, this regressive transfer should increase person i's intertemporal poverty.
The alternative functional form for person i's intertemporal poverty index suggested by these authors is

where ![]() is the individual income poverty function in period
is the individual income poverty function in period ![]() and
and ![]() is the same as in equation (5.3). Standard examples of
is the same as in equation (5.3). Standard examples of ![]() can be
can be ![]() and
and ![]() , where
, where ![]() and
and ![]() are parameters. These two functions correspond respectively to the Foster et al. (1984) and Chakravarty (1983) poverty indices. The parameter
are parameters. These two functions correspond respectively to the Foster et al. (1984) and Chakravarty (1983) poverty indices. The parameter ![]() attaches higher weight to longer poverty spells reflecting the idea that continuous enlargement of the size of a poverty block intensifies a person's intertemporal poverty experience. However,
attaches higher weight to longer poverty spells reflecting the idea that continuous enlargement of the size of a poverty block intensifies a person's intertemporal poverty experience. However, ![]() is a violator of the time replication invariance axiom. The authors argued that for looking at poverty differences between two intertemporal distributions with sizes
is a violator of the time replication invariance axiom. The authors argued that for looking at poverty differences between two intertemporal distributions with sizes ![]() and
and ![]() , where
, where ![]() , one can choose a subsample of
, one can choose a subsample of ![]() periods of the second distribution and make the necessary comparison. Their index fails to take into account the act of poverty mitigation. The authors also suggested an aggregate index of intertemporal poverty by considering an average of an increasing strictly convex transformation of
periods of the second distribution and make the necessary comparison. Their index fails to take into account the act of poverty mitigation. The authors also suggested an aggregate index of intertemporal poverty by considering an average of an increasing strictly convex transformation of ![]() values over the entire population.
values over the entire population.
The key factor underlying the Mendola–Busetta path of measuring intertemporal poverty is the “cumulative hardship” property, which requires intensification of intertemporal poverty as periodwise poverty situations become closer even if the postswitch stations of poverty periods are not contiguous. It is weaker than the block monotonicity axiom, which requires augmentation of intertemporal poverty only when postrotated locations of poverty periods are contiguous.
The cumulative hardship postulate is consistent with the Hoy and Zheng (2011, 2015) chronic poverty axiom, which we state next on the space of intertemporal poverty profiles:
- Chronic Poverty: Suppose that there are only two distinct and nonadjacent poverty periods
 in the intertemporal poverty profile
in the intertemporal poverty profile  , where
, where  and
and  . Now, if
. Now, if 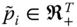 is obtained from
is obtained from 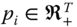 by exchanging temporal locations of these two poverty situations to
by exchanging temporal locations of these two poverty situations to 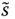 and
and 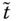 , where
, where 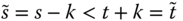 for some
for some 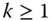 , then
, then 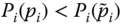 .
.
This statement of the axiom has a minor difference with the Hoy–Zheng formulation since we replace their weak inequality ![]() by the strict inequality
by the strict inequality ![]() . All indices that verify this axiom are members of the class that can be identified under the category “the closeness approach.” The proposals
. All indices that verify this axiom are members of the class that can be identified under the category “the closeness approach.” The proposals ![]() ,
, ![]() , and
, and ![]() are violators of this axiom since in this axiom, it is not unambiguously required that the postswitch locations are contiguous.
are violators of this axiom since in this axiom, it is not unambiguously required that the postswitch locations are contiguous.
The Mendola and Busetta (2012) index of individual intertemporal poverty for determining the extent of poverty in a profile spanning ![]() periods is defined as
periods is defined as
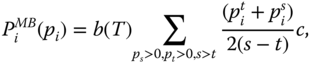
where ![]() is a normalization coefficient and
is a normalization coefficient and ![]() is a decay factor discounting the individual's early period poverty happenings. Although it satisfies the chronic poverty axiom, it is a violator of the decomposability axioms analyzed earlier and the two poverty mitigation axioms.
is a decay factor discounting the individual's early period poverty happenings. Although it satisfies the chronic poverty axiom, it is a violator of the decomposability axioms analyzed earlier and the two poverty mitigation axioms.
Essential to the Hoy and Zheng (2011) closeness-reliant proposal is the chronic poverty axiom. According to these authors, each period of poverty and an individual's entire lifetime are important ingredients of an individual's lifetime poverty. They characterized the following functional form of individual intertemporal poverty index using an axiomatic framework:
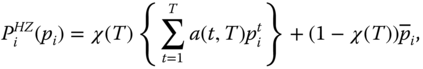
where  , with
, with ![]() being the one-dimensional poverty index;
being the one-dimensional poverty index; ![]() and.
and. ![]() . The term
. The term 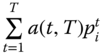 is a weighted average of periodwise poverty experiences of the person, and
is a weighted average of periodwise poverty experiences of the person, and ![]() is the extent of poverty associated with the person's lifetime average income. In the polar case
is the extent of poverty associated with the person's lifetime average income. In the polar case ![]() , intertemporal poverty is represented by the person's deprivation arising from the shortfall of his lifetime average income from the threshold limit. Consequently, poverty situations of different periods do not play any role here. In other words, knowledge of period-by-period poverty extents is not necessary. In contrast, when
, intertemporal poverty is represented by the person's deprivation arising from the shortfall of his lifetime average income from the threshold limit. Consequently, poverty situations of different periods do not play any role here. In other words, knowledge of period-by-period poverty extents is not necessary. In contrast, when ![]() , a recollection period-by-period poverty experience is required to determine the overall intertemporal poverty of the person. Hence, the parameter
, a recollection period-by-period poverty experience is required to determine the overall intertemporal poverty of the person. Hence, the parameter ![]() may be interpreted as representing a “memory factor” in the sense that the extreme cases
may be interpreted as representing a “memory factor” in the sense that the extreme cases ![]() and
and ![]() correspond, respectively, to “perfect recall” and “no recall” of poverty episodes. A value of
correspond, respectively, to “perfect recall” and “no recall” of poverty episodes. A value of ![]() lying between 0 and 1 shows that each term of the across-periods poverty sequence
lying between 0 and 1 shows that each term of the across-periods poverty sequence ![]() and lifetime poverty value
and lifetime poverty value ![]() are decisive factors in the evaluation of individual intertemporal poverty. In this intermediate case, the index upholds the strong poverty mitigation axiom.
are decisive factors in the evaluation of individual intertemporal poverty. In this intermediate case, the index upholds the strong poverty mitigation axiom.
Hoy and Zheng (2011) showed that satisfaction of the early poverty axiom by ![]() requires that
requires that ![]() is a decreasing function of
is a decreasing function of ![]() . The early poverty axiom demands that poverty episodes in early phases of life have more harmful effects on life. Poverty in childhood periods is likely to have detrimental effects on physical and mental conditions of a person later in life. Similarly, verification of the chronic poverty axiom by
. The early poverty axiom demands that poverty episodes in early phases of life have more harmful effects on life. Poverty in childhood periods is likely to have detrimental effects on physical and mental conditions of a person later in life. Similarly, verification of the chronic poverty axiom by ![]() necessitates that
necessitates that ![]() is strictly concave in
is strictly concave in ![]() . Examples of the function
. Examples of the function ![]() that meet these requirements are
that meet these requirements are ![]() and
and ![]() , where
, where ![]() and
and ![]() are constants.
are constants.
As noted by Zheng (2012), the additive structure of ![]() does not enable us to take into account across-periods poverty interactions. To overcome this, Zheng (2012) developed an axiomatic characterization of the following class of gravitational indices of intertemporal poverty
does not enable us to take into account across-periods poverty interactions. To overcome this, Zheng (2012) developed an axiomatic characterization of the following class of gravitational indices of intertemporal poverty
where ![]() is continuous in its arguments, increasing in the first two arguments, decreasing in the third argument,
is continuous in its arguments, increasing in the first two arguments, decreasing in the third argument, ![]() , and
, and ![]() . Zheng (2012) refers to this class as gravitational class since its formulation relies on Newton's Universal Law of Gravitation – “the force is proportional to the product of two masses and inversely proportional to the square of distance between the point masses.”
. Zheng (2012) refers to this class as gravitational class since its formulation relies on Newton's Universal Law of Gravitation – “the force is proportional to the product of two masses and inversely proportional to the square of distance between the point masses.”
Two illustrative examples of the family (5.18) are

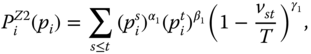
where ![]() , and
, and ![]() are positive constants. As these two examples indicate,
are positive constants. As these two examples indicate, ![]() is increasing in each pair of poverty experiences, and as the gap between any two poverty spells reduces so that
is increasing in each pair of poverty experiences, and as the gap between any two poverty spells reduces so that ![]() decreases,
decreases, ![]() increases.
increases.
5.4 An Exploration of the Counting Approaches to Multidimensional Intertemporal Deprivations
While in the preceding subsection, our scrutiny was restricted to unidimensional variants of the block-approach-contingent multidimensional enquiry, in this section, we scrutinize some alternative proposals for analyzing multidimensional intertemporal deprivations using the counting approach.
The Nicholas and Ray (2011) suggestion for quantifying multidimensional intertemporal deprivation combines the Chakravarty and D'Ambrosio (2006); Bossert et al. (2012), and Gradin et al. (2012) approaches. Essential to this counting-dependent generalization is the number of periods in which a person becomes deprived in different dimensions. In terms of the notation we have introduced in the chapter, this proposal can formally be defined as
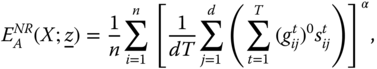
where ![]() , desired to capture the impact of the spread of the deprivation spells, is a nonnegative increasing function of
, desired to capture the impact of the spread of the deprivation spells, is a nonnegative increasing function of ![]() , the length of the deprivation spell to which individual i's deprivation occurrence in dimension
, the length of the deprivation spell to which individual i's deprivation occurrence in dimension ![]() in period
in period ![]() corresponds, and
corresponds, and ![]() is a parameter. For
is a parameter. For ![]() ,
, ![]() becomes the proportion of persons that are deprived in at least one dimension for at least one period. Clearly,
becomes the proportion of persons that are deprived in at least one dimension for at least one period. Clearly, ![]() upholds the multidimensional version of the block monotonicity axiom, stated in terms of number of dimensionwise deprivations of a person across periods. The index may or may not satisfy the time replication invariance principle, although it is population replication invariant. Its transgression of the time replication invariance is evident if we choose
upholds the multidimensional version of the block monotonicity axiom, stated in terms of number of dimensionwise deprivations of a person across periods. The index may or may not satisfy the time replication invariance principle, although it is population replication invariant. Its transgression of the time replication invariance is evident if we choose ![]() , where
, where ![]() is a constant. Consequently, it is not suitable for comparison of intertemporal deprivations across profiles with different lengths of time profiles.
is a constant. Consequently, it is not suitable for comparison of intertemporal deprivations across profiles with different lengths of time profiles.
The concern of Bossert et al. (2014) counting approach is the intertemporal deprivation in material living conditions. Assume that there are ![]() dimensions of materials living conditions. Let us consider a binary variable
dimensions of materials living conditions. Let us consider a binary variable ![]() , where a value of 1 indicates that person
, where a value of 1 indicates that person ![]() is deprived with respect to dimension
is deprived with respect to dimension ![]() in period
in period ![]() , whereas a value of 0 identifies him as nondeprived in the dimension–period pair
, whereas a value of 0 identifies him as nondeprived in the dimension–period pair ![]() . Then person i's material deprivation in period
. Then person i's material deprivation in period ![]() is given by
is given by 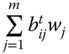 , where
, where ![]() is a positive weight assigned to dimension
is a positive weight assigned to dimension ![]() . A simple index of material deprivation for the person, when we follow the Foster (2009)-type aggregation rule, is given by
. A simple index of material deprivation for the person, when we follow the Foster (2009)-type aggregation rule, is given by ![]() , the average value of periodwise deprivations. Formally,
, the average value of periodwise deprivations. Formally,
for all ![]() . The corresponding aggregate intertemporal material deprivation
. The corresponding aggregate intertemporal material deprivation ![]() is the average of intertemporal material deprivation values across persons. More precisely, for all
is the average of intertemporal material deprivation values across persons. More precisely, for all ![]() ,
,
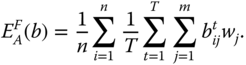
In order to discuss adaption of the Bossert et al. (2012) approach to the current setting, we say that person ![]() is deprived in period
is deprived in period ![]() if and only if he is deprived with respect to at least one dimension in the period. This is the same as the requirement that
if and only if he is deprived with respect to at least one dimension in the period. This is the same as the requirement that  . The sum
. The sum 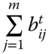 is the deprivation score of person
is the deprivation score of person ![]() in period
in period ![]() . In order to be identified as deprived in a period, the concerned person's deprivation score in the period must be at least 1. Equivalently, we are following here the union method of identification of deprivation. Given that person
. In order to be identified as deprived in a period, the concerned person's deprivation score in the period must be at least 1. Equivalently, we are following here the union method of identification of deprivation. Given that person ![]() is deprived in period
is deprived in period ![]() in
in ![]() , let
, let ![]() be the maximal number of consecutive periods including
be the maximal number of consecutive periods including ![]() in which person is deprived, where
in which person is deprived, where ![]() is arbitrary. Similarly, if person
is arbitrary. Similarly, if person ![]() is nondeprived in period
is nondeprived in period ![]() in
in ![]() , let
, let ![]() stand for the maximal number of consecutive periods including
stand for the maximal number of consecutive periods including ![]() in which person is nondeprived (see Bossert et al., 2014). Thus, if
in which person is nondeprived (see Bossert et al., 2014). Thus, if ![]() and the person is deprived only in periods 2 and 3, then
and the person is deprived only in periods 2 and 3, then ![]() ,
, ![]() and
and ![]() . Bossert et al. (2014) suggested the use of the following as a numerical representation of individual material deprivation
. Bossert et al. (2014) suggested the use of the following as a numerical representation of individual material deprivation

where ![]() is arbitrary. According to these authors, the aggregate intertemporal material deprivation can be ascertained, for any arbitrary
is arbitrary. According to these authors, the aggregate intertemporal material deprivation can be ascertained, for any arbitrary ![]() , by
, by
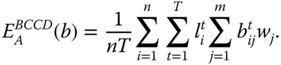
This population replication invariant aggregate intertemporal deprivation measure endorses the time replication invariance principle as well.
Finally, we describe how the Hojman and Kast (2009) recommendation can be redesigned in the context of material deprivation. At the individual level, intertemporal deprivation has two constituents; the first indicates the quantity of individual intertemporal material deprivation, as determined by (5.22), and the second represents changes in individual intertemporal material deprivation over time, measured by weighted sum of upward and downward shifts of individual deprivation over time. To understand this, consider two situations ![]() and
and ![]() with
with ![]() , where in the former, the person is deprived in periods 2 and 3, whereas in the latter, he is deprived in periods 1 and 3. The Hojman–Kast approach demands that
, where in the former, the person is deprived in periods 2 and 3, whereas in the latter, he is deprived in periods 1 and 3. The Hojman–Kast approach demands that ![]() should be regarded as more intertemporally deprived than
should be regarded as more intertemporally deprived than ![]() . The individual material deprivation levels are the same in the two situations. In the former, there is only one poverty production in the movement from period 1 to period 2. In the latter, there is one poverty ruination in the step from period 1 to period 2, which is then followed by a single poverty formation in the move from period 2 to period 3. This expresses the view that poverty formation (destruction) takes place under an increase (a reduction) in deprivation.
. The individual material deprivation levels are the same in the two situations. In the former, there is only one poverty production in the movement from period 1 to period 2. In the latter, there is one poverty ruination in the step from period 1 to period 2, which is then followed by a single poverty formation in the move from period 2 to period 3. This expresses the view that poverty formation (destruction) takes place under an increase (a reduction) in deprivation.
To formalize the aforementioned discussion analytically, for any arbitrary ![]() and
and ![]() , we introduce two indicator functions, formally defined as
, we introduce two indicator functions, formally defined as
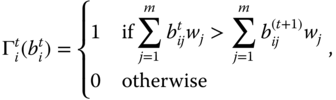
and
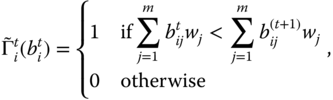
for all ![]() . They are desired to seize, respectively, the gains (reductions in individual material deprivation) and losses (enhancement of individual material deprivation).
. They are desired to seize, respectively, the gains (reductions in individual material deprivation) and losses (enhancement of individual material deprivation).
Then for any individual ![]() , intertemporal material deprivation, in the Hojman–Kast framework, is given by
, intertemporal material deprivation, in the Hojman–Kast framework, is given by
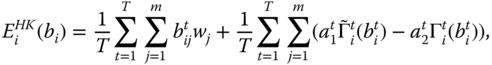
where ![]() is arbitrary, and
is arbitrary, and ![]() and
and ![]() are positive constants such that
are positive constants such that ![]() for all
for all ![]() . If the inequality
. If the inequality ![]() holds, then losses are assigned higher weights than gains in the aggregation. If
holds, then losses are assigned higher weights than gains in the aggregation. If ![]() , then they get equal importance; an increase in deprivation can be exactly matched by a reduction of the same amount.
, then they get equal importance; an increase in deprivation can be exactly matched by a reduction of the same amount.
Aggregate intertemporal deprivation in the Hojman–Kast framework is determined by ![]() . Formally, for all
. Formally, for all ![]() ,
,
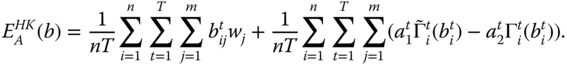
One common feature of the counting-dependent proposals investigated in this section is that they apply to both ratio-scale and ordinal dimensions of well-being.
5.5 The Multidimensional Duration Approach
Because of close connection between one- and multidimensional duration propositions for poverty measurement, it will be rewarding to analyze some one-dimensional submissions briefly. In view of this, our organization of this section is divided into several subsections.
5.5.1 A Review of One-Dimensional Duration-Reliant Offers
Recall the notation we have introduced in Section 5.3.3. We denote individual i's censored income in period ![]() by
by ![]() and the time-invariant income poverty line by
and the time-invariant income poverty line by ![]() , where
, where ![]() and
and ![]() . The income deprivation indicator of person
. The income deprivation indicator of person ![]() in period
in period ![]() is
is ![]() . The duration approach identifies a person as chronically income poor (chronically poor, for short), if he remains in income poverty for at least a certain fraction of time periods
. The duration approach identifies a person as chronically income poor (chronically poor, for short), if he remains in income poverty for at least a certain fraction of time periods ![]() . Equivalently, the person is chronically poor, by this method of identification, if he becomes income deprived in at least
. Equivalently, the person is chronically poor, by this method of identification, if he becomes income deprived in at least ![]() periods, where
periods, where ![]() , that is,
, that is, ![]() is the minimum number of periods for which
is the minimum number of periods for which ![]() holds. It should be clear that the value of
holds. It should be clear that the value of ![]() is unique. For instance, if we have observations on achievements for 11 periods and
is unique. For instance, if we have observations on achievements for 11 periods and ![]() , then
, then ![]() .
.
We refer to ![]() as the duration threshold. Several suggestions have been made in the literature concerning the choice of
as the duration threshold. Several suggestions have been made in the literature concerning the choice of ![]() . For instance, according to Gaiha and Deolikar (1993), those families with incomes below the poverty line in at least five out of nine periods of observations can be taken as chronically poor. Hulme and Shepherd (2003) argued that the necessary condition for a person to be identified as suffering from chronic capability deprivation is poverty experience for at least five successive years (see Hoy and Zheng, 2015, for further discussion). However, our definition of chronic poverty does not require poverty experiences in consecutive periods. Unless specified, we will assume that
. For instance, according to Gaiha and Deolikar (1993), those families with incomes below the poverty line in at least five out of nine periods of observations can be taken as chronically poor. Hulme and Shepherd (2003) argued that the necessary condition for a person to be identified as suffering from chronic capability deprivation is poverty experience for at least five successive years (see Hoy and Zheng, 2015, for further discussion). However, our definition of chronic poverty does not require poverty experiences in consecutive periods. Unless specified, we will assume that ![]() is given.
is given.
Let ![]() be a panel of income distributions of
be a panel of income distributions of ![]() persons over
persons over ![]() periods. The tth column of the panel gives the distribution of income among
periods. The tth column of the panel gives the distribution of income among ![]() persons in period
persons in period ![]() . Similarly, the ith row of the panel shows person i's incomes in
. Similarly, the ith row of the panel shows person i's incomes in ![]() periods. Let
periods. Let ![]() be the set of chronically poor persons in
be the set of chronically poor persons in ![]() . In other words,
. In other words, ![]() is the set of all the persons who remain in poverty for at least
is the set of all the persons who remain in poverty for at least ![]() periods of time. Then
periods of time. Then ![]() , the cardinality of the set
, the cardinality of the set ![]() , gives the number of chronically poor persons in
, gives the number of chronically poor persons in ![]() . The fraction
. The fraction ![]() is the chronic head-count ratio, the proportion of persons that are chronically poor in
is the chronic head-count ratio, the proportion of persons that are chronically poor in ![]() .
.
The chronic income poverty index suggested by Foster (2009) is defined as
where ![]() is a parameter. We can rewrite (5.30) as
is a parameter. We can rewrite (5.30) as 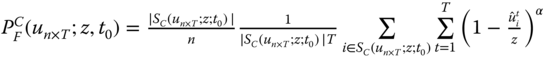 , the product of the chronic head-count ratio and the average of the transformed deprivations
, the product of the chronic head-count ratio and the average of the transformed deprivations ![]() of the chronically poor across all periods. As Foster (2009) mentioned,
of the chronically poor across all periods. As Foster (2009) mentioned, ![]() satisfies several useful properties. For
satisfies several useful properties. For ![]() , the index becomes the duration-adjusted head-count ratio
, the index becomes the duration-adjusted head-count ratio ![]() , where
, where ![]() is the average duration of poverty among the chronically poor, given by
is the average duration of poverty among the chronically poor, given by  .
.
According to Jalan and Ravallion (1998), a person is regarded as chronically poor if the mean of his periodwise incomes falls below the poverty line. Let ![]() be the panel of income distributions in which for any
be the panel of income distributions in which for any ![]() ,
, ![]() is replaced by
is replaced by ![]() for all
for all ![]() , where
, where 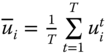 is the average income of person
is the average income of person ![]() across
across ![]() periods. In other words,
periods. In other words, ![]() is obtained from
is obtained from ![]() by replacing the entries in the ith row by the common number
by replacing the entries in the ith row by the common number ![]() , for all
, for all ![]() .
.
The Jalan–Ravallion index of chronic income poverty, ![]() , can then be obtained by aggregating the squared deprivations
, can then be obtained by aggregating the squared deprivations ![]() of all chronically poor persons in the smoothed panel
of all chronically poor persons in the smoothed panel ![]() . Formally,
. Formally,
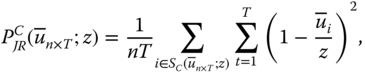
where the set ![]() of chronically poor persons now consists of all those persons whose average incomes over the entire length of the period profile
of chronically poor persons now consists of all those persons whose average incomes over the entire length of the period profile ![]() fall below the poverty line. Evidently, in this case, the chronic poverty identification problem is a one-period issue: if the mean income of a person over all the periods is below the poverty threshold, then he is chronically poor, otherwise not. This analysis clearly shows that, given the one-period notion of identification of the chronically poor, the Jalan–Ravallion index can be calculated using the type of aggregation invoked in Foster (2009), under the additional assumption that
fall below the poverty line. Evidently, in this case, the chronic poverty identification problem is a one-period issue: if the mean income of a person over all the periods is below the poverty threshold, then he is chronically poor, otherwise not. This analysis clearly shows that, given the one-period notion of identification of the chronically poor, the Jalan–Ravallion index can be calculated using the type of aggregation invoked in Foster (2009), under the additional assumption that ![]() .
.
The Foster (2009) approach can, in fact, be extended to the entire family of subgroup-decomposable income poverty indices. The general ditto of ![]() can be defined as
can be defined as
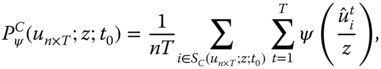
where ![]() is continuous, decreasing, and strictly convex. For
is continuous, decreasing, and strictly convex. For ![]() becomes Foster's (2009) proposal. Alternatively, if we choose
becomes Foster's (2009) proposal. Alternatively, if we choose ![]() , then
, then ![]() becomes a chronic poverty translation of the Chakravarty (1983) income poverty index (see Chakravarty, 2009). We can also apply the Jalan–Ravallion identification criterion to
becomes a chronic poverty translation of the Chakravarty (1983) income poverty index (see Chakravarty, 2009). We can also apply the Jalan–Ravallion identification criterion to ![]() to get variants of
to get variants of ![]() .
.
5.5.2 Axioms for a Chronic Multidimensional Poverty Quantifier
Throughout this and the next two subsections, we follow the notation adopted in Section 5.2. Given a well-defined method of identification of the multidimensionally poor in each period, the duration approach identifies a person as chronic multidimensionally poor if he remains in poverty for some exogenously given ![]() periods of time. As before, we adopt the union method of identification of poor.
periods of time. As before, we adopt the union method of identification of poor.
This duration-dependent approach involves a two-step identification problem. The first step requires identification of the multidimensionally poor persons in each period. The exercise at the second step is to identify the chronically poor among these multidimensionally poor persons in different periods. Recall our notation that ![]() stands for the set of all
stands for the set of all ![]() dimensional intertemporal distribution matrices when the population size is
dimensional intertemporal distribution matrices when the population size is ![]() , and
, and ![]() denotes the set of such matrices for all possible population sizes (assuming that
denotes the set of such matrices for all possible population sizes (assuming that ![]() and
and ![]() are given).
are given).
For all ![]() ,
, ![]() , let
, let ![]() be the set of all persons who are chronically poor in
be the set of all persons who are chronically poor in ![]() , that is, the set of all persons who are counted as multidimensionally poor for at least
, that is, the set of all persons who are counted as multidimensionally poor for at least ![]() periods in the intertemporal distribution matrix
periods in the intertemporal distribution matrix ![]() . Formally,
. Formally, 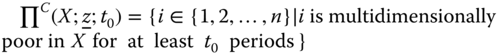 . We denote the number of chronically poor persons in
. We denote the number of chronically poor persons in ![]() by
by ![]() . A multidimensional chronic poverty index in this framework can be written as a function
. A multidimensional chronic poverty index in this framework can be written as a function ![]() , where
, where ![]() .
.
As an illustrative example assume that ![]() and
and ![]() . The social matrices for the four periods are
. The social matrices for the four periods are  ,
,  ,
,  ,
,  , and the vector of common poverty cutoffs is
, and the vector of common poverty cutoffs is ![]() . The entries in the first row of matrix
. The entries in the first row of matrix ![]() indicate person 1's achievements in period
indicate person 1's achievements in period ![]() , where
, where ![]() . Similarly, figures in the other rows of the four matrices can be explained. By the union method of identification of the poor, while person
. Similarly, figures in the other rows of the four matrices can be explained. By the union method of identification of the poor, while person ![]() is poor in all the four periods, person 3 is poor only in period 4. On the other hand, person 1 is poor in periods 1 and 4. Assume that the duration threshold
is poor in all the four periods, person 3 is poor only in period 4. On the other hand, person 1 is poor in periods 1 and 4. Assume that the duration threshold ![]() . Then although persons 1 and 2 are chronically poor, person 3 is not so. It may be worthy to note that by the intersection identification procedure, persons 1 and 2 are poor in period 1. However, nobody is chronically poor by this notion of identification.
. Then although persons 1 and 2 are chronically poor, person 3 is not so. It may be worthy to note that by the intersection identification procedure, persons 1 and 2 are poor in period 1. However, nobody is chronically poor by this notion of identification.
The corresponding intertemporal social matrix with 12 rows and 2 columns, denoted by ![]() , is now obtained by placing the rows of
, is now obtained by placing the rows of ![]() , where
, where ![]() , contiguously as rows of
, contiguously as rows of ![]() from above to below. In consequence, the entries in rows 1, 4, 7, and 10 of
from above to below. In consequence, the entries in rows 1, 4, 7, and 10 of ![]() quantify person 1's achievements in periods 1, 2, 3, and 4, respectively, in the two dimensions. Other rows of
quantify person 1's achievements in periods 1, 2, 3, and 4, respectively, in the two dimensions. Other rows of ![]() can be explained analogously. The number
can be explained analogously. The number ![]() here is 2 and the corresponding set consists of persons 1 and 2. We will use the matrix
here is 2 and the corresponding set consists of persons 1 and 2. We will use the matrix ![]() to illustrate the axioms defined for a general index.
to illustrate the axioms defined for a general index.
The explicit representation of the intertemporal social matrix ![]() , associated with our example, is given by
, associated with our example, is given by
The following axioms can now be stated for a general multidimensional chronic poverty index ![]() . Of these, the first two axioms parallel the Bourguignon–Chakravarty focus axioms. The four axioms that follow these are directly adapted to the chronic poverty setup from the literature. Each of the next five axioms is a multidimensional version of Foster's (2009) corresponding unidimensional postulate. They are followed by a chronic twin of the Alkire and Foster (2011) dimensional monotonicity axiom. The remaining postulates are chronic reproductions of the corresponding properties proposed in Chapter 3.
. Of these, the first two axioms parallel the Bourguignon–Chakravarty focus axioms. The four axioms that follow these are directly adapted to the chronic poverty setup from the literature. Each of the next five axioms is a multidimensional version of Foster's (2009) corresponding unidimensional postulate. They are followed by a chronic twin of the Alkire and Foster (2011) dimensional monotonicity axiom. The remaining postulates are chronic reproductions of the corresponding properties proposed in Chapter 3.
- Chronic Weak Focus: For all
 ,
,  ,
, 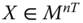 , suppose that person
, suppose that person 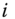 is not chronically poor in
is not chronically poor in 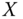 , and
, and 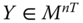 is obtained from
is obtained from 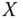 as follows:
as follows:  for a triplet
for a triplet 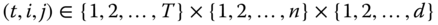 , where
, where  and
and  for all triplets
for all triplets  . Then
. Then 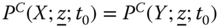 .
.
According to this axiom, an increase in the achievement in a dimension of a chronically nonpoor person in any period does not change the value of the poverty index. That is, the poverty index is independent of the achievements of all persons who are chronically nonpoor. In the matrix ![]() , person 3 is chronically nonpoor. An increase in his achievement in dimension 1 in period 4 from 3 to 4 reduces his poverty level in the period but does not affect his chronic poverty status.
, person 3 is chronically nonpoor. An increase in his achievement in dimension 1 in period 4 from 3 to 4 reduces his poverty level in the period but does not affect his chronic poverty status.
- Chronic Strong Focus: For all
 ,
,  ,
,  , suppose that
, suppose that 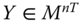 is obtained from
is obtained from 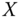 as follows:
as follows: 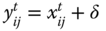 for a triplet
for a triplet 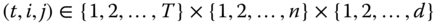 , where
, where 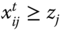 ,
, 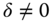 is such that
is such that 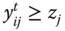 and
and 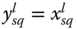 for all triplets
for all triplets 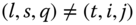 . Then
. Then 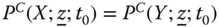 .
.
In this case, person ![]() may or may not be chronically poor. In either case, if his achievement in a nondeprived dimension
may or may not be chronically poor. In either case, if his achievement in a nondeprived dimension ![]() in some period
in some period ![]() increases, the poverty index remains unaffected. If person
increases, the poverty index remains unaffected. If person ![]() is chronically nonpoor, then the strong focus axiom reduces to its weak version. In
is chronically nonpoor, then the strong focus axiom reduces to its weak version. In ![]() person 1, who is chronically poor, is nondeprived in dimension 1 in period 3. His chronic poverty position remains unaltered, if this achievement increases from 9 to any higher level.
person 1, who is chronically poor, is nondeprived in dimension 1 in period 3. His chronic poverty position remains unaltered, if this achievement increases from 9 to any higher level.
- Period-Restricted Anonymity: For all
 ,
, 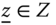 ,
, 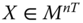 , suppose that
, suppose that 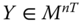 is obtained from
is obtained from 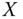 as follows:
as follows: 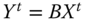 , where
, where  is any
is any  permutation matrix,
permutation matrix,  is arbitrary, and
is arbitrary, and 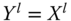 for all
for all  . Then
. Then 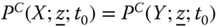 .
.
This postulate demands that a rearrangement of the rows of the distribution matrix in any period, keeping the distribution matrices in all other periods unchanged, does not affect chronic poverty. Thus, in our social matrix ![]() , if we exchange only the first two rows, that is, the first row now becomes (2,2), whereas the second row is given by (3,3) and all other rows remain unaltered, then the chronic poverty levels of the new intertemporal matrix and the original matrix
, if we exchange only the first two rows, that is, the first row now becomes (2,2), whereas the second row is given by (3,3) and all other rows remain unaltered, then the chronic poverty levels of the new intertemporal matrix and the original matrix ![]() are the same.
are the same.
The next axiom becomes helpful in cross-population comparisons of chronic poverty.
- Chronic Population Replication Invariance: For all
 ,
, 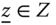 ,
, 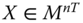 ,
, 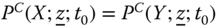 ,where
,where 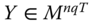 is the
is the 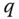 -fold replication of
-fold replication of 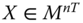 ,
, 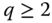 being a positive integer, that is, in
being a positive integer, that is, in 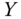 each row of
each row of 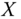 appears
appears 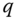 times.
times.
This axiom ensures that chronic poverty is measured in per-capita terms. Consequently, comparison of chronic poverty levels of two societies whose population sizes are different becomes possible. If the intertemporal matrix ![]() is replicated twice, in the resulting matrix
is replicated twice, in the resulting matrix ![]() , each row of
, each row of ![]() appears twice and the postulate requires that
appears twice and the postulate requires that ![]() .
.
- Chronic Strong Ratio-Scale Invariance: For all
 ,
,  ,
, 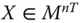 , suppose that
, suppose that 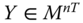 is obtained from
is obtained from 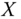 as follows: for all
as follows: for all  ,
, 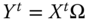 , where
, where  is any
is any 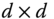 positive diagonal matrix. Then
positive diagonal matrix. Then 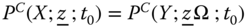 .
.
According to this axiom, if all the achievements in any dimension in all the periods and the corresponding threshold limit are subjected to the same equiproportionate change, then chronic poverty remains unchanged. A weaker form of this axiom, chronic ratio-scale invariance, demands that the proportionality factor is the same across the dimensions in all the periods. For four ![]() matrices associated with
matrices associated with ![]() , define
, define ![]() by
by ![]() and let the corresponding intertemporal matrix be
and let the corresponding intertemporal matrix be ![]() , where
, where ![]() . Then the strong invariance postulate demands that
. Then the strong invariance postulate demands that ![]() .
.
The postulate, subgroup decomposability, establishes consistency between local and global evaluations of chronic poverty in a specific way.
- Chronic Subgroup Decomposability: For all
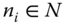 ,
, 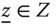 ,
,  ,
,
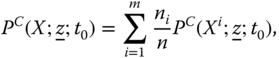
where
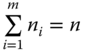 and
and 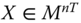 is obtained by placing the matrices
is obtained by placing the matrices 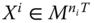 from above to below for
from above to below for  , where
, where 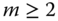 .
.
The formulation of the axiom indicates that for any division of the population into two or more nonoverlapping subgroups, aggregate chronic poverty is the population share weighted average of its subgroup brothers. Since the numbering of the matrices ![]() is arbitrary, the arrangement of the rows of
is arbitrary, the arrangement of the rows of ![]() is also arbitrary. Under an alternative numbering of the matrices, the positioning of the rows of
is also arbitrary. Under an alternative numbering of the matrices, the positioning of the rows of ![]() will be in the manner consistent with the numbering. Suppose that a reduction in chronic poverty in one subgroup, say, as a result of implementation of some targeted poverty alleviation policy, takes place. Then, under the ceteris paribus condition that poverty extents remain fixed in all other subgroups, this shrinkage in the particular subgroup's poverty must lead to a reduction in overall chronic poverty.
will be in the manner consistent with the numbering. Suppose that a reduction in chronic poverty in one subgroup, say, as a result of implementation of some targeted poverty alleviation policy, takes place. Then, under the ceteris paribus condition that poverty extents remain fixed in all other subgroups, this shrinkage in the particular subgroup's poverty must lead to a reduction in overall chronic poverty.
To illustrate this axiom, suppose that the three individuals we have considered in our example have been partitioned into two subgroups ![]() and
and ![]() , with respect to their regions of residence, say, where
, with respect to their regions of residence, say, where ![]() consists of person 1 and the other subgroup consists of persons 2 and 3. Then the axiom claims that
consists of person 1 and the other subgroup consists of persons 2 and 3. Then the axiom claims that ![]() ,where
,where ![]() and
and ![]() denote the intertemporal social matrices associated with the subgroups
denote the intertemporal social matrices associated with the subgroups ![]() and
and ![]() , respectively.3
, respectively.3
- Time Anonymity: For all
 ,
, 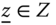 ,
, 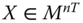 , if the sequence of matrices
, if the sequence of matrices 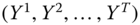 is obtained by a reordering of the sequence of period-by-period matrices
is obtained by a reordering of the sequence of period-by-period matrices 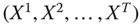 under
under 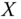 , then
, then 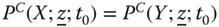 .
.
This desideratum claims that an interchange of positions two periodwise distribution matrices in the sequence of timings ![]() does not affect chronic poverty. Consequently, if the distribution matrix that appears in period
does not affect chronic poverty. Consequently, if the distribution matrix that appears in period ![]() under
under ![]() appears in period
appears in period ![]() under
under ![]() , and for the remaining periods the distribution matrices under
, and for the remaining periods the distribution matrices under ![]() and
and ![]() are the same, then chronic poverty in
are the same, then chronic poverty in ![]() will be equal to that in
will be equal to that in ![]() . In the illustrative matrix
. In the illustrative matrix ![]() , suppose that the positions of
, suppose that the positions of ![]() and
and ![]() are interchanged, and the positions of
are interchanged, and the positions of ![]() and
and ![]() are kept unchanged. If we denote the resulting intertemporal distribution matrix by
are kept unchanged. If we denote the resulting intertemporal distribution matrix by ![]() , then the time anonymity axiom asserts that
, then the time anonymity axiom asserts that ![]() .
.
Clearly, an intertemporal poverty index that verifies the block monotonicity axiom so that higher weights are assigned to poverty blocks with larger sizes is a violator of this postulate. Evidently, the time anonymity axiom does not make any distinction between two situations with the same number of poverty spells where in the former, the poverty spells appear consecutively, but in the latter, they are separated by at least one zero-poverty spell. It treats the profiles ![]() and
and ![]() as identically intertemporally poor. But the block approach regards the latter as poorer than the former because in the former, the lengths of the two poverty blocks are 3 and 1, respectively, whereas in the latter, the single poverty block has a length of 4. The time anonymity axiom brings out a major distinguishing feature between the two approaches. An index that agrees with this axiom also fails to meet the Hoy–Zheng chronic poverty axiom.
as identically intertemporally poor. But the block approach regards the latter as poorer than the former because in the former, the lengths of the two poverty blocks are 3 and 1, respectively, whereas in the latter, the single poverty block has a length of 4. The time anonymity axiom brings out a major distinguishing feature between the two approaches. An index that agrees with this axiom also fails to meet the Hoy–Zheng chronic poverty axiom.
- Chronic Monotonicity: For all
 ,
, 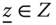 ,
, 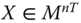 , suppose that the matrix
, suppose that the matrix 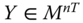 is obtained from
is obtained from 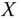 as follows:
as follows: 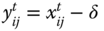 for a triplet
for a triplet 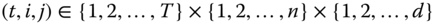 , where person
, where person 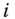 is chronically poor,
is chronically poor, 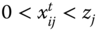 ,
, 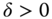 , and
, and 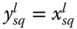 for all triplets
for all triplets 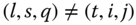 . Then
. Then 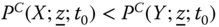 .
.
If achievement in a deprived dimension of a chronically poor person reduces, then a natural requirement is that poverty should go up. This is what the chronic monotonicity axiom demands. In ![]() , if achievement in dimension 2 in period 1 of person 2, a chronically poor person, goes down from 2 to 1, then poverty should indicate an upward trend.
, if achievement in dimension 2 in period 1 of person 2, a chronically poor person, goes down from 2 to 1, then poverty should indicate an upward trend.
- Time Monotonicity: For all
 ,
,  ,
, 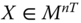 , suppose that person
, suppose that person 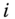 is chronically poor in
is chronically poor in 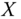 and
and 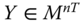 is related to
is related to 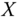 as follows:
as follows:  for a triplet
for a triplet  , and
, and  for all triplets
for all triplets 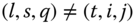 . Then
. Then 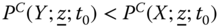 .
.
Poverty should go up under an increase in the number of periods of deprivation suffered by a chronically poor person in some dimension. Our time monotonicity axiom states this necessity. In the matrix ![]() , person 1 is chronically poor but nondeprived in dimension 1 in period 2. If this achievement gets slashed from 7 to 4, then his duration of deprivation in the dimension increases from 2 to 3. Hence, chronic poverty should go up.
, person 1 is chronically poor but nondeprived in dimension 1 in period 2. If this achievement gets slashed from 7 to 4, then his duration of deprivation in the dimension increases from 2 to 3. Hence, chronic poverty should go up.
- Duration Monotonicity: For all
 ,
, 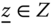 ,
, 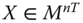 , given the duration threshold
, given the duration threshold 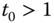 , if
, if 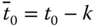 , where
, where 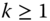 is an integer such that
is an integer such that 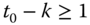 , then
, then 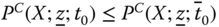 .
.
If the duration threshold goes down, then there is a possibility that some newer persons who were not chronically poor originally become chronic poverty stricken now. Hence, we are adding some new chronically poor persons without changing the statuses of the existing poor. Consequently, chronic poverty should not go down under a reduction in the duration threshold. In our social matrix ![]() , suppose that
, suppose that ![]() reduces from 2 to 1, then all the three persons become chronically poor, whereas for
reduces from 2 to 1, then all the three persons become chronically poor, whereas for ![]() , only two persons are chronically poor. Accordingly,
, only two persons are chronically poor. Accordingly, ![]() .
.
None of the axioms stated so far was concerned with the inequality among the chronically poor. In the case of cross-sectional multidimensional poverty, if there is a Pigou–Dalton bundle of transfers of achievements, in deprived dimensions, from a poorer poor to a richer poor that do not change their statuses, then the posttransfer social distribution should have higher multidimensional poverty than the pretransfer one.
Given ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , suppose that in all the dimensions of
, suppose that in all the dimensions of ![]() , the common set of deprived dimensions of the chronically poor persons
, the common set of deprived dimensions of the chronically poor persons ![]() and
and ![]() in period
in period ![]() , the former has higher deprivations than the latter. More precisely, for all
, the former has higher deprivations than the latter. More precisely, for all ![]() ,
, ![]() , where
, where ![]() ,with
,with ![]() and
and ![]() being arbitrary. Assume that
being arbitrary. Assume that ![]() is nonempty.
is nonempty.
We have assumed at the outset that the same set of deprived dimensions of the chronically poor persons ![]() and
and ![]() in period
in period ![]() , with the additional characteristic that
, with the additional characteristic that ![]() has higher deprivations than
has higher deprivations than ![]() , is nonempty. Condition (i) of Definition 5.4 demands that all individuals except persons
, is nonempty. Condition (i) of Definition 5.4 demands that all individuals except persons ![]() and
and ![]() have identical achievements in all the dimensions in both
have identical achievements in all the dimensions in both ![]() and
and ![]() . Part (a) of condition (ii) says that each of persons
. Part (a) of condition (ii) says that each of persons ![]() and
and ![]() has identical achievements in all nondeprived dimensions in period
has identical achievements in all nondeprived dimensions in period ![]() . According to part (b) of condition (ii), we get
. According to part (b) of condition (ii), we get ![]() and
and ![]() by dimensionwise regressive transfers of achievements from person
by dimensionwise regressive transfers of achievements from person ![]() to person
to person ![]() in their common set of deprived dimensions, where the size of the transfer is nonnegative for any dimension in the set, and for at least one deprived dimension, the transfer has a positive size. In part (b) of condition (ii), it is ensured that the size of the transfer in any dimension does not allow the recipient to be nondeprived in the dimension. Finally, condition (iii) of the definition requires that in all the periods other than
in their common set of deprived dimensions, where the size of the transfer is nonnegative for any dimension in the set, and for at least one deprived dimension, the transfer has a positive size. In part (b) of condition (ii), it is ensured that the size of the transfer in any dimension does not allow the recipient to be nondeprived in the dimension. Finally, condition (iii) of the definition requires that in all the periods other than ![]() , social matrices in both
, social matrices in both ![]() and
and ![]() are the same. Since for any
are the same. Since for any ![]() ,
, ![]() cannot exceed
cannot exceed ![]() , it is confirmed that
, it is confirmed that ![]() .
.
This bundle of regressive transfers increases inequality in the achievement distributions among the poor. The following may be regarded as the chronic poverty ditto of this property:
- Chronic Transfer: For all
 ,
,  ,
, 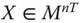 ,
, 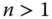 , if
, if 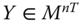 is obtained from
is obtained from 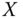 by a Pigou–Dalton bundle of regressive transfers between two chronically poor persons, then
by a Pigou–Dalton bundle of regressive transfers between two chronically poor persons, then 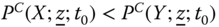 .
.
In the matrix ![]() , persons 1 and 2 are chronically poor, and person 2 has higher deprivations than person 1 in both the dimensions in period 1. Then a Pigou–Dalton bundle of regressive transfers consisting of sizes of 1 and 0.5 units of achievements in dimensions 1 and 2, respectively, from person 2 to person 1 will raise chronic poverty.
, persons 1 and 2 are chronically poor, and person 2 has higher deprivations than person 1 in both the dimensions in period 1. Then a Pigou–Dalton bundle of regressive transfers consisting of sizes of 1 and 0.5 units of achievements in dimensions 1 and 2, respectively, from person 2 to person 1 will raise chronic poverty.
- Chronic Dimensional Monotonicity: For all
 ,
,  ,
, 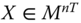 , suppose that person
, suppose that person  is chronically poor in
is chronically poor in  , and
, and  is related to
is related to  as follows:
as follows: 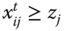 ,
, 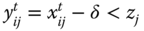 for a triplet
for a triplet  , and
, and 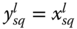 for all triplets
for all triplets 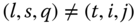 , where
, where  . Then
. Then 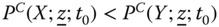 .
.
This property insists that chronic poverty goes up when a chronically poor person who is nondeprived in a dimension in some period becomes deprived in the dimension in that period. In the distribution matrix ![]() , person 1 is chronically poor but nondeprived in dimension 2 in period 4. If this achievement falls down to a level below the threshold limit, say from 5 to 3, then the person becomes deprived in dimension 2 in period 4. This expansion in the number of deprived dimensions of the chronically poor, person 1, should augment chronic poverty.
, person 1 is chronically poor but nondeprived in dimension 2 in period 4. If this achievement falls down to a level below the threshold limit, say from 5 to 3, then the person becomes deprived in dimension 2 in period 4. This expansion in the number of deprived dimensions of the chronically poor, person 1, should augment chronic poverty.
The next axiom is concerning association between dimensions of well-being. Consequently, it represents a unique feature of multidimensional chronic poverty analysis.
- Definition: Suppose that persons
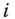 and
and 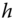 are chronically poor in the intertemporal social matrix
are chronically poor in the intertemporal social matrix 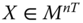 . Assume also that they are deprived in dimensions
. Assume also that they are deprived in dimensions 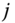 and
and 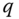 in some period
in some period 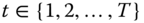 and (i)
and (i) 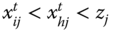 , (ii)
, (ii) 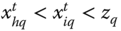 , (iii)
, (iii)  for all
for all 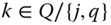 . Next, suppose that
. Next, suppose that 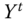 is obtained from
is obtained from 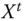 as follows: (iv)
as follows: (iv) 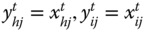 , (v)
, (v) 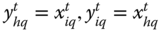 , (vi)
, (vi) 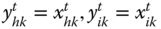 for all
for all  , and (vii)
, and (vii) 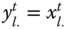 for all
for all  , where
, where 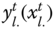 is the lth row of
is the lth row of 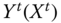 . If
. If 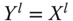 for all
for all 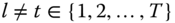 , then we say that
, then we say that 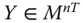 is obtained from
is obtained from 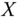 by a correlation-increasing switch between two chronically poor persons. Conversely, it can be said that
by a correlation-increasing switch between two chronically poor persons. Conversely, it can be said that 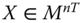 is derived from
is derived from 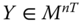 by a correlation-decreasing switch between two persons who are chronically poor.
by a correlation-decreasing switch between two persons who are chronically poor.
Conditions (i) and (ii) of the aforementioned definition state that in ![]() , person
, person ![]() has lower achievement than person
has lower achievement than person ![]() in dimension
in dimension ![]() , and the reverse inequality holds in dimension
, and the reverse inequality holds in dimension ![]() . According to condition (iii), in all other dimensions, achievements of person
. According to condition (iii), in all other dimensions, achievements of person ![]() are at least as large as those of person
are at least as large as those of person ![]() . Condition (iv) formally states that in period
. Condition (iv) formally states that in period ![]() , a switch between achievements of persons
, a switch between achievements of persons ![]() and
and ![]() in dimension
in dimension ![]() has been performed. Conditions (iv) and (v) jointly ensure that in the postswitch situation, person
has been performed. Conditions (iv) and (v) jointly ensure that in the postswitch situation, person ![]() has higher achievements than person
has higher achievements than person ![]() in both the dimensions
in both the dimensions ![]() and
and ![]() in the period. This swap of achievements between persons
in the period. This swap of achievements between persons ![]() and
and ![]() increases the correlation between the dimensional achievements. Note that in
increases the correlation between the dimensional achievements. Note that in ![]() in no dimension, person
in no dimension, person ![]() has higher achievement than person
has higher achievement than person ![]() .
.
- Increasing Chronic Poverty under Correlation-Increasing Switch: For all
 ,
, 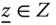 ,
, 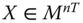 ,
, 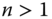 , if
, if 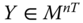 is obtained from
is obtained from 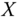 by a correlation-increasing switch between two chronically poor persons, then
by a correlation-increasing switch between two chronically poor persons, then  given that the two dimensions affected by the switch are substitutes.
given that the two dimensions affected by the switch are substitutes.
Similarly, when the underlying dimensions are complements, the reverse inequality ![]() holds. If the dimensions are independents, the perfect equality
holds. If the dimensions are independents, the perfect equality ![]() is achieved.
is achieved.
Suppose that the matrix ![]() is derived from
is derived from ![]() by a switch of achievements in dimension 2 of persons 1 and 2 in period 1. Assume that all other entries in the two matrices are the same. We can then say that
by a switch of achievements in dimension 2 of persons 1 and 2 in period 1. Assume that all other entries in the two matrices are the same. We can then say that ![]() is obtained from
is obtained from ![]() by a correlation-decreasing switch.
by a correlation-decreasing switch.
- Chronic Monotonicity in Threshold Limits: For all
 ,
, 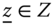 ,
, 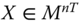 , suppose that person
, suppose that person 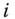 , who is chronically poor in
, who is chronically poor in  , is deprived in dimension
, is deprived in dimension  in period
in period 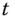 so that
so that 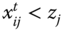 . Then
. Then 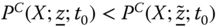 , where
, where  , for
, for 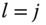 ,
,  for
for 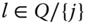 , and
, and 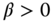 is constant.
is constant.
This postulate asserts that chronic poverty increases under an increase in the threshold limit of a dimension in which a chronically poor person is deprived in some period. In the social matrix ![]() , person 1 is chronically poor and deprived in dimension 2 in period 1. If the threshold limit of the dimension increases from 4 to 5, say, then the person's deprivation in the dimension in period 2 also goes up. This increased deprivation of person 1 leads to a higher chronic poverty. More precisely,
, person 1 is chronically poor and deprived in dimension 2 in period 1. If the threshold limit of the dimension increases from 4 to 5, say, then the person's deprivation in the dimension in period 2 also goes up. This increased deprivation of person 1 leads to a higher chronic poverty. More precisely, ![]() .
.
The following axioms also seem appropriate for a duration-based index.
- Chronic Boundedness: For all
 ,
, 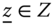 ,
, 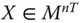 ,
,  , where (a)
, where (a) 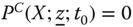 if
if 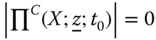 , and (b)
, and (b)  if
if 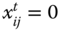 for all triplets
for all triplets  .
.
This axiom claims that the chronic poverty index is bounded between 0 and 1, where the lower bound, showing minimal poverty (0), is achieved if there is no chronically poor person in the society. In contrast, the index attains its upper bound, representing maximum poverty (1), when everybody in the society is maximally deprived in all the dimensions in all periods.
The next axiom is self-explanatory.
- Chronic Continuity: Given
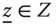 , for any arbitrary population size
, for any arbitrary population size  ,
, 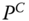 varies continuously with changes in achievements in each period provided that individuals' poverty statuses remain unchanged in all the periods.
varies continuously with changes in achievements in each period provided that individuals' poverty statuses remain unchanged in all the periods.
5.5.2 The Bourguignon–Chakravarty Approach to Chronic Multidimensional Poverty Measurement
This subsection proposes a scalar representation of multidimensional chronic poverty in a society and evaluates it with respect to the axioms introduced earlier. It follows the Bourguignon and Chakravarty (2003) aggregation rule and, in consequence, can be regarded as the chronic twin of the Bourguignon–Chakravarty multidimensional poverty index.
The numerical representation of multidimensional chronic poverty, we suggest, is given by
where ![]() ,
, ![]() are sensitivity parameters along the Bourguignon–Chakravarty lines of multidimensional poverty measurement; with
are sensitivity parameters along the Bourguignon–Chakravarty lines of multidimensional poverty measurement; with ![]() ,
, ![]() , and
, and ![]() being arbitrary. As we will see, adoption of this functional form will capacitate us to identify any pair of dimensions in terms of a well-defined notion of association between them. This chronic poverty metric is time replication invariant as well.
being arbitrary. As we will see, adoption of this functional form will capacitate us to identify any pair of dimensions in terms of a well-defined notion of association between them. This chronic poverty metric is time replication invariant as well.
Person i's deprivation indicator in dimension ![]() in the tth period is given by
in the tth period is given by ![]() . The third bracketed term in (5.33) is the simple unweighted average of transformed values of such indicators over all dimensions in the period for the chronically poor person
. The third bracketed term in (5.33) is the simple unweighted average of transformed values of such indicators over all dimensions in the period for the chronically poor person ![]() , where the transformed values are generated by applying the nonnegative increasing, strictly convex transformation
, where the transformed values are generated by applying the nonnegative increasing, strictly convex transformation ![]() ,
, ![]() . These periodic dimensional averages are then aggregated across periods to arrive at
. These periodic dimensional averages are then aggregated across periods to arrive at  , where
, where ![]() . These quantities have been calculated for any arbitrary chronically poor person
. These quantities have been calculated for any arbitrary chronically poor person ![]() in the population. If we sum these values over all chronically poor persons in the society and divide the resulting expression by the population size
in the population. If we sum these values over all chronically poor persons in the society and divide the resulting expression by the population size ![]() , then we arrive at the summary standard in (5.33).
, then we arrive at the summary standard in (5.33).
Now, person ![]() is fully deprived in any dimension
is fully deprived in any dimension ![]() in a year
in a year ![]() , if
, if ![]() . If this situation of maximum deprivation occurs for all periods in all the dimensions for a chronically poor person
. If this situation of maximum deprivation occurs for all periods in all the dimensions for a chronically poor person ![]() , then the sum
, then the sum 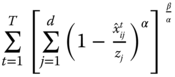 becomes
becomes ![]() for all
for all ![]() and
and ![]() . If all the persons in the society are chronically poor and are characterized by maximum deprivation for all (period, dimension) combinations, then the value of the expression
. If all the persons in the society are chronically poor and are characterized by maximum deprivation for all (period, dimension) combinations, then the value of the expression 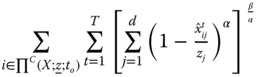 is
is ![]() . This in turn establishes that
. This in turn establishes that ![]() is bounded above by 1. It attains the lower bound 0 if nobody is chronically poor.
is bounded above by 1. It attains the lower bound 0 if nobody is chronically poor.
The following proposition, which is easy to demonstrate, describes some properties of ![]() .
.
The index can be expressed as the sum of dimensionwise indices when ![]() . Using this breakdown, we can calculate contribution of each dimension to the chronic poverty of the society (see Chapter 3). One can search for the factors that are likely to relegate people into poverty. Given a positive
. Using this breakdown, we can calculate contribution of each dimension to the chronic poverty of the society (see Chapter 3). One can search for the factors that are likely to relegate people into poverty. Given a positive ![]() , as
, as ![]() ,
, ![]() approaches
approaches ![]() , where
, where ![]() is the chronic head-count ratio, the proportion of persons that are chronically poor in
is the chronic head-count ratio, the proportion of persons that are chronically poor in ![]() , and
, and ![]() is the average number of (period, dimension) combinations in which the chronically poor persons are deprived, that is,
is the average number of (period, dimension) combinations in which the chronically poor persons are deprived, that is, 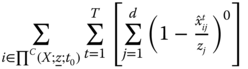 , expressed as a fraction of dT. The normalized quantity
, expressed as a fraction of dT. The normalized quantity ![]() is the average duration of poverty among all chronic multidimensionally poor persons. Then the fraction
is the average duration of poverty among all chronic multidimensionally poor persons. Then the fraction ![]() is the multidimensional twin of the duration-adjusted head-count ratio. On the other hand, for
is the multidimensional twin of the duration-adjusted head-count ratio. On the other hand, for ![]() , the index becomes
, the index becomes 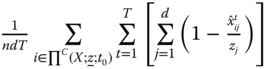 , the sum of deprivations experienced by the chronically poor persons across all dimensions and periods, divided by
, the sum of deprivations experienced by the chronically poor persons across all dimensions and periods, divided by ![]() , the maximum possible value that this number can assume. We can write it alternatively as
, the maximum possible value that this number can assume. We can write it alternatively as
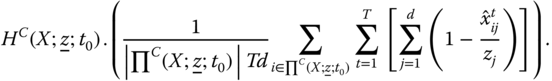
The component 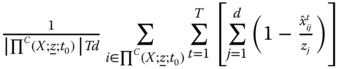 of this multiplicative decomposition is the average deprivation of the chronically poor persons in the poverty spells across all dimensions and periods. Each of the two terms of this simple multiplicative decomposition conveys significant information on different aspects of chronic poverty, confronted by the society. The first term tells us the extent of poverty arising from the fraction of population affected by chronic poverty. When this term divides the overall chronic poverty value
of this multiplicative decomposition is the average deprivation of the chronically poor persons in the poverty spells across all dimensions and periods. Each of the two terms of this simple multiplicative decomposition conveys significant information on different aspects of chronic poverty, confronted by the society. The first term tells us the extent of poverty arising from the fraction of population affected by chronic poverty. When this term divides the overall chronic poverty value 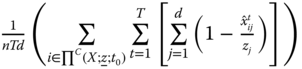 , we are left with the third bracketed term of the decomposition, which indicates the average depth of deprivation felt by the chronically poor persons in all
, we are left with the third bracketed term of the decomposition, which indicates the average depth of deprivation felt by the chronically poor persons in all ![]() dimensions throughout the period profile
dimensions throughout the period profile ![]() . Evidently, while the former simply counts the proportion of persons affected by chronic multidimensional poverty, the latter represents its intensity. Each of these factors is quite important from policy perspective.
. Evidently, while the former simply counts the proportion of persons affected by chronic multidimensional poverty, the latter represents its intensity. Each of these factors is quite important from policy perspective.
In order to illustrate the calculation of ![]() , let us consider again the social matrix
, let us consider again the social matrix ![]() . Assume, as before, that
. Assume, as before, that ![]() and
and ![]() . Recall that under these specifications, only persons 1 and 2 are chronically poor. Then the corresponding
. Recall that under these specifications, only persons 1 and 2 are chronically poor. Then the corresponding ![]() dimensional deprivation matrix whose entries represent deprivations of the chronically poor persons is given by
dimensional deprivation matrix whose entries represent deprivations of the chronically poor persons is given by

The entries in the 1st, 3rd, 5th, and 7th rows of ![]() indicate deprivations of person 1 in the two dimensions in periods 1, 2, 3, and 4, respectively. Entries in the 2nd, 4th, 6th, and 8th rows register similar figures for person 2. Since person 3 is chronically nonpoor, we do not include his deprivations in the matrix. The sum 3.4 of all possible entries in
indicate deprivations of person 1 in the two dimensions in periods 1, 2, 3, and 4, respectively. Entries in the 2nd, 4th, 6th, and 8th rows register similar figures for person 2. Since person 3 is chronically nonpoor, we do not include his deprivations in the matrix. The sum 3.4 of all possible entries in ![]() divided by
divided by ![]() is the value of
is the value of ![]() when
when ![]() . This value then becomes
. This value then becomes ![]() . The head count ratio is
. The head count ratio is ![]() . As a result, the average deprivation of the chronically poor person is
. As a result, the average deprivation of the chronically poor person is ![]() . We can similarly calculate
. We can similarly calculate ![]() for other choices of
for other choices of ![]() and
and ![]() .
.
In our analysis in the earlier subsection, if we assume that the duration threshold ![]() , then the resulting situation should include deprivations of all the poor persons for the determination of overall poverty. For any
, then the resulting situation should include deprivations of all the poor persons for the determination of overall poverty. For any ![]() ,
, ![]() , and
, and ![]() , we denote this by
, we denote this by ![]() . In contrast, for arbitrary
. In contrast, for arbitrary ![]() ,
, ![]() , and
, and ![]() , any restriction imposing a given positive value of
, any restriction imposing a given positive value of ![]() means that
means that ![]() takes into account only deprivations of the chronically poor persons. In consequence, it is reasonable to regard the difference
takes into account only deprivations of the chronically poor persons. In consequence, it is reasonable to regard the difference
as a transient multidimensional poverty standard, where ![]() ,
, ![]() , and
, and ![]() are chosen arbitrarily. The decomposition (5.35) capacitates us to judge the contributions of both transient and chronic poverty, which may be helpful in analyzing the lifetime poverty.
are chosen arbitrarily. The decomposition (5.35) capacitates us to judge the contributions of both transient and chronic poverty, which may be helpful in analyzing the lifetime poverty.
Recall that in ![]() , person 3 is deprived only in the dimension 1 in period 4 and the value of the corresponding deprivation indicator is 0.4. This deprivation of person 3, in addition to those that are relevant to
, person 3 is deprived only in the dimension 1 in period 4 and the value of the corresponding deprivation indicator is 0.4. This deprivation of person 3, in addition to those that are relevant to ![]() , should be included for the calculation of the overall poverty
, should be included for the calculation of the overall poverty ![]() . For
. For ![]() , the aggregate poverty
, the aggregate poverty ![]() is
is ![]() . Consequently, the level of the related transient poverty is
. Consequently, the level of the related transient poverty is ![]() . The head-count ratio also increases from
. The head-count ratio also increases from ![]() to 1, which shows that the transient head-count ratio here is
to 1, which shows that the transient head-count ratio here is ![]() .
.
5.6 Intertemporal Poverty Orderings
An important issue of investigation in intertemporal poverty analysis is to rank lifetime poverty profiles of different persons or of a society by members of some class of poverty indices. Duclos, Sahn, and Younger developed intertemporal poverty orderings that parallel the Bresson and Duclos (2015) bidimensional poverty dominances. (See Chapter 3.) In this section, we provide a discussion on this.
The authors considered a bidimensional individual well-being standard ![]() , where
, where ![]() may be taken as a person's income during his working life and
may be taken as a person's income during his working life and ![]() may be regarded as his retired income. This standard is assumed to be continuous and nondecreasing in its arguments. Intertemporal poverty is defined by the situations
may be regarded as his retired income. This standard is assumed to be continuous and nondecreasing in its arguments. Intertemporal poverty is defined by the situations ![]() in which
in which ![]() . Consequently, the set of points
. Consequently, the set of points ![]() , satisfying the constraint
, satisfying the constraint ![]() , represents the intertemporal poverty domain. A person with achievement vector
, represents the intertemporal poverty domain. A person with achievement vector ![]() that fulfills the inequality
that fulfills the inequality ![]() is treated as poor in this setup. The poverty frontier, which separates the poor from the nonpoor, is represented by a locus
is treated as poor in this setup. The poverty frontier, which separates the poor from the nonpoor, is represented by a locus ![]() .
.
Exchange between two periods' incomes is permitted. In consequence, a person's poverty remains unchanged if instead of enjoying incomes ![]() and
and ![]() in periods 1 and 2, respectively, he enjoys
in periods 1 and 2, respectively, he enjoys ![]() in period 2 and
in period 2 and ![]() in period 1. This is equivalent to the requirement poverty intertemporal poverty spells are equally valued (Calvo and Dercon, 2009). In other words, the rate of time discounting parameter takes on the value 1. The poverty frontier is then defined by a locus
in period 1. This is equivalent to the requirement poverty intertemporal poverty spells are equally valued (Calvo and Dercon, 2009). In other words, the rate of time discounting parameter takes on the value 1. The poverty frontier is then defined by a locus ![]() . In other words, the frontier is symmetric with respect to its arguments. Hence, if for any
. In other words, the frontier is symmetric with respect to its arguments. Hence, if for any ![]() ,
, ![]() holds, then it must be the case that
holds, then it must be the case that ![]() .
.
Bresson and Duclos (2015) demonstrated that under perfect substitutability, of two intertemporal profiles, one is regarded as more intertemporally poverty stricken than the other by all subgroup-decomposable poverty indices that are continuous along the poverty frontier and nonincreasing in incomes if and only if the sum of proportions of intertemporal income profiles whose incomes fall within two rectangles with common breadth ![]() and length
and length ![]() along two axes is higher for the former than for the latter. Each of these rectangles corresponds to those persons who have low incomes in one period. The common breadth
along two axes is higher for the former than for the latter. Each of these rectangles corresponds to those persons who have low incomes in one period. The common breadth ![]() is the length of a side of a square, which represents the two-dimensional poverty space here. Since the choice of the common length
is the length of a side of a square, which represents the two-dimensional poverty space here. Since the choice of the common length ![]() and breadth
and breadth ![]() can be arbitrary, this condition should be checked for all possible breadths and lengths of the rectangles below the frontier (see Figure 5.1). Evidently, all those persons who are deprived in both the periods, that is, whose incomes are in the two-dimensional poverty space, are counted twice.
can be arbitrary, this condition should be checked for all possible breadths and lengths of the rectangles below the frontier (see Figure 5.1). Evidently, all those persons who are deprived in both the periods, that is, whose incomes are in the two-dimensional poverty space, are counted twice.
Figure 5.1 Intertemporal poverty ordering.
We can define ![]() as the minimum permanent income as that level of income, which if enjoyed in each period, empowers a person to get away from poverty. More precisely,
as the minimum permanent income as that level of income, which if enjoyed in each period, empowers a person to get away from poverty. More precisely, ![]() . In this two-period setup, suppose that a person is identified as chronically poor if his income in each period falls below
. In this two-period setup, suppose that a person is identified as chronically poor if his income in each period falls below ![]() (Hulme and Shepherd, 2003). Then all those persons who are not chronically poor but whose incomes are below the frontier are transiently poor. More precisely, transiently poor are those whose incomes are below the frontier but not in the two-dimensional space.4
(Hulme and Shepherd, 2003). Then all those persons who are not chronically poor but whose incomes are below the frontier are transiently poor. More precisely, transiently poor are those whose incomes are below the frontier but not in the two-dimensional space.4
5.7 Concluding Remarks
The significance of time in assessing a person's poverty position in a society has received considerable attention from both researchers and policy-makers. The concern with intertemporal poverty is, in fact, long established (see, e.g., Godley, 1847). Since for many people in the world, poverty is a situation from which it is difficult to escape over time, it becomes important to look at poverty over multiple periods. Long disclosure to poverty has highly significant implications on future planning of individuals. Investigation of poverty from a dynamic perspective standpoint is highly likely to provide helpful insights for poverty reduction policies (World Bank, 2000). This of course requires information on panel data on different dimensions of well-being of the population. It may be justifiable to mention that duration-contingent approaches have been employed to measure other economic indices, such as unemployment rates. (See, e.g., Sengupta, 2009 and Shorrocks, 2009b.)
Research on axiomatic formulations of intertemporal poverty in multidimensional frameworks has started very recently. In this chapter, we made an attempt to discuss how different episodes of poverty and nonpoverty of an individual should be taken into consideration in evaluating his lifetime poverty. Throughout the chapter, it has been assumed implicitly that all the individuals live for the entire period of analysis. This is a limitation. Demises of some people at early ages may affect the analysis significantly (Kanbur and Mukherjee, 2007).
Since the history of axiomatic foundations of this literature is not old, there are weighty future tasks for the literature. A concrete line of investigation can be the contention of extending the results when threshold limits are not the same across periods. Appropriate reformulations of the axioms and investigations of their implications will be a worthy exercise.
References
- Addison, T., D. Hulme, and R. Kanbur (eds.). 2009. Poverty Dynamics: Interdisciplinary Perspectives. Oxford: Oxford University Press.
- Alkire, S., M. Apablaza, S.R. Chakravarty, and G. Yalonetzky. 2017. Measuring Chronic Multidimensional Poverty. Journal of Policy Modelling. In Press.
- Alkire, S. and J.E. Foster. 2011. Counting and Multidimensional Poverty Measurement. Journal of Public Economics 95: 476–487.
- Alkire, S., J.E. Foster, S. Seth, M.E. Santos, J.M. Roche, and P. Ballon. 2015. Multidimensional Poverty Measurement and Analysis. New York: Oxford University Press.
- Arranz, J.M. and O. Cantó. 2012. Measuring the Effect of Spell Recurrence on Poverty Dynamics - Evidence from Spain. Journal of Economic Inequality 10: 191–217.
- Baluch, B. and J. Hoddinott (eds.) 2000. Special Issue on Economic Mobility and Poverty Dynamics in Developing Countries. Journal of Development Studies 36: 1–200.
- Baluch B. and E. Masset 2003. Do Monetary and Non-monetary Indicators Tell the Same Story about Chronic Poverty? A Study of Vietnam in the 1990s. World Development 31: 441–53.
- Bane M. and D. Ellwood. 1986. Slipping into and out of Poverty. Journal of Human Resources 21: 1–23.
- Betti, G. and A. Lemmi (eds.). 2014. Poverty and Social Exclusion: New Methods of Analysis. London: Routledge.
- Blackorby, C., W. Bossert, and D. Donaldson. 2005. Population Issues in Social Choice Theory, Welfare Economics and Ethics. Cambridge: Cambridge University Press.
- Blackorby, C. and D. Donaldson. 1984. Social Criteria for Evaluating Population Change. Journal of Public Economics 25: 13–33.
- Bossert, W., L. Ceriani, S.R. Chakravarty, and C. D'Ambrosio. 2014. Inter-temporal Material Deprivation. In G. Betti and A. Lemmi (eds.)128–142.
- Bossert, W., S.R. Chakravarty, and C. D'Ambrosio. 2012. Poverty and Time. Journal of Economic Inequality 10: 145–162.
- Bourguignon, F. and S.R. Chakravarty. 2003. The Measurement of Multidimensional Poverty. Journal of Economic Inequality 1: 25 – 49.
- Bourguignon, F. and C. Morrison (2002). Inequality among World Citizens: 1820–1992. American Economic Review 92: 727–744.
- Bresson, F. and J.-Y. Duclos. 2015. Intertemporal Poverty Comparisons. Social Choice and Welfare 44: 567–616.
- Calvo S. and S. Dercon. 2009. Chronic Poverty and All That: The Measurement of Poverty over Time. T. Addison, D. Hulme, and R. Kanbur (eds.), 29–58.
- Cappellari, L. and S.P. Jenkins. 2004. Modeling Low Income Transitions. Journal of Applied Econometrics 19: 593–610.
- Carter, M.R. and C.B. Barrett. 2006. The Economics of Poverty Traps and Persistent Poverty: An Asset-based Approach. Journal of Development Studies 42: 178–199.
- Chakravarty, S.R. 1983. A New Index of Poverty. Mathematical Social Sciences 6: 307 –313.
- Chakravarty, S.R. 2009. Inequality, Polarization and Poverty: Advances in Distributional Analysis. New York: Springer.
- Chakravarty, S.R. and C. D'Ambrosio. 2006. The Measurement of Social Exclusion. Review of Income and Wealth 52: 377–398.
- Chronic Poverty Research Center. 2005. The Chronic Poverty Report 2004-5. Manchester: University of Manchester.
- Decancq, K., A. Decoster, and E. Schokkaert. 2006. The Evolution of World Inequality in Well-Being. World Development 37: 11–25.
- Duclos, J.-Y., A. Araar, and J. Giles. 2010. Chronic and Transient Poverty: Measurement and Estimation. Journal of Development Economics 91: 266–277.
- Duncan, G.J. and W. Rodgers. 1991. Has Children Poverty Become More Persistent? American Sociological Review 56: 538–550.
- Dutta, I., L. Roope, and H. Zank. 2013. On Inter-temporal Poverty Measures: The Role of Affluence and Want. Social Choice and Welfare 41: 741–62.
- Foster J.E. 2009. A Class of Chronic Poverty Measures. In T. Addison, D. Hulme, and R. Kanbur (eds.), 59–76.
- Foster, J.E., J. Greer, and E. Thorbecke. 1984. A Class of Decomposable Poverty Measures. Econometrica 52: 761–766.
- Foster, J.E. and M.E. Santos. 2014. Measuring Chronic Poverty. In G. Betti and A. Lemmi (eds.), 143–165.
- Gaiha, R. 1989. Are the Chronically Poor also the Poorest in Rural India? Development and Change 20: 295–322.
- Gaiha, R. and A.B. Deolikar. 1993. Persistent, Expected and Innate Poverty: Estimates for Semi -arid Rural South India 1975-1984. Cambridge Journal of Economics 17: 409–21.
- Godley, J.R. 1847. Observations on an Irish Poor Law (Addressed to the Committee of Landed Properties, Assembled in Dublin). Dublin: Grant and Bolton.
- Gradin, C., C. del Rio, and O. Cantó. 2012. Measuring Poverty Accounting for Time. Review of Income and Wealth 58: 330–54.
- Green, M. and D. Hulme. 2005. From Correlates and Characteristics to Causes: Thinking about Poverty from a Chronic Poverty Perspective. World Development 33: 867–879.
- Hojman, D. and F. Kast. 2009. On the Measurement of Poverty Dynamics. Faculty Research Working Paper 09-035. Harvard Kennedy School.
- Hoy, M., B.S. Thompson, and B. Zheng (2012). Empirical Issues in Lifetime Poverty Measurement. Journal of Economic Inequality 10: 163–189.
- Hoy, M. and B. Zheng. 2011. Measuring Lifetime Poverty. Journal of Economic Theory 146: 2544–2562.
- Hoy, M. and B. Zheng. 2015. Measuring Lifetime/Inter-temporal Poverty. Research on Economic Inequality. Forthcoming.
- Hulme, D., K. Moore, and A. Shepherd. 2001. Chronic Poverty: Meanings and Analytical Frameworks. CPRC Working Paper 2.
- Hulme, D. and A. Shepherd. 2003. Conceptualizing Chronic Poverty. World Development 31: 403–423.
- Jalan J. and M. Ravallion. 1998. Transient Poverty in Post-reform Rural China. Journal of Comparative Economics 26: 338–357.
- Jenkins, S.P. 2000. Modeling Household Income Dynamics. Journal of Population Economics 13: 529–567.
- Kanbur, R. and D. Mukherjee. 2007. Premature Mortality and Poverty Measurement. Bulletin of Economic Research 59: 339–359.
- Kurosaki, T. 2006. The Measurement of Transient Poverty: Theory and Application to Pakistan. Journal of Economic Inequality 4: 325–346.
- Levy, F. 1997. How big is the American underclass? Working Paper. Washington D.C.: Urban Institute.
- Lillard, L. and R. Willis. 1978. Dynamic Aspects of Earnings Mobility. Econometrica 46: 985–1012.
- Lybbert, T.J., C.B. Barrett, S. Desta, and D.L. Coppock. 2004. Stochastic Wealth Dynamics and Risk Management among a Poor Population. Economic Journal 114: 750–77.
- McKay, A., and D. Lawson. 2003. Assessing the Extent and Nature of Chronic Poverty in Low Income Countries: Issues and Evidence. World Development 31: 425–439.
- Mehta, A.K. and A.K. Shah. 2003. Chronic Poverty in India: Incidence, Causes and Policies. World Development 31: 473–490.
- Mendola, D. and A. Busetta. 2012. The Importance of Consecutive Spells of Poverty: A Path-dependent Index of Longitudinal Poverty. Review of Income and Wealth 58: 355–74.
- Morduch, J. 1994. Poverty and Vulnerability. American Economic Review Papers and Proceedings 84: 221–225.
- Narayan, D. and P. Petesch (eds.) 2007. Moving Out of Poverty: Cross-Disciplinary Perspectives on Mobility. Washington, DC: World Bank.
- Nicholas, A. and R. Ray. 2011. Duration and Persistence in Multidimensional Deprivation: Methodology and Australian Application. Economic Record 88: 106–126.
- Porter C. and N.N. Quinn. 2008. Inter-temporal Poverty Measurement: Tradeoffs and Policy Options. CSAE Working Paper 2008-21.
- Porter C. and N.N. Quinn. 2014. Measuring Inter-temporal Poverty: Policy Options for the Poverty Analyst. In G. Betti and A. Lemmi (eds.) (2014), 166–193.
- Ravallion, M. 1988. Expected Poverty under Risk-induced Welfare Variability. Economic Journal 98: 1171–1182.
- Ravallion, M., D. van de Walle, and M. Gautam. (1995). Testing a Social Safety Net. Journal of Public Economics 57: 175–199.
- Rodgers, J.R. and J.L. Rodgers. 2003. Chronic Poverty in the United States. Journal of Human Resources 28: 25–54.
- Sen, A.K. 1992. Inequality Re-examined. Cambridge, MA: Harvard University Press.
- Sengupta, M. 2009. Unemployment Duration and the Measurement of Unemployment. Journal of Economic Inequality 7: 273–294.
- Shorrocks, A.F. 1983. Ranking Income Distributions. Economica 50: 3–17.
- Shorrocks, A.F. 2009a. Spell Incidence, Spell Duration and the Measurement of Unemployment. Journal of Economic Inequality 7: 295–310.
- Shorrocks, A.F. 2009b. On the Measurement of Unemployment. Journal of Economic Inequality 7: 311–327.
- Walker, R. 1995. The Dynamics of Poverty and Social Exclusion. In G. Room (ed.) Beyond the Threshold. Bristol: Policy Press, 102–128.
- World Bank. 2000. World Development Report 2000/2001: Attacking Poverty. New York: Oxford University Press.
- Yaqub, S. 2000a. Inter-temporal Welfare Dynamics: Extent and Causes. Paper presented at the Globalization, New Opportunities, New Vulnerabilities Workshop. Washington, DC: Brookings Institution.
- Yaqub, S. 2000b. Chronic Poverty: Scrutinizing Estimates, Patterns, Correlates and Explanations. Chronic Poverty Research Centre Working Paper No. 21. Manchester: University of Manchester.
- Zheng, B. 2012. Measuring Chronic Poverty: A Gravitational Approach. Working Paper, Department of Economics. Colorado Denver: University of Colorado.