1. Introduction: Why Look Beyond Hadoop Map-Reduce?
Perhaps you are a video service provider and would like to optimize the end user experience by choosing the appropriate content distribution network based on dynamic network conditions. Or you are a government regulatory body that needs to classify Internet pages into porn or non-porn in order to filter porn pages—which has to be achieved at high throughput and in real-time. Or you are a telecom/mobile service provider, or you work for one, and you are worried about customer churn (churn refers to a customer leaving the provider and choosing a competitor, or new customers joining in leaving competitors). How you wish you had known that the last customer who was on the phone with your call center had tweeted with negative sentiments about you a day before. Or you are a retail storeowner and you would love to have predictions about the customers’ buying patterns after they enter the store so that you can run promotions on your products and expect an increase in sales. Or you are a healthcare insurance provider for whom it is imperative to compute the probability that a customer is likely to be hospitalized in the next year so that you can fix appropriate premiums. Or you are a Chief Technology Officer (CTO) of a financial product company who wishes that you could have real-time trading/predictive algorithms that can help your bottom line. Or you work for an electronic manufacturing company and you would like to predict failures and identify root causes during test runs so that the subsequent real-runs are effective. Welcome to the world of possibilities, thanks to big data analytics.
Analytics has been around for a long time now—North Carolina State University ran a project called “Statistical Analysis System (SAS)” for agricultural research in the late 1960s that led to the formation of the SAS Company. The only difference between the terms analysis and analytics is that analytics is about analyzing data and converting it into actionable insights. The term Business Intelligence (BI) is also used often to refer to analysis in a business environment, possibly originating in a 1958 article by Peter Luhn (Luhn 1958). Lots of BI applications were run over data warehouses, even quite recently. The evolution of “big data” in contrast to the “analytics” term has been quite recent, as explained next.
The term big data seems to have been used first by John R. Mashey, then chief scientist of Silicon Graphics Inc. (SGI), in a Usenix conference invited talk titled “Big Data and the Next Big Wave of InfraStress,” the transcript of which is available at http://static.usenix.org/event/usenix99/invited_talks/mashey.pdf. The term was also used in a paper (Bryson et al. 1999) published in the Communications of the Association for Computing Machinery (ACM). The report (Laney 2001) from the META group (now Gartner) was the first to identify the 3 Vs (volume, variety, and velocity) perspective of big data. Google’s seminal paper on Map-Reduce (MR; Dean and Ghemawat 2004) was the trigger that led to lots of developments in the big data space. Though the MR paradigm was known in the functional programming literature, the paper provided scalable implementations of the paradigm on a cluster of nodes. The paper, along with Apache Hadoop, the open source implementation of the MR paradigm, enabled end users to process large data sets on a cluster of nodes—a usability paradigm shift. Hadoop, which comprises the MR implementation, along with the Hadoop Distributed File System (HDFS), has now become the de facto standard for data processing, with a lot of industrial game changers such as Disney, Sears, Walmart, and AT&T having their own Hadoop cluster installations.
Hadoop Suitability
Hadoop is good for a number of use cases, including those in which the data can be partitioned into independent chunks—the embarrassingly parallel applications, as is widely known. Hindrances to widespread adoption of Hadoop across Enterprises include the following:
• Lack of Object Database Connectivity (ODBC)—A lot of BI tools are forced to build separate Hadoop connectors.
• Hadoop’s lack of suitability for all types of applications:
• If data splits are interrelated or computation needs to access data across splits, this might involve joins and might not run efficiently over Hadoop. For example, imagine that you have a set of stocks and the set of values of those stocks at various time points. It is required to compute correlations across stocks—can you check when Apple falls? What is the probability of Samsung too falling the next day? The computation cannot be split into independent chunks—you may have to compute correlation between stocks in different chunks, if the chunks carry different stocks. If the data is split along the time line, you would still need to compute correlation between stock prices at different points of time, which may be in different chunks.
• For iterative computations, Hadoop MR is not well-suited for two reasons. One is the overhead of fetching data from HDFS for each iteration (which can be amortized by a distributed caching layer), and the other is the lack of long-lived MR jobs in Hadoop. Typically, there is a termination condition check that must be executed outside of the MR job, so as to determine whether the computation is complete. This implies that new MR jobs need to be initialized for each iteration in Hadoop—the overhead of initialization could overwhelm computation for the iteration and could cause significant performance hits.
The other perspective of Hadoop suitability can be understood by looking at the characterization of the computation paradigms required for analytics on massive data sets, from the National Academies Press (NRC 2013). They term the seven categories as seven “giants” in contrast with the “dwarf” terminology that was used to characterize fundamental computational tasks in the super-computing literature (Asanovic et al. 2006). These are the seven “giants”:
1. Basic statistics: This category involves basic statistical operations such as computing the mean, median, and variance, as well as things like order statistics and counting. The operations are typically O(N) for N points and are typically embarrassingly parallel, so perfect for Hadoop.
2. Linear algebraic computations: These computations involve linear systems, eigenvalue problems, inverses from problems such as linear regression, and Principal Component Analysis (PCA). Linear regression is doable over Hadoop (Mahout has the implementation), whereas PCA is not easy. Moreover, a formulation of multivariate statistics in matrix form is difficult to realize over Hadoop. Examples of this type include kernel PCA and kernel regression.
3. Generalized N-body problems: These are problems that involve distances, kernels, or other kinds of similarity between points or sets of points (tuples). Computational complexity is typically O(N2) or even O(N3). The typical problems include range searches, nearest neighbor search problems, and nonlinear dimension reduction methods. The simpler solutions of N-body problems such as k-means clustering are solvable over Hadoop, but not the complex ones such as kernel PCA, kernel Support Vector Machines (SVM), and kernel discriminant analysis.
4. Graph theoretic computations: Problems that involve graph as the data or that can be modeled graphically fall into this category. The computations on graph data include centrality, commute distances, and ranking. When the statistical model is a graph, graph search is important, as are computing probabilities which are operations known as inference. Some graph theoretic computations that can be posed as linear algebra problems can be solved over Hadoop, within the limitations specified under giant 2. Euclidean graph problems are hard to realize over Hadoop as they become generalized N-body problems. Moreover, major computational challenges arise when you are dealing with large sparse graphs; partitioning them across a cluster is hard.
5. Optimizations: Optimization problems involve minimizing (convex) or maximizing (concave) a function that can be referred to as an objective, a loss, a cost, or an energy function. These problems can be solved in various ways. Stochastic approaches are amenable to be implemented in Hadoop. (Mahout has an implementation of stochastic gradient descent.) Linear or quadratic programming approaches are harder to realize over Hadoop, because they involve complex iterations and operations on large matrices, especially at high dimensions. One approach to solve optimization problems has been shown to be solvable on Hadoop, but by realizing a construct known as All-Reduce (Agarwal et al. 2011). However, this approach might not be fault-tolerant and might not be generalizable. Conjugate gradient descent (CGD), due to its iterative nature, is also hard to realize over Hadoop. The work of Stephen Boyd and his colleagues from Stanford has precisely addressed this giant. Their paper (Boyd et al. 2011) provides insights on how to combine dual decomposition and augmented Lagrangian into an optimization algorithm known as Alternating Direction Method of Multipliers (ADMM). The ADMM has been realized efficiently over Message Passing Interface (MPI), whereas the Hadoop implementation would require several iterations and might not be so efficient.
6. Integrations: The mathematical operation of integration of functions is important in big data analytics. They arise in Bayesian inference as well as in random effects models. Quadrature approaches that are sufficient for low-dimensional integrals might be realizable on Hadoop, but not those for high-dimensional integration which arise in Bayesian inference approach for big data analytical problems. (Most recent applications of big data deal with high-dimensional data—this is corroborated among others by Boyd et al. 2011.) For example, one common approach for solving high-dimensional integrals is the Markov Chain Monte Carlo (MCMC) (Andrieu 2003), which is hard to realize over Hadoop. MCMC is iterative in nature because the chain must converge to a stationary distribution, which might happen after several iterations only.
7. Alignment problems: The alignment problems are those that involve matching between data objects or sets of objects. They occur in various domains—image de-duplication, matching catalogs from different instruments in astronomy, multiple sequence alignments used in computational biology, and so on. The simpler approaches in which the alignment problem can be posed as a linear algebra problem can be realized over Hadoop. But the other forms might be hard to realize over Hadoop—when either dynamic programming is used or Hidden Markov Models (HMMs) are used. It must be noted that dynamic programming needs iterations/recursions. The catalog cross-matching problem can be posed as a generalized N-body problem, and the discussion outlined earlier in point 3 applies.
To summarize, giant 1 is perfect for Hadoop, and in all other giants, simpler problems or smaller versions of the giants are doable in Hadoop—in fact, we can call them dwarfs, Hadoopable problems/algorithms! The limitations of Hadoop and its lack of suitability for certain classes of applications have motivated some researchers to come up with alternatives. Researchers at the University of Berkeley have proposed “Spark” as one such alternative—in other words, Spark could be seen as the next-generation data processing alternative to Hadoop in the big data space. In the previous seven giants categorization, Spark would be efficient for
• Complex linear algebraic problems (giant 2)
• Generalized N-body problems (giant 3), such as kernel SVMs and kernel PCA
• Certain optimization problems (giant 4), for example, approaches involving CGD
An effort has been made to apply Spark for another giant, namely, graph theoretic computations in GraphX (Xin et al. 2013). It would be an interesting area of further research to estimate the efficiency of Spark for other classes of problems or other giants such as integrations and alignment problems.
The key idea distinguishing Spark is its in-memory computation, allowing data to be cached in memory across iterations/interactions. Initial performance studies have shown that Spark can be 100 times faster than Hadoop for certain applications. This book explores Spark as well as the other components of the Berkeley Data Analytics Stack (BDAS), a data processing alternative to Hadoop, especially in the realm of big data analytics that involves realizing machine learning (ML) algorithms. When using the term big data analytics, I refer to the capability to ask questions on large data sets and answer them appropriately, possibly by using ML techniques as the foundation. I will also discuss the alternatives to Spark in this space—systems such as HaLoop and Twister.
The other dimension for which the beyond-Hadoop thinking is required is for real-time analytics. It can be inferred that Hadoop is basically a batch processing system and is not well suited for real-time computations. Consequently, if analytical algorithms are required to be run in real time or near real time, Storm from Twitter has emerged as an interesting alternative in this space, although there are other promising contenders, including S4 from Yahoo and Akka from Typesafe. Storm has matured faster and has more production use cases than the others. Thus, I will discuss Storm in more detail in the later chapters of this book—though I will also attempt a comparison with the other alternatives for real-time analytics.
The third dimension where beyond-Hadoop thinking is required is when there are specific complex data structures that need specialized processing—a graph is one such example. Twitter, Facebook, and LinkedIn, as well as a host of other social networking sites, have such graphs. They need to perform operations on the graphs, for example, searching for people you might know on LinkedIn or a graph search in Facebook (Perry 2013). There have been some efforts to use Hadoop for graph processing, such as Intel’s GraphBuilder. However, as outlined in the GraphBuilder paper (Jain et al. 2013), it is targeted at construction and transformation and is useful for building the initial graph from structured or unstructured data. GraphLab (Low et al. 2012) has emerged as an important alternative for processing graphs efficiently. By processing, I mean running page ranking or other ML algorithms on the graph. GraphBuilder can be used for constructing the graph, which can then be fed into GraphLab for processing. GraphLab is focused on giant 4, graph theoretic computations. The use of GraphLab for any of the other giants is an interesting topic of further research.
The emerging focus of big data analytics is to make traditional techniques, such as market basket analysis, scale, and work on large data sets. This is reflected in the approach of SAS and other traditional vendors to build Hadoop connectors. The other emerging approach for analytics focuses on new algorithms or techniques from ML and data mining for solving complex analytical problems, including those in video and real-time analytics. My perspective is that Hadoop is just one such paradigm, with a whole new set of others that are emerging, including Bulk Synchronous Parallel (BSP)-based paradigms and graph processing paradigms, which are more suited to realize iterative ML algorithms. The following discussion should help clarify the big data analytics spectrum, especially from an ML realization perspective. This should help put in perspective some of the key aspects of the book and establish the beyond-Hadoop thinking along the three dimensions of real-time analytics, graph computations, and batch analytics that involve complex problems (giants 2 through 7).
Big Data Analytics: Evolution of Machine Learning Realizations
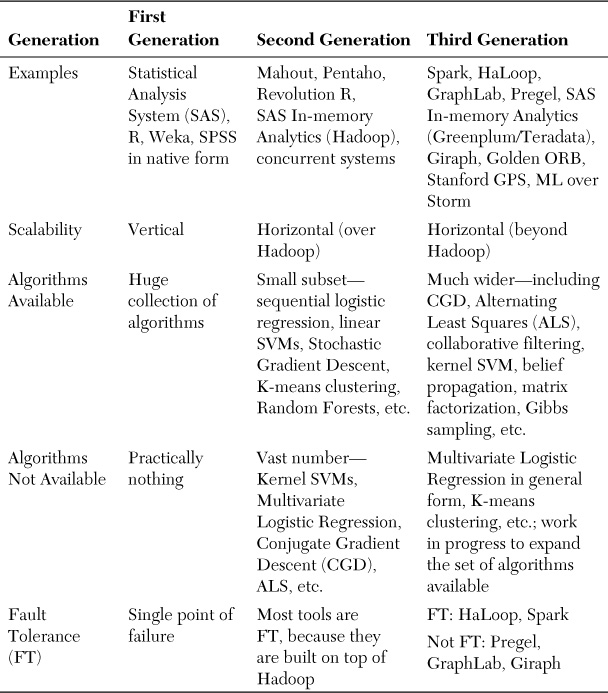
I will explain the different paradigms available for implementing ML algorithms, both from the literature and from the open source community. First of all, here’s a view of the three generations of ML tools available today:
1. The traditional ML tools for ML and statistical analysis, including SAS, SPSS from IBM, Weka, and the R language. These allow deep analysis on smaller data sets—data sets that can fit the memory of the node on which the tool runs.
2. Second-generation ML tools such as Mahout, Pentaho, and RapidMiner. These allow what I call a shallow analysis of big data. Efforts to scale traditional tools over Hadoop, including the work of Revolution Analytics (RHadoop) and SAS over Hadoop, would fall into the second-generation category.
3. The third-generation tools such as Spark, Twister, HaLoop, Hama, and GraphLab. These facilitate deeper analysis of big data. Recent efforts by traditional vendors such as SAS in-memory analytics also fall into this category.
First-Generation ML Tools/Paradigms
The first-generation ML tools can facilitate deep analytics because they have a wide set of ML algorithms. However, not all of them can work on large data sets—like terabytes or petabytes of data—due to scalability limitations (limited by the nondistributed nature of the tool). In other words, they are vertically scalable (you can increase the processing power of the node on which the tool runs), but not horizontally scalable (not all of them can run on a cluster). The first-generation tool vendors are addressing those limitations by building Hadoop connectors as well as providing clustering options—meaning that the vendors have made efforts to reengineer the tools such as R and SAS to scale horizontally. This would come under the second-/third-generation tools and is covered subsequently.
Second-Generation ML Tools/Paradigms
The second-generation tools (we can now term the traditional ML tools such as SAS as first-generation tools) such as Mahout (http://mahout.apache.org), Rapidminer, and Pentaho provide the capability to scale to large data sets by implementing the algorithms over Hadoop, the open source MR implementation. These tools are maturing fast and are open source (especially Mahout). Mahout has a set of algorithms for clustering and classification, as well as a very good recommendation algorithm (Konstan and Riedl 2012). Mahout can thus be said to work on big data, with a number of production use cases, mainly for the recommendation system. I have also used Mahout in a production system for realizing recommendation algorithms in financial domain and found it to be scalable, though not without issues. (I had to tweak the source significantly.) One observation about Mahout is that it implements only a smaller subset of ML algorithms over Hadoop—only 25 algorithms are of production quality, with only 8 or 9 usable over Hadoop, meaning scalable over large data sets. These include the linear regression, linear SVM, the K-means clustering, and so forth. It does provide a fast sequential implementation of the logistic regression, with parallelized training. However, as several others have also noted (see Quora.com, for instance), it does not have implementations of nonlinear SVMs or multivariate logistic regression (discrete choice model, as it is otherwise known).
Overall, this book is not intended for Mahout bashing. However, my point is that it is quite hard to implement certain ML algorithms including the kernel SVM and CGD (note that Mahout has an implementation of stochastic gradient descent) over Hadoop. This has been pointed out by several others as well—for instance, see the paper by Professor Srirama (Srirama et al. 2012). This paper makes detailed comparisons between Hadoop and Twister MR (Ekanayake et al. 2010) with regard to iterative algorithms such as CGD and shows that the overheads can be significant for Hadoop. What do I mean by iterative? A set of entities that perform a certain computation, wait for results from neighbors or other entities, and start the next iteration. The CGD is a perfect example of iterative ML algorithm—each CGD can be broken down into daxpy, ddot, and matmul as the primitives. I will explain these three primitives: daxpy is an operation that takes a vector x, multiplies it by a constant k, and adds another vector y to it; ddot computes the dot product of two vectors x and y; matmul multiplies a matrix by a vector and produces a vector output. This means 1 MR per primitive, leading to 6 MRs per iteration and eventually 100s of MRs per CG computation, as well as a few gigabytes (GB)s of communication even for small matrices. In essence, the setup cost per iteration (which includes reading from HDFS into memory) overwhelms the computation for that iteration, leading to performance degradation in Hadoop MR. In contrast, Twister distinguishes between static and variable data, allowing data to be in memory across MR iterations, as well as a combine phase for collecting all reduce phase outputs and, hence, performs significantly better.
The other second-generation tools are the traditional tools that have been scaled to work over Hadoop. The choices in this space include the work done by Revolution Analytics, among others, to scale R over Hadoop and the work to implement a scalable runtime over Hadoop for R programs (Venkataraman et al. 2012). The SAS in-memory analytics, part of the High Performance Analytics toolkit from SAS, is another attempt at scaling a traditional tool by using a Hadoop cluster. However, the recently released version works over Greenplum/Teradata in addition to Hadoop—this could then be seen as a third-generation approach. The other interesting work is by a small start-up known as Concurrent Systems, which is providing a Predictive Modeling Markup Language (PMML) runtime over Hadoop. PMML is like the eXtensible Markup Language (XML) of modeling, allowing models to be saved in descriptive language files. Traditional tools such as R and SAS allow the models to be saved as PMML files. The runtime over Hadoop would allow these model files to be scaled over a Hadoop cluster, so this also falls in our second-generation tools/paradigms.
Third-Generation ML Tools/Paradigms
The limitations of Hadoop and its lack of suitability for certain classes of applications have motivated some researchers to come up with alternatives. The efforts in the third generation have been to look beyond Hadoop for analytics along different dimensions. I discuss the approaches along the three dimensions, namely, iterative ML algorithms, real-time analytics, and graph processing.
Iterative Machine Learning Algorithms
Researchers at the University of Berkeley have proposed “Spark” (Zaharia et al. 2010) as one such alternative—in other words, Spark could be seen as the next-generation data processing alternative to Hadoop in the big data space. The key idea distinguishing Spark is its in-memory computation, allowing data to be cached in memory across iterations/interactions. The main motivation for Spark was that the commonly used MR paradigm, while being suitable for some applications that can be expressed as acyclic data flows, was not suitable for other applications, such as those that need to reuse working sets across iterations. So they proposed a new paradigm for cluster computing that can provide similar guarantees or fault tolerance (FT) as MR but would also be suitable for iterative and interactive applications. The Berkeley researchers have proposed BDAS as a collection of technologies that help in running data analytics tasks across a cluster of nodes. The lowest-level component of the BDAS is Mesos, the cluster manager that helps in task allocation and resource management tasks of the cluster. The second component is the Tachyon file system built on top of Mesos. Tachyon provides a distributed file system abstraction and provides interfaces for file operations across the cluster. Spark, the computation paradigm, is realized over Tachyon and Mesos in a specific embodiment, although it could be realized without Tachyon and even without Mesos for clustering. Shark, which is realized over Spark, provides a Structured Query Language (SQL) abstraction over a cluster—similar to the abstraction Hive provides over Hadoop. Zacharia et al. article explores Spark, which is the main ingredient over which ML algorithms can be built.
The HaLoop work (Bu et al. 2010) also extends Hadoop for iterative ML algorithms—HaLoop not only provides a programming abstraction for expressing iterative applications, but also uses the notion of caching to share data across iterations and for fixpoint verification (termination of iteration), thereby improving efficiency. Twister (http://iterativemapreduce.org) is another effort similar to HaLoop.
Real-time Analytics
The second dimension for beyond-Hadoop thinking comes from real-time analytics. Twitter from Storm has emerged as the best contender in this space. Storm is a scalable Complex Event Processing (CEP) engine that enables complex computations on event streams in real time. The components of a Storm cluster are
• Spouts that read data from various sources. HDFS spout, Kafka spout, and Transmission Control Protocol (TCP) stream spout are examples.
• Bolts that process the data. They run the computations on the streams. ML algorithms on the streams typically run here.
• Topology. This is an application-specific wiring together of spouts and bolts—topology gets executed on a cluster of nodes.
An architecture comprising a Kafka (a distributed queuing system from LinkedIn) cluster as a high-speed data ingestor and a Storm cluster for processing/analytics works well in practice, with a Kafka spout reading data from the Kafka cluster at high speed. The Kafka cluster stores up the events in the queue. This is necessary because the Storm cluster is heavy in processing due to the ML involved. The details of this architecture, as well as the steps needed to run ML algorithms in a Storm cluster, are covered in subsequent chapters of the book. Storm is also compared to the other contenders in real-time computing, including S4 from Yahoo and Akka from Typesafe.
Graph Processing Dimension
The other important tool that has looked beyond Hadoop MR comes from Google—the Pregel framework for realizing graph computations (Malewicz et al. 2010). Computations in Pregel comprise a series of iterations, known as supersteps. Each vertex in the graph is associated with a user-defined compute function; Pregel ensures at each superstep that the user-defined compute function is invoked in parallel on each edge. The vertices can send messages through the edges and exchange values with other vertices. There is also the global barrier—which moves forward after all compute functions are terminated. Readers familiar with BSP can see why Pregel is a perfect example of BSP—a set of entities computing user-defined functions in parallel with global synchronization and able to exchange messages.
Apache Hama (Seo et al. 2010) is the open source equivalent of Pregel, being an implementation of the BSP. Hama realizes BSP over the HDFS, as well as the Dryad engine from Microsoft. It might be that they do not want to be seen as being different from the Hadoop community. But the important thing is that BSP is an inherently well-suited paradigm for iterative computations, and Hama has parallel implementations of the CGD, which I said is not easy to realize over Hadoop. It must be noted that the BSP engine in Hama is realized over MPI, the father (and mother) of parallel programming literature (www.mcs.anl.gov/research/projects/mpi/). The other projects that are inspired by Pregel are Apache Giraph, Golden Orb, and Stanford GPS.
GraphLab (Gonzalez et al. 2012) has emerged as a state-of-the-art graph processing paradigm. GraphLab originated as an academic project from the University of Washington and Carnegie Mellon University (CMU). GraphLab provides useful abstractions for processing graphs across a cluster of nodes deterministically. PowerGraph, the subsequent version of GraphLab, makes it efficient to process natural graphs or power law graphs—graphs that have a high number of poorly connected vertices and a low number of highly connected vertices. Performance evaluations on the Twitter graph for page-ranking and triangle counting problems have verified the efficiency of GraphLab compared to other approaches. The focus of this book is mainly on Giraph, GraphLab, and related efforts.
Table 1.1 carries a comparison of the various paradigms across different nonfunctional features such as scalability, FT, and the algorithms that have been implemented. It can be inferred that although the traditional tools have worked on only a single node and might not scale horizontally and might also have single points of failure, recent reengineering efforts have made them move across generations. The other point to be noted is that most of the graph processing paradigms are not fault-tolerant, whereas Spark and HaLoop are among the third-generation tools that provide FT.
Closing Remarks
This chapter has set the tone for the book by discussing the limitations of Hadoop along the lines of the seven giants. It has also brought out the three dimensions along which thinking beyond Hadoop is necessary:
1. Real-time analytics: Storm and Spark streaming are the choices.
2. Analytics involving iterative ML: Spark is the technology of choice.
3. Specialized data structures and processing requirements for these: GraphLab is an important paradigm to process large graphs.
These are elaborated in the subsequent chapters of this book. Happy reading!
References
Agarwal, Alekh, Olivier Chapelle, Miroslav Dudík, and John Langford. 2011. “A Reliable Effective Terascale Linear Learning System.” CoRR abs/1110.4198.
Andrieu, Christopher, N. de Freitas, A. Doucet, and M. I. Jordan. 2003. “An Introduction to MCMC for Machine Learning.” Machine Learning 50(1-2):5-43.
Asanovic, K., R. Bodik, B. C. Catanzaro, J. J. Gebis, P. Husbands, K. Keutzer, D. A. Patterson, W. L. Plishker, J. Shalf, S. W. Williams, and K. A. Yelick. 2006. “The Landscape of Parallel Computing Research: A View from Berkeley.” University of California, Berkeley, Technical Report No. UCB/EECS-2006-183. Available at www.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-183.html. Last accessed September 11, 2013.
Boyd, Stephen, Neal Parikh, Eric Chu, Borja Peleato, and Jonathan Eckstein. 2011. “Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers.” Foundation and Trends in Machine Learning 3(1)(January):1-122.
Bryson, Steve, David Kenwright, Michael Cox, David Ellsworth, and Robert Haimes. 1999. “Visually Exploring Gigabyte Data Sets in Real Time.” Communications of the ACM 42(8)(August):82-90.
Bu, Yingyi, Bill Howe, Magdalena Balazinska, and Michael D. Ernst. 2010. “HaLoop: Efficient Iterative Data Processing on Large Clusters.” In Proceedings of the VLDB Endowment 3(1-2)(September):285-296.
Dean, Jeffrey, and Sanjay Ghemawat. 2008. “MapReduce: Simplified Data Processing on Large Clusters.” In Proceedings of the 6th Conference on Symposium on Operating Systems Design and Implementation (OSDI ‘04). USENIX Association, Berkeley, CA, USA, (6):10-10.
Ekanayake, Jaliya, Hui Li, Bingjing Zhang, Thilina Gunarathne, Seung-Hee Bae, Judy Qiu, and Geoffrey Fox. 2010. “Twister: A Runtime for Iterative MapReduce.” In Proceedings of the 19th ACM International Symposium on High-Performance Distributed Computing. June 21-25, Chicago, Illinois. Available at http://dl.acm.org/citation.cfm?id=1851593.
Gonzalez, Joseph E., Yucheng Low, Haijie Gu, Danny Bickson, and Carlos Guestrin. 2012. “PowerGraph: Distributed Graph-Parallel Computation on Natural Graphs.” In Proceedings of the 10th USENIX Symposium on Operating Systems Design and Implementation (OSDI ‘12).
Jain, Nilesh, Guangdeng Liao, and Theodore L. Willke. 2013. “GraphBuilder: Scalable Graph ETL Framework.” In First International Workshop on Graph Data Management Experiences and Systems (GRADES ‘13). ACM, New York, NY, USA, (4):6 pages. DOI=10.1145/2484425.2484429.
Konstan, Joseph A., and John Riedl. 2012. “Deconstructing Recommender Systems.” IEEE Spectrum.
Laney, Douglas. 2001. “3D Data Management: Controlling Data Volume, Velocity, and Variety.” Gartner Inc. Retrieved February 6, 2001. Last accessed September 11, 2013. Available at http://blogs.gartner.com/doug-laney/files/2012/01/ad949-3D-Data-Management-Controlling-Data-Volume-Velocity-and-Variety.pdf.
Low, Yucheng, Danny Bickson, Joseph Gonzalez, Carlos Guestrin, Aapo Kyrola, and Joseph M. Hellerstein. 2012. “Distributed GraphLab: A Framework for Machine Learning and Data Mining in the Cloud.” In Proceedings of the VLDB Endowment 5(8)(April):716-727.
Luhn, H. P. 1958. “A Business Intelligence System.” IBM Journal 2(4):314. doi:10.1147/rd.24.0314.
Malewicz, Grzegorz, Matthew H. Austern, Aart J. C. Bik, James C. Dehnert, Ilan Horn, Naty Leiser, and Grzegorz Czajkowski. 2010. “Pregel: A System for Large-scale Graph Processing.” In Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data (SIGMOD ‘10). ACM, New York, NY, USA, 135-146.
[NRC] National Research Council. 2013. “Frontiers in Massive Data Analysis.” Washington, DC: The National Academies Press.
Perry, Tekla S. 2013. “The Making of Facebook Graph Search.” IEEE Spectrum. Available at http://spectrum.ieee.org/telecom/internet/the-making-of-facebooks-graph-search.
Seo, Sangwon, Edward J. Yoon, Jaehong Kim, Seongwook Jin, Jin-Soo Kim, and Seungryoul Maeng. 2010. “HAMA: An Efficient Matrix Computation with the MapReduce Framework.” In Proceedings of the 2010 IEEE Second International Conference on Cloud Computing Technology and Science (CLOUDCOM ‘10). IEEE Computer Society, Washington, DC, USA, 721-726.
Srirama, Satish Narayana, Pelle Jakovits, and Eero Vainikko. 2012. “Adapting Scientific Computing Problems to Clouds Using MapReduce.” Future Generation Computer System 28(1)(January):184-192.
Venkataraman, Shivaram, Indrajit Roy, Alvin AuYoung, and Robert S. Schreiber. 2012. “Using R for Iterative and Incremental Processing.” In Proceedings of the 4th USENIX Conference on Hot Topics in Cloud Computing (HotCloud ‘12). USENIX Association, Berkeley, CA, USA, 11.
Xin, Reynold S., Joseph E. Gonzalez, Michael J. Franklin, and Ion Stoica. 2013. “GraphX: A Resilient Distributed Graph System on Spark.” In First International Workshop on Graph Data Management Experiences and Systems (GRADES ‘13). ACM, New York, NY, USA, (2):6 pages.
Zaharia, Matei, Mosharaf Chowdhury, Michael J. Franklin, Scott Shenker, and Ion Stoica. 2010. “Spark: Cluster Computing with Working Sets.” In Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing (HotCloud ‘10). USENIX Association, Berkeley, CA, USA, 10.