2.7 The Interleaver
The interleaver ![]() bijectively maps the binary codewords
bijectively maps the binary codewords ![]() into the codewords
into the codewords ![]() . The interleaver is determined by the interleaving vector
. The interleaver is determined by the interleaving vector ![]() which defines the mapping between
which defines the mapping between ![]() and
and ![]() as follows:
as follows:
where ![]() (see (2.80)) and
(see (2.80)) and
The sequences ![]() and
and ![]() are obtained, respectively, by reading columnwise the elements of the sequences of binary vectors
are obtained, respectively, by reading columnwise the elements of the sequences of binary vectors ![]() and
and ![]() . Very often, we will skip the notation which includes the interleaving vector
. Very often, we will skip the notation which includes the interleaving vector ![]() , i.e., we use
, i.e., we use ![]() .
.
We now define two simple and well-known interleavers.
As the interleaving transforms the code ![]() into the code
into the code ![]() , considerations in the domain of the codewords
, considerations in the domain of the codewords ![]() may help clarify the relationships between modulation and coding. In what follows, we “reuse” the DS-related definitions from Section 2.6.
may help clarify the relationships between modulation and coding. In what follows, we “reuse” the DS-related definitions from Section 2.6.
Further, we adapt Definition 2.23 as follows.
We note that the interleaving does not change the HW of the codewords, and thus, we have ![]() . On the other hand, in general,
. On the other hand, in general, ![]() . In fact, the GHW
. In fact, the GHW ![]() used in
used in ![]() and in
and in ![]() has, in general, different dimensions:
has, in general, different dimensions: ![]() for
for ![]() and
and ![]() for
for ![]() .
.
At this point, it is also useful to define the generalized input-output distance spectrum (GIODS) of the code ![]() , which relates the input sequences
, which relates the input sequences ![]() and the corresponding codewords
and the corresponding codewords ![]() .
.
It is then convenient to introduce the input-dependent distance spectrum (IDS) and generalized input-dependent distance spectrum (GIDS) of the encoder.
As the IDS and GIDS defined above relate the codewords ![]() and the input sequences
and the input sequences ![]() , they depend on the encoding operation. They are thus different from the DS or GDS in Definitions 2.21 and 2.23 which are defined solely for the codewords, i.e., in abstraction of how the encoding is done.
, they depend on the encoding operation. They are thus different from the DS or GDS in Definitions 2.21 and 2.23 which are defined solely for the codewords, i.e., in abstraction of how the encoding is done.
The following relationships are obtained via marginalization of the GIODS
The codewords ![]() and
and ![]() are related to each other via the bijective operation of interleaving, which owes its presence to considerations similar to those we evoked in Section 2.6 to motivate the introduction of the DS. We repeat here the assertion we made that the “protection” against decoding errors can be related to the HW of the codewords (or the HD between pairs of codewords). Then,in order to simplify the decoder's task of distinguishing between the binary codewords, we postulate, not only to have a large distance between all pairs of codewords, but also to transmit every bit of the binary difference between the codewords, using different symbols
are related to each other via the bijective operation of interleaving, which owes its presence to considerations similar to those we evoked in Section 2.6 to motivate the introduction of the DS. We repeat here the assertion we made that the “protection” against decoding errors can be related to the HW of the codewords (or the HD between pairs of codewords). Then,in order to simplify the decoder's task of distinguishing between the binary codewords, we postulate, not only to have a large distance between all pairs of codewords, but also to transmit every bit of the binary difference between the codewords, using different symbols ![]() . In such a case, we decrease the probability that the respective observations
. In such a case, we decrease the probability that the respective observations ![]() are simultaneously affected by the channel in an adverse manner. These considerations motivate the following definition.
are simultaneously affected by the channel in an adverse manner. These considerations motivate the following definition.
Clearly, the codeword diversity ![]() is bounded as
is bounded as
We thus say that the codeword ![]() achieves its maximum diversity if
achieves its maximum diversity if ![]() , which depends on how the interleaver allocates all the nonzero elements in
, which depends on how the interleaver allocates all the nonzero elements in ![]() to different labels
to different labels ![]() . In addition, if
. In addition, if ![]() , the codeword cannot achieve its maximum diversity. From now on, we only consider the cases
, the codeword cannot achieve its maximum diversity. From now on, we only consider the cases ![]() .
.
The interleaver diversity efficiency is bounded as ![]() , where interleavers that achieve the upper bound are desirable. This is justified by the assertions we made above, namely that it is desirable to transmit bits in which the codewords differ using independent symbols. As a yardstick to compare the diversity efficiency of different interleavers, we define the random interleaver.
, where interleavers that achieve the upper bound are desirable. This is justified by the assertions we made above, namely that it is desirable to transmit bits in which the codewords differ using independent symbols. As a yardstick to compare the diversity efficiency of different interleavers, we define the random interleaver.
We note that the codewords ![]() are generated in a deterministic manner, but for a random interleaver, the mapping between
are generated in a deterministic manner, but for a random interleaver, the mapping between ![]() and
and ![]() is random. Therefore, both the codeword diversity
is random. Therefore, both the codeword diversity ![]() and the interleaver diversity efficiency
and the interleaver diversity efficiency ![]() are random. To evaluate them meaningfully, we then use expectations, i.e., we consider their average with respect to the distribution of the interleaving vector
are random. To evaluate them meaningfully, we then use expectations, i.e., we consider their average with respect to the distribution of the interleaving vector ![]() given in (2.119).10
given in (2.119).10
For large ![]() , treating
, treating ![]() as a continuous variable, we may apply a first-order Taylor-series approximation of
as a continuous variable, we may apply a first-order Taylor-series approximation of ![]() around
around ![]() , to obtain
, to obtain
From now, we will refer to ![]() as the average complementary interleaver diversity efficiency.
as the average complementary interleaver diversity efficiency.
In Fig. 2.23, we show the expression (2.121) as well as the approximation in (2.127). We observe that the average complementary interleaver diversity efficiency is strongly affected by an increase in ![]() . For example, when
. For example, when ![]() , to keep the average complementary interleaver diversity efficiency at
, to keep the average complementary interleaver diversity efficiency at ![]() ,
, ![]() is necessary for
is necessary for ![]() but we need
but we need ![]() when
when ![]() . It is also interesting to note from Fig. 2.23 that a random interleaver does not guarantee an average interleaver diversity
. It is also interesting to note from Fig. 2.23 that a random interleaver does not guarantee an average interleaver diversity ![]() , even for large
, even for large ![]() .
.

Figure 2.23 Average complementary interleaver diversity efficiency (solid lines) and its large- approximation (2.127) (dashed lines) for
approximation (2.127) (dashed lines) for 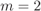 (hollow markers, e.g.,
(hollow markers, e.g.,  ) and for
) and for 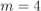 (filled markers, e.g., •)
(filled markers, e.g., •)
Another property of the code ![]() we are interested in is related to the way the codewords' weights are distributed across the bit positions after interleaving, which we formalize in the following.
we are interested in is related to the way the codewords' weights are distributed across the bit positions after interleaving, which we formalize in the following.
Up to now, we have considered two effects of the interleaving of the code ![]() independently: the GDS in Definition 2.36 deals with the assignment of
independently: the GDS in Definition 2.36 deals with the assignment of ![]() nonzero bits from
nonzero bits from ![]() into different positions
into different positions ![]() at the modulator's input, while the interleaver diversity efficiency in Definition 2.40 deals with the assignment of these
at the modulator's input, while the interleaver diversity efficiency in Definition 2.40 deals with the assignment of these ![]() bits into labels at different time instants
bits into labels at different time instants ![]() . We may also jointly consider these two “dimensions” of the interleaving. Namely, for all
. We may also jointly consider these two “dimensions” of the interleaving. Namely, for all ![]() with
with ![]() , we have
, we have
i.e., the ratio between the number of codewords in the set ![]() which achieve their maximum diversity and the number of codewords in the set
which achieve their maximum diversity and the number of codewords in the set ![]() depends solely on
depends solely on ![]() . The proof of (2.140) can be made along the lines of the proofs of Theorems 2.43 and 2.45.
. The proof of (2.140) can be made along the lines of the proofs of Theorems 2.43 and 2.45.
Theorem 2.45 takes advantage of the enumeration over all possible interleavers ![]() , which makes the enumeration over all codewords unnecessary. As we can use any codeword
, which makes the enumeration over all codewords unnecessary. As we can use any codeword ![]() , the assignment of the bits
, the assignment of the bits ![]() to the position
to the position ![]() in the label
in the label ![]() becomes independent of the codeword
becomes independent of the codeword ![]() . Thus, we can simply treat the assigned position
. Thus, we can simply treat the assigned position ![]() as a random variable
as a random variable ![]() . The assignment is not “biased” toward any position
. The assignment is not “biased” toward any position ![]() , so
, so ![]() has a uniform distribution on the set
has a uniform distribution on the set ![]() , which leads to (2.139). Such a model is depicted in Fig. 2.24.
, which leads to (2.139). Such a model is depicted in Fig. 2.24.
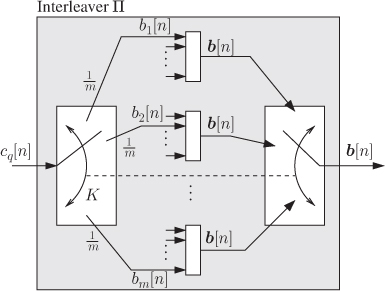
Figure 2.24 Model of the random interleaver: the bits 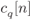 are mapped to the bit positions
are mapped to the bit positions  within the label
within the label  , where
, where  is a uniformly distributed random variable, i.e.,
is a uniformly distributed random variable, i.e., 
The concept of random interleavers leads to the random position-assignment model from Fig. 2.24. Of course, in practice, a fixed interleaving vector ![]() is used. However, we will be able to apply the simple model depicted in Fig. 2.24 to analyze also a fixed interleaver, provided that it inherits some of the properties of the random interleaver. In such a case, we talk about quasirandom interleavers which we define in the following.
is used. However, we will be able to apply the simple model depicted in Fig. 2.24 to analyze also a fixed interleaver, provided that it inherits some of the properties of the random interleaver. In such a case, we talk about quasirandom interleavers which we define in the following.
As we refer to properties of the interleavers for ![]() , when discussing their effects, we have in mind a particular family of interleavers which defines how to obtain the interleaving vector
, when discussing their effects, we have in mind a particular family of interleavers which defines how to obtain the interleaving vector ![]() for each value of
for each value of ![]() . Therefore, strictly speaking, the definition above applies to a family of interleavers and not to a particular interleaver with interleaving vector
. Therefore, strictly speaking, the definition above applies to a family of interleavers and not to a particular interleaver with interleaving vector ![]() .
.
The essential difference between the random interleaving and quasirandom interleaving lies in the analysis of the DS or GDS. In the case of random interleaving, instead of enumerating all possible codewords ![]() , we fix one of them and average the spectrum over all possible realizations of the interleaver. In the case of a fixed (quasirandom) interleaving, we enumerate the codewords
, we fix one of them and average the spectrum over all possible realizations of the interleaver. In the case of a fixed (quasirandom) interleaving, we enumerate the codewords ![]() produced by interleaving all the codewords
produced by interleaving all the codewords ![]() from
from ![]() . The property of quasirandomness assumes that the enumeration over the codewords will produces the same average (spectrum) as the enumeration over the interleavers.
. The property of quasirandomness assumes that the enumeration over the codewords will produces the same average (spectrum) as the enumeration over the interleavers.
Of course, quasirandomness is a property which depends on the code and how the family of interleavers is defined. In the following example, we analyze a CC and two particular interleavers in the light of the conditions of quasirandomness.

Figure 2.25 Complementary interleaver diversity efficiency 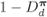 for the CENC with
for the CENC with  and two types of interleavers: (a) rectangular and (b) pseudorandom
and two types of interleavers: (a) rectangular and (b) pseudorandom

Figure 2.26 Values of  for
for  when using a rectangular interleaver for different values of
when using a rectangular interleaver for different values of  : (a)
: (a) 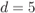 , (b)
, (b)  , (c)
, (c) 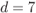 , and (d)
, and (d) 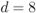 . The thick solid lines are the distributions of the random interleaver
. The thick solid lines are the distributions of the random interleaver 

Figure 2.27 Values of  for
for  when using a pseudorandom interleaver for different values of
when using a pseudorandom interleaver for different values of 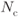 : (a)
: (a)  , (b)
, (b)  , (c)
, (c)  , and (d)
, and (d) 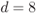 . The thick solid lines are the distributions of the random interleaver
. The thick solid lines are the distributions of the random interleaver 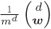
2.8 Bibliographical Notes
TCM was originally proposed at ISIT 1976 [1] and then developed in [2–4]. TCM quickly became a very popular research topic and improved TCM paradigms were soon proposed: rotationally invariant TCM [5, 6], multidimensional TCM [3, 7–9], TCM based on cosets and lattices [10, 11], TCM with nonequally spaced symbols [12–15], etc. TCM went also quickly from research to practice; it was introduced in the modem standards in the early 1990s (V.32 [16] and V.32bis [17]) increasing the transmission rates up to 14.4 kbps. TCM is a well-studied topic and extensive information about it can be found, e.g., in [18, 19, Section 8.12], [20, Chapter 4], [21, Section 8.2], [22, Chapter 14], [23, Chapter 18]. TCM for fading channels is studied in [20, Chapter 5].
MLC was proposed by Imai and Hirakawa in [24, 25]. MLC with MSD as well as the design rules for selecting the ![]() rates of the encoders were analyzed in detail in [26, 27]. MLC for fading channels, which includes bit interleavers in each level, has been proposed in [28], and MLC using capacity-approaching (turbo) codes was proposed in [29].
rates of the encoders were analyzed in detail in [26, 27]. MLC for fading channels, which includes bit interleavers in each level, has been proposed in [28], and MLC using capacity-approaching (turbo) codes was proposed in [29].
BICM was introduced in [30] and later analyzed from an information-theoretic point of view in [31, 32]. BICM-ID was introduced in [33–35] where BICM was recognized as a serial concatenation of encoders (the encoder and the mapper) and further studied in [36–40]. For relevant references about the topics related to BICM treated in this book, we refer the reader to the end of each chapter.
The discrete-time AWGN model and the detection of signals in a continuous-time AWGN channel is a well-studied topic in the literature, see, e.g., [19, Chapter 3], [41, Chapter 2], [42, Chapter 5], [43, Section 2.5], [44, Chapters 26 and 28]. For more details about models for fading channels, we refer the reader to [19, Chapter 13] or to [42, Chapter 3]. In particular, more details on the Nakagami fading distribution [45] are given in [42, Section 3.2.2].
The BRGC was introduced in [46] and studied for uncoded transmission in [47, 48] where its asymptotic optimality for PAM, PSK, and QAM constellations was proved. For more details about Gray labelings, we refer the reader also to [49]. The expansion used to define the BRGC was introduced in [47]. An alternative construction that can be used is based on reflections, which is detailed in [47, Section IV]. The FBC was analyzed in [50] for uncoded transmission and the BSGC was recently introduced in [51].
For 8PSK and in the context of BICM-ID, other labelings have been proposed; see [52] and references therein. For example, the SSP labeling was proposed in [40, Fig. 2 (c)], (later found via an algorithmic search in [38, Fig. 2 (a)], and called M8), or the MSP labeling [53, Fig. 2 (b)]. These two labelings are shown in Fig. 2.17 (b) and (c). The M16 labeling used in BICM-ID for 16QAM was first proposed in [38, Fig. 2 (b)].
The design of bit labelings for improving the performance of BICM-ID has been studied in [37, 38, 54–59] and references therein. Most of the works consider one-to-one mappers (i.e., a bijective mapping from labels to constellation symbols); however, when signal shaping is considered, a many-to-one mapping (![]() ) may be useful, as shown in [59, Section 6.2].
) may be useful, as shown in [59, Section 6.2].
The channel capacity defined in 1948 by Shannon [60] spurred a great deal of activity and approaching Shannon's limit became one of the most important problems among researchers for about 45 years. The complexity of encoding/decoding was always an issue but these limits have been continuously pushed by the development of integrated circuits. CENCs provided a low-complexity encoding strategy and the Viterbi algorithm [61] gave a clever and relatively low-complexity decoding method. Introduced by Elias [62] in 1955, CENCs were studied extensively and their detailed description can be found in popular textbooks, e.g., [23, Chapter 11], [63, Chapter 5], [64]. The name for CENCs with ODS was coined by Frenger et al. in [65], however, most of the newly reported spectra in [65] had already been presented in [66, Tables III–V], [67, Tables II–IV], as later clarified in [68].
TCs were invented by Berrou et al. [69] and surprised the coding community with their performance maintaining relatively simple encoding and decoding via iterative processing. Since then, they have been analyzed in detail in many works and textbooks, e.g., [63, Chapter 8.2; 23, Chapter 16]; TCs are also used in many communication standards such as 3G and 4G telephony [70, Section 16.5.3], digital video broadcasting (DVB) standards [71], as well as in deep space communications [72, 73].
Most often, the BICM literature assumes that random interleaving with infinite length is used [31], which leads to the simple random multiplexing model we have shown in Fig. 2.24. The formulas describing the diversity efficiency of the finite-length interleaver can be found in [32, Chapter 4.3].
References
- [1] Ungerboeck, G. and Csajka, I. (1976) On improving data-link performance by increasing channel alphabet and introducing sequence decoding. International Symposium on Information Theory (ISIT), June 1976, Ronneby, Sweden (book of abstracts).
- [2] Ungerboeck, G. (1982) Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory, 28 (1), 55–67.
- [3] Ungerboeck, G. (1987) Trellis-coded modulation with redundant signal sets Part I: introduction. IEEE Commun. Mag., 25 (2), 5–11.
- [4] Ungerboeck, G. (1987) Trellis-coded modulation with redundant signal sets Part II: state of the art. IEEE Commun. Mag., 25 (2), 12–21.
- [5] Wei, L.-F. (1984) Rotationally invariant convolutional channel coding with expanded signal space—Part I: 180°. IEEE J. Sel. Areas Commun., SAC-2 (5), 659–671.
- [6] Wei, L.-F. (1984) Rotationally invariant convolutional channel coding with expanded signal space—Part II: Nonlinear codes. IEEE J. Sel. Areas Commun., SAC-2 (5), 672–686.
- [7] Wei, L.-F. (1987) Trellis-coded modulation with multidimensional constellations. IEEE Trans. Inf. Theory, IT-33 (4), 483–501.
- [8] Gersho, A. and Lawrence, V. B. (1984) Multidimensional signal constellations for voiceband data transmission. IEEE J. Sel. Areas Commun., SAC-2 (5), 687–702.
- [9] Forney, G. D. Jr., Gallager, R., Lang, G. R., Longstaff, F. M., and Qureshi, S. U. (1984) Efficient modulation for band-limited channels. IEEE J. Sel. Areas Commun., SAC-2 (5), 632–647.
- [10] Calderbank, A. R. and Sloane, N. J. A. (1987) New trellis codes based on lattices and cosets. IEEE Trans. Inf. Theory, IT-33 (2), 177–195.
- [11] Forney, G. D. Jr. (1988) Coset codes I: introduction and geometrical classification. IEEE Trans. Inf. Theory, 34 (6), 1123–1151 (invited paper).
- [12] Calderbank, R. and Mazo, J. E. (1984) A new description of trellis codes. IEEE Trans. Inf. Theory, IT-30 (6), 784–791.
- [13] van der Vleuten, R. J. and Weber, J. H. (1996) Optimized signal constellations of trellis-coded modulation on AWGN channels. IEEE Trans. Commun., 44 (6), 646–648.
- [14] Simon, M. K. and Divsalar, D. (1985) Combined trellis coding with asymmetric MPSK modulation. Jet Propulsion Laboratory, Pasadena, CA, JPL Pub. 85-24, May 1985.
- [15] Divsalar, D., Simon, M., and Yuen, J. (1987) Trellis coding with asymmetric modulations. IEEE Trans. Commun., 35 (2), 130–3141.
- [16] ITU (1993) A family of 2-wire, duplex modems operating at data signalling rates of up to 9600 bit/s for use on the general switched telephone network and on leased telephone-type circuits. ITU-T Recommendation V.32, Tech. Rep., International Telecommunication Union (ITU).
- [17] ITU (1991) A duplex modem operating at data signalling rates of up to 14 400 bit/s for use on the general switched telephone network and on leased point-to-point 2-wire telephone-type circuits. ITU-T Recommendation V.32 bis, Tech. Rep., International Telecommunication Union (ITU).
- [18] Biglieri, E., Divsalar, D., McLane, P. J., and Simon, M. K. (1992) Introduction to Trellis-Coded Modulation with Applications, Prentice Hall.
- [19] Proakis, J. G. and Salehi, M. (2008) Digital Communications, 5th edn, McGraw-Hill.
- [20] Jamali, S. H. and Le-Ngoc, T. (1994) Coded-Modulation Techniques for Fading Channels, Kluwer Academic Publishers.
- [21] Burr, A. (2001) Modulation and Coding for Wireless Communications, Prentice Hall.
- [22] Wicker, S. B. (1995) Error Control Systems for Digital Communication and Storage, Prentice Hall.
- [23] Lin, S. and Costello, D. J. Jr. (2004) Error Control Coding, 2nd edn, Prentice Hall, Englewood Cliffs, NJ.
- [24] Imai, H. and Hirakawa, S. (1977) A new multilevel coding method using error-correcting codes. IEEE Trans. Inf. Theory, IT-23 (3), 371–377.
- [25] Imai, H. and Hirakawa, S. (1977) Correction to ‘A new multilevel coding method using error-correcting codes’. IEEE Trans. Inf. Theory, IT-23 (6), 784.
- [26] Wachsmann, U., Fischer, R. F. H., and Huber, J. B. (1999) Multilevel codes: theoretical concepts and practical design rules. IEEE Trans. Inf. Theory, 45 (5), 1361–1391.
- [27] Beygi, L., Agrell, E., Karlsson, M., and Makki, B. (2010) A novel rate allocation method for multilevel coded modulation. IEEE International Symposium on Information Theory (ISIT), June 2010, Austin, TX.
- [28] Kofman, Y., Zehavi, E., and Shamai, S. (1994) Performance analysis of a multilevel coded modulation system. IEEE Trans. Commun., 42 (2/3/4), 299–312.
- [29] Wachsmann, U. and Huber, J. B. (1995) Power and bandwidth efficient digital communication using turbo codes in multilevel codes. Eur. Trans. Telecommun., 6 (5), 557–567.
- [30] Zehavi, E. (1992) 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun., 40 (3), 873–884.
- [31] Caire, G., Taricco, G., and Biglieri, E. (1998) Bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 44 (3), 927–946.
- [32] Guillén i Fàbregas, A., Martinez, A., and Caire, G. (2008) Bit-interleaved coded modulation. Found. Trends Commun. Inf. Theory, 5 (1–2), 1–153.
- [33] Li, X. and Ritcey, J. A. (1997) Bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett., 1 (6), 169–171.
- [34] ten Brink, S., Speidel, J., and Yan, R.-H. (1998) Iterative demapping for QPSK modulation. IEE Electron. Lett., 34 (15), 1459–1460.
- [35] Benedetto, S., Montorsi, G., Divsalar, D., and Pollara, F. (1998) Soft-input soft-output modules for the construction and distributed iterative decoding of code networks. Eur. Trans. Telecommun., 9 (2), 155–172.
- [36] Chindapol, A. and Ritcey, J. A. (2001) Design, analysis, and performance evaluation for BICM-ID with square QAM constellations in Rayleigh fading channels. IEEE J. Sel. Areas Commun., 19 (5), 944–957.
- [37] Tüchler, M. (2004) Design of serially concatenated systems depending on the block length. IEEE Trans. Commun., 52 (2), 209–218.
- [38] Schreckenbach, F., Görtz, N., Hagenauer, J., and Bauch, G. (2003) Optimization of symbol mappings for bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett., 7 (12), 593–595.
- [39] Szczecinski, L., Chafnaji, H., and Hermosilla, C. (2005) Modulation doping for iterative demapping of bit-interleaved coded modulation. IEEE Commun. Lett., 9 (12), 1031–1033.
- [40] Li, X., Chindapol, A., and Ritcey, J. A. (2002) Bit-interlaved coded modulation with iterative decoding and 8PSK signaling. IEEE Trans. Commun., 50 (6), 1250–1257.
- [41] Viterbi, A. J. and Omura, J. K. (1979) Principles of Digital Communications and Coding, McGraw-Hill.
- [42] Goldsmith, A. (2005) Wireless Communications, Cambridge University Press, New York.
- [43] Anderson, J. B. (2005) Digital Transmission Engineering, 2nd edn, John Wiley & Sons, Inc.
- [44] Lapidoth, A. (2009) A Foundation in Digital Communication, Cambridge University Press.
- [45] Nakagami, M. (1960) The
 -distribution, a general formula of intensity distribution of rapid fading, in Statistical Methods in Radio Wave Propagation (ed. W.G. Hoffman), Pergamon, Oxford.
-distribution, a general formula of intensity distribution of rapid fading, in Statistical Methods in Radio Wave Propagation (ed. W.G. Hoffman), Pergamon, Oxford. - [46] Gray, F. (1953) Pulse code communications. US patent 2 632 058.
- [47] Agrell, E., Lassing, J., Ström, E. G., and Ottosson, T. (2004) On the optimality of the binary reflected Gray code. IEEE Trans. Inf. Theory, 50 (12), 3170–3182.
- [48] Agrell, E., Lassing, J., Ström, E. G., and Ottosson, T. (2007) Gray coding for multilevel constellations in Gaussian noise. IEEE Trans. Inf. Theory, 53 (1), 224–235.
- [49] Savage, C. (1997) A survey of combinatorial Gray codes. SIAM Rev., 39 (4), 605–629.
- [50] Lassing, J., Ström, E. G., Agrell, E., and Ottosson, T. (2003) Unequal bit-error protection in coherent
 -ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL.
-ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL. - [51] Agrell, E. and Alvarado, A. (2011) Optimal alphabets and binary labelings for BICM at low SNR. IEEE Trans. Inf. Theory, 57 (10), 6650–6672.
- [52] Brännström, F. and Rasmussen, L. K. (2009) Classification of unique mappings for 8PSK based on bit-wise distance spectra. IEEE Trans. Inf. Theory, 55 (3), 1131–1145.
- [53] Tran, N. H. and Nguyen, H. H. (2006) Signal mappings of 8-ary constellations for bit interleaved coded modulation with iterative decoding. IEEE Trans. Broadcast., 52 (1), 92–99.
- [54] Tan, J. and Stüber, G. L. (2002) Analysis and design of interleaver mappings for iteratively decoded BICM. IEEE International Conference on Communications (ICC), May 2002, New York City, NY.
- [55] ten Brink, S. (2001) Convergence behaviour of iteratively decoded parallel concatenated codes. IEEE Trans. Commun., 49 (10), 1727–1737.
- [56] Zhao, L., Lampe, L., and Huber, J. (2003) Study of bit-interleaved coded space-time modulation with different labeling. IEEE Information Theory Workshop (ITW), March 2003, Paris, France.
- [57] Clevorn, T., Godtmann, S., and Vary, P. (2006) Optimized mappings for iteratively decoded BICM on Rayleigh channels with IQ interleaving. IEEE Vehicular Technology Conference (VTC-Spring), May 2006, Melbourne, Australia.
- [58] Tan, J. and Stüber, G. L. (2005) Analysis and design of symbol mappers for iteratively decoded BICM. IEEE Trans. Wireless Commun., 4 (2), 662–672.
- [59] Schreckenbach, F. Iterative decoding of bit-interleaved coded modulation. PhD dissertation, Technische Universität München, Munich, Germany, 2007.
- [60] Shannon, C. E. (1948) A mathematical theory of communications. Bell Syst. Tech. J., 27, 379–423 and 623–656.
- [61] Viterbi, A. J. (1967) Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory, 13 (2), 260–269.
- [62] Elias, P. (1955) Coding for noisy channels. IRE Conv. Rec., 3, 37–46.
- [63] Morelos-Zaragoza, R. H. (2002) The Art of Error Correcting Coding, 2nd edn, John Wiley & Sons.
- [64] Johannesson, R. and Zigangirov, K. S. (1999) Fundamentals of Convolutional Coding, 1st edn, IEEE Press.
- [65] Frenger, P., Orten, P., and Ottosson, T. (1999) Convolutional codes with optimum distance spectrum. IEEE Trans. Commun., 3 (11), 317–319.
- [66] Chang, J.-J., Hwang, D.-J., and Lin, M.-C. (1997) Some extended results on the search for good convolutional codes. IEEE Trans. Inf. Theory, 43 (6), 1682–1697.
- [67] Bocharova, I. E. and Kudryashov, B. D. (1997) Rational rate punctured convolutional codes for soft-decision Viterbi decoding. IEEE Trans. Inf. Theory, 43 (4), 1305–1313.
- [68] Frenger, P. K., Orten, P., and Ottosson, T. (2001) Comments and additions to recent papers on new convolutional codes. IEEE Trans. Inf. Theory, 47 (3), 1199–1201.
- [69] Berrou, C., Glavieux, A., and Thitimajshima, P. (1993) Near Shannon limit error-correcting coding and decoding: Turbo codes. IEEE International Conference on Communications (ICC), May 1993, Geneva, Switzerland.
- [70] Dahlman, E., Parkvall, S., Sköld, J., and Beming, P. (2008) 3G Evolution: HSPA and LTE for Mobile Broadband, 2nd edn, Academic Press.
- [71] ETSI (2009) Digital video broadcasting (DVB); Frame structure channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2). Technical Report ETSI EN 301 790 V1.5.1 (2009-05), ETSI.
- [72] Divsalar, D. and Pollara, F. (1995) Turbo codes for deep-space communications. TDA Progress Report 42-120, Jet Propulsion Laboratory, Pasadena, CA, pp. 29–39.
- [73] Divsalar, D. and Pollara, F. (1995) On the design of turbo codes. TDA Progress Report 42-123, Jet Propulsion Laboratory, Pasadena, CA, pp. 99–121.
