1.1 Coded Modulation

The main challenge in the design of communication systems is to reliably transmit digital information (very often, bits generated by the source) over a medium which we call the communication channel or simply the channel. This is done by mapping a sequence of bits to a sequence of symbols . These symbols are then used to vary (modulate) parameters of the continuous-time waveforms (such as amplitude, phase, and/or frequency), which are sent over the channel every seconds, i.e., at a symbol rate . The transmission rate of the system is thus equal to

1.1

where the bandwidth occupied by the waveforms is directly proportional to the symbol rate . Depending on the channel and the frequency used to carry the information, the waveforms may be electromagnetic, acoustic, optical, etc.

Throughout this book we will make abstraction of the actual waveforms and instead, consider a discrete-time model where the sequence of symbols is transmitted through the channel resulting in a sequence of received symbols . In this discrete-time model, both the transmitted and received symbol at each time instant are -dimensional column vectors. We also assume that linear modulation is used, that the transmitted waveforms satisfy the Nyquist condition, and that the channel is memoryless. Therefore, assuming perfect time/frequency synchronization, it is enough to model the relationship between the transmitted and received signals at time , i.e.,

1.2

In (1.2), we use to model the channel attenuation (gain) and to model an unknown interfering signal (most often the noise). Using this model, we analyze the transmission rate (also known as spectral efficiency):

1.3

which is independent of , thus allowing us to make abstraction of the bandwidth of the waveforms used for transmission. Clearly, and are related via

1.4

The process of mapping the information bits to the symbols is known as coding and are called codewords. We will often relate to well-known results stemming from the works of Shannon [1, 2] which defined the fundamental limits for reliable communication over the channel. Modeling the transmitted and received symbols and as random vectors and with distributions and , the rate is upper bounded by the mutual information (MI) . As long as , the probability of decoding error (i.e., choosing the wrong information sequence) can be made arbitrarily small when goes to infinity. The maximum achievable rate , called the channel capacity, is obtained by maximizing over the distribution of the symbols , and it represents the ultimate transmission rate for the channel. In the case when is modeled as a Gaussian vector, the probability density function (PDF) that maximizes the MI is also Gaussian, which is one of the most popular results establishing limits for a reliable transmission.

The achievability proof is typically based on random-coding arguments, where, to create the codewords which form the codebook , the symbols are generated from the distribution . At the receiver's side, the decoder decides in favor of the most likely sequence from the codebook, i.e., it uses the maximum likelihood (ML) decoding rule:

1.5

When grows, however, the suggested encoding and decoding cannot be used as practical means for the construction of the coding scheme. First, because storing the codewords results in excessive memory requirements, and second, because an exhaustive enumeration over codewords in the set in (1.5) would be prohibitively complex. In practice, the codebook is not randomly generated, but instead, obtained using an appropriately defined deterministic algorithm taking information bits as input. The structure of the code should simplify the decoding but also the encoding, i.e., the transmitter can generate the codewords on the fly (the codewords do not need to be stored).

To make the encoding and decoding practical, some “structure” has to be imposed on the codewords. The first constraint typically imposed is that the transmitted symbols are taken from a discrete predefined set , called a constellation. Moreover, the structure of the code should also simplify the decoding, as only the codewords complying with the constraints of the imposed structure are to be considered.

Consider the simple case of (i.e., is in fact a scalar), when the constellation is given by , i.e., a -ary pulse amplitude modulation (PAM) (2PAM) constellation, and when the received symbol is corrupted by additive white Gaussian noise (AWGN), i.e., where is a zero-mean Gaussian random variable with variance . We show in Fig. 1.1 the MI for this case and compare it with the capacity which relies on the optimization of the distribution of . This figure indicates that for , both values are practically identical. This allows us to focus on the design of binary codes with rate that can operate reliably without bothering about the theoretical suboptimality of the chosen constellation. This has been in fact the focus of research for many years, resulting in various binary codes being developed and used in practice. Initially, convolutional codes (CCs) received quite a lot of attention, but more recently, the focus has been on “capacity-approaching” codes such as turbo codes (TCs) or low-density parity-check (LDPC) codes. Their performance is deemed to be very “close” to the limits defined by the MI, even though the decoding does not rely on the ML rule in (1.5).

One particular problem becomes evident when analyzing Fig 1.1: the MI curve for 2PAM saturates at , and thus, it is impossible to transmit at rates . From (1.4) and , we conclude that if we want to increase the transmission rate , we need to increase the rate , and therefore, the transmission bandwidth. This is usually called bandwidth expansion and might be unacceptable in many cases, including modern wireless communication systems with stringent constraints on the available frequency bands.

The solution to the problem of increasing the transmission rate without bandwidth expansion is to use a high-order constellation and move the upper bound on from to . Combining coding with nonbinary modulation (i.e., high-order constellations) is often referred to as coded modulation (CM), to emphasize that not only coding but also the mapping from the code bits to the constellation symbols is important. The core problem in CM design is to choose the appropriate coding scheme that generates symbols from the constellation and results in reliable transmission at rate . On the practical side, we also need a CM which is easy to implement and which—because of the ever-increasing importance of wireless communications—allows us to adjust the coding rate to the channel state, usually known as adaptive modulation and coding (AMC).

A well-known CM is the so-called trellis-coded modulation (TCM), where convolutional encoders (CENCs) are carefully combined with a high-order constellation . However, in the past decades, a new CM became prevalent and is the focus of this work: bit-interleaved coded modulation (BICM). The key component in BICM is a (suboptimal) two-step decoding process. First, logarithmic likelihood ratios (LLRs, also known as L-values) are calculated, and then a soft-input binary decoder is used. In the next section, we give a brief outline of the historical developments in the area of CM, with a particular emphasis on BICM.

1.2 The Road Toward BICM

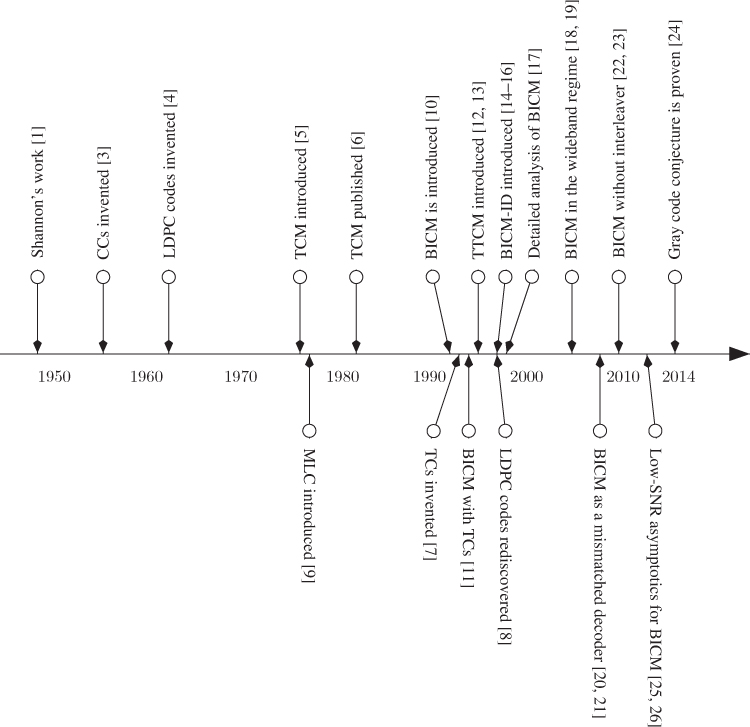
The area of CM has been explored for many years. In what follows, we show some of the milestones in this area, which culminated with the introduction of BICM. In Fig. 1.2, we show a timeline of the CM developments, with emphasis on BICM.

The early works on CM in the 1970s include those by de Buda [27, 28], Massey [29], Miyakawa et al. [30], Anderson and Taylor [31], and Aulin [32]. The first breakthroughs for coding for came with Ungerboeck and Csajka's TCM [5, 6, 33, 34] and Imai and Hirakawa's multilevel coding (MLC) [9, 35]. For a detailed historical overview of the early works on CM, we refer the reader to [36, Section 1.2] and [37, pp. 952–953]. Also, good summaries of the efforts made over the years to approach Shannon's limit can be found in [38, 39].

BICM's birth is attributed to the paper by Zehavi [10]. More particularly, Zehavi compared BICM based on CCs to TCM and showed that while BICM loses to TCM in terms of Euclidean distance (ED), it wins in terms of diversity. This fundamental observation spurred interest in BICM.

BICM was then analyzed in [17] by Caire et al., where achievable rates for BICM were shown to be very close to those reached by CM, provided that a Gray labeling was used. Gray codes were then conjectured to be the optimal binary labeling for BICM. These information-theoretic arguments were important because at the time [10] appeared, capacity-approaching codes (TCs) invented by Berrou et al. [7] were already being used together with binary modulation. Furthermore, CM inspired by the turbo principle were being devised at that time, in particular, the so-called turbo trellis-coded modulation (TTCM) [12, 13, 40–43]. In TTCM, coding and modulation were tightly coupled, and thus, changing the targeted spectral efficiency typically required a change in the CM design.

BICM appeared then as an alternative to “capacity-approaching” CM such as TTCM, where, to eliminate the rigidity of such systems, a small decrease in terms of achievable rate was an acceptable price to pay. In 1994, the combination of a capacity-approaching TC using the BICM paradigm was proposed for the first time [11]. This combination is based on a fairly simple implementation and turned out to perform very well, as later shown, e.g., in [44].

In 2003, Le Goff [45] analyzed the relationship between achievable rates and the performance of practical coding schemes. It was argued that the gap between the CM and BICM rates translates into performance differences between TCM and BICM when both are based on “capacity-approaching” codes. However, these differences are in most cases so small that it may be difficult to relate them to the performance loss of different practical coding schemes whose “strengths” are difficult to compare. For example, the results in [45, Fig. 6], show that the TTCM of [13, 40] outperforms BICM for (by a fraction of a decibel), however, for BICM outperforms the TTCM of [42]. This comparison illustrates well the fact that using TCM based on a concatenated coding does not guarantee the “strength” of the resulting system. In fact, this example highlights the flexibility of BICM whose coding rate was chosen arbitrarily without any implementation hassle, in contrast to changing the rate for TCM, which usually requires a change of the encoding structure.

Recognizing the bit-to-symbol mapper as an encoder, BICM was later cast into the framework of serially concatenated codes in [14–16]. This led to the introduction of bit-interleaved coded modulation with iterative demapping (BICM-ID) studied, e.g., in [46–50]. From the very start, the key role of the binary labeling for BICM-ID was recognized and extensively studied in the literature; for details about this, we refer the reader to [47, 48, 51–56] and references therein.

An information-theoretic analysis of BICM¹ was always at the forefront of analytical developments. One of the most important information-theoretic papers in this area is [17], where a formal model to analyze the rates achievable in BICM was proposed. Later, Martinez et al. [20] recognized BICM as a mismatched decoder and the model of [17] was refined. It was also shown in [20] that in terms of achievable rates, the interleaver plays no role, and that the key element is the suboptimal (mismatched) decoder. This observation is closely linked to the results in [22, 23] where it is shown that when BICM with CCs is used in nonfading channels, a better error probability can be obtained if the interleaver is completely removed from the transceivers. BICM in the wideband regime was first studied in [18, 19, 57], and later generalized to multidimensional constellations and arbitrary input distributions in [25, 26]. The long-standing Gray code conjecture for BICM was recently proven for one-dimensional constellations in [24].

1.3 Why Everybody Loves BICM

Striving for a simple and flexible CM, we may need to trade off its performance. Indeed, this is what happens in practice. BICM is most often the answer to a simplicity and flexibility requirement, while the performance loss with respect to the potentially optimal/better CM are moderate, or at least acceptable. In our view, the main reasons that make BICM systems particularly appealing and explain their omnipresence in practical communication systems are the following.

1. Flexibility: Tributary to the bit-level operation, BICM provides a high design flexibility. Unlike other CM (e.g., TCM or TTCM) where owing to the well-structured relationship between the encoder and the modulator, the encoder and coding rate must be carefully matched to the constellation, BICM allows the designer to choose the constellation and the encoder independently. This is why BICM is usually considered to be a pragmatic approach to CM. This “unstructured” transmission characteristic of BICM yields a flexibility so high that it allows for a straightforward implementation of the so-called irregular modulation (where modulation varies within the transmitted block of symbols) [58] or irregular coding (where the coding/puncturing may vary within the block of bits) [47]. The flexibility is particularly important in wireless communications where the stream of data must be matched to the structures imposed by a multiuser communication context (such as slots and frames) when transmitting over variable channel conditions. The flexibility of BICM can be hardly beaten as all operations are done at the bit level. For example, to get the most out of a varying channel, puncturing, rate matching, bit padding, and other operations typical in wireless standards can be done with arbitrary (up to a bit level) granularity. Performing similar operations in other CM paradigms is less straightforward.
2. Robustness: As BICM uses one decoder, only one parameter (the rate) is to be adjusted, which makes AMC not only easy to implement but also more robust to changes in the channel variations. This may be contrasted with MLC, where multiple decoders are needed (which may or may not collaborate with each other) and their respective rates have to be jointly adjusted to the channel conditions. Although BICM and MLC may be ultimately fit into the same framework (see [59] for details), we will maintain their conventional separation and consider MLC as a different CM paradigm. However, many elements of the analysis we propose in this book are applicable also to MLC, particularly those related to the analysis of the reliability metrics for the code bits.
3. Negligible Losses in Scalar Channels: The appearance of “capacity-approaching” binary codes made the difference between optimal CM systems and BICM negligible for most practical purposes, when transmitting over scalar channels. The eventual differences of fractions of a decibel (if any) are not very relevant from a system-level perspective, and in most cases, can be considered a small price to pay compared to the advantages BICM systems offer.
4. Increased Diversity: When transmitting over fading channels, and thanks to the interleaving, the L-values used in the decision process are calculated from symbols affected by independent channel realizations, which increases the so-called transmission diversity. This particular observation (first made in [10]) spurred the initial interest in BICM. While this property is often evoked as the raison d'être of BICM, we note that communication systems such as third-generation partnership project (3GPP) or long-term evolution (LTE) are designed to operate with packetized transmission. As often the packets are much shorter than the channel coherence time, the time diversity is limited. In multicarrier transmission such as orthogonal frequency-division multiplexing (OFDM), the frequency diversity depends on the frequency selectivity of the channel and may be easier to exploit. Nevertheless, with the appearance of capacity-approaching codes such as TCs or LDPC codes, the diversity is less relevant than other parameters of the channel, such as the capacity, which these codes approach closely.

Nothing comes for free, and there are some drawbacks to using BICM:

1. Suboptimality: Owing to the bitwise processing, the BICM decoder is suboptimal. From an information-theoretic point of view, this translates into a decrease in achievable rates when compared to those obtained using an optimal decoder. These losses are small for transmission over scalar channels where a constellation with a Gray labeling is used. On the other hand, the losses become more important in multiple-input multiple-output (MIMO) channels, where the effective bit-to-symbol mapping is affected by the random channel variations. In these cases, the use of nonbinary codes might offer advantage over BICM. When using “weak” codes such as CCs, the suboptimality is observed also in nonfading scalar channels but may be remedied to some extent by appropriate modification (or even removal) of the interleaver.
2. Long Interleavers/Delays: To ensure independence of the L-values which the demapper calculates and passes to the channel decoder, relatively long interleavers might be required. This, in turn, causes a mandatory packet-based decoding, i.e., no symbol-after-symbol decoding can be performed. This fact, however, is less important with the presence of “capacity-approaching” codes, which rely on iterative decoding, and thus, inherently require packet-based processing.

1.4 Outline of the Contents

This book provides an exhaustive analysis of BICM, paying special attention to those properties that are of particular interest when compared to other CM paradigm. The book is therefore intended for those interested in theoretical aspects of CM transmission in general, and BICM in particular.

In order to give an overview of the chapters in this book, we consider the simple model of BICM transmission in Fig. 1.3. A block of binary data of length is encoded by a binary encoder (ENC) which produces binary codewords of length . The codewords are interleaved at bit level, and the resulting bitstream is separated into groups of bits that are mapped to symbols of an -ary constellation , where . The symbols are transmitted over the channel whose outcome is used at the receiver to calculate a posteriori probabilities for the transmitted bits, which are then used for decoding. Instead of probabilities, reliability metrics are most often expressed in the form of an LLR, also known as an L-value. These L-values are then deinterleaved and passed to the channel decoder.

• Chapter 2 introduces the basic definitions, concepts, and notational convention used throughout the book. CM transmission is discussed, as well as channel models, constellations, and binary labelings used in the book. A brief summary of CCs and TCs is also presented.
• Chapter 3 defines the L-values and their approximations/simplifications. The well-known maximum a posteriori (MAP) and ML decoding strategies are compared against the (suboptimal) BICM decoder shown in Fig. 1.3.
• Chapter 4 takes a closer look at the theoretical limits of CM with special attention paid to BICM. Achievable rates for BICM as a function of the constellation shape, the input distribution, and the binary labeling are studied.
• Chapter 5 characterizes the BICM channel in Fig. 1.3 as a binary-input real-output entity focusing on the probabilistic models of the L-values. PDFs of the L-values for one- and two-dimensional constellations are developed.
• Chapter 6 explains how to evaluate the performance of transmission without coding as well as different methods that can be used to approximate the performance of the encoder–decoder pair in BICM transmission.
• Chapter 7 deals with the problem of mismatched L-values. Suitable strategies for correcting the mismatched L-values are presented. Special attention is paid to the correction based on a linear scaling.
• Chapter 8 shows how to exploit unequal error protection (UEP) inherently present in BICM and caused by the binary labeling of the constellation. The performance evaluation tools developed in the previous chapters are refined and a design of the interleaver and the encoder is proposed, taking advantage of UEP.
• Chapter 9 studies the use of a BICM receiver for trellis codes in nonfading channels. This is motivated by results that show that for the AWGN channel and CENCs, the use of a trellis encoder (without an interleaver) and a BICM receiver has an improved performance when compared to standard BICM configurations. Equivalences between different encoders and the optimal selection of CCs are also analyzed.

There are some important issues related to BICM which are not addressed in this work. In what follows, we list some of the ones we feel deserve a more in-depth study.

1. BICM for MIMO (or more generally for high-dimensional constellations) has to rely on an efficient and most likely suboptimal calculation of the L-values. This is caused by the fact that by increasing the size of the constellation and the number of antennas, the enumeration of a large number of terms becomes the computational bottleneck of the receiver. Finding suitable suboptimal detection schemes as well as methods for their characterization is a challenging issue.
2. BICM-ID devised in the early years of BICM is a theoretically interesting solution treating the BICM transmitter as a serially concatenated code. A remarkable improvement with iterations is obtained by custom-tailoring the labeling to the channel and the encoder. However, a complexity–performance trade-off analysis does not seem to provide a clear-cut answer to their ultimate usefulness in scalar channels. This is a promising solution when the channel introduces uncontrollable interference, as in the case of MIMO transmission.
3. Cooperative transmission is an increasingly popular subject and analyzing BICM transmission in the presence of multiple nodes using cooperative modulation schemes, network coding, and physical network coding is a promising venue to explore.

References

1. [1] Shannon, C. E. (1948) A mathematical theory of communications. Bell Syst. Tech. J., 27, 379–423 and 623–656.
2. [2] Shannon, C. E. (1949) Communication in the presence of noise. Proc. IRE, 37 (1), 10–21.
3. [3] Elias, P. (1955) Coding for noisy channels. IRE Conv. Rec., 3, 37–46.
4. [4] Gallager, R. (1962) Low-density parity-check codes. IRE Trans. Inf. Theory, IT-8, 21–28.
5. [5] Ungerboeck, G. and Csajka, I. (1976) On improving data-link performance by increasing channel alphabet and introducing sequence decoding. International Symposium on Information Theory (ISIT), June 1976, Ronneby, Sweden (book of abstracts).
6. [6] Ungerboeck, G. (1982) Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory, 28 (1), 55–67.
7. [7] Berrou, C., Glavieux, A., and Thitimajshima, P. (1993) Near Shannon limit error-correcting coding and decoding: Turbo codes. IEEE International Conference on Communications (ICC), May 1993, Geneva, Switzerland.
8. [8] MacKay, D. J. C. and Neal, R. M. (1997) Near Shannon limit performance of low density parity check codes. Electron. Lett., 33 (6), 457–458.
9. [9] Imai, H. and Hirakawa, S. (1977) A new multilevel coding method using error-correcting codes. IEEE Trans. Inf. Theory, IT-23 (3), 371–377.
10. [10] Zehavi, E. (1992) 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun., 40 (3), 873–884.
11. [11] Le Goff, S., Glavieux, A., and Berrou, C. (1994) Turbo-codes and high spectral efficiency modulation. IEEE International Conference on Communications (ICC), May 1994, New Orleans, LA.
12. [12] Benedetto, S., Divsalar, D., Montorsi, G., and Pollara, F. (1995) Bandwidth efficient parallel concatenated coding schemes. Electron. Lett., 31 (24), 2067–2069.
13. [13] Divsalar, D. and Pollara, F. (1995) On the design of turbo codes. TDA Progress Report 42-123, Jet Propulsion Laboratory, Pasadena, CA, pp. 99–121.
14. [14] Li, X. and Ritcey, J. A. (1997) Bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett., 1 (6), 169–171.
15. [15] ten Brink, S., Speidel, J., and Yan, R.- H. (1998) Iterative demapping for QPSK modulation. IEE Electron. Lett., 34 (15), 1459–1460.
16. [16] Benedetto, S., Montorsi, G., Divsalar, D., and Pollara, F. (1998) Soft-input soft-output modules for the construction and distributed iterative decoding of code networks. Eur. Trans. Telecommun., 9 (2), 155–172.
17. [17] Caire, G., Taricco, G., and Biglieri, E. (1998) Bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 44 (3), 927–946.
18. [18] Martinez, A., Guillén i Fàbregas, A., and Caire, G. (2008) Bit-interleaved coded modulation in the wideband regime. IEEE Trans. Inf. Theory, 54 (12), 5447–5455.
19. [19] Stierstorfer, C. and Fischer, R. F. H. (2008) Mappings for BICM in UWB scenarios. International ITG Conference on Source and Channel Coding (SCC), January 2008, Ulm, Germany.
20. [20] Martinez, A., Guillén i Fàbregas, A., Caire, G., and Willems, F. M. J. (2009) Bit-interleaved coded modulation revisited: a mismatched decoding perspective. IEEE Trans. Inf. Theory, 55 (6), 2756–2765.
21. [21] Guillén i Fàbregas, A., Martinez, A., and Caire, G. (2008) Bit-interleaved coded modulation. Found. Trends Commun. Inf. Theory, 5 (1–2), 1–153.
22. [22] Stierstorfer, C., Fischer, R. F. H., and Huber, J. B. (2010) Optimizing BICM with convolutional codes for transmission over the AWGN channel. International Zurich Seminar on Communications, March 2010, Zurich, Switzerland.
23. [23] Alvarado, A., Szczecinski, L., and Agrell, E. (2011) On BICM receivers for TCM transmission. IEEE Trans. Commun., 59 (10), 2692–2702.
24. [24] Alvarado, A., Brännström, F., Agrell, E., and Koch, T. (2014) High-SNR asymptotics of mutual information for discrete constellations with applications to BICM. IEEE Trans. Inf. Theory, 60 (2), 1061–1076.
25. [25] Agrell, E. and Alvarado, A. (2011) Optimal alphabets and binary labelings for BICM at low SNR. IEEE Trans. Inf. Theory, 57 (10), 6650–6672.
26. [26] Agrell, E. and Alvarado, A. (2013) Signal shaping for BICM at low SNR. IEEE Trans. Inf. Theory, 59 (4), 2396–2410.
27. [27] de Buda, R. (1972) Fast FSK signals and their demodulation. Can. Electron. Eng. J., 1, 28–34.
28. [28] de Buda, R. (1972) Coherent demodulation of frequency-shift keying with low deviation ratio. IEEE Trans. Commun., COM-20, 429–435.
29. [29] Massey, J. L. (1974) Coding and modulation in digital communications. International Zurich Seminar on Digital Communications, March 1974, Zurich, Switzerland.
30. [30] Miyakawa, H., Harashima, H., and Tanaka, Y. (1975) A new digital modulation scheme–Multi-mode binary CPFSK. 3rd International Conference Digital Satellite Communications, November 1975, Kyoto, Japan.
31. [31] Anderson, J. B. and Taylor, D. P. (1978) A bandwidth-efficient class of signal-space codes. IEEE Trans. Inf. Theory, IT-24 (6), 703–712.
32. [32] Aulin, T. (1979) CPM–A power and bandwidth efficient digital constant envelope modulation scheme. PhD dissertation, Lund University, Lund, Sweden.
33. [33] Ungerboeck, G. (1987) Trellis-coded modulation with redundant signal sets Part I: Introduction. IEEE Commun. Mag., 25 (2), 5–11.
34. [34] Ungerboeck, G. (1987) Trellis-coded modulation with redundant signal sets Part II: state of the art. IEEE Commun. Mag., 25 (2), 12–21.
35. [35] Imai, H. and Hirakawa, S. (1977) Correction to ‘A new multilevel coding method using error-correcting codes’. IEEE Trans. Inf. Theory, IT-23 (6), 784.
36. [36] Anderson, J. B. and Svensson, A. (2003) Coded Modulation Systems, Springer.
37. [37] Lin, S. and Costello, D. J. Jr. (2004) Error Control Coding, 2nd edn, Prentice Hall, Englewood Cliffs, NJ.
38. [38] Costello, D. J. Jr. and Forney, G. D. Jr. (2007) Channel coding: the road to channel capacity. Proc. IEEE, 95 (6), 1150–1177.
39. [39] Forney, G. D. Jr. and Ungerboeck, G. (1998) Modulation and coding for linear Gaussian channels. IEEE Trans. Inf. Theory, 44 (6), 2384–2415 (Invited Paper).
40. [40] Benedetto, S. and Montorsi, G. (1996) Design of parallel concatenated convolutional codes. IEEE Trans. Commun., 44 (5), 591–600.
41. [41] Benedetto, S., Divsalar, D., Montorsi, G., and Pollara, F. (1996) Parallel concatenated trellis coded modulation. IEEE International Conference on Communications (ICC), June 1996, Dallas, TX.
42. [42] Robertson, P. and Wörz, T. (1998) Bandwidth-efficient turbo trellis-coded modulation using punctured component codes. IEEE J. Sel. Areas Commun., 16 (2), 206–218.
43. [43] Blackert, W. J. and Wilson, S. G. (1996) Turbo trellis coded modulation. Conference on Information Sciences and Systems (CISS), March 1996, Princeton, NJ.
44. [44] Abramovici, I. and Shamai, S. (1999) On turbo encoded BICM. Ann. Telecommun., 54 (3–4), 225–234.
45. [45] Goff, S. Y. L. (2003) Signal constellations for bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 49 (1), 307–313.
46. [46] Chindapol, A. and Ritcey, J. A. (2001) Design, analysis, and performance evaluation for BICM-ID with square QAM constellations in Rayleigh fading channels. IEEE J. Sel. Areas Commun., 19 (5), 944–957.
47. [47] Tüchler, M. (2004) Design of serially concatenated systems depending on the block length. IEEE Trans. Commun., 52 (2), 209–218.
48. [48] Schreckenbach, F., Görtz, N., Hagenauer, J. and Bauch, G. (2003) Optimization of symbol mappings for bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett., 7 (12), 593–595.
49. [49] Szczecinski, L., Chafnaji, H., and Hermosilla, C. (2005) Modulation doping for iterative demapping of bit-interleaved coded modulation. IEEE Commun. Lett., 9 (12), 1031–1033.
50. [50] Li, X., Chindapol, A., and Ritcey, J. A. (2002) Bit-interlaved coded modulation with iterative decoding and 8PSK signaling. IEEE Trans. Commun., 50 (6), 1250–1257.
51. [51] Tan, J. and Stüber, G. L. (2002) Analysis and design of interleaver mappings for iteratively decoded BICM. IEEE International Conference on Communications (ICC), May 2002, New York City, NY.
52. [52] ten Brink, S. (2001) Convergence behaviour of iteratively decoded parallel concatenated codes. IEEE Trans. Commun., 49 (10), 1727–1737.
53. [53] Zhao, L., Lampe, L., and Huber, J. (2003) Study of bit-interleaved coded space-time modulation with different labeling. IEEE Information Theory Workshop (ITW), March 2003, Paris, France.
54. [54] Clevorn, T., Godtmann, S., and Vary, P. (2006) Optimized mappings for iteratively decoded BICM on Rayleigh channels with IQ interleaving. IEEE Vehicular Technology Conference (VTC-Spring), May 2006, Melbourne, Australia.
55. [55] Tan, J. and Stüber, G. L. (2005) Analysis and design of symbol mappers for iteratively decoded BICM. IEEE Trans. Wireless Commun., 4 (2), 662–672.
56. [56] Schreckenbach, F. (2007) Iterative decoding of bit-interleaved coded modulation. PhD dissertation, Technische Universität München, Munich, Germany.
57. [57] Alvarado, A., Agrell, E., Guillén i Fàbregas, A., and Martinez, A. (2010) Corrections to ‘Bit-interleaved coded modulation in the wideband regime’. IEEE Trans. Inf. Theory, 56 (12), 6513.
58. [58] Schreckenbach, F. and Bauch, G. (2006) Bit-interleaved coded irregular modulation. Eur. Trans. Telecommun., 17 (2), 269–282.
59. [59] Wachsmann, U., Fischer, R. F. H., and Huber, J. B. (1999) Multilevel codes: theoretical concepts and practical design rules. IEEE Trans. Inf. Theory, 45 (5), 1361–1391.