Chapter 8
Interleaver Design
In binary modulation all the bits receive the same “treatment” when transmitted over the channel, i.e., the L-values have the same conditional probability density function (PDF). The error probability is also the same for all bits, i.e., each bit is equally “protected” against errors. High-order modulations, on the other hand, introduce unequal error protection (UEP). This is an inherent property of bit-interleaved coded modulation (BICM) and depends on the labeling and the form of the constellation. While previously we considered the use of quasi-random interleavers (which average out the UEP), in this chapter we want to take advantage of the UEP. To this end, we propose to design interleavers for BICM, which requires the analytical tools developed in the previous chapters to be refined.
This chapter is organized as follows. In Section 8.1 we introduce the idea of UEP and study a particular interleaver that takes into account the presence of the UEP: the so-called multiple-input interleaver (M-interleaver). In Section 8.1.1 we study the performance of BICM with M-interleavers generalizing the results from Chapter 6. In Section 8.1.1 we also study the problem of a joint interleaver and code design for such BICM transceivers.
8.1 UEP in BICM and M-interleavers
UEP may be easily explained using the communication-theoretic tools of Chapter 6 or the information-theoretic tools of Chapter 4. Let us revisit these concepts through a simple example.

Figure 8.1 UEP for 8PAM constellation labeled by the BRGC over the AWGN channel: (a) BEP for uncoded transmission in (6.26) and (b) normalized BICM-GMI and the bit-wise MIs 
Example 8.1 illustrates the concept of UEP caused by the binary labeling. In what follows we focus on its communication-theoretic analysis. Namely, we characterize the performance of the BICM decoder by explicitly taking into account the fact that the L-values calculated by the demapper for different bit positions have different distributions.
8.1.1 Preserving UEP in BICM
Let us consider a model for the BICM transmission, which generalizes the BICM channel in Fig. 5.1. This is done in Fig. 8.2 where all the elements appearing after the encoder and before the decoder are treated as a BICM channel with a vectorial input ![]() and a vectorial output
and a vectorial output ![]() . In this way, the code bits from the
. In this way, the code bits from the ![]() different classes are explicitly shown in Fig. 8.2 as the inputs to the BICM channel.
different classes are explicitly shown in Fig. 8.2 as the inputs to the BICM channel.

Figure 8.2 Refined model of the BICM channel: the  classes of code bits are identified at the inputs of the BICM channel
classes of code bits are identified at the inputs of the BICM channel

Figure 8.3 Zehavi's BICM channel: (a) each class of the code bits is individually interleaved and mapped to a given input of the mapper (multiple interleavers) and (b) equivalent parallel channel model defined by the conditional PDFs  ,
,  (parallel channel model)
(parallel channel model)
As discussed in Section 6.2.4, if the interleaver complies with the conditions of quasirandomness (see Definition 2.46), the L-values ![]() may be considered independent. Using similar considerations, for
may be considered independent. Using similar considerations, for ![]() , we can replace all the elements of the generalized BICM channel by a set of parallel channels. This is shown in Fig. 8.3 (b), where each channel yields L-values having distribution
, we can replace all the elements of the generalized BICM channel by a set of parallel channels. This is shown in Fig. 8.3 (b), where each channel yields L-values having distribution ![]() .
.
Let us now compare the conventional single-input interleaver (S-interleaver) ![]() with the M-interleaver shown in Fig. 8.3. The S-interleaver is the one we studied in the previous chapters and operates without differentiating the classes of code bits. For the S-interleaver, according to the considerations in Section 6.2 leading to (6.227), we have
with the M-interleaver shown in Fig. 8.3. The S-interleaver is the one we studied in the previous chapters and operates without differentiating the classes of code bits. For the S-interleaver, according to the considerations in Section 6.2 leading to (6.227), we have
For the M-interleaver with ![]() , the
, the ![]() th L-values
th L-values ![]() is the deinterleaved version of
is the deinterleaved version of ![]() , so we obtain
, so we obtain
Thus, using the S-interleaver we average the PDFs of the L-values and remove the effect of UEP. Eliminating UEP was, in fact, considered useful in some works on BICM (as it simplifies the analysis). On the other hand, the M-interleaver considered above allows us to preserve the UEP introduced by the binary labeling. While the idea of using M-interleavers was already present in the early works on BICM, this concept was not thoroughly studied in the literature.
We will show that the M-interleaver we propose are a generalization of S-interleavers, and thus, with an appropriate design, we can only obtain performance gains. This is shown in Section 8.1.4. From now, we refer to BICM transmission with S-interleavers as BICM-S, and BICM with M-interleaver will be called BICM-M. Further, in order to exploit the presence of UEP, we will generalize the M-interleaver to deal with the case of ![]() and derive performance metrics that will allow us to design such M-interleavers.
and derive performance metrics that will allow us to design such M-interleavers.
The order in which we enumerate the classes of bits is arbitrary and so is the numbering of the mapper's inputs. Instead of changing the order of the encoder's output or the order of the mapper's inputs, we may modify the M-interleaver shown in Example 8.2. For example, we may pass the bits from the first encoder's output to the second mapper's input (and not the first one as we did in Example 8.2), those from the second encoder's output to the third mapper's input, and those from the third encoder's output to the first mapper's input. In general, there are ![]() possible permutations, each changing the structure of the transceiver. One of the questions we will answer in this chapter is whether such a permutation changes the performance of the receiver for a given encoder. Choosing the most appropriate permutation becomes a part of interleaver design.
possible permutations, each changing the structure of the transceiver. One of the questions we will answer in this chapter is whether such a permutation changes the performance of the receiver for a given encoder. Choosing the most appropriate permutation becomes a part of interleaver design.
8.1.2 The M-Interleaver
In order to deal with the more general case ![]() , we propose a particular interleaver shown in Fig. 8.4, where we use
, we propose a particular interleaver shown in Fig. 8.4, where we use ![]() interleavers at the input, the deterministic bit-reorganizing multiplexer (MUX) and
interleavers at the input, the deterministic bit-reorganizing multiplexer (MUX) and ![]() interleavers at the output of the MUX.
interleavers at the output of the MUX.

Figure 8.4 The M-interleaver: the input sequences  are passed through
are passed through  interleavers
interleavers  and the resulting sequences
and the resulting sequences  are reorganized by a deterministic MUX into sequences
are reorganized by a deterministic MUX into sequences  , which are next interleaved into output sequences
, which are next interleaved into output sequences 
The role of the MUX is to reorganize the interleaved bits' sequences ![]() . These sequences
. These sequences ![]() are first divided into subsequences as follows:
are first divided into subsequences as follows:
where each subsequence ![]() contains
contains ![]() bits and
bits and ![]() is constrained to be such that
is constrained to be such that ![]() . Next, the subsequences are concatenated into output sequences
. Next, the subsequences are concatenated into output sequences
each of them composed of ![]() bits, as required to generate
bits, as required to generate ![]() labels
labels ![]() .
.

Figure 8.5 Example of interleaving via the M-interleaver with 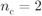 ,
,  . The values defining the MUX are
. The values defining the MUX are  ,
,  ,
,  ,
,  , and
, and 
The M-interleaver is then defined by a matrix ![]() with entries
with entries ![]() , which have to satisfy two obvious constraints. The first one is that all the bits
, which have to satisfy two obvious constraints. The first one is that all the bits ![]() must be assigned to one of the mapper's input, i.e.,
must be assigned to one of the mapper's input, i.e.,
which translates into
The second constraint is that each mapper's input is equally “loaded” with bits from the encoder's output
or equivalently,
The matrix ![]() can then be written as
can then be written as
where the last row and the last column of ![]() take into account the constraints imposed on
take into account the constraints imposed on ![]() . Consequently, when designing
. Consequently, when designing ![]() , only
, only ![]() for
for ![]() and
and ![]() may be freely set (considering also
may be freely set (considering also ![]()
![]() ).
).
The motivation behind the structure of the M-interleaver should be now clear: we would like to assign the code bits to the protected positions so as to improve the performance of the receiver. However, we cannot do it arbitrarily. For example, we cannot assign all the bits ![]() to the most protected positions (in Example 8.1 this would be the position
to the most protected positions (in Example 8.1 this would be the position ![]() ) as this will violate the constraints defined in (8.8).
) as this will violate the constraints defined in (8.8).
We note here that the particular case of ![]() , i.e., when the matrix
, i.e., when the matrix ![]() is square and each row/column contains only one nonzero element, the double set of interleavers—input (
is square and each row/column contains only one nonzero element, the double set of interleavers—input (![]() ) and output (
) and output (![]() )—is not necessary. When
)—is not necessary. When ![]() we may use just one set of interleavers as is shown already in Fig. 8.3. Having two sets of interleavers, however, is necessary for the more general case
we may use just one set of interleavers as is shown already in Fig. 8.3. Having two sets of interleavers, however, is necessary for the more general case ![]() .
.
8.1.3 Modeling the M-Interleaver
We recall that the S-interleaver in Fig. 2.24 is modeled as a random MUX assigning the code bits belonging to the class ![]() to the
to the ![]() th position of the mapper. The randomness comes from the fact that the interleavers are generated randomly, and then, the position
th position of the mapper. The randomness comes from the fact that the interleavers are generated randomly, and then, the position ![]() is random as well, which we denote by
is random as well, which we denote by ![]() . For S-interleavers we considered up to now, this variable was uniformly distributed.
. For S-interleavers we considered up to now, this variable was uniformly distributed.
To analyze the M-interleaver and take advantage of the considerations in Section 2.7 and Section 6.2, we model the interleaving vectors ![]() and
and ![]() as random variables drawn with equal probability from the set of all possible permutations. Then,
as random variables drawn with equal probability from the set of all possible permutations. Then,
where ![]() means that
means that ![]() belongs to the subsequence
belongs to the subsequence ![]() , i.e., it is assigned to the mapper's output
, i.e., it is assigned to the mapper's output ![]() . Similarly,
. Similarly,
i.e., for any position ![]() , the bit
, the bit ![]() is obtained from the
is obtained from the ![]() th code bits' class with probability
th code bits' class with probability ![]() .
.
To adapt the model Fig. 2.24 to the case of the M-interleaver, we first need to consider a random switch indexed by ![]() , i.e., we use
, i.e., we use ![]() instead of
instead of ![]() . We also replace the values of the assignment probabilities as shown in Fig. 8.6. Now
. We also replace the values of the assignment probabilities as shown in Fig. 8.6. Now ![]() has a meaning of the probability that the bit belonging to the class
has a meaning of the probability that the bit belonging to the class ![]() is mapped to the position
is mapped to the position ![]() of the mapper, i.e.,
of the mapper, i.e., ![]() .
.
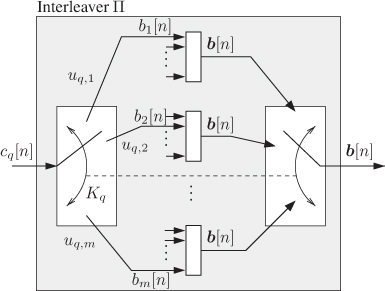
Figure 8.6 Probabilistic model of the M-interleaver defined in Section 8.1.2: the bits  are multiplexed to the position
are multiplexed to the position  within the label
within the label  , where
, where  is a random variable with distribution
is a random variable with distribution 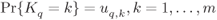
The immediate consequence of the random assignment of the bits ![]() to the positions
to the positions ![]() is that the corresponding L-value
is that the corresponding L-value ![]() has a distribution that changes with
has a distribution that changes with ![]() . Thus the PDFs for
. Thus the PDFs for ![]() are given by
are given by
Using the PDFs of the L-values in (8.15) we transform the BICM channel in Fig. 8.2 to a set of parallel BICO channels with channel transition probabilities ![]() , which is shown in Fig. 8.3 (b).
, which is shown in Fig. 8.3 (b).
In the case of Zehavi's interleaving in Example 8.2, using (8.10) and (8.15) we recover the formulas we already had in (8.2). In the case of the S-interleaver, the matrix ![]() should be chosen as
should be chosen as
so using (8.15) we obtain the PDF
which coincides, as expected, with (8.1).
We emphasize that in order to obtain the formula (8.15) and use it further to evaluate the performance of the decoder, we need to satisfy the conditions of quasi-randomness, similar to those we explained in Section 2.7. We do not dwell on this anymore and simply assume that such conditions are fulfilled.
8.1.4 Performance Evaluation
We have established a parallel channel model (see Fig. 8.3 (b)), which relies solely on the knowledge of the PDF of the L-values ![]() associated with the classes of code bits. To study the performance of the decoders, we should distinguish amongst the codewords according to the input they provide to the parallel channels. Assuming that the joint symmetry condition in (3.75) is satisfied, this input depends on the generalized Hamming weight (GHW) of the codeword
associated with the classes of code bits. To study the performance of the decoders, we should distinguish amongst the codewords according to the input they provide to the parallel channels. Assuming that the joint symmetry condition in (3.75) is satisfied, this input depends on the generalized Hamming weight (GHW) of the codeword ![]() . Namely,for each codeword
. Namely,for each codeword ![]() with
with ![]() the metric
the metric ![]() of the BICM decoder is given by the sum of
of the BICM decoder is given by the sum of ![]() L-values with PDF
L-values with PDF ![]() ,
, ![]() L-values with PDF
L-values with PDF ![]() , and so on. This is what we showed already in (6.211), and consequently, the PDF of the metric
, and so on. This is what we showed already in (6.211), and consequently, the PDF of the metric ![]() is given by
is given by
Then using the same approximation strategies as in Section 6.2.4 we obtain an approximation for the word-error probability (WEP):

where ![]() is the generalized distance spectrum (GDS) of the code
is the generalized distance spectrum (GDS) of the code ![]() in Definition 2.23, and
in Definition 2.23, and
In analogy to Example 6.22, the following example shows the performance of BICM with convolutional encoders (CENCs), but now using M-interleaver.
In the following example we show how to compute the GIWD ![]() and the GWD
and the GWD ![]() for a CENC, which follow as a generalization of the procedure in Example 6.23.
for a CENC, which follow as a generalization of the procedure in Example 6.23.

Figure 8.7 Generalized state machine for  used in the analysis of BICM-M
used in the analysis of BICM-M
By using a vector of dummy variables ![]() , the procedure shown in Example 8.6 (
, the procedure shown in Example 8.6 (![]() ) can be extended to any value of
) can be extended to any value of ![]() , and in general, the GWD and GIWD can be expressed in terms of an
, and in general, the GWD and GIWD can be expressed in terms of an ![]() dimensional vector
dimensional vector ![]() . Once the GIWD of the encoder is calculated, in order to predict the BEP performance of BICM-M via (8.22), we only need to compute
. Once the GIWD of the encoder is calculated, in order to predict the BEP performance of BICM-M via (8.22), we only need to compute ![]() in (8.20). This is done in the following section by exploiting the Gaussian simplifications we introduced in Section 6.4.
in (8.20). This is done in the following section by exploiting the Gaussian simplifications we introduced in Section 6.4.
8.2 Exploiting UEP in  Constellations
Constellations
In Section 8.1 we defined the models to characterize the performance of BICM-M. In order to efficiently optimize the transceiver, we need closed-form expressions that relate the performance of the decoder to the multiplexing matrix ![]() and the channel model. In this section we turn our attention to the relatively simple case of
and the channel model. In this section we turn our attention to the relatively simple case of ![]() PAM constellations for which we obtained simplified forms for the PDFs of the L-values (see Section 5.5).
PAM constellations for which we obtained simplified forms for the PDFs of the L-values (see Section 5.5).
8.2.1 The Generalized BICM Channel
For ![]() PAM constellations labeled by the BRGC, the results in Section 6.4.2 tell us that the conditional PDF of the max-log L-values can be approximated via a Gaussian function. After marginalization over all transmitted symbols (assumed equiprobable), we obtain
PAM constellations labeled by the BRGC, the results in Section 6.4.2 tell us that the conditional PDF of the max-log L-values can be approximated via a Gaussian function. After marginalization over all transmitted symbols (assumed equiprobable), we obtain
where ![]() is given by (6.386),
is given by (6.386), ![]() by (6.387), and
by (6.387), and ![]() by (6.388).
by (6.388).
As the L-values ![]() in (8.35) are modeled as a mixture of Gaussian random variables, and the L-values
in (8.35) are modeled as a mixture of Gaussian random variables, and the L-values ![]() are a mixture of L-values
are a mixture of L-values ![]() (see (8.15)), the L-values
(see (8.15)), the L-values ![]() are also a Gaussian mixture. The way the Gaussian PDFs are mixed is defined by
are also a Gaussian mixture. The way the Gaussian PDFs are mixed is defined by ![]() in (8.9) and by the constellation bit-wise Euclidean distance spectrum (CBEDS) matrix
in (8.9) and by the constellation bit-wise Euclidean distance spectrum (CBEDS) matrix ![]() , which gathers all parameters
, which gathers all parameters ![]() , as defined in (6.374). More specifically, if we define the matrix
, as defined in (6.374). More specifically, if we define the matrix ![]() of dimensions
of dimensions ![]()
the PDF of the L-values at the ![]() th decoder's input is given by
th decoder's input is given by
From (8.37), ![]() can be interpreted as the probability of observing the
can be interpreted as the probability of observing the ![]() th Gaussian PDF at the
th Gaussian PDF at the ![]() th parallel channel in Fig. 8.3 (b).
th parallel channel in Fig. 8.3 (b).
8.2.2 Performance Evaluation
The expression in (8.37) gives an analytical approximation for the PDFs of the L-values for BICM-M. In this section we study the performance of such BICM-M transceivers. From now on, we limit our considerations to the parameters defined by the zero-crossing model (ZcM) approximation (see Section 6.4.2), which proved to yield more accurate results than those obtained from the consistent model (CoM) (see Section 6.4.4). The next theorem shows how the pairwise-error probability (PEP) in (8.20) can be approximated.

Figure 8.8 BEP approximation in (8.22) based on Theorem 8.8 (lines) and simulated BEP (markers) for BICM-M,  , 4PAM (
, 4PAM ( ) and the three interleavers defined in (8.51). We used the ODS CENC
) and the three interleavers defined in (8.51). We used the ODS CENC  from Table 2.1 (
from Table 2.1 ( ) and the TENC in Example 2.31. The interleaver size of the TENC
) and the TENC in Example 2.31. The interleaver size of the TENC 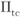 is
is  and 10 iterations are performed by the turbo decoder
and 10 iterations are performed by the turbo decoder
We note that all combinations in (8.49) are in general tedious to evaluate (specially for large values of ![]() and/or
and/or ![]() ), and thus, we propose further approximations. One straightforward simplification is to consider, for each
), and thus, we propose further approximations. One straightforward simplification is to consider, for each ![]() , only the Gaussian density with the smallest mean-to-standard deviation ratio (e.g.,
, only the Gaussian density with the smallest mean-to-standard deviation ratio (e.g., ![]() ). The intuition behind this approximation is that the error terms related to other Gaussian functions decrease quickly with
). The intuition behind this approximation is that the error terms related to other Gaussian functions decrease quickly with ![]() . This approximation yields the following approximation on the BEP:
. This approximation yields the following approximation on the BEP:
The expression in (8.52) is quite simple to evaluate compared to the original expression based on (8.45), and it still takes into account the optimization parameters (MUX and encoder).
We can also obtain the following asymptotic approximation
which we expect to be tight as ![]() . This result provides us with a new criterion to select the optimum encoder and interleaver (see Section 8.2.3).
. This result provides us with a new criterion to select the optimum encoder and interleaver (see Section 8.2.3).
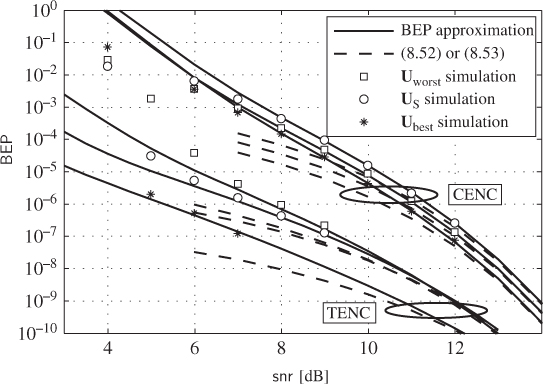
Figure 8.9 BEP approximation in (8.22) based on Theorem 8.8 (lines) and simulated BEP (markers) for BICM-M for the rate  ODS CENC
ODS CENC  from Table 2.1 (
from Table 2.1 ( ) and for the TENC in Example 2.31 for
) and for the TENC in Example 2.31 for  and 8PAM (
and 8PAM ( ,
,  ). The interleaver size of the TENC
). The interleaver size of the TENC  is
is  and 10 iterations are performed by the turbo decoder. The asymptotic bounds based on (8.52) for the TENC and on (8.53) for the CENC are also shown
and 10 iterations are performed by the turbo decoder. The asymptotic bounds based on (8.52) for the TENC and on (8.53) for the CENC are also shown
Analyzing the approximation of the BEP expression (8.22) together with (8.45), we can appreciate three terms: ![]() , which depends only on the encoder;
, which depends only on the encoder; ![]() , which depends only on the channel (see (8.46)); and
, which depends only on the channel (see (8.46)); and ![]() , which depends on the interleaver (see (8.36)). Assuming that the constellation and the labeling are fixed, the optimum performance of the system will be achieved by a joint design of the interleaver and the encoder. We study this in the following section.
, which depends on the interleaver (see (8.36)). Assuming that the constellation and the labeling are fixed, the optimum performance of the system will be achieved by a joint design of the interleaver and the encoder. We study this in the following section.
8.2.3 Joint Encoder and Interleaver Design
It is well known that ODS CENCs in Table 2.1 are the optimum CENCs for binary transmission. However, according to (8.53), when UEP is introduced by the channel, the optimization criterion is different, i.e., a joint optimization of the MUX (i.e., how the code bits are assigned to different bit positions in the constellation) and the CENC should be done. More specifically, the expression in (8.53) shows that we first need to optimize the free Hamming distance (FHD) of the encoder and then we need to optimize the GIWD of the encoder and the MUX matrix ![]() . To formally define the optimum design for a given constraint length
. To formally define the optimum design for a given constraint length ![]() and code rate
and code rate ![]() , we define
, we define ![]() as the set of encoders in
as the set of encoders in ![]() that give MFHD, where
that give MFHD, where ![]() is the CENC universe defined in Section 2.6.1.
is the CENC universe defined in Section 2.6.1.
Note that for given values of ![]() and
and ![]() , the problem of selecting the optimum interleaver configuration (selection of
, the problem of selecting the optimum interleaver configuration (selection of ![]() ) is a continuous multidimensional optimization problem. For simplicity, however, the optimization is performed over only a limited number of points. Using Definition 8.11, an exhaustive search for pairs
) is a continuous multidimensional optimization problem. For simplicity, however, the optimization is performed over only a limited number of points. Using Definition 8.11, an exhaustive search for pairs ![]() with constraint length up to
with constraint length up to ![]() was performed. Three different configurations were tested: code rate
was performed. Three different configurations were tested: code rate ![]() (
(![]() ,
, ![]() ) with 4PAM (
) with 4PAM (![]() ), 8PAM (
), 8PAM (![]() ), or 16PAM (
), or 16PAM (![]() ). The (simplified) optimization space for
). The (simplified) optimization space for ![]() in these cases was
in these cases was ![]() for
for ![]() ,
, ![]() for
for ![]() , and
, and ![]() for
for ![]() . The results are presented in Table 8.1, where we highlight CENCs found that are different (in terms of their IWD) from the ODS CENCs in Table 2.1. Among the 24 combinations studied, 6 resulted in new optimal encoders.
. The results are presented in Table 8.1, where we highlight CENCs found that are different (in terms of their IWD) from the ODS CENCs in Table 2.1. Among the 24 combinations studied, 6 resulted in new optimal encoders.
Table 8.1 Optimum CENC and multiplexers (MUXs) for ![]() wit 4PAM, 8PAM, and 16PAM. New encoders found, better than the ODS CENCs in Table 2.1, are highlighted
wit 4PAM, 8PAM, and 16PAM. New encoders found, better than the ODS CENCs in Table 2.1, are highlighted
| 4PAM ( |
8PAM ( |
16PAM ( |
||||||||
| 2 | 5 | |||||||||
| 3 | 6 | |||||||||
| 4 | 7 | |||||||||
| 5 | 8 | |||||||||
| 6 | 10 | |||||||||
| 7 | 10 | |||||||||
| 8 | 12 | |||||||||
| 9 | 12 | |||||||||
The cost function in (8.55) is shown in Fig. 8.10 as a function of the interleaver parameter ![]() for
for ![]() , 4PAM, and
, 4PAM, and ![]() . The ODS CENC
. The ODS CENC ![]() is shown with a thick black line. Analyzing this curve, it is clear that the performance of this encoder can be optimized by setting
is shown with a thick black line. Analyzing this curve, it is clear that the performance of this encoder can be optimized by setting ![]() , and that the curve has a maximum for
, and that the curve has a maximum for ![]() , which will result in the worst interleaver design for this particular encoder. The cost function obtained for the encoder
, which will result in the worst interleaver design for this particular encoder. The cost function obtained for the encoder ![]() (thick dashed line) attains the smallest value among all other encoders (including the ODS one). Consequently, if the MUX is adequately designed setting
(thick dashed line) attains the smallest value among all other encoders (including the ODS one). Consequently, if the MUX is adequately designed setting ![]() (best BICM-M), this encoder is the optimal encoder for this particular configuration. However, if the interleaver is not optimized, e.g., setting
(best BICM-M), this encoder is the optimal encoder for this particular configuration. However, if the interleaver is not optimized, e.g., setting ![]() (BICM-S), the new encoder is not optimal anymore.
(BICM-S), the new encoder is not optimal anymore.

Figure 8.10 Cost function in (8.55) for all possible encoders in  for
for  (
( ,
, 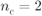 ), 4PAM, and
), 4PAM, and  as a function of the MUX parameter
as a function of the MUX parameter  . The thick solid line represents the ODS CENC
. The thick solid line represents the ODS CENC  , and the thick dashed line the optimum BICM-M design based on
, and the thick dashed line the optimum BICM-M design based on 
We conclude by showing in Fig. 8.11 the performance of the optimum design ![]() compared with all encoders with
compared with all encoders with ![]() and
and ![]() (enumerated using the variable
(enumerated using the variable ![]() ) using the best and the worst interleaver design (
) using the best and the worst interleaver design (![]() and
and ![]() ). The lines represent the range of variation between the best and the worst interleaver design, i.e., any other interleaver configuration will have a coefficient between the corresponding pair of markers. We note that the optimum design may significantly outperform other encoders, e.g., 16PAM and
). The lines represent the range of variation between the best and the worst interleaver design, i.e., any other interleaver configuration will have a coefficient between the corresponding pair of markers. We note that the optimum design may significantly outperform other encoders, e.g., 16PAM and ![]() in Fig. 8.11. The improvement with respect to ODS CENCs is less evident but clear. Thus, the results presented in this section indicate that optimizing the interleaver and encoder should be a mandatory step in the design of BICM-M.
in Fig. 8.11. The improvement with respect to ODS CENCs is less evident but clear. Thus, the results presented in this section indicate that optimizing the interleaver and encoder should be a mandatory step in the design of BICM-M.

Figure 8.11 Cost function in (8.55) for all the 21 possible encoders in 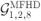 , for the best and worst interleaver design:
, for the best and worst interleaver design: 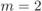 (‘
(‘ ’),
’),  (‘
(‘ ’), and
’), and  (‘
(‘ ’). The lines represent the range of variation between the best and the worst interleaver design
’). The lines represent the range of variation between the best and the worst interleaver design
8.3 Bibliographical Notes
UEP in terms of BEP for uncoded transmission with ![]() PSK and
PSK and ![]() QAM constellations labeled by the BRGC has been studied in [1] and for 16QAM and 64QAM in [2, Figs. 5.2 and 5.4]. Unequal power allocation for systematic/parity bits to impose UEP is an idea first used for turbo-encoded BICM in [3] and later analyzed in [4–8]. UEP for turbo-encoded schemes has been studied in [3 4, 6 8–10]. The influence of the block length and code rate for optimal power allocation was analyzed in [4 11] and interleaver design aiming to assign the code bits to different bit positions for high-order modulation schemes was studied in [12].
QAM constellations labeled by the BRGC has been studied in [1] and for 16QAM and 64QAM in [2, Figs. 5.2 and 5.4]. Unequal power allocation for systematic/parity bits to impose UEP is an idea first used for turbo-encoded BICM in [3] and later analyzed in [4–8]. UEP for turbo-encoded schemes has been studied in [3 4, 6 8–10]. The influence of the block length and code rate for optimal power allocation was analyzed in [4 11] and interleaver design aiming to assign the code bits to different bit positions for high-order modulation schemes was studied in [12].
The BICM transceivers with M-interleaver we analyzed in this chapter in fact correspond to the original model introduced by Zehavi in [13] for BICM (and also for BICM with iterative demapping (BICM-ID) in [14]), where the application of parallel interleavers was postulated. Over the years, different names have been given to these interleavers: e.g., “in-line” 15, “intralevel” [16], “M” [17], “dual” [18], or “modular” [19]. BICM-M has been studied in [17 20], BICM-ID with M-interleavers in [14], BICM for serially concatenated systems in [15], and orthogonal frequency-division multiplexing (OFDM)-based BICM in [16] (see also [21]). BICM-M has also been proposed in the third-generation partnership project (3GPP) standard [18 22]. Nevertheless, most of the existing literature on BICM and BICM-ID still follows the framework set in [23] and assumes the use of one singe-input interleaver (BICM-S). This simplifies the analysis of the resulting system, but leads to suboptimality, as we have shown in this chapter.
The generalized transfer function of the encoder was briefly introduced in the original paper of Zehavi [13, eq. ((4.8))] and the GIWD in [19, Section IV-A]. As the PEP computation for BICM-M is not straightforward, the application of the GIWD of the encoder was not very popular. This problem was solved by the analytical expressions for the PDF of the L-values (and their Gaussian approximations) we introduced in Chapter 5. This was first done in [24] for Gaussian channels and later in [25] for fading channels. BICM-ID with M-interleavers was shown to outperform BICM-ID with a single interleaver in [26] (see also [27, Chapter 4]).
References
- [1] Lassing, J., Ström, E. G., Agrell, E., and Ottosson, T. (2003) Unequal bit-error protection in coherent
 -ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL.
-ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL. - [2] Hanzo, L., Webb, W., and Keller, T. (2000) Single- and Multi-Carrier Quadrature Amplitude Modulation, John Wiley & Sons.
- [3] Hokfelt, J. and Maseng, T. (1996) Optimizing the energy of different bitstreams of turbo code. International Turbo Coding Seminar, August 1996, Lund, Sweden.
- [4] Salah, M. M., Raines, R. A., Temple, M. A., and Bailey, T. G. (2000) Energy allocation strategies for turbo codes with short frames. The International Conference on Information Technology: Coding and Computing (ITCC), March 2000, Las Vegas, NV.
- [5] Zhang, W. and Wang, X. (2004) Optimal energy allocations for turbo codes based on distributions of low weight codewords. Electron. Lett., 20 (19), 1205–1206.
- [6] Duman, T. and Salehi, M. (1997) On optimal power allocation for turbo codes. International Symposium on Information Theory (ISIT), June 1997, Ulm, Germany.
- [7] Mohammadi, A. H. S. and Khandani, A. K. (1997) Unequal error protection on the turbo-encoder output bits. IEEE International Conference on Communications (ICC), June 1997, Montreal, QC, Canada.
- [8] Mohammadi, A. H. S. and Khandani, A. K. (1999) Unequal power allocation to the turbo-encoder output bits with applications to CDMA systems. IEEE Trans. Commun., 47 (11), 1609–1610.
- [9] Aydinlik, M. and Salehi, M. (2008) Turbo coded modulation for unequal error protection. IEEE Trans. Commun., 56 (4), 555–564.
- [10] Kousa, M. A. and Mugaibel, A. H. (2002) Puncturing effects on turbo codes. Proc. IEE, 149 (3), 132–138.
- [11] Choi, Y. M. and Lee, P. J. (1999) Analysis of turbo codes with symmetric modulation. Electron. Lett., 35 (1), 35–36.
- [12] Rosnes, E. and Ytrehus, O. (2006) On the design of bit-interleaved turbo-coded modulation with low error floors. IEEE Trans. Commun., 54 (9), 1563–1573.
- [13] Zehavi, E. (1992) 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun., 40 (3), 873–884.
- [14] Li, X. and Ritcey, J. A. (1997) Bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett., 1 (6), 169–171.
- [15] Nilsson, A. and Aulin, T. M. (2005) On in-line bit interleaving for serially concatenated systems. IEEE International Conference on Communications (ICC), May 2005, Seoul, Korea.
- [16] Stierstorfer, C. and Fischer, R. F. H. (2007) Intralevel interleaving for BICM in OFDM scenarios. 12th International OFDM Workshop, August 2007, Hamburg, Germany.
- [17] Abramovici, I. and Shamai, S. (1999) On turbo encoded BICM. Ann. Telecommun., 54 (3–4), 225–234.
- [18] Dahlman, E., Parkvall, S., Sköld, J., and Beming, P. (2008) 3G Evolution: HSPA and LTE for Mobile Broadband, 2nd edn, Academic Press.
- [19] Li, X., Chindapol, A., and Ritcey, J. A. (2002) Bit-interlaved coded modulation with iterative decoding and 8PSK signaling. IEEE Trans. Commun., 50 (6), 1250–1257.
- [20] Hansson, U. and Aulin, T. (1996) Channel symbol expansion diversity—improved coded modulation for the Rayleigh fading channel. IEEE International Conference on Communications (ICC), June 1996, Dallas, TX.
- [21] Stierstorfer, C. (2009) A bit-level-based approach to coded multicarrier transmission. PhD dissertation, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany.
- [22] 3GPP (2009) Universal mobile telecommunications system (UMTS); multiplexing and channel coding (FDD). Technical Report TS 25.212, V8.5.0 Release 8, 3GPP.
- [23] Caire, G., Taricco, G., and Biglieri, E. (1998) Bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 44 (3), 927–946.
- [24] Alvarado, A., Agrell, E., Szczecinski, L., and Svensson, A. (2010) Exploiting UEP in QAM-based BICM: Interleaver and code design. IEEE Trans. Commun., 58 (2), 500–510.
- [25] Hossain, Md. J., Alvarado, A., and Szczecinski, L. (2011) Towards fully optimized BICM transceivers. IEEE Trans. Commun., 59 (11), 3027–3039.
- [26] Alvarado, A., Szczecinski, L., Agrell, E., and Svensson, A. (2010) On BICM-ID with multiple interleavers. IEEE Commun. Lett., 14 (9), 785–787.
- [27] Alvarado, A. (2010) Towards fully optimized BICM transmissions. PhD dissertation, Chalmers University of Technology, Göteborg, Sweden.





