6
Cognition, Instruction, and the Quest for Meaning
When the first Carnegie Cognition Symposium on cognition and instruction was held (Klahr, 1976), the field was in its infancy, and many of the presentations were only tangentially related to instruction. Now, as the chapters in Parts I and II of this volume reveal, researchers are producing substantial quantities of rigorous research directly relevant to instruction. As the subtitle of this volume indicates, it has been “25 years of progress” for the field of cognition and instruction.
We should keep in mind, however, that the term “progress” has two different senses. One indicates improvement (i.e., technological progress); the other indicates change but not necessarily improvement (i.e., progress toward the inevitable). As we consider the accomplishments of this field, we should ask ourselves which changes represent improvement and which represent change but not necessarily improvement.
COGNITION AND INSTRUCTION: A TETRAHEDRAL FRAMEWORK
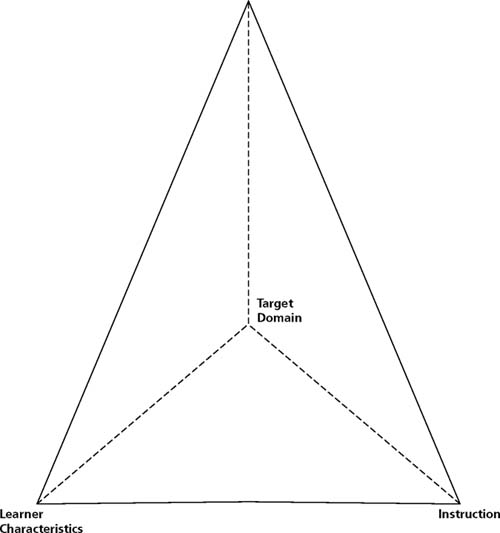
The central message that I derive from these chapters is that the way to produce optimal learning is to lead learners to interact with the target domain in meaningful ways. This perspective suggests a tetrahedral framework for thinking about cognition and instruction (Fig. 6.1). At the apex of the tetrahedron is learning; at the other vertices are learner characteristics, the target domain, and instruction. This framework has three
advantages. First, it identifies variables that are central to understanding cognition and instruction, with each face defining a key intersection of three variables. Second, it reminds us that in analyses of cognition of instruction, learning is at the apex; instruction, the target domain, and learner characteristics matter only as they influence learning. Third, the faces of the tetrahedron provide a framework for organizing issues in the field in general and in the present set of chapters in particular. The remainder of this discussion examines issues concerning each of the three faces with learning at the apex.
Target Domain, Instruction, and Learning
What aspects of the target domain should be emphasized in instruction (i.e., “What should be learned?”). At one level, the answers suggested by the present chapters, all of which focus on math and science, are quite traditional; students should learn about ratios and proportions, forces and motion, density and weight, integers, rational numbers, functions, and so on. At another level, however, the chapters in the present volume reflect a more abstract, higher level characterization of target domains and instructional goals than was prevalent in the volume on this topic 25 years ago. Minstrell focuses on promoting scientific discourse skills (chap. 4). Palincsar and Magnusson encourage students to critically evaluate science texts and to understand the thought processes of other scientists (chap. 5). Lehrer, Schauble, Strom, and Pligge's program promotes understanding of the nature of mathematical argument, as well as of the epistemology of science (chap. 2). The goals of Kalchman, Moss, and Case's (chap. 1) and Klahr, Chen, and Toth's (chap. 3) research are somewhat less lofty, but they still are very high-level relative to typical classroom activities as well as to past research on cognition and instruction. Promoting number sense and scientific experimentation skills hardly qualifies as part of the back to basics movement.
To some extent, the views that very high-level goals are central to each target domain and that they should be emphasized in instruction reflect choices of the symposium organizers. They selected the participants and thus, indirectly, the approaches that would be included. However, their choices seem representative of current emphases in the field of cognition and instruction. This emphasis may be a reaction to practices in typical classrooms, where activities aimed at inculcating low-level skills dominate day-to-day activities. Alternatively, it may reflect a more absolute belief that the high-level skills are the most important ones and should be emphasized even if it means that lower level skills receive less practice.
This change from lower level goals certainly represents progress, but it is unclear whether it is progress in the sense of improvement or only in the sense of change. Before we will know, researchers interested in cognition and instruction will need to answer two questions. First, what kinds of evidence do we have that learning would be improved if high-level thinking skills were emphasized to a greater extent than they are? Given time pressures, educators need to choose among competing priorities. What evidence is there that would convince teachers who are skeptical but not cynical about pursuing high-level goals that changing their current approaches would be worthwhile? Comprehensive comparisons of the degree to which children receiving high-level instruction or traditional instruction attain both low-level and high-level objectives are needed to answer this question. Longitudinal comparisons of learning over time would be especially useful, because they would help distinguish between two plausible hypotheses. By one hypothesis, children whose instruction emphasizes high-level skills should be especially motivated to learn more about the domain in the future, and therefore should improve over time relative to those in traditional classrooms. By the other hypothesis, children whose instruction emphasizes high-level skills will be increasingly handicapped by insufficient mastery of the basics and therefore will fall behind over time. The present group of authors clearly hold the first hypothesis; I suspect that they are right, but I would like to see the data.
A second, related question is: What kinds of supports, if any, will be sufficient to allow classroom teachers to inculcate high-level thinking skills if the broader society decides to assign them high priority? Teachers may emphasize low-level skills not because they believe that those skills are the most important but because they understand them and are comfortable teaching them. The fact that professors, graduate students, and trained research assistants can effectively teach high-level content does not imply that most teachers could do the same. What type of help will poor, unmotivated teachers, as well as excellent, highly motivated ones, need to help students understand the thinking of other scientists, to critically evaluate science texts, and to develop scientific discourse skills? I suspect that in many cases, a great deal of help would be needed.
Another major issue within the target domain/instruction/learning area concerns how particular target domains can best be taught. The presenters in this group share the assumption that hands-on activity, guided by instructors' questions, notebooks, and text materials, is the best method for constructing deep knowledge of mathematics and science. Again, the present set of chapters include numerous appealing examples of how such hands-on learning can occur: The whole number and rational number board games used by Kalchman, Moss, and Case (chap. 1), the elbow construction project used by Lehrer, Schauble, Strom, and Pligge (chap. 2), the ramps and springs used to demonstrate experimental design principles by Klahr, Chen, and Toth (chap. 3), and so on. As with the emphasis on high-level instructional/learning goals, the emphasis on hands-on learning is appealing and the results are promising. Again, however, we need evidence that hands-on learning is worth the extra time and effort that would be required for teachers in the classroom to adopt the approach. We also need to ask what types of supports teachers would need to do so.
LEARNER CHARACTERISTICS, INSTRUCTION, AND LEARNING
In the subtitle of their chapter, Klahr, Chen, and Toth (chap. 3) ask if the relation between cognitive development and cognition and instruction is like that of two ships proceeding from different directions toward a single destination, with both ships' beacons illuminating that destination, or like that of ships passing in the night, with beacons trained on different destinations. Their chapter, and that of others in this group, suggests that there is a fair amount of overlapping illumination. This makes sense, given the centrality in both areas of the relation between learner characteristics and learning and the interest of some cognitive developmental researchers in instruction.
A number of themes in current research on cognitive development are evident in these chapters. One is that young children have greater learning capabilities than is usually realized. Palincsar and Magnusson demonstrate that third graders can gain a sophisticated understanding of reflection and refraction of light (chap. 5). Klahr, Chen, and Toth show that fourth graders can learn and transfer scientific experimentation skills (chap. 3). Lehrer, Schauble, Strom, and Pligge find that fifth graders can generate mathematical models of scientific data (chap. 2). Kalchman, Moss, and Case report that sixth graders can gain an understanding of mathematical functions that in some ways is superior to that of eleventh-grade honors students taught with more conventional methods (chap. 1).
A second area of overlap between research on cognitive development and research on cognition and instruction is a shared emphasis on the ways that systematic misconceptions interfere with children's learning. This theme is illustrated especially impressively in Minstrell's system for classifying and addressing errors that reflect different misconceptions about falling objects (chap. 4). It also is aptly illustrated by the probes regarding reflection of light offered by the teacher in Palincsar and Magnusson's chapter (chap. 5). A third theme is the importance of learner characteristics, such as age and conceptual knowledge, on the effectiveness of instruction. Such influences are particularly emphasized by Klahr, Chen, and Toth (chap. 3) and by Kalchman, Moss, and Case (chap. 1). A final shared theme of all of the chapters in this group, as well as of most contemporary research on cognitive development, is that learning is a constructive process, with learners continually striving to understand their experiences. As Palincsar and Magnusson point out, this is true regardless of whether children are learning from text or from physical experience (chap. 5). As Klahr, Chen, and Toth point out, it is true regardless of whether the instructional approach is classified as discovery learning or conceptually oriented didactic instruction (chap. 3).
Instruction always requires going beyond both theory and empirical findings; in many cases, intuitions and past experience are the only bases for making crucial decisions. Although knowledge of cognitive developmental theories and empirical findings may account for part of the instructional success enjoyed by the present group of investigators, the validity of their intuitions and their creative application of their past experience probably play a larger role. Their intuitions raise several questions that need to be addressed by cognitive developmental research:
- At the outset of their instructional program, Klahr, Chen, and Toth present children flawed experiments as a way of motivating them to learn how to perform valid ones (chap. 3). Do children learn more effectively when the negative consequences of flawed existing procedures are shown to them before they receive instruction in superior ones?
- Kalchman, Moss, and Case hypothesize that there is a central conceptual structure for rational numbers and another for functions, and that learning these is essential for understanding mathematics beyond arithmetic (chap. 1). What is the evidence that children who acquire these central conceptual structures immediately understand, or are quicker to learn, aspects of mathematics other than rational numbers and functions?
- Palincsar and Magnusson require children to commit to claims about how light works before instruction begins (chap. 5). They believe that such commitment enhances learning. Does it?
- Palincsar and Magnusson also hypothesize that greater learning will occur if children do not examine text-based descriptions of phenomena until they have substantial first-hand experience with the phenomena (chap. 5). Are they right?
Thus, just as theories and findings from cognitive development can help guide instructional efforts, so ideas and findings from cognition and instruction can help guide cognitive developmental research.
LEARNER CHARACTERISTICS, TARGET DOMAIN, AND LEARNING
A common theme in all of these chapters is that regardless of the age and knowledge of the learner, learning of mathematics and science should be organized around the pursuit of meaning. For example, in chap. 2, Lehrer, Schauble, Strom, and Pligge comment, “In reform classrooms … mathematical cognition is a joint product of individuals' attempts to achieve meaning…about the nature of mathematics,” (p. 42) and Minstrell notes that teachers need to make sense of experiences in the classroom (chap. 4).
This theme would not be surprising if we were talking about learning of literature or history. In those areas, the pursuit of meaning has always been viewed as central. The view also would not be surprising if we were talking about students at elite universities learning the deep structure of mathematics or physics. Most researchers who study both psychology and education agree that regardless of the content area or the population of students, the pursuit of meaning should be emphasized. However, the popularity of back to basics movements indicates that many people are skeptical and will need to be convinced of the importance and feasibility of the goal before it will be given high priority in classrooms. Again, researchers who study cognition and instruction need to provide evidence indicating that focusing on meaning represents progress in the sense of improvement, not just in the sense of change.
Emphasizing the pursuit of meaning in mathematics and science raises the issue of what meaning means in these contexts. My understanding of it is a generalized version of the kind of number sense that Kalchman, Moss, and Case try to inculcate in students (chap. 1). Meaningful understanding implies fluent translation among alternative representations and ability to integrate facts, concepts, and procedures in a way that consistent conclusions can be derived via different routes. One of the most hopeful results of the programs described in Parts I and II is the frequency with which they seem to lead students to acquire such meaningful understanding. Thus, Lehrer, Schauble, Strom, and Pligge note that most students who participate in the program demonstrated multiple understandings of similarity: As a ratio, a line, and an algebraic expression (chap. 2). Similarly, Kalchman, Moss, and Case cite the example of a student who, when asked to express one eighth as a decimal, moved fluently between fractional, percentage, and decimal representations, “Well one eighth is half of one fourth. And one quarter is 25%, so half of that is 121/2%. So as a decimal, that would have to be point 12 and a half. So that is point 12 point 5, so that means that it is .125” (chap. 1, p. 20).
Research from cognitive development also suggests that encouraging children to pursue meaning enhances learning of mathematics and science. For example, asking children to explain why the correct answer is correct leads to more learning than simply telling them that the correct answer is correct (Bielaczyc, Pirolli, & Brown, 1995; Chi, Bassok, Lewis, Reimann, & Glasser, 1989; Siegler, 1995). Moreover, asking them to explain both why correct answers are correct and why incorrect answers are incorrect leads to more learning than only asking why correct answers are correct (Siegler, in press). Requests to explain phenomena enhance learning with populations varying from preschoolers to adults and with domains ranging from number conservation to ecosystems to computer programming. Better learners spontaneously generate such explanations more often than less good learners (Bielaczyc et al., 1995; Chi, de Leeuw, Chi, & LaVancher, 1989), and requesting such explanations from randomly selected children or adults causes them to learn more (Chi, de Leeuw, Chi, & LaVancher, 1994; Siegler, in press).
The findings from the present group of chapters raise several questions. First, how can we assess the degree to which children possess meaningful understanding of a domain? More precise specification of the knowledge needed to understand a given area in a meaningful way, and objective measures of that knowledge, are a logical next step in this area. Second, are young children capable of grasping all kinds of meaning in mathematics and science, or are some kinds of meaning best pursued at older ages? Referring to sixth graders learning about mathematical functions, Kalchman, Moss, and Case suggest that “there are some problems specific to the domain that are beyond the ability of some younger students, possibly because of their earlier stage of intellectual development and their limited experience with more advanced ideas in mathematics” (chap. 1, p. 35). What ideas are children unable to understand at given ages, and how exactly does their general intellectual stage limit their learning? Third, can we inculcate in children a “habit of mind” to pursue meaning in all domains? We know that on particular tasks, some children seek explanations far more than do other children. We do not know whether explanation seeking is a general characteristic of some children but not of others; whether explanation seeking is general for a given child within a given domain, but not across different domains; or whether individual children's explanation seeking varies greatly on different tasks within the same domain. We also do not know whether it is possible to instruct children in ways that increase their likelihood of seeking meaning on a broader range of tasks and domains. The answers to this last question will have a lot to do with the long-term success of encouraging children to pursue meaning.
REFERENCES
Bielaczyc, K., Pirolli, P. L., & Brown, A. L. (1995). Training in self-explanation and self-regulation strategies: Investigating the effects of knowledge acquisition activities on problem solving. Cognition and Instruction, 13, 221–252.
Chi, M. T. H., Bassok, M., Lewis, M., Reimann, P., & Glasser, R. (1989). Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science, 13, 145–182.
Chi, M. T. H., de Leeuw, N., Chiu, M.-H., & LaVancher, C. (1994). Eliciting self-explanations improves understanding. Cognitive Science, 18, 439–477.
Klahr, D. (1976). Cognition and instruction. Hillsdale, NJ: Lawrence Erlbaum Associates.
Siegler, R. S. (1995). How does change occur: A microgenetic study of number conservation. Cognitive Psychology, 28, 225–273.
Siegler, R. S. (in press). Microgenetic studies of self-explanations. In N. s & J. Parziale (Eds.), Microdevelopment: Transition processes in development and learning. New York: Cambridge University Press.