Chapter 14. Encryption and Hashing Concepts
This chapter covers the following subjects:
![]() Cryptography Concepts: This section covers the basic terminology of cryptography, including encryption, ciphers, and keys. It also discusses private versus public keys, symmetric versus asymmetric encryption, and public key encryption.
Cryptography Concepts: This section covers the basic terminology of cryptography, including encryption, ciphers, and keys. It also discusses private versus public keys, symmetric versus asymmetric encryption, and public key encryption.
![]() Encryption Algorithms: This section delves into the various symmetric algorithms, such as DES and AES, and some of the popular asymmetric algorithms such as RSA and elliptic curve.
Encryption Algorithms: This section delves into the various symmetric algorithms, such as DES and AES, and some of the popular asymmetric algorithms such as RSA and elliptic curve.
![]() Hashing Basics: Here, we investigate the most common way to verify the integrity of files: hashing. We cover basic hashing concepts and cryptographic hash functions, such as MD5, SHA, and NTLM.
Hashing Basics: Here, we investigate the most common way to verify the integrity of files: hashing. We cover basic hashing concepts and cryptographic hash functions, such as MD5, SHA, and NTLM.
When data is encrypted, it is modified in such a way that it cannot be understood by anyone who does not have the correct key. If you have the correct key, you can decrypt the data, and it will once again become intelligible. Though almost everyone has dealt with encrypted data and/or encrypted Internet sessions of some sort, chances are that the majority of the readers of this book will have limited hands-on experience with encryption. Because of this, I have written this chapter, and the following one, in a very to-the-point manner with simple analogous examples. I cover only what you need to know about encryption concepts, methods, and types. Encryption by itself is an entire IT field, but the CompTIA Security+ exam requires that you know only the basics—the exam objectives only scrape the surface of encryption concepts. Keep all this in mind as you go through this chapter and the next. I have provided some links to more advanced encryption books and websites in the View Recommended Resources document online, although reading them is not necessary for the exam. That being said, the “basics” of cryptography is a pretty huge chunk of information—there is a lot to cover, and some of the topics can be difficult to understand.
It can help to pose the following question: What is it that we need to encrypt? Without a doubt, it is the data that needs to be encrypted, but more specifically three types of data: data in use, data at rest, and data in transit. Data in use can be described as actively used data undergoing constant change; for example, it could be stored in databases or spreadsheets. Data at rest is inactive data that is archived—backed up to tape or otherwise. Data in transit (also known as data in motion) is data that crosses the network or data that currently resides in computer memory. Consider thinking in these terms as we progress through the chapter.
Foundation Topics
Cryptography Concepts
Cryptography is the practice of hiding the meaning of a message. The word is roughly derived from the Greek words kryptos (meaning “hidden”) and graphein (meaning “to write”). However, in cryptography it is not the message that is hidden, but rather the significance of the message.
Let me give a basic example of cryptography. When I was younger, some of the kids I knew would keep a black book with names, phone numbers, and so on. You probably wouldn’t use a black book today, but I digress... Anyway, a couple of those people did something that fascinated me—they would modify phone numbers according to a code they had developed. This was done to hide the true phone number of a special friend from their parents, or from teachers, and so on. It was a basic form of encryption, although at the time I didn’t realize it. I just referred to it as a “code.”
Essentially, it worked like this:
The person with the black book would take a real phone number such as 555-0386. They would then modify the number by stepping each number backward or forward x number of steps. Let’s say the person decided to step each number between 0 and 9 backward by three steps; the resulting coded phone number would be 222-7053. I’m sure you see how that was done, but let’s break it down so that we can make an analogy to today’s data encryption. Table 14-1 shows the entire code used.
Table 14-1 Black Book Phone Number Encryption
| Original Number | Modifier | Modified Number |
| 0 | Minus 3 | 7 |
| 1 | 8 | |
| 2 | 9 | |
| 3 | 0 | |
| 4 | 1 | |
| 5 | 2 | |
| 6 | 3 | |
| 7 | 4 | |
| 8 | 5 | |
| 9 | 6 |
In this example, each number between 0 and 9 corresponds to a number three digits behind it. By the way, the numbers cycle through: For example, the number 0 goes three steps back, starting at 0, to 9, 8, and then 7 in an “around-the-bend” fashion. This is an example of cryptographic substitution.
Note
This is based on the Caesar Cipher (more accurately the Caesar Shift Cipher), where messages sent in ancient Rome would have each letter shifted by one or more places. You may also have heard of the ROT13 substitution cipher—this replaces (or rotates) a letter with the letter 13 steps after it.
Let’s analogize. Each of the components in the table can be likened to today’s computer-based encryption concepts:
![]() The original number is like to original file data.
The original number is like to original file data.
![]() The modifier is like to an encryption key.
The modifier is like to an encryption key.
![]() The modified number is like to encrypted file data.
The modified number is like to encrypted file data.
I call this the “Black Book Example,” but I would guess that others have used similar analogies. Of course, this is a basic example; however, it should serve to help you to associate actual computer-based encryption techniques with this more tangible idea.
Now, for other people to figure out the original phone numbers in the black book, they would have to do the following:
Step 1. Gain access to the black book. This is just like gaining access to data. Depending on how well the black book is secured, this by itself could be difficult.
Step 2. Break the code. This would be known as decrypting the data. Of course, if the owner of the black book was silly enough to put the phone number encryption table in the book, well, then game over; it would be easy to decode. But if the owner was smart enough to memorize the code (and tell it to no one), making it a secret code, it would be much more difficult for another person to crack. Plus, the person could make the code more advanced; for example, look at Table 14-2.
Table 14-2 Advanced Black Book Phone Number Encryption
| Original Number | Modifier | Modified Number |
| 0 | Minus 9 | 1 |
| 1 | Minus 8 | 3 |
| 2 | Minus 7 | 5 |
| 3 | Minus 6 | 7 |
| 4 | Minus 5 | 9 |
| 5 | Minus 4 | 1b |
| 6 | Minus 3 | 3b |
| 7 | Minus 2 | 5b |
| 8 | Minus 1 | 7b |
| 9 | Minus 0 | 9b |
In this example, there is a different modifier (or key) for each original number. Because the modified numbers have duplicates, we place a letter next to each of the various duplicates to differentiate. This is tougher to decrypt due to the increased level of variations, but on the flipside, it is that much harder to memorize. Likewise, computers have a harder time processing more advanced encryption codes, and hackers (or crackers) have a difficult time processing their decryption.
At this point, only one person has legitimate access to the encryption codes. However, what if the person wanted to share phone numbers with another person, but still keep the numbers secret from everyone else? This would be known as a secret key.
We refer to this basic concept as we go through this chapter and the next.
Now that we have given a basic example, let’s define some terminology in a more technical way. We start with cryptography, encryption, ciphers, and keys. You might want to read through this list twice because each definition builds on the last.
![]() Cryptography: By definition, cryptography is the practice and study of hiding information, or more accurately, hiding the meaning of the information. It is used in e-commerce and with passwords. Most commonly, encryption is used to hide a message’s meaning and make it secret.
Cryptography: By definition, cryptography is the practice and study of hiding information, or more accurately, hiding the meaning of the information. It is used in e-commerce and with passwords. Most commonly, encryption is used to hide a message’s meaning and make it secret.
![]() Encryption: Encryption is the process of changing information using an algorithm (or cipher) into another form that is unreadable by others—unless they possess the key to that data. Encryption is used to secure communications and to protect data as it is transferred from one place to another. The reverse, decryption, can be accomplished in two ways: First, by using the proper key to unlock the data, and second, by cracking the original encryption key. Encryption enforces confidentiality of data.
Encryption: Encryption is the process of changing information using an algorithm (or cipher) into another form that is unreadable by others—unless they possess the key to that data. Encryption is used to secure communications and to protect data as it is transferred from one place to another. The reverse, decryption, can be accomplished in two ways: First, by using the proper key to unlock the data, and second, by cracking the original encryption key. Encryption enforces confidentiality of data.
![]() Cipher: A cipher is an algorithm that can perform encryption or decryption. A basic example would be to take the plaintext word “code” and encrypt it as a ciphertext using a specific algorithm. The end result could be anything, depending on the algorithm used, but, for example, let’s say the end result was the ciphertext “zlab.” I don’t know about you, but “zlab” looks like gibberish to me. (Although if you Google it, I’m sure you’ll find all kinds of endless fun.) You’ve probably already guessed at my cipher—each letter of the plaintext word “code” was stepped back three letters in the alphabet. Historical ciphers use substitution methods such as this, and transposition methods as well. However, actual algorithms today are much more complex. Algorithms are well-defined instructions that describe computations from their initial state to their final state. IF-THEN statements are examples of computer algorithms. The entire set of instructions is the cipher. We cover the various types of ciphers (again, also known as algorithms) in the section “Encryption Algorithms” later in this chapter.
Cipher: A cipher is an algorithm that can perform encryption or decryption. A basic example would be to take the plaintext word “code” and encrypt it as a ciphertext using a specific algorithm. The end result could be anything, depending on the algorithm used, but, for example, let’s say the end result was the ciphertext “zlab.” I don’t know about you, but “zlab” looks like gibberish to me. (Although if you Google it, I’m sure you’ll find all kinds of endless fun.) You’ve probably already guessed at my cipher—each letter of the plaintext word “code” was stepped back three letters in the alphabet. Historical ciphers use substitution methods such as this, and transposition methods as well. However, actual algorithms today are much more complex. Algorithms are well-defined instructions that describe computations from their initial state to their final state. IF-THEN statements are examples of computer algorithms. The entire set of instructions is the cipher. We cover the various types of ciphers (again, also known as algorithms) in the section “Encryption Algorithms” later in this chapter.
![]() Key: The key is the essential piece of information that determines the output of a cipher. It is indispensable; without it there would be no result to the cipher computation. In the previous bullet, the key was the act of stepping back three letters. In the first black book example, the key was stepping back three numbers (a modifier of minus 3). Just like a person can’t unlock a lock without the proper key, a computer can’t decrypt information without the proper key (using normal methods). The only way to provide security is if the key is kept secret—or in the case that there are multiple keys, if one of them is kept secret. The terms key and cipher are sometimes used interchangeably, but you should remember that the key is the vital portion of the cipher that determines its output. The length of the key determines its strength. Shorter, weaker keys are desirable to attackers attempting to access encrypted data. When two users exchange encrypted messages, it starts with a key exchange. The method of this exchange will vary depending on the type of cryptographic algorithm.
Key: The key is the essential piece of information that determines the output of a cipher. It is indispensable; without it there would be no result to the cipher computation. In the previous bullet, the key was the act of stepping back three letters. In the first black book example, the key was stepping back three numbers (a modifier of minus 3). Just like a person can’t unlock a lock without the proper key, a computer can’t decrypt information without the proper key (using normal methods). The only way to provide security is if the key is kept secret—or in the case that there are multiple keys, if one of them is kept secret. The terms key and cipher are sometimes used interchangeably, but you should remember that the key is the vital portion of the cipher that determines its output. The length of the key determines its strength. Shorter, weaker keys are desirable to attackers attempting to access encrypted data. When two users exchange encrypted messages, it starts with a key exchange. The method of this exchange will vary depending on the type of cryptographic algorithm.
Keys can be private or public. A private key is only known to a specific user or users who keep the key a secret. A public key is known to all parties involved in encrypted transactions within a given group. An example of a private key would be the usage of an encrypted smart card for authentication. Smart cards, ExpressCard/PC Card technology, and USB flash drives are examples of devices that can store keys. When private keys are stored on these types of devices and delivered outside of a network, it is known as out-of-band key exchange. An example of a public key would be when two people want to communicate securely with each other over the Internet; they would require a public key that each of them knows. When this key transfer happens over a network, it is known as in-band key exchange.
Encryption types, such as AES or RSA, are known as ciphers, key algorithms, or simply as algorithms; we refer to them as algorithms during the rest of this chapter and the next. There are basically two classifications of key algorithms: symmetric and asymmetric.
Symmetric Versus Asymmetric Key Algorithms
Some cryptographic systems use symmetric keys only, others use asymmetric keys only, and some use both symmetric and asymmetric. It is important to know the differences between the two, and how they can be used together.
Symmetric Key Algorithms
The symmetric key algorithm is a class of cipher that uses a single key, identical keys, or closely related keys for both encryption and decryption. The term symmetric key is also referred to as the following: secret key, private key, single key, and shared key. Examples of symmetric key algorithms include DES, 3DES, RC, and AES, all of which we discuss later in this chapter. Another example of a technology that uses symmetric keys is Kerberos. By default, Kerberos makes use of a third party known as a key distribution center (KDC) for the secure transmission of symmetric keys, also referred to as tickets.
Note
Kerberos can optionally use public key cryptography (covered later in this chapter) by making use of asymmetric keys. This is done during specific authentication stages. Kerberos is covered in more depth in Chapter 10, “Physical Security and Authentication Models.”
The private key is common in the workplace. Let’s say that a user encrypts a file with a private key. Generally, that same key (or a very similar private key) is needed to decrypt the data. Imagine that the user left the organization and that user’s account (and therefore the user’s key) was deleted. How would you get the data back? Well, if the system has a recovery agent, you could use that to decrypt the file; otherwise, the data will not be recoverable! It’s important to understand that private keys, and by extension, symmetric key systems, must be approached carefully or data could become lost.
Following are two types of symmetric key algorithms:
![]() A stream cipher is a type of algorithm that encrypts each binary digit in the data stream, one bit at a time.
A stream cipher is a type of algorithm that encrypts each binary digit in the data stream, one bit at a time.
![]() A block cipher is a type of algorithm that encrypts a group of bits collectively as individual units known as blocks. For example, the Advanced Encryption Standard (AES) algorithm can use 128-bit or 256-bit block ciphers. Block ciphers can work in different modes including: Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB), Galois/Counter Mode (GCM), and Counter (CTR). The modes define how a message is divided into blocks and encrypted. For example, ECB divides a message into blocks of plaintext and each block is encrypted separately. CBC is a commonly used mode that builds on ECB by XORing each block of plaintext with the previous ciphertext block that was created. CBC is one of the modes that require a unique binary sequence (an initialization vector, or IV) for each encryption operation. The IV can be a vulnerability, as in the CBC IV attack, where a predictable IV can lead to the deciphering of all blocks, because each one is based on the block previous. Secure coding concepts should be employed when using CBC or a separate block mode should be selected altogether such as GCM, which is considered to be a more efficient mode. The mode chosen will depend on the purpose of the encryption and the application it is being developed for.
A block cipher is a type of algorithm that encrypts a group of bits collectively as individual units known as blocks. For example, the Advanced Encryption Standard (AES) algorithm can use 128-bit or 256-bit block ciphers. Block ciphers can work in different modes including: Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB), Galois/Counter Mode (GCM), and Counter (CTR). The modes define how a message is divided into blocks and encrypted. For example, ECB divides a message into blocks of plaintext and each block is encrypted separately. CBC is a commonly used mode that builds on ECB by XORing each block of plaintext with the previous ciphertext block that was created. CBC is one of the modes that require a unique binary sequence (an initialization vector, or IV) for each encryption operation. The IV can be a vulnerability, as in the CBC IV attack, where a predictable IV can lead to the deciphering of all blocks, because each one is based on the block previous. Secure coding concepts should be employed when using CBC or a separate block mode should be selected altogether such as GCM, which is considered to be a more efficient mode. The mode chosen will depend on the purpose of the encryption and the application it is being developed for.
Symmetric key algorithms require a secure initial exchange of one or more secret keys to both the sender and the receiver. In our black book example, we mentioned that people might possibly want to share their cipher with someone else. To do so, they would need to make sure that they were alone and that no one was eavesdropping. It is also so with computers. The secure initial exchange of secret keys can be difficult depending on the circumstances. It is also possible to encrypt the initial exchange of the secret keys!
Symmetric encryption is the preferred option when encrypting and sending large amounts of data. This is in part because it usually takes far less time to encrypt and decrypt data than asymmetric encryption does.
Asymmetric Key Algorithms
Asymmetric key algorithms use a pair of different keys to encrypt and decrypt data. The keys might be related, but they are not identical or even close to it in the way symmetric keys are. The two asymmetric keys are related mathematically. Imagine that you are the night shift security guard for a warehouse that stores CPUs. When your shift is over you are required to lock up. But the warehouse uses a special lock. Your key can only lock the warehouse door; it cannot unlock it. Conversely, the morning watchman has a key that can only unlock the door but not lock it. There are physical and electronic locks of this manner. This is analogous to asymmetric keys used in encryption. One key is used to encrypt data; the other, dissimilar key is used to decrypt the data. Because of the difference in keys, asymmetric key management schemes (such as PKI) are considered to be the most complicated. Examples of asymmetric key algorithms include RSA, the Diffie-Hellman system, and elliptic curve cryptography. SSL and TLS protocols use asymmetric key algorithms but generally do so in a public key cryptographic environment.
Public Key Cryptography
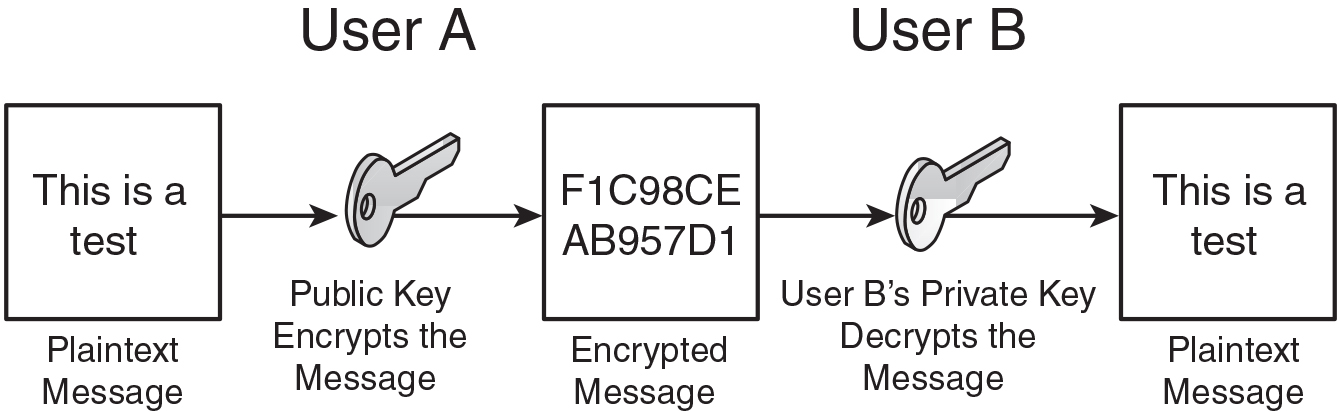
Public key cryptography uses asymmetric keys alone or in addition to symmetric keys. It doesn’t need the secure exchange of secret keys mentioned in the symmetric key section. Instead, the asymmetric key algorithm creates a secret private key and a published public key. The public key is well known, and anyone can use it to encrypt messages. However, only the owner(s) of the paired or corresponding private key can decrypt the message. The security of the system is based on the secrecy of the private key. If the private key is compromised, the entire system will lose its effectiveness. This is illustrated in Figure 14-1.
Public key cryptography can become more intense. In some schemes, the private key is used to sign a message, and anyone can check the signature with the public key. This signing is done with a digital signature. A digital signature authenticates a document through math, letting the recipient know that the document was created and sent by the actual sender, and not someone else. So, it ensures integrity and non-repudiation, and it protects against forgery and tampering. The basic order of functions for the usage of asymmetric keys in this case would be encrypt, sign, decrypt, and verify.
Note
Digital signatures can also be hashed (more on hashing later) for comparison once the document gets to its final destination.
In the Diffie-Hellman scheme, each user generates a public/private key pair and distributes a public key to everyone else. After two or more users obtain a copy of the others’ public keys, they can be used to create a shared secret used as the key for a symmetric cipher. Due to the varying methods of public key cryptography, the whole subject can become somewhat confusing. Remember that there will always be a private key and a public key involved, and that public key cryptography can use asymmetric keys alone or in addition to symmetric keys.
Internet standards, such as SSL/TLS and PGP, use public key cryptography. Don’t confuse the term public key cryptography with public key infrastructure (PKI). Although they are related, they are not the same. PKI is an entire system of hardware, software, policies, and so on, that binds public keys with user identities by way of certificates and a certificate authority (server or other such device). A certificate is an electronic document that uses a digital signature to bind the key with the identity. We cover PKI more in Chapter 15, “PKI and Encryption Protocols.”
Key Management
Key management deals with the relationship between users and keys; it’s important to manage the generation, exchange, storage, and usage of those keys. It is crucial technically, and organizationally, because issues can present themselves due to poorly designed key systems and poor management. Keys must be chosen and stored securely. The generation of strong keys is probably the most important concept. Some algorithms have weak keys that make cryptanalysis easy. For example, DES uses a considerably weaker key than AES; the stronger the key, the stronger the key management. We detail several methods for the exchange of keys later in this chapter, including encapsulating one key within another, using key indicators, and exchanging symmetric session keys with an asymmetric key algorithm—in effect, ciphering our cipher. (We’ll talk more about session keys in Chapter 15.) Secure storage of keys often depends on users and passwords, or other authentication schemes. Proper storage of keys allows for availability, part of the CIA triad. Finally, keys should be replaced frequently. If a particular user uses a key for too long, it increases the chances of the key being cracked. Keys, like passwords, should be changed and/or recycled often.
Steganography
Although I have placed steganography within the cryptography section, it actually isn’t cryptography, although it might be used with cryptography. Steganography is the science (and art) of writing hidden messages; it is a form of security through obscurity. The goal is that no one aside from the sender and receiver should even suspect that the hidden message exists. The advantage of steganography is that the clearly visible messages look to be just that, regular old messages that wouldn’t usually attract attention to themselves. Most people know when they come into contact with an encrypted message, but far fewer people identify when a steganographic message has crossed their path. The classic example of steganography is from ancient Greece. A messenger would shave his head, and a leader would write a message on the person’s scalp with indelible ink. After the messenger’s hair grew long enough to hide the message, he would then deliver the message (time was not of the essence). When the messenger arrived at his destination, he would shave his head and the recipient could read the message. In Greek, steganos means “covered,” and this is one example of hiding a message by covering it.
Steganography can hide messages within encrypted documents by inserting extra encrypted information. The hidden messages can also be found in sound files, image files, slowed-down video files, and regular Word documents or Excel spreadsheets. Messages can also be concealed within VoIP conversations (known as Lost Audio Packets Steganography, or LACK), and within any streaming service as well. They can also be obscured on a compromised wireless network with the HICCUPS system (Hidden Communication System for Corrupted Networks).
A common example of steganography is when using graphic files to send hidden messages. In this scenario, the least significant bit of each byte is replaced. For example, we could shade the color of a pixel (or triad) just slightly. This slight change would change the binary number associated with the color, enabling us to insert information. The color blue is represented as three bytes of data numbered 0, 0, and 255. We could change the color blue slightly to 1, 0, 255. This would not make the graphic look any different to the naked eye, but the change would be there nonetheless. This would be done in several or more pixels of the graphic to form the message. For this to work, the recipient would first need to have possession of the original file. Then the sender would transmit the modified steganographic file to be compared with the original by the recipient. There are several programs available on the Internet that facilitate and automate this process. Remember that one of the goals of steganography is to provide obfuscation, meaning making something obscure and unclear. This can be difficult to do manually, and more difficult to undo manually, so use reliable vendor-provided tools to aid in the process.
Encryption Algorithms
We mentioned previously that ciphers (or algorithms) can encrypt or decrypt data with the help of a key. We also pointed out that algorithms are well-defined instructions that describe computations from their initial state to their final state. In addition, we mentioned that there are symmetric and asymmetric algorithms. Now, let’s talk about some of the actual algorithmic standards within both of those classifications. We start with symmetric types, including DES, 3DES, AES, and RC, and afterward move on to asymmetric types, including RSA, Diffie-Hellman, and the elliptic curve.
DES and 3DES
The Data Encryption Standard (DES) is an older type of block cipher selected by the U.S. federal government back in the 1970s as its encryption standard. But due to its weak key, it is now considered deprecated and has been replaced by other standards. Being a block cipher, it groups 64 bits together into encryption units. Today, a 64-bit cipher is not considered powerful enough; also, and more important, the key size is 56-bit, which can be cracked fairly easily with a brute-force attack or linear cryptanalysis attack. In addition to this, there are some theoretical weaknesses to the cipher itself. DES was replaced by Triple DES (3DES) in 1999. The actual algorithm is sometimes referred to as the Data Encryption Algorithm (DEA). The algorithm is based on the Feistel cipher, which has very similar, if not identical, encryption and decryption processes, reducing the amount of code required.
Note
The International Data Encryption Algorithm (IDEA) was designed as a replacement to DES and is an optional algorithm in the OpenPGP standard, though it suffers from a simple key schedule resulting in weak keys.
Triple DES, also known as 3DES or the Triple Data Encryption Algorithm (TDEA), is similar to DES but applies the cipher algorithm three times to each cipher block. The cipher block size is still 64-bit, but the key size can now be as much as 168-bit (three times the size of DES). This was a smart approach to defeating brute-force attacks without having to completely redesign the DES protocol. However, both DES and 3DES have been overshadowed by AES, which became the preferred standard in late 2001.
AES
In the late 1990s, the National Institute of Standards and Technology (NIST) started a competition to develop a more advanced type of encryption. There were 15 submissions, including Serpent, Twofish, RC6, and others, but the selected winner was Rijndael. This submission was then further developed into the Advanced Encryption Standard (AES) and became the U.S. federal government standard in 2002. AES is the successor to DES/3DES and is another symmetric key encryption standard composed of three different versions of block ciphers: AES-128, AES-192, and AES-256. Actually, each of these has the same 128-bit cipher block size, but the key sizes for each are 128-bit, 192-bit, and 256-bit, respectively.
AES is based on the substitution-permutation network, which takes plaintext and the key and applies x number of rounds to create the ciphertext. These rounds consist of substitution boxes and permutation boxes (usually in groups of 4×4 bytes) that convert the plaintext input bits to ciphertext output bits. AES specifies 10, 12, or 14 rounds for each of the respective versions.
AES is fast, uses minimal resources, and can be used on a variety of platforms. For example, it is the encryption algorithm of choice if you have a wireless network running the WPA2 protocol; the IEEE 802.11i standard specifies the usage of AES with WPA2, and in the process deprecates WEP. (See Chapter 9, “Securing Network Media and Devices,” for more about WEP and WPA.) You will also find AES as the encrypting protocol for remote control applications. These are examples of data in motion (also called data in transit). Any network session that uses AES would fall into this category. But memory encryption would fall into that category as well. For example, there are programs that can encrypt passwords and other personally identifiable information (PII) as it is passing through RAM. They often use AES or Twofish.
In addition, AES is a good choice for transferring encrypted data quickly to a USB flash drive. It is also used as the Windows Encrypting File System (EFS) algorithm and in whole disk encryption techniques such as BitLocker.
AES is purportedly susceptible to the related-key attack, if the attacker has some information about the mathematical relationship between several different keys. Side-channel attacks can also circumvent the AES cipher using malware to obtain privilege escalation. These are ways of attacking the implementation of the protocol, but not the protocol itself.
Generally, AES is considered the strongest type of symmetric encryption for many scenarios. As of now, AES is used worldwide and has not been outright compromised, and some industry experts think it never will be.
You may have heard of the terms DEK, KEK, and MEK. These are different types of keys used during the encryption process. AES provides a good place to discuss these. Let’s say you have data that you need encrypted and you decide to use AES to do so. When AES encrypts the data, it does so with a data encryption key (DEK). To make an encryption system more secure, you can store that DEK in an encrypted format. This is done with a key encryption key (KEK) and can be stored in a separate location for additional security if need be. A master encrypting key (MEK), or simply master key, is another type of key that describes either a DEK or KEK being used. For example, in a secure storage scenario, the master key will be a DEK that is used to encrypt data that is put in a user’s protected storage area. It is encrypted by a KEK that is based on the user’s password. That is a very basic explanation of DEK, KEK, and MEK. For the Security+ exam you should be able to define them, and understand that they can be instrumental in dealing with secure storage of data, potentially in multiple locations. However, unless you are a developer, you most likely won’t be working with each type of key individually.
RC
RC stands for different things depending on who you talk to. Officially, it is known as Rivest Cipher but is playfully known as Ron’s Code as well. There are multiple RC versions, most of which are not related aside from the fact that they are all encryption algorithms.
RC4 is a somewhat widely used stream cipher in protocols such as SSL, WEP, and RDP. It is known for its speed and simplicity. However, it is avoided when designing newer applications and technologies due to several vulnerabilities; when used with WEP on wireless networks, it can be cracked quickly with the use of aircrack-ptw. One way to avoid this to a certain extent is to use the Temporal Key Integrity Protocol (TKIP) with WEP. However, it still is recommended that AES and WPA2 be used in wireless networks. Some versions of Microsoft Remote Desktop Services use RC4 128-bit. However, Microsoft recommends disabling RC4 if at all possible, and using other encryption, such as Federal Information Processing Standard (FIPS)-compliant encryption (IPsec and EFS) and TLS for authentication.
Note
FIPS-compliant could be in the form of a hardware- or software-based crypto-module. For example, FIPS 140-1 and 140-2 specify Microsoft as a proper vendor; see this link for more: http://csrc.nist.gov/groups/STM/cmvp/documents/140-1/140val-all.htm. Microsoft includes a software library known as the Cryptographic Service Provider (CSP) that implements the Microsoft CryptoSPI (a system program interface).
RC5 is a block cipher noted for its simplicity and for its variable size (32-, 64-, or 128-bit). The strongest RC5 block cipher that has been cracked via brute-force as of the writing of this book is a 64-bit RC5 key, in 2001. This was done by distributed.net, a nonprofit organization which at the time had 30 TFLOPS of computational power. It is also working on cracking the 72-bit version of RC5, with substantially higher throughput at its disposal. This is cause for concern for some—because Moore’s Law tells us of the effective doubling of CPU power every two years or so—but you must remember that stronger algorithms such as AES 256-bit are exponentially harder to crack.
RC6 is a block cipher entered into the AES competition and was one of the five finalists. Though it was not selected, it is a patented algorithm offered by RSA Security as an alternative to AES. It is similar to AES in block size and key size options but uses different mathematical methods than Rijndael.
Blowfish and Twofish
Blowfish and Twofish are two ciphers designed by Bruce Schneier. The original Blowfish is a block cipher designed as an alternative to DES (the name also pertains to a suite of products). It has a 64-bit block size and variable key size between 32 and 448 bits. Bruce Schneier recommends the newer Twofish cipher, which has a block size of 128 bits and a key size up to 256 bits and is also based on Feistel. There is also a newer Threefish block cipher with key sizes up to 1024-bit. These symmetrical ciphers have not been compromised, but they do have minor weaknesses that can be exploited by birthday attacks and key separation.
Summary of Symmetric Algorithms
Table 14-3 gives some comparisons of the algorithms up to this point and their key size. Key size is the number of bits in a cipher. It is also referred to as key length or key strength.
Table 14-3 Summary of Symmetric Algorithms
| Algorithm Acronym | Full Name | Maximum/Typical Key Size |
| DES | Data Encryption Standard | 56-bit |
| 3DES | Triple DES | 168-bit |
| AES | Advanced Encryption Standard | 256-bit |
| RC4 | Rivest Cipher version 4 | 128-bit typical |
| RC5 | Rivest Cipher version 5 | 64-bit typical |
| RC6 | Rivest Cipher version 6 | 256-bit typical |
| Twofish | Twofish | 128-, 192-, 256-bit |
RSA
Let’s talk about some asymmetric key algorithms. The original and very common RSA (which stands for Rivest, Shamir, and Adleman, the creators) is a public key cryptography algorithm. As long as the proper size keys are used, it is considered to be a secure protocol and is used in many e-commerce scenarios. It is slower than symmetric key algorithms but has advantages of being suitable for signing and for encryption. It works well with credit card security and TLS/SSL. Key lengths for RSA are much longer than in symmetric cryptosystems. For example, 512-bit RSA keys have proven to be breakable over a decade ago; however, 1024-bit keys are currently considered unbreakable by most known technologies, but RSA still recommends using the longer 2048-bit key, which should deter even the most powerful super hackers. It is important to note that asymmetric algorithm keys need to be much larger than their symmetric key counterparts to be as effective. For example, a 128-bit symmetric key is essentially equal to a 2304-bit asymmetric key in strength.
The RSA algorithm uses what is known as integer factorization cryptography. It works by first multiplying two distinct prime numbers that cannot be factored. Then it moves on to some more advanced math in order to derive a set of two numbers. Finally, from these two numbers, it creates a private and public key pair.
The private key is used to decrypt data that has been encrypted with the public key. For example, if Alice (User A) sends Bob (User B) a message, Alice can find out Bob’s public key from a central source and encrypt a message to Bob using Bob’s public key. When Bob receives it, he decrypts it with his private key.
Bob can also authenticate himself to Alice, for example by using his private key to encrypt a digital certificate. When Alice receives it, she can use his public key to decrypt it. These concepts are summarized in Table 14-4.
Table 14-4 Summary of RSA Public and Private Key Usage
| Task | Which Person’s Key to Use | What Kind of Key |
| Send an encrypted message | Receiver’s | Public key |
| Decrypt an encrypted message | Receiver’s | Private key |
| Send an encrypted signature | Sender’s | Private key |
| Decrypt an encrypted signature | Sender’s | Public key |
Other examples of RSA encryption include tokens in the form of SecurID USB dongles, and devices such as hardware security modules (HSMs) and trusted platform modules (TPMs). All these devices can store RSA asymmetric keys and can be used to assist in user authentication. RSA key distribution is vulnerable to man-in-the-middle attacks. However, these attacks are defensible through the use of digital certificates and other parts of a PKI system that we detail in the next chapter. It is also susceptible to timing attacks that can be defended against through the use of cryptographic blinding: This blind computation provides encryption without knowing actual input or output information. Due to other types of attacks, it is recommended that a secure padding scheme be used. Padding schemes work differently depending on the type of cryptography. In public key cryptography, padding is the addition of random material to a message to be sufficient, and incorporating a proof, making it more difficult to crack. A padding scheme is always involved, and algorithm makers such as RSA are always releasing improved versions.
In 2000, RSA Security released the RSA algorithm to the public. Therefore, no licensing fees are required if an organization decides to use or modify the algorithm. RSA published a group of standards known as PKCS (Public-Key Cryptography Standards) in an effort to promote its various public key techniques. For example, PKCS #1 defines the mathematical properties of RSA public and private keys. Another example is PKCS #11, which defines how HSMs utilize RSA. The entire list of standards can be found at the following link:
https://www.emc.com/emc-plus/rsa-labs/standards-initiatives/public-key-cryptography-standards.htm
Diffie-Hellman
The Diffie-Hellman key exchange, invented in the 1970s, was the first practical method for establishing a shared secret key over an unprotected communications channel. This asymmetric algorithm was developed shortly before the original RSA algorithm. It is also known as the Diffie-Hellman-Merkle key exchange due to Ralph Merkle’s conceptual involvement.
Diffie-Hellman relies on secure key exchange before data can be transferred. This key exchange establishes a shared secret key that can be used for secret communications but over a public network. Originally, fictitious names were chosen for the “users”: Alice and Bob. Basically, Alice and Bob agree to initial prime and base numbers. Then, each of them selects secret integers and sends an equation based on those to each other. Each of them computes the other’s equation to complete the shared secret, which then allows for encrypted data to be transmitted. The secret integers are discarded at the end of the session. These were originally static keys, meaning that they were used for a long period of time.
Diffie-Hellman is considered secure against eavesdroppers due to the difficulty of mathematically solving the Diffie-Hellman problem. However, it is vulnerable to man-in-the-middle attacks. To prevent this, some method of authentication is used such as password authentication. This algorithm is used by the Transport Layer Security (TLS) protocol during encrypted web sessions. When used in this manner, it works in ephemeral mode, meaning that keys are generated during each portion of the key establishment process, and are used for shorter periods of time than with static keys. It is this ephemeral process that achieves perfect forward secrecy (PFS), which ensures that the compromise of one message will not lead to the compromise of another message. This ephemeral version of Diffie-Hellman is called DHE, or sometimes Ephemeral Diffie-Hellman (EDH), because it uses an ephemeral key, meaning that the cryptographic key is generated for each execution of the key establishment process. One of the drawbacks to DHE is that it requires more computational power; however, there is an elliptic curve alternative, which we talk about in the next section.
Note
The Diffie-Hellman algorithm can also be used within a public key infrastructure (PKI), though the RSA algorithm is far more common.
Elliptic Curve
Elliptic curve cryptography (ECC) is a type of public key cryptography based on the structure of an elliptic curve. It uses logarithms calculated against a finite field and is based on the difficulty of certain mathematical problems. It uses smaller keys than most other encryption methods. Keys are created by graphing specific points on the curve, which were generated mathematically. All parties involved must agree on the elements that define the curve. This asymmetric algorithm has a compact design, leading to reduced computational power compared to other asymmetric algorithms, yet it creates keys that are difficult to crack.
Other algorithms have been adapted to work with elliptic curves, including Diffie-Hellman and the Digital Signature Algorithm (DSA). The Diffie-Hellman version (known as Elliptic Curve Diffie-Hellman, or ECDH) uses elliptic curve public/private key pairs to establish the secret key. Another variant, Elliptic Curve Diffie-Hellman Ephemeral (ECDHE), runs in ephemeral mode, which as previously stated makes sure that a compromised message won’t start a chain reaction, and that other messages maintain their integrity. By its very design, the elliptic curve solves the problem of the extra computational power required by DHE. DSA is a U.S. federal government standard public key encryption algorithm used in digital signatures. The elliptic version is known as ECDSA. In general, the size of the public key in an elliptic curve–based algorithm can be 1/6 the size of the non-elliptic curve version. For example, ECDSA has a public key that is 160 bits, but regular DSA uses a public key that is 1024 bits. This is part of the reasoning behind the reduced amount of CPU power needed.
ECC is used with smart cards, wireless security, and other communications such as VoIP and IPsec (with DSA). It can be susceptible to side-channel attacks (SCAs), which are attacks based on leaked information gained from the physical implementation (number and type of curves) of the cryptosystem, and fault attacks (a type of SCA), plus there are concerns about backdoors into the algorithm’s random generator. Elliptic curve cryptography (as well as RSA and other algorithms) is also theoretically vulnerable to quantum cryptanalysis–based computing attacks.
More Encryption Types
We have a couple more encryption types to speak of. They don’t quite fit into the other sections, so I figured I would place them here. The first is the one-time pad, and the second is the Pretty Good Privacy (PGP) application and encryption method.
One-Time Pad
A one-time pad (also known as the Vernam cipher, named after the engineer Gilbert Vernam) is a stream cipher that encrypts plaintext with a secret random key that is the same length as the plaintext. It uses a string of bits that is generated at random (known as a keystream). Encryption is accomplished by combining the keystream with the plaintext message using the bitwise XOR operator to produce the ciphertext. Because the keystream is randomized, even an attacker with a plethora of computational resources on hand can only guess the plaintext if the attacker sees the ciphertext.
Unlike other encryption types, it can be computed by hand with a pencil and paper (thus the word “pad” in the name), although today computers will be used to create a one-time pad algorithm for use with technology. It has been proven as impossible to crack if used correctly and is known as being “information-theoretically secure”; it is the only cryptosystem with theoretically perfect secrecy. This means that it provides no information about the original message to a person trying to decrypt it illegitimately. However, issues with this type of encryption have stopped it from being widely used. Because of this, the acronym OTP is more commonly associated with “one-time passwords,” which we talk about later in this chapter.
One of the issues with a one-time pad is that it requires perfect randomness. The problem with computer-based random number generators is that they usually aren’t truly random because high-quality random numbers are difficult to generate; instead, they are pseudorandom number generators (PRNGs), discussed a bit later. Another issue is that the exchange of the one-time pad data must be equal to the length of the message. It also requires proper disposal, which is difficult due to data remanence.
Regardless of these issues, the one-time pad can be useful in scenarios in which two users in a secure environment are required to also communicate with each other from two other separate secure environments. The one-time pad is also used in superencryption (or multiple encryption), which is encrypting an already encrypted message. In addition, it is commonly used in quantum cryptography, which uses quantum mechanics to guarantee secure communications. These last two concepts are far beyond the Security+ exam, but they show the actual purpose for this encryption type.
PGP
Pretty Good Privacy (PGP) is an encryption program used primarily for signing, encrypting, and decrypting e-mails in an attempt to increase the security of e-mail communications. You might remember that we previously discussed weaknesses of e-mail client programs when sending via POP3 and SMTP servers. PGP uses (actually wrote) the encryption specifications as shown in the OpenPGP standard; other similar programs use this as well. Today, PGP has an entire suite of tools that can encrypt e-mail, accomplish whole disk encryption, and encrypt zip files and instant messages. PGP uses a symmetric session key (also referred to as a preshared key, or PSK), and as such, you might hear PGP referred to as a program that uses symmetric encryption, but it also uses asymmetric RSA for digital signatures and for sending the session key. Because of this it is known as a hybrid cryptosystem, combining the best of conventional systems and public key cryptography.
When encrypting data, PGP uses key sizes of at least 128 bits. Newer versions allow for RSA or DSA key sizes ranging from 512 bits to 2048 bits. The larger the key, the more secure the encryption is, but the longer it takes to generate the keys; although, this is done only once when establishing a connection with another user. The program uses a combination of hashing, data compression, symmetric key cryptography, and public key cryptography. New versions of the program are not fully compatible with older versions because the older versions cannot decrypt the data that was generated by a newer version. This is one of the issues when using PGP; users must be sure to work with the same version. Newer versions of PGP support OpenPGP and S/MIME, which allows for secure communications with just about everyone.
Because it works with RSA, the security of PGP is based on the key size. It is considered secure and uncrackable as long as a sufficient key size is used. As an example, it has been suggested that a 2048-bit key should be safe against the strongest of well-funded adversaries with knowledgeable people and the latest in supercomputers until at least the year 2020; 1024-bit keys are considered strong enough for all but the most sensitive data environments.
Around the turn of the millennium, the creator of PGP, and many other security-minded people that used PGP, sensed that an open source alternative would be beneficial to the cryptographic community. This was presented to, and accepted by, the IETF, and a new standard called OpenPGP was developed. With this open source code, others could write software that could easily integrate with PGP (or replace it). One example of this is the GNU Privacy Guard (GPG, or GNuPG), which is compliant with the OpenPGP standard. Over time this has been developed for several platforms including various Linux GUIs, macOS/OS X, and Windows. GPG is a combination of symmetric key encryption and public key encryption.
PGP and its derivatives are used by many businesses and individuals worldwide so that files can be easily encrypted before transit. The original PGP (developed by Philip Zimmerman) has changed hands several times and, as of this writing, is owned by Symantec, which offers it as part of its products (for a fee). There are also several versions of PGP, as well as GNuPG, available for download for free. A good starting point is the following link: http://openpgp.org/.
Pseudorandom Number Generators
The pseudorandom number generator (PRNG) is used by cryptographic applications that require unpredictable output. They are primarily coded in C or Java and are developed within a cryptography application such as a key generator program. Within that program there is a specific utility, for example SHA2PRNG, that is used to create the PRNG. (Remember to use SHA-256—as of the writing of this book—or higher.) For additional “randomness” a programmer will increase entropy, often by collecting system noise. One of the threats to PRNGs is the random number generator attack, which exploits weaknesses in the code. This can be prevented by implementing randomness, using AES, using newer versions of SHA, and maintaining physical control of the system where the PRNG is developed and stored.
Hashing Basics
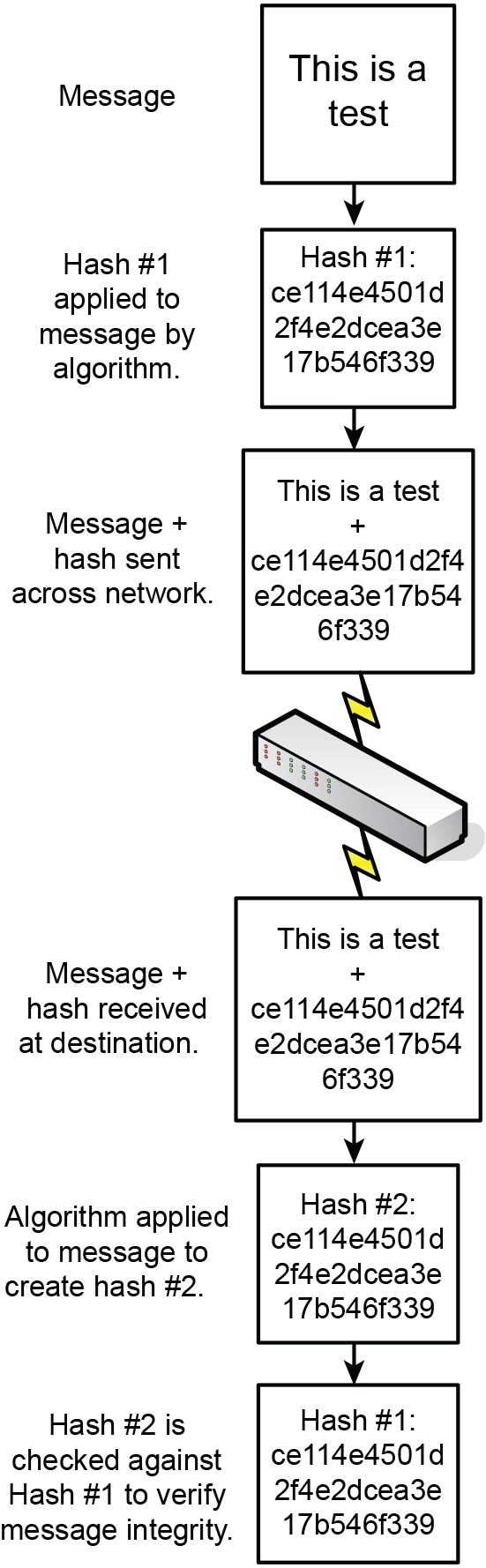
A hash is a summary of a file or message, often in numeric format. Hashes are used in digital signatures, in file and message authentication, and as a way to protect the integrity of sensitive data; for example, data entered into databases, or perhaps entire hard drives. A hash is generated through the use of a hash function to verify the integrity of the file or message, most commonly after transit over a network. A hash function is a mathematical procedure that converts a variable-sized amount of data into a smaller block of data. The hash function is designed to take an arbitrary data block from the file or message, use that as an input, and from that block produce a fixed-length hash value. Basically, the hash is created at the source and is recalculated and compared with the original hash at the destination. Figure 14-2 illustrates this process. Note the hash that was created starting with ce114e and so on. This is the summary, or message digest, of the file to be sent. It is an actual representation of an MD5 hash (covered shortly) of a plaintext file with the words “This is a test,” as shown in the message portion of Figure 14-2.
Because the hash is a condensed version of the file/message, or a portion of it, it is also known as a message digest. It provides integrity to data so that a user knows that the message is intact, hasn’t been modified during transit, and comes from the source the user expects. A hash can fall into the category of a one-way function. This means it is easy to compute when generated but difficult (or impossible) to compute in reverse. In the case of a hash, a condensed version of the message, initial computation is relatively easy (compared to other algorithms), but the original message should not be re-created from the hash. Contrast this concept to encryption methods that indeed can be reversed. A hash can be created without the use of an algorithm, but generally, the ones used in the field require some kind of cryptographic algorithm.
Cryptographic Hash Functions
Cryptographic hash functions are hash functions based on block ciphers. The methods used resemble that of cipher modes used in encryption. Examples of cryptographic hash functions include MD5 and SHA. Let’s discuss a few types of hash functions now.
MD5
The Message-Digest algorithm 5 (MD5) is the newest of a series of algorithms designed by Ron Rivest. It uses a 128-bit key. This is a widely used hashing algorithm; at some point you have probably seen MD5 hashes when downloading files. This is an example of the attempt at providing integrity. By checking the hash produced by the downloaded file against the original hash, you can verify the file’s integrity with a level of certainty. However, MD5 hashes are susceptible to collisions. A collision occurs when two different files end up using the same hash. Due to this low collision resistance, MD5 is considered to be harmful today. MD5 is also vulnerable to threats such as rainbow tables and pre-image attacks. The best solution to protect against these attacks is to use a stronger type of hashing function such as SHA-2 or higher.
Note
A rainbow table is a precomputed table used to reverse engineer a cryptographic hash function. Rainbow tables are most often used to crack passwords.
SHA
The Secure Hash Algorithm (SHA) is one of a number of hash functions designed by the U.S. National Security Agency (NSA) and published by the NIST. They are used widely in the U.S. government. SHA-1 is no longer considered to be secure because there is the potential for successful collision-based attacks. It employs a 160-bit hash, and as of 2017 has been deprecated. Any websites or other applications using SHA-1 are required to be updated to a higher level of SHA or other hashing algorithm. SHA-2 is more secure; it has 256-bit and 512-bit block sizes, plus truncated derivatives of each. Keccak was selected from a group of algorithms in 2012 as the SHA-3 winner, but is not meant as a replacement for SHA-2, because no compromise of SHA-2 has yet been demonstrated (as of the writing of this book).
It is important that a hashing algorithm be collision-resistant. If it has the capability to avoid the same output from two guessed inputs (by an attacker attempting a collision attack), it is collision-resistant. When it comes to cryptography, “perfect hashing” is not possible because usually unknowns are involved, such as the data to be used to create the hash, and what hash values have been created in the past. Though perfect is not possible, it is possible to increase collision resistance by using a more powerful hashing algorithm.
Because MD5 and SHA-1 have vulnerabilities, some government agencies started using SHA-2 as early as 2011 (and most likely will use SHA-3 at some point). For added security, a software key (computed with either SHA or MD-5) might be compared to a hardware key. Some software activations require this in fact—if the hardware and software hash values don’t match, then the software won’t activate.
RIPEMD and HMAC
RIPEMD stands for the RACE Integrity Primitives Evaluation Message Digest. The original RIPEMD (128-bit) had a collision reported, and therefore it is recommended to use RIPEMD-160 (160-bit), RIPEMD-256, or RIPEMD-320. The commonly used RIPEMD-160 is a 160-bit message digest algorithm used in cryptographic hashing. It is used less commonly than SHA and was designed as an open source hashing algorithm.
HMAC stands for Hash-based Message Authentication Code. Let’s step back for a moment: Message Authentication Code (MAC) is a short piece of information—a small algorithm—used to authenticate a message and to provide integrity and authenticity assurances on the message. It checks the integrity of the cipher used and notifies the receiver if there were any modifications to the encrypted data. This way, the data cannot be denied (repudiated) when received.
Building on this concept, HMAC is a calculation of a MAC through the use of a cryptographic hash function such as MD5 or SHA-1. If for example SHA-1 is used, the corresponding MAC would be known as HMAC-SHA1, or better yet, if using SHA-2 (due to SHA-1 deprecation) then you would probably use HMAC-SHA256 (or higher). Warning: Be very careful selecting the type and version of hash function that you use!
LANMAN, NTLM, and NTLMv2
Passwords can also be hashed using algorithms. Some password hashes are more secure than others, whereas older ones have been cracked and are therefore compromised. This section details the Windows-based LANMAN, NTLM, and NTLMv2 hashes starting from the oldest. These three types of authentication are what attempts to make your login to the Windows computer secure, unless you log in to a domain where Kerberos is used by default.
LANMAN
The LANMAN hash, also known as the LAN Manager hash or simply LM hash, was the original hash used to store Windows passwords. It was used in Windows operating systems before Windows NT but is supported by some versions of Windows in an attempt to be backward compatible. This backward compatibility can be a security risk because the LM hash has several weaknesses and can be cracked easily.
Its function is based on the deprecated DES algorithm and can only be a maximum of 14 characters. These weaknesses are compounded by the fact that the ASCII password is broken into two pieces, one of which is converted to uppercase, essentially removing a large portion of the character set. Plus, it can store a maximum of only seven uppercase characters. Due to this, brute-force attacks can crack alphanumeric LM hashes in a matter of hours.
Due to all these weaknesses, it is highly recommended that the LANMAN hash be disabled on operating systems that run it by default. It should also be checked on operating systems such as Windows Vista/Server 2008 and higher that are supposed to have it disabled by default, just in case the setting was modified.
The following step-by-step procedure shows how to disable the storage of LM hashes in Windows:
Step 1. Open the Run prompt and type secpol.msc to display the Local Security Policy window.
Step 2. Navigate to Local Policies > Security Options.
Step 3. In the right pane, double-click the policy named Network Security: Do Not Store LAN Manager Hash Value on Next Password Change.
Step 4. Click Enabled (if it isn’t already), as shown in Figure 14-3, and click OK. (Remember that in a situation such as this you are enabling a negative.)
Note
For Windows Server domain controllers, you need to access the Group Policy Editor, not Local Group Policy. Generally, this would be done at the default domain policy, but it could also be accomplished at a single OU’s policy, if necessary.
You can also disable the storage of LM hash passwords by modifying the Registry. This process is necessary for older versions of Windows. For more information, see the link to Microsoft’s website in the “View Recommended Resources” document on the accompanying website.
If, for whatever reason, the storing of LM hashes for passwords cannot be turned off, Microsoft recommends using a 15-character-minimum password. When this is done, an LM hash and an NTLM hash value are stored. In this situation, the LM hash cannot be used solely to authenticate the user; therefore, it cannot be solely cracked. The NTLM hash would have to be cracked as well. Because 15 characters might be beyond some organizations’ policies—or some users’ ability, for that matter—it is highly recommended that the LM hash policy be disabled.
NTLM and NTLMv2
Well, we talked a lot about why the LM hash is insufficient. Let’s get into the replacements. The first is the NTLM hash, also known as the NT LAN Manager hash. The NTLM algorithm was first supplied with Windows NT 3.1; it provides Unicode support and, more important to this conversation, the RC4 cipher. Although the RC4 cipher enables a more powerful hash known as NTLM for storing passwords, the systems it ran on were still configured to be backward compatible with the LM hash. So, as long as the LM hash was not disabled, those systems were still at the same risk as older systems that ran the LM hash only. Windows Vista and Windows Server 2008 operating systems (and higher) disable the older LM hash by default.
While NTLM uses cyclic redundancy checks (CRCs) and message digest algorithms for integrity, the main issue with NTLM is that it is based on the RC4 cipher, and not any recent cryptographic methods such as AES or SHA-256. RC4 has been compromised, and therefore the NTLM hash is compromised. Due to the weakness of NTLM, we need a stronger hashing algorithm: NTLMv2.
The NTLMv2 hash uses an HMAC-MD5 hash, making it difficult to crack; it is a 128-bit system. NTLMv2 has been available since Windows NT 4.0 SP4 and is used by default on newer Windows operating systems. Even though NTLMv2 responds to the security issues of the LM hash and NTLM, most Microsoft domains use Kerberos as the logon authentication scheme because of its level of security when dealing with one computer logging in to another or in to an entire network/domain. NTLMv2 is used either when Kerberos isn’t available, users log in with local accounts, or a connecting OS doesn’t support Kerberos.
Hashing Attacks
A cryptographic hash is difficult to reverse engineer, but not impossible. A powerful computer can decrypt some hashes...it just takes time. But time is of the essence, and so attackers will attempt other methods, such as creating collisions, using side-channel attacks, or utilizing privilege escalation. Let’s discuss a couple of ways that hashes can be exploited.
Pass the Hash
A pass the hash attack is when an attacker obtains the password hash of one or more user accounts and reapplies the hash to a server or other system in order to fool the system into thinking that the attacker is authentic. The goal is for the attacker to gain access to the system, often a Windows Server, and gain another user’s credentials with the potential to escalate privileges.
The attack starts with the attacker obtaining the hashes from a target system. That’s the hard part. Access to the system is required in one way or another, then the attacker can use a hash dumping utility to collect the hashes for user passwords. Next, the attacker utilizes a “pass the hash” program to place the hashes within the server. For example, within the Local Security Authority Subsystem Service (LSASS) in Windows Server. This can be done using a side-channel attack so that the attacker can impersonate one of the users. If done properly, the attacker does not need to know the password of an account, does need to brute-force the password, and does not need to reverse engineer the hash. While the attack can be carried out on an individual client system also, it is more often something that is focused on Windows Servers (namely domain controllers) because they house many user account credentials.
Prevention includes the following: Only allowing clients that are trusted operating systems to connect to a server; configuring Windows domain trusts securely; using multifactor authentication; using tokens; and implementing the principle of least privilege for user accounts. When employing least privilege, be sure to include domain accounts and local admin accounts. Finally, standard network security discussed in Chapter 6 through 9 should also be implemented, including IDS/IPS solutions, firewall restrictions, and so on.
Happy Birthday!
Not when a birthday attack is involved. A birthday attack is an attack on a hashing system that attempts to send two different messages with the same hash function, causing a collision. It is based on the birthday problem in probability theory (also known as the birthday paradox). This can be summed up simply as the following: A randomly chosen group of people will have a pair of persons with the same calendar date birthday. Given a standard calendar year of 365 days, the probability of this occurring with 366 people is 100% (367 people on a leap year). So far, this makes sense and sounds logical.
The paradox (thoughtfully and mathematically) comes into play when fewer people are involved. With only 57 people, there is a 99% probability of a match (a much higher percentage than one would think), and with only 23 people, there is a 50% probability. Imagine that and blow out your candles! And by this, I mean use hashing functions with strong collision resistance. Because if attackers can find any two messages that digest the same way (use the same hash value), they can deceive a user into receiving the wrong message. To protect against a birthday attack, use a secure transmission medium, such as SSH, or encrypt the entire message that has been hashed.
Additional Password Hashing Concepts
Remember that hashed passwords are one-way functions. The process of hashing takes the password and converts it into a fixed-length binary value that cannot be reversed. The converted number is usually represented in hexadecimal. Due to the nature of the conversion, even slightly different passwords will have completely different hashes.
Know that password hashes can be cracked. I know, I said the number cannot be reversed, and it can’t, because it is a one-way function. But the hash can be cracked in a variety of ways. A person could try to guess the password, or use the dictionary attack method, or try the brute-force attack method. Attackers will also make use of lookup tables, reverse lookup tables, and rainbow tables. These vulnerabilities make your password policies—and the type of hash you use—very important. Of course, in some scenarios, you might be limited as to the length of password you can have your users select. For example, let’s say you are using a web server technology with a somewhat weak password methodology, and you are concerned about hash collisions. There are other ways to increase the security of the password.
One way is to use key stretching. A key stretching technique will take a weak key, process it, and output an enhanced and more powerful key. Often, this process will increase the size of the key to 128 bits, making attacks such as brute-force attacks much more difficult, if not impossible. Examples of key stretching software include PBKDF2 and bcrypt.
These utilities also incorporate salting to protect against dictionary attacks, brute-forcing, and rainbow table attacks. Salting is additional random data that is added to a one-way cryptographic hash. It is one character or more, but defined in bits. The person with the weaker web server password key, or perhaps the admin with the NTLM hash, would do well to consider key stretching or salting. Another technique used is the nonce (number used once). It can be added to password-based authentication schemes where a secure hash function (such as SHA) is used. It is a unique number (that is difficult for attackers to find) that can only be used once. As such, it helps to protect users from replay attacks.
Of course, an admin needs to remember that the primary line of defense when it comes to passwords is to use complexity and length; not just one or the other. There are a couple of myths connected with passwords in general. The first is that complexity is better than length. This isn’t always true; it will depend on the type of attack (dictionary or brute-force), the level of complexity, and the length of the password. So again, if at all possible, define policies that specify complexity plus length. And if length cannot be incorporated into your password scheme, use key stretching, or salting, or strongly consider using a different hash altogether. Another myth is that password checkers ensure strong passwords. Password checkers can help you get an idea of whether a password is secure, but may interpret some weak passwords as strong.
Remember also to limit the number of times that a password can be tried via policy; for example, limiting password attempts to five or even as little as three (remember the three strikes and you’re out rule?). Also, define delays between consecutive password attempts. This is especially important on websites. It can help to defend against exhaustive key searches. Better yet, use one-time passwords (OTPs), such as the HMAC-based OTP (HOTP). Extend that concept by supporting a time-based moving factor that must be changed each time a new password is generated, and you have the time-based OTP (TOTP).
It may seem like we’ve covered a dizzying array of password technologies and acronyms, but we can quickly get our bearings by creating a checklist and going through it every time we design a password scheme: Use a strong hash, and if not possible, utilize key stretching. Incorporate salting. Consider OTPs, and create meticulously defined policies governing passwords. Finally, if working on a website that accepts passwords (especially public passwords), implement secure programming techniques, particularly input validation.
Chapter Review Activities
Use the features in this section to study and review the topics in this chapter.
Chapter Summary
If there’s one thing you should take away from this chapter it’s that my phone number was probably never in any black books, either as plaintext or as ciphertext! (Just making sure you are reading the chapter summaries...be thankful I am not anthropomorphizing computers this time.) Seriously, though, it’s amazing how many children can easily understand and design code with which to hide information. It’s not surprising that there are so many cryptographers and cryptanalysts in this day and age, and a huge assortment of ciphers to work with.
The art of secret communication can basically be broken down into two categories: steganography and cryptography. Both have been used for millennia. But one is inherently insecure, and the other is inherently crackable. Steganography hides the entire message, but if the message is found, the message is instantly compromised. Remember the discussion of the Greek messenger who shaved his head, had a message written on his scalp, and re-grew his hair? If he had been asked by a guard at a border to shave his head (and had complied), the message would have been seen right away. That’s why insecurity is built right into the scheme. Cryptography, on the other hand, is used to hide the meaning of the message. The message could be there for everyone to see, but they won’t understand it unless they have the key to the message. Of course, all ciphers can be cracked; it’s built into their DNA, so to speak. But, with the proper key size and appropriately designed ciphers, it can be very difficult, if not impossible, to crack the code. So, encryption is the weapon of choice for most data transfers.
However, you will also see some scenarios where a message is encrypted and then hidden as well, effectively combining the two concepts of cryptography and steganography. For example, User A might e-mail User B with an attachment containing a photo of the Grand Canyon—a slightly altered Grand Canyon, where some of the pixels’ colors have been changed, but the changes are not visible to the naked eye. User B already has an unaltered version of the original photo stored on the computer. User B compares the two, and locates all of the modified pixels (or has a program do it). The modified colors could translate to letters in the alphabet: for example, a certain shade of red’s three-byte color would be written numerically as FF 00 66 (255 0 102 in decimal). It could have been decided earlier that the third number of the three bytes would be the modified color. Furthermore, 102 is equal to the letter f in ASCII, which might be the first letter of the first sentence of a message. The process would continue until the complete message emerges from a group of modified colors. That’s pretty hidden, wouldn’t you say? But now, encryption could be employed based on a predetermined code. It could be as simple as a Caesar Cipher where the letters are shifted over three places, so instead of the ciphertext f, we get the plaintext c. So now, the message is hidden and the meaning of the message is hidden. And we can get as complex as we want with the cipher, either by utilizing a published algorithm or by designing our own.
Dating back to ancient times, cryptographers would create a code, and cryptanalysts would attempt to crack it. Every time a code was cracked, it was then considered compromised, and a new code would be created. This concept has been even more pronounced during the computer age. That’s why there are so many algorithms in this chapter—the cyclic mousetrap effect has been in play for decades.
Symmetric algorithms use a single key, or more than one identical key (or very similar keys). One of the most powerful symmetric algorithms is the Advanced Encryption Standard (AES), which can have a maximum key length of 256 bits. That is considered uncrackable, so instead of trying to crack the code, attackers will usually attempt to maneuver around it and assault the implementation of the algorithm. Asymmetric algorithms, on the other hand, use a pair of different keys for encryption and decryption. For instance, take public key cryptography, where there will be a well-known public key that is used to encrypt messages, and a secret private key that is used to decrypt them. A common example of an asymmetric algorithm is RSA.
It is often desirable to create a summary of a message, known as a hash. Hashes are used in digital downloads to allow users to verify the integrity of a message or file. They are also used to protect passwords. A common hash used on the Internet is SHA-2—remember, SHA-1 is deprecated and should be replaced if it’s currently in use. A common hash used to protect passwords in Windows is NTLMv2.
By combining all of these techniques and technologies, you can provide a decent amount of security for your files and passwords—essentially protecting your data and the access to that data.
Review Key Topics
Review the most important topics in the chapter, noted with the Key Topic icon in the outer margin of the page. Table 14-5 lists a reference of these key topics and the page number on which each is found.
Table 14-5 Key Topics for Chapter 14
| Key Topic Element | Description | Page Number |
| Table 14-1 | Black book phone number encryption | 323 |
| Figure 14-1 | Illustration of public key cryptography | 327 |
| Table 14-3 | Summary of symmetric algorithms | 331 |
| Table 14-4 | Summary of RSA public and private key usage | 332 |
| Figure 14-2 | Illustration of the hashing process | 337 |
| Figure 14-3 | LM hash in the Local Group Policy | 340 |
Define Key Terms
Define the following key terms from this chapter, and check your answers in the glossary:
encryption
Data Encryption Standard (DES)
Triple DES (3DES)
Advanced Encryption Standard (AES)
elliptic curve cryptography (ECC)
Elliptic Curve Diffie-Hellman Ephemeral (ECDHE)
pseudorandom number generator (PRNG)
Message-Digest algorithm 5 (MD5)
Complete the Real-World Scenarios
Complete the Real-World Scenarios found on the companion website (www.pearsonitcertification.com/title/9780134846057). You will find a PDF containing the scenario and questions, and also supporting videos and simulations.
Review Questions
Answer the following review questions. Check your answers in Appendix A, “Answers to the Review Questions.”
1. Which type of encryption technology is used with the BitLocker application?
A. Symmetric
B. Asymmetric
C. Hashing
D. WPA2
2. Which of the following will provide an integrity check?
A. Public key
B. Private key
C. WEP
D. Hash
3. Why would an attacker use steganography?
A. To hide information
B. For data integrity
C. To encrypt information
D. For wireless access
4. You need to encrypt and send a large amount of data. Which of the following would be the best option?
A. Symmetric encryption
B. Hashing algorithm
C. Asymmetric encryption
D. PKI
5. Imagine that you are an attacker. Which would be most desirable when attempting to compromise encrypted data?
A. A weak key
B. The algorithm used by the encryption protocol
C. Captured traffic
D. A block cipher
6. What is another term for secret key encryption?
A. PKI
B. Asymmetrical
C. Symmetrical
D. Public key
7. Your boss wants you to set up an authentication scheme in which employees will use smart cards to log in to the company network. What kind of key should be used to accomplish this?
A. Private key
B. Public key
C. Cipher key
D. Shared key
8. The IT director wants you to use a cryptographic algorithm that cannot be decoded by being reversed. Which of the following would be the best option?
A. Asymmetric
B. Symmetric
C. PKI
D. One-way function
9. Which of the following concepts does the Diffie-Hellman algorithm rely on?
A. Usernames and passwords
B. VPN tunneling
C. Biometrics
D. Key exchange
10. What does steganography replace in graphic files?
A. The least significant bit of each byte
B. The most significant bit of each byte
C. The least significant byte of each bit
D. The most significant byte of each bit
11. What does it mean if a hashing algorithm creates the same hash for two different downloads?
A. A hash is not encrypted.
B. A hashing chain has occurred.
C. A one-way hash has occurred.
D. A collision has occurred.
12. Which of the following methods will best verify that a download from the Internet has not been modified since the manufacturer released it?
A. Compare the final LANMAN hash with the original.
B. Download the patch file over an AES encrypted VPN connection.
C. Download the patch file through an SSL connection.
D. Compare the final MD5 hash with the original.
13. Which of the following encryption methods deals with two distinct, large prime numbers and the inability to factor those prime numbers?
A. SHA-1
B. RSA
C. WPA
D. Symmetric
14. Which of the following is not a symmetric key algorithm?
A. RC4
C. 3DES
D. Rijndael
15. You are attempting to move data to a USB flash drive. Which of the following enables a rapid and secure connection?
A. SHA-2
B. 3DES
C. AES-256
D. MD5
16. Which of the following is used by PGP to encrypt the session key before it is sent?
A. Asymmetric key distribution system
B. Asymmetric scheme
C. Symmetric key distribution system
D. Symmetric scheme
17. Which of the following encryption algorithms is used to encrypt and decrypt data?
A. SHA-256
B. RC5
C. MD5
D. NTLM
18. Of the following, which statement correctly describes the difference between a secure cipher and a secure hash?
A. A hash produces a variable output for any input size; a cipher does not.
B. A cipher produces the same size output for any input size; a hash does not.
C. A hash can be reversed; a cipher cannot.
D. A cipher can be reversed; a hash cannot.
19. When encrypting credit card data, which would be the most secure algorithm with the least CPU utilization?
A. AES
B. 3DES
C. SHA-512
D. MD5
20. A hash algorithm has the capability to avoid the same output from two guessed inputs. What is this known as?
A. Collision resistance
B. Collision strength
C. Collision cipher
D. Collision metric
21. Which of the following is the weakest encryption type?
B. RSA
C. AES
D. SHA
22. Give two examples of hardware devices that can store keys. (Select the two best answers.)
A. Smart card
B. Network adapter
C. PCI Express card
D. USB flash drive
23. What type of attack sends two different messages using the same hash function, which end up causing a collision?
A. Birthday attack
B. Bluesnarfing
C. Man-in-the-middle attack
D. Logic bomb
24. Which of the following might a public key be used to accomplish?
A. To decrypt the hash of a digital signature
B. To encrypt web browser traffic
C. To digitally sign a message
D. To decrypt wireless messages
25. Which of the following combines the keystream with the plaintext message using the bitwise XOR operator to produce the ciphertext?
A. One-time pad
B. Obfuscation
C. PBKDF2
D. ECDH
26. WEP improperly uses an encryption protocol and therefore is considered to be insecure. What encryption protocol does it use?
A. AES
B. RSA
C. RC6
D. RC4
27. The fundamental difference between symmetric key systems and asymmetric key systems is that symmetric key systems do which of the following?
A. Use the same key on each end
B. Use different keys on each end
C. Use multiple keys for non-repudiation purposes
D. Use public key cryptography
28. Last week, one of the users in your organization encrypted a file with a private key. This week the user left the organization, and unfortunately the systems administrator deleted the user’s account. What are the most probable outcomes of this situation? (Select the two best answers.)
A. The data is not recoverable.
B. The former user’s account can be re-created to access the file.
C. The file can be decrypted with a PKI.
D. The data can be decrypted using the recovery agent.
E. The data can be decrypted using the root user account.
29. You are tasked with ensuring that messages being sent and received between two systems are both encrypted and authenticated. Which of the following protocols accomplishes this?
A. Diffie-Hellman
B. BitLocker
C. RSA
D. SHA-384
30. Which of the following is not a valid cryptographic hash function?
A. RC4
B. SHA-512
C. MD5
D. RIPEMD
31. A network stream of data needs to be encrypted. Jason, a security administrator, selects a cipher that will encrypt 128 bits at a time before sending the data across the network. Which of the following has Jason chosen?
A. Stream cipher
B. Block cipher
C. Hashing algorithm
D. RC4
32. You are tasked with selecting an asymmetric encryption method that allows for the same level of encryption strength, but with a lesser key length than is typically necessary. Which encryption method fulfills your requirement?
A. RSA
B. ECC
C. DHE
D. Twofish