Chapter 4: Introducing Hash Functions and Digital Signatures

Since time immemorial, most contracts, meaning any kind of agreement between people or groups, have been written on paper and signed manually using a particular signature at the end of the document to authenticate the signatory. This was possible because, physically, the signatories were in the same place at the moment of signing. The signatories could usually trust each other because a third trustable person (a notary or legal entity) guaranteed their identities as a super-party entity.

Nowadays, people wanting to sign contracts often don't know each other and frequently share documents to be signed via email, signing them without a trustable third party to guarantee their identities.

Imagine that you are signing a contract with a third party and will be sending it via the internet. Now, consider the third party as untrustable, and you don't want to expose the document's contents to an unknown person via an unsecured channel such as the internet. How is it possible in this case to verify whether the signatures are correct and acceptable?

Moreover, how is it possible to hide the document's content and, at the same time, allow a signature on the document?

Digital signatures come to our aid to make this possible. This chapter will also show how hash functions are very useful for digitally signing encrypted documents so that anyone can identify the signers, and at the same time, the document is not exposed to prying eyes.

In this chapter, we will cover the following topics:

• Hash functions
• Digital signatures with RSA and El Gamal
• Blind signatures

So, let's start by introducing hash functions and their main scopes. Then we will go deeper into categorizing digital signature algorithms.

A basic explanation of hash functions

Hash functions are widely used in cryptography for many applications. As we have already seen in Chapter 3, Asymmetric Algorithms, one of these applications is blinding an exchanged message when it is digitally signed. What does this mean? When Alice and Bob exchange a message using any asymmetric algorithm, in order to identify the sender, it commonly requires a signature. Generally, we can say that the signature is performed on the message [M]. For reasons we will learn later, it's discouraged to sign the secret message directly, so the sender has to first transform the message [M] into a function (M'), which everyone can see. This function is called the hash of M, and it will be represented in this chapter with these notations: f(H) or h[M].

We will focus more on the relations between hashes and digital signatures later on in this chapter. However, I have inserted hash functions in this chapter alongside digital signatures principally because hash functions are crucial for signing a message, even though we can find several applications related to hash functions outside of the scope of digital signatures, such as applications linked to the blockchain, like distributed hash tables. They also find utility in the search engine space.

So, the first question we have is: what is a hash function?

The answer can be found in the meaning of the word: to reduce into pieces, which in this case refers to the contents of a message or any other information being reduced into a smaller portion.

Given an arbitrary-length message [M] as input, running a hash function f(H), we obtain an output (message digest) of a determined fixed dimension (M').

If you remember the bit expansion (Exp-function), seen in Chapter 2, Introduction to Symmetric Encryption, this is conceptually close to hashes. The bit expansion function works with a given input of bits that has to be expanded. We have the opposite task with hash functions, where the input dimension is bigger than the hash's bit value.

We call a hash function (or simply a hash) a unidirectional function. We will see later that this property of being one-way is essential in classifying hash functions.

Being a unidirectional or one-way function means that it is easy to calculate the result in one direction, but very difficult (if not impossible) to get back to the original message from the output of the function.

Let's see the properties verified in a hash function:

• Given an input message [M], its digest message h(M) can be calculated very quickly.
• It should be almost impossible (-%) to come back from the output (M') calculated through h(M) to the original message [M].
• It should be computationally intractable to find two different input messages [m1] and [m2], such that:

  h(m1) = h(m2)

In this case, we can say that the f(h) function is strongly collision-free.

To provide an example of a hash function, if we want the message digest of the entire content of Wikipedia, it becomes a fixed-length bit as follows:

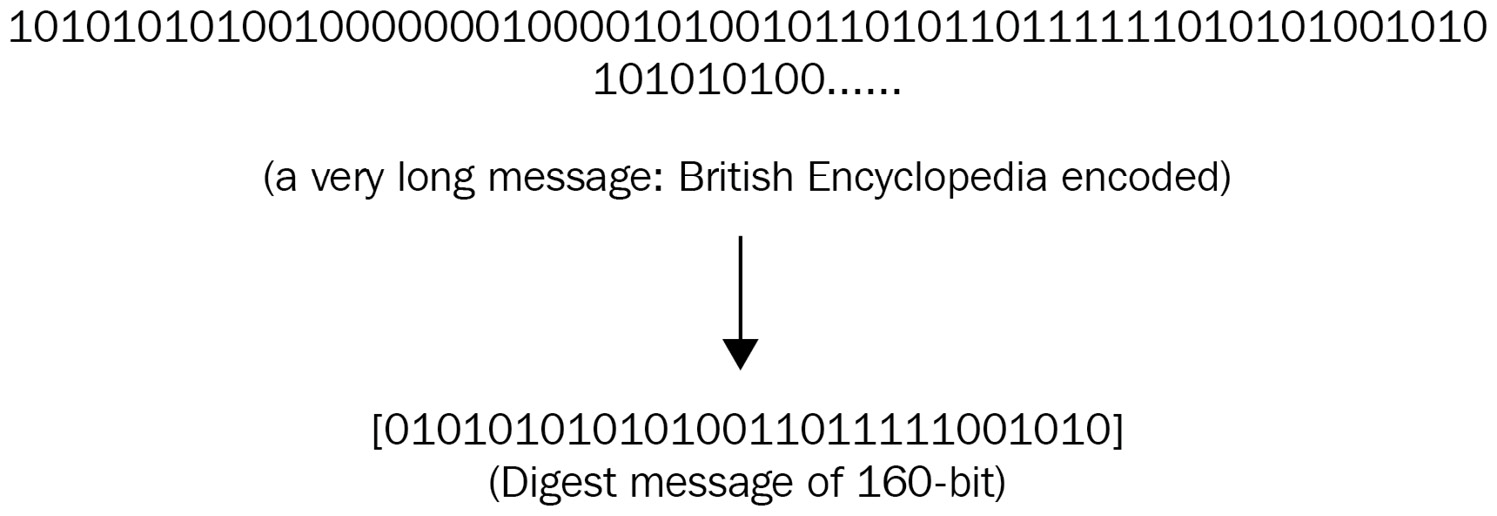
Figure 4.1 – Example of hash digest

Another excellent metaphor for hash functions could be a funnel mincer like the following, which digests plaintext as input and outputs a fixed-length hash:

Figure 4.2 – Hash functions symbolized by a "funnel mincer"

The next question is: why and where are hash functions used?

Recalling what we said at the beginning, in cryptography, hash functions are widely used for a range of different scopes:

• Hash functions are commonly used in asymmetric encryption to avoid exposing the original message [M] when collecting digital signatures on it (we will see this later in this chapter). Instead, the hash of the original message proves the identity of the transmitter using (M') as a surrogate.
• Hashes are used to check the integrity of a message. In this case, based on the digital hash of the original message (M'), the receiver can easily detect whether someone has modified the original message [M]. Indeed, by changing only 1 bit among the entire content of the British Encyclopedia [M], for example, its hash function, h(M), will have a completely different hash value h(M') than the previous one. This particularity of hash functions is essential because we need a strong function to verify that the original content has not been modified.
• Furthermore, hash functions are used for indexing databases. We will see these functions throughout this book. We will use them a lot in the implementation of our Crypto Search Engine detailed in Chapter 9, Crypto Search Engine, and will also see them in Chapter 8, Quantum Cryptography. Indeed, hash functions are candidates for being quantum resistant, which means that hash functions can overcome a quantum computer's attack under certain conditions.
• The foundational concept of performing a secure hash function is that given an output h(M), it is difficult to get the original message from this output.

A function that respects such a characteristic is the discrete logarithm, which we have already seen in our examination of asymmetric encryption:

g^[a] ≡ y (mod p)

Where, as you may remember, given the output (y) and also knowing (g), it is very difficult to find the secret private key [a].

However, a function like this seems to be too slow to be considered for practical implementations. As you have seen above, one of the particularities of hashes is to be quick to calculate. As we have seen what hash functions are and their characteristics, now we will look at the main algorithms that implement hash functions.

Overview of the main hash algorithms

Since a hash algorithm is a particular kind of mathematical function that produces a fixed output of bits starting from a variable input, it should be collision-free, which means that it will be difficult to produce two hash functions for the same input value and vice versa.

There are many types of hash algorithms, but the most common and important ones are MD5, SHA-2, and CRC32, and in this chapter, we will focus on the Secure Hash Algorithm (SHA) family.

Finally, for your knowledge, there is RIPEMD-160, an algorithm developed by EU scientists in the early 1990s available in 160 bits and in other versions of 256 bits and 320 bits. This algorithm didn't have the same success as the SHA family, but could be the right candidate for security as it has never been broken so far.

The SHA family, developed by the National Security Agency (NSA), is the object of study in this chapter. I will provide the necessary knowledge to understand and learn how the SHA family works. In particular, SHA-256 is currently the hash function used in Bitcoin as Proof of Work (PoW) when mining cryptocurrency. The process of creating new Bitcoins is called mining; it is done by solving an extremely complicated math problem, and this problem is based on SHA-256. At a high level, Bitcoin mining is a system in which all the transactions are devolved to the miners. Selecting one megabyte worth of transactions, miners bundle them as an input into SHA-256 and attempt to find a specific output the network accepts. The first miner to find this output receives a reward represented by a certain amount of Bitcoin. We will look at the SHA family in more detail later in this book, but now let's go on to analyze at a high level other hash functions, such as MD5.

We can start by familiarizing ourselves with hash functions, experimenting with a simple example of an MD5 hash.

You can try to use the MD5 Generator to hash your files. My name converted into hexadecimal notation with MD5 is as follows:

Figure 4.3 – MD5 hash function example

As I told you before, the MD family was found to be insecure. Attacks against MD5 have been demonstrated, valid also for RIPEMD, based on differential analysis and the ability to create collisions between two different input messages.

So, let's go on to explore the mathematics behind hash functions and how they are implemented.

Logic and notations to implement hash functions

This section will give you some more knowledge about the operations performed inside hash functions and their notations.

Recalling Boolean logic, I will outline more symbols here than those already seen in Chapter 2, Introduction to Symmetric Encryption, and shore up some basic concepts.

Operating in Boolean logic means, as we saw in Chapter 2, Introduction to Symmetric Encryption, performing operations on bits. For instance, taking two numbers in decimal notation and then transposing the mathematical and logical operations on their corresponding binary notations, we get the following results:

• X ∧ Y = AND logical conjunction – this is a bitwise multiplication (mod 2). So, the result is 1 when both the variables are 1, and the result is 0 in all other cases:

  X=60 —————-—>   00111100

  Y=240 ————-—>   11110000

  AND= 48————->   00110000

• X ∨ Y = OR logical disjunction – a bitwise operation (mod 2) in which the result is 1 when we have at least 1 as a variable in the operation, and the result is 0 in other cases:

  X=60 —————-—>   00111100

  Y=240 ——————>   11110000

  OR = 252 ———>   11111100

• X ⊕ Y = XOR bitwise sum (mod 2) – we have already seen the XOR operation. XOR means that the result is 1 when bits are different, and the result is 0 in all other cases:

  a=60 —————-—>   00111100

  b=240 ——————>   11110000

  XOR=204 ————>   11001100

Other operations useful for implementing hash functions are the following:

• ¬X: This operation (the NOT or inversion operator ~) converts the bit 1 to 0 and 0 to 1.

  So, for example, let's take the following binary string:

  01010101

  It will become the following:

  10101010

• X << r: This is the shift left bit operation. This operation means to shift (X) bits to the left of r positions.

  In the following example, you can see what happens when we shift to the left by 1 bit:

Figure 4.4 – Scheme of the shift left bit operation

So, for example, we have decimal number 23, which is 00010111 in byte notation. If we do a shift left, we get the following:

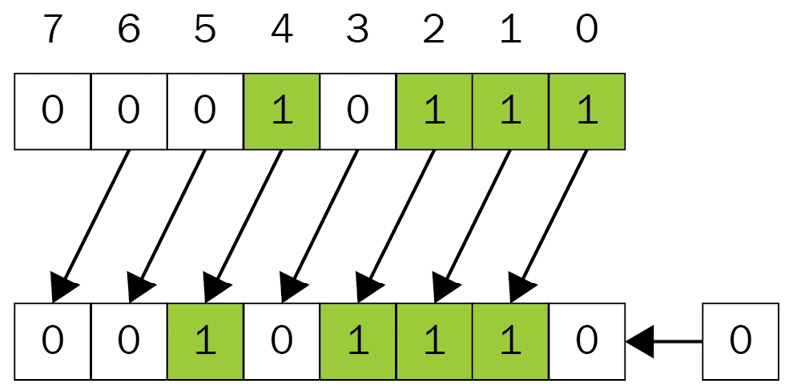
Figure 4.5 – Example of the shift left bit operation (1 position)

The result of the operation after the shift left bit is (00101110)2 = 46 in decimal notation.

• X >> r: This is the shift right bit operation. This is a similar operation as the previous, but it shifts the bits to the right.

  The following diagram shows the scheme of the shift right bit operation:

Figure 4.6 – Scheme of the shift right bit operation (1 position)

As before, let's consider this for the decimal number 23, which is 00010111 in byte notation. If we do a shift right bit operation, we will get the decimal number 11 as the result, as you can see in the following example:

Figure 4.7 – Example of the shift right bit operation (1 position)

• X↩r: This is left bit rotation. This operator (also represented as <<<) means a circular rotation of bits, similar to shift, but with the key difference here that the initial part becomes the final part. It's used in the SHA-1 algorithm to rotate the variables A and B, respectively, by 5 and 30 positions (A<<<5; B<<<30) as will be further explained in the following section.

Figure 4.8 – Scheme of left bit rotation (1 position)

If we apply left bit rotation to our example of the number 23 as expressed in binary notation, we get the following:

Figure 4.9 – Example of left bit rotation

In this case, the result of the left bit rotation operation is the same as the shift left bit operation: (00101110)2 = 46. But, if we perform a right bit rotation, we will get the following:

Figure 4.10 – Example of right bit rotation

In this case, the result of the operation is (10001011)2 = 139 expressed in decimal notation.

• ⊞: This operator represents the modular sum (X+Y) (mod 2^32) and is used in SHA to represent this operation, as you will see later in our examination of the SHA-1 algorithm (Figure 4.14).

After having analyzed the logic operators used to perform hash functions, two more issues have to be considered in order to implement hash functions:

• In SHA, for example, there are some constants (Kt) that go from 0 to n (we will look at this in the following section).
• The notations are generally expressed in hexadecimal.

Let's now see how the hexadecimal system works.

It uses the binary numbers for 0 to 9, consisting of 4 bits per number, for example:

0= 0000

1= 0001

2= 0010

………

9= 1001

Then, from 10 to 16 we have 6 capital letters, A, B, C, D, E, F, to reach a total of 16 (hex) numbers:

A= 1010

B= 1011

……….

F= 1111

For a better and clearer understanding, in the following figure, you can see a comparison between the binary, hexadecimal, and decimal systems:

Figure 4.11 – Comparison between binary, hexadecimal, and decimal systems

The hexadecimal system is used to represent bytes, where 1 byte is an 8-digit binary number.

For example, 1 byte (8 bits) is expressed as (1111 0010)2 = [F2]16 = 242.

Now that we have the instruments to define a hash function, let's go ahead and implement SHA-1, which is the simplest model in the SHA family.

Explanation of the SHA-1 algorithm

Secure Hash Algorithm 1 (SHA-1) was designed by the NSA. Since 2005, it has been considered insecure and was replaced by its successors, SHA-2 and SHA-3. In this section, we will examine SHA-1 simply as a case study to better understand how hash functions are implemented.

SHA-1 returns a 160-bit output based on an iterative procedure. This concept will become clearer in the next few lines.

As for other hash functions, the message [m] made of variable bit input, is broken into 512-bit fixed-length blocks: m= [m1,m2,m3,....ml].

In the last part of this section, you will see how an input message [m] of 2,800 bits will be transformed into blocks [m1,m2,.....ml] of 512 bits each.

The blocks are elaborated through a compression function f(H) (it will be better analyzed later in Step 3 of the algorithm) that combines the current block with the result obtained in the previous round. There are four rounds and they correspond to the variable (t), whose range is divided into four t-rounds as shown in Figure 4.12, each one made of 20 steps (for a total of 80 steps). Each iteration can be seen as a counter that runs along the values of each range made of 20 values. As you can see from Figures 4.12 and 4.13, each iteration uses the constants (Kt) and the operations ft (B,C,D) of the corresponding round.

Each round updates the sub-registers (A,B,C,D,E) after the other. At the end of the 4th round, when t = 79, the sub-registers (A,B,C,D,E) are added to the sub-registers (H0, H1, H2, H3, H4) to perform the 160 bits final hash value.

Let's now examine the issue of constants in SHA-1.

Constants are fixed numbers expressed in hexadecimal defined with particular criteria. An important criterion adopted to choose the constants in SHA is to avoid collisions. Collisions happen when a hash function gives the same result for two different blocks starting from different constants. So, even though someone might think it would be a good idea to change the values of the constants, don't try to change them because that could cause a collision problem.

In SHA-1, for example, the given constants are as follows:

Figure 4.12 – The Kt constants in SHA-1

Where, in different ranges of (t), different values correspond with the constants (Kt), as you see in the preceding figure.

Besides the constants, we have the function ft (B,C,D) defined as follows:

Figure 4.13 – The ft function

The first initial register of SHA-1 is X0, a 160-bit hash function generated by five sub-registers (H0, H1, H2, H3, H4) consisting of 32 bits each. We will see the initialization of these sub-registers in Step 2 using constants expressed in hexadecimal numbers.

Now let's explain the SHA-1 algorithm by dividing the process into four steps to obtain the final hash value of 160 bits:

• Step 1 – Starting with a message [m], operate a concatenation of bits such that:

  y= m1 ‖ m2 ‖ m3 ‖ … ‖mL

  Where the ‖ symbol stands for the concatenation of bits expressed by each block of message [ml] consisting of 512 bits.

• Step 2 – Initialization of the sub registers: H0 = 67452301, H1 = EFCDAB89, H2 = 98BADCFE, H3 = 10325476, H4 = C3D2E1F0.

  You may notice that these constants are expressed in hexadecimal notation. They were chosen by the NSA, the designers of this algorithm.

• Step 3 – For j = 0, 1, … ,L-1, execute the following instructions:

  a) mi = W0 ‖ W1……….. ‖W15,

  where each (Wj) consists of 32 bits.

  b) For t = 16 to 79, put:

  Wt = (Wt-3 ⊕ Wt-8 ⊕ Wt-14 ⊕ Wt-16) ↩ 1

  c) At the beginning, we put:

  A = H0, B = H1, C = H2, D = H3, E = H4

  Each variable (A,B,C,D,E) is of 32 bits length for a total length of the sub-register of 160 bits.

  d) For 80 iterations, where 0 ≤ t ≤79, execute the following steps in succession:

  T = (A ↩ 5) + ft((B,C, D) +E + Wt + KtE = D, D = C, C = (B ↩ 30), B = A, A = T

  e) The sub-registers (A,B,C,D,E) are added to the sub-registers (H0, H1, H2, H3, H4):

  H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E

• Step 4 – Take the following as output:

  H0 ‖ H1 ‖ H2 ‖ H3 ‖ H4.

  This is the hash value of 160 bits.

Here you can see a scheme of SHA-1 (the sub-registers are A, B, C, D, E):

Figure 4.14 – SHA-1 scheme of the operations in each sub-register

Important Note

Remember from the previous section on the logic and notations that:

X↩r is left bit rotation, also represented as <<<, and means a circular rotation of bits. So, in the case of A ↩ 5, it means that bits rotate 5 positions to the left, while in the case of B ↩ 30 bits, bits rotate 30 positions to the left.

⊞: This operator represents the modular sum (X+Y) (mod 2^32).

Notes and example on SHA-1

In this section, we will analyze the SHA-1 algorithm in a little more detail.

Since Steps 1 and 2 are just message initialization and sub-register initialization, the algorithm's core is in Step 3, where you can see a series of mathematical operations consisting of bit concatenation, XOR, bit shift, bit transposition, and bit addition.

Finally, Step 4 reduces the output to 160 bits just because each sub-register H0, H1, H2, H3, and H4 is 32 bits. In Step 1, we mentioned that the minimum block message provided in the input has to be 512 bits. The message [m] could be divided into blocks of 512 bits, and if the original message is shorter than 512 bits, we have to apply a padding operation, involving the addition of bits to complete the block.

SHA-1 is used to compute a message digest of 160-bit length for an arbitrary message that is provided as input. The input message is a bit string, so the length of the message is the number of bits that make up the message (that is, an empty message has length 0). If the number of bits in a message is a multiple of 8 (a byte), for compactness, we can represent the message in hexadecimal. Conversely, if the message is not a multiple of a byte, then we have to apply padding. The purpose of the padding is to make the total length of a padded message a multiple of 512. As SHA-1 sequentially processes blocks of 512 bits when computing the message digest, the trick to getting a strong message digest is that the hash function has to provide the best grade of confusion/diffusion on the bits involved in the iterative operations.

The process of padding consists of the following sequence of passages:

1. SHA-1 starts by taking the original message and appends 1 bit followed by a sequence of 0 bits.
2. The 0 bits are added to ensure that the length of the new message is a multiple of 512 bits.
3. For this scope, the new message will have a final length of n*512.

For example, if the original message has a length of 2800 bits, it will be padded with 1 bit at the end followed by 207 bits. So, we will have 2800 + 1 + 207 = 3008 bits. Then to make the result of the padding a multiple of 512, using the division algorithm, notice that 3008 = 5 * 512 + 448, so to get to a multiple of 512, we pad the message with 64 zeros. So, we finally obtain 3008 + 64 = 3072, which is the number of bits of the padded message, divisible by 512 (bits per block).

Example of one block encoded with SHA- 1

Let's understand this with the help of a practical example:

• Step 1 – Padding the message:

  Suppose we want to encode the message abc using SHA-1, which in binary system is expressed as:

  abc = 01100001 01100010 01100011

  In hex, the string is:

  abc = 616263

  As you can see in the following figure, the message is padded by appending 1, followed by enough 0s until the length of the message becomes 448 bits. Since the message abc is 24 bits in length, 423 further bits are added. The length of the message represented by 64 bits is then added to the end, producing a message that is 512 bits long:

Figure 4.15 – Padding of the message in SHA-1

• Step 2 – Initialization of the sub-registers:

  The initial hash value for the sub-registers H0, H1, H2, H3, and H4 will be:

  H[0] = 67452301

  H[1] = EFCDAB89

  H[2] = 98BADCFE

  H[3] = 10325476

  H[4] = C3D2E1F0

• Step 3 – Block contents:

  W[0] = 61626380 W[1] = 00000000 W[2] = 00000000 W[3] = 00000000 W[4] = 00000000 W[5] = 00000000 W[6] = 00000000 W[7] = 00000000 W[8] = 00000000 W[9] = 00000000 W[10] = 00000000 W[11] = 00000000 W[12] = 00000000 W[13] = 00000000 W[14] = 00000000 W[15] = 00000018

  Iterations on the sub-registers:

            A        B        C        D        E

  t = 0: 0116FC33 67452301 7BF36AE2 98BADCFE 10325476

  t = 1: 8990536D 0116FC33 59D148C0 7BF36AE2 98BADCFE

  ..........

  Tt = 79: 42541B35 5738D5E1 21834873 681E6DF6 D8FDF6AD

  Addition of the sub-registers:

  H[0] = 67452301 + 42541B35 = A9993E36

  H[1] = EFCDAB89 + 5738D5E1 = 4706816A

  H[2] = 98BADCFE + 21834873 = BA3E2571

  H[3] = 10325476 + 681E6DF6 = 7850C26C

  H[4] = C3D2E1F0 + D8FDF6AD = 9CD0D89D

• Step 4 – Result:

  After performing the four rounds, the final message digest of the string abc of 160-bit hash is:

  A9993E36 4706816A BA3E2571 7850C26C 9CD0D89D

Figure 4.16 – A complete round in SHA-1

Now that we have learned about hash functions, we are prepared to explore digital signatures.

Authentication and digital signatures

In cryptography, the authentication problem is one of the most interesting and difficult problems to solve. Authentication is one of the most sensitive functions (as well as the most used) for the procedure of access control.

Authentication is based on three methods:

• On something that only the user knows (for example, a password)
• On something that only the user holds (a smart card, device, or a token)
• On something that characterizes the user (for example, fingerprints, an iris scan, and in general biometric characteristics of a person)

In addition to these three methods, there is one more method involving something that only the user holds, related to something that uniquely characterizes them: brain waves. For example, when you look at a picture or think about it, the brain waves activated by your brain are unique, different from any other brain waves that characterize another person.

This invention is related to the authentication between human/computer. In other words, with Brain Password, it is possible to unlock devices such as computers and telephones and get access to web applications. I will introduce brain passwords in Chapter 6, New Algorithms in Public/Private Key Cryptography.

In the next section, we will analyze an authentication method based on digital signatures. Keep in mind (as we will see later on) that there are similar methods of authentication based, for example, on zero knowledge, which will be covered further in Chapter 5, Introduction to Zero-Knowledge Protocols.

Let's see how a method of authentication based on a digital signature over public/private key encryption works.

Let's consider an example where Alice wants to transmit a message to Bob. She knows Bob's public key (as in RSA), so Alice encrypts the message [M] with RSA and sends it to Bob.

Let's look at some of the common problems faced when Alice transmits the message:

1. How can Bob be sure that this message comes from Alice (authentication problem)?
2. After Bob has received the message, Alice could always deny that she is the transmitter (non-repudiation).
3. Another possible issue is that the message [M] could be manipulated by someone who intercepted it (a Man-in-the-Middle (MiM) attack) and subsequently, the attacker could change part of the content. This is a case of integrity loss of the message.
4. Finally, here's another consideration (and probably the first time you'll see it in a textbook): the message could be intercepted and spied on by the attacker, who recovers the content but decides not to modify it. How can the receiver and the transmitter be sure that this doesn't happen? For example, how can you be sure that your telecommunication provider or the cloud that hosts your data don't spy on your messages? I refer to this as the spying problem.

To answer the last question, you could rightly say that since the message [M] is encrypted, it is difficult – if not impossible – for the attacker to recover the secret message without knowing the key.

I will demonstrate that (under some conditions) it is possible to spy on an encrypted message, even if the attacker doesn't know the secret key for decryption.

We will discuss problems 1, 2, and 3 in this chapter. As for problem 4, I will explain an attack method for spying and the relative way to repair this problem in Chapter 6, New Algorithms in Public/Private Key Cryptography.

A digital signature is a proof that the sender of the message [M] instructs the receiver to do the following:

• Prove their identity
• Prove that the message [M] has not been manipulated
• Provide for the non-repudiation of the message

Let's see how digital signatures can help us to avoid all these problems and also how it is possible to sign a message based on the type of algorithm and the different ways of using signatures.

We will first look at RSA digital signatures, and will then analyze the other methods of signatures in public-private key algorithms.

RSA digital signatures

As I have told you before, it's possible to sign a message in different ways; we will now explore how to mathematically sign one and how anyone can verify a signature.

Recalling the RSA algorithm from Chapter 3, Asymmetric Encryption, we know that the process of encryption for Bob is as follows:

Perform encryption based on the public key of Alice (Na) and define the secret elements within the square brackets [M]:

[M]^e ≡ c (mod Na)

(Na) is the public key of the receiver (Alice).

Therefore, Bob will encrypt the message [M] with Alice's public key, and Alice will decrypt [M] with her private key [da] by performing the following operation:

c^[da] ≡ [M] (mod Na)

Where the parameter [da] is the private key of Alice, given by the operation:

INV (e) ≡ [da] mod(p-1)(q-1)

The process for the digital signing and verification of Bob's identity is as follows:

• Step 1: Bob chooses two big prime numbers, [p1, q1], and keeps them secret.
• Step 2: Bob calculates Nb = [p1] * [q1] and publishes (Nb) as his public key.
• Step 3: Bob calculates his private key [db] such that:

  INV (e) ≡ [db] mod (p1-1)(q1-1)

• Step 4: Bob performs the signature:

  S ≡ [M]^[db] (mod Nb)

  Where (S) and (Nb) are public and [db] is secret.

  What about [M]?

  [M], the message, is supposed to be secret and shared only between Bob and Alice. However, a digital signature should be verified by everyone. We will deal with this issue later on. Now let's verify the signature (S).

• Step 5: Verifying the signature:

  Signature verification is the inverse process of the above. Alice (or anyone) can verify the following:

  S^e ≡ [M] (mod Nb)

  If the preceding equation is verified, then Alice accepts the message [M].

Before analyzing the issue of [M], let's understand this algorithm with the help of a numerical example.

Numerical example:

Recalling the RSA example from Chapter 3, Asymmetric Encryption, we have the following numerical parameters given by the RSA algorithm:

[M] = 88

e = 9007

Alice's parameters were as follows:

[p] = 101

[q] = 67

Na = 6767

Let's perform all of the steps of RSA to show the comprehensive process of digitally signing the message:

• Step 1 – Bob's encryption is as follows:

  [M] ^e ≡ c (mod N)

  88^9007 ≡ 6621 (mod 6767)

  c = 6621

• Step 2 – Bob's signature (S) for the message [M] will be generated as follows:

  Bob chooses two prime numbers, [p, q]:

  [p] = 211

  [q] = 113

  Nb= 211*113 = 23843

  9007 * [db] ≡ 1 (mod (211-1)*(113-1))

  Solving the modular equation for [db], we have the following:

  [db] = 9103

  Now, Bob can sign the message:

  [M]^[db] ≡ S (mod Nb)

  88^9103 ≡ 19354 (mod 23843)

  S = 19354

  Bob sends to Alice the pair (c, S) = (6621, 19354).

• Step 3 – Alice's decryption will be as follows:

  c^[da] ≡ [M] (mod Na)

  Alice calculates [da]:

  9007 * [da] ≡ 1 (mod (101-1)*(67-1))

  [da] = 3943

  Alice decrypts the cryptogram (c) and obtains the message [M]:

  c^[da] ≡ [M] (mod Na)

  6621^3943 ≡ 88 (mod 6767)

• Step 4 – Verification of Bob's identity:

  If the signature (S) elevated to the parameter (e) gives the message [M], then Alice can be sure that the message was sent by Bob:

  S^e ≡ [M] (mod Nb)

  19354^9007 = 88 (mod 23843)

  Indeed, Alice obtains the message M=88.

  Important Note

  I hope someone has noticed that the message [M] can be verified by anyone, and not only by Alice, because (S, e, Nb) are public parameters. So, if Bob uses the original message [M], instead of its hash h[M] to gain the signature (S) (see above for the encryption procedure), everyone who knows Bob's public key could easily recover the message [M]!

It's just a matter of solving the following equation to recover the secret message [M]:

S^e ≡ x (mod Nb)

Where the parameters (S, e, Nb) are all known.

In this case, hash functions come to our aid. Performing the hash function h[M] = (m), Bob will send the couple (c, S) , signing (m) instead of [M].

Alice already got the encrypted message [M], so only Alice can verify it:

h[M] = m

If it is TRUE, then Bob's identity will be verified by Alice; if it is FALSE, Bob's claim of identity will be refused.

Why do digital signatures work?

If anyone else who isn't Bob tries to use this signature, they will struggle with the discrete logarithm problem. Indeed, generating [db] in the following equation is a hard problem for the attacker to solve:

m^[db] ≡ S (mod Nb)

Also, even if (m, S) are known by the attacker, it is still very difficult to calculate [db]. In this case, we are dealing with a discrete logarithm problem like what we saw in Chapter 3, Asymmetric Algorithms.

Let's try to understand what happens if Eve (an attacker) tries to modify the signature with the help of an example:

Eve (the attacker) exchanges [db] with (de), computing a fake digital signature (S'):

m^(de) ≡ S' (mod Nb)

If Eve is able to trick Alice to accept the signature (S'), then Eve can make an MiM attack by pretending to be Bob, substituting (S') with the real signature (S).

But when Alice verifies the signature (S'), she recognizes that it doesn't correspond to the correct signature performed by Bob because the hash of the message is (m'), not (m):

(S')^e ≡ m' (mod Nb)

m' ≢ m

So, Alice refuses the digital signature.

That is why cryptographers also need to pay a lot of attention to the collisions between hashes.

Now that we have got a different result, that is, (m') instead of (m), Alice understands there is a problem and doesn't accept the message [M].

This is the scope of the signature (S).

The preceding attack is a simple trick, but there are some more intelligent and sneaky attacks that we will see later on, in Chapter 6, New Algorithms in Public/Private Key Cryptography, when I will explain unconventional attacks.

Digital signatures with the ElGamal algorithm

ElGamal is a public-private key algorithm, as we saw in Chapter 3, Asymmetric Algorithms, based on the Diffie-Hellman key exchange.

In ElGamal, we have different ways of signing the message than RSA, but all are equally valid.

Recalling the ElGamal encryption technique, we have the following elements:

• (g, p): Public parameters
• [k]: Alice's private key
• [M]: The secret message
• B ≡ g^[b] (mod p): Bob's public key
• A ≡ g^[a] (mod p): Alice's public key

Alice's encryption:

y1 ≡ g^[k] (mod p)

y2 ≡ [M]*B^[k] (mod p)

Note

The elements inside the square brackets indicate secret parameters; all the others are public.

Now, if Alice wants to add her digital signature to the message, she will make a hash of the message, h[M], to protect the message [M], and will then transmit the result to Bob in order to prove her identity.

To sign the message [M], Alice first has to generate the hash of the message h[M]:

h[M] = m

Now, Alice can operate with the digest value of [M]——>(m) in cleartext because, as we have learned before, it is almost impossible to return to [M] from its cryptographic hash (m).

Alice calculates the signature (S) such that:

• Step 1 – Making the inverse of [k] in (mod p-1):

  [INVk] ≡ k^(-1) (mod p-1)

• Step 2 – Performing the equation:

  S ≡ [INVk]* (m - [a] *y1) (mod p-1)

  Alice sends to Bob the public parameters (m, y1, S).

• Step 3 – In the first verification, Bob performs V1:

  V1 ≡ A^(y1) * y1^(S) (mod p)

  After the decryption step, if h[M] = m, Bob obtains the second parameter of verification, V2:

  V2 ≡ g^m (mod p)

  Finally, if V1 = V2, Bob accepts the message.

Now, let's better understand this algorithm with the help of a numerical example.

Numerical example:

Let's suppose that the value of the secret message is:

[M]= 88

We assign the following values to the other public parameters:

g = 7

p = 200003

h[M] = 77

The first step is the "Key initialization" of the private and public keys:

[b] = 2367 (private key of Bob)

[a] = 5433 (private key of Alice)

[k] = 23 (random secret number of Alice)

B = 151854 (public key of Bob)

A = 43725 (public key of Alice)

y1 ≡ g^[k] (mod p) = 7^23 (mod 200003) = 90914

After the initialization process, Alice calculates the inverse of the key (Step 1) and then the signature (Step 2):

• Step 1 – Alice computes the inverse of [k] in (mod p-1):

  [INVk] ≡ [k]^(-1) (mod p-1) = 23^-1 (mod 200003 - 1) = 34783

• Step 2 – Alice can get now the signature (S):

  S ≡ [INVk]* (m - [a] *y1) (mod p-1)

  S ≡ 34783 * (77 – 5433 * 90914) (mod 200003 - 1)

  S = 72577

  Alice sends to Bob the public parameters (m, y1, S)= (77, 90914, 72577)

• Step 3 – With those parameters Bob can perform the first verification (V1). Consequently, he computes V2. If V2 = V1 Bob accepts the digital signature (S):

  V1 ≡ A^(y1) * y1^(S) (mod p)

  V1 ≡ 43725 ^ (90914) * 90914 ^ 72577 (mod 200003) = 76561

  V1 = 76561

  Bob's verification (V2):

  V2 ≡ g^m (mod p)

  V2 ≡ 7^ 77 (mod 200003) = 76561

  V2 = 76561

  Bob verifies that V1= V2.

Considering the underlying problem that makes this algorithm work, we can say that it is the same as the discrete logarithm. Indeed, let's analyze the verification function:

V1 ≡ A^(y1) * y1^(S) (mod p)

All the elements are made by discrete powers, and as we already know, it's a hard problem (for now) to get back from a discrete power even if the exponent or the base is known. It is not sufficient to say that discrete powers and logarithms ensure the security of this algorithm. As we saw in Chapter 3, Asymmetric Cryptography, the following function could also be an issue:

y2 ≡ [M]*B^[k] (mod p)

It's given by multiplication. If we are able to recover [k], then we have discovered [M].

So, the algorithm suffers not only from the discrete logarithm problem but also from the factorization problem.

Now that you have learned about the uses and implementations of digital signatures, let's move forward to explore another interesting cryptographic protocol: blind signatures.

Blind signatures

David Chaum invented blind signatures. He struggled a lot to find a cryptographic system to anonymize digital payments. In 1990, David funded eCash, a system that adopted an untraceable currency. Unfortunately, the project went bankrupt in 1998, but Chaum will be forever remembered as one of the pioneers of digital money and one of the fathers of modern cryptocurrency, along with Bitcoin.

The underlying problems that Chaum wanted to solve were the following:

• To find an algorithm that was able to avoid the double-spending problem for electronic payments.
• To make the digital system secure and anonymous to guarantee the privacy of the user.

In 1982, Chaum wrote an article entitled Blind Signatures for Untraceable Payments. The following is an explanation of how the blind signatures described in the article work and how to implement them.

Signing a message blind means to sign something without knowing the content. It could be used not only for digital payments but also if Bob, for example, wants to publicly register something that he created without making known to others the details of his invention. Another application of blind signatures is in electronic voting machines, where someone makes a choice (say, in an election for the president or for a party, for example). In this case, the result of the vote (the transmitted message) has to be known by the receiver obviously, but the identity of the voter has to remain a secret if the voter wants to be sure that their vote will be counted (that is the proper function of blind signatures).

I will expose an innovative blind signature scheme for the MBXI cipher in Chapter 6, New Algorithms in Public/Private Key Cryptography, where I will introduce new ciphers in private/public keys, including the MBXI, invented and patented by me in 2011.

Let's see now how David Chaum's protocol works by performing a blind signature with RSA.

Blind signature with RSA

Suppose Bob has an important secret he doesn't want to expose to the public until a determined date. For example, he discovered a formidable cure for coronavirus and he aspires to get the Nobel Prize.

Alice represents the commission for the Nobel Prize.

Alice picks up two big secret primes [pa, qa]:

• [pa*qa] = Na, which is Alice's public key.
• (e) is the same public parameter already defined in RSA.

The parameter [da] is Alice's private key, given by this operation:

INV (e) ≡ [da] mod(pa-1)(qa-1)

Suppose that [M1] is the secret belonging to Bob. I have just called it [M1] to distinguish it from the regular [M].

Bob picks up a random number [k] and keeps it secret.

Now Bob can go ahead with the blind signature protocol on [M1]:

• Step 1 – Bob performs encryption (t) on [M1] to blind the message:

  t ≡ [M1] * [k]^e (mod Na)

  Bob sends (t) to Alice.

• Step 2 – Alice can perform the blind signature given by the following operation:

  S ≡ t^[da] (mod Na)

  Alice sends (S) to Bob, who can verify whether the blind signature corresponds to the message [M1].

• Step 3 – Verification:

  Bob calculates (V):

  S/k ≡ V (mod Na)

  Then he can verify the following:

  V^e ≡ [M1] (mod Na)

  If the last operation is TRUE, it means Alice has effectively signed blind [M1]. In this case, Bob can be sure of the following:

  [M1]^[da] ≡ V (mod Na)

Since no one except Alice could have performed function (S) without being able to solve the discrete logarithm problem (as already seen in Chapter 3, Asymmetric Algorithms), the signer must be Alice, for sure. This sentence remains valid until any other variable occurs; for example, when someone finds a logical way to solve the discrete logarithm or a quantum computer reaches enough qubits to break the algorithm, as we'll see in Chapter 8, Quantum Cryptography.

Let's see an example to better understand the protocol.

Numerical example:

1. The parameters defined by Alice are as follows:

   pa = 67

   qa = 101

   So, the public key (Na) is the following:

   67*101 = Na = 6767

   da ≡ 1/e (mod (pa-1) * (qa-1))

   Reduce [e*x == 1, x, Modulus -> (pa - 1)*(qa - 1)]

   [da] = 1553

   e = 17

2. Bob picks up a random number, [k]:

   k = 29

   Bob calculates (t):

   t ≡ M1* k^e ≡ 88 * 29^17 = 3524 (mod 6767)

3. Bob sends (t) to Alice ———————————> Alice can now blind-sign (t):

   S ≡ t^[da] ≡ 3524^1553 = 1533 (mod 6767)

4. Bob can verify (S) <———————— Alice sends (S = 1553) to Bob:

   S/k ≡ V (mod Na)

   1533/29 = 2853 (mod 6767)

   Reduce [k*x == S, x, Modulus -> Na]

   x = 2853

   V = 2853

   if:

   V^e ≡ [M1] (mod Na)

   2853^17 ≡ 88 (mod 6767)

   Then, Bob accepts the signature (S).

As you can see from this example and the explanation of blind signatures, Alice is sure that Bob's discovery (the coronavirus cure) belongs to him, and Bob can preserve his invention without declaring the exact content of it before a certain date.

Notes on the blind signature protocol

You can do a double-check on [M1], so you will be able to realize that Alice has really signed [M1] without knowing anything about its value:

M1^[da] ≡ V (mod Na)

88^1553 ≡ 2853 (mod 6767)

A warning about blind signatures is necessary, as Alice doesn't know what she is going to sign because [M1] is hidden inside (t). So, Bob could also attempt to convince Alice to sign a $1 million check. There is a lot of danger in adopting such protocols.

Another consideration concerns possible attacks.

As you see here, we are faced with a factorization problem:

t ≡ M1* [k]^e (mod Na)

We can see that (t) is the product of [X*Y]:

X = M1 <———— Factorization problem

Y = k^e

It doesn't matter if the attacker is unable to determine [k], as they can always attempt to find [M1] by factoring (t), if [M1] is a small number, for example. It's simply the case of M1=0, because of course (t) will be zero and the message can be discovered by the attacker to be M = 0.

On the other hand, if we assume, for example, that (k^e) is a small number, since [k] is random, then the attacker can perform this operation:

Reduce [(k^e)*x == t, x, Modulus -> Na]

x = MESSAGE

In this case, if, unfortunately, [k^e] (mod Na) results in a small number, the attacker can recover the message [M1].

As you will understand after reading the next chapter, blind signatures are the precursor to zero-knowledge protocols; the object of study in the next Chapter 5, Introduction to Zero-Knowledge Protocols. Indeed, some of the elements we find here, such as random [k] and the execution of blind signatures, and the last step of verification, V = S/k, performed by the receiver, utilize the logic that inspired zero-knowledge protocols.

Summary

In this chapter, we have analyzed hash functions, digital signatures, and blind signatures. After introducing hash functions, we started by describing the mathematical operations behind these one-way functions followed by an explanation of SHA-1. We then explained digital signatures with RSA and ElGamal with practical numerical examples and examined the possible vulnerabilities.

Finally, the blind signature protocol was introduced as a cryptographic instrument for implementing electronic voting and digital payment systems.

Therefore, you have now learned what a hash function is and how to implement it. You also know what digital signatures are, and in particular, you got familiar with the signature schemes in RSA and ELGamal. We also learned about the vulnerabilities that could lead to digital signatures being exposed, and how to repair them.

Finally, you have learned what blind signatures are useful for and their fields of application.

These topics are essential because we will use them abundantly in the following chapters of this book. They will be particularly useful in understanding the zero-knowledge protocols explained in Chapter 5, Introduction to Zero-Knowledge Protocols, and the other algorithms discussed in Chapter 6, New Algorithms in Public/Private Key Cryptography. Finally, Chapter 6 will examine new methods of attack against digital signatures.

Now that you have learned the fundamentals of digital signatures, it is time to analyze zero-knowledge protocols in detail in the next chapter.