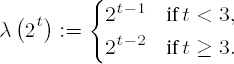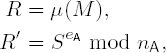The next question was the obvious one, "Can this be done with ordinary encipherment? Can we produce a secure encrypted message, readable by the authorised recipient without any prior secret exchange of the key etc?" . . . I published the existence theorem in 1970.
As we approach the end of our story we would like to investigate the possibility of testing what we have labored over chapter by chapter against a realistic and current example, one that clearly demonstrates the connection between the theme of cryptographic application and the deployment of our programmed functions. We shall make a brief excursion into the principle of asymmetric cryptosystems and then turn our attention to the RSA algorithm as the classic example of such a system, which was published in 1978 by its inventors/discoverers, Ronald Rivest, Adi Shamir, and Leonard Adleman (see [Rive], [Elli]), and which by now has been implemented worldwide.[49] The RSA algorithm is patented in the United States of America, but the patent expired on 20 September 2000. Against the free use of the RSA algorithm stood the claims of RSA Security, who possessed rights to the trade name "RSA," which triggered vehement discussion in connection with work on the standard P1363 [IEEE], with in some cases rather grotesque results, for example, the suggestion of rechristening the RSA procedure "biprime cryptography." There have also appeared less serious suggestions, such as FRA (former RSA algorithm), RAL (Ron, Adi, Leonard), and QRZ (RSA – 1). Upon expiry of their patent RSA Security weighed in with its opinion:
Clearly, the terms "RSA algorithm," "RSA public-key algorithm," "RSA cryptosystem," and "RSA public-key cryptosystem" are well established in standards and open academic literature. RSA Security does not intend to prohibit the use of these terms by individuals or organizations that are implementing the RSA algorithm ("RSA-Security—Behind the Patent," September 2000).[50]
The fundamental idea behind asymmetric cryptosystems was published in 1976 by Whitfield Diffie and Martin Hellman in the groundbreaking article "New Directions in Cryptography" (see [Diff]). Asymmetric cryptosystems, in contrast to symmetric algorithms, do not use a secret key employed both for encryption and decryption of a message, but a pair of keys for each participant consisting of a public key E for encryption and a different, secret, key D for decryption. If the keys are applied to a message M one after another in sequence, then the following relation must hold:
One might picture this arrangement as a lock that can be closed with one key but for which one needs a second key to unlock it.
For the sake of security of such a procedure it is necessary that a secret key D not be able to be derived from the public key E, or that such a derivation be infeasible on the basis of time and cost constraints.
In contrast to symmetric systems, asymmetric systems enable certain simplifications in working with keys, since only the public key of a participant A need be transmitted to a communication partner B for the latter to be in a position to encrypt a message that only participant A, as possessor of the secret key, can decrypt. This principle contributes decisively to the openness of communication: For two partners to communicate securely it suffices to agree on an asymmetric encryption procedure and exchange public keys. No secret key information needs to be transmitted. However, before our euphoria gets out of hand we should note that in general, one cannot avoid some form of key management even for asymmetric cryptosystems. As a participant in a supposedly secure communication one would like to be certain that the public keys of other participants are authentic, so that an attacker, with the nefarious goal of intercepting secret information, cannot undetected interpose him- or herself and give out his or her key as the public key under the guise of its being that of the trusted partner. To ensure the authenticity of public keys there have appeared surprisingly complex procedures, and in fact, there are already laws on the books that govern such matters. We shall go into this in more detail below.
The principle of asymmetric cryptosystems has even more far-reaching consequences: It permits the generation of digital signatures in which the function of the key is turned on its head. To generate a digital signature a message is "encrypted" with a secret key, and the result of this operation is transmitted together with the message. Now anyone who knows the associated public key can "decrypt" the "encrypted" message and compare the result with the original message. Only the possessor of the secret key can generate a digital signature that can withstand such a comparison. We note that in the case of digital signatures the terms "encryption" and "decryption" are not quite the correct ones, so that we shall speak rather of "generation" and "verification" of a digital signature.
A requirement for the implementation of an asymmetric encryption system for the generation of digital signatures is that the association of D (M) and M can be reliably verified. The possibility of such a verification exists if the mathematical operations of encryption and decryption are commutative, that is, if their execution one after the other leads to the same, original, result regardless of the order in which they are applied:
By application of the public key E to D (M) it can be checked in this case whether D (M) is valid as a digital signature applied to the message M.
The principle of digital signatures has attained its present importance in two important directions:
The laws on digital and electronic signatures in Europe and the United States create a basis for the future use of digital signatures in legal transactions.
The increasing use of the Internet for electronic commerce has generated a strong demand for digital signatures for identification and authentication of those taking part in commercial transactions, for authenticating digital information, and for ensuring the security of financial transactions.
It is interesting to observe that the use of the terms "electronic signature" and "digital signature" bring into focus the two different approaches to signature laws: For an electronic signature all means of identification used by one party, such as electronic characters, letters, symbols, and images, are employed to authenticate a document. A digital signature, on the other hand, is realized as an electronic authentication procedure based on information-technological processes that is employed to verify the integrity and authenticity of a transmitted text. Confusion arises because these two terms are frequently used interchangeably, thus mixing up two different technical processes (see, for example, [Mied]).
While the laws on electronic signatures in general leave open just what algorithms will be used for the implementation of digital signatures, most protocols being discussed or already implemented for identification, authentication, and authorization in the area of electronic transactions over the Internet are based on the RSA algorithm, which suggests that it will continue to dominate the field. The generation of digital signatures by means of the RSA algorithm is thus a particularly current example of the application of our FLINT/C functions.
The author is aware that the following paragraphs represent a painfully brief introduction to an enormously significant cryptographic principle. Nevertheless, such brevity seems to be justified by the large number of extensive publications on this topic. The reader wishing to know more is referred to [Beut], [Fumy], [Salo], and [Stin] as introductory sources, to the more comprehensive works [MOV] and [Schn], and to the more mathematically oriented monographs [Kobl], [Kran], and [HKW].
All that is merely probable is probably false.
We shall now present a brief outline of the mathematical properties of the RSA algorithm, and we shall see how the RSA procedure can be implemented both as an asymmetric cryptosystem and an asymmetric signature scheme. Following the mathematical principles of the RSA algorithm we shall develop C++ classes with RSA functions for encryption and decryption as well as for the generation and authentication of digital signatures. In this way we shall clarify the possibilities offered for the implementation of the methods of our LINT class.
The most important aspect of the RSA algorithm is the pair of keys, which have a particular mathematical form: An RSA key pair consists of three basic components: the modulus n, the public key component e (encryption), and the secret key component d (decryption). The pairs
We first generate the modulus n as the product n = pq of two prime numbers p and q. If
We illustrate this principle with the help of a small example: We choose p = 7 and q = 11. Then we have n = 77 and
Equipped now with such keys (we shall soon discuss what constitutes a realistic size for the various key components) and appropriate software, communication partners can securely exchange information with each other. To demonstrate the procedure we consider the process by which a participant Ms. A sends an RSA-encoded message to a communication partner Mr. B:
Bgenerates his RSA key with components nB, dB, and eB. He then gives the public key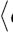
Now
Awould like to send an encrypted message M toB(0 ≤ M < nB). SinceAhas received fromBhis public key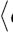
and sends the encrypted value C to
B.After
Bhas obtained the encrypted message C fromA, thenBdecodes this message by calculatingusing his secret key
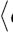
It is not difficult to see why this works. Because d • e ≡ 1 mod
where we have made use of the theorem of Euler quoted on page 177, from which we deduce that M
gcd(M, n) = 1. For the more theoretically interesting case that gcd(M, n) > 1, equation (17.3) holds as well: For relatively prime p and q, we have the isomorphism • An alternative to key generation is the use of univeral exponents λ := lcm(p − 1, q − 1) instead of
Then for all a € •×n, we have aλ(m) ≡ 1 mod n. For a proof, see page 15 of [Kran]. As above, this can also be extended to the case gcd(M, n) = 1, since from ev = 1 + kλ(n) we have ve ≡ 1 mod gcd(p − 1, q − 1), and so in •p and •q we have Mve = M. On account of the isomorphism •
It is clear that the security of the RSA algorithm depends on the ease of factorability of n. If n can be factored into its components p and q, then the secret key d can be determined from the public key e. Conversely, the factorization of n can be easily accomplished if both key components d and e are known: If k := de − 1, then k is a multiple of
Possibilities for attacking the RSA algorithm other than factorization of the modulus are either as expensive as this or rely on the special weaknesses of individual protocols used in implementing the RSA cryptosystem, but do not rely on the RSA algorithm itself. Based on the current state of knowledge the following conditions lead to opportunities to attack the RSA algorithm:
Common modulus
The use of a common modulus for several participants leads to an obvious weakness: Based on what we have just said, each participant can use his or her own key components e and d to factorize the common modulus n = pq. From a knowledge of the factors p and q as well as the public key components of other participants with the same modulus their secret keys can be calculated.
Small public exponents
Since the computational time for the RSA algorithm for a given modulus depends directly on the size of the exponents e and d, it would appear attractive to choose these as small as possible. For example, 3, as the smallest possible exponent, requires only one squaring and one multiplication modulo n, so why not save valuable computing time in this way?
Let us assume that an attacker was able to capture three encoded messages C1, C2, and C3, each of which encodes the same plain text M, encoded with the keys
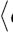
It is highly probable that
gcd(ni, nj) = 1 for i ≠ j, so that the attacker can use the Chinese remainder theorem (cf. page 203) to find a value C for whichSince it is also true that M3 < n1n2n3, we have that C is actually equal to M3, and the attacker can obtain M directly by calculating
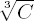
Small secret exponents and small intervals between p and q
Even more problematic than small public exponents are small secret exponents: M. Wiener [Wien] showed already in 1990 how, given a key
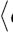
It is plausible that the modulus n can be easily factored when p ≈ q ≈
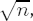
Work of B. de Weger, extended with proven methods of attack by Wiener, Boneh, and Durfee, shows how the security of the procedure depends on the sizes of both the secret key and the difference of the prime factors |p − q|: Let |p − q| = nβ and d = nδ. The modulus n = pq can be factored efficiently if 2
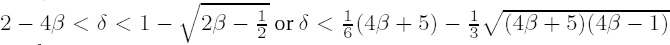
As a consequence of his results, de Weger recommends choosing p, q, and d such that δ + 2β > 7/4. For δ ≥
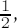
This is in accord with suggestions to be found elsewhere, according to which 0.5 < |log2p − log2q| < 30 should hold (see [EESSI]).
Encryption of small texts
Boneh, Joux, and Nguyen have presented a particularly efficient method with which it is frequently possible to determine, for an arbitrary public key
Weaknesses in implementation
In addition to the weaknesses caused by the choice of parameters there is a host of potential implementation problems that can adversely affect the security of the RSA algorithm, as is the case with any encryption procedure. Certainly, the greatest care must be taken with implementations completely in software that are not protected from outside attack by measures implemented in hardware. Reading from memory contents, observation of bus activity or CPU states, can lead to the disclosure of secret key information. At the minimum, all data in main memory that in any way are correlated with the secret components of the RSA algorithm (or any other cryptosystem) should be erased immediately after use with active overwriting (for example, with the function
purge_l(), which appears on page 164).The functions in the FLINT/C library are already equipped for this purpose. In secure mode local variables and allocated memory are overwritten with zeros before termination of the function and are thereby deleted. Here a certain degree of care is necessary, since the optimization capabilities of the compiler are so highly developed that a simple instruction at the end of a function that can be seen to have no effect on the function's termination might simply be ignored. And there is more: One must take into account that calls to the function
memset()in the C standard library are ignored if the compiler cannot recognize any useful purpose in calling it.The following example illustrates these effects. The function
f_l()uses two automatic variables:CLINT key_landUSHORT secret. At the end of the function, whose contents are of no further interest here, memory should be overwritten by assigning0tosecretand, respectively, by a call tomemset()in the case ofkey_l. The C code looks like this:int f_l (CLINT n_l) { CLINT key_l; USHORT secret;.../* overwrite the variables */ secret = 0; memset (key_l, 0, sizeof (key_l)); return 0; }And what does the compiler make of this (Microsoft Visual C/C++ 6.0, compilation with
cl -c -FAs -O2)?PUBLIC _f ; COMDAT _f _TEXT SEGMENT _ key _l$ = −516 _ secret $ = −520 _f PROC NEAR ; COMDAT ; 5 : CLINT key _l; ; 6 : USHORT secret;
...; 18 : /* overwrite the variables */ ; 19 : secret = 0; ; 20 : memset (key_l, 0, sizeof (key _l)); ; 21 : return 0; xor eax, eax ; 22 : } add esp, 532 ; 00000214H ret 0 _f ENDP _TEXT ENDSThe assembler code generated by the compiler documents that the instructions to delete the variables
key_landsecretare passed over without effect. From the point of view of optimization this is a desirable result. Even the inline version of the functionmemset()is simply optimized away. For security-critical applications, however, this strategy is simply too clever.The active deletion of security-critical variables by overwriting must therefore be implemented in such a way that it is actually carried out. One should note that in this case assertions can prevent the checking for effectiveness, since the presence of the assertions forces the compiler to execute the code. When the assertions are turned off, then optimization again goes into effect.
For the FLINT/C package the following function is implemented, which accepts a variable number of arguments and treats them according to their size as standard integer types and sets them to 0, or for other data structures calls
memset()and lets it do the overwriting:static void purgevars_l (int noofvars, ...) { va_list ap; size_t size; va_start (ap, noofvars); for (; noofvars > 0; -noofvars) { switch (size = va_arg (ap, size_t)) { case 1: *va_arg (ap, char *) = 0; break; case 2: *va_arg (ap, short *) = 0; break; case 4: *va_arg (ap, long *) = 0; break; default: memset (va_arg(ap, char *), 0, size); } } va_end (ap); }The function expects pairs of the form (byte length of the variable, pointer to the variable) as arguments, prefixed in
noofvarsby the number of such pairs.As an extension of this function the macro
PURGEVARS_L()is defined by#ifdef FLINT_SECURE #define PURGEVARS_L(X) purgevars_l X #else #define PURGEVARS_L(X) (void)0 #endif /* FLINT_SECURE */
so that security mode can be turned on and off as required. Deletion of the variables in
f()can take place as follows:/* overwrite the variables */ PURGEVARS_L ((2, sizeof (secret), & secret, sizeof (key_l), key_l));The compiler cannot ignore the call to this function on the principle of optimization strategy, which could be accomplished only by an extraordinarily effective global optimization. In any case, the effect of such security measures should be checked by means of code inspection:
PUBLIC _f EXTRN _purgevars_l:NEAR ; COMDAT_f _TEXT SEGMENT _key_l$ = −516 _secret$ = −520 _f PROC NEAR ; COMDAT ; 9 : { sub esp, 520 ; 00000208H ; 10 : CLINT key_l; ; 11 : USHORT secret;...; 18 : /* overwrite the variables */ ; 19 : PURGEVARS_L ((2, sizeof (secret), &secret, sizeof (key_l), key_l)); lea eax, DWORD PTR _key_l$[esp+532] push eax lea ecx, DWORD PTR _secret$[esp+536] push 514 ; 00000202H push ecx push 2 push 2 call _purgevars_l ; 20 : return 0; xor eax, eax ; 21 : } add esp, 552 ; 00000228H ret 0 _f ENDP _TEXT ENDSAs a further protective measure in connection with the implementation of security-critical applications we should mention a comprehensive mechanism for error handling that sees to it that even in the case of invalid arguments or other exceptional situations no sensitive information is divulged. Likewise, suitable measures should be considered for establishing the authenticity of the code of a cryptographic application, so that the insertion of Trojan horses is prevented or at least detected before the code can be executed. Taking a cue from the story of the Trojan War, Trojan horse is the name given to software that has been altered in such a way that it apparently functions correctly but has additional undesirable effects such as the transmittal of secret key information to an attacker via an Internet connection.
To get a grip on such problems, frequently, in practice, for cryptographic operations, "security boxes," or "S-Boxes" for short, are implemented, whose hardware is protected against attack by encapsulation in conjunction with detectors or sensors.
If all these known traps are avoided, then there remains only the risk that the modulus will be factored, and this risk can be effectively eliminated by choosing sufficiently large prime numbers. To be sure, it has not been proved that there is no easier method to break the RSA algorithm than factorization, and there is also no proof that factorization of large integers is truly as difficult a problem as it presently seems to be, but these issues have not adversely affected the practical application of the algorithm to date: The RSA algorithm is the most commonly implemented asymmetric cryptosystem worldwide, and its use in the generation of digital signatures continues to increase.
There are many places in the literature where it is recommended that so-called strong primes p and q be used in order to protect the modulus against some of the simpler factorization methods. A prime p is called strong in this connection if
p − 1 has a large prime divisor r,
p + 1 has a large prime divisor s,
r − 1 has a large prime divisor t.
The importance of strong prime numbers to the security of the RSA algorithm is not everywhere equally emphasized. Recently, there has been an increase in the number of voices that assert that while the use of strong prime numbers is not harmful, it also does not accomplish a great deal (cf. [MOV], Section 8.2.3, Note 8.8, as well as [RegT], Appendix 1.4) or even that they should not be used (see [Schn], Section 11.5). In the program example that follows we shall therefore do without the generation of strong primes. For those who are nonetheless interested, we sketch here a procedure for constructing such primes:
The first step in the construction of a strong prime p with lp binary digits consists in the search for primes s and t satisfying log2(s) ≈ log2(t) ≈
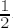
We now invoke the Chinese remainder theorem (see page 203) to calculate a solution of the simultaneous congruences x ≡ 1 mod r and x ≡ −1 mod s by setting x0 := 1 − 2r−1s mod rs, where r−1 is the multiplicative inverse of r modulo s.
For our prime number search we use an odd initial value: We generate a random number z with a number of digits close to but less than (sometimes denoted by
Whether or not strong primes are used for keys, in every case it is practical to have available a function that generates primes of a specified length or within a specified interval. A procedure for this that additionally ensures that a prime p thus generated satisfies the further condition gcd(p − 1, f) = 1 for a specified number f is given in [IEEE], page 73. Here is the algorithm in a slightly altered form.
Algorithm to generate a prime p such that pmin ≤ p ≤ pmax
Generate a random number p, pmin ≤ p ≤ pmax.
If p is even, set p ← p + 1.
If p > pmax, set p ← pmin + p mod (pmax + 1) and go to step 2.
Compute d
:= gcd(p − 1, f) (cf. Section 10.1). If d = 1, test p for primality (cf. Section 10.5). If p is prime, then output p and terminate the algorithm. Otherwise, set p ← p + 2 and go to step 3.
A realization of this procedure as a C++ function is contained in the FLINT/C package (source file flintpp.cpp).
generation of a prime number p within an interval [pmin, pmax] satisfying the additional condition | |
Syntax: | LINT findprime(const LINT& pmin, const LINT& pmax, const LINT& f); |
Input: |
|
Return: |
|
LINT findprime (const LINT& pmin, const LINT& pmax, const LINT& f)
{
if (pmin.status == E_LINT_INV) LINT::panic (E_LINT_VAL, "findprime", 1, __LINE__);
if (pmax.status == E_LINT_INV) LINT::panic (E_LINT_VAL, "findprime", 2, __LINE__);
if (pmin > pmax) LINT::panic (E_LINT_VAL, "findprime", 1, __LINE__);
if (f.status == E_LINT_INV) LINT::panic (E_LINT_VAL, "findprime", 3, __LINE__);
if (f.iseven()) // 0 < f must be odd
LINT::panic (E_LINT_VAL, "findprime", 3, __LINE__);
LINT p = randBBS (pmin, pmax);
LINT t = pmax - pmin;
if (p.iseven())
{
++p;
}
if (p > pmax)
{
p = pmin + p % (t + 1);
}
while ((gcd (p - 1, f) != 1) || !p.isprime())
{
++p;
++p;
while (p > pmax)
{
p = pmin + p % (t + 1);if (p.iseven())
{
++p;
}
}
}
return p;
}Additionally, the function findprime() is overloaded so that instead of the interval boundaries pmin and pmax a binary length can be set.
Function: | generation of a prime number p within the interval [2l−1, 2l − 1] satisfying the additional condition |
Syntax: | LINT findprime(USHORT l, const LINT& f); |
Input: |
|
Return: |
|
With regard to the key length to be chosen, a look at the development worldwide of attempts at factorization is most informative: In April 1996 after months-long cooperative work at universities and research laboratories in the USA and Europe under the direction of A.K. Lenstra[51] the RSA modulus
RSA-130 = 18070820886874048059516561644059055662781025167694013 4917012702145005666254024404838734112759081 2303371781887966563182013214880557
with 130 decimal places was factored as
RSA-130 = 39685999459597454290161126162883786067576449112810064 832555157243 × 4553449864673597218840368689727440886435630126320506 9600999044599.
Then in February 1999, RSA-140 was factored into its two 70-digit factors. This success was accomplished under the direction of Herman J. J. te Riele of CWI in the Netherlands with teams from the Netherlands, Australia, France, Great Britain, and the USA.[52] RSA-130 and RSA-140 came from a list of 42 RSA moduli published in 1991 by the firm RSA Data Security, Inc. as encouragement to the cryptographic research community.[53] The calculations that led to the factorization of RSA-130 and RSA-140 were divided among a large number of workstations and the results collated. The calculational effort to factor RSA-140 was estimated to be 2000 MIPS years[54] (for RSA-130 it was about 1000 MIPS years).
Only a short time later, namely at the end of August 1999, news of the factorization of RSA-155 flashed across the globe. At a cost of about 8000 MIPS years the next number in the list of RSA challenges had been laid to rest, again under the direction of Herman te Riele with international participation. With the factorization of
RSA-155 = 1094173864157052742180970732204035761200373294544920599 0913842131476349984288934784717997257891267332497 625752899781833797076537244027146743531593354333897
into the two 78-digit factors
RSA-155 = 10263959282974110577205419657399167590071656780803 8066803341933521790711307779 × 1066034883801684548209272203600128786792079585759 89291522270608237193062808643
the magical threshold of 512 was crossed, a length that for many years had been considered safe for key lengths.
After the factorization of the next RSA challenge, RSA-160, with the participation of the Gernab Institute for Security in Information Technology (BSI) in Bonn, in April 2003, it was in December 2003 that a consortium of the University of Bonn; the Max Planck Institute for Mathematics, in Bonn; the Institute for experimental Mathematics, in Essen; and the BSI factored the 174-digit number
RSA-576 = 18819881292060796383869723946165043980716356337941738 2700763356422988859715234665485319060606504743045 3173880113033967161996923212057340318795506569962 21305168759307650257059
into two 87-digit factors:
RSA-576 = 39807508642406493739712550055038649119906436234252670 8406385189575946388957261768583317 × 47277214610743530253622307197304822463291469530209711 6459852171130520711256363590397527.
The question of what key length is to be considered adequate for the RSA algorithm is revised each time progress in factorization is made. A. K. Lenstra and Eric R. Verheul [LeVe] provide some concrete advice in this regard in their description of a model for the determination of recommended key lengths for many types of cryptosystems. Beginning with a set of well-founded and conservative assumptions, combined with current findings, they calculate some prognoses as to minimum key lengths to recommend in the future and display them in tabular form. The values shown in Table 17-1, which are valid for asymmetric procedures like RSA, El-Gamal, and Diffie–Hellman, are taken from their results.
Table 17-1. Recommended key lengths according to Lenstra and Verheul
|
|
|---|---|
2001 | 990 |
2005 | 1149 |
2010 | 1369 |
2015 | 1613 |
2020 | 1881 |
2025 | 2174 |
We may conclude that an RSA key should possess no fewer than 1024 binary digits if it is to provide a comfortable margin of safety for critical applications. We may conclude as well, however, that successes in factorization are gradually approaching this value, and one must keep careful tabs on developments. It is therefore worthwhile to distinguish different application purposes and for sensitive applications to consider using 2048 or more binary digits (cf. [Schn], Chapter 7, and [RegT], Appendix 1.4).[55] With the FLINT/C package we are well equipped to produce such key lengths. We need not be too concerned that the expense of factorization decreases in proportion to the speed of new hardware, since this same hardware allows us to create longer keys as required. The security of the RSA algorithm can thus always be ensured by keeping sufficiently ahead of the progress in factorization.
How many such keys are available? Are there enough so that every man, woman, and child on the planet (and perhaps even their pet cats and dogs) can be provided one or more RSA keys? To this the prime number theorem provides the answer, according to which the number of prime numbers less than an integer x is asymptotically approximated by x/ ln x (cf. page 220): Moduli of length 1024 bits are generated as products of two prime numbers each of length approximately 512 bits. There are about 2512/512 such primes, that is, about 10151, each pair of which forms a modulus. If we let N = 10151, then there are N(N − 1)/2 such pairs, which comes to about 10300 different moduli for which additionally that number again can be chosen for secret key components. This overwhelmingly large number is difficult to grasp, but consider, for example, that the entire visible universe contains "only" about 1080 elementary particles (cf. [Saga], Chapter 9). To put it another way, if every person on Earth were given ten new moduli every day, then the process could continue for 10287 years without a modulus being reused, and to date Earth has existed "only" a few billion years.
Finally, that an arbitrary text can be represented as a positive integer is obvious: By associating a unique integer to each letter of an alphabet texts can be interpreted in any number of ways as integers. A common example is the numerical representation of characters via ASCII code. An ASCII-encoded text can be turned into a single integer by considering the code value of an individual character as a digit to base 256. The probability that such a process would result in an integer M for which gcd(M, n) > 1, that is, such that M contains as a factor one of the factors p, q, of an RSA key n, is vanishingly small. If M is too large for the modulus n of an RSA key, that is, larger than n − 1, then the text can be divided into blocks whose numerical representations M1, M2, M3, . . . all are less than n. These blocks must then be individually encrypted.
For texts of considerable length this becomes tiresome, and therefore one seldom uses the RSA algorithm for the encryption of long texts. For this purpose one may employ symmetric cryptosystems (such as Triple-DES, IDEA, or Rijndael; see Chapter 11 and [Schn], Chapters 12, 13, 14), with which the process goes much more quickly and with equivalent security. For an encrypted transmittal of the necessary key, which must be kept secret with symmetric procedures, the RSA algorithm is perfectly suited.
"Please, your Majesty," said the Knave, "I didn't write it, and they can't prove that I did: there's no name signed at the end."
To clarify how the RSA algorithm is used for generating digital signatures we consider the following process, by which a participant A sends a message M with her digital signature to a participant B, upon which B checks the validity of the signature.
Agenerates her RSA key with components nA, dA, and eA. She then transmits her public key
Awould now like to send a message M with her signature toB. To this endAgenerates the redundancy R = μ(M) with R < nAusing a redundancy function μ (see below). ThenAcalculates the signatureand sends (M, S) to
B.Bpossesses the public key
with the public key
Bnow checks whether R′ = R. If this is the case, thenBaccepts the digital signature ofA. Otherwise,Brejects it.
Digital signatures that must be checked by a separate transmittal of the signed message M are called digital signatures with appendix.
The signature procedures with appendix are used primarily for signing messages of variable lengths whose numerical representation exceeds the modulus, so that M ≥ n. In principle, one could, as we did above, divide the message into blocks M1, M2, M3, . . . of suitable lengths Mi < n and encrypt and sign each block separately. However, leaving aside the fact that in such a case a counterfeiting problem arises consisting in the possibility of mixing up the order of the blocks and the signatures belonging to the blocks, there are two further compelling reasons to employ, instead of construction of blocks, the function μ that we named the redundancy function in the paragraph above in which we discussed calculating a digital signature.
The first is that a redundancy function
The second reason is that the RSA algorithm has an undesirable property for creating signatures: For two messages M1 and M2 the multiplicative relation
holds, which supports the counterfeiting of signatures if no measures are taken against it.
On account of this property, called homomorphism, of the RSA function it would be possible without the inclusion of redundancy R to have messages digitally signed with a "hidden" signature. To do this one could select a secret message M and a harmless message M1, from which a further message M2 := M M1 mod nA is formed. If one succeeded in getting a person or authority A to digitally sign the messages M1 and M2, then one would obtain the signatures S1 = MdA1 mod nA and S2 = MdA2 mod nA, 1 from which one can create the signature to M by calculating S2S−11 mod nA, which was probably not what A had in mind, though nonetheless A may not have noticed this when generating the signatures S1 and S2: The message M would in this case be said to have a hidden signature.
To be sure, one could counter that with high probability M2 does not represent a meaningful text and that anyway, A would not be well advised to sign M1 or M2 at a stranger's request and without examining the contents with care. Yet one should not rely on such assumptions of reasonableness when it comes to human behavior in order to justify the weaknesses of a cryptographic protocol, especially when such weaknesses can be eliminated, such as in this case by including redundancy. In order to achieve this redundancy, the redundancy function μ must satisfy the property
for all M1, M2 €
Supplementary to the signature procedures with appendix there are additional methods known that make it possible to extract the signed message from the signature itself, the so-called digital signatures with message recovery (cf. [MOV], Chapter 11, [ISO2], and [ISO3]). Digital signatures with message recovery based on the RSA algorithm are particularly suited for short messages with a binary length less than one-half the binary length of the modulus.
However, in every case the security properties of redundancy functions should be carefully examined, such as is demonstrated by the procedure published in 1999 by Coron, Naccache, and Stern for attacking such schemes. The procedure is based on an attacker having access to a large number of RSA signatures attached to messages whose representation as an integer is divisible exclusively by small primes. Based on such a makeup of the messages it is possible under favorable conditions, without knowledge of the signature key, to construct additional signatures to additional messages, which would amount to counterfeiting these signatures (cf. [Coro]). The ISO has reacted to this development: In October 1999 the workgroup SC 27 removed the standard [ISO2] from circulation and published the following announcement:
Based on various attacks on RSA digital signature schemes . . ., it is the consensus of ISO/IEC JTC 1/SC 27 that IS 9796:1991 no longer provides sufficient security for application-independent digital signatures and is recommended to be withdrawn.[56]
The withdrawn standard refers to digital signatures for which the RSA function is applied directly to a short message. Signatures with appendix, which arise by way of a hash function, are not included.
A widely distributed redundancy scheme for which the attack of Coron, Naccache, and Stern has at best a theoretical significance and represents no real threat is set by the PKCS #1 format of RSA laboratories (cf. [RDS1], [Coro], pages 11–13, and [RDS2]). The PKCS #1 format specifies how a so-called encryption block EB should appear as input value to an encryption or signing operation:
At the head, after the introductory 00 byte, is a byte BT that describes the block type (01 for private key operations, that is, signatures; 02 for public key operations, that is, encryption) and then at least eight filler bytes PS1 . . . PSl, l > 8, with the value FF (hex) in the case of signing and nonzero random values in the case of encryption. There follows 00 as separator byte, and then come finally the data bytes D1 . . . Dn: the payload, so to speak. The number l of filler bytes PSi depends on the size of the modulus m and the number n of data bytes: If k is defined by
then
and for the number n of data bytes, it follows that
The minimum number 8 ≤ l of filler bytes is required for encryption for reasons of security. It is thus possible to prevent an attacker from attaching a catalog of encrypted messages to a public key and comparing the result with a given encrypted text to determine the plain text without knowing the associated secret key.[57]
In particular, when one and the same message is encrypted with several keys, it is important that the PSi be random numbers that are determined anew for each encryption operation.
In the signing case the data bytes Di are typically constructed from an identifier for a hash function H and the value H(M) of this hash function (called the hash value), which represents the text M to be signed. The resulting data structure is called the DigestInfo. The number of data bytes depends in this case on the constant length of the hash value, independent of the length of the text. This is particularly advantageous when M is much longer than H(M). We shall not go into the precise process for the construction of the data structure DigestInfo, but simply assume that the data bytes correspond to the value H(M) (but see in this connection [RDS1]).
From the cryptographic point of view there are several fundamental requirements to place on hash functions so as not to diminish the security of a redundancy scheme based on such a function and thereby call the entire signing procedure into question. When we consider the use of hash and redundancy functions in connection with digital signatures and the possibilities for manipulating them that might arise, we observe the following:
In accordance with our considerations thus far, we start with the assumption that a digital signature with appendix relates to a redundancy R = μ(M) whose principal component is the hash value of the text to be signed. Two texts M and M′ for which H(M) = H(M′), and consequently μ(M) = μ(M′), possess the same signature S = Rd = μ(M)d = μ(M′)d mod n. The recipient of a signature to the text M could now conclude that the signature actually refers to the text M′, which in general would be contrary to the intent of the sender. Likewise, the sender could assume actually to have signed the text M′. The point here is that texts M ≠ M′ with H(M) = H(M′) always exist, due to the fact that infinitely many texts are mapped to finitely many hash values. This is the price to be paid for the convenience of hash values of fixed length.[58]
Since we must also assume the existence of texts that possess identical signatures in relation to a particular hash or redundancy function (where we assume that the same signature key has been used), then it is crucial that such texts not be easy to find or to construct.
In sum, a hash function should be easy to compute, but this should not be the case for the inverse mapping. That is, given a value H of a hash function it should not be easy to find a preimage that is mapped to H. Functions with this property are called one-way functions. Furthermore, a hash function must be collision-free, meaning that it must not be easy to find two different preimages of a given hash value. Until the present, these properties were satisfied by hash functions such as the widely used functions RIPEMD-160 (cf. [DoBP]) and the Secure Hash Algorithm SHA-1 (cf. [ISO1]). It now appears, however, that for digital signatures in the near term (according to NIST and [RegT] from 2010 on), lengths of hash values of 256 bits and greater will be required.
In recent months, reports of the discovery of collisions have provoked a discussion about a requirement to migrate to new hash algorithms. In 2004, results were published related to the hash functions MD4, MD5, HAVAL128, RIPEMD, SHA-0,[59] and a weak variant of SHA-1 with a reduced number of passes (see [WFLY]). In the meantime, while all of these algorithms have come to be considered broken, and in particular are considered unsuitable for use in creating digital signatures, a similar development for SHA-1 seems to be in store, with uncertainty reigning while the drama runs its course. Even if reports on this issue in February 2005, whose sensational publication seems to have been more for serving the interests of those bearing the tidings than of the situation itself, have not led to the outright rejection of the algorithm, the noose seems to be tightening. However, a panicked reaction based on vague suppositions should be rejected, given its worldwide use and the significance of SHA-1 for countless applications.
Given the many different uses to which SHA-1 is being put, it is not very productive to debate what measures may need to be taken before the possible consequences of new methods of attack for individual application areas and thereby the actions to be taken are carefully analyzed. A closer look will show that in most cases, no rush to action is required, and instead, the measures already taken in the mid and long terms should suffice. New hash functions will be needed that will meet security needs for the foreseeable future, given what is known about the newest methods of attack, and these new functions should not be finding themselves in the headlines every half year. Whether the answer already exists in SHA-224, SHA-256, SHA-384, or SHA-512 (see [F180]) needs to be investigated. An increase in the block length may not suffice to compensate for possible weaknesses in the functional building blocks of a hash algorithm. It is always possible that methods of attack will be developed whose effect is independent of the block length, as has been discussed in relation to the hash algorithms that we have mentioned.
How one finds suitable algorithms has been demonstrated by the European Union in the development of RIPEMD in connection with the RIPE project,[60] and in the USA with the competition for the development of the AES. Within the framework of a public international competition, new candidates for hash algorithms with the greatest possible transparency can be put to the test and the most suitable algorithms adopted. The only disadvantage of such a process is that it costs time: In the case of AES it was about three years from the announcement of the competition until a victor was crowned, and four years altogether before the standard was published in 2001. Given this experience, until 2010 is enough time for the development and standardization of new hash functions, although the migration to a new algorithm (or, better, two or three of them) will take time.
Whether in specific applications a switch to other transitional algorithms might be necessary, and what consequences might be thereby associated, can be evaluated only on a case by case basis.
We shall not go into further detail on this topic, which is very important to cryptography. The interested reader is referred to [Pren] or [MOV], Chapter 9, as well as the literature cited therein, above all literature on the current state of affairs. Algorithms for transforming texts or hash values into natural numbers can be found in [IEEE], Chapter 12: "Encoding Methods" (we already have available the corresponding functions clint2byte_l() and byte2clint_l(); cf. page 152). Implementations of RIPEMD-160, SHA-1, and SHA-256 can be found in ripemd.c, sha1.c, and sha256.c in the downloadable source code.
In thinking about the signature protocol described above we are immediately confronted with the following question: How can B know whether he is in possession of the authentic public key of A? Without such certainty B cannot trust the signature, even if it can be verified as described above. This becomes critical when A and B do not know each other personally or when there has been no personal exchange of public keys, which is the normal case in communication over the Internet.
To make it possible for B nonetheless to trust in the authenticity of A's digital signature, A can present her communication partner a certificate from a certification authority that attests to the authenticity of A's public key. An informal "receipt," which one may believe or not, is, of course, inadequate. A certificate is rather a data set that has been formatted according to some standard[61] that among other things speaks to the identity of A as well as her public key and that itself has been digitally signed by the certification authority.
The genuineness of a participant's key can be verified with the help of the information contained in the certificate. Applications that support such verification in software already exist. The future multiplicity of such applications, whose technical and organizational basis will be based on so-called public key infrastructures (PKI), can today only be guessed at. Concrete uses are emerging in the digital signing of e-mail, the validation of commercial transactions, e-commerce and m-commerce, electronic banking, document management, and administrative procedures (see Figure 17-1).
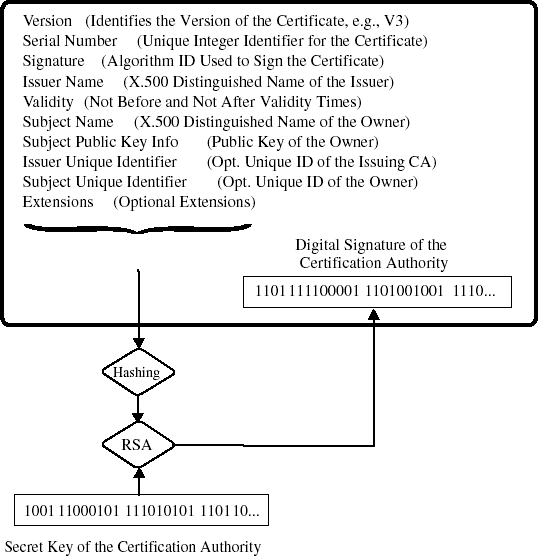
On the assumption that B knows the public key of the certification authority, B can now verify the certificate presented by A and thereafter A's signature to become convinced of the authenticity of the information.
The example presented in Figure 17-2, which shows a client's digitally signed bank statement together with the certificate of the bank presented by a certification authority, demonstrates this process.
Such a bank statement has the advantage that it can reach the client over any electronic transmittal path, such as e-mail, in which it would be further encrypted to protect the confidentiality of the information.
However, the problem of trust has not been hereby miraculously cleared up, but merely shifted: Now B need no longer believe directly in the validity of A's key (in the above example that of the bank), but in exchange must check the genuineness of the certificate presented by A. For certainty to be attained, the validity of certificates must be verified anew for every occurrence, either from the source that issued the certificate or an authority that represents it. Such a procedure can succeed only if the following conditions are met:
the public key of the certification authority is known;
the certification authority takes the greatest care in the identification of the receivers of certificates and in the protection of their private certification keys.
To achieve the first of these desiderata the public key of the certification authority can be certified by an additional, higher, authority, and so forth, resulting in a hierarchy of certification authorities and certificates. However, verification along such a hierarchy assumes that the public key of the highest certification authority, the root certification authority, is known and can be accepted as authentic. Trust in this key must thus be established by other means through suitable technical or organizational measures.
The second condition holds, of course, for all authorities of a certification hierarchy. A certification authority, in the sense of granting legal force to a signature, must establish the organizational and technical processes for which detailed requirements have been set in law or associated implementing orders.
At the end of 1999, a European Union directive was adopted that established a framework for the use of electronic signatures in Europe (cf. [EU99]). The guideline was enacted to avoid conflicting regulations among the individual member states. In decisive points, it requires regulations that deviate from SigG in its original 1997 version, in which it joins the "technical-legal approach," which is also followed by the SigG of 1997, with the "market-economy approach" to form a "hybrid approach." The technical-legal approach is represented by "advanced" and "qualified electronic signatures," and the market-economy approach by "electronic signatures."
In the area of the market-economy approach, no technical requirements are made on the "electronic." For qualified electronic signatures, the technical and organizational requirements are regulated, which contributes to the actual security of these signatures, as the basis for legal consequences being able to be linked to qualified electronic signatures.
Important components of the regulations for guaranteeing the actual security are, in addition to the liability of certification service providers, the requirements for technical security of the components used and the security requirements for the facilities and processes of the certification service providers, as well as their supervision.
A corresponding revision of the German signature law was concluded in the first quarter of 2001 (see [SigG]), in which the guidelines of the EU were implemented. The significant change with respect to the old version of the law is the acceptance of "qualified electronic signatures," which now are permitted as a substitute for written signatures and as admissible evidence in court.
The goal of this law is to create basic conditions for qualified electronic signatures. The use of electronic signatures is optional, though certain regulations could require them in specific instances. In particular, regulations could be established regarding the use of qualified electronic signatures in the work of public institutions.
We now leave this interesting topic, which can pursued further in [Bies], [Glad], [Adam], [Mied], and [Fegh], and turn our attention, finally, to the implementation of C++ classes that provide for encryption and the generation of digital signatures.
In this section we develop a C++ class RSAkey that contains the functions
as well as a class RSApub for the storage and application of public keys only with the functions
RSApub::RSApub()for importing a public key from an object of the classRSAkey;RSApub::crypt()for encrypting a text;RSApub::authenticate()for authenticating a digital signature.
The idea is not merely to look at cryptographic keys as numbers with particular cryptographic properties, but to consider them as objects that bring with themselves the methods for their application and make them available to the outside world but that nonetheless restrictively prevent unmediated access to private key data. Objects of the class RSAkey thus contain, after the generation of a key, a public and a private RSA key component as private elements, as well as the public functions for encryption and signing. Alternatively, the constructor functions enable the generation of keys
with fixed length and internal initialization of the BBS random number generator;
with adjustable length and internal initialization of the BBS random number generator;
with adjustable length and passing of a
LINTinitialization value for the BBS random number generator via the calling program.
Objects of the class RSApub contain only the public key, which they must import from an RSAkey object, and the public functions for encryption and verification of a signature. To generate an object of the RSApub class, then, an initialized RSAkey object must already exist. In contrast to objects of type RSAkey, RSApub objects are considered unreliable and can be more freely handled than RSAkey objects, which in serious applications may be transmitted or stored in data media only in encrypted form or protected by special hardware measures.
Before we realize these example classes we would like to set ourselves some boundary conditions that will limit the implementation cost at something appropriate for what is merely an example: For the sake of simplicity, input values for RSA encryption will be accepted only if they are smaller than the modulus; a subdivision of longer texts into blocks will not occur. Furthermore, we shall leave aside the more costly functional and security-related features that would be necessary in a full-fledged implementation of the RSA classes (see in this regard the pointer on page 384).
However, we do not wish to do without an effective possibility of speeding up the calculations for decryption or signing. By application of the Chinese remainder theorem (see page 203) the RSA operations with the secret key d can be made about four times as fast as with the usual method of calculating a single power: Given a secret key
Calculate a1 ← mdp mod p and a2 ← mdq mod q.
Calculate c ← a1 + p ((a2 − a1)r mod q).
After step 1 we have a1 ≡ mdq ≡ md mod p and a2 ≡ mdq ≡ md mod q. To see this, just use the little theorem of Fermat (cf. page 177), according to which mp−1 ≡ 1 mod p, respectively mq−1 ≡ 1 mod q. From d = l(p − 1) + dp with integral l it follows that
and analogously, we have the same for md mod q. An application of the Garner algorithm (see page 207) with m1 := p, m2 := q, and r := 2 shows us at once that c in step 2 represents the desired solution. Rapid decryption is implemented in the auxiliary function RSAkey::fastdecrypt(). All exponents modulo p, q, or n are calculated via Montgomery exponentiation with the LINT function (cf. page 344).
// Selection from the include file rsakey.h
. . .
#include "flintpp.h"
#include "ripemd.h"
#define BLOCKTYPE_SIGN 01
#define BLOCKTYPE_ENCR 02
// The RSA key structure with all key components
typedef struct
{
LINT pubexp, prvexp, mod, p, q, ep, eq, r;
USHORT bitlen_mod;// binary length of modulus
USHORT bytelen_mod; // length of modulus in bytes
} KEYSTRUCT;// the structure with the public key components
typedef struct
{
LINT pubexp, mod;
USHORT bitlen_mod;// binary length of the modulus
USHORT bytelen_mod; // length of modulus in bytes
} PKEYSTRUCT;
class RSAkey
{
public:
inline RSAkey (void) {};
RSAkey (int);
RSAkey (int, const LINT&);
PKEYSTRUCT export_public (void) const;
UCHAR* decrypt (const LINT&, int*);
LINT sign (const UCHAR*, int);
private:
KEYSTRUCT key;
// auxiliary functions
int makekey (int, const LINT& = 1);
int testkey (void);
LINT fastdecrypt (const LINT&);
};
class RSApub
{
public:
inline RSApub (void) {};
RSApub (const RSAkey&);
LINT crypt (const UCHAR*, int);
int verify (const UCHAR*,ž int, const LINT&);
private:
PKEYSTRUCT pkey;
};
// selection from module rsakey.cpp
...
#include "rsakey.h"
////////////////////////////////////////////////////////////////////////
// member functions of the class RSAkey
// constructor generates RSA keys of specified binary length
RSAkey::RSAkey (int bitlen)
{int done;
seedBBS ((unsigned long)time (NULL));
do
{
done = RSAkey::makekey (bitlen);
}
while (!done);
}
// constructor, generates RSA keys of specified binary length to the
// optional public exponent PubExp. The initialization of random number
// generator randBBS() is carried out with the specified LINT argument rnd.
// If PubExp == 1 or it is absent, then the public exponent is chosen
// randomly. If PubExp is even, then an error status is generated
// via makekey(), which can be caught by try() and catch() if
// error handling is activated using Exceptions.
RSAkey::RSAkey (int bitlen, const LINT& rand, const LINT& PubExp)
{
int done;
seedBBS (rand);
do
{
done = RSAkey::makekey (bitlen, PubExp);
}
while (!done);
}
// export function for public key components
PKEYSTRUCT RSAkey::export_public (void) const
{
PKEYSTRUCT pktmp;
pktmp.pubexp = key.pubexp;
pktmp.mod = key.mod;
pktmp.bitlen_mod = key.bitlen_mod;
pktmp.bytelen_mod = key.bytelen_mod;
return pktmp;
}
// RSA decryption
UCHAR* RSAkey::decrypt (const LINT& Ciph, int* LenMess)
{
UCHAR* EB = lint2byte (fastdecrypt (Ciph), LenEB);
UCHAR* Mess = NULL;
// Parse decrypted encryption block, PKCS#1 formatted
if (BLOCKTYPE_ENCR != parse_pkcs1 (Mess, EB, LenEB, key.bytelen_mod))
{// wrong block type or incorrect format
return (UCHAR*)NULL;
}
else
{
return Mess; // return pointer to message
}
}
// RSA signing
LINT RSAkey::sign (const UCHAR* Mess, int LenMess)
{
int LenEncryptionBlock = key.bytelen_mod - 1;
UCHAR HashRes[RMDVER>>3];
UCHAR* EncryptionBlock = new UCHAR[LenEncryptionBlock];
ripemd160 (HashRes, (UCHAR*)Mess, (ULONG)LenMess);
if (NULL == format_pkcs1 (EncryptionBlock, LenEncryptionBLock,
BLOCKTYPE_SIGN, HashRes, RMDVER >> 3))
{
delete [] EncryptionBlock;
return LINT (0);// error in formatting: message too long
}
// change encryption block into LINT number (constructor 3)
LINT m = LINT (EncryptionBlock, LenEncryptionBlock);
delete [] EncryptionBlock;
return fastdecrypt (m);
}
////////////////////////////////////////////////////////////////////////
// private auxiliary functions of the class RSAkey
// ... among other things: RSA key generation according to IEEE P1363, Annex A
// If parameter PubExp == 1 or is absent, a public exponent
// of length half the modulus is determined randomly.
int RSAkey::makekey (int length, const LINT& PubExp)
{
// generate prime p such that 2 ˆ (m - r - 1) <= p > 2 ˆ (m - r), where
// m =  (length + 1)/2
(length + 1)/2 and r random in interval 2 <= r < 15
USHORT m = ((length + 1) >> 1) - 2 - usrandBBS_l () % 13;
key.p = findprime (m, PubExp);
// determine interval bounds qmin and qmax for prime q
// set qmin =
and r random in interval 2 <= r < 15
USHORT m = ((length + 1) >> 1) - 2 - usrandBBS_l () % 13;
key.p = findprime (m, PubExp);
// determine interval bounds qmin and qmax for prime q
// set qmin =  (2 ˆ (length - 1))/p + 1
(2 ˆ (length - 1))/p + 1 LINT qmin = LINT(0).setbit (length - 1)/key.p + 1;
// set qmax =
LINT qmin = LINT(0).setbit (length - 1)/key.p + 1;
// set qmax =  (2 ˆ length - 1)/p)
(2 ˆ length - 1)/p) LINT qmax = (((LINT(0).setbit (length - 1) - 1) << 1) + 1)/key.p;
LINT qmax = (((LINT(0).setbit (length - 1) - 1) << 1) + 1)/key.p;// generate prime q > p with length qmin <= q <= qmax
key.q = findprime (qmin, qmax, PubExp);
// generate modulus mod = p*q such that 2 ˆ (length - 1) <= mod < 2 ˆ length
key.mod = key.p * key.q;
// calculate Euler phi function
LINT phi_n = key.mod - key.p - key.q + 1;
// generate public exponent if not specified in PubExp
if (1 == PubExp)
{
key.pubexp = randBBS (length/2) | 1; // half the length of the modulus
while (gcd (key.pubexp, phi_n) != 1)
{
++key.pubexp;
++key.pubexp;
}
}
else
{
key.pubexp = PubExp;
}
// generate secret exponent
key.prvexp = key.pubexp.inv (phi_n);
// generate secret components for rapid decryption
key.ep = key.prvexp % (key.p - 1);
key.eq = key.prvexp % (key.q - 1);
key.r = inv (key.p, key.q);
return testkey();
}
// test function for RSA-key
int RSAkey::testkey (void)
{
LINT mess = randBBS (ld (key.mod) >> 1);
return (mess == fastdecrypt (mexpkm (mess, key.pubexp, key.mod)));
}
// rapid RSA decryption
LINT RSAkey::fastdecrypt (const LINT& mess)
{
LINT m, w;
m = mexpkm (mess, key.ep, key.p);
w = mexpkm (mess, key.eq, key.q);
w.msub (m, key.q);
w = w.mmul (key.r, key.q) * key.p;return (w + m);
}
////////////////////////////////////////////////////////////////////////
// member functions of the class RSApub
// constructor RSApub()
RSApub::RSApub (const RSAkey& k)
{
pkey = k.export();// import public key from k
}
// RSA encryption
LINT RSApub::crypt (const UCHAR* Mess, int LenMess)
{
int LenEncryptionBlock = key.bytelen_mod - 1;
UCHAR* EncryptionBlock = new UCHAR[LenEncryptionBlock];
// format encryption block according to PKCS #1
if (NULL == format_pkcs1 (EncryptionBlock, LenEncryptionBlock,
BLOCKTYPE_ENCR, Mess, (ULONG)LenMess))
{
delete [] EncryptionBlock;
return LINT (0); // formatting error: message too long
}
// transform encryption block into LINT number (constructor 3)
LINT m = LINT (EncryptionBlock, LenEncryptionBlock);
delete [] EncryptionBlock;
return (mexpkm (m, pkey.pubexp, pkey.mod));
}
// verification of RSA signature
int RSApub::verify (const UCHAR* Mess, int LenMess, const LINT& Signature)
{
int length, BlockType verification = 0;
UCHAR m H1[RMDVER>>3];
UCHAR* H2 = NULL;
UCHAR* EB = lint2byte (mexpkm (Signature, pkey.pubexp, pkey.mod), &length);
ripemd160 (H1 (UCHAR*)Mess, (ULONG)LenMess);
// take data from decrypted PKCS #1 encryption block
BlockType = parse_pkcs1 (H2, EB, &length, pkey.bytelen_mod);
if ((BlockType == 0 || BlockType == 1) && // Block Type Signature
(HashRes2 > NULL) && (length == (RMDVER >> 3)))
{
verification = !memcmp ((char *)H1, (char *)H2, RMDVER >> 3);
}return verification; }
The class implementations RSAkey and RSApub contain in addition the following operators, which are not discussed further here:
RSAkey& operator= (const RSAkey&); friend int operator== (const RSAkey&, const RSAkey&); friend int operator!= (const RSAkey&, const RSAkey&); friend fstream& operator<< (fstream&, const RSAkey&); friend fstream& operator>> (fstream&, RSAkey&);
and
RSApub& operator= (const RSApub&); friend int operator== (const RSApub&, const RSApub&); friend int operator!= (const RSApub&, const RSApub&); friend fstream& operator<< (fstream&, const RSApub&); friend fstream& operator>> (fstream&, RSApub&);
These are for elementwise allocation, tests for equality and inequality, as well as reading and writing of keys to and from mass storage. However, one must note that the private key components are stored in plain text, just as the public key is. For a real application the secret keys must be stored in encrypted form and in a secure environment.
There are also the member functions
RSAkey::purge (void), RSApub::purge (void),
which delete keys by overwriting their LINT components with zeros. The formatting of message blocks for encryption or signing corresponding to the PKCS #1 specification is taken over by the function
UCHAR* format_pkcs1 (const UCHAR* EB, int LenEB, UCHAR BlockType, const UCHAR* Data, int LenData);
The analysis of decrypted message blocks for verifying the format and for the extraction of useful data is handled by the function
int parse_pkcs1 (UCHAR*& PayLoad, const UCHAR* EB, int* LenData);
The classes RSAkey and RSApub are extendable in a number of ways. For example, one could imagine a constructor that accepts a public key as parameter and generates a suitable modulus and secret key. For a practical implementation the inclusion of additional hash functions may be necessary. Message blocking is also required. The list of worthwhile extensions is long, and a full discussion would break the bounds and the binding of this book.
An example test application of the classes RSAkey and RSApub is to be found in the module rsademo.cpp contained in the FLINT/C package. The program is translated with
gcc -O2 -DFLINT_ASM -o rsademo rsademo.cpp rsakey.cpp
flintpp.cpp randompp.cpp flint.c aes.c ripemd.c sha256.c entropy.c random.c
-lflint -lstdc++if one implements, for example, the GNU C/C++ compiler gcc under Linux and uses the assembler functions in libflint.a.
[49] According to http://www.rsasecurity.com by 1999 over three hundred million products containing RSA functions had been sold.
[50] http://www.rsasecurity.com/solutions/developers/total-solution/faq.html.
[51] Lenstra: Arjen K.: Factorization of RSA-130 using the Number Field Sieve, http://dbs.cwi.nl.herman.NFSrecords/RSA-130; see also [Cowi].
[52] E-mail from [email protected] in Number Theory Network of 4 February 1999. See also http://www.rsasecurity.com.
[53] http://www.rsasecurity.com.
[54] MIPS = mega instructions per second measures the speed of a computer. A computer works at 1 MIPS if is can execute 700,000 additions and 300,000 multiplications per second.
[55] It is useful to choose RSA keys of binary length a multiple of 8, in conformity with the convention that such keys should end at the end of a byte.
[56] ISO/IEC JTC 1/SC27: Recommendation on the withdrawal of IS 9796:1991, 6 October 1991.
[57] We have already mentioned the attack of Boneh, Joux, and Nguyen.
[58] In the language of mathematics we would say that hash functions H :
[59] This was an earlier version of SHA-1 from 1993, which in 1995 was replaced by SHA-1, which was designed to overcome specific weaknesses.
[60] RIPEMD has been further developed to RIPEMD160 [DoBP]. Although RIPEMD160 has meanwhile been rejected in favor of SHA-1, this algorithm in its current state remains unbroken.
[61] Widely used is ISO 9594-8, which is equivalent to the ITU-T (formerly CCITT) recommendation X.509v3.