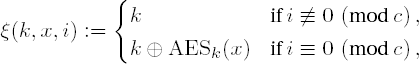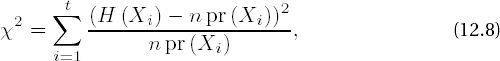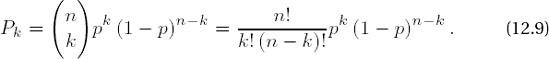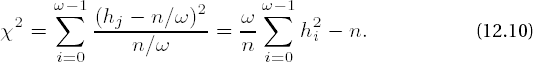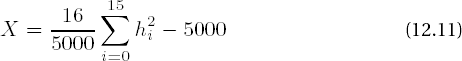Mathematics is full of pseudorandomness—plenty enough to supply all would-be creators for all time.
Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.
Sequences of "random" numerical values are used in many statistical procedures, in numerical mathematics, in physics, and also in number-theoretic applications to replace statistical observations or to automate the input of variable quantities. Random numbers are used:
to select random samples from a larger set,
in cryptography to generate keys and in running security protocols,
as initial values in procedures to generate prime numbers,
to test computer programs (a topic to which we shall return),
for fun,
as well as in many additional applications. In computer simulations of natural phenomena random numbers can be used to represent measured values, thereby representing a natural process (Monte Carlo methods). Random numbers are useful even when numbers are required that can be selected arbitrarily. Before we set out in this chapter to produce some functions for the generation of large random numbers, which will be required, in particular, for cryptographic applications, we should take care of some methodological preparations.
There are many sources of random numbers, but we should be sure to differentiate between genuine random numbers, which arise as the result of random experiments, and pseudorandom numbers, which are generated algorithmically. Genuine random numbers arise from such processes as the tossing of coins or dice, spinning a (fair) roulette wheel, observing processes of radioactive decay with the aid of suitable measuring equipment, and evaluating the output of electronic components. In contrast to these, pseudorandom numbers are computed by algorithms, generated with the aid of pseudorandom number generators, which are deterministic, in that they depend only on an initial state and initial value (seed), and therefore are both predictable and reproducible. Pseudorandom numbers thus do not arise randomly in the strict sense of the word. The reason that this situation can frequently be ignored is that we are in possession of algorithms that are able to produce pseudorandom numbers of "high quality," where we shall have to explain what we mean by this term.
The first thing that we establish is that in fact, it makes no sense to talk about a single number being "random," but that mathematical requirements for randomness are always satisfied by sequences of numbers. Knuth speaks of a sequence of independent random numbers with a particular distribution, in which every number is produced randomly and independently of all other numbers of the sequence, and every number assumes a value within a certain range of values with a certain probability (see [Knut], Section 3.1). We use the terms "random" and "independent" here to mean that the events leading to the selection of concrete numbers are too complex in their formation and interaction to be detected by statistical or other tests.
This ideal is theoretically unachievable by generating numbers using deterministic procedures. Yet the goal of many different algorithmic techniques is to approach this ideal as closely as possible. The logical structure of deterministic random number generators can be described by a quintuple (S, R,
Therefore, we first select from the many possibilities at hand a proven and frequently used procedure for generating pseudorandom numbers (for the sake of brevity we shall frequently drop the "pseudo" and speak simply of random numbers, random sequences, and random number generators) and spend some time with the method of linear congruences. Beginning with an initial value X0 the elements of a sequence are generated by the linear recursion
This procedure was developed in 1951 by D. Lehmer, and it has enjoyed considerable popularity since that time, since despite their simplicity, linear congruences can produce random sequences with excellent statistical properties, where their quality, as one might expect, depends on the choice of parameters a, b, and m. In [Knut] it is shown that linear congruences with carefully chosen parameters can pass through the hoops of statistical tests with flying colors, but that on the other hand, a random selection of parameters almost always leads to a poor generator. The moral is this: Be careful in your choice of parameters!
The choice of m as a power of two has at once the advantage that forming the residue modulo m can be accomplished with a mathematical AND. An accompanying disadvantage is that the least-significant binary digits of numbers thus generated demonstrate less random behavior than the most-significant digits, and thus one must be careful in working with such numbers. In general, one must look out for poor random properties of such numbers formed from sequential values of a linear congruence generator modulo a prime divisor of the modulus m, so that the choice of m as a prime number should also be considered, since in this case individual binary digits are no worse than any others.
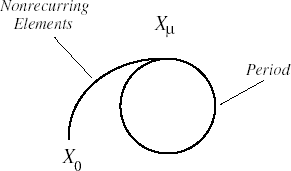
The choice of a and m has influence on the periodic behavior of the sequence: Since only finitely many, namely at most m, distinct sequence values can appear, the sequence begins to repeat at the latest with the generation of the (m + 1)st number. That is, the sequence is periodic. (One says also that the sequence enters a period or a cycle.) The entry point into a cycle need not be the initial value X0, but can be some later value Xμ. The numbers X0, X1, X2, . . . , Xμ−1 are called the nonrecurring elements. We may thus indicate the periodic behavior of the sequence as shown in Figure 12-1.
Since the regular repetition of numbers in short cycles represents poor random behavior according to all reasonable criteria, we must strive to maximize the length of the cycles or indeed to find generators that possess only cycles of maximum length. We can establish criteria by which a linear congruence sequence with parameters a, b, and m possesses exactly the maximal period length. Namely, the following conditions should be fulfilled:
gcd(b, m) = 1.
For all primes p one has p | m p | (a − 1).
4 | m 4 | (a − 1).
For a proof and additional details see [Knut], Section 3.2.1.2.
As an example of parameters that fulfill these criteria let us consider the linear congruence that the ISO-C standard recommends as exemplary for the function rand():
where m = 2k, with k determined by 2k − 1 being the largest number representable by the type unsigned int. The number Xi+1 is not returned as the value of rand(), but rather Xi+1/216 mod (RAND_MAX + 1), so that the function rand() generates all values between 0 and RAND_MAX. The macro RAND_MAX is defined in stdio.h and should have a value of at least 32267 (see [Pla1], p. 337). Here the recommendation of Knuth to do without the least-significant binary digits in the case of power-of-two moduli has apparently been taken into account. We easily determine that the above requirements (i)–(iii) are satisfied and that therefore a sequence produced by this generator possesses the maximum period length 2k.
Whether this happens to be the case for a particular implementation of the C library, whose source code is usually unavailable,[36] can be tested under favorable circumstances with the aid of the following algorithm by R. P. Brent. The Brent algorithm determines the period length λ of a sequence that is computed by the recursion Xi+1 = F (Xi) on a set of values D using the generating function F : D ← D and an initial value X0 € D. One needs at most 2 • max {μ, λ} calculations of the function F (cf.[HKW], 4.2).
Algorithm of Brent for determining the period length λ of a sequence generated by X0, Xi+1 = F (Xi)
Set y ← X0, r ← 1, and k ← 0.
Set x ← y, j ← k, and r ← r + r.
Set k ← k + 1 and y ← F (y); repeat this step until x = y or k ≥ r.
If x ≠ y, go to step 2. Otherwise, output λ = k − j.
This process is successful only if in step 3 one actually sees the actual sequence values F (y) and not, as in the above ISO recommendation, only their most-significant parts.
We turn first to the actual subject of this chapter and supply ourselves with functions for generating random numbers in CLINT integer format. As our starting point for the generation of prime numbers, we would like to be able to create large numbers with a specified number of binary digits; for these, the highest bit should be set to 1, and the remaining bits should be randomly generated.
First we construct a linear congruence generator from whose sequential values we will take the digits of a CLINT random number. The parameters a = 6364136223846793005 and m = 264 for our generator are taken from the table with results of the spectral test in Knuth ([Knut], pages 102–104). The sequence Xi+1 = (Xi • a + 1) mod m thus generated possesses a maximal period length λ = m as well as good statistical properties, as we conclude from the test results presented in the table. The generator is implemented in the following function rand64_l(). On each call to rand64_l() the next number in the sequence is generated and then stored in the global CLINT object SEED64, declared as static. The parameter a is stored in the global variable A64. The function returns a pointer to SEED64.
Function: | linear congruence generator with period length 264 |
Syntax: |
|
Return: | pointer to |
clint *
rand64_l (void)
{
mul_l (SEED64, A64, SEED64);
inc_l (SEED64);Note
The reduction modulo 264 proceeds simply by setting the length field of SEED64 and costs almost no computational time.
SETDIGITS_L (SEED64, MIN (DIGITS_L (SEED64), 4)); return ((clint *)SEED64); }
Next, we require a function for setting the initial values for rand64_l(). This function is called seed64_l(), and it accepts a CLINT object as input, from which it takes at most four of the most-significant digits as initial values in SEED64. The previous value of SEED64 is copied into the static CLINT object BUFF64, and a pointer to BUFF64 is returned.
Function: | set an initial value for |
Syntax: | |
Input: |
|
Return: | pointer to |
The next function returns random numbers of type ULONG. All numbers are generated with a call to rand64_l(), where the most-significant digits of SEED64 are used to build a number of the requested type.
Function: | generation of a random number of type |
Syntax: | |
Return: | random number of type |
ULONG
ulrand64_l (void)
{
ULONG val;
USHORT l;
rand64_l();
l = DIGITS_L (SEED64);
switch (l)
{
case 4:
case 3:
case 2:
val = (ULONG)SEED64[l-1];
val += ((ULONG)SEED64[l] << BITPERDGT);
break;
case 1:
val = (ULONG)SEED64[l];
break;
default:
val = 0;
}
return val;
}The FLINT/C package contains the additional functions ucrand64_l(void) and usrand64_l(void), which generate random numbers of types UCHAR and USHORT, respectively. However, we shall not discuss them here. We now present the function rand_l(), which generates large random numbers of CLINT type, with the number of binary digits to be specified.
Function: | generation of a random number of type |
Syntax: |
|
Input: |
|
Output: |
|
void
rand_l (CLINT r_l, int l)
{
USHORT i, j, ls, lr;Note
The requested number of binary digits l is first bounded by the maximum permitted value for CLINT objects. Then the number ls of required USHORT digits and the position lr of the most-significant binary digit of the most-significant USHORT are determined.
l = MIN (l, CLINTMAXBIT); ls = (USHORT)l >> LDBITPERDGT; lr = (USHORT)l & (BITPERDGT - 1UL);
Note
Now the digits of r_l are generated by successive calls to the function usrand64_l(). The least-significant binary digits of SEED64 are therefore not used for the construction of CLINT digits.
for (i = 1; i <= ls; i++)
{
r_l[i] = usrand64_l ();
}Note
Now follows the precise manufacture of r_l by setting the most-significant bit in position lr − 1 of the (ls + 1)st USHORT digit to 1 and the most-significant bits to 0. If lr == 0, then the most-significant bit of the USHORT digit ls is set to 1.
if (lr > 0)
{
r_l[++ls] = usrand64_l ();
j = 1U << (lr - 1); /* j <- 2 ^ (lr - 1) */
r_l[ls] = (r_l[ls] | j) & ((j << 1) - 1);
}
else
{
r_l[ls] |= BASEDIV2;
}
SETDIGITS_L (r_l, ls);
}We now come to the cryptographic number generators that can be used for sensitive purposes based on their properties, on the assumption that they have been properly implemented and secret start values are used (more on this later). We will first construct the BBS generator, then a random number generator based on the symmetric algorithm AES, and then another that rests on a chain of the cryptographic hash functions RIPEMD-160 and SHA-1. With the use of AES, we build on the previous chapter; with hash functions, whose properties are collected in Chapter 17, we are somewhat anticipating things.
We will realize random number generators in such a way that they are reentrant, so that they can be simultaneously and independently used by several functions without their interfering with one another. That this is a good idea will become immediately clear when one considers how a function calls a random number generator whose internal state has just been deleted by another function. In this case, the second function will not obtain useful results. This scenario is heightened when the functions are executed in parallel processes or threads.
For example, if cryptographic keys are generated within a process or thread, and during this process the status of the random number generator being used is deleted by another process (that is, set to zero), then the random number generator will thereafter no longer produce reliable values, which could lead to sharply reduced quality of the keys produced by the affected process.
A way out of this problem is provided by the reentrant property, which we achieve by storing the internal states of the random number generators in separate buffers, which are managed individually and used exclusively by the calling functions.
For the derivation of start values for cryptographic random number generators, so-called entropy sources are required, which while observable, are neither predictable nor able to be influenced. Every sequence of pseudorandom numbers that proceeds deterministically is at most as secure as its start value. An attacker who knows or can guess the start value of a pseudorandom sequence thereby knows the entire random sequence or the keys or passwords derived from it. The notion of entropy is borrowed from physics, where it is used as a measure of disorder in closed systems. The idea that good start values are achieved from the observation of the greatest possible disorder seems to be more intuitive and compelling than to speak of the "randomness of start values."
For our purposes, we will use primarily artificial sources of entropy, in particular, certain system statistics such as the number of clock ticks for certain processes, measures of external events such as mouse movements or the times between keyboard events or mouse clicks by users.
Such parameters are best combined with one another in a mixture, such as through the use of hash functions.
Functions for obtaining entropy are also offered by various operating systems, for example, by Linux and by the Win32 CryptoAPI under Windows. The Win32 CryptoAPI offers the function CryptGenRandom(), which takes entropy from a variety of sources available to the operating system. Here it is necessary to bind the link library ADVAPI32.LIB in order to use the Win32 DLL ADVAPI32.DLL (see [HoLe]).
Linux and FreeBSD offer entropy via the virtual devices /dev/random and /dev/urandom. The associated driver manages a 512-byte entropy pool, which is filled with the results of a variety of continuously monitored unpredictable events. The most productive source of these random events is the keyboard: The last digit of the microsecond-precise time measurement between two keyboard events can be neither predicted nor reproduced. Further sources are times associated with mouse movements, hardware interrupts, and block devices from the kernel. When the entropy pool is queried, 64-byte blocks from the pool are processed sequentially with the hash function SHA-1, and the result of this operation is played back into the pool. The hash function is then applied again to the first 64 bytes of the pool, and the result is finally returned to the calling function as a random value. The process is repeated as often as necessary until the required number of bytes is returned, and read access is terminated. The device file /dev/random always outputs only as many bits as corresponds to the available entropy in the pool. If the requests exceed this amount, then the virtual device is blocked, and it returns additional random bytes only after a sufficient number of events have occurred that can be observed for the production of entropy.
In contrast to /dev/random, the device file /dev/urandom returns values continuously even when the entropy pool is exhausted. In this case, the device returns random values determined in the manner described previously (see [Tso]).
The following function uses, depending on platform and availability, both sources for generating start values. Under Windows, in addition, the 64 result bytes of the WIN32 function QueryPerformanceCounter() are used for collecting entropy. Moreover, the system time is queried, and optionally, a character string of the calling function is accepted so that a user entry, such as input from the keyboard, can be considered in the generation of the start value. The values thus obtained are once more compressed with the hash function RIPEMD-160 to a 20-byte result, which is returned in this form and also as a large integer in CLINT format.
Function: | Generation of entropy for the initialization of pseudorandom number generators. In addition to an optional user-defined character string, entropy bytes are read from system-specific sources: For Win32: Value from For Linux: Entropy is read from Altogether, Additionally, a hash value is generated from the entropy data. |
Syntax: | int GetEntropy_l (CLINT Seed_l, char *Hashres, int AddEntropy, char *RndStr, int LenRndStr); |
Input: |
|
Output: |
If |
Return: | 0 if all O.K. n > 0 if n is less than the required number of entropy bytes that could be read
|
int
GetEntropy_l (CLINT Seed_l, UCHAR *Hashres, int AddEntropy,
char *RndStr, int LenRndStr)
{
unsigned i, j, nextfree = 0;
unsigned MissingEntropy = MAX(AddEntropy, sizeof (time_t));
UCHAR *Seedbytes;
int BytesRead;
int LenSeedbytes = LenRndStr + MissingEntropy +
sizeof (time_t) + 2*sizeof (ULONG);
RMDSTAT hws;
time_t SeedTime;
FILE *fp;
#if defined _WIN32 && defined _MSC_VER
LARGE_INTEGER PCountBuff;
HCRYPTPROV hProvider = 0;
#endif /* defined _WIN32 && defined _MSC_VER? */
if ((Seedbytes = (UCHAR*)malloc(LenSeedbytes)) == NULL)
{
return E_CLINT_MAL;
}
if (RndStr != NULL && LenRndStr > 0)
{
memcpy (Seedbytes, RndStr, LenRndStr);
nextfree = LenRndStr;
}Note
Bring system time into the buffer Seedbytes.
SeedTime = (time_t)time(NULL);
for (i = 0; i < sizeof(time_t); i++)
{
j = i << 3;
Seedbytes[nextfree+i] = (UCHAR)((SeedTime >> j) & (time_t)0xff);
}
nextfree += sizeof (time_t);
MissingEntropy -= sizeof (time_t);Note
Entropy from WIN32 API (link to ADVAPI32.LIB is required.
#if defined _WIN32 && defined _MSC_VER
if (MissingEntropy)
{Note
Chain with 64-bit value from QueryPerformanceCounter()
QueryPerformanceCounter (&PCountBuff);
for (i = 0; i < sizeof (DWORD); i++)
{
j = i << 3;
Seedbytes[nextfree + i] =
(char)((PCountBuff.HighPart >> j) & (DWORD)0xff);
Seedbytes[nextfree + sizeof (DWORD) + i] =
(char)((PCountBuff.LowPart >> j) & (DWORD)0xff);
}
nextfree += 2*sizeof (DWORD);
MissingEntropy -= 2*sizeof (DWORD);
}Note
Chain with values from CryptGenRandom():
if (CryptAcquireContext(&hProvider, NULL, NULL, PROV_RSA_FULL,
CRYPT_VERIFYCONTEXT))
{
if (CryptGenRandom (hProvider, MissingEntropy, &Seedbytes[nextfree]))
{
nextfree += MissingEntropy;
MissingEntropy = 0;
}
}
if (hProvider)
{
CryptReleaseContext (hProvider, 0);
}
#endif /* defined _WIN32 && _MSC_VER */Note
Fetch entropy from /dev/urandom if this source is available.
if ((fp = fopen("/dev/urandom", "r")) != NULL)
{
BytesRead = fread(&Seedbytes[nextfree], sizeof (UCHAR), MissingEntropy, fp);
nextfree += BytesRead;
MissingEntropy −= BytesRead;
fclose (fp);
}Note
Hash the chained entropy values.
if (Hashres != NULL)
{
ripeinit (&hws);
ripefinish (Hashres, &hws, Seedbytes, nextfree);
}Note
Seed as an integer in CLINT format.
if (Seed_l != NULL)
{
byte2clint_l (Seed_l, Seedbytes, nextfree);
}Note
Overwrite and deallocate seed.
SeedTime = 0; local_memset (Seedbytes, 0, LenSeedbytes); local_memset (&hws, 0, sizeof (hws)); free (Seedbytes); return MissingEntropy; }
For an extensive discussion and ideas for obtaining start values, see [Gut1], [Gut2], [East], [Matt].[37]
A random number generator that has been well researched with regard to its cryptographic properties is the BBS bit generator of L. Blum, M. Blum, and M. Shub, which is based on results of complexity theory. We would like now to describe the process and then implement it, although without getting into the theoretical details, for which see [Blum] or [HKW], Chapter IV and Section VI.5.
We require two prime numbers p, q congruent to 3 modulo 4, which we multiply together to obtain a modulus n, as well as a number X that is relatively prime to n. From X0 := X2 (mod n), we obtain the start value X0 for a sequence of integers that we calculate by successive squaring modulo n:
As random numbers we remove from each value Xi the least-significant bit. We may thus make a formal description of the generator: The state set is denoted by S := { 0, 1, . . . , n − 1 }, the random values are defined by R := { 0, 1 }, the state transitions are described by the function
A random sequence constructed of binary digits thus obtained can be considered secure in the cryptographic sense: The ability to predict previous or future binary digits from a portion of those that have already been calculated is possible only if the factors p and q of the modulus are known. If these are kept secret, then according to current knowledge, the modulus n must be factored for one to be able to predict further bits of a BBS random sequence with probability greater than
With the aid of the function prime_l, prime numbers p ≡ q ≡ 3 (mod 4) are determined, both with approximately the same number of binary digits (this results in the modulus being as difficult as possible to factor, and the security of the BBS generator depends on this), and the modulus n = pq is created.[38]
Beginning with the start value X0, the next numbers in the sequence Xi+1 = Xi (mod n) are computed using the function SwitchRandBBS_l(), which outputs as random bit the least-significant bit of Xi+1. The value Xi+1 is stored in a buffer as the current state of the generator, which is managed by the calling function. We will return to the question of how this buffer is to be initialized with a suitable start value with the first call to SwitchRandBBS_l(). But first let us implement the function.
deterministic random number generator, after Blum–Blum–Shub | |
Syntax: | int SwitchRandBBS_l (STATEBBS *rstate); |
Input: |
|
Output: |
|
Return: | value from {0, 1} |
int
SwitchRandBBS_l (STATEBBS *rstate)
{Note
Continue the generator with modular squaring.
msqr_l (rstate->XBBS, rstate->XBBS, rstate->MODBBS);
Note
Output the least-significant bit of rstate->XBBS.
return (*LSDPTR_L (rstate->XBBS) & 1); }
The initialization of the BBS generator is accomplished with the help of the function InitRandBBS_l(), which in turn calls two additional functions: The function GetEntropy_l generates a start value seed_l, from which using the second function, seedBBS_l(), the initial state of the generator is calculated. The place where fresh chance comes into play in GetEntropy_l and how a start value is processed have already been discussed in the previous section.
Function: | initialization of the Blum–Blum–Shub pseudorandom number generator including obtaining entropy |
Syntax: | int
InitRandBBS_l (STATEBBS *rstate, char * UsrStr,
int LenUsrStr, int AddEntropy); |
Input: |
|
Output: |
|
Return: | 0 if all O.K. n > 0: number of requested but not generated bytes |
int
InitRandBBS_l (STATEBBS *rstate, char *UsrStr, int LenUsrStr, int AddEntropy)
{
CLINT Seed_l;
int MissingEntropy;Note
Generation of the requested entropy and from that the start value
MissingEntropy = GetEntropy_l (Seed_l, NULL, AddEntropy, UsrStr, LenUsrStr);
Note
Generation of the internal start state
SeedBBS_l (rstate, Seed_l);
Note
Deletion of the start value by overwriting
local_memset (Seed_l, 0, sizeof (CLINT)); return MissingEntropy; }
The actual initialization of the generator is accomplished by the function seedBBS_l:
Function: | set initial values for |
Syntax: | |
Input: |
|
Output: |
|
Return: |
|
int
seedBBS_l (STATEBBS *rstate CLINT seed_l)
{
CLINT g_l;
str2clint_l (rstate->MODBBS, (char *)MODBBSSTR, 16);
gcd_l (rstate->MODBBS, seed_l, g_l);
if (!EQONE_L (g_l))
{
return E_CLINT_RCP;
}
msqr_l (seed_l, rstate->XBBS, rstate->MODBBS);Note
Set the flag: PRNG is initialized.
rstate->RadBBSInit = 1; return E_CLINT_OK; }
Random numbers of type UCHAR are generated by the function bRandBBS_l(), the analogue of the function ucrand64_l():
Function: | generation of a random number of type |
Syntax: |
|
Input: |
|
Ouput: |
|
Return: | random number of type |
UCHAR
bRandBBS_l (STATEBBS *rstate)
{
int i;
UCHAR r = SwitchRandBBS_l (rstate);
for (i = 1; i < (sizeof (UCHAR) << 3); i++)
{
r = (r << 1) + SwitchRandBBS_l (rstate);
}
return r;
}For completeness, we should mention the functions sRandBBS_l() and lRandBBS_l(), which generate random numbers of types USHORT and ULONG.
We still lack the function RandBBS_l, which generates random numbers r_l with exactly l binary digits r_l in the interval 2l−1 ≤ r_l ≤ 2l − 1. Since this corresponds to a great extent to the function rand_l(), we shall omit an extensive description, instead presenting only the function header. Of course, these functions are contained in the FLINT/C package. To delete state buffers, the function PurgeRandBBS_l() is available.
Function: | generation of a random number of type |
Syntax: | int RandBBS_l (CLINT r_l, STATEBBS *rstate, int l); |
Input: |
|
Ouput: |
|
Return: |
|
An additional possibility for constructing random number generators is offered by symmetric block encryption systems, whose statistical and cryptographic properties have been shown to be well suited to the generation of pseudorandom numbers. We can clarify this with the help of the Advanced Encryption Standard, which as representative of modern block encryption systems stands out in relation to security and speed.[39]
With the code space K, the space D of clear text blocks, and the set C := {0, . . . , c − 1 } for a constant c, state sets are defined by RandAES via S := K × D × C. The state function is described by
with
and the output function via
The constant c specifies how frequently the key is updated, to prevent a conclusion from being drawn about one state from the previous state. The price for more security is the time it takes to initialize the key. The most secure, but slowest, variant of the generator is obtained with c = 1.
The output of the generator is varied using the counter i in such a way that in sequential steps, various byte positions are selected from the output values.
The initialization of the AES-based pseudorandom number generator RandAES is accomplished via the function InitRandAES_l:
initialization of the AES pseudorandom number generator and production of entropy | |
Syntax: | int
InitRandAES_l (STATEAES *rstate, char *UsrStr,
int LenUsrStr, int AddEntropy, int update); |
Input: |
|
Ouput: |
|
Return: | 0 if all O.K. n > 0: number of requested but not generated entropy bytes |
int
InitRandAES_l (STATEAES *rstate, char *UsrStr, int LenUsrStr,
int AddEntropy, int update)
{
int MissingEntropy, i;Note
Generation of the start value. In MissingEntropy is stored how many of the requested entropy bytes were unavailable.
MissingEntropy = GetEntropy_l (NULL, rstate->XAES, AddEntropy,
UsrStr, LenUsrStr);Note
Initialization of AES.
for (i = 0; i < 32; i++)
{
rstate->RandAESKey[i] ^= RandAESKey[i];
}
AESInit_l (&rstate->RandAESWorksp, AES_ECB, 192, NULL,
&rstate->RandAESSched, rstate->RandAESKey, 256, AES_ENC);Note
First state change, creation of start state
AESCrypt_l (rstate->XAES, &rstate->RandAESWorksp,
&rstate->RandAESSched, rstate->XAES, 24);Note
Set frequency of key update as parameter
rstate->UpdateKeyAES = update;
Note
Initialization of the step counter
rstate->RoundAES = 1;
Note
Set the initialization flag.
rstate->RandAESInit = 1; return MissingEntropy; }
The state function SwitchRandAES_l() is realized as follows:
Function: | Deterministic random number generator based on the Advanced Encryption Standard (AES) |
Syntax: |
|
Input: |
|
Ouput: |
|
Return: | random value of length one byte |
UCHAR
SwitchRandAES_l (STATEAES *rstate)
{
int i;
UCHAR rbyte;Note
State change via application of the function
The content of the buffer rstate->XAES corresponds to the function argument x.
AESCrypt_l (rstate->XAES, &rstate->RandAESWorksp,
&rstate->RandAESSched, rstate->XAES, 24);rbyte = rstate->XAES[(rstate->RoundAES)++ & 15];
Note
Key update if the parameter is set and the prescribed number of rounds is reached
if (rstate->UpdateKeyAES)
{
if (0 == (rstate->RoundAES % rstate->UpdateKeyAES))
{
for (i = 0; i < 32; i++)
{
rstate->RandAESKey[i] ^= rstate->XAES[i];
}
AESInit_l (&rstate->RandAESWorksp, AES_ECB, 192, NULL,
&rstate->RandAESSched, rstate->RandAESKey, 256, AES_ENC);
}
}
return rbyte;
}Random values r_l in the interval 2l−1 ≤ r_l ≤ 2l − 1 are specified with the function RandAES_l(), whose function header is given here:
Function: | generation of a random number of type |
Syntax: | int RandAES_1 (CLINT r_l, STATEAES *rstate, int l); |
Input: |
|
Ouput: |
|
Return: |
|
Additionally, in random.h are defined the macros bRandAES_l(), sRandAES_l(), and lRandAES_l(), each of which expects an initialized state buffer as argument, and they generate random numbers of types UCHAR, USHORT, and ULONG from these buffers.
The deletion of the generator takes place in analogy to RandBBS with the following function:
Function: | deletion of the internal state of RandAES |
Syntax: | void PurgeRandAES_1 (STATEAES *rstate); |
Input: |
|
Ouput: |
|
The following pseudorandom number generator will be built from the hash functions SHA-1 and RIPEMD-160. Both functions can be calculated extremely quickly, which leads to a generator with excellent performance.
With the definitions D := { 0, . . . , 2160 − 1}, C := {0, . . . , c − 1 }, S := D × C, and R := { 0, . . . , 28 − 1 } for input values, counters, states, and output values, the state function is described by
and the output function determined by
As in the case of RandAES, the output is varied with the help of the counter i in such a way that in successive steps, varying byte positions are selected as output values. The initialization of the generator takes place via the function InitRandRMDSHA1_l():
initialization of the RIPEMD-160/SHA-1 pseudorandom number generator together with entropy creation | |
Syntax: | int
InitRandRMDSHA1_l (STATERMDSHA1 *rstate, char * UsrStr,
int LenUsrStr, int AddEntropy); |
Input: |
|
Output: |
|
Return: | 0 if all O.K. n > 0: number of requested but not generated entropy bytes |
int
InitRandRMDSHA1_l (STATERMDSHA1 *rstate, char *UsrStr,
int LenUsrStr, int AddEntropy)
{
int MissingEntropy;Note
Generation of start value. In MissingEntropy is stored the number of requested entropy bytes that were not available.
MissingEntropy = GetEntropy_l (NULL, rstate->XRMDSHA1, AddEntropy,
UsrStr, LenUsrStr);Note
First state transition, creation of start state.
ripemd160_l (rstate->XRMDSHA1, rstate->XRMDSHA1, 20);
Note
Initialization of the step counter i.
rstate->RoundRMDSHA1 = 1;
Note
Set the initialization flag.
rstate->RandRMDSHA1Init = 1; return MissingEntropy; }
The state function SwitchRandRMDSHA1_l() outputs a random byte each time it is called:
Function: | Deterministic random number generator based on the hash functions SHA-1 and RIPEMD-160 |
Syntax: |
|
Input: |
|
Output: |
|
Return: | random value of length one byte |
UCHAR
SwitchRandRMDSHA1_l (STATERMDSHA1 *rstate)
{
UCHAR rbyte;sha1_l (rstate->SRMDSHA1, rstate->XRMDSHA1, 20); rbyte = rstate->SRMDSHA1[(rstate->RoundRMDSHA1)++ & 15];
ripemd160_l (rstate->XRMDSHA1, rstate->XRMDSHA1, 20); return rbyte; }
Random numbers r_l in the interval 2l−1 ≤ r_l ≤ 2l − 1 are generated via the function RandRMDHSA1_l(), whose function header is given here:
Generation of a random number of type | |
Syntax: | int RandRMDSAH1_l (CLINT r_l, STATERMDSHA1 *rstate, int l); |
Input: |
|
Output: |
|
Return: |
|
For this generator as well there are associated macros bRandRMDSHA1_l(), sRandRMDSHA1_l(), and lRandRMDSHA1_l() in the module random.h, which expect as argument the appropriate initialized buffer from which random integers of types UCHAR, USHORT, and ULONG are generated.
Finally, for sensitive applications, one needs a function for deleting the internal state of the random number generator:
Function: | deletion of the internal state of RandRMDSHA-1 |
Syntax: | void PurgeRandSHA_l (STATERMDSHA1 *rstate); |
Input: |
|
Ouput: |
|
For investigating the quality of random number generators, a large number of theoretical and empirical tests have been developed that are suitable for detecting the structural properties of sequences of random numbers.
Depending on the area of application, in addition to the statistical requirements on such sequences, one must also consider that random sequences that are to be used in cryptographic applications must not be predictable without the knowledge of secret information or reproducible from a small number of representatives, so as to keep attackers from being able to reconstruct a cryptographic key or sequence of keys derived from the sequence.
As an example, the German Institute for Security in Information Technology has specified in [BSI2] functionality classes and quality criteria for evaluating deterministic random number generators. The specification establishes four classes of increasing security:
- K1
A sequence of random vectors composed of random numbers should with high probability contain no identical consecutive elements. Statistical properties of the generated random numbers are unimportant. The length of the random vectors and the probability of error depend on the application.
- K2
The generated random numbers should be indistinguishable from true random numbers based on statistical tests. The tests to be applied are the monobit test, poker test, runs and longruns tests from [BSI2] and [FIPS], as well as the additional statistical test of autocorrelation. Altogether, what is checked is how well a given sequence of bits (or a part of such a sequence) satisfies the following conditions:
Zeros and ones appear equally often.
After a sequence of n zeros (respectively ones), the next bit will be a one (zero) with probability one-half.
A given output contains no information about the next output.
- K3
It should be impossible for all practical purposes for an attacker to be able to calculate or guess from a known sequence of generated random numbers any previous or future random numbers or an inner state of the generator.
- K4
It should be impossible for all practical purposes for an attacker to calculate or guess from an inner state of the generator previous random numbers or states.
As motivation for dealing with tests for evaluation of property K2, we look first at the chi-squared test (also written "X2 test"), which with the Kolmogorov–Smirnov test is among the most important tests of goodness of fit. The chi-squared test gives information on how well an empirically obtained probability distribution corresponds to a theoretically expected distribution. The chi-squared test computes the statistic
where for t distinct events Xi we designate H (Xi) the observed frequency of the event Xi, pr (Xi) the probability for the occurrence of Xi, and n the number of observations. For the case to which these distributions correspond, the statistic X2, viewed as a random variable, has the expected value E (X2) = t − 1. The threshold values that lead to the rejection of the test hypothesis of equality of the distributions for given error probabilities can be read from tables of the chi-squared distribution for t − 1 degrees of freedom (cf. [Bos1], Section 4.1).
The chi-squared test is employed in connection with many empirical tests to measure their results for correspondence with the theoretically calculated test distributions. The test is particularly simple to apply for sequences of uniformly distributed (which is our test hypothesis!) random numbers Xi in a range of values W = {{0, . . . , ω − 1}: We assume that each of the numbers in W is taken with the same probability p = 1/ω and thus expect that among n random numbers Xi each number from W appears approximately n/ω times (where we assume n > ω). However, this should not be exactly the case, because the probability Pk that among n random numbers Xi a specific value ω € W appears k times is given by
This binomial distribution indeed has the largest values for k ≈ n/ω , but the probabilities P0 = (1 − p)n and Pn = pn are not equal to zero. Under the assumption of random behavior we therefore expect to observe in the sequence of the Xi frequencies hw of individual values ω € W according to the binomial distribution. Whether this actually occurs is established by the chi-squared test in calculating
The test is repeated for several random samples (partial sequences of Xi). A rough approximation to the chi-squared distribution allows us to deduce that in most cases the test result X2 must lie in the interval [ω − 2√ω,ω + 2√ω]. Otherwise, the given sequence would attest to a lack of randomness. Based on this, the probability of an error, namely, that an actually "good" random sequence is declared "bad" based on the result of the chi-squared test, is about two percent. It is in this sense that the error probability of 10−6 that results from the given bounds is to be interpreted in the following tests. The bounds are set such that a "halfway reasonable" probability generator would almost always pass the test, so that known attacks against cryptographic algorithms based on statistical weaknesses in random number generators would fail (see [BSI2], page 7).[40]
The linear congruence generator in the ISO-C standard that we considered above passes this simple test, as do the pseudorandom number generators that we shall implement below for the FLINT/C package.
For a random sequence of 2500 bytes, or 20 000 bits, a test is made whether approximately the same number of zeros and ones occurs. The test is passed with error probability 10−6 if the number of ones (that is, set bits) in a sequence of 20 000 bits lies in the interval [9 654, 10 346] (see [BSI2] and [FIPS]).
The poker test is a special case of the chi-squared test with ω = 16 and n = 5000. A generated sequence of random numbers is divided into segments of four bits, and the frequencies of the sixteen possible sequences of zeros and ones are counted.
For an execution of the test, a sequence of 20 000 bits is divided into 5000 segments of four bits each. The frequencies hi, 0 ≤ i ≤ 15, of the sixteen four-bit arrangements are counted. For the test to be passed, the value
must lie, according to the specifications in [BSI2] and [FIPS], in the interval [1.03,57.40], which corresponds to an error probability of 10−6. Measured values outside the previously mentioned interval ω − 2√ωω, + 2√ω] = [8, 24], on the other hand, are rejected with the higher error probability 0.02.
A run is a sequence of identical bits (zeros or ones). The test counts the frequencies of runs of various lengths and checks for deviations from expected values. In a sequence of 20 000 bits, all runs of the same type (length and bit value, e.g., runs of 2 ones) are counted. The test is passed if the numbers lie in the intervals shown in Table 12-1 (error probability of 10-6).
As an extension of the runs test, the longruns test checks whether there exists a sequence of identical bits longer than a given length. The test is passed if there is no run of length 34 or longer in a sequence of 20 000 bits.
The autocorrelation test provides information about possible existing dependencies within a generated bit sequence. For a sequence of 10 000 bits, b1, . . . , b10000, and for t in the range 1 ≤ t ≤ 5000, the values
are computed. The test is passed with probability of error 10−6 if all the Zt lie in the interval [2327, 2673] (see [BSI2] and [FIPS]).
To demonstrate the properties K2, the required statistical tests for the output width of 8 bits for the random number generators presented here were carried out. In 2313 individual tests, over 20 000 random bits were calculated. All test results lay within the required bounds. The average values were calculated, and they are presented in Table 12-2. Therefore, the generators presented here can be placed in class K2.
Class K3 requires that it be impossible for an attacker to determine predecessors or successors of a given subsequence ri, ri+1, . . . , ri+j, nor to determine any internal state. For the generator RandAES, this would be equivalent to serious attack possibilities against the encryption procedure AES, which would lead to being able to take ciphered text and produce bits of clear text or of a key. No such attacks are known. Furthermore, the AES is considered a high-strength cryptographic mechanism, so that the generator can be placed in class K3.
If the parameter c is set to the value 1, then in each round, a new key
Table 12-2. Test results of the FLINT/C random number generators
| Rand64 | RandRMDSHA-1 | Tolerance Interval | ||
|---|---|---|---|---|---|
Monobit | 9997.29 | 10000.11 | 9999.15 | 9998.66 | [9654, 10346] |
Poker | 15.11 | 14.70 | 15.19 | 15.01 | [1.03, 57.40] |
Runs length 1 | 2499.55 | 2501.69 | 2500.02 | 2499.86 | [2267, 2733] |
Runs length 2 | 1250.29 | 1249.31 | 1249.38 | 1249.48 | [1079, 1421] |
Runs length 3 | 625.05 | 624.95 | 625.07 | 625.22 | [502 748] |
Runs length 4 | 312.16 | 312.32 | 312.87 | 312.59 | [233, 402] |
Runs length 5 | 156.29 | 156.22 | 156.15 | 156.11 | [90 223] |
Runs length 6 | 156.36 | 156.34 | 156.23 | 156.41 | [90, 233] |
Longruns | 0.00 | 0.00 | 0.00 | 0.00 | [0 0] |
Autocorrelation | 2500.79 | 2500.06 | 2501.00 | 2500.10 | [2327 2673] |
from knowledge of the internal state si, and therefore, with knowledge of the internal state of RandAES, it is even impossible to determine from a subsequence any predecessors of that subsequence. For c = 1, then, RandAES can be placed in class K4.
The argumentation for RandRMDSHA1 is similar. Because of the unidirectional properties of SHA-1, one cannot draw conclusions about the internal state of the generator from a subsequence, and therefore, no predecessors or successors can be determined. This ensures membership in class K3. Because of the same property in RIPEMD-160, no previous states can be derived from an internal state of the generator, without which again no predecessors can be determined. Thus the random number generator RandRMDSHA-1 can be placed in class K4.
For RandBBS an argument has already been presented that supports placing the generator in class K4.
An extensive overview of this field can be found in [Knut]. In particular, a comprehensive presentation of the theoretical evaluation of random number generators is provided in [Nied]. Ideas for constructing random number generators presented in this chapter have been taken from [Sali], as well as the type of representation of the test results in Table 12-2. Some pragmatic ideas for testing random sequences are contained in [FIPS].
In this section we will prepare several functions for generating random numbers and random prime numbers with additional boundary conditions that are not specialized to a specific random number generator. Rather, the choice of the generator to use is supported by a parameter. Here it is necessary to pass the appropriate state memory as parameter. The structure
struct InternalStatePRNG
{
STATERMDSHA1 StateRMDSHA1;
STATEAES StateAES;
STATEBBS StateBBS;
int Generator;
};extended by setting
typedef struct InternalStatePRNG STATEPRNG;
contains the state memory of the individual random number generators previously presented as well as the status variable Generator, which specifies for which random number generator the structure was initialized.
With this definition, the functions InitRand_l(), Rand_l(), lRand_l(), sRand_l(), bRand_l(), and PurgeRand_l() were created. With InitRand_l() a generator is initialized that is then used for subsequent calls of the random functions. The random functions themselves require as parameter a pointer to the initialized structure STATEPRNG.
Initialization of a yet to be specified random generator with generation of entropy | |
Syntax: | int InitRand_l (STATEPRNG *xrstate, char *UsrStr, int LenUsrStr, int AddEntropy, int Generator); |
Input: |
FLINT_RND64 FLINT_RNDRMDSHA1 FLINT_RNDAES FLINT_RNDBBS) |
Output: |
|
Return: | 0: OK n > 0: number of requested but not generated entropy bytes n < 0 : specified generator does not exist; |
int
InitRand_l (STATEPRNG *xrstate, char *UsrStr, int LenUsrStr,
int AddEntropy, int Generator)
{
int error;
switch (Generator)
{
case FLINT_RNDBBS:
error = InitRandBBS_l (&xrstate->StateBBS, (char*)UsrStr,
LenUsrStr, AddEntropy);
xrstate->Generator = FLINT_RNDBBS;
break;
case FLINT_RNDRMDSHA1:
error = InitRandRMDSHA1_l (&xrstate->StateRMDSHA1, (char*)UsrStr,
LenUsrStr, AddEntropy);
xrstate->Generator = FLINT_RNDRMDSHA1;
break;
case FLINT_RNDAES:
error = InitRandAES_l (&xrstate->StateAES, (char*)UsrStr,
LenUsrStr, AddEntropy, 10);
xrstate->Generator = FLINT_RNDAES;
break;
case FLINT_RND64:
error = InitRand64_l ((char*)UsrStr, LenUsrStr, AddEntropy);
xrstate->Generator = FLINT_RND64;
break;
default:
InitRand64_l ((char*)UsrStr, LenUsrStr, AddEntropy);
xrstate->Generator = FLINT_RND64;
error = -AddEntropy;
}
return error;
}int
Rand_l (CLINT r_l, STATEPRNG *xrstate, int l)
{
int error = E_CLINT_OK;
switch (xrstate->Generator)
{
case FLINT_RNDBBS:
error = RandBBS_l (r_l, &xrstate->StateBBS,
MIN (l, (int)CLINTMAXBIT));
break;
case FLINT_RNDAES:
error = RandAES_l (r_l, &xrstate->StateAES,
MIN (l, (int)CLINTMAXBIT));
break;case FLINT_RNDRMDSHA1:
error = RandRMDSHA1_l (r_l, &xrstate->StateRMDSHA1,
MIN (l, (int)CLINTMAXBIT));
break;
case FLINT_RND64:
rand_l (r_l, MIN (l, (int)CLINTMAXBIT));
break;
default:
rand_l (r_l, MIN (l, (int)CLINTMAXBIT));
error = E_CLINT_RIN;
}
return error;
}The remaining random functions should be executed only with their associated signatures.
Function: | generation of a pseudorandom number of types |
Syntax: | UCHAR bRand_l (STATEPRNG *xrstate); USHORT sRand_l (STATEPRNG *xrstate); ULONG lRand_l (STATEPRNG *xrstate); |
Input: |
|
Output: |
|
Return: | pseudorandom number of type |
With the following function, the internal state of a random number generator is deleted:
deletion of the internal state of a pseudorandom number generator | |
Syntax: | int PurgeRand_l (STATEPRNG *xrstate); |
Input: |
|
Output: |
|
Return: |
|
There follow some interesting functions with whose help we can determine large random prime numbers. We begin with the search for random numbers that lie within a prescribed interval [rmin, rmax]. This is a generalization of our function Rand_l().
Function: | determination of a pseudorandom number pseudorandom number generators; previous initialization by calling initialization function |
Syntax: | int
RandlMinMax_l (CLINT r_l, STATEPRNG *xrstate,
CLINT rmin_l,CLINT rmax_l); |
Input: |
|
Output: |
|
Return: |
|
int
RandMinMax_l (CLINT r_l, STATEPRNG *xrstate, CLINT rmin_l, CLINT rmax_l)
{
CLINT t_l;
int error = E_CLINT_OK;
USHORT l = ld_l (rmax_l);Note
Plausibility: Is rmin_l ≤ rmax_l?
if (GT_L (rmin_l, rmax_l))
{
return E_CLINT_RGE;
}Note
Form auxiliary variable t_l := rmax_l - rmin_l + 1.
sub_l (rmax_l, rmin_l, t_l); inc_l (t_l);
Note
Search for random number less than or equal to 2
switch (xrstate->Generator)
{
case FLINT_RNDAES:
error = RandAES_l (r_l, &xrstate->StateAES,
MIN (l, (int)CLINTMAXBIT));
break;
case FLINT_RNDRMDSHA1:
error = RandRMDSHA1_l (r_l, &xrstate->StateRMDSHA1,
MIN (l, (int)CLINTMAXBIT));
break;
case FLINT_RNDBBS:
error = RandBBS_l (r_l, &xrstate->StateBBS,
MIN (l, (int)CLINTMAXBIT));
break;case FLINT_RND64:
rand_l (r_l, MIN (l, (int)CLINTMAXBIT));
error = rand_l (r_l, MIN (l, (int)CLINTMAXBIT));
break;
default:
return E_CLINT_RNG;
}
if (E_CLINT_OK != error)
{
return error;
}Note
Calculate r_l mod t_l + rmin_l.
mod_l (r_l, t_l, r_l); add_l (r_l, rmin_l, r_l); return error; }
With the help of the function RandMinMax_l(), we can begin our search for prime numbers p that lie within the interval [rmin, rmax] and that satisfy the additional condition that p − 1 is relatively prime to a specified number f. We search for these numbers with the following algorithm and associated function FindPrimeMinMaxGcd_l():
Algorithm for determining a random prime number p with rmin ≤ p ≤ rmax that satisfies the additional condition gcd(p − 1, f) = 1, after [IEEE]
Set kmin ← ⌈(rmin − 1)/2⌉ and kmax

Generate randomly an integer k satisfying kmin ≤ k ≤ kmax.
Set ← 2k + 1.
Compute d ←
gcd(p − 1, f).If d = 1, test p for primality. If p is prime, set d ←
gcd(p − 1, f). Otherwise, go to step 2.
Determine a prime | |
Syntax: | int
FindPrimeMinMaxGcd_l (CLINT p_l, STATEPRNG *xrstate,
CLINT rmin_l, CLINT rmax_l, CLINT f_l); |
Input: |
|
Output: |
|
Return: |
|
int
FindPrimeMinMaxGcd_l (CLINT p_l, STATEPRNG *xrstate, CLINT rmin_l,
CLINT rmax_l, CLINT f_l)
{
CLINT t_l, rmin1_l, g_l;
CLINT Pi_rmin_l, Pi_rmax_l, NoofCandidates_l, junk_l;
int error;Note
Check whether f_l is odd.
if (ISEVEN_L (f_l))
{
return E_CLINT_RGE;
}Note
Estimate the number of prime numbers in the interval [rmin_l rmax_l], and store the result in NoofCandidates_l.
udiv_l (rmin_l, ld_l (rmin_l), Pi_rmin_l, junk_l); udiv_l (rmax_l, ld_l (rmax_l), Pi_rmax_l, junk_l); sub_l (Pi_rmax_l, Pi_rmin_l, NoofCandidates_l);
Note
Set rmin_l ← ⌈(rmin_l − 1)/2⌉.
dec_l (rmin_l);
div_l (rmin_l, two_l, rmin_l, junk_l);
if (GTZ_L (junk_l))
{
inc_l (rmin_l);
}Note
Set rmax_l ←
dec_l (rmax_l);
shr_l (rmax_l);
do
{Note
Test the breakoff condition for whether number of prime candidates has been reduced to zero. If this is the case, then no prime will be found within the given boundary conditions. This is indicated by the error code E_CLINT_RGE.
if (EQZ_L (NoofCandidates_l))
{
return (E_CLINT_RGE);
}Note
Determination of a random number.
if (E_CLINT_OK != (error = RandMinMax_l (p_l, xrstate, rmin_l, rmax_l)))
{
return error;}
Note
Set the prime number candidate p_l ← 2*p_l + 1; thus p_l is odd.
shl_l (p_l);
inc_l (p_l);
cpy_l (rmin1_l, p_l);
dec_l (rmin1_l);
gcd_l (rmin1_l, f_l, g_l);
dec_l (NoofCandidates_l);
}
while (!(EQONE_L (g_l) && ISPRIME_L (p_l)));
return error;
}The following two functions are by-products, so to speak, of the previous function. We first generate pseudorandom prime numbers with a specified number of binary digits and with the additional property of being relatively prime to a specified integer. For this we use the function FindPrimeMinMaxGcd_l():
Determination of a pseudorandom prime number | |
Syntax: | int
FindPrime_l (CLINT p_l, STATEPRNG *xrstate,
USHORT l, CLINT f_l); |
Input: |
|
Output: |
|
Return: |
|
int
FindPrimeGcd_l (CLINT p_l, STATEPRNG *xrstate, USHORT l, CLINT f_l)
{
CLINT pmin_l;
clint pmax_l[CLINTMAXSHORT + 1]; int error;
if (0 == l)
{
return E_CLINT_RGE;
}
SETZERO_L (pmin_l);
SETZERO_L (pmax_l);
setbit_l (pmin_l, l - 1);
setbit_l (pmax_l, l);
dec_l (pmax_l);
error = FindPrimeMinMaxGcd_l (p_l, xrstate, pmin_l, pmax_l, f_l);
return error;
}In the last step we wish to avoid the condition of relative primality by passing one as a parameter in the call FindPrimeGcd_l (p_l, xrstate, l, one_l):
Determination of a pseudorandom prime number | |
Syntax: | int FindPrime_l (CLINT p_l, STATEPRNG *xrstate, USHORT l); |
Input: |
|
Output: |
|
Return: |
|
int
FindPrime_l (CLINT p_l, STATEPRNG *xrstate, USHORT l)
{
return (FindPrimeGcd_l (p_l, xrstate, l, one_l));
}[36] The GNU-C library, of the Free Software Foundation, and the EMX-C library, by Eberhard Mattes, are excellent exceptions. The rand() function of the EMX library uses the parameters a = 69069, b = 5, and m = 232. The multiplier a = 69069 suggested by G. Marsaglia produces, together with the modulus m = 232, good statistical results and a maximal period length (see [Knut], pp. 102–104).
[37] For highly sensitive applications, the generation of start values or even entire random sequences of genuine random numbers using suitable hardware components is always to be preferred.
[38] Several such moduli of various lengths are contained in the FLINT/C package, though without the associated factors, which are known only to the author ;-).
[39] AES is used in an extended form with a block length of 192 bits. The standard requires 128 bits, while the underlying algorithm Rijndael is designed for block lengths of 256 bits.
[40] Take note that the test is valid only for a sufficiently large number of samples: This number must be at least n = 5ω (see [Bos2], Section 6.1), with an even larger number to be preferred.