7. Artificial Neural Networks
In Chapter 6, we examined the intricacies of artificial neurons. The theme of the current chapter is the natural extension of that: We cover how individual neural units are linked together to form artificial neural networks, including deep learning networks.
The Input Layer
In our Shallow Net in Keras Jupyter notebook (a schematic of which is available in Figure 5.4), we crafted an artificial neural network with the following layers:
An input layer consisting of 784 neurons, one for each of the 784 pixels in an MNIST image
A hidden layer composed of 64 sigmoid neurons
An output layer consisting of 10 softmax neurons, one for each of the 10 classes of digits
Of these three, the input layer is the most straightforward to detail. We start with it and then move on to discussion of the hidden and output layers.
Neurons in the input layer don’t perform any calculations; they are simply placeholders for input data. This placeholding is essential because the use of artificial neural networks involves performing computations on matrices that have predefined dimensions. At least one of these predefined dimensions in the network architecture corresponds directly to the shape of the input data.
Dense Layers
There are many kinds of hidden layers, but as mentioned in Chapter 4, the most general type is the dense layer, which can also be called a fully connected layer. Dense layers are found in many deep learning architectures, including the majority of the models we go over in this book. Their definition is uncomplicated: Each of the neurons in a given dense layer receive information from every one of the neurons in the preceding layer of the network. In other words, a dense layer is fully connected to the layer before it!
While they might not be as specialized nor as efficient as the other flavors of hidden layers we dig into in Part III, dense layers are broadly useful, because they can nonlinearly recombine the information provided by the preceding layer of the network.1 Reviewing the TensorFlow Playground demo from the end of Chapter 1, we’re now better positioned to appreciate the deep learning model we built. Breaking it down layer by layer, the network in Figures 1.18 and 1.19 has the following layers:
1. This statement assumes that the dense layer is made up of neurons with a nonlinear activation function like the sigmoid, tanh, and ReLU neurons introduced in Chapter 6, which should be a safe assumption.
An input layer with two neurons: one for storing the vertical position of a given dot within the grid on the far right, and the other for storing the dot’s horizontal position.
A hidden layer composed of eight ReLU neurons. Visually, we can see that this is a dense layer because each of the eight neurons in it is connected to (i.e., is receiving information from) both of the input-layer neurons, for a total of 16 (= 8 × 2) incoming connections.
Another hidden layer composed of eight ReLU neurons. We can again discern that this is a dense layer because each of its eight neurons receives input from each of the eight neurons in the preceding layer, for a total of 64 (= 8 × 8) inbound connections. Note in Figure 1.19 how the neurons in this layer are nonlinearly recombining the straight-edge features provided by the neurons in the first hidden layer to produce more-elaborate features like curves and circles.2
A third dense hidden layer, this one consisting of four ReLU neurons for a total of 32 (= 4 × 8) connecting inputs. This layer nonlinearly recombines the features from the previous hidden layer to learn more-complex features that begin to look directly relevant to the binary (orange versus blue) classification problem shown in the grid on the right in Figure 1.18.
A fourth and final dense hidden layer. With its two ReLU neurons, it receives a total of 8 (= 2 × 4) inputs from the previous layer. The neurons in this layer devise such elaborate features via nonlinear recombination that they visually approximate the overall boundary dividing blue from orange on the far-right grid.
An output layer made up of a single sigmoid neuron. Sigmoid is the typical choice of neuron for a binary classification problem like this one. As shown in Figure 6.9, the sigmoid function outputs activations that range from 0 up to 1, allowing us to obtain the network’s estimated probability that a given input x is a positive case (a blue dot in the current example). Like the hidden layers, the output layer is dense, too: Its neuron receives information from both neurons of the final hidden layer for a total of 2 (= 1 × 2) connections.
2. By returning to playground.tensorflow.org you can observe these features closely by hovering over these neurons with your mouse.
In summary, every layer within the networks provided by the TensorFlow Playground is a dense layer. We can call such a network a dense network, and we’ll experiment with these versatile creatures for the remainder of Part II.3
3. Elsewhere, you may find dense networks referred to as feedforward neural networks or multilayer perceptrons (MLPs). We prefer not to use the former term because other model architectures, such as convolutional neural networks (formally introduced in Chapter 10), are feedforward networks (that is, any network that doesn’t include a loop) as well. Meanwhile, we prefer not to use the latter term because MLPs, confusingly, don’t involve the perceptron neural units we cover in Chapter 6.
A Hot Dog-Detecting Dense Network
Let’s further strengthen your comprehension of dense networks by returning to two old flames of ours from Chapter 6: a frivolous hot dog-detecting binary classifier and the mathematical notation we used to define artificial neurons. As shown in Figure 7.1, our hot dog classifier is no longer a single neuron; in this chapter, it is a dense network of artificial neurons. More specifically, with this network architecture, the following differences apply:
We have reduced the number of input neurons down to two for simplicity.
The first input neuron, x1, represents the volume of ketchup (in, say, milliliters, which abbreviates to mL) on the object being considered by the network. (We are no longer working with perceptrons, so we are no longer restricted to binary inputs only.)
The second input neuron, x2, represents milliliters of mustard.
We have two dense hidden layers.
The first hidden layer has three ReLU neurons.
The second hidden layer has two ReLU neurons.
The output neuron is denoted by y in the network. This is a binary classification problem, so—as outlined in the previous section—this neuron should be sigmoid. As in our perceptron examples in Chapter 6, y = 1 corresponds to the presence of a hot dog and y = 0 corresponds to the presence of some other object.

Figure 7.1 A dense network of artificial neurons, highlighting the inputs to the neuron labeled a1
Forward Propagation Through the First Hidden Layer
Having described the architecture of our hot dog-detecting network, let’s turn our attention to its functionality by focusing on the neuron labeled a1.4 This particular neuron, like its siblings a2 and a3, receives input regarding a given object’s “ketchup-y-ness” and “mustard-y-ness” from x1 and x2, respectively. Despite receiving the same data as a2 and a3, a1 treats these data uniquely by having its own unique parameters. Remembering Figure 6.7, “the most important equation in this book”—w · x + b—you may grasp this behavior more concretely. Breaking this equation down for the neuron labeled a1, we consider that it has two inputs from the preceding layer: x1 and x2. This neuron also has two weights: w1 (which applies to the importance of the ketchup measurement x1) and w2 (which applies to the importance of the mustard measurement x2). With these five pieces of information we can calculate z, the weighted input to that neuron:
4. We’re using a shorthand notation for conveniently identifying neurons in this chapter. See Appendix A for a more precise and formal notation used for neural networks.
In turn, with the z value for the neuron labeled a1, we can calculate the activation a it outputs. Because the neuron labeled a1 is a ReLU neuron, we use the equation introduced with respect to Figure 6.11:
To make this computation of the output of neuron a1 tangible, let’s concoct some numbers and work through the arithmetic together:
x1 is 4.0 mL of ketchup for a given object presented to the network
x2 is 3.0 mL of mustard for that same object
w1 = –0.5
w2 = 1.5
b = –0.9
To calculate z let’s start with Equation 7.1 and then fill in our contrived values:
Finally, to compute a—the activation output of the neuron labeled a1—we can leverage Equation 7.2:
As suggested by the right-facing arrow along the bottom of Figure 7.1, executing the calculations through an artificial neural network from the input layer (the x values) through to the output layer (y) is called forward propagation. Just now, we detailed the process for forward propagating through a single neuron in the first hidden layer of our hot dog-detecting network. To forward propagate through the remaining neurons of the first hidden layer—that is, to calculate the a values for the neurons labeled a2 and a3—we would follow the same process as we did for the neuron labeled a1. The inputs x1 and x2 are identical for all three neurons, but despite being fed the same measurements of ketchup and mustard, each neuron in the first hidden layer will output a different activation a because the parameters w1, w2, and b vary for each of the neurons in the layer.
Forward Propagation Through Subsequent Layers
The process of forward propagating through the remaining layers of the network is essentially the same as propagating through the first hidden layer, but for clarity’s sake, let’s work through an example together. In Figure 7.2, we assume that we’ve already calculated the activation value a for each of the neurons in the first hidden layer. Returning our focus to the neuron labeled a1, the activation it outputs (a1 = 1.6) becomes one of the three inputs into the neuron labeled a4 (and, as highlighted in the figure, this same activation of a = 1.6 is also fed as one of the three inputs into the neuron labeled a5).
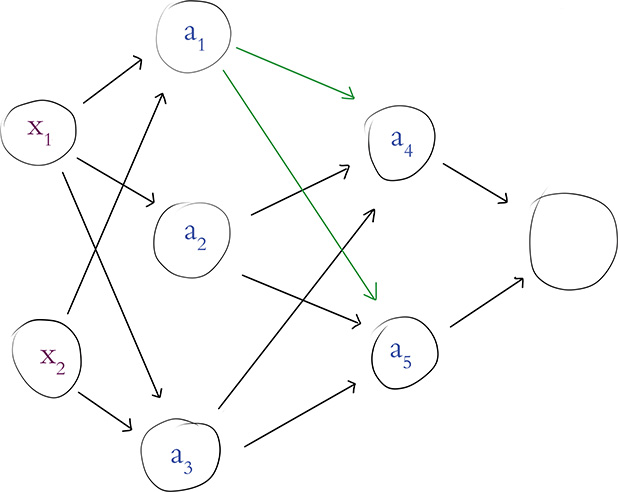
Figure 7.2 Our hot dog-detecting network from Figure 7.1, now highlighting the activation output of neuron a1, which is provided as an input to both neuron a4 and neuron a5
To provide an example of forward propagation through the second hidden layer, let’s compute a for the neuron labeled a4. Again, we employ the all-important equation w · x + b. For brevity’s sake, we’ve combined it with the ReLU activation function:
This is sufficiently similar to Equations 7.3 and 7.4 that it would be superfluous to walk through the arithmetic again with feigned values. As we propagate through the second hidden layer, the only twist is that the layer’s inputs (i.e., x in the equation w · x + b) do not come from outside the network; instead they are provided by the first hidden layer. Thus, in Equation 7.5:
x1 is the value a = 1.6, which we obtained earlier from the neuron labeled a1
x2 is the activation output a (whatever it happens to equal) from the neuron labeled a2
x3 is likewise a unique activation a from the neuron labeled a3
In this manner, the neuron labeled a4 is able to nonlinearly recombine the information provided by the three neurons of the first hidden layer. The neuron labeled a5 also nonlinearly recombines this information, but it would do it in its own distinctive way: The unique parameters w1, w2, w3, and b for this neuron would lead it to output a unique a activation of its own.
Having illustrated forward propagation through all of the hidden layers of our hot dog-detecting network, let’s round the process off by propagating through the output layer. Figure 7.3 highlights that our single output neuron receives its inputs from the neurons labeled a4 and a5. Let’s begin by calculating z for this output neuron. The formula is identical to Equation 7.1, which we used to calculate z for the neuron labeled a1, except that the (contrived, as usual) values we plug in to the variables are different:
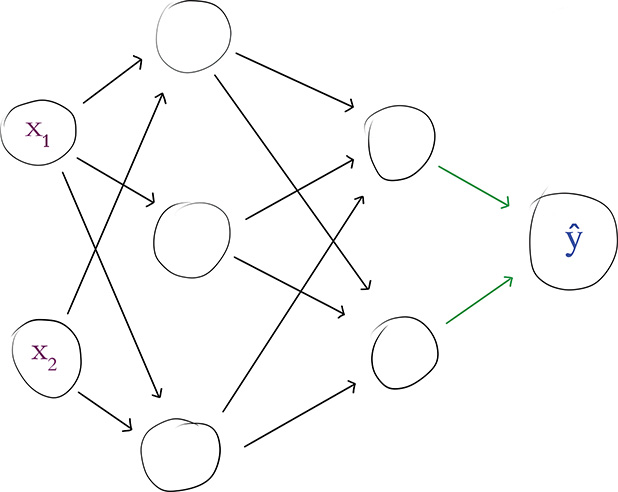
Figure 7.3 Our hot dog-detecting network, with the activations providing input to the output neuron ŷ highlighted
The output neuron is sigmoid, so to compute its activation a we pass its z value through the sigmoid function from Figure 6.9:
We are lazy, so we didn’t work out the final line of this equation manually. Instead, we used the Sigmoid Function Jupyter notebook that we created in Chapter 6. By executing the line sigmoid(-2.0) within it, our machine did the heavy lifting for us and kindly informed us that a comes out to about 0.1192.
The activation a computed by the sigmoid neuron in the output layer is a special case, because it is the final output of our entire hot dog-detecting neural network. Because it’s so special, we assign it a distinctive designation: ŷ. This variable is a version of the letter y that wears an object called a caret to keep its head warm, and so we call it “why hat.” The value represented by ŷ is the network’s guess as to whether a given object is a hot dog or not a hot dog, and we can express this in probabilistic language. Given the inputs x1 and x2 that we fed into the network—that is, 4.0 mL of ketchup and 3.0 mL of mustard—the network estimates that there is an 11.92 percent chance that an object with those particular condiment measurements is a hot dog.5 If the object presented to the network was indeed a hot dog (y = 1), then this ŷ of 0.1192 was pretty far off the mark. On the other hand, if the object was truly not a hot dog (y = 0), then the ŷ is quite good. We formalize the evaluation of ŷ predictions in Chapter 8, but the general notion is that the closer ŷ is to the true value y, the better.
5. Don’t say we didn’t warn you from the start that this was a silly example! If we’re lucky, its outlandishness will make it memorable.
The Softmax Layer of a Fast Food-Classifying Network
As demonstrated thus far in the chapter, the sigmoid neuron suits us well as an output neuron if we’re building a network to distinguish two classes, such as a blue dot versus an orange dot, or a hot dog versus something other than a hot dog. In many other circumstances, however, you have more than two classes to distinguish between. For example, the MNIST dataset consists of the 10 numerical digits, so our Shallow Net in Keras from Chapter 6 had to accommodate 10 output probabilities—one representing each digit.
When concerned with a multiclass problem, the solution is to use a softmax layer as the output layer of our network. Softmax is in fact the activation function that we specified for the output layer in our Shallow Net in Keras Jupyter notebook (Example 5.6), but we initially suggested you not concern yourself with that detail. Now, a couple of chapters later, the time to unravel softmax has arrived.
In Figure 7.4, we provide a new architecture that builds upon our binary hot dog classifier. The schematic is the same—right down to its volumes-of-ketchup-and-mustard inputs—except that instead of having a single output neuron, we now have three. This multiclass output layer is still dense, so each of the three neurons receives information from both of the neurons in the final hidden layer. Continuing on with our proclivity for fast food, let’s say that now:
y1 represents hot dogs.
y2 is for burgers.
y3 is for pizza.
Note that with this configuration, there can be no alternatives to hot dogs, burgers, or pizza. The assumption is that all objects presented to the network belong to one of these three classes of fast food, and one of the classes only.
Because the sigmoid function applies solely to binary problems, the output neurons in Figure 7.4 take advantage of the softmax activation function. Let’s use code from our Softmax Demo Jupyter notebook to elucidate how this activation function operates. The only dependency is the exp function, which calculates the natural exponential of whatever value it’s given. More specifically, if we pass some value x into it with the command exp(x), we will get back ex. The effect of this exponentiation will become clear as we move through the forthcoming example. We import the exp function into the notebook by using from math import exp.
To concoct a particular example, let’s say that we presented a slice of pizza to the network in Figure 7.4. This pizza slice has negligible amounts of ketchup and mustard on it, and so x1 and x2 are near-0 values. Provided these inputs, we use forward propagation to pass information through the network toward the output layer. Based on the information that the three neurons receive from the final hidden layer, they individually use our old friend w · x+b to calculate three unique (and, for the purposes of this example, contrived) z values:
z for the neuron labeled ŷ1, which represents hot dogs, comes out to -1.0.
For the neuron labeled ŷ2, which represents burgers, z is 1.0.
For the pizza neuron ŷ3, z comes out to 5.0.

Figure 7.4 Our food-detecting network, now with three softmax neurons in the output layer
These values indicate that the network estimates that the object presented to it is most likely to be pizza and least likely to be a hot dog. Expressed as z, however, it isn’t straightforward to intuit how much more likely the network predicts the object to be pizza relative to the other two classes. This is where the softmax function comes in.
After importing our dependency, we create a list named z to store our three z values:
z = [-1.0, 1.0, 5.0]
Applying the softmax function to this list involves a three-step process. The first step is to calculate the exponential of each of the z values. More explicitly:
exp(z[0])comes out to0.3679for hot dog.6exp(z[1])gives us2.718for burger.exp(z[2])gives us the much, much larger (exponentially so!)148.4for pizza.
6. Recall that Python uses zero indexing, so z[0] corresponds to the z of neuron ŷ1.
The second step of the softmax function is to sum up our exponentials:
total = exp(z[0]) + exp(z[1]) + exp(z[2])
With this total variable we can execute the third and final step, which provides proportions for each of our three classes relative to the sum of all of the classes:
exp(z[0])/totaloutputs a ŷ1 value of0.002428, indicating that the network estimates there’s a ~0.2 percent chance that the object presented to it is a hot dog.exp(z[1])/totaloutputs a ŷ2 value of0.01794, indicating an estimated ~1.8 percent chance that it’s a burger.exp(z[2])/totaloutputs a ŷ3 value of0.9796, for an estimated ~98.0 percent chance that the object is pizza.
Given this arithmetic, the etymology of the “softmax” name should now be discernible: The function returns z with the highest value (the max), but it does so softly. That is, instead of indicating that there’s a 100 percent chance the object is pizza and a 0 percent chance it’s either of the other two fast food classes (that would be a hard max function), the network hedges its bets, to an extent, and provides a likelihood that the object is each of the three classes. This leaves us to make the decision about how much confidence we would require to accept a neural network’s guess.7
7. Confidence thresholds may vary based on your particular application, but typically we’d simply accept whichever class has the highest likelihood. This class can, for example, be identified with the argmax() (argument maximum) function in Python, which returns the index position (i.e., the class label) of the largest value.
Revisiting Our Shallow Network
With the knowledge of dense networks that you’ve developed over the course of this chapter, we can return to our Shallow Net in Keras notebook and understand the model summary within it. Example 5.6 shows the three lines of Keras code we use to architect a shallow neural network for classifying MNIST digits. As detailed in Chapter 5, over those three lines of code we instantiate a model object and add layers of artificial neurons to it. By calling the summary() method on the model, we see the model-summarizing table provided in Figure 7.5. The table has three columns:
Layer (type): the name and type of each of our layersOutput Shape: the dimensionality of the layerParam #: the number of parameters (weights w and biases b) associated with the layer

Figure 7.5 A summary of the model object from our Shallow Net in Keras Jupyter notebook
The input layer performs no calculations and never has any of its own parameters, so no information on it is displayed directly. The first row in the table, therefore, corresponds to the first hidden layer of the network. The table indicates that this layer:
Is called
dense_1; this is a default name because we did not designate one explicitlyIs a
Denselayer, as we specified in Example 5.6Is composed of 64 neurons, as we further specified in Example 5.6
Has 50,240 parameters associated with it, broken down into the following:
50,176 weights, corresponding to each of the 64 neurons in this dense layer receiving input from each of the 784 neurons in the input layer (64 × 784)
Plus 64 biases, one for each of the neurons in the layer
Giving us a total of 50,240 parameters: nparameters = nw + nb = 50176 + 64 = 50240
The second row of the table in Figure 7.5 corresponds to the model’s output layer. The table tells us that this layer:
Is called
dense_2Is a
Denselayer, as we specified it to beConsists of 10 neurons—again, as we specified
Has 650 parameters associated with it, as follows:
640 weights, corresponding to each of the 10 neurons receiving input from each of the 64 neurons in the hidden layer (64 × 10)
Plus 10 biases, one for each of the output neurons
From the parameter counts for each layer, we can calculate for ourselves the Total params line displayed in Figure 7.5:
All 50,890 of these parameters are Trainable params because—during the subsequent model.fit() call in the Shallow Net in Keras notebook—they are permitted to be tuned during model training. This is the norm, but as you’ll see in Part III, there are situations when it is fruitful to freeze some of the parameters in a model, rendering them Non-trainable params.
Summary
In this chapter, we detailed how artificial neurons are networked together to approximate an output y given some inputs x. In the remaining chapters of Part II, we detail how a network learns to improve its approximations of y by using training data to tune the parameters of its constituent artificial neurons. Simultaneously, we broaden our coverage of best practices for designing and training artificial neural networks so that you can include additional hidden layers and form a high-caliber deep learning model.
Key Concepts
Here are the essential foundational concepts thus far. New terms from the current chapter are highlighted in purple.
parameters:
weight w
bias b
activation a
artificial neurons:
sigmoid
tanh
ReLU
input layer
hidden layer
output layer
layer types:
dense (fully connected)
softmax
forward propagation
