Chapter 21 Asynchronous Network Computing with Process Failures
In this chapter, we consider what can and what cannot be computed in asynchronous networks in the presence of process stopping failures. Here, we only consider process failures and assume that communication is reliable.
We begin by showing that, for the purpose of obtaining computability results, it does not matter whether we consider send/receive or broadcast systems.
Then we (re-)state the fundamental impossibility result for the problem of distributed agreement in the asynchronous network model. This result says that the agreement problem cannot be solved in asynchronous networks, even if there is guaranteed to be no more than one process failure. In Chapter 12, we discussed this problem and gave an analogous impossibility result for the asynchronous shared memory setting. As we noted at the beginning of Chapter 12, such impossibility results have practical implications for distributed applications in which agreement is required. These include database systems requiring agreement on whether transactions commit or abort, communication systems requiring agreement on message delivery, and process control systems requiring agreement on fault diagnoses. The impossibility results imply that no purely asynchronous algorithm can work correctly.
In the rest of this chapter, we describe some ways around this fundamental difficulty: using randomization, strengthening the model with mechanisms for failure detection, agreeing on a set of values rather than just one, and agreeing approximately rather than exactly.
This chapter rests heavily on previous chapters, especially Chapters 7, 12, and 17. In particular, many results about computability in asynchronous networks follow directly from analogous results about computability in asynchronous read/write shared memory systems, by means of general transformations.
21.1 The Network Model
The model we assume throughout this chapter is an asynchronous broadcast system with reliable broadcast channels and process stopping failures (modelled with stop events). We could equally well have considered send/receive systems with reliable FIFO send/receive channels between all pairs of distinct processes: it turns out that the two models are the same from the point of view of computability. It is not hard to see that the broadcast model is at least as powerful as the send/receive model. The following theorem shows that it is not more powerful.
Theorem 21.1 If A is any asynchronous broadcast system with a reliable broadcast channel, then there is an asynchronous send/receive system B with reliable FIFO send/receive channels that has the same user interface as A and that “simulates” A, as follows. For every execution α of B, there is an execution α′ of A such that the following conditions hold:
- α and α′ are indistinguishable to U (the composition of the users Ui).
- For each i, a stopi occurs in a exactly if it does in α′.
Moreouer, if α is fair, then α′ is also fair.
Proof Sketch. System B has one process Qi for each process Pi of A. Each Qi is responsible for simulating Pi, plus participating in the simulation of the broadcast channel.
Qi simulates a bcast(m)i output of Pi by performing send(m, t)i,j outputs for all j ≠ i, where t is a local integer-valued tag, and then performing an internal step simulating receive(m)i,i. The tag values used by Qi start with 1 and are incremented with each successive bcast. If Qi receives a message (m, t) sent by Qj, it helps in the simulation of Pj’s broadcast by relaying the message—specifically, it sends (m, t, j) to all processes other than i and j. If Qi receives (m, t, j) from k, it continues helping by sending (m, t, j) to all processes other than i, j, and k to which Qi has not already sent (m, t, j).
Meanwhile, Qi collects tagged messages (m, i) originally broadcast by each Pj, j ≠ i; these are either received directly from Qj or via relays. At certain times, Qi is allowed to perform an internal step simulating a receive(m)j,i event of the A system. Specifically, Qi can do this when Qi has a message (m, t) originally broadcast by Pj, Qi has already relayed (m, t, j) to all processes other than i and j, and Qi has already simulated receivej,i events for messages from Pj with all tag values strictly less than t.
Some key facts for the proof are as follows. First, note that no process Qi simulates a receive(m)j,i event for any j until after it has succeeded in sending the corresponding (m, t) to all the other processes, and thus after it has been guaranteed that all processes will eventually receive (m, t) from j. Second, note that although a process Qi can receive messages originally broadcast by Pj out of the order in which they were broadcast by Pj, the tags allow Qi to sort these messages into the proper order. Third, note that if a message with tag t is sent by any process Qi, then it must be that messages originating at Pi with all smaller tag values have previously been sent to all processes.
Theorem 21.1 implies that it does not matter, from the point of view of computability, whether we consider broadcast systems or send/receive systems. Of course, the complexity is different—the total number of receive events might be multiplied by approximately n in the simulation described above—but we will not worry much about complexity in this chapter. We choose to consider broadcast systems because they make the impossibility results appear slightly stronger and because they make the algorithms easier to write.
21.2 Impossibility of Agreement in the Presence of Faults
We use the definition of the agreement problem in Section 12.1. Although it was formulated there for shared memory systems, it also makes sense for asynchronous (broadcast or send/receive) network systems. We review it here.
The user interface of the system A consists of init(v)i input actions and decide(v)i output actions, where v ∈ V and 1 ≤ i ≤ n; A also has stopi input actions. All the actions with subscript i are said to occur on port i. Each user Ui has outputs init(v)i and inputs decide(v)i, v ∈ V. U is assumed to perform at most one initi action in any execution.
A sequence of initi and decidei actions is well-formed for i provided that it is some prefix of a sequence of the form initi(v), decidei(w). We consider the following conditions on the combined system consisting of A and the users Ui:
Well-formedness: In any execution, and for any i, the interactions between Ui and A are well-formed for i.
Agreement: In any execution, all decision values are identical.
Validity: In any execution, if all init actions that occur contain the same value v, then v is the only possible decision value.
Failure-free termination: In any fair failure-free execution in which init events occur on all ports, a decide event occurs on each port.
We say that an asynchronous network system solves the agreement problem if it guarantees well-formedness, agreement, validity, and failure-free termination (for all collections of users). We also consider
f-failure termination, 0 ≤ f ≤ n: In any fair execution in which init events occur on all ports, if there are stop events on at most f ports, then a decide event occurs on every non-failing port.
Wait-free termination is defined to be the special case of f-failure termination where f = n.
Of course, it is easy to solve the agreement problem in the asynchronous broadcast model if there are no fault-tolerance requirements. For example, each process could simply broadcast its initial value and apply some appropriate agreed-upon function to the vector of initial values it receives. Since all processes are guaranteed to receive the same vector of values, all will obtain the same result.
The main impossibility result for broadcast systems (repeated from Section 17.2.3) is
Theorem 21.2 There is no algorithm in the asynchronous broadcast model with a reliable broadcast channel that solves the agreement problem and guarantees 1-failure termination.
The proof given in Section 17.2.3 is based on a transformation from asynchronous broadcast systems to asynchronous shared memory systems (Theorem 17.8) and an impossibility result for the agreement problem in the asynchronous shared memory model (Theorem 12.8). It is also possible to prove the impossibility result directly, using a proof similar to that of Theorem 12.8. We leave this alternative proof for an exercise.
21.3 A Randomized Algorithm
Theorem 21.2 says that the agreement problem cannot be solved in an asynchronous network system, even for only a single stopping failure. However, the problem is so fundamental to distributed computing that it is important to find ways around this inherent limitation. In order to obtain an algorithm, we must be willing either to weaken the correctness requirements, strengthen the model, or both.
In this section, we do both. We show that the agreement problem can be solved in a randomized asynchronous network. This model is stronger than the ordinary asynchronous network model, because it allows the processes to make random choices during the computation. On the other hand, the correctness conditions are slightly weaker than before: although well-formedness, agreement, and validity are still guaranteed, the termination condition is now probabilistic. Namely, all the nonfaulty processes will decide by time t after the arrival of all inputs, with probability at least p(t), where p is a particular monotone nonde-creasing, unbounded function. This implies eventual termination with probability 1.
In the subsequent sections, we consider other ways around the inherent limitation expressed by Theorem 21.2, including the use of failure detectors, allowing more than one decision value, and allowing approximate instead of exact agreement.
The algorithm, by Ben-Or, works for n > 3f and V = {0,1}. Formally, it is an instance of the probabilistic model described in Section 8.8.
BenOr algorithm:
Each process Piihas local variables x and y, initially null. An init(v)i input causes process Pi to set x := v. Pi executes a series of stages numbered 1,2,…, each stage consisting of two rounds. Pi begins stage 1 after it receives its initial value in an initi input. It continues performing the algorithm forever, even after it decides.
At each stage s ≥ 1, Pi does the following:
Round 1: Pi broadcasts ("first", s, v), where v is its current value of x, then waits to obtain n – f messages of the form ("first", s,*). If all of these have the same value v, then Pi sets y := v; otherwise it sets y := null.
Round 2: Pi broadcasts ("second", s,v), where v is its current value of y, then waits to obtain n – f messages of the form ( "second", s, *). There are three cases: First, if all of these have the same value v ≠ null, then Pi sets x := v and performs a decide(v)i if it has not already done so. Second, if at least n – 2f of these messages, but not all of the messages, have the same value v ≠ null, then Pi sets x := v (but does not decide). (The assumption that n > 3f implies that there cannot be two different such values v.) Otherwise, Pi sets x to either 0 or 1, choosing randomly with equal probability.
Notice the similarity between the organization of the BenOr algorithm and that of the TurpinCoan algorithm in Section 6.3.3.
Lemma 21.3 The BenOr algorithm guarantees well-formedness, agreement, and validity.
Proof. Well-formedness is straightforward. For validity, suppose that all init events that occur in an execution contain the same value v. Then it is easy to see that any process that completes stage 1 must decide on v in that stage. This is because the only value sent or received by any process in a ("first", 1, *) message is v, so the only value sent in a ("second", 1, *) message is v.
For agreement, suppose that process Pi decides v at stage s and no process decides at any smaller-numbered stage. Then it must be that Pi receives n – f ("second", s, v) messages. This implies that any other process Pj that completes stage s receives at least n – 2i ("second", s, v) messages, since it hears from all but at most f of the processes that Pi hears from. This means that Pj cannot decide on a value different from v at stage s; moreover, Pj sets x := v at stage s. Since this is true for all Pj that complete stage s, it follows (as in the argument for validity) that any process that completes stage s + 1 must decide v at stage s + 1.
Now we consider termination. First, it is not hard to see that the algorithm continues to progress through successive stages; this fact does not depend on the probabilities.
Lemma 21.4 In every fair execution of the BenOr algorithm in which init events occur on all ports, each nonfaulty process completes infinitely many stages. Moreover, if ℓ is an upper bound on the time for each process task, and d is an upper bound on the delivery time for the oldest message in transit from each Pi to each Pj, then each nonfaulty process completes each stage s by O(s(d + ℓ)) time after the last init event.
However, Lemma 21.4 does not imply that each nonfaulty process eventually decides. It turns out that this property is not guaranteed by the BenOr algorithm, but only holds probabilisticallyi
Example 21.3.1 An execution with no decisions
We describe a fair execution of the BenOr algorithm for n = 3f + 1 in which no process ever decides. Every stage s proceeds in the same way, as follows.
Some number m of the processes, f + 1 ≤ m ≤ 2f, start with x = 0, and the rest start with xi= 1. After round 1, all processes have y = null, and at round 2, all processes choose their new values of x randomly. Then some number m′ of the random choices, f + 1 ≤ m′ ≤ 2f, turn out to be 0 and the rest 1, leading to a situation where m′ of the processes begin stage s + 1 with x = 0 and the rest with x = 1.
As in Section 11.4, we imagine that all the nondeterministic choices in the algorithm—here, which action occurs next and when, and what is the resulting state—are under the control of an adversary. We constrain the adversary to enforce the fairness conditions of all the process I/O automata and the broadcast channel automaton. We also constrain it to observe the usual time restrictions: an upper bound ℓ on time for tasks within processes and an upper bound of d on the delivery time for the oldest message in transit from each Pi to each Pj. Finally, we require that the adversary allow init events on all ports. We assume that the adversary has complete knowledge of the past execution. Any such adversary determines a probability distribution on the executions of the algorithm.
Lemma 21.5 For any adversary and any s ≥ 0, with probability at least ![]() , all nonfaulty processes decide within s + 1 stages.
, all nonfaulty processes decide within s + 1 stages.
Proof Sketch. The case s = 0 is trivial. Consider any stage s 7ge; 1. We argue that with probability at least![]() , all nonfaulty processes choose the same value of x at the end of stage s (no matter how the random choices are resolved for other stages). In this case, by the argument for agreement, all nonfaulty processes decide by the end of stage s + 1.
, all nonfaulty processes choose the same value of x at the end of stage s (no matter how the random choices are resolved for other stages). In this case, by the argument for agreement, all nonfaulty processes decide by the end of stage s + 1.
For this stage s, consider any shortest finite execution α in which some non-faulty process, say Pi, has received n – f ("first", s, *) messages. (Thus, α ends with the delivery of one of these messages.) If at least f + 1 of these messages contain a particular value v, then define v to be a good value after a; there can be either one or two good values. We claim that if there is only one good value v after α, then every ("second", s, *) message that is sent in any extension of α must contain either value v or value null. This is because if Pi receives f + 1 copies of v, then every other process receives at least one copy of v and so cannot send a ("second", s, ![]() ) message. (Here we use the notation
) message. (Here we use the notation ![]() to denote the value 1 — v.) Similarly, if there are two good values after α, then every ("second", s,*) message that is sent in any extension of α must contain null.
to denote the value 1 — v.) Similarly, if there are two good values after α, then every ("second", s,*) message that is sent in any extension of α must contain null.
It follows that if there is only one good value v, then v is the only value that can be "forced" to be any process’s value of x at the end of stage s by a nonrandom assignment, in any extension of α. Similarly, if there are two good values, then no value can be forced in this way. Since no process makes a random choice for stage s in α, the determination of values that can be forced at stage s is made before any random choices for stage s.
Thus, if there is exactly one good value, then with probability at least ![]() , all processes that choose their values of x randomly will choose the good value, thus agreeing with those that choose nonrandomly. Similarly, if there are two good values, then with probability at least
, all processes that choose their values of x randomly will choose the good value, thus agreeing with those that choose nonrandomly. Similarly, if there are two good values, then with probability at least ![]() , all processes will (randomly) choose the same value of x. In either case, with probability at least
, all processes will (randomly) choose the same value of x. In either case, with probability at least ![]() , all nonfaulty processes end up with the same value of x at the end of stage s.
, all nonfaulty processes end up with the same value of x at the end of stage s.
Now, the argument for each stage s only depends on the random choices at stage s, and these are independent of the choices at other stages. So we can combine the probabilities for different stages, to see that with probability at least 1 – (1 – ![]() )s, all nonfaulty processes obtain the same value of x at the end of some stage s′, 1 ≤ s′ ≤ s. Therefore, with probability at least 1 – (1 –
)s, all nonfaulty processes obtain the same value of x at the end of some stage s′, 1 ≤ s′ ≤ s. Therefore, with probability at least 1 – (1 – ![]() )s, all nonfaulty processes decide within s + 1 stages.
)s, all nonfaulty processes decide within s + 1 stages.
Now define a function T from ![]() to
to ![]() such that each nonfaulty process completes each stage s by T(s) time after the last init event. By Lemma 21.4, we can choose T(s) to be O(s(d + ℓ)). Also, define p(t) to be 0 if t < T(1) and
such that each nonfaulty process completes each stage s by T(s) time after the last init event. By Lemma 21.4, we can choose T(s) to be O(s(d + ℓ)). Also, define p(t) to be 0 if t < T(1) and ![]() if s 7ge; 1 and T(s) ≤ t < T(s + 1). Lemmas 21.5 and 21.4 then imply
if s 7ge; 1 and T(s) ≤ t < T(s + 1). Lemmas 21.5 and 21.4 then imply
Lemma 21.6 For any adversary and any t ≥ 0, with probability p(t), all non-faulty processes decide within time t after the last init event.
The main correctness result is
Theorem 21.7 The BenOr algorithm guarantees well-formedness, agreement, and validity. It also guarantees that, with probability 1, all nonfaulty processes eventually decide.
Proof. By Lemmas 21.3, 21.6, and 21.4. (Lemma 21.4 is needed to show that p(t) is unbounded.)
Randomized versus nonrandomized protocols. One reason the BenOr algorithm is significant is that it demonstrates an inherent difference between the randomized and nonrandomized asynchronous network models. Namely, the agreement problem cannot be solved at all in the presence of process failures in the nonrandomized model, but can be solved easily (with probability 1) in the randomized model. A similar contrast is shown by the LehmannRabin algorithm in Section 11.4.
Reducing the complexity. The BenOr algorithm is not practical, because its probabilistic time bound is high. It is possible to improve the time complexity by increasing the probability that different processes’ random values at the same stage are the same. However, this requires the use of cryptographic techniques, which are outside the model given here.
21.4 Failure Detectors
Another way to solve the agreement problem in fault-prone asynchronous networks is to strengthen the model by adding a new type of system component known as a failure detector. A failure detector is a module that provides information to the processes in an asynchronous network about previous process failures. There are different sorts of failure detectors, based on whether the information about stopping is always correct and on whether it is complete. The simplest one is a perfect failure detector, which is guaranteed to report only failures that have actually happened and to eventually report all such failures to all other non-failed processes.
Formally, we consider a system A that has the same structure as an asynchronous network system, except that it has additional input actions inform-stopped(j)i for each pair i and j of ports, i ≠ j. A perfect failure detector for system A is a single I/O automaton that has the actions stopi, 1 ≤ i ≤ n, as inputs, and the actions inform-stopped(j)i, 1 ≤ i, j &13; n, i ≠ j, as outputs. The idea is that the failure detector learns about stopping failures that occur anywhere in the network and informs the other processes about them. An inform-stopped(j)i action is intended as an announcement at port i that process j has stopped. Figure 21.1 shows the architecture for a simple three-process system. The following algorithm solves the agreement problem when used with a perfect failure detector:
PerfectFDAgreement algorithm (informal):
Each process Pi attempts to stabilize two pieces of data:
- A vector val, indexed by {1,…, n}, with values in V ∪ {null}. If val(j) = v 7isin; V, it means that Pi has learned that Pj’s initial value is v.
- A set stopped of process indices. If j ∈ stopped, it means that Pi has learned that Pj has stopped.
Process Pi continually broadcasts its current val and stopped data and updates it upon receipt of new data from processes not in stopped. It ignores messages from processes it has already placed in stopped. Pi also keeps track of processes that "ratify" its data, that is, from which it receives the same (vol, stopped) data that it already has. When Pi reaches a point where its data has "stabilized," that is, when it has received ratifications for its current data from all non-stopped processes, then Pi decides on the non-null value corresponding to the smallest index in its val vector.
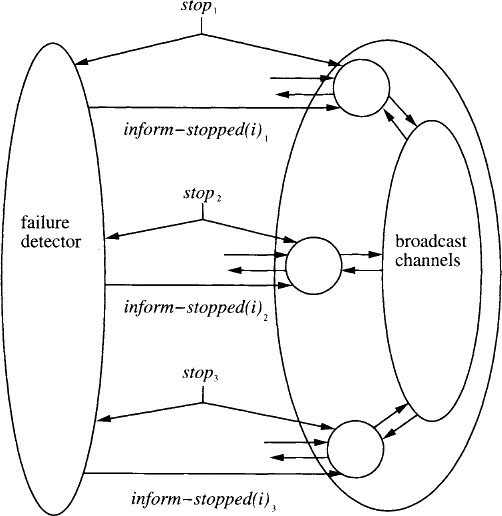
Figure 21.1: Architecture for asynchronous broadcast system witha perfact failure detector.
The code follows. Let W denote the set of vectors indexed by {1,…, n}, of elements of V ∩ {null}. We define a partial ordering on pairs (w, I), where w ∈ W and I ⊆ {1,…, n}. Namely, we write (w, I) ≤d (w′,I′) and say that (w′, I′) dominates (w, I), provided that both of the following hold:
This captures the idea that (w′,I′) contains at least all the information that (w, I) does.
To avoid confusion, we do not explicitly describe the behavior of Pi after a stopi event occurs. It is just as usual—the process stops.

Theorem 21.8 PerfectFDAgreement, when used with any perfect failure detector, solves the agreement problem and guarantees wait-free termination.
Proof. Well-formedness and validity are easy to see. For wait-free termination, consider a fair execution α in which init events occur on all ports and let i be any non-failing port; we show that Pi eventually decides in α. Note that every time Pi’s data (vali, stoppedj) changes in α, it must be that the new pair dominates the old pair. Since there are only finitely many possible pairs, eventually this data reaches final values (wfinal, Ifinal). If Pi decides before this point, then we are done, so suppose that it does not. Then we claim that eventually thereafter, ratifiedi ∪ stoppedi = {1,…, n}, which is enough to imply that a decidei event occurs. To prove this claim, it is enough to show that every process j ≠ i that never fails eventually ratifies this pair (wfinal, Ifinal).
So consider any j ≠i that never fails. Eventually, a message containing (wfinal, Ifinal) is broadcast by Pi and received by Pj, after which Pj’s pair always dominates (wfinal Ifinal). But Pj’s pair can never strictly dominate (w final,Ifinal), since if it did, Pj would eventually succeed in communicating this new information to Pj. So, eventually, Pj’s pair becomes and remains equal to (wfinal, Ifinal). Then, eventually, a message containing (wfinal,Ifinal) is broadcast by Pj and received by Pj. This places j in ratifiedi, as needed.
Finally we argue agreement. Suppose that Pi is the first process that decides and let w and I be the values of vali and stoppedi, respectively, when the decidei event, π, occurs. Then all processes in I fail in α prior to π and so can never decide. Let J = {1,…, n} – I; we argue that all processes in J that decide must decide on the same value as Pi.
Each process j in J must be in ratifiedi when π occurs, so must have (w, I) as its local data at some point tj before π. We claim that each process j in J must keep vol = w forever after point tj in α, which implies that if it decides, it agrees with Pi.
So suppose that this is not the case and let j be the first process in J to acquire a val vector containing information that is not in w (i.e., some element of the vector is in V, whereas the corresponding element of w is null). Then this acquisition must occur as a result of a receivek, j event occurring after point tj, where the broadcasting process Pk has, at the time of the broadcast, a val vector containing information not in w. Since Pj ignores all processes in I after point tj, it must be that the broadcasting process Pk is in J. But this contradicts the choice of j as the first process in J to acquire information not in w.
Complexity. The communication complexity and time complexity of the Perfect-FDAgreement algorithm are unbounded. This is not so terrible, because we are only addressing computability issues in this chapter. However, it is possible to devise similar protocols with bounded complexity. We leave this for an exercise.
21.5 k-Agreement
Now we consider weakening the problem statement. The k-agreement problem, as described in Sections 7.1 and 12.5 for the synchronous network setting and asynchronous shared memory setting, respectively, is a variation on the agreement problem that can be solved in asynchronous networks with a limited number (f < k) of faults. We use the same problem definition as in Section 12.5: that is, this problem has the same well-formedness and termination conditions as the ordinary agreement problem, and the agreement and validity conditions are replaced by the following, where k is any integer, k ≥ 1.
Agreement: In any execution, there is a subset W of V, |W| = k, such that all decision values are in W.
Validity: In any execution, any decision value for any process is the initial value of some process.
The agreement condition is weaker than that for ordinary agreement in that it permits k decision values rather than just 1. The validity condition is a slight strengthening of the validity condition for ordinary agreement. There is a trivial algorithm to solve the k-set agreement problem in an asynchronous broadcast network, where f < k:
TrivialKAgreement algorithm:
Processes P1, P2,… Pk (only) broadcast their initial values. Every process Pi decides on the first value it receives.
Theorem 21.9 TrivialK Agreement solves the k-agreement problem and guarantees f-failure termination, if f < k.
It is also not hard to devise a fc-agreement algorithm that is similar to Perfect-FDAgreement, based on stable vectors. We leave this for an exercise. Alternatively, we can obtain fe-agreement algorithms for the asynchronous network model from algorithms for the asynchronous shared memory model, using Theorem 17.5 to translate from the shared memory model to the network model; however, this approach has the disadvantage that it only works if n > 2f, whereas Trivial-KAgreement and the algorithm based on stable vectors also work if n < 2f.
It turns out that the k-agreement problem cannot be solved if the number of failures is ≥ k.
Theorem 21.10 The k-agreement problem is not solvable with k-failure termination in the asynchronous broadcast model.
Proof. By Theorems 12.13 and 17.8.
21.6 Approximate Agreement
Again we weaken the problem statement. Another variation on the agreement problem is the approximate agreement problem, as described in Sections 7.2 and 12.5 for the synchronous network setting and the asynchronous shared memory setting, respectively. We use the same problem definition as in Section 12.5. That is, the set V of values is the set of real numbers, and processes are permitted to send real-valued data in messages. Instead of having to agree exactly, as in the agreement problem, the requirement is that they agree to within a small positive tolerance e. The problem has the same well-formedness and termination conditions as the ordinary agreement problem, and the agreement and validity conditions are replaced by the following.
Agreement: In any execution, any two decision values are within e of each other.
Validity: In any execution, any decision value is within the range of the initial values.
An algorithm similar to the ConvergeApproxAgreement algorithm of Section 7.2 works for the asynchronous setting with stopping failures, provided that n > 3f. Each process Pi executes a series of stages, at each of which it waits to hear from any n – f processes rather than from all n processes. (It cannot wait to hear from all processes, because up to f processes might stop.) Because we are now considering stopping failures only, it is not necessary for Pi to "reduce" its multiset of values by discarding the extreme values. The mean and select functions used in the following description, as well as some notions like the width of a multiset of reals, are defined in Section 7.2.
A synch Approx Agreement algorithm:
We assume that n > 3f. Each Pi maintains a variable val containing its latest estimate. This gets initialized to the value v that arrives in an init(v)i input. At each stage, Pi does the following: First, it broadcasts its val value, tagged with the stage number s. Then it collects the first n – f values it receives for stage s into a multiset W. Finally, it sets val to mean(s elect (W)).
It should be obvious that the val chosen by any process at any stage s is in the range of the vals chosen by all the processes at stage s – 1 (or the initial val values, if s = 1). We claim that, at each stage, the width of the multiset of vals is reduced by a factor of at least ![]() . Since n > 3f, this yields convergence.
. Since n > 3f, this yields convergence.
Lemma 21.11 Let v and v′ be the values of vali and vali chosen by two processes Pi and Pi, at stage s of an execution of AsynchApproxAgreement. Then

where d is the width of the range of the val values chosen at stage s – 1, if s ≥ 2, and d is the width of the initial values, if s = 1.
Proof. Analogous to that of Lemma 7.17.
Termination. So far everything we have said about AsynchApproxAgreement works if we just assume that n > 2f (rather than n > 3f). But we do not yet have a complete algorithm, because we have not said when processes actually decide. We use the extra processes to help in achieving termination.
We cannot use the simple termination strategy that we used for Converge-ApproxAgreement, because a process cannot wait to hear from all processes at stage 1 and thus cannot always determine an upper bound on the range of the multiset of initial values. However, we can modify this strategy slightly by adding a special initialization stage, stage 0, to the beginning of the algorithm. In stage 0, each process Pi broadcasts its val, collects a multiset of n – f vals, and chooses the median of the multiset as its new val for use in stage 1. Since n > 3f, it is easy to check that any val chosen by any process Pi at stage 0 is in the range of the multiset collected by any process Pj at stage 0. Thus, each Pi can use the range of the multiset it collects at stage 0 to compute a stage number by which it is sure that the val values of any two processes at stage s are at most e apart. The rest of this strategy is as for ConvergeApproxAgreement.
The AsynchApproxAgreement algorithm is not optimal, in the sense that the problem can actually be solved for any n > 2f. However, a more complicated algorithm is needed. For example, an algorithm that works for n > 2f can be obtained from a shared memory approximate agreement algorithm A, based on single-writer/multi-reader shared registers, that guarantees wait-free termination. Theorem 12.14 asserts that such an algorithm A exists (and you can find one in [24]). Then Theorem 17.5 can be used to infer the existence of an asynchronous network algorithm that solves the approximate agreement problem and guarantees f-failure termination, for n > 2f.1 On the other hand, it is not hard to see that the approximate agreement problem cannot be solved if n ≤ 2f.
Theorem 21.12 The approximate agreement problem is not solvable with f-failure termination in the asynchronous broadcast model if n > 2/.
Proof Sketch. The proof is similar to that of Theorem 17.6. Briefly, we suppose that such an algorithm exists and let G1 be the set 1,…,n – f and G2 be the set n – f + 1,…, n. We consider a fair execution α1 in which all processes begin with value v1 and all processes with indices in G2 fail right at the start. By f-failure termination, all processes in G1 must eventually decide, and the validity condition implies that they must decide v1. Symmetrically, we consider a second fair execution α2 in which all processes begin with v2, where ![]() , and all processes with indices in G1 fail at the start. In α2, all processes in G2 must eventually decide v2.
, and all processes with indices in G1 fail at the start. In α2, all processes in G2 must eventually decide v2.
We then construct a finite execution α as in the proof of Theorem 17.6, by combining α1 and α2. In α, the processes in G1 decide v1 and those in G2 decide v2, which contradicts the agreement condition.
21.7 Computability in Asynchronous Networks*
The same construction that is used in the proofs of Theorems 17.6 and 21.12 can be used to show that many other problems of global coordination cannot be solved in asynchronous networks if half of the processes might fail.
As we did in Section 12.5, we can consider the solvability of arbitrary decision problems in asynchronous networks. Ordinary agreement, k-agreement, and approximate agreement problems are all examples of decision problems, and we have already given the main results about the computability of these problems in asynchronous networks. As for the read/write shared memory model, we state a theorem that gives some conditions that imply that a problem cannot be solved with 1-failure termination in the asynchronous network model.
Theorem 21.13 Let D be a decision mapping whose decision problem is solvable with 1-failure termination in the asynchronous broadcast model. Then there must be a decision mapping D′ with D′(w) ⊆ D(w) for all w, such that both of the following hold:
- If input vectors w and w′ differ in exactly one position, then there exist y ∈ D′(w) and y′ ∈ D∈(w′) such that y and y’ differ in at most one position.
- For each w, the graph defined by D’(w) is connected.
Proof. By Theorems 12.15 and 17.8.
In general, impossibility results for computabiliy in the read/write shared memory setting carry over to the network setting using Theorem 17.8. Algorithms carry over also, using Theorem 17.5, but only under the restrictions needed for Theorem 17.5, including the requirement that n > 2f.
21.8 Bibliographic Notes
Theorem 21.2, the impossibility of agreement in the presence of stopping failures, was first proved by Fischer, Lynch, and Paterson [123]. Their original proof was given directly in terms of the asynchronous broadcast model rather than via a transformation. Loui and Abu-Amara [199] observed that Theorem 21.2 could be extended to the read/write shared memory model, using essentially the same proof. Our proof of Theorem 12.8 follows the presentation of Loui and Abu-Amara. The original proof by Fischer, Lynch, and Paterson, reorganized somewhat according to suggestions by Bridgland and Watro [58] is outlined in Exercises 21.2, 21.3, and 21.4.
The BenOr algorithm was invented by Ben-Or [46]. Later work by Rabin [248] and by Feldman [114] produced other randomized algorithms with much better (in fact, constant) time complexity. These use "secret sharing" techniques to increase the probability that the random values chosen by different processes at the same stage are the same.
The notion of a failure detector was defined and developed by Chandra and Toueg [66] and by Chandra, Hadzilacos, and Toueg [65]. Those papers describe not only the perfect failure detector discussed here but also many less perfect variations, including failure detectors that falsely identify processes as faulty and failure detectors that fail to notify all processes about failures. Such weaker failure detectors can also be used to solve the agreement problem, and some can be implemented in practical distributed systems using timeouts. Failure detectors are also discussed by Hadzilacos and Toueg [143].
We have already discussed the origins of the k-agreement problem and the approximate agreement problem in the Bibliographic Notes for Chapters 7 and 12. Attiya, Bar-Noy, Dolev, Roller, Peleg, and Reischuk [19, 20, 40] describe some other interesting problems that are solvable in asynchronous networks with failures, including a problem of process renaming and a problem of slotted exclusion. Bridgland and Watro [58] describe a resource-allocation problem that is solvable in asynchronous networks with failures. The idea of a stable vector algorithm is due to Attiya et al. [20].
The proof of Theorem 21.12 is adapted from proofs by Bracha and Toueg [56] and Attiya, Bar-Noy, Dolev, Peleg, and Reischuk [20]. Biran, Moran, and Zaks [51] characterized the decision problems that can be solved in an asynchronous network with 1-failure termination, based on an earlier impossibility result by Moran and Wolfstahl [230]. Theorem 21.13 is adapted from these two papers.
21.9 Exercises
21.1. Prove Theorem 21.1.
21.2. Suppose V = {0, 1}. If A is an asynchronous broadcast system that solves the agreement problem, then define 0-valence, 1-valence, univalence and bivalence for finite executions of A, and also define initializations of A, in the same way as in Section 12.2.2.
(a) Give an example of such a system A in which there is a bivalent initialization.
(b) Given an example of such a system A in which all initializations are univalent.
(c) Prove that if A guarantees 1-failure termination, then there is a bivalent initialization.
21.3. Let V, A be as in Exercise 21.2. Define a decider execution α to be a finite failure-free input-first execution satisfying the following conditions, for some i:
(a) α is bivalent.
(b) There exists a 0-valent failure-free extension α0 of α such that the portion of α0 after α consists of steps of process i only.
(c) There exists a 1-valent failure-free extension α1 of α such that the portion of α1 after α consists of steps of process i only.
That is, a single process i can operate on its own in two different ways (e.g., interleaving locally controlled and message-receiving steps in two different ways, or else receiving two different sequences of messages), in such a way as to resolve the final decision in two different ways.
Prove that if A has a bivalent initialization, then A has a decider. Note that we have assumed only that A solves the agreement problem; we have made no fault-tolerance assumptions. (Hint: Consider the proof of Lemma 12.7.)
21.4. Use the results of Exercises 21.2 and 21.3 to prove Theorem 21.2.
21.5. Reconsider the agreement problem of this chapter, using the broadcast model. This time consider a more constrained fault model than general stopping failures, in which processes can only fail at the beginning of computation. (That is, all stop events precede all other events.) Can the agreement problem be solved in this model, guaranteeing
(a) 1-failure termination?
(b) f-failure termination, where n < 2f?
(c) wait-free termination?
In each case, give either an algorithm or an impossibility proof.
21.6. Design a variant of the BenOr algorithm in which all nonfaulty processes eventually halt.
21.7. Design variants of the BenOr randomized agreement algorithm that work for the following cases:
(a) The synchronous network model with stopping failures.
(b) The synchronous network model with Byzantine failures.
(c) The asynchronous network model with Byzantine failures. (As mentioned in Section 14.1.1, a Byzantine failure of a process Pi is modelled by allowing Pi to be replaced by an arbitrary I/O automaton with the same external interface.)
In each case, try to design the algorithm to work for as few processes as possible, relative to the number f of tolerated failures.
21.8. Design a randomized asynchronous algorithm for agreement with stopping failures, using an arbitrary value set V rather than just {0, 1}. Try to minimize the number of processes. (Hint: Combine the ideas of the TurpinCoan algorithm with those of the BenOr algorithm.)
21.9. Repeat Exercise 21.8 for the case of Byzantine failures.
21.10. Devise an alternative protocol to PerfectFD Agreement that also uses a perfect failure detector to achieve wait-free agreement but that has "small" communication and time complexity. Try to obtain the smallest communication and time complexity that you can.
21.11. Define an imperfect failure detector as follows. It has the same external interface as a perfect failure detector, with the addition of an inform-not-stopped(j)i action for each j and i, j ≠ i. This is used to correct a previous inform-stopped(j)i action, that is, to notify process Pi that Pj has in fact not stopped, in spite of a previous erroneous notification. An imperfect failure detector can alternate inform-stopped(j)i and inform-not-stopped(j)i events any number of times. However, in any fair execution a of the failure detector, there can be only finitely many such events for any i and j, and the final such event must contain the correct information—saying whether or not stopj occurs in α.
Suppose that n > 2f. Devise an algorithm that solves the agreement problem guaranteeing f-failure termination, using any imperfect failure detector.
21.12. Prove that there is no algorithm to solve the agreement problem guaranteeing f-failure termination, using an arbitrary imperfect failure detector as defined in Exercise 21.11, in case n ≤ 2f.
21.13. Give precondition-effect code for a "stable vector" algorithm similar to PerfectFDAgreement, to solve the k-agreement problem. Prove that it works correctly, if f < k. (Hint: The state only contains the components val, ratified, and decided but not the stopped component. A decision can be made when |ratified| ≥ n – f.)
21.14. Define a finite execution a of a k-agreement algorithm to be m-valent if there are exactly m distinct decision values that appear in extensions of α, and define an initialization as in Section 12.2.2. Prove (without using Theorem 21.10) that any k-agreement algorithm in the asynchronous broadcast model that guarantees k-failure termination must have a k + 1-valent initial execution. (Hint: Use ideas from Section 7.1, including Sperner’s Lemma.)
21.15. Give complete precondition-effect code for the AsynchApproxAgreement algorithm, including the termination protocol. Prove correctness.
21.16. Modify the AsynchApproxAgreement algorithm and its proof to work for the case of Byzantine failures. How many processes are needed? (Hint: Use ideas from the ConvergeApproxAgreement algorithm for the synchronous Byzantine setting.)
21.17. Prove the most general impossibility result you can, using the construction in the proof of Theorem 21.12.
21.18. Give a general characterization of the decision problems (as defined in Section 12.5) that can be solved in asynchronous networks with 1-failure termination. (Warning: This is very hard.)
1In order to apply Theorem 17.5, we need for A to satisfy the "turn" restriction given in Section 17.1.1. The shared memory approximate agreement algorithm can be constructed so as to satisfy this condition.
