In this chapter we present two implementations used to build computationally efficient, linear phase, finite impulse response (FIR) filters. We discuss these special FIR filters now because their behavior will be easier to understand using the z-transform concepts introduced in the last chapter.
The first filter type presented is called frequency sampling filters. They are in that special class of linear phase finite impulse response (FIR) filters built with recursive structures (using feedback). The Section 7.1 material is a bit advanced for DSP beginners, but it deserves study for two reasons. First, these filters can be very efficient (minimized computational workload) for narrowband lowpass filtering applications; and second, understanding their operation and design reinforces much of the DSP theory covered in previous chapters.
Section 7.2 discusses interpolated lowpass FIR filters. These filters, implemented with nonrecursive structures (no feedback), cascade multiple FIR filters to reduce computational workload. Their implementation is an innovative approach where more than one unit time delay separates the multipliers in a traditional tapped delay line structure.
The common thread among these two filter types is they're lean mean filtering machines. They wring every last drop of computational efficiency from a guaranteed stable, linear phase filter. In many lowpass filtering applications these FIR filter types can attain greatly reduced computational workloads compared to the traditional Parks-McClellan–designed FIR filters discussed in Chapter 5.
This section describes a class of digital filters, called frequency sampling filters, used to implement linear-phase FIR filter designs. Although frequency sampling filters were developed over 35 years ago, the advent of the powerful Parks-McClellan nonrecursive FIR filter design method has driven them to near obscurity. In the 1970s, frequency sampling filter implementations lost favor to the point where their coverage in today's DSP classrooms and textbooks ranges from very brief to nonexistent. However, we'll show how frequency sampling filters remain more computationally efficient than Parks-McClellan–designed filters for certain applications where the desired passband width is less than roughly one fifth the sample rate. The purpose of this material is to introduce the DSP practitioner to the structure, performance, and design of frequency sampling filters; and to present a detailed comparison between a proposed high-performance frequency sampling filter implementation and its nonrecursive FIR filter equivalent. In addition, we'll clarify and expand the literature of frequency sampling filters concerning the practical issues of phase linearity, filter stability, gain normalization, and computational workload using design examples.
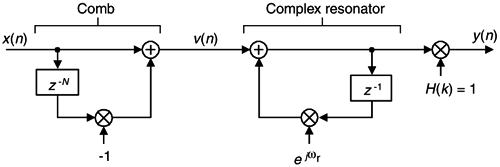
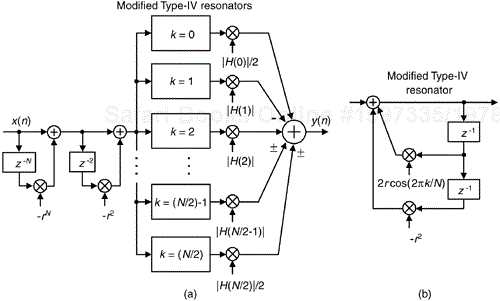
Frequency sampling filters were founded upon the fact that the traditional N-tap nonrecursive (direct convolution) FIR filter in Figure 7-1(a) can be implemented as a comb filter in cascade with a bank of N complex resonators as shown in Figure 7-1(b). We call the filter in Figure 7-1(b) a general frequency sampling filter (FSF), and its equivalence to the nonrecursive FIR filter has been verified[1–3]. While the h(k) coefficients, where 0 < k < N–1, of N-tap nonrecursive FIR filters are typically real-valued, in general they can be complex. That's the initial assumption made in equating the two filters in Figure 7-1. The H(k) gain factors, the discrete Fourier transform of the h(k) time-domain coefficients, are in the general case complex values represented by |H(k)|ejø(k).
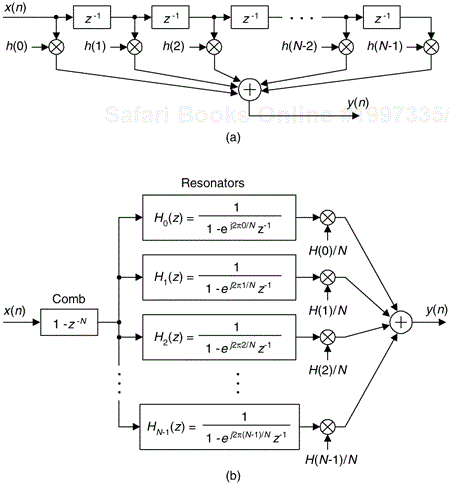
Figure 7-1. FIR filters: (a) N-tap nonrecursive; (b) equivalent N-section frequency sampling filter.
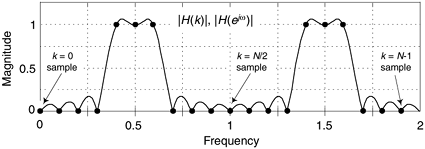
The basis of FSF design is the definition of a desired FIR filter frequency response in the form of H(k) frequency-domain samples, whose magnitudes are depicted as dots in Figure 7-2. Next, those complex H(k) sample values as used as gain factors following the resonators in the FSF structure (block diagram). If you haven't seen it before, please don't be intimidated by this apparently complicated FSF structure. We'll soon understand every part of it, and how those parts work together.
Later we'll develop the math to determine the interpolated (actual) frequency magnitude response |H(ejω)| of an FSF shown by the continuous curve in Figure 7-2. In this figure, the frequency axis labeling convention is a normalized angle measured in π radians with the depicted ω frequency range covering 0 to 2π radians, corresponding to a cyclic frequency range of 0 to fs, where fs is the sample rate in Hz.
To avoid confusion, we remind the reader there is a popular nonrecursive FIR filter design technique known as the frequency sampling design method described in the DSP literature. That design scheme begins (in a manner similar to an FSF design) with the definition of desired H(k) frequency response samples, then an inverse discrete Fourier transform is performed on those samples to obtain a time-domain impulse response sequence that's used as the h(k) coefficients in the nonrecursive N-tap FIR structure of Figure 7-1(a). In the FSF design method described here, the desired frequency-domain H(k) sample values are the coefficients used in the FSF structure of Figure 7-1(b), which is typically called the frequency sampling implementation of an FIR filter.
Although more complicated than nonrecursive FIR filters, FSFs deserve study because in many narrowband filtering situations they can implement a linear-phase FIR filter at a reduced computational workload relative to an N-tap nonrecursive FIR filter. The computation reduction occurs because, while all of the h(k) coefficients are used in the nonrecursive FIR filter implementation, most of the H(k) values will be zero-valued, corresponding to the stopband, and need not be implemented. To understand the function and benefits of FSFs, we start by considering the behavior of the comb filter and then review the performance of a single digital resonator.
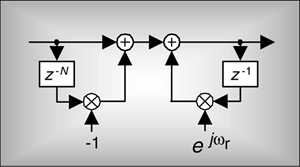
A single section of a complex FSF is a comb filter followed by a single complex digital resonator as shown in Figure 7-3.
The 1/N gain factor following a resonator in Figure 7-1(b) is omitted, for simplicity, from the single-section complex FSF. (The effect of including the 1/N factor will be discussed later.) To understand the single-section FSF's operation, we first review the characteristics of the nonrecursive comb filter whose time-domain difference equation is
with its output equal to the input sequence minus the input delayed by N samples. A single-section FSF z-domain transfer function is
The frequency response of a comb filter, derived in Appendix G, Section 1, is
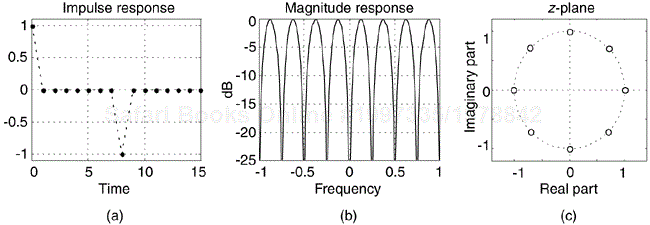
with a magnitude response of |Hcomb(ejω)| = 2|sin(ωN/2)| whose maximum value is 2. It's meaningful to view the comb filter's time-domain impulse response and frequency-domain magnitude response shown in Figure 7-4 for N = 8. The magnitude response makes it clear why the term “comb” is used.
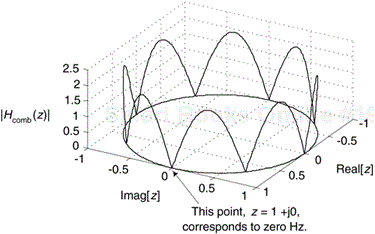
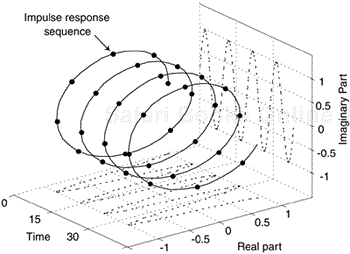
Equation (7-2) leads to a key feature of this comb filter: its transfer function has N periodically spaced zeros around the z-plane's unit circle shown in Figure 7-4(c). Each of those zeros, located at z(k) = ej2πk/N, where k = 0, 1, 2, . . ., N–1, corresponds to a magnitude null in Figure 7-4(b), where the normalized frequency axis is labeled from –π to +π radians. Those z(k) values are the N roots of unity when we set Eq. (7-2) equal to zero yielding z(k)N = (ej2πk/N)N = 1. We can combine the magnitude response (on a linear scale) and z-plane information in the three-dimensional z-plane depiction shown in Figure 7-5, where we see the intersection of the |Hcomb(z)| surface and the unit circle. Breaking the curve at the z = –1 point, and laying it flat, corresponds to the magnitude curve in Figure 7-4(b).
To preview where we're going, soon we'll build an FSF by cascading the comb filter with a digital resonator having a transfer function pole lying on top of one of the comb's z-plane zeros, resulting in a linear-phase bandpass filter. With this thought in mind, let's characterize the digital resonator in Figure 7-3.
The complex resonator's time-domain difference equation is
where the angle ωr, -π ≤ ωr ≤ π determines the resonant frequency of our resonator. We show this by considering the resonator's z-domain transfer function
and the resonator's complex time-domain impulse response, for ωr = π/4, in Figure 7-6.
The ωr = π/4 resonator's impulse response is a complex sinusoid, the real part (a cosine sequence) of which is plotted in Figure 7-7(a), and can be considered infinite in duration. (The imaginary part of the impulse response is, as we would expect, a sinewave sequence.) The frequency magnitude response is very narrow and centered at ωr. The resonator's Hres(z) has a single zero at z = 0, but what concerns us most is its pole, at ![]() , on the unit circle at an angle of ωr as shown in Figure 7-7(c). We can think of the resonator as an infinite impulse response (IIR) filter that's conditionally stable because its pole is neither inside nor outside the unit circle.
, on the unit circle at an angle of ωr as shown in Figure 7-7(c). We can think of the resonator as an infinite impulse response (IIR) filter that's conditionally stable because its pole is neither inside nor outside the unit circle.
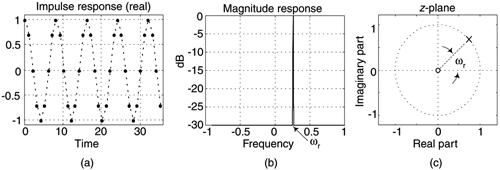
Figure 7-7. Time and frequency-domain characteristics of a single complex digital resonator with ωr = π/4.
We now analyze the single-section complex FSF in Figure 7-3. The z-domain transfer function of this FSF is the product of the individual transfer functions and H(k), or
If we restrict the resonator's resonant frequency ωr to be 2πk/N, where k = 0, 1, 2, . . ., N–1, then the resonator's z-domain pole will be located atop one of the comb's zeros and we'll have an FSF transfer function of
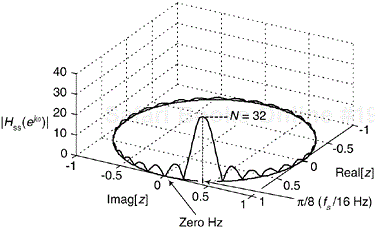
where the subscript “ss” in Eq. (7-7) means a single-section complex FSF. We can understand a single-section FSF by reviewing its time and frequency-domain behavior for N = 32, k = 2, and H(2) = 1 shown in Figure 7-8.
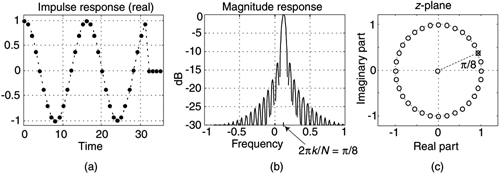
Figure 7-8. Time and frequency-domain characteristics of a single-section complex FSF where N = 32, k = 2, and H(2) = 1.
Figure 7-8 is rich in information. We see that the complex FSF's impulse response is a truncated complex sinusoid whose real part is shown in Figure 7-8(a). The positive impulse from the comb filter started the resonator oscillation at zero time. Then at just the right sample, N = 32 samples later—which is k = 2 cycles of the sinusoid—the negative impulse from the comb arrives at the resonator to cancel all further oscillation. The frequency magnitude response, being the Fourier transform of the truncated sinusoidal impulse response, takes the form of a sin(x)/x-like function. In the z-plane plot of Figure 7-8, the resonator's pole is indeed located atop the comb filter's k = 2 zero on the unit circle canceling the frequency magnitude response null at 2πk/N = π/8 radians. (Let's remind ourselves that a normalized angular frequency of 2πk/N radians corresponds to a cyclic frequency of kfs/N where fs is the sample rate in Hz. Thus the filter in Figure 7-8 resonates at fs/16 Hz.)
We can determine the FSF's interpolated frequency response by evaluating the Hss(z) transfer function on the unit circle. Substituting ejω for z in Hss(z) in Eq. (7-7), as detailed Appendix G, Section 2, we obtain an Hss(ejω) frequency response of
Evaluating |Hss(ejω)| over the frequency range of –π < ω < π yields the curve in Figure 7-8(b). Our single-section FSF has linear phase because the e–jπk/N term in Eq. (7-8) is a fixed phase angle based on constants N and k, the angle of H(k) is fixed, and the e–jω(N–1)/2 phase term is a linear function of frequency (ω). As derived in Appendix G, Section 2, the maximum magnitude response of a single-section complex FSF is N when |H(k)| = 1. We illustrate this fact in Figure 7-9.
In order to build useful FSFs we use multiple resonator sections, as indicated in Figure 7-1(b), to provide bandpass FIR filtering. For example, let's build a three-section complex bandpass FSF by establishing the parameters of N = 32 with the non-zero frequency samples H(2), H(3), and H(4). The desired frequency magnitude response is shown in Figure 7-10(a) with the bandpass FSF structure provided in Figure 7-10(b).
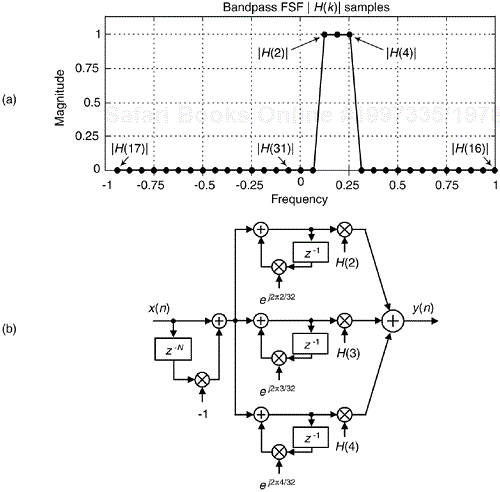
Figure 7-10. Three-section N = 32 complex FSF: (a) desired frequency magnitude response; (b) implementation.
Exploring this scenario, recall that the z-domain transfer function of parallel filters is the sum of the individual transfer functions. So, the transfer function of an N-section complex FSF from Eq. (7-7) is
where the subscript “cplx” means a complex multisection FSF.
Let's pause for a moment to understand Eq. (7-9). The first factor on the right side represents a comb filter, and the comb is in cascade (multiplication) with the sum of ratio terms. The summation of the ratios (each ratio is a resonator) means those resonators are connected in parallel. Recall from Section 6.8.1 that the combined transfer function of filters connected in parallel is the sum of the individual transfer functions. It's important to be comfortable with the form of Eq. (7-9) because we'll be seeing many similar expressions in the material to come.
So a comb filter is driving a bank of resonators. For an N = 32 complex FSF we could have up to 32 resonators, but in practice only a few resonators are needed for narrowband filters. In Figure 7-10, we used only three resonators. That's the beauty of FSFs: most of the H(k) gain values in Eq. (7-9) are zero-valued and those resonators are not implemented, keeping the FSF computationally efficient.
Using the same steps as in Appendix G, Section 2, we can write the frequency response of a multisection complex FSF, such as in Figure 7-10, as
The designer of a multisection complex FSF can achieve any desired filter phase response by specifying the ø(k) phase angle value of each non-zero complex H(k) = |H(k)|ejø(k) gain factor. However, to build a linear-phase complex FSF, the designer must: (a) specify the ø(k) phase values to be a linear function of frequency, and (b) define the ø(k) phase sequence so its slope is –(N–1)/2. This second condition forces the FSF to have a positive time delay of (N–1)/2 samples, as would the N-tap nonrecursive FIR filter in Figure 7-1(a). The following expressions for ø(k), with N being even, satisfy those two conditions.
If N is odd, the linear-phase H(k) phase values are
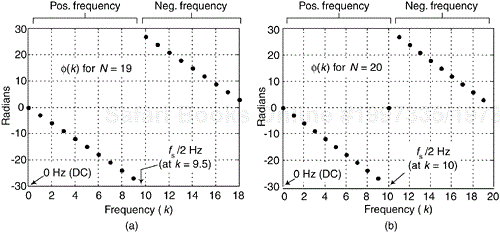
Two example linear-phase ø(k) sequences, for N = 19 and N = 20, are shown in Figure 7-11. The ø(0) = 0 values set the phase to be zero at zero Hz, and the ø(N/2) = 0, at the cyclic frequency of fs/2 in Figure 7-11(b), ensures a symmetrical time-domain impulse response.
Assigning the appropriate phase for the non-zero H(k) gain factors is, however, only half the story in building a multisection FSF. There's good news to be told. Examination of the frequency response Eq. (7-10) shows us a simple way to achieve phase linearity in practice. Substituting |H(k)|ejø(k), with ø(k) defined by Eq. (7-11) above, for H(k) in Eq. (7-10) provides the expression for the frequency response of an even-N multisection linear-phase complex FSF,
where the subscript “lp” indicates linear-phase.
Equation (7-13) is not as complicated as it looks. It merely says that the total FSF frequency response is the sum of individual resonators' sin(x)/x-like frequency responses. The first term within the brackets represents the resonator centered at k = N/2 (fs/2). The first summation is the positive-frequency resonators and the second summation represents the negative-frequency resonators.
The (–1)k terms in the numerators of Eq. (7-13) deserve our attention because they are an alternating sequence of plus and minus ones. Thus a single-section frequency response will be 180° out of phase relative to its neighboring section. That is, the outputs of neighboring single-section FSFs will have a fixed π radians phase difference over the passband common to both filters as shown in Figure 7-12. (The occurrence of the (-1)k factors in Eq. (7-13) is established in Appendix G, Section 3.)
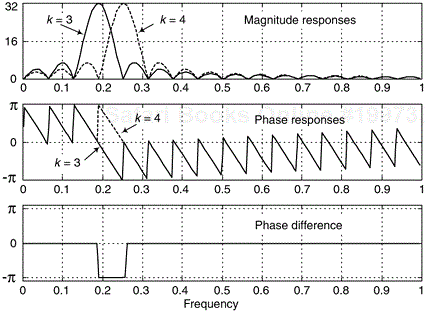
Figure 7-12. Comparison of the magnitude and phase responses, and phase difference, between the k = 3 and the k = 4 FSFs, when N = 32.
The effect of those (–1)k factors is profound, and not emphasized nearly enough in the literature of FSFs. Rather than defining each non-zero complex H(k) gain factor with their linearly increasing phase angles ø(k), we can build a linear-phase multisection FSF by using just the |H(k)| magnitude values and incorporating the alternating signs for those real-valued gain factors. In addition, if the non-zero |H(k)| gain factors are all equal to one, we avoid Figure 7-10's gain factor multiplications altogether, as shown in Figure 7-13(a).
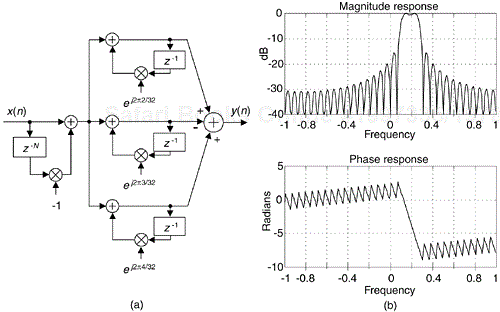
Figure 7-13. Simplified N = 32 three-section linear-phase complex bandpass FSF: (a) implementation; (b) frequency response.
The unity-valued |H(k)| gain factors and the alternating-signed summation allows the complex gain multiplies in Figure 7-10(b) to be replaced by simple adds and subtracts as in Figure 7-13(a). We add the even-k and subtract the odd-k resonator outputs. Figure 7-13(b) confirms the linear phase, with phase discontinuities at the magnitude nulls, of these multisection complex FSFs. The transfer function of the simplified complex linear phase FSF is
(We didn't use the “lp” subscript in Eq. (7-14) because, from here on out, all our complex FSFs will be linear phase.)
So far we've discussed complex FSFs with pole/zero cancellation on the unit circle. However, in practice, exact cancellation requires infinite-precision arithmetic. Real-world binary word quantization errors in the FSF's coefficients can make the filter poles lie outside the unit circle. The result would be an unstable filter, whose impulse response is no longer finite in duration, which must be avoided. (This is a beautiful example of the time-honored phrase, “In theory, there's no difference between theory and practice. In practice, sometimes the theory doesn't work.”) Even if a pole is located only very slightly outside the unit circle, roundoff noise will grow as time increases, corrupting the output samples of the filter. We prevent this problem by moving the comb filter's zeros and the resonators' poles just inside the unit circle, as depicted in Figure 7-14(a). Now the zeros and a pole are located on a circle of radius r, where the damping factor r is just slightly less than 1.
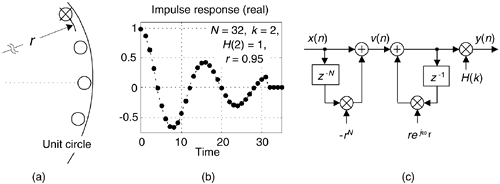
Figure 7-14. Ensuring FSF stability: (a) poles and zeros are inside the unit circle; (b) real part of a stable single-section FSF impulse response; (c) FSF structure.
We call r the damping factor because a single-stage FSF impulse response becomes a damped sinusoid. For example, the real part of the impulse response of a single-stage complex FSF, where N = 32, k = 2, H(2) = 2, and r = 0.95, is shown in Figure 7-14(b). Compare that impulse response to Figure 7-8(a). The structure of a single-section FSF with zeros and a pole inside the unit circle is shown in Figure 7-14(c).
The comb filter's feedforward coefficient is –rN because the new z-domain transfer function of this comb filter is
with the N zeros for this comb being located at zr<1(k) = rej2πk/N, where k = 0, 1, 2, . . ., N–1.
Those zr<1(k) values are the N roots of rN when we set Eq. (7-15) equal to zero, yielding zr<1(k)N = (rej2πk/N)N = rN. The z-domain transfer function of the resonator in Figure 7-14(b), with its pole located at a radius of r, at an angle of 2πk/N, is
leading us to the transfer function of a guaranteed-stable single-section complex FSF of
whose implementation is shown in Figure 7-14(c). The subscript “gs,ss” means a guaranteed-stable single-section FSF. The z-domain transfer function of a guaranteed-stable N-section complex FSF is
where the subscript “gs,cplx” means a guaranteed-stable complex multisection FSF. The frequency response of a guaranteed-stable multisection complex FSF (derived in Appendix G, Section 4) is
If we modify the bandpass FSF structure in Figure 7-13(a) to force the zeros and poles inside the unit circle, we have the structure shown in Figure 7-15(a). The frequency-domain effects of zeros and poles inside the unit circle are significant, as can be seen in Figure 7-15(b) for the two cases where r = 0.95 and r = 0.9999.
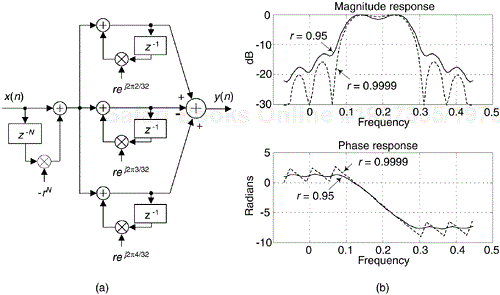
Figure 7-15. Guaranteed-stable N = 32 three-section linear-phase complex bandpass FSF: (a) implementation; (b) frequency response for two values of damping factor r.
Figure 7-15(b) shows how a value of r = 0.95 badly corrupts our complex bandpass FSF performance; the stop band attenuation is degraded, and significant phase nonlinearity is apparent. Damping factor r values less than unity cause phase nonlinearity because the filter is in a nonreciprocal zero condition. Recall a key characteristic of FIR filters: to maintain linear phase, any z-plane zero located inside the unit circle at z = zr<1(k), where zr<1(k) is not equal to 0, must be accompanied by a zero at a reciprocal location, namely z = 1/zr<1(k) outside the unit circle. We do not satisfy this condition here, leading to phase nonlinearity. (The reader should have anticipated nonlinear phase due to the asymmetrical impulse response in Figure 7-14(b).) The closer we can place the zeros to the unit circle, the more linear the phase response. So the recommendation is to define r to be as close to unity as your binary number format allows[4]. If integer arithmetic is used, set r = 1–1/2B, where B is the number of bits used to represent a filter coefficient magnitude.
Another stabilization method worth considering is decrementing the largest component (either real or imaginary) of a resonator's ej2πk/N feedback coefficient by one least significant bit. This technique can be applied selectively to problematic resonators and is effective in combating instability due to rounding errors which result in finite-precision ej2πk/N coefficients having magnitudes greater than unity.
Thus far we're reviewed FSFs with complex coefficients and frequency magnitude responses not symmetrical about zero Hz. Next we explore FSFs with real-only coefficients having conjugate-symmetric frequency magnitude and phase responses.
We can obtain real-FSF structures (real-valued coefficients) by forcing our complex N-section FSF, where N is even, to have conjugate poles, by ensuring all non-zero H(k) gain factors are accompanied by conjugate H(N–k) gain factors, so that H(N–k) = H*(k). That is, we can build real-valued FSFs if we use conjugate pole pairs located at angles of ±2πk/N radians. The transfer function of such an FSF (derived in Appendix G, Section 5) is
where the subscript “gs,real” means a guaranteed-stable real-valued multisection FSF, and øk is the desired phase angle of the kth section. Eq. (7-20) defines the structure of a Type-I real FSF to be as shown in Figure 7-16(a), requiring five multiplies per resonator output sample. The implementation of a real pole-pair resonator, using real-only arithmetic, is shown in Figure 7-16(b).
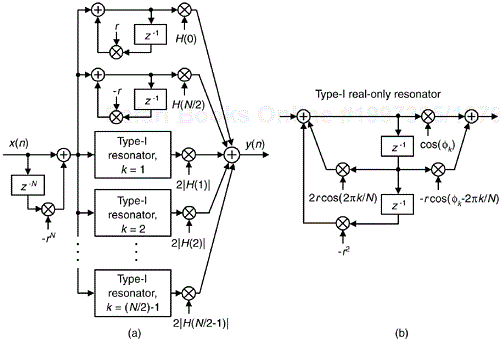
Figure 7-16. Guaranteed-stable, even-N, Type-I real FSF: (a) structure; (b) using real-only resonator coefficients.
Of course, for lowpass FSFs the stage associated with the H(N/2) gain factor in Figure 7-16 would not be implemented, and for bandpass FSFs neither stage associated with the H(0) and H(N/2) gain factors would be implemented. The behavior of a single-section Type-I real FSF with N = 32, k = 3, H(3) = 1, r = 0.99999, and ø3 = 0 is provided in Figure 7-17.
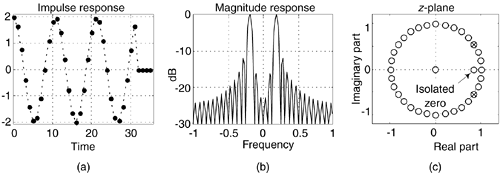
Figure 7-17. Time and frequency-domain characteristics of a single-section Type-I FSF when N = 32, k = 3, H(3) = 1, r = 0.99999, and φ3 = 0.
An alternate version of the Type-I FSF, with a simplified resonator structure, can be developed by setting all øk values equal to zero and moving the gain factor of 2 inside the resonators. Next we incorporate the alternating signs in the final summation, as shown in Figure 7-18 to achieve linear phase just as we did to arrive at the linear-phase multisection complex FSF in Figure 7-13(a) by adding the even-k and subtracting the odd-k resonator outputs. The “±” symbol in Figure 7-18(a) warns us that when N is even, k = (N/2)–1 can be odd or even.
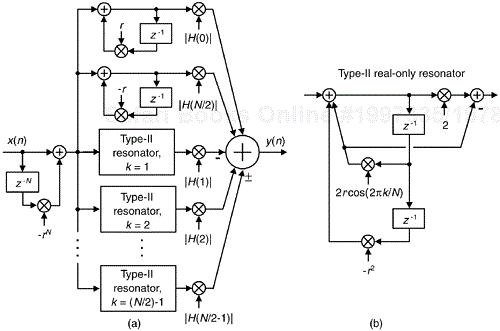
Figure 7-18. Linear-phase, even-N, Type-II real FSF: (a) structure; (b) real-only resonator implementation.
If the non-zero |H(k)| gain factors are unity, this Type-II real FSF requires only three multiplies per section output sample. When a resonator's multiply by 2 can be performed by a hardware binary arithmetic left shift, only two multiplies are needed per output sample. The transfer function of this real-valued FSF is
Neither the Type-I or the Type-II FSF have exactly linear phase. While the phase nonlinearity is relatively small, their passband group delays can have a peak-to-peak fluctuation of up to two sample periods (2/fs) when used in multisection applications. This phase nonlinearity is unavoidable because those FSFs have isolated zeros located at z = rcos(2πk/N), when øk = 0, as shown in Figure 7-17(c). Because the isolated zeros inside the unit circle have no accompanying reciprocal zeros located outside the unit circle at z = 1/[rcos(2πk/N)], sadly, this causes phase nonlinearity.
While the Type-I and -II FSFs are the most common types described in the literature of FSFs, their inability to yield exact linear phase has not received sufficient attention or analysis. In the next section we take steps to obtain linear phase by repositioning the isolated zero.
We can achieve exact real-FSF phase linearity by modifying the Type-I real FSF resonator's feedforward coefficients, in Figure 7-16(b), moving the isolated zero on top of the comb filter's zero located at z = r. We do this by setting øk = πk/N. The numerator of the transfer function of one section of the real FSF, from Eq. (7-20), is cos(øk)–rcos(øk–2πk/N)z–1. If we set this expression equal to zero, and let øk = πk/N, we find the shifted isolated zero location zo is
or
Substituting πk/N for øk in Eq. (7-20) yields the transfer function of a linear-phase Type-III real FSF as
The implementation of the linear-phase Type-III real FSF is shown in Figure 7-19, requiring four multiplies per section output sample.
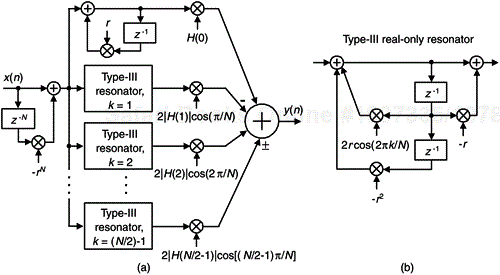
Figure 7-19. Even-N, linear-phase, Type-III real FSF: (a) structure; (b) real-only resonator implementation.
Notice that the H(N/2), fs/2, section is absent in Figure 7-19(a). We justify this as follows: the even-N Type-I, -II, & -III real FSF sections have impulse responses comprising N non-zero samples. As such, their k = N/2 sections' impulse responses, comprising even-length sequences of alternating plus and minus ones, are not symmetrical. This asymmetry would corrupt the exact linear phase should a k = N/2 section be included. Consequently, as with even-length nonrecursive FIR filters, even-N Type-I, -II, & -III real FSFs cannot be used to implement linear-phase highpass filters.
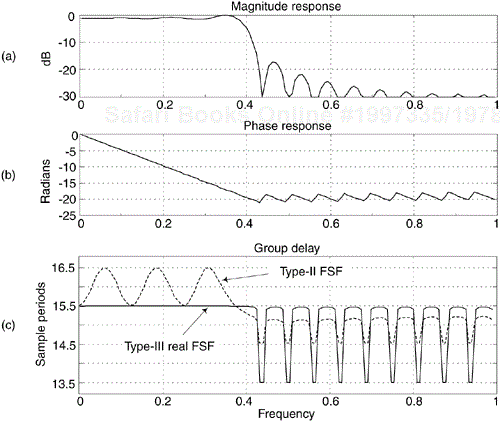
Figure 7-20 shows the frequency-domain performance of an eight-section Type-III FSF for N = 32, where the eight sections begin at DC (0 ≤ k ≤ 7). Figure 7-20(c) provides a group delay comparison between the Type-III FSF and an equivalent eight-section Type-II FSF showing the improved Type-III phase linearity having a constant group delay of (N-1)/2 samples over the passband.
We've reviewed the structure and behavior of a complex FSF whose complex resonator stages had poles residing atop the zeros of a comb filter, resulting in a recursive FIR filter. Next, to ensure filter implementation stability, we forced the pole/zero locations to be just inside the unit circle. We examined a guaranteed-stable even-N Type-I real FSF having resonators with conjugate pole pairs resulting in an FSF with real-valued coefficients. Next, we modified the Type-I real FSF structure yielding the more computationally efficient but only moderately linear-phase Type-II real FSF. Finally, we modified the coefficients of the Type-I real FSF, and added post-resonator gain factors resulting in the exact linear-phase Type-III real FSF. During this development, we realized that the even-N Type-I, -II, and -III real FSFs cannot be used to implement linear-phase highpass filters.
In the remainder of this section we introduce a proposed resonator structure that provides superior filtering properties compared to the Type-I, -II, & -III resonators. Next we'll examine the use of non-zero transition band filter sections to improve overall FSF passband ripple and stopband attenuation, followed by a discussion of several issues regarding modeling and designing FSFs. We'll compare the performance of real FSFs to their equivalent Parks-McClellan-designed N-tap nonrecursive FIR filters. Finally, a detailed FSF design procedure is presented.
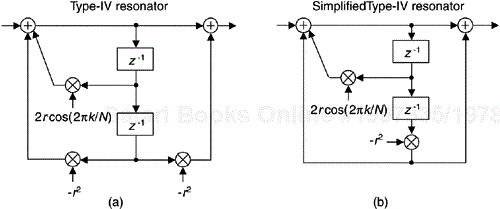
There are many real-valued resonators that can be used in FSFs, but of particular interest to us is the Type-IV resonator presented in Figure 7-21(a).
This resonator deserves attention because it:
is guaranteed-stable,
exhibits highly linear phase,
uses real-valued coefficients,
is computationally efficient,
can implement highpass FIR filters, and
yields stopband attenuation performance superior to the Type-I, -II, and -III FSFs.
From here on in, the Type IV will be our FSF of choice.
Cascading Type-IV resonators with a comb filter provides a Type-IV real-only FSF with a transfer function of
where N is even. (Note, when N is odd, k = N/2 is not an integer and the |H(N/2)| term does not exist.) As derived in Appendix G, Section 6, the Type-IV FSF frequency response is
The even-N frequency and resonance magnitude responses for a single Type-IV FSF section are
and
Its resonant magnitude gains at k = 0 (DC), and k = N/2 (fs/2), are
To reduce the number of resonator multiply operations, it is tempting to combine the dual –r2 factors in Figure 7-21(a) to simplify the Type-IV resonator as shown in Figure 7-21(b). However, a modification reducing both the number of multiply and addition operations is to implement the (1–r2z–2) term in the numerator of Eq. (7-23) as a second-order comb filter as shown in Figure 7-22(a)[5]. This transforms the Type-IV resonator to that shown in Figure 7-22(b). The |H(0)|/2 and |H(N/2)|/2 gain factors compensate for the gain of 2N for a Type-IV resonator in Eq. (7-27).
The “±” symbols in Figure 7-22(a) remind us, again, when N is even, k = N/2 could be odd or even. This FSF has the very agreeable characteristic of having an impulse response whose length is N+1 samples. Thus, unlike the Type-I, -II, and -III FSFs, an even-N Type-IV FSF's k = N/2 section impulse response (alternating ±1s) is symmetrical, and Type-IV FSFs can be used to build linear-phase highpass filters. When N is odd, the k = N/2 section is absent in Figure 7-22, and the odd-N Type-IV transfer function is identical to Eq. (7-23), with the summation's upper limit being (N–1)/2 instead of N/2.
We've covered a lot of ground thus far. Table 7-1 summarizes what we've discussed concerning real-valued FSFs. The table lists the average passband group delay measured in sample periods, the number of multiplies and additions necessary per output sample for a single FSF section, and a few remarks regarding the behavior of the various real FSFs. The section gains at their resonant frequencies, assuming the desired |H(k)| gain factors are unity, is N for all four of the real-valued FSFs.
Table 7-1. Summary of Even-N Real FSF Properties
Real FSF type | Group delay | Multiplies | Adds | Remarks |
|---|---|---|---|---|
Type-I (Figure 7-16) |
| 5 | 3 | Real-coefficient FSF. Phase is only moderately linear. |
Type-II (Figure 7-18) |
| 3 | 3 | Modified, and more efficient, version of the Type-I FSF. Phase is only moderately linear. A binary left shift may eliminate one resonator multiply. |
Type-III (Figure 7-19) |
| 4 | 3 | Very linear phase. Cannot implement a linear-phase highpass filter. |
Type-IV (Figure 7-22) |
| 2 | 2 | Very linear phase. Improved stopband attenuation. Usable for lowpass, bandpass, or highpass filtering. |
We derived several different H(ejω) frequency response equations here, not so much to use them for modeling FSF performance, but to examine them in order to help define the structure of our FSF block diagrams. For example, it was analyzing the properties of HType-IV(ejω) that motivated the use of the 1/2 gain factors in the Type-IV FSF structure.
When modeling the FSFs, fortunately it's not necessary to write code to calculate frequency-domain responses using the various H(ejω) equations provided here. All that's necessary is code to compute the time-domain impulse response of the FSF being modeled, pad the impulse response with enough zeros so the padded sequence is 10–20 times the length of the original, perform a discrete Fourier transform (DFT) on the padded sequence, and plot the resulting interpolated frequency-domain magnitude and phase. Of course, forcing your padded sequence length to be an integer power of two enables the use of the efficient FFT to calculate frequency-domain responses. Alternatively, many commercial signal processing software packages have built-in functions to calculate filter frequency response curves based solely on the filter's transfer function coefficients.
We can increase FSF stopband attenuation if we carefully define |H(k)| magnitude samples in the transition region, between the passband and stopband. For example, consider a lowpass Type-IV FSF having seven sections of unity gain, with N = 32 whose desired performance is shown in Figure 7-23(a), and whose interpolated (actual) frequency magnitude response is provided in Figure 7-23(b).
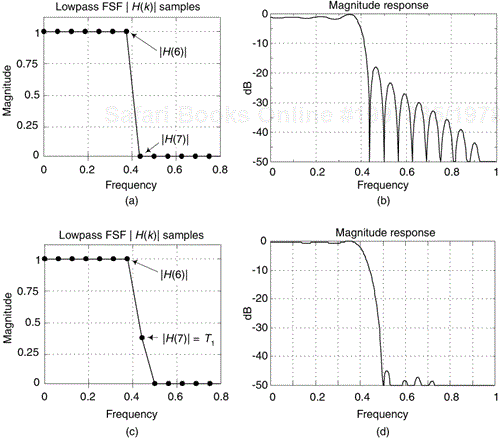
Figure 7-23. Seven-section, N = 32, Type-IV FSF: (a) desired frequency response; (b) actual performance; (c) using one transition sample; (d) improved stopband attenuation.
The assignment of a transition magnitude sample, coefficient T1 whose value is between 0 and 1 as in Figure 7-23(c), reduces the abruptness in the transition region between the passband and the stopband of our desired magnitude response. Setting T1 = 0.389 results in reduced passband ripple and the improved stopband sidelobe suppression shown in Figure 7-23(d). The price we pay for the improved performance is the computational cost of an additional FSF section and increased width of the transition region.
Assigning a coefficient value of T1 = 0.389 was not arbitrary or magic. Measuring the maximum stopband sidelobe level for various values of 0 ≤ T1 ≤ 1 reveals the existence of an optimum value for T1. Figure 7-24 shows that the maximum stopband sidelobe level is minimized when T1 = 0.389. The minimum sidelobe level of –46 dB (when T1 = 0.389) corresponds to the height of the maximum stopband sidelobe in Figure 7-23(d). This venerable and well known method of employing a transition region coefficient to reduce passband ripple and minimize stopband sidelobe levels also applies to bandpass FSF design where the transition sample is used just before and just after the filter's passband unity-magnitude |H(k)| samples.
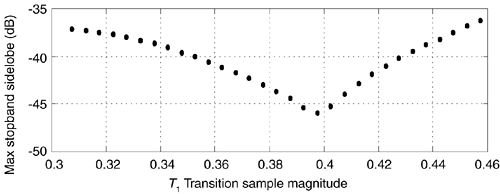
Figure 7-24. Maximum stopband sidelobe level as a function of the transition region coefficient value for a seven-section Type-IV real FSF when N = 32.
Further stopband sidelobe level suppression is possible if two transition coefficients, T1 and T2, are used such that 0 ≤ T2 ≤ T1 ≤ 1. (Note: for lowpass filters, if T1 is the |H(k)| sample, then T2 is the |H(k+1)| sample.) Each additional transition coefficient used improves the stopband attenuation by approximately 25 dB. However, finding the optimum values for the T coefficients is a daunting task. Optimum transition region coefficient values depend on the number of unity-gain FSF sections, the value of N, and the number of coefficients used. Unfortunately, there's no closed form equation available to calculate optimum transition coefficient values; we must search for them empirically.
If one coefficient (T1) is used, finding its optimum value can be considered a one-dimensional search. If two coefficients are used, the search becomes two dimensional, and so on. Fortunately, descriptions of linear algebra search technique are available[1,6–8], and commercial mathematical software packages have built-in optimization functions to facilitate this computationally intensive search. For the Type-I/II FSFs, tables of optimum transition region coefficients for various N, and number of FSF sections used, have been published[1], with a subset of those tables provided as an appendix in a textbook[2]. For the higher performance Type-IV FSF, tables of optimum coefficient values have been compiled by this author and provided in Appendix H. With this good news in mind, shortly we'll look at a real-world FSF design example to appreciate the benefits of FSFs.
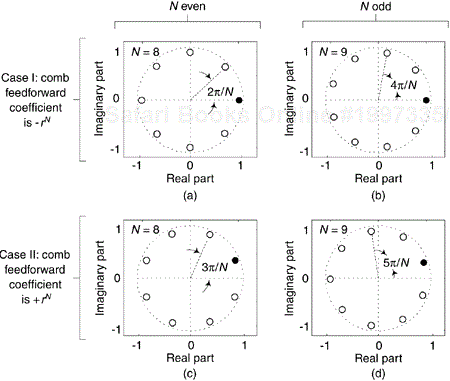
With the primary comb filter in Figure 7-22 having a feedforward coefficient of -rN, its even-N transfer function zeros are equally spaced around and inside the unit circle, as shown in Figure 7-4(c) and Figure 7-25(a), so the k = 1 zero is at an angle of 2π/N radians. In this Case I, if N is odd the comb's zeros are spaced as shown in Figure 7-25(b). An alternate situation, Case II, exists when the comb filter's feedforward coefficient is +rN. In this mode, an even-N comb filter's zeros are rotated counterclockwise on the unit circle by π/N radians as shown in Figure 7-25(c) where the comb's k = 1 zero is at an angle of 3π/N radians[5]. The k = 0 zeros are shown as solid dots.
The structure of a Case II FSF is identical to that of a Case I FSF. However, the Case II resonators' coefficients must be altered to rotate the poles by π/N radians to ensure pole/zero cancellation. As such, the transfer function of a Case II, even-N, Type-IV FSF is
Because a Case II FSF cannot have a pole or a zero at z = 1 (DC), these FSFs are unable to implement lowpass filters. Table 7-2 lists the filtering capabilities of the various Case I and Case II Type-IV FSFs.
Their inability to implement lowpass filtering limits the utility of Case II FSFs, but their resonator's shifted center frequencies do provide some additional flexibility in defining the cutoff frequencies of bandpass and highpass filters. The remainder of this material considers only the Case I Type-IV FSFs.
During the formative years of FIR filter theory (early 1970s) a computer program was made available for designing nonrecursive FIR filters using the Parks-McClellan (PM) method[9]. This filter design technique provided complete control in defining desired passband ripple, stopband attenuation, and transition region width. (FIR filters designed using the PM method are often called optimal FIR, Remez Exchange, Chebyshev approximation, or equiripple filters.) Many of the early descriptions of the PM design method included a graphical comparison of various lowpass FIR filter design methods similar to that redrawn in Figure 7-26[7,10–11]. In this figure, a given filter's normalized (to impulse response length N, and the sample rate fs) transition bandwidth is plotted as a function of its minimum stopband attenuation. (Passband peak-to-peak ripple values, measured in dB, are provided numerically within the figure.)
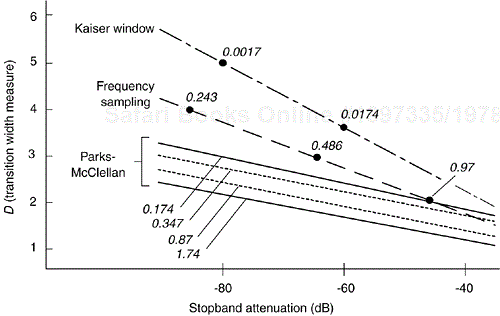
Figure 7-26. Comparison of the Kaiser window, frequency sampling, and Parks-McClellan designed FIR filters.
Because the normalized transition bandwidth measure D in Figure 7-26 is roughly independent of N, this diagram is considered to be a valid performance comparison of the three FIR filter design methods. For a given passband ripple and stopband attenuation, the PM-designed FIR filter could exhibit the most narrow transition bandwidth, thus the highest performance filter. The wide dissemination of Figure 7-26 justifiably biased filter designers toward the PM design method. (During his discussion of Figure 7-26, one author boldly declared “The smaller is D, the better is the filter.”[10]) Given its flexibility, improved performance, and ease of use, the PM method quickly became the predominant FIR filter design technique. Consequently, in the 1970s FSF implementations lost favor to the point where they're rarely mentioned in today's DSP classrooms or textbooks.
Table 7-2. Type-IV FSF Modes of Operation
Type-IV FSF | Lowpass | Bandpass | Highpass |
|---|---|---|---|
Case I, N even | Yes | Yes | Yes |
Case I, N odd | Yes | Yes | No |
Case II, N even | No | Yes | No |
Case II, N odd | No | Yes | Yes |
However, from a computational workload standpoint, Figure 7-26 is like modern swimwear: what it shows is important; what it does not show is vital. That design comparison does not account for those situations where both frequency sampling and PM filters meet the filter performance requirements, but the frequency sampling implementation is more computationally efficient. The following FIR filter design example illustrates this issue and shows why FSFs should be included in our bag of FIR filter design tools.
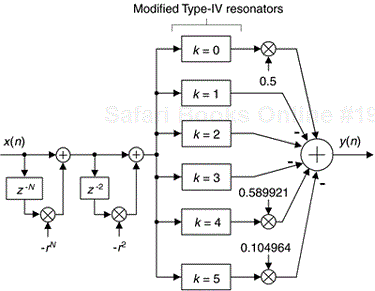
Consider the design of a linear-phase lowpass FIR filter with the cutoff frequency being 0.05 times the sample rate fs. The stopband must begin at 0.095 times fs, maximum passband ripple is 0.3 dB peak to peak, and the minimum stopband attenuation must be 65 dB. If we designed a six-section Type-IV FSF with N = 62 and r = 0.99999, its frequency-domain performance satisfies our requirements and is the solid curve in Figure 7-27(a).
![An N = 62, six-section Type-IV real FSF [solid] versus a 60-tap PM-designed filter [dashed]: (a) frequency magnitude response; (b) passband response detail.](http://imgdetail.ebookreading.net/math_science_engineering/11/0131089897/0131089897__understanding-digital-signal__0131089897__graphics__07fig27_alt.gif)
Figure 7-27. An N = 62, six-section Type-IV real FSF [solid] versus a 60-tap PM-designed filter [dashed]: (a) frequency magnitude response; (b) passband response detail.
For this FSF, two transition region coefficients of |H(4)| = T1 = 0.589921, and |H(5)| = T2 = 0.104964 were used. Included in Figure 7-27(a), the dashed curve, is the magnitude response of a PM-designed 60-tap nonrecursive FIR filter. Both filters meet the performance requirements and have linear phase. The structure of the Type-IV FSF is provided in Figure 7-28. A PM-designed filter implemented using a folded nonrecursive FIR structure, exploiting its impulse response symmetry to halve the number of multipliers, requires 30 multiplies and 59 adds per output sample. We see the computational savings of the Type-IV FSF which requires only 17 multiplies and 19 adds per output sample. (Note, the FSF's H(k) gain factors are all zero for 6 ≤ k ≤ 31.)
In this section we answer the burning question, When is it smarter (more computationally efficient) to use a Type-IV FSF instead of a PM-designed FIR filter? The computational workload of a PM-designed FIR filter is directly related to the length of its time-domain impulse response, which in turn is inversely proportional to the filter transition bandwidth. The more narrow the transition bandwidth, the greater the nonrecursive FIR filter's computational workload measured in arithmetic operations per output sample. On the other hand, the computational workload of an FSF is roughly proportional to its passband width. The more FSF sections needed for wider bandwidths and the more transition region coefficients used, the higher the FSF's computational workload. So in comparing the computational workload of FSFs to PM-designed FIR filters, both transition bandwidth and passband width must be considered.
Figure 7-29 provides a computational comparison between even-N Type-IV FSFs and PM-designed nonrecursive lowpass FIR filters. The curves represent desired filter performance parameters where a Type-IV FSF and a PM designed filter have approximately equal computational workloads per output sample. (The bandwidth values in the figure axis are normalized to the sample rate, so for example a frequency value of 0.1 equals fs/10.) If the desired FIR filter transition region width and passband width combination (a point) lies beneath the curves in Figure 7-29, then a Type-IV FSF is computationally more efficient than a PM-designed filter. Figure 7-29(a) is a comparison accounting only for multiply operations. For filter implementations where multiplies and adds require equal processor clock cycles, Figure 7-29(b) provides the appropriate comparison. The solitary black dot in the figure indicates the comparison-curves location for the above Figure 7-27 Type-IV FSF filter example. (A Type-IV FSF design example using the curves in Figure 7-29 will be presented later.)
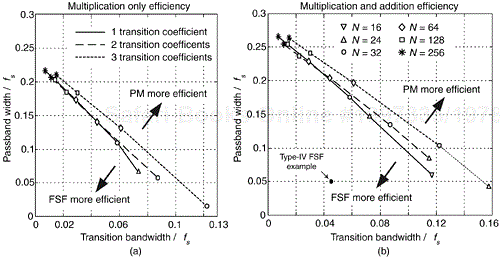
Figure 7-29. Computational workload comparison between even-N lowpass Type-IV FSFs and nonrecursive PM FIR filters: (a) only multiplications considered; (b) multiplications and additions considered. (No 1/N gain factor used.)
The assumptions made in creating Figure 7-29 are that an even-N Type-IV FSF, damping factor r = 0.99999, and no 1/N gain scaling from Figure 7-1(b) is used. The PM filter implementation used in the comparison assumes a symmetrical impulse response, an M-tap folded structure requiring M/2 multiplies, and M-1 additions. The performance criteria levied on the PM filter are typical Type-IV FSF properties (when floating-point coefficients are used) given in Table 7-3.
The Type-IV resonators have a gain of N, so the subsequent gain of the FSF in Figure 7-28 is N. For FSF implementations using floating point numbers, this gain may not be a major design issue. In filters implemented with fixed point numbers, the gain of N could cause overflow errors, and a gain reduction by a scaling factor of 1/N may be necessary. Occasionally, in the literature, a 1/N scaling factor is shown as a single multiply just prior to an FSF's comb filter[2,12]. This scale factor implementation is likely to cause an intolerable increase in the input signal quantization noise. A more practical approach is to apply the 1/N scaling at the output of each FSF section, prior to the final summation, as indicated in Figure 7-1(b). Thus every FSF resonator output is multiplied by a non-unity value, increasing the computational workload of the FSF. In this situation, the computational comparison between even-N Type-IV FSFs and PM filters becomes as shown in Figure 7-30.
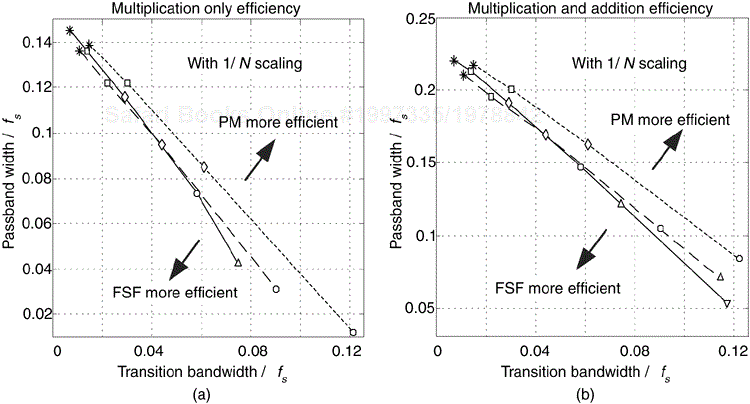
Figure 7-30. Computational workload comparison between even-N lowpass Type-IV FSFs, with resonator output 1/N scaling included, and nonrecursive PM FIR filters: (a) only multiplications considered; (b) multiplications and additions considered.
Of course, if N is an integer power of two, some hardware implementations may enable resonator output 1/N scaling with hard-wired binary arithmetic right shifts to avoid explicit multiply operations. In this situation, the computational workload comparison in Figure 7-29 applies.
Table 7-3. Typical Even-N Type-IV FSF Properties
Parameter | 1-coefficient | 2-coefficient | 3-coefficient |
|---|---|---|---|
Passband peak-peak ripple (dB) | 0.7 | 0.35 | 0.16 |
Minimum stopband attenuation (dB) | –45 | –68 | –95 |
As of this writing, programmable-DSP chips typically cannot take advantage of the folded FIR filter structure assumed in the creation of Figures 7-29 and 7-30. In this case, an M-tap direct convolution FIR filter has the disadvantage that it must perform the full M multiplies per output sample. However, DSP chips have the advantage of zero-overhead looping and single-clock-cycle multiply and accumulate (MAC) capabilities making them more efficient for direct convolution FIR filtering than for filtering using the recursive FSF structures. Thus, a DSP chip implementation's disadvantage of more necessary computations and its advantage of faster execution of those computations roughly cancel each other. With those thoughts in mind, we're safe to use Figures 7-29 and 7-30 as guides in deciding whether to use a Type-IV FSF or a PM-designed FIR filter in a programmable DSP chip filtering application.
Finally we conclude, from the last two figures, that Type-IV FSFs are more computationally efficient than PM-designed FIR filters in lowpass applications where the passband is less than approximately fs/5 and the transition bandwidth is less than roughly fs/8.
The design of a practical Type-IV FSF comprises three stages: (1) determine if an FSF can meet the desired filter performance requirements, (2) determine if a candidate FSF is more, or less, computationally efficient than an equivalent PM-designed filter, and (3) design the FSF and verify its performance. To aid in the first stage of the design, Figure 7-31 shows the typical minimum stopband attenuation of Type-IV FSFs, as a function of transition bandwidth, for various numbers of transition region coefficients. (Various values for N, and typical passband ripple performance, are given within Figure 7-31 as general reference parameters.)
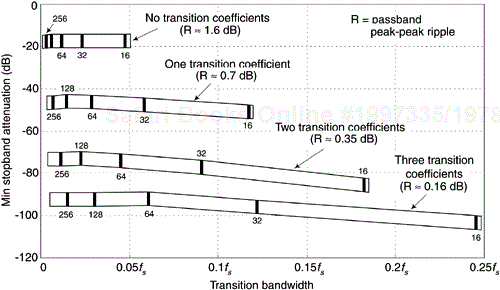
Figure 7-31. Typical Type-IV lowpass FSF stopband attenuation performance as a function of transition bandwidth.
In designing an FSF, we find the value N to be a function of the desired filter transition bandwidth. The number of FSF sections required is determined by both N and the desired filter bandwidth. Specifically, given a linear-phase FIR filter's desired passband width, passband ripple, transition bandwidth, and minimum stopband attenuation, the design of a linear-phase lowpass Type-IV FSF proceeds as follows:
Using Figure 7-31, determine which performance band in the figure satisfies the desired minimum stopband attenuation. This step defines the number of transition coefficients necessary to meet stopband attenuation requirements.
Ensure that your desired transition bandwidth value resides within the chosen shaded band. (If the transition bandwidth value lies to the right of a shaded band, a PM-designed filter will be more computationally efficient than a Type-IV FSF and the FSF design proceeds no further.)
Determine if the typical passband ripple performance, provided in Figure 7-31, for the candidate shaded band is acceptable. If so, a Type-IV FSF can meet the desired lowpass filter performance requirements. If not, a PM design should be investigated.
Based on arithmetic implementation priorities, determine the appropriate computational workload comparison chart to be used from Figure 7-29 or Figure 7-30 in determining if an FSF is more efficient than a PM-designed nonrecursive filter.
Using the desired filter's transition bandwidth and passband width as coordinates of a point on the selected computational workload comparison chart, determine if that point lies beneath the appropriate curve. If so, an FSF can meet the filter performance requirements with fewer computations per filter output sample than a PM-designed filter. (If the transition bandwidth/passband point lies above the appropriate curve, a PM design should be investigated and the FSF design proceeds no further.)
Assuming the designer has reached this step of the evaluation process, the design of a Type-IV FSF proceeds by selecting the filter order N. The value of N depends on the desired transition bandwidth and the number of transition coefficients from step 1 and, when the transition bandwidth is normalized to fs, can be estimated using
The required number of unity-gain FSF sections, integer M, is roughly proportional to the desired normalized double-sided passband width divided by the FSF's frequency resolution (fs/N), and is estimated using
Given the initial integer values for N and M, find the appropriate optimized transition coefficient gain values from the compiled tables in Appendix H. If the tables do not contain optimized coefficients for the given N and M values, the designer may calculate approximate coefficients by linear interpolation of the tabulated values. Alternatively, an optimization software program may be used to find optimized transition coefficients.
Using the values for N, M, and the optimized transition coefficients, determine the interpolated (actual) frequency response of the filter as a function those filter parameters. This frequency response can be obtained by evaluating Eq. (7-24). More conveniently, the frequency response can be determined with a commercial signal processing software package to perform the DFT of the FSF's impulse response sequence, or by using the transfer function coefficients in Eq. (7-23).
Next the fun begins, as the values for N and M are modified slightly, and steps 8 and 9 are repeated, as the design process converges to a minimum value of M to minimize the computational workload, and optimized transition coefficients maximizing stopband attenuation.
When optimized filter parameters are obtained, they are used in an Type-IV FSF implementation, as in Figure 7-28.
The final FSF design step is to sit back and enjoy a job well done.
The Type-IV FSF example presented in Figures 7-27 and 7-28 provides an illustration of the above steps 6 and 7. The initial design estimates for N and M are

Repeated iterations of steps 8–11 converged to the parameters of N = 62 and M = 6 that satisfy the desired filter performance specifications.
We've introduced the structure, performance, and design of frequency sampling FIR filters. Special emphasis was given to the practical issues of phase linearity, stability, and computational workload of these filters. In addition, we presented a detailed comparison between the high-performance Type-IV FSF and its nonrecursive FIR equivalent. Performance curves were presented to help the designer choose between a Type-IV FSF and a Parks-McClellan–designed FIR filter for a given narrowband linear-phase filtering application. We found that:
Type-IV FSFs are more computationally efficient, for certain stopband attenuation levels, than Parks-McClellan–designed nonrecursive FIR filters in lowpass (or highpass) applications where the passband is less than fs/5 and the transition bandwidth is less than fs/8. (See Figures 7-29 and 7-30.)
FSFs are modular. Their components (sections) are computationally identical and well understood;
tables of optimum transition region coefficients, used to improve Type-IV FSF performance, can be generated (as was done in Appendix H); and
although FSFs use recursive structures, they can be designed to be guaranteed stable, and have linear phase.
In this section we cover another class of digital filters called interpolated FIR filters, used to build narrowband lowpass FIR filters that can be more computationally efficient than traditional Parks-McClellan–designed FIR filters. Interpolated FIR filters can reduce traditional narrowband lowpass FIR filter computational workloads by more than 80 percent. In their description, we'll introduce interpolated FIR filters with a simple example, discuss how filter parameter selection is made, provide filter performance curves, and go through a simple lowpass filter design example showing their computational savings over traditional FIR filters[13,14].
Interpolated FIR (IFIR) filters are based upon the behavior of an N-tap nonrecursive linear-phase FIR filter when each of its single-unit delays are replaced with M-unit delays, with the expansion factor M being an integer, as shown in Figure 7-32(a). If the hp(k) impulse response of a 9-tap FIR filter is that shown in Figure 7-32(b), the impulse response of an expanded FIR filter, where for example M = 3, is the hsh(k) in Figure 7-32(c). The M-unit delays result in the zero-valued samples, the white dots, in the hsh(k) impulse response. Our variable k is merely an integer time-domain index where 0 ≤ k ≤ N–1. To define our terminology, we'll call the original FIR filter the prototype filter—that's why we used the subscript “p” in hp(k)—and we'll call the filter with expanded delays the shaping subfilter. Soon we'll see why this terminology is sensible.
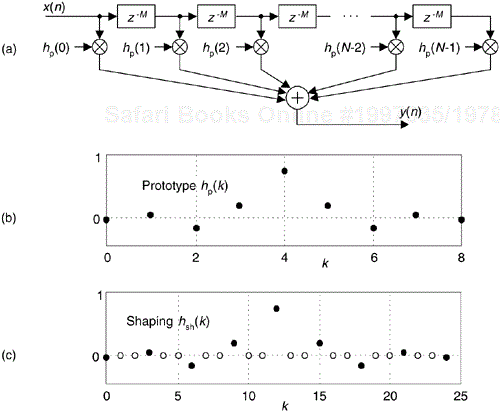
Figure 7-32. Filter relationships: (a) shaping FIR filter with M-unit delays between the taps; (b) impulse response of a prototype FIR filter; (c) impulse response of an expanded-delay shaping FIR filter with M = 3.
We can express a prototype FIR filter's z-domain transfer function as
where Np is the length of hp. The transfer function of a general shaping FIR filter, with z in Eq. (7-31) replaced with zM, is
If the number of coefficients in the prototype filter is Np, the shaping filter has Np nonzero coefficients and an expanded impulse response length of
Later we'll see how Ksh has an important effect on the implementation of IFIR filters.
The frequency-domain effect of those M-unit delays is shown in Figure 7-33. As we should expect, an M-fold expansion of the time-domain filter impulse response causes an M-fold compression (and repetition) of the frequency-domain |Hp(f)| magnitude response as in Figure 7-33(b). The frequency axis of these curves is normalized to fs, with fs being the input signal sample rate. For example, the normalized frequency fpass is equivalent to a cyclic frequency of fpassfs Hz. Those repetitive passbands in |Hsh(f)| centered about integer multiples of 1/M (fs/M Hz) are called images, and on them we now focus our attention.
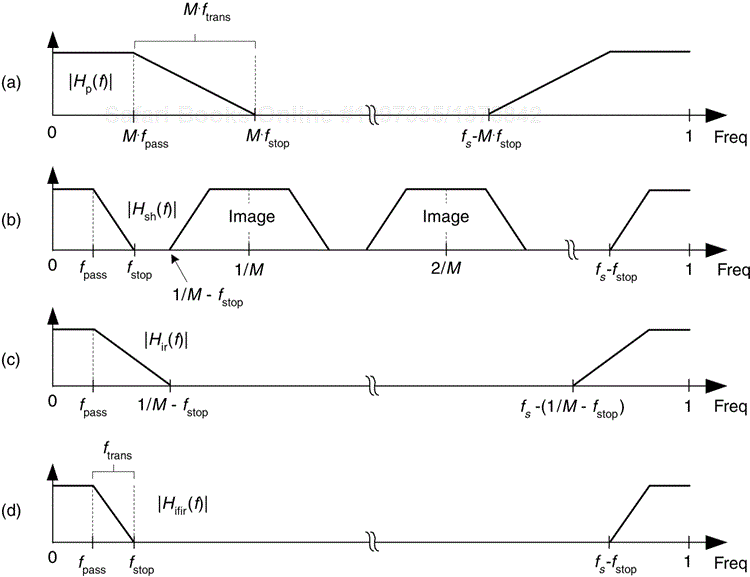
Figure 7-33. IFIR filter magnitudes responses: (a) the prototype filter; (b) shaping subfilter; (c) image-reject subfilter; (d) final IFIR filter.
If we follow the shaping subfilter with a lowpass image-reject subfilter, Figure 7-33(c), whose task is to attenuate the image passbands, we can realize a multistage filter whose frequency response is shown in Figure 7-33(d). The resultant |Hifir(f)| frequency magnitude response is, of course, the product
The structure of the cascaded subfilters is the so-called IFIR filter shown in Figure 7-34(a), with its interpolated impulse response given in Figure 7-34(b).
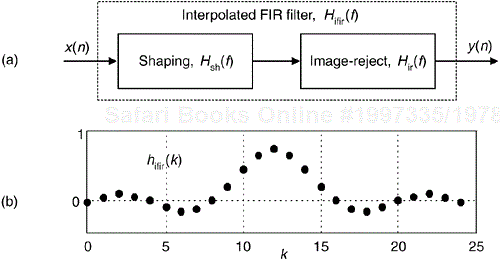
Figure 7-34. Lowpass interpolated FIR filter: (a) cascade structure; (b) resultant impulse response.
If the original desired lowpass filter's passband width is fpass, its stopband begins at fstop, and the transition region width is ftrans = fstop–fpass, then the prototype subfilter's normalized frequency parameters are defined as
The image-reject subfilter's frequency parameters are
The stopband attenuations of the prototype filter and image-reject subfilter are identical and set equal to the desired IFIR filter stopband attenuation. The word “interpolated” in the acronym IFIR is used because the image-reject subfilter interpolates the zero-valued samples in the shaping subfilter's hsh(k) impulse response making the overall IFIR filter's impulse response, hifir(k) in Figure 7-34(b), nearly equivalent to a traditional Ksh-length nonrecursive FIR filter. (Did you notice hifir(k) is an interpolated version of the hp(k) in Figure 7-32(b)?) Some authors emphasize this attribute by referring to the image-reject subfilter as an interpolator. The sample rate remains unchanged within an IFIR filter, so no actual signal interpolation takes place.
To give you an incentive to continue reading, the following example shows the terrific computational advantage of using IFIR filters. Consider the design of a desired linear-phase FIR filter whose normalized passband width is fpass = 0.1, its passband ripple is 0.1 dB, the transition region width is ftrans = 0.02, and the stopband attenuation is 60 dB. (The passband ripple is a peak-peak specification measured in dB.) With an expansion factor of M = 3, the |Hp(f)| frequency magnitude response of the prototype filter is shown in Figure 7-35(a). The normalized frequency axis for these curves is such that a value of 0.5 on the abscissa represents the cyclic frequency fs/2 Hz, half the sample rate. The frequency response of the shaping subfilter, for M = 3, is provided in Figure 7-35(b), with an image passband centered about (1/M) Hz. The response of the image-reject subfilter is the solid curve in Figure 7-35(c), with the response of the overall IFIR filter provided in Figure 7-35(d).
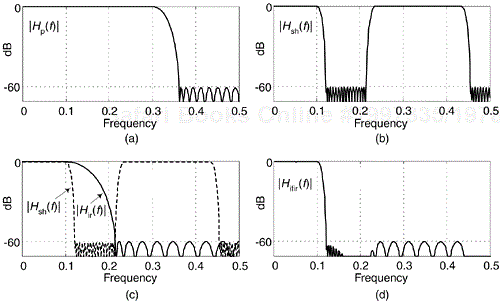
Figure 7-35. Example lowpass IFIR filter magnitudes responses: (a) the prototype filter; (b) shaping subfilter; (c) image-reject subfilter; (d) final IFIR filter.
Satisfying the original desired filter specifications in Figure 7-35(d) would require a traditional single-stage FIR filter with Ntfir = 137 taps, where the “tfir” subscript means traditional FIR. In our IFIR filter, the shaping and the image-reject subfilters require Np = 45 and Nir = 25 taps respectively, for a total of Nifir = 70 taps. We can define the percent reduction in computational workload of an IFIR filter, over a traditional FIR filter, as
As such, the above example IFIR filter has achieved a computational workload reduction, over a traditional FIR filter, of
Figure 7-35 shows how the transition region width (the shape) of |Hifir(f)| is determined by the transition region width of |Hsh(f)|, and this justifies the decision to call hsh(k) the “shaping” subfilter.
The expansion factor M deserves our attention because it can have a profound effect on the computational efficiency of IFIR filters. To show this, had we used M = 2 in our Figure 7-35 example we would have realized an IFIR filter described by the M = 2 column in Table 7-4, in which case the computation reduction over a conventional FIR filter is 43%. With M = 2, a reduced amount of frequency-domain compression occurred in Hsh(f), which mandated more taps in hsh(k) than needed in the M = 3 case.
Table 7-4. IFIR Filter Computation Reduction vs. M
Expansion factor M | Number of taps | Computation reduction % | ||
|---|---|---|---|---|
hsh(k) | hir(k) | IFIR total | ||
2 | 69 | 8 | 77 | 43 |
3 | 45 | 25 | 70 | 49 |
4 | 35 | 95 | 130 | 8 |
Now had M = 4 been used, the computation reduction would only be 8% as shown in Table 7-4. This is because the Hsh(f) passband images would be so close together that a high-performance (increased number of taps) image-reject subfilter would be required. As so often happens in signal processing designs, there is a trade-off to be made. We would like to use a large value for M to compress the Hsh(f)'s transition region width as much as possible, but a large M reduces the transition region width of the image-reject subfilter which increases the number of taps in hir(k) and its computational workload. In our Figure 7-35 IFIR filter example, an expansion factor of M = 3 is optimum because it yields the greatest computation reduction over a traditional single-stage nonrecursive FIR filter.
As indicated in Figure 7-33(b), the maximum M is the largest integer satisfying 1/M–fstop ≥ fstop, ensuring no passband image overlap. This yields an upper bound on M of
where ⌊x⌋ indicates truncation of x to an integer. Thus the acceptable expansion factors are integers in the range 2 ≤ M ≤ Mmax. Evaluating Eq. (7-38) for the Figure 7-35 IFIR filter example yields
justifying the range of M used in Table 7-4.
To estimate the computation reduction of IFIR filters, an algorithm is needed to compute the number of taps, N, in a traditional nonrecursive FIR filter. Several authors have proposed empirical relationships for estimating N for traditional nonrecursive FIR filters based on passband ripple, stopband attenuation, and transition region width[8, 15–17]. A particularly simple expression for N, giving results consistent with other estimates for passband ripple values near 0.1 dB, is
where Atten is the stopband attenuation measured in dB, and fpass and fstop are the normalized frequencies in Figure 7-33(d)[17]. Likewise, the number of taps in the prototype and image-reject subfilters can be estimated using
As it turns out, IFIR filter computational workload reduction depends on the expansion factor M, the passband width, and transition region width of the desired IFIR filter. To show this, we substitute the expressions from Eq. (7-39) into Eq. (7-37) and write
Equation (7-40) is plotted in Figure 7-36(a), for a passband width of one tenth the sample rate (fpass = 0.1) showing the percent computation reduction afforded by an IFIR filter vs. transition region width for expansion factors of 2, 3, and 4. Focusing on Figure 7-36(a), we see when the transition region width is large (say, ftrans = 0.07). The IFIR filter's passband plus transition region width is so wide, relative to the passband width, that only an expansion factor of M = 2 will avoid passband image overlap.
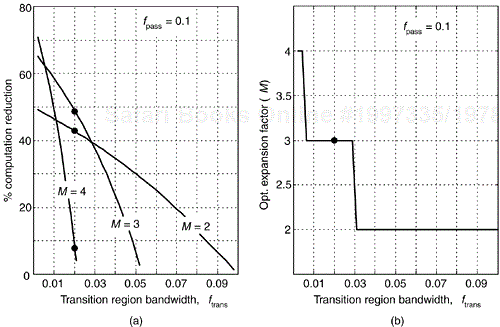
Figure 7-36. IFIR filter performance versus transition region width for fpass = 0.1: (a) percent computation reduction; (b) optimum expansion factors.
At smaller transition region widths, expansion factors of 3 and 4 are possible. For example, over the transition region width range of roughly 0.005 to 0.028, an expansion factor of M = 3 provides greater computation reduction than using M = 2. The optimum (greatest percent computation reduction) expansion factor, as a function of transition region width, is shown in Figure 7-36(b). The black dots in Figure 7-36 represent the Figure 7-35 IFIR filter example with a transition region width of ftrans = 0.02.
To see how the percent computation reduction of IFIR filters vary with the desired passband width, Figure 7-37 shows IFIR filter performance when the desired passband width is 5% of the sample rate (fpass = 0.05). The numbers on the curves in Figure 7-37(a) are the expansion factors.
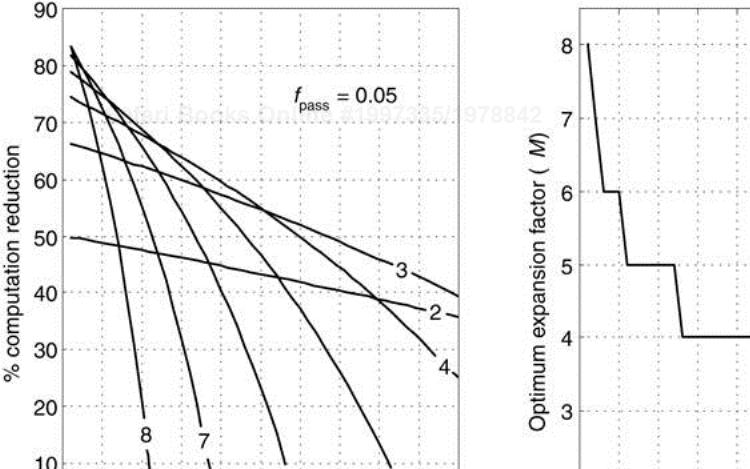
Figure 7-37. IFIR filter performance vs. transition region width for fpass = 0.05: (a) percent computation reduction; (b) optimum expansion factors.
The optimum M values vs. transition region width are presented in Figure 7-37(b). The curves in Figure 7-37(a) illustrate, as the first ratio within the brackets of Eq. (7-40) indicates, that when the transition region width approaches zero, the percent computation reduction approaches 100(M–1)/M.
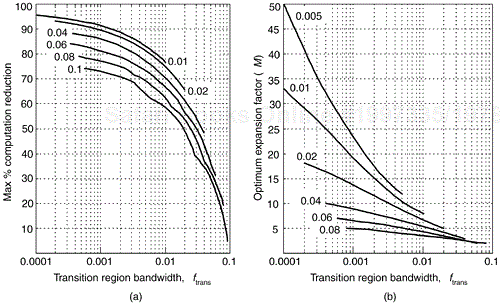
We continue describing the efficiency of IFIR filters by considering the bold curve in Figure 7-38(a), which is the maximum percent computation reduction as a function of transition region width for the fpass = 0.1 IFIR filter described for Figure 7-36(a). The bold curve is plotted on a logarithmic frequency axis, to show maximum percent computation reduction over a wider transition region width range, in Figure 7-38(b).
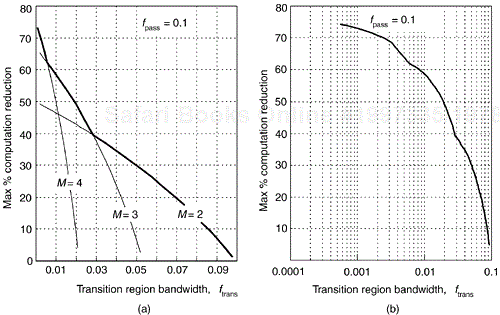
Figure 7-38. Maximum percent computation reduction versus transition region width for fpass = 0.1: (a) plotted on a linear axis; (b) using a logarithmic axis.
Next, we duplicate the Figure 7-38(b) curve in Figure 7-39(a), and include the maximum percent computation reduction vs. transition region width curves for five other IFIR filters having different passband widths showing how significant computation reduction can be achieved by using lowpass IFIR filters. The optimum expansion factors, used to compute the curves in Figure 7-39(a), are shown in Figure 7-39(b). To keep the lower portion of Figure 7-39(b) from being too cluttered, curve fitting was performed to convert the stairstep curves to smooth curves. Shortly we'll see how the curves in Figure 7-39(b) are used in an IFIR filter design example.
The computation reduction of IFIR filters is based on the assumption that they are implemented as two separate subfilters, as in Figure 7-34. We have resisted the temptation to combine the two subfilters into a single filter whose coefficients are the convolution of the subfilters' impulse responses. Such a maneuver would eliminate the zero-valued coefficients of the shaping subfilter, and we'd lose all computation reduction.
The curves in Figure 7-39(b) indicate an important implementation issue when using IFIR filters. With decreasing IFIR filter passband width, larger expansion factors, M, can be used. When using programmable DSP chips, larger values of M require that a larger block of hardware data memory, in the form of a circular buffer, be allocated to hold a sufficient number of input x(n) samples for the shaping subfilter. The size of this data memory must be equal to Ksh, as indicated in Eq. (7-33). Some authors refer to this data memory allocation requirement, to accommodate all the stuffed zeros in the hsh(k) impulse response, as a disadvantage of IFIR filters. This is a misleading viewpoint because, as it turns out, the Ksh length of hsh(k) is only few percent larger than the length of the impulse response of a traditional FIR filter having the same performance as an IFIR filter. So, from a data storage standpoint, the price we pay to use IFIR filters is a slight increase in the memory of size to accommodate Ksh, plus the data memory of size Kir needed for the image-reject subfilter. In practice, for narrowband lowpass IFIR filters, Kir is typically less than 10% of Ksh. The Ksh-sized data memory allocation, for the shaping subfilter, is not necessary in field programmable gate array (FPGA) IFIR filter implementations because FPGA area is not a strong function of the expansion factor M[18].
When implementing an IFIR filter with a programmable DSP chip, the filter's computation reduction gain can only be realized if the chip's architecture enables zero-overhead looping through the circular data memory using an increment equal to the expansion factor M. That looping capability ensures that only the nonzero-valued coefficients of hsh(k) are used in the shaping subfilter computations.
In practice, the shaping and image-reject subfilters should be implemented with a folded nonrecursive FIR structure, exploiting their impulse response symmetry, to reduce the number of necessary multiplications by a factor of two. (See Section 13.7.) Using a folded structure does not alter the performance curves provided in Figure 7-39. Regarding an IFIR filter's implementation in fixed-point hardware, its sensitivity to coefficient quantization errors is no greater than the errors exhibited by traditional FIR filters[13].
The design of practical lowpass IFIR filters is straightforward, and comprises four steps:
Define the desired lowpass filter performance requirements.
Determine a candidate value for the expansion factor M.
Design and evaluate the shaping and image-reject subfilters.
Investigate IFIR performance for alternate expansion factors near the initial M value.
As a design example, refer to Figure 7-33(d) and assume we want to build a lowpass IFIR filter with fpass = 0.02, a peak-to-peak passband ripple of 0.5 dB, a transition region bandwidth of ftrans = 0.01 (thus fstop = 0.03), and 50 dB of stopband attenuation. First, we find the ftrans = 0.01 point on the abscissa of Figure 7-39(b) and follow it up to the point where it intersects the fpass = 0.02 curve. This intersection indicates we should start our design with an expansion factor of M = 7. (The same intersection point in Figure 7-39(a) suggests we can achieve a computational workload reduction of roughly 80%.)
With M = 7, and applying Eq. (7-35), we use our favorite traditional FIR filter design software to design a linear-phase prototype FIR filter with the following parameters:
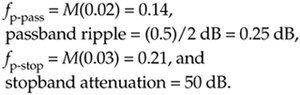
(Notice how we used our cascaded filters' passband ripple rule of thumb from Section 6.8.1 to specify the prototype filter's passband ripple to be half our final desired ripple. We'll do the same for the image-reject subfilter.) Such a prototype FIR filter will have Np = 33 taps and, from Eq. (7-33), when expanded by M = 7 the shaping subfilter will have an impulse response length of Ksh = 225 samples.
Next, using Eq. (7-36) we design a image-reject subfilter having the following parameters:
This image-reject subfilter will have Nir = 27 taps, and when cascaded with the shaping subfilter will yield an IFIR filter requiring 60 multiplications per filter output sample. The frequency response of the IFIR filter is shown in Figure 7-40(a), with passband response detail provided in Figure 7-40(b).
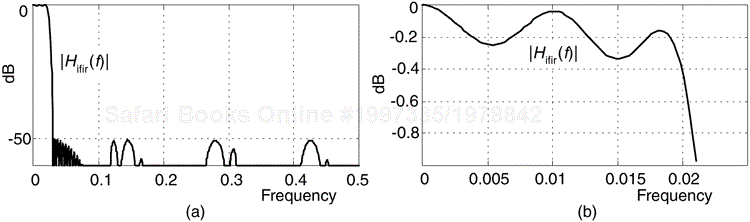
Figure 7-40. IFIR filter design example magnitudes responses: (a) full response; (b) passband response detail.
A traditional FIR filter satisfying our design example specifications would require approximately Ntfir = 240 taps. Because the IFIR filter requires only 60 multiplications per output sample, using Eq. (7-37), we have realized a computational workload reduction of 75%. The final IFIR filter design step is to sit back and enjoy a job well done.
Further modeling of our design example for alternate expansion factors yields the IFIR filter performance results in Table 7-5. There we see how the M expansion factors of 5 through 8 provide very similar computational reductions and Ksh-sized data storage requirements for the shaping subfilter.
IFIR filters are suitable whenever narrowband lowpass linear-phase filtering is required, for example the filtering prior to decimation for narrowband channel selection within wireless communications receivers, or in digital television. IFIR filters are essential components in sharp-transition wideband frequency-response masking FIR filters[19,20]. In addition, IFIR filters can also be employed in narrowband two-dimensional filtering applications.
Additional, and more complicated, IFIR design methods have been described in the literature. Improved computational workload reduction, on the order of 30–40% beyond that presented here, has been reported using an intricate design scheme when the Figure 7-34 image-reject subfilter is replaced with multiple stages of filtering[21].
To conclude our linear-phase narrowband IFIR filter material, we reiterate: they can achieve significant computational workload reduction (as large as 90%) relative to traditional nonrecursive FIR filters, at the cost of less than a 10% increase in hardware data memory requirements. Happily, IFIR implementation is a straightforward cascade of filters designed using readily available traditional FIR filter design software.