As we study the literature of digital signal processing, we'll encounter some creative techniques that professionals use to make their algorithms more efficient. These practical techniques are straightforward examples of the philosophy “don't work hard, work smart,” and studying them will give us a deeper understanding of the underlying mathematical subtleties of DSP. In this chapter, we present a collection of these tricks of the trade, in no particular order, and explore several of them in detail because doing so reinforces the lessons we've learned in previous chapters.
Frequency translation is often called for in digital signal processing algorithms. There are simple schemes for inducing frequency translation by 1/2 and 1/4 of the signal sequence sample rate. Let's take a look at these mixing schemes.
First we'll consider a technique for frequency translating an input sequence by fs/2 by merely multiplying a sequence by (–1)n = 1,–1,1,–1, ..., etc., where fs is the signal sample rate in Hz. This process may seem a bit mysterious at first, but it can be explained in a straightforward way if we review Figure 13-1(a).There we see that multiplying a time domain signal sequence by the (–1)n mixing sequence is equivalent to multiplying the signal sequence by a sampled cosinusoid where the mixing sequence samples are shown as the dots in Figure 13-1(a). Because the mixing sequence's cosine repeats every two sample values, its frequency is fs/2. Figure 13-1(b) and (c) show the discrete Fourier transform (DFT) magnitude and phase of a 32-sample (–1)n sequence. As such, the right half of those figures represents the negative frequency range.
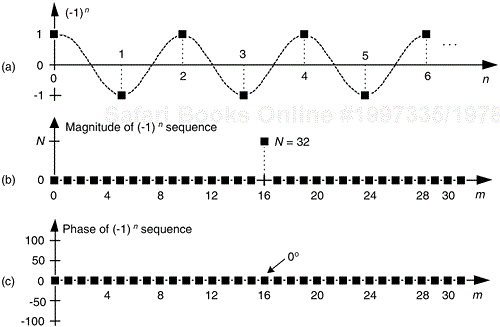
Figure 13-1. Mixing sequence comprising (–1)n = 1,–1,1,–1, etc: (a) time-domain sequence; (b) frequency-domain magnitudes for 32 samples; (c) frequency-domain phase.
Let's demonstrate this (–1)n mixing by an example. Consider a real x(n) signal sequence having 32 samples of the sum of three sinusoids whose |X(m)| frequency magnitude and φ(m) phase spectra are as shown in Figure 13-2(a) and (b). If we multiply that time signal sequence by (–1)n, the resulting x1,–1(n) time sequence will have the magnitude and phase spectra are that shown in Figure 13-2(c) and (d). Multiplying a time signal by our (–1)n, cosine shifts half its spectral energy up by fs/2 and half its spectral energy down by –fs/2. Notice in these non-circular frequency depictions that as we count up, or down, in frequency we wrap around the end points.
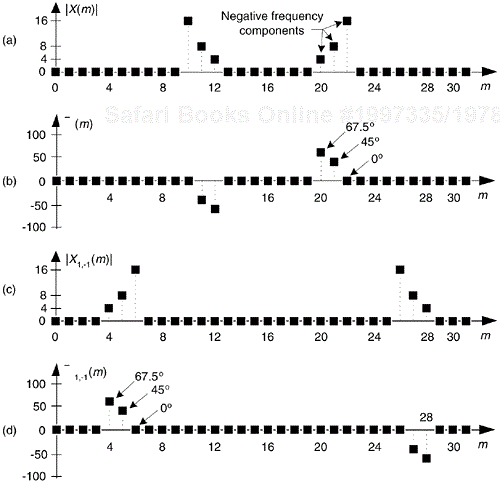
Figure 13-2. A signal and its frequency translation by fs/2: (a) original signal magnitude spectrum; (b) original phase; (c) the magnitude spectrum of the translated signal; (d) translated phase.
Here's a terrific opportunity for the DSP novice to convolve the (–1)n spectrum in Figure 13-1 with the X(m) spectrum to obtain the frequency-translated X1,–1(m) signal spectrum. Please do so; that exercise will help you comprehend the nature of discrete sequences and their time and frequency-domain relationships by way of the convolution theorem.
Remember now, we didn't really perform any explicit multiplications—the whole idea here is to avoid multiplications, we merely changed the sign of alternating x(n) samples to get x1,–1(n). One way to look at the X1,–1(m) magnitudes in Figure 13-2(c) is to see that multiplication by the (–1)n mixing sequence flips the positive frequency band of X(m) [X(0) to X(16)] about the fs/4 Hz point, and flips the negative frequency band of X(m) [X(17) to X(31)] about the –fs/4 Hz sample. This process can be used to invert the spectra of real signals when bandpass sampling is used as described in Section 2.4. By the way, in the DSP literature be aware that some clever authors may represent the (–1)n sequence with its equivalent expressions of
Two other simple mixing sequences form the real and imaginary parts of a complex –fs/4 oscillator used for frequency down-conversion to obtain a quadrature version (complex and centered at 0 Hz) of a real bandpass signal originally centered at fs/4. The real (in-phase) mixing sequence is cos(πn/2) = 1,0,–1,0, etc. shown in Figure 13-3(a). That mixing sequence's quadrature companion is –sin(πn/2) = 0,–1,0,1, etc. as shown in Figure 13-3(b). The spectral magnitudes of those two sequence are identical as shown in Figure 13-3(c), but their phase spectrum has a 90° shift relationship (what we call quadrature).
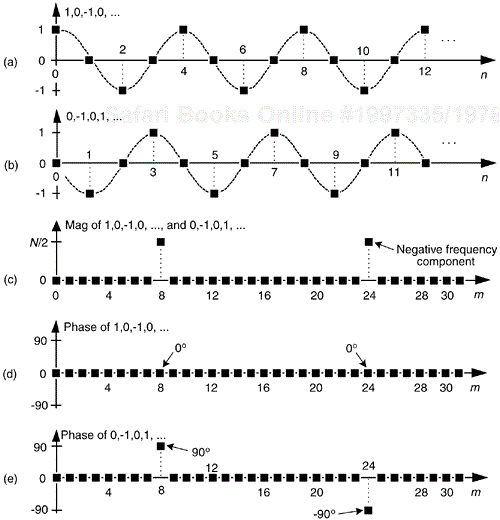
Figure 13-3. Quadrature mixing sequences for downconversion by fs/4: (a) in-phase mixing sequence; (b) quadrature phase mixing sequence; (c) the frequency magnitudes of both sequences for N = 32 samples; (d) the phase of the cosine sequence; (e) phase of the sine sequence.
If we multiply the x(n) sequence whose spectrum is that in Figure 13-2(a) and (b) by the in-phase (cosine) mixing sequence, the product will have the I(m) spectrum shown in Figures 13-4(a) and (b). Again, X(m)'s spectral energy is translated up and down in frequency, only this time the translation is by ±fs/4. Multiplying x(n) by the quadrature phase (sine) sequence yields the Q(m) spectrum in Figure 13-4(a) and (c).
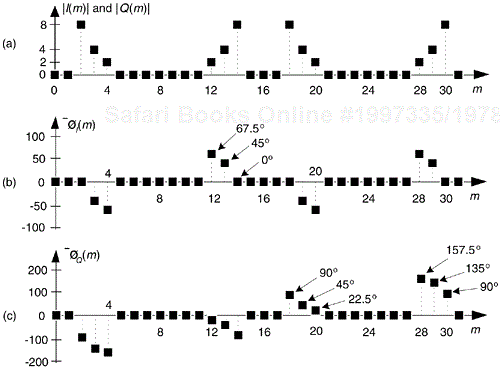
Figure 13-4. Spectra after translation down by fs/4: (a) I(m) and Q(m) spectral magnitudes; (b) phase of I(m) ; (c) phase of Q(m).
Because their time sample values are merely 1, –1, and 0, the quadrature mixing sequences are useful because downconversion by fs/4 can be implemented without multiplication. That's why these mixing sequences are of so much interest: downconversion of an input time sequence is accomplished merely with data assignment, or signal routing.
To downconvert a general x(n) = xreal(n) + jximag(n) sequence by fs/4, the value assignments are:
If your implementation is hardwired gates, the above data assignments are performed by means of routing signals (and their negatives). Although we've focused on downconversion so far, it's worth mentioning that upconversion of a general x(n) sequence by fs/4 can be performed with the following data assignments:
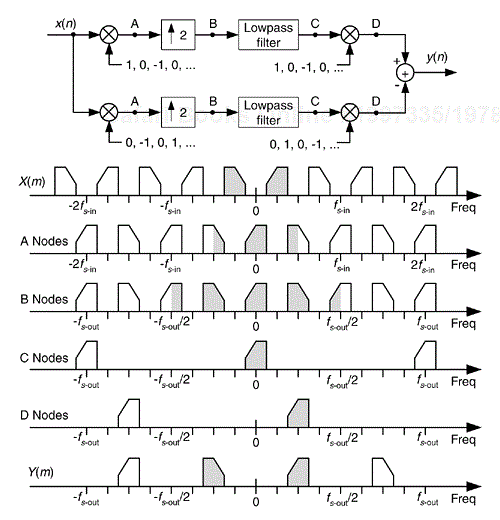
There's an efficient way to perform the complex down-conversion and filtering of a real signal by fs/4 process we considered for the quadrature sampling scheme in Section 8.9. We can use a novel technique to greatly reduce the computational workload of the linear-phase lowpass filters[1–3]. In addition, decimation of the complex down-converted sequence by a factor of two is inherent, with no effort on our part, in this process.
Considering Figure 13-5(a), notice that if an original x(n) sequence was real-only, and its spectrum is centered at fs/4, multiplying x(n) by cos(πn/2) = 1,0,–1,0, for the in-phase path and –sin(πn/2) = 0,–1,0,1, for the quadrature phase path to down-convert x(n)'s spectrum to 0 Hz, yields the new complex sequence xnew(n) = xi(n) + xq(n), or
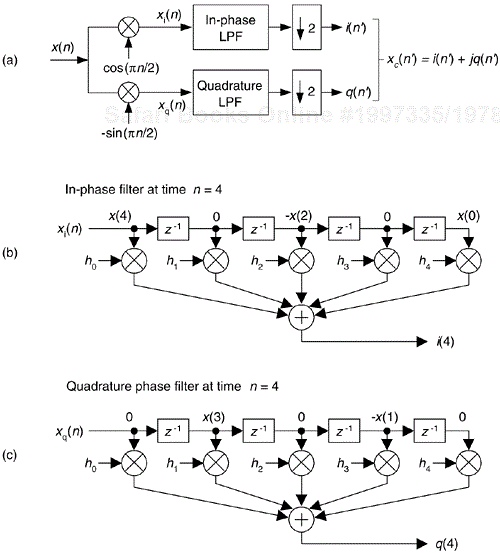
Figure 13-5. Down-conversion by fs/4 and filtering: (a) the process; (b) the data in the in-phase filter; (c) data within the quadrature phase filter.
Next, we want to lowpass filter (LPF) both the xi(n) and xq(n) sequences followed by decimation by a factor of two.
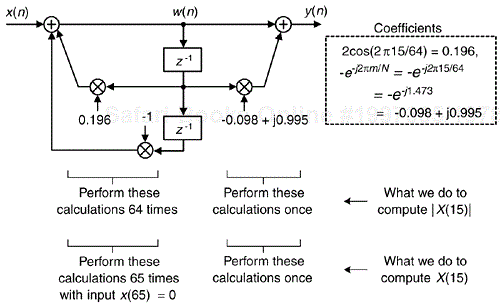
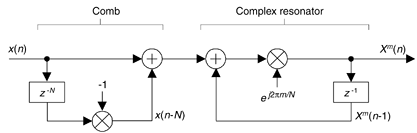
Here's the trick. Let's say we're using five-tap FIR filters and at the n = 4 time index; the data residing in the two lowpass filters would be that shown in Figure 13-5(b) and (c). Due to the alternating zero-valued samples in the xi(n) and xq(n) sequences, we see that only five non-zero multiplies are being performed at this time instant. Those computations, at time index n = 4, are shown in the third row of the rightmost column in Table 13-1. Because we're decimating by two, we ignore the time index n = 5 computations. The necessary computations during the next time index (n = 6) are given in the fourth row of Table 13-1, where again only five non-zero multiplies are computed.
A review of Table 13-1 tells us we can multiplex the real-valued x(n) sequence, multiply the multiplexed sequences by the repeating mixing sequence 1,–1, ..., etc., and apply the resulting xi(n) and xq(n) sequences to two filters, as shown in Figure 13-6(a). Those two filters have decimated coefficients in the sense that their coefficients are the alternating h(k) coefficients from the original lowpass filter in Figure 13-5. The two new filters are depicted in Figure 13-6(b), showing the necessary computations at time index n = 4. Using this new process, we've reduced our multiplication workload by a factor of two. The original data multiplexing in Figure 13-6(a) is what implemented our desired decimation by two.
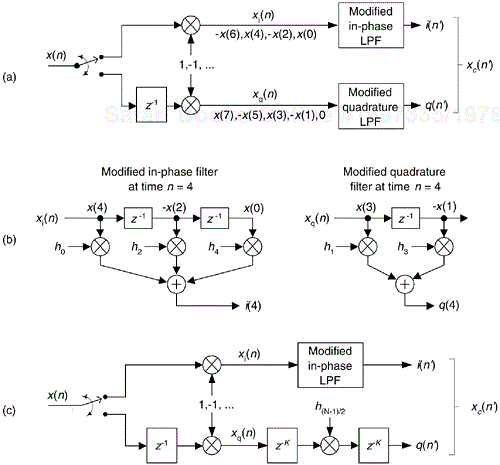
Figure 13-6. Efficient down-conversion, filtering and decimation: (a) process block diagram; (b) the modified filters and data at time n = 4; (c) process when a half-band filter is used.
Table 13-1. Filter Data and Necessary Computations after Decimation by Two
Time | Data in the Filters | Necessary Computations | ||||
|---|---|---|---|---|---|---|
n = 0 | x(0) | – | – | – | – | i(0) = x(0)h0 |
h0 | h1 | h2 | h3 | h4 | ||
0 | – | – | – | – | q(0) = 0 | |
n = 2 | –x(2) | 0 | x(0) | – | – | i(2) = x(0)h2 –x(2)h0 |
h0 | h1 | h2 | h3 | h4 | ||
0 | –x(1) | 0 | – | – | q(2) = –x(1)h1 | |
n = 4 | x(4) | 0 | –x(2) | 0 | x(0) | i(4) = x(0)h4 –x(2)h2 +x(4)h0 |
h0 | h1 | h2 | h3 | h4 | ||
0 | x(3) | 0 | –x(1) | 0 | q(4) = –x(1)h3 +x(3)h1 | |
n = 6 | –x(6) | 0 | x(4) | 0 | –x(2) | i(6) = –x(2)h4 +x(4)h2 –x(6)h0 |
h0 | h1 | h2 | h3 | h4 | ||
0 | –x(5) | 0 | x(3) | 0 | q(6) = x(3)h3 –x(5)h1 | |
n = 8 | x(8) | 0 | –x(6) | 0 | x(4) | i(8) = x(4)h4 –x(6)h2 +x(8)h0 |
h0 | h1 | h2 | h3 | h4 | ||
0 | x(7) | 0 | –x(5) | 0 | q(8) = –x(5)h3 +x(7)h1dn7 | |
Here's another feature of this efficient down-conversion structure. If half-band filters are used in Figure 13-5(a), then only one of the coefficients in the modified quadrature lowpass filter is non-zero. This means we can implement the quadrature-path filtering as K unit delays, a single multiply by the original half-band filter's center coefficient, followed by another K delay as depicted in Figure 13-6(c). For an original N-tap half-band filter, K is the integer part of N/4. If the original half-band filter's h(N–1)/2 center coefficient is 0.5, as is often the case, we can implement its multiply by an arithmetic right shift of the delayed xq(n).
This down-conversion process is indeed slick. Here's another attribute. If the original lowpass filter in Figure 13-5(a) has an odd number of taps, the coefficients of the modified filters in Figure 13-6(b) will be symmetrical and we can use the folded FIR filter scheme (Section 13.7) to reduce the number of multipliers (at the expense of additional adders) by almost another factor of two!
Finally, if we need to invert the output xc(n') spectrum, there are two ways to do so. We can negate the 1,–1, sequence driving the mixer in the quadrature path, or we can swap the order of the single unit delay and the mixer in the quadrature path.
The quadrature processing techniques employed in spectrum analysis, computer graphics, and digital communications routinely require high speed determination of the magnitude of a complex number (vector V) given its real and imaginary parts, i.e., the in-phase part I and the quadrature-phase part Q. This magnitude calculation requires a square root operation because the magnitude of V is
Assuming that the sum I2 + Q2 is available, the problem is efficiently to perform the square root operation.
There are several ways to obtain square roots. The optimum technique depends on the capabilities of the available hardware and software. For example, when performing a square root using a high-level software language, we employ whatever software square root function is available. Although accurate, software routines can be very slow. By contrast, if a system must accomplish a square root operation in 50 nanoseconds, high-speed magnitude approximations are required[4,5]. Let's look at a neat magnitude approximation scheme that's particularly hardware efficient.
There is a technique called the αMax+βMin (read as “alpha max plus beta min”) algorithm for calculating the magnitude of a complex vector.[†] It's a linear approximation to the vector magnitude problem that requires the determination of which orthogonal vector, I or Q, has the greater absolute value. If the maximum absolute value of I or Q is designated by Max, and the minimum absolute value of either I or Q is Min, an approximation of |V| using the αMax+βMin algorithm is expressed as
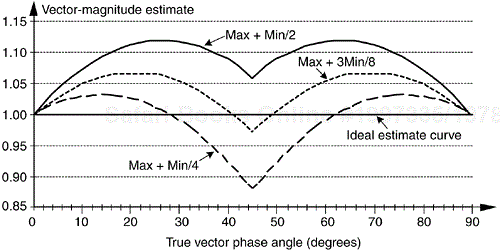
There are several pairs for the α and β constants that provide varying degrees of vector magnitude approximation accuracy to within 0.1 dB[4,7]. The αMax+βMin algorithms in Reference [10] determine a vector magnitude at whatever speed it takes a system to perform a magnitude comparison, two multiplications, and one addition. But those algorithms require, as a minimum, a 16-bit multiplier to achieve reasonably accurate results. If, however, hardware multipliers are not available, all is not lost. By restricting the α and β constants to reciprocals of integer powers of two, Eq. (13-6) lends itself well to implementation in binary integer arithmetic. A prevailing application of the αMax+βMin algorithm uses α = 1.0 and β = 0.5[8–10]. The 0.5 multiplication operation is performed by shifting the minimum quadrature vector magnitude, Min, to the right by one bit. We can gauge the accuracy of any vector magnitude estimation algorithm by plotting its error as a function of vector phase angle. Let's do that. The αMax+βMin estimate for a complex vector of unity magnitude, using
over the vector angular range of 0 to 90 degrees, is shown as the solid curve in Figure 13-7. (The curves in Figure 13-7 repeat every 90°.)
An ideal estimation curve for a unity magnitude vector would have a value of one. We'll use this ideal estimation curve as a yardstick to measure the merit of various αMax+βMin algorithms. Let's make sure we know what the solid curve in Figure 13-7 is telling us. It indicates that a unity magnitude vector oriented at an angle of approximately 26° will be estimated by Eq. (13-7) to have a magnitude of 1.118 instead of the correct magnitude of one. The error then, at 26°, is 11.8%, or 0.97 dB. Analyzing the entire solid curve in Figure 13-7 results in an average error, over the 0 to 90° range, of 8.6% (0.71 dB). Figure 13-7 also presents the error curves for the α = 1 and β = 1/4, and the α = 1 and β = 3/8 values.
Although the values for α and β in Figure 13-7 yield rather accurate vector magnitude estimates, there are other values for α and β that deserve our attention because they result in smaller error standard deviations. Consider the α = 7/8 and β = 7/16 pair where its error curve is the solid curve in Figure 13-8. A further improvement can be obtained using α = 15/16 and β = 15/32 having an error shown by the dashed curve in Figure 13-8. The α = 15/16 and β = 15/32 pair give rather good results when compared to the optimum floating point values of α = 0.96043387 and β = 0.397824735 reported in Reference [11], whose error is the dotted curve in Figure 13-8.
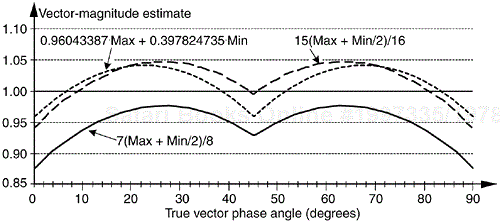
Figure 13-8. αMax+βMin estimates for α = 7/8, β = 7/16; α = 15/16, β = 15/32; and α = 0.96043387, β = 0.397824735.
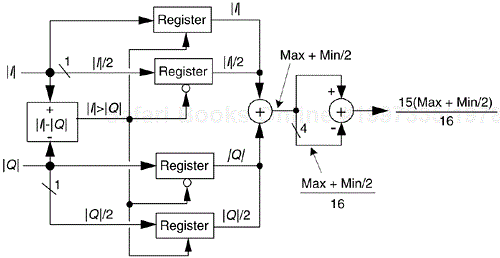
Although using β = 15/16 and β = 15/32 appears to require two multiplications and one addition, its digital hardware implementation can be straightforward, as shown in Figure 13-9. The diagonal lines, 1 for example, denote a hardwired shift of one bit to the right to implement a divide-by-two operation by truncation. Likewise, the 4 symbol indicates a right shift by four bits to realize a divide-by-16 operation. The |I|>|Q| control line is TRUE when the magnitude of I is greater than the magnitude of Q, so that Max = |I| and Min = |Q|. This condition enables the registers to apply the values |I| and |Q|/2 to the adder. When |I| > |Q| is FALSE, the registers apply the values |Q| and |I|/2 to the adder. Notice that the output of the adder, Max + Min/2, is the result of Eq. (13-26). Equation (13-29) is implemented via the subtraction of (Max + Min/2)/16 from Max + Min/2.
In Figure 13-9, all implied multiplications are performed by hardwired bit shifting and the total execution time is limited only by the delay times associated with the hardware components.
One thing to keep in mind. Because the various |V| estimations can exceed the correct normalized vector magnitude value, i.e., some magnitude estimates are greater than one. This means that although the correct magnitude value may be within the system's full-scale word width, an algorithm result may exceed the word width of the system and cause overflow errors. With αMax+βMin algorithms the user must be certain that no true vector magnitude exceeds the value that will produce an estimated magnitude greater than the maximum allowable word width.
The penalty we pay for the convenience of having α and β as powers of two is the error induced by the division-by-truncation process, and we haven't taken that error into account thus far. The error curves in Figure 13-7 and Figure 13-8 were obtained using a software simulation with its floating point accuracy, and are useful in evaluating different α and β values. However, the true error introduced by the αMax+βMin algorithm will be somewhat different, due to division errors when truncation is used with finite word widths. For αMax+βMin schemes, the truncation errors are a function of the data's word width, the algorithm used, the values of both |I| and |Q|, and the vector's phase angle. (These errors due to truncation compound the errors already inherent in our αMax+βMin algorithms.) However, modeling has shown that for an 8-bit system (maximum vector magnitude = 255) the truncation error is less than 1%. As the system word width increases the truncation errors approach 0%, this means that truncation errors add very little to the inherent αMax+βMin algorithm errors.
The relative performance of the various algorithms is summarized in Table 13-2.
The last column in Table 13-2 illustrates the maximum allowable true vector magnitude as a function of the system's full-scale (F.S.) word width to avoid overflow errors.
So, the αMax+βMin algorithm enables high speed vector magnitude computation without the need for math coprocessor or hardware multiplier chips. Of course, with the recent availability of high-speed floating point multiplier integrated circuits—with their ability to multiply in one or two clock cycles—α and β may not always need to be restricted to reciprocals of integer powers of two. It's also worth mentioning that this algorithm can be nicely implemented in a single hardware integrated circuit (for example, a field programmable gate array) affording high speed operation.
Table 13-2. αMax+βMin Algorithm Comparisons
Algorithm |V| ≈ | Largest error (%) | Largest error (dB) | Average error (%) | Average error (dB) | Max |V| (% F.S.) |
|---|---|---|---|---|---|
Max + Min/2 | 11.8% | 0.97 dB | 8.6% | 0.71 dB | 89.4% |
Max + Min/4 | –11.6% | –1.07 dB | –0.64% | –0.06 dB | 97.0% |
Max + 3Min/8 | 6.8% | 0.57 dB | 3.97% | 0.34 dB | 93.6% |
7(Max + Min/2)/8 | –12.5% | –1.16 dB | –4.99% | –0.45 dB | 100% |
15(Max + Min/2)/16 | –6.25% | –0.56 dB | 1.79% | 0.15 dB | 95.4% |
There's an interesting technique for minimizing the calculations necessary to implement windowing of FFT input data to reduce spectral leakage. There are times when we need the FFT of unwindowed time domain data, while at the same time we also want the FFT of that same time-domain data with a window function applied. In this situation, we don't have to perform two separate FFTs. We can perform the FFT of the unwindowed data and then we can perform frequency-domain windowing on that FFT results to reduce leakage. Let's see how.
Recall from Section 3.9 that the expressions for the Hanning and the Hamming windows were wHan(n) = 0.5 –0.5cos(2πn/N) and wHam(n) = 0.54 –0.46cos(2πn/N), respectively. They both have the general cosine function form of
for n = 0, 1, 2, ..., N–1. Looking at the frequency response of the general cosine window function, using the definition of the DFT, the transform of Eq. (13-8) is
Because ![]() , Eq. (13-9) can be written as
, Eq. (13-9) can be written as
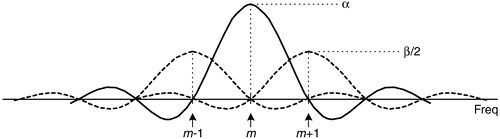
Equation (13-10) looks pretty complicated, but using the derivation from Section 3.13 for expressions like those summations we find that Eq. (13-10) merely results in the superposition of three sin(x)/x functions in the frequency domain. Their amplitudes are shown in Figure 13-10.
Notice that the two translated sin(x)/x functions have side lobes with opposite phase from that of the center sin(x)/x function. This means that α times the mth bin output, minus β/2 times the (m–1)th bin output, minus β/2 times the (m+1)th bin output will minimize the sidelobes of the mth bin. This frequency domain convolution process is equivalent to multiplying the input time data sequence by the N-valued window function w(n) in Eq. (13-8)[12–14].
For example, let's say the output of the mth FFT bin is X(m) = am + jbm, and the outputs of its two neighboring bins are X(m–1) = a–1 + jb–1 and X(m+1) = a+1 + jb+1. Then frequency-domain windowing for the mth bin of the unwindowed X(m) is as follows:
To compute a windowed N-point FFT, Xthree-term(m), we can apply Eq. (13-11), requiring 4N additions and 3N multiplications, to the unwindowed N-point FFT result X(m) and avoid having to perform the N multiplications of time domain windowing and a second FFT with its Nlog2(N) additions and 2Nlog2(N) multiplications. (In this case, we called our windowed results Xthree-term(m) because we're performing a convolution of a three-term W(m) sequence with the X(m) sequence.)
The neat situation here are the frequency-domain coefficients values, α and β, for the Hanning window. They're both 0.5, and the multiplications in Eq. (13-11) can be performed in hardware with two binary right shifts by a single bit for α = 0.5 and two shifts for each of the two β/2 = 0.25 factors, for a total of six binary shifts. If a gain of four is acceptable, we can get away with only two left shifts (one for the real and one for the imaginary parts of X(m)) using
In application specific integrated circuit (ASIC) and field-programmable gate array (FPGA) hardware implementations, where multiplies are to be avoided, the binary shifts can be eliminated through hard-wired data routing. Thus only additions are necessary to implement frequency-domain Hanning windowing. The issues we need to consider are which window function is best for the application, and the efficiency of available hardware in performing the frequency domain multiplications. Frequency-domain Hamming windowing can be implemented but, unfortunately, not with simple binary shifts.
Along with the Hanning and Hamming windows, Reference [14] describes a family of windows known as Blackman windows that provide further FFT spectral leakage reduction when performing frequency-domain windowing. (Note: Reference [14] reportedly has two typographical errors in the 4-Term (–74 dB) window coefficients column on its page 65. Reference [15] specifies those coefficients to be 0.40217, 0.49703, 0.09892, and 0.00188.) Blackman windows have five non-zero frequency-domain coefficients, and their use requires the following five-term convolution:
Table 13-3 provides the frequency-domain coefficients for several common window functions.
Let's end our discussion of the frequency-domain windowing trick by saying this scheme can be efficient because we don't have to window the entire set of FFT data; windowing need only be performed on those FFT bin outputs of interest to us. An application of frequency-domain windowing is presented in Section 13.18.
The multiplication of two complex numbers is one of the most common functions performed in digital signal processing. It's mandatory in all discrete and fast Fourier transformation algorithms, necessary for graphics transformations, and used in processing digital communications signals. Be it in hardware or software, it's always to our benefit to streamline the processing necessary to perform a complex multiply whenever we can. If the available hardware can perform three additions faster than a single multiplication, there's a way to speed up a complex multiply operation [16].
The multiplication of two complex numbers, a + jb and c + jd, results in the complex product
We can see that Eq. (13-14) requires four multiplications and two additions. (From a computational standpoint we'll assume a subtraction is equivalent to an addition.) Instead of using Eq. (13-14), we can calculate the following intermediate values
We then perform the following operations to get the final R and I
The reader is invited to plug the k values from Eq. (13-15) into Eq. (13-16) to verify that the expressions in Eq. (13-16) are equivalent to Eq. (13-14). The intermediate values in Eq. (13-15) required three additions and three multiplications, while the results in Eq. (13-16) required two more additions. So we traded one of the multiplications required in Eq. (13-14) for three addition operations needed by Eq. (13-15) and Eq. (13-16). If our hardware uses fewer clock cycles to perform three additions than a single multiplication, we may well gain overall processing speed by using Eq. (13-15) and Eq. (13-16) instead of Eq. (13-14) for complex multiplication.
Upon recognizing its linearity property and understanding the odd and even symmetries of the transform's output, the early investigators of the fast Fourier transform (FFT) realized that two separate, real N-point input data sequences could be transformed using a single N-point complex FFT. They also developed a technique using a single N-point complex FFT to transform a 2N-point real input sequence. Let's see how these two techniques work.
The standard FFT algorithms were developed to accept complex inputs; that is, the FFT's normal input x(n) sequence is assumed to comprise real and imaginary parts, such as
In typical signal processing schemes, FFT input data sequences are usually real. The most common example of this is the FFT input samples coming from an A/D converter that provides real integer values of some continuous (analog) signal. In this case the FFT's imaginary xi(n)'s inputs are all zero. So initial FFT computations performed on the xi(n) inputs represent wasted operations. Early FFT pioneers recognized this inefficiency, studied the problem, and developed a technique where two independent N-point, real input data sequences could be transformed by a single N-point complex FFT. We call this scheme the Two N-Point Real FFTs algorithm. The derivation of this technique is straightforward and described in the literature[17–19]. If two N-point, real input sequences are a(n) and b(n), they'll have discrete Fourier transforms represented by Xa(m) and Xb(m). If we treat the a(n) sequence as the real part of an FFT input and the b(n) sequence as the imaginary part of the FFT input, then
Applying the x(n) values from Eq. (13-18) to the standard DFT,
we'll get an DFT output X(m) where m goes from 0 to N–1. (We're assuming, of course, that the DFT is implemented by way of an FFT algorithm.) Using the superscript * symbol to represent the complex conjugate, we can extract the two desired FFT outputs Xa(m) and Xb(m) from X(m) by using the following:
and
Let's break Eqs. (13-20) and (13-21) into their real and imaginary parts to get expressions for Xa(m) and Xb(m) that are easier to understand and implement. Using the notation showing X(m)'s real and imaginary parts, where X(m) = Xr(m) + jXi(m), we can rewrite Eq. (13-20) as
where m = 1, 2, 3, . . ., N–1. What about the first Xa(m), when m = 0? Well, this is where we run into a bind if we actually try to implement Eq. (13-20) directly. Letting m = 0 in Eq. (13-40), we quickly realize that the first term in the numerator, X*(N–0) = X*(N), isn't available because the X(N) sample does not exist in the output of an N-point FFT! We resolve this problem by remembering that X(m) is periodic with a period N, so X(N) = X(0).[†] When m = 0, Eq. (13-20) becomes
Next, simplifying Eq. (13-21),
where, again, m = 1, 2, 3, . . ., N–1. By the same argument used for Eq. (13-23), when m = 0, Xb(0) in Eq. (13-24) becomes
This discussion brings up a good point for beginners to keep in mind. In the literature Eqs. (13-20) and (13-21) are often presented without any discussion of the m = 0 problem. So, whenever you're grinding through an algebraic derivation or have some equations tossed out at you, be a little skeptical. Try the equations out on an example—see if they're true. (After all, both authors and book typesetters are human and sometimes make mistakes. We had an old saying in Ohio for this situation: “Trust everybody, but cut the cards.”) Following this advice, let's prove that this Two N-Point Real FFTs algorithm really does work by applying the 8-point data sequences from Chapter 3's DFT Examples to Eqs. (13-22) through (13-25). Taking the 8-point input data sequence from Section 3.1's DFT Example 1 and denoting it a(n),
Taking the 8-point input data sequence from Section 3.6's DFT Example 2 and calling it b(n),
Combining the sequences in Eqs. (13-26) and (13-27) into a single complex sequence x(n),
Now, taking the 8-point FFT of the complex sequence in Eq. (13-28) we get
So from Eq. (13-23),
To get the rest of Xa(m), we have to plug the FFT output's X(m) and X(N–m) values into Eq. (13-22).[†] Doing so,


So Eq. (13-22) really does extract Xa(m) from the X(m) sequence in Eq. (13-29). We can see that we need not solve Eq. (13-22) when m is greater than 4 (or N/2) because Xa(m) will always be conjugate symmetric. Because Xa(7) = Xa(1), Xa(6) = Xa(2), etc., only the first N/2 elements in Xa(m) are independent and need be calculated.
OK, let's keep going and use Eqs. (13-24) and (13-25) to extract Xb(m) from the FFT output. From Eq. (13-25),
Plugging the FFT's output values into Eq. (13-24) to get the next four Xb(m)s, we have

The question arises “With the additional processing required by Eqs. (13-22) and (13-24) after the initial FFT, how much computational saving (or loss) is to be had by this Two N-Point Real FFTs algorithm?” We can estimate the efficiency of this algorithm by considering the number of arithmetic operations required relative to two separate N-point radix-2 FFTs. First, we estimate the number of arithmetic operations in two separate N-point complex FFTs.
From Section 4.2, we know that a standard radix-2 N-point complex FFT comprises (N/2) log2N butterfly operations. If we use the optimized butterfly structure, each butterfly requires one complex multiplication and two complex additions. Now, one complex multiplication requires two real additions and four real multiplications, and one complex addition requires two real additions.[†] So a single FFT butterfly operation comprises four real multiplications and six real additions. This means that a single N-point complex FFT requires (4N/2)·log2N real multiplications, and (6N/2)·log2N real additions. Finally, we can say that two separate N-point complex radix-2 FFTs require
Next, we need to determine the computational workload of the Two N-Point Real FFTs algorithm. If we add up the number of real multiplications and real additions required by the algorithm's N-point complex FFT, plus those required by Eq. (13-22) to get Xa(m), and those required by Eq. (13-24) to get Xb(m), the Two N-Point Real FFTs algorithm requires
Equations (13-31) and (13-31') assume that we're calculating only the first N/2 independent elements of Xa(m) and Xb(m). The single N term in Eq. (13-31) accounts for the N/2 divide by 2 operations in Eq. (13-22) and the N/2 divide by 2 operations in Eq. (13-24).
OK, now we can find out how efficient the Two N-Point Real FFTs algorithm is compared to two separate complex N-point radix-2 FFTs. This comparison, however, depends on the hardware used for the calculations. If our arithmetic hardware takes many more clock cycles to perform a multiplication than an addition, then the difference between multiplications in Eqs. (13-30) and (13-31) is the most important comparison. In this case, the percentage gain in computational saving of the Two N-Point Real FFTs algorithm relative to two separate N-point complex FFTs is the difference in their necessary multiplications over the number of multiplications needed for two separate N-point complex FFTs, or
The computational (multiplications only) saving from Eq. (13-32) is plotted as the top curve of Figure 13-11. In terms of multiplications, for N≥32, the Two N-Point Real FFTs algorithm saves us over 45 percent in computational workload compared to two separate N-point complex FFTs.
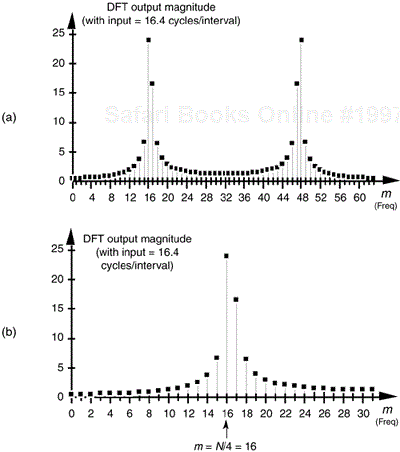
Figure 13-11. Computational saving of the Two N-Point Real FFTs algorithm over that of two separate N-point complex FFTs. The top curve indicates the saving when only multiplications are considered. The bottom curve is the saving when both additions and multiplications are used in the comparison.
For hardware using high-speed multiplier integrated circuits, multiplication and addition can take roughly equivalent clock cycles. This makes addition operations just as important and time consuming as multiplications. Thus the difference between those combined arithmetic operations in Eqs. (13-30) plus (13-30') and Eqs. (13-31) plus (13-31') is the appropriate comparison. In this case, the percentage gain in computational saving of our algorithm over two FFTs is their total arithmetic operational difference over the total arithmetic operations in two separate N-point complex FFTs, or
The full computational (multiplications and additions) saving from Eq. (13-33) is plotted as the bottom curve of Figure 13-11. This concludes our discussion and illustration of how a single N-point complex FFT can be used to transform two separate N-point real input data sequences.
Similar to the scheme above where two separate N-point real data sequences are transformed using a single N-point FFT, a technique exists where a 2N-point real sequence can be transformed with a single complex N-point FFT. This 2N-Point Real FFT algorithm, whose derivation is also described in the literature, requires that the 2N-sample real input sequence be separated into two parts[19,20]. Not broken in two, but unzipped—separating the even and odd sequence samples. The N even- indexed input samples are loaded into the real part of a complex N-point input sequence x(n). Likewise, the input's N odd-indexed samples are loaded into x(n)'s imaginary parts. To illustrate this process, let's say we have a 2N-sample real input data sequence a(n) where 0 ≤ n ≤ 2N–1. We want a(n)'s 2N-point transform Xa(m). Loading a(n)'s odd/even sequence values appropriately into an N-point complex FFT's input sequence, x(n),
Applying the N complex values in Eq. (13-34) to an N-point complex FFT, we'll get an FFT output X(m) = Xr(m) + jXi(m), where m goes from 0 to N–1. To extract the desired 2N-Point Real FFT algorithm output Xa(m) = Xa,real(m) + jXa,imag(m) from X(m), let's define the following relationships
The values resulting from Eqs. (13-35) through (13-38) are, then, used as factors in the following expressions to obtain the real and imaginary parts of our final Xa(m):
and
Remember now, the original a(n) input index n goes from 0 to 2N–1, and our N-point FFT output index m goes from 0 to N–1. We apply 2N real input time-domain samples to this algorithm and get back N complex frequency-domain samples representing the first half of the equivalent 2N-point complex FFT, Xa(0) through Xa(N–1). Because this algorithm's a(n) input is constrained to be real, Xa(N) through Xa(2N–1) are merely the complex conjugates of their Xa(0) through Xa(N–1) counterparts and need not be calculated. To help us keep all of this straight, Figure 13-12 depicts the computational steps of the 2N-Point Real FFT algorithm.
To demonstrate this process by way of example, let's apply the 8-point data sequence from Eq. (13-26) to the 2N-Point Real FFT algorithm. Partitioning those Eq. (13-26) samples as dictated by Eq. (13-34), we have our new FFT input sequence:
With N = 4 in this example, taking the 4-point FFT of the complex sequence in Eq. (13-41) we get
Using these values, we now get the intermediate factors from Eqs. (13-35) through (13-38). Calculating our first ![]() value, again we're reminded that X(m) is periodic with a period N, so X(4) = X(0), and
value, again we're reminded that X(m) is periodic with a period N, so X(4) = X(0), and ![]() Continuing to use Eqs. (13-35) through (13-38),
Continuing to use Eqs. (13-35) through (13-38),
Using the intermediate values from Eq. (13-43) in Eqs. (13-39) and (13-40),
Evaluating the sine and cosine terms in Eq. (13-44),
Combining the results of the terms in Eq. (13-45), we have our final correct answer of
After going through all the steps required by Eqs. (13-35) through (13-40), the reader might question the efficiency of this 2N-Point Real FFT algorithm. Using the same process as the above Two N-Point Real FFTs algorithm analysis, let's show that the 2N-Point Real FFT algorithm does provide some modest computational saving. First, we know that a single 2N-Point radix-2 FFT has (2N/2) · log22N = N · (log2N+1) butterflies and requires
and
If we add up the number of real multiplications and real additions required by the algorithm's N-point complex FFT, plus those required by Eqs. (13-35) through (13-38) and those required by Eqs. (13-39) and (13-40), the complete 2N-Point Real FFT algorithm requires
and
OK, using the same hardware considerations (multiplications only) we used to arrive at Eq. (13-32), the percentage gain in multiplication saving of the 2N-Point Real FFT algorithm relative to a 2N-point complex FFT is
The computational (multiplications only) saving from Eq. (13-49) is plotted as the bottom curve of Figure 13-13. In terms of multiplications, the 2N-Point Real FFT algorithm provides a saving of >30% when N ≥ 128 or whenever we transform input data sequences whose lengths are ≥256.
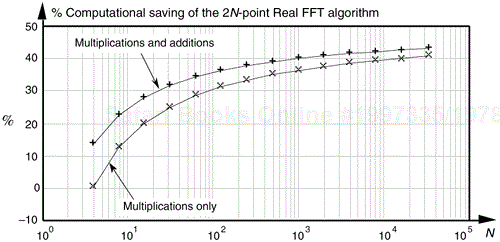
Figure 13-13. Computational saving of the 2N-Point Real FFT algorithm over that of a single 2N-point complex FFT. The top curve is the saving when both additions and multiplications are used in the comparison. The bottom curve indicates the saving when only multiplications are considered.
Again, for hardware using high-speed multipliers, we consider both multiplication and addition operations. The difference between those combined arithmetic operations in Eqs. (13-47) plus (13-47') and Eqs. (13-48) plus (13-48') is the appropriate comparison. In this case, the percentage gain in computational saving of our algorithm is
The full computational (multiplications and additions) saving from Eq. (13-50) is plotted as a function of N in the top curve of Figure 13-13.
There are many signal processing applications where the capability to perform the inverse FFT is necessary. This can be a problem if available hardware, or software routines, have only the capability to perform the forward FFT. Fortunately, there are two slick ways to perform the inverse FFT using the forward FFT algorithm.
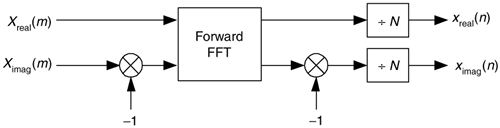
The first inverse FFT calculation scheme is implemented following the processes shown in Figure 13-14.
To see how this works, consider the expressions for the forward and inverse DFTs. They are
To reiterate our goal, we want to use the process in Eq. (13-51) to implement Eq. (13-52). The first step of our approach is to use complex conjugation. Remember, conjugation (represented by the superscript * symbol) is the reversal of the sign of a complex number's imaginary exponent—if x = ejø, then x* = e–jø. So, as a first step we take the complex conjugate of both sides of Eq. (13-52) to give us
One of the properties of complex numbers, discussed in Appendix A, is that the conjugate of a product is equal to the product of the conjugates. That is, if c = ab, then c* = (ab)* = a*b*. Using this, we can show the conjugate of the right side of Eq. (13-53) to be
Hold on; we're almost there. Notice the similarity of Eq. (13-54) to our original forward DFT expression Eq. (13-51). If we perform a forward DFT on the conjugate of the X(m) in Eq. (13-54), and divide the results by N, we get the conjugate of our desired time samples x(n). Taking the conjugate of both sides of Eq. (13-54), we get a more straightforward expression for x(n):
The second inverse FFT calculation technique is implemented following the interesting data flow shown in Figure 13-15.
In this clever inverse FFT scheme we don't bother with conjugation. Instead, we merely swap the real and imaginary parts of sequences of complex data[21]. To see why this process works, let's look at the inverse DFT equation again while separating the input X(m) term into its real and imaginary parts and remembering that ejø = cos(ø) + jsin(ø).
Multiplying the complex terms in Eq. (13-56) gives us
Equation (13-57) is the general expression for the inverse DFT and we'll now quickly show that the process in Figure 13-15 implements this equation. With X(m) = Xreal(m) + jXimag(m), then swapping these terms gives us
The forward DFT of our Xswap(m) is
Multiplying the complex terms in Eq. (13-59) gives us
Swapping the real and imaginary parts of the results of this forward DFT gives us what we're after:
If we divided Eq. (13-61) by N, it would be exactly equal to the inverse DFT expression in Eq. (13-57), and that's what we set out to show.
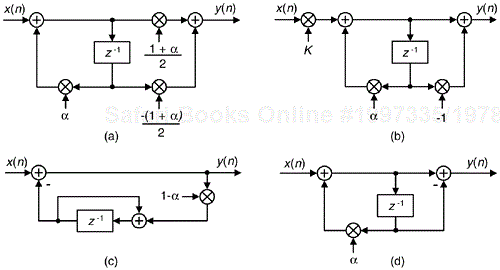
If we implement a linear phase FIR digital filter using the standard structure in Figure 13-16(a), there's a way to reduce the number of multipliers when the filter has an odd number of taps. Let's look at the top of Figure 13-16(a) where the five-tap FIR filter coefficients are h(0) through h(4) and the y(n) output is
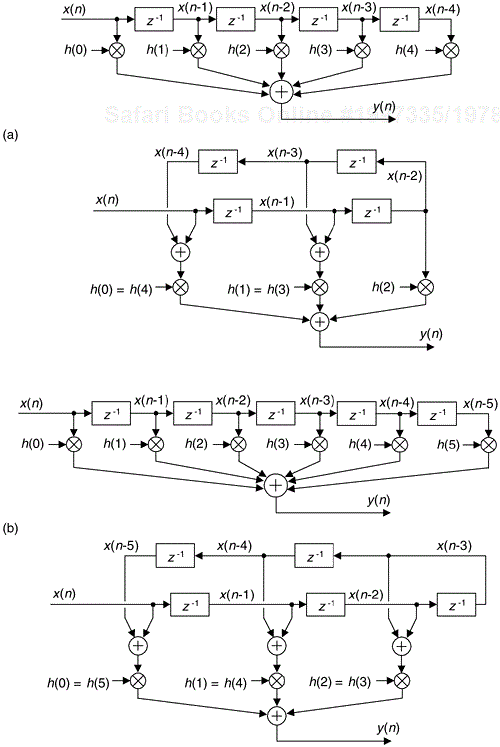
Figure 13-16. Conventional and simplified structures of an FIR filter: (a) with an odd number of taps; (b) with an even number of taps.
If the FIR filter's coefficients are symmetrical we can reduce the number of necessary multipliers. That is, if h(4) = h(0), and h(3) = h(1), we can implement Eq. (13-62) by
where only three multiplications are necessary as shown at the bottom of Figure 13-16(a). In our five-tap filter case, we've eliminated two multipliers at the expense of implementing two additional adders. This minimum-multiplier structure is called a “folded” FIR filter.
In the general case of symmetrical-coefficient FIR filters with S taps, we can trade (S–1)/2 multipliers for (S–1)/2 adders when S is an odd number. So in the case of an odd number of taps, we need only perform (S–1)/2 + 1 multiplications for each filter output sample. For an even number of symmetrical taps as shown in Figure 13-16(b), the savings afforded by this technique reduces the necessary number of multiplications to S/2.
As of this writing, typical programmable-DSP chips cannot take advantage of the folded FIR filter structure because it requires a single addition before each multiply and accumulate operation.
In Section 12.3 we discussed the mathematical details, and ill effects, of quantization noise in analog-to-digital (A/D) converters. DSP practitioners commonly use two tricks to reduce converter quantization noise. Those schemes are called oversampling and dithering.
The process of oversampling to reduce A/D converter quantization noise is straightforward. We merely sample an analog signal at an fs sample rate higher than the minimum rate needed to satisfy the Nyquist criterion (twice the analog signal's bandwidth), and then lowpass filter. What could be simpler? The theory behind oversampling is based on the assumption that an A/D converter's total quantization noise power (variance) is the converter's least significant bit (lsb) value squared over 12, or
We derived that expression in Section 12.3. The next assumption is: the quantization noise values are truly random, and in the frequency domain the quantization noise has a flat spectrum. (These assumptions are valid if the A/D converter is being driven by an analog signal that covers most of the converter's analog input voltage range, and is not highly periodic.) Next we consider the notion of quantization noise power spectral density (PSD), a frequency-domain characterization of quantization noise measured in noise power per hertz as shown in Figure 13-17. Thus we can consider the idea that quantization noise can be represented as a certain amount of power (watts, if we wish) per unit bandwidth.
In our world of discrete systems, the flat noise spectrum assumption results in the total quantization noise (a fixed value based on the converter's lsb voltage) being distributed equally in the frequency domain, from –fs/2 to +fs/2 as indicated in Figure 13-17. The amplitude of this quantization noise PSD is the rectangle area (total quantization noise power) divided by the rectangle width (fs), or
measured in watts/Hz.
The next question is: “How can we reduce the PSDnoise level defined by Eq. (13-65)?” We could reduce the lsb value (volts) in the numerator by using an A/D converter with additional bits. That would make the lsb value smaller and certainly reduce PSDnoise, but that's an expensive solution. Extra converter bits cost money. Better yet, let's increase the denominator of Eq. (13-65) by increasing the sample rate fs.
Consider a low-level discrete signal of interest whose spectrum is depicted in Figure 13-18(a). By increasing the fs,old sample rate to some larger value fs,new (oversampling), we spread the total noise power density (a fixed value) over a wider frequency range as shown in Figure 13-18(b). The area under the shaded curves in Figure 13-18(a) and 13-18(b) are equal. Next we lowpass filter the converter's output samples. At the output of the filter, the quantization noise level contaminating our signal will be reduced from that at the input of the filter.
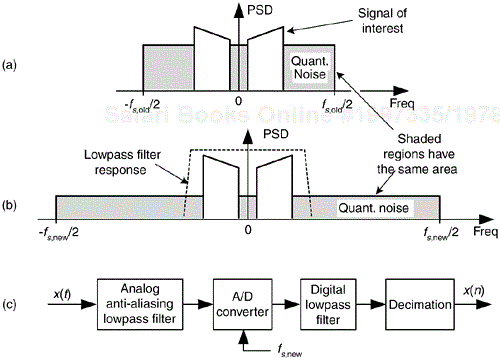
Figure 13-18. Oversampling example: (a) noise PSD at an fs,old samples rate; (b) noise PSD at the higher fs,new samples rate; (c) processing steps.
The improvement in signal to quantization noise ratio, measured in dB, achieved by oversampling is:
For example: if fs,old = 100 kHz, and fs,new = 400 kHz, the SNRA/D-gain = 10log10(4) = 6.02 dB. Thus oversampling by a factor of 4 (and filtering), we gain a single bit's worth of quantization noise reduction. Consequently we can achieve N+1-bit performance from an N-bit A/D converter, because we gain signal amplitude resolution at the expense of higher sampling speed. After digital filtering, we can decimate to the lower fs,old without degrading the improved SNR. Of course, the number of bits used for the lowpass filter's coefficients and registers must exceed the original number of A/D converter bits, or this oversampling scheme doesn't work.
With the use of a digital lowpass filter, depending on the interfering analog noise in x(t), it's possible to use a lower performance (simpler) analog anti-aliasing filter relative to the analog filter necessary at the lower sampling rate.
Dithering, another technique used to minimize the effects of A/D quantization noise, is the process of adding noise to our analog signal prior to A/D conversion. This scheme, which doesn't seem at all like a good idea, can indeed be useful and is easily illustrated with an example. Consider digitizing the low-level analog sinusoid shown in Figure 13-19(a), whose peak voltage just exceeds a single A/D converter least significant bit (lsb) voltage level, yielding the converter output x1(n) samples in Figure 13-19(b). The x1(n) output sequence is clipped. This generates all sorts of spectral harmonics. Another way to explain the spectral harmonics is to recognize the periodicity of the quantization noise in Figure 13-19(c).
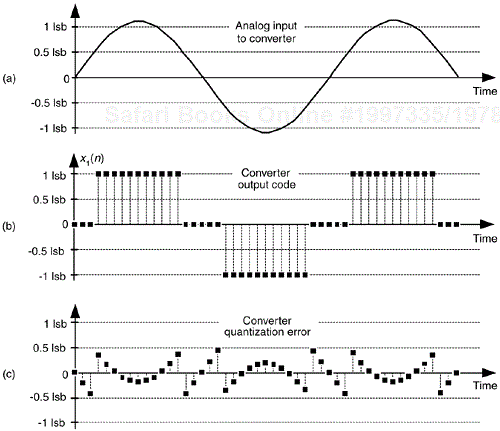
Figure 13-19. Dithering: (a) a low-level analog signal; (b) the A/D converter output sequence; (c) the quantization error in the converter's output.
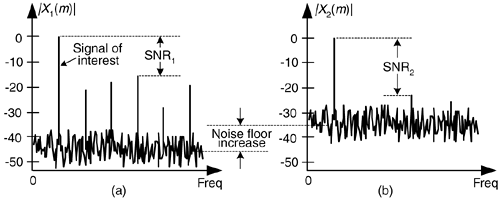
We show the spectrum of x1(n) in Figure 13-20(a) where the spurious quantization noise harmonics are apparent. It's worthwhile to note that averaging multiple spectra will not enable us to pull some spectral component of interest up above those spurious harmonics in Figure 13-20(a). Because the quantization noise is highly correlated with our input sinewave—the quantization noise has the same time period as the input sinewave—spectral averaging will also raise the noise harmonic levels. Dithering to the rescue.
Dithering is the technique where random analog noise is added to the analog input sinusoid before it is digitized. This technique results in a noisy analog signal that crosses additional converter lsb boundaries and yields a quantization noise that's much more random, with a reduced level of undesirable spectral harmonics as shown in Figure 13-20(b). Dithering raises the average spectral noise floor but increases our signal to noise ratio SNR2. Dithering forces the quantization noise to lose its coherence with the original input signal, and we could then perform signal averaging if desired.
Dithering is indeed useful when we're digitizing
low-amplitude analog signals,
highly periodic analog signals (like a sinewave with an even number of cycles in the sample time interval), and
slowly varying (very low frequency, including DC) analog signals.
The standard implementation of dithering is shown in Figure 13-21(a). The typical amount of random wideband analog noise used in the this process, provided by a noise diode or noise generator ICs, has a rms level equivalent to 1/3 to 1 lsb voltage level.
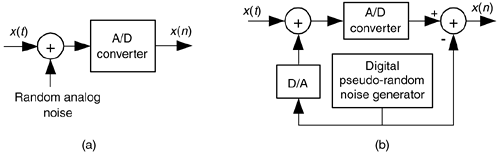
Figure 13-21. Dithering implementations: (a) standard dithering process; (b) advanced dithering with noise subtraction.
For high-performance audio applications, engineers have found that adding dither noise from two separate noise generators improves background audio low-level noise suppression. The probability density function (PDF) of the sum of two noise sources (having rectangular PDFs) is the convolution of their individual PDFs. Because the convolution of two rectangular functions is triangular, this dual-noise-source dithering scheme is called triangular dither. Typical triangular dither noise has rms levels equivalent to, roughly, 2 lsb voltage levels.
In the situation where our signal of interest occupies some well defined portion of the full frequency band, injecting narrowband dither noise having an rms level equivalent to 4 to 6 lsb voltage levels, whose spectral energy is outside that signal band, would be advantageous. (Remember though: the dither signal can't be too narrowband, like a sinewave. Quantization noise from a sinewave signal would generate more spurious harmonics!) That narrowband dither noise can then be removed by follow-on digital filtering.
One last note about dithering: to improve our ability to detect low-level signals, we could add the analog dither noise and then subtract that noise from the digitized data, as shown in Figure 13-21(b). This way, we randomized the quantization noise, but reduced the amount of total noise power injected in the analog signal. This scheme is used in commercial analog test equipment[22,23].
We can take advantage of digital signal processing techniques to facilitate the testing of A/D converters. In this section we present two schemes for measuring converter performance; first, a technique using the FFT to estimate overall converter noise, and second, a histogram analysis scheme to detect missing converter output codes.
The combination A/D converter quantization noise, missing bits, harmonic distortion, and other nonlinearities can be characterized by analyzing the spectral content of the converter's output. Converter performance degradation caused by these nonlinearities is not difficult to recognize because they show up as spurious spectral components and increased background noise levels in the A/D converter's output samples. The traditional test method involves applying a sinusoidal analog voltage to an A/D converter's input and examining the spectrum of the converter's digitized time-domain output samples. We can use the FFT to compute the spectrum of an A/D converter's output samples, but we have to minimize FFT spectral leakage to improve the sensitivity of our spectral measurements. Traditional time-domain windowing, however, provides insufficient FFT leakage reduction for high-performance A/D converter testing.
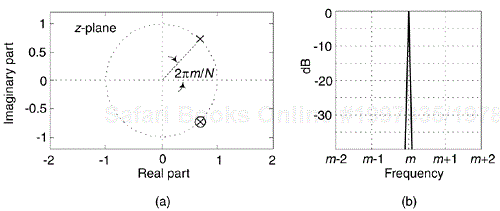
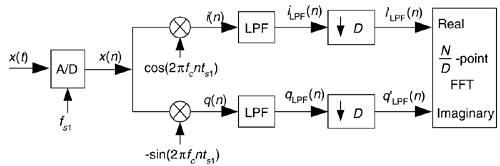
The trick to circumventing this FFT leakage problem is to use an sinusoidal analog input voltage whose frequency is an integer fraction of the A/D converter's clock frequency as shown in Figure 13-22(a). That frequency is mfs/N, where m is an integer, fs is the clock frequency (sample rate), and N is the FFT size. Figure 13-22(a) shows the x(n) time domain output of an ideal A/D converter when its analog input is a sinewave having exactly eight cycles over N = 128 converter output samples. In this case, the input frequency normalized to the sample rate fs is 8fs/128 Hz. Recall from Chapter 3 that the expression mfs/N defined the analysis frequencies, or bin centers, of the DFT, and a DFT input sinusoid whose frequency is at a bin center causes no spectral leakage.

Figure 13-22. Ideal A/D converter output when the input is an analog 8fs/128 Hz sinusoid: (a) output time samples; (b) spectral magnitude in dB.
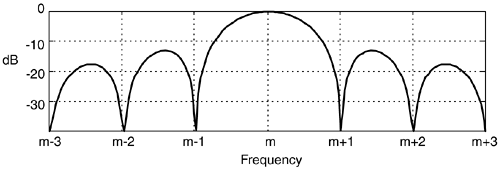
The first half of a 128-point FFT of x(n) is shown in the logarithmic plot in Figure 13-22(b) where the input tone lies exactly at the m = 8 bin center and FFT leakage has been sufficiently reduced. Specifically, if the sample rate were 1 MHz, then the A/D's input analog tone would have to be exactly 8(106/128) = 62.5 kHz. In order to implement this scheme we need to ensure that the analog test generator be synchronized, exactly, with the A/D converter's clock frequency of fs Hz. Achieving this synchronization is why this A/D converter testing procedure is referred to as coherent sampling[24–26]. That is, the analog signal generator and the A/D clock generator providing fs must not drift in frequency relative to each other—they must remain coherent. (We must take care here from a semantic viewpoint because the quadrature sampling schemes described in Chapter 8 are also sometimes called coherent sampling, and they are unrelated to this A/D converter testing procedure.)
As it turns out, some values of m are more advantageous than others. Notice in Figure 13-22(a), that when m = 8, only nine different amplitude values are output by the A/D converter. Those values are repeated over and over. As shown in Figure 13-23, when m = 7 we exercise many more than nine different A/D output values.
Because it's best to test as many A/D output binary words as possible, while keeping the quantization noise sufficiently random, users of this A/D testing scheme have discovered another trick. They found that making m an odd prime number (3, 5, 7, 11, etc.) minimizes the number of redundant A/D output word values.
Figure 13-24(a) illustrates an extreme example of nonlinear A/D converter operation, with several discrete output samples having dropped bits in the time domain x(n) with m = 8. The FFT of this distorted x(n) is provided in Figure 13-24(b) where we can see the increased background noise level due to the A/D converter's nonlinearities compared to Figure 13-22(b).
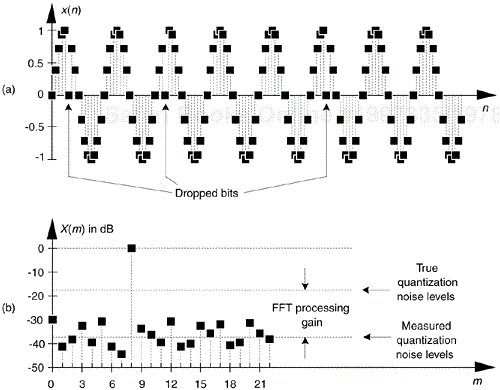
Figure 13-24. Non-ideal A/D converter output showing several dropped bits: (a) time samples; (b) spectral magnitude in dB.
The true A/D converter quantization noise levels will be higher than those measured in Figure 13-24(b). That's because the inherent processing gain of the FFT (discussed in Section 3.12.1) will pull the high-level m = 8 spectral component up out of the background quantization noise. Consequently, if we use this A/D converter test technique, we must account for the FFT's processing gain of 10log10(N/2) as indicated in Figure 13-24(b).
To fully characterize the dynamic performance of an A/D converter we'd need to perform this testing technique at many different input frequencies and amplitudes.[†] The key issue here is that when any input frequency is mfs/N, where m is less than N/2 to satisfy the Nyquist sampling criterion, we can take full advantage of the FFT's processing capability while minimizing spectral leakage.
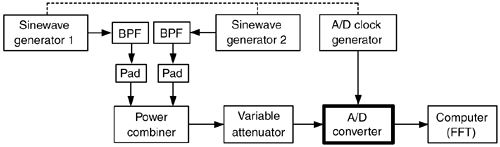
In closing, applying the sum of two analog tones to an A/D converter's input is often done to quantify the intermodulation distortion performance of a converter, which in turn characterizes the converter's dynamic range. In doing so, both input tones must comply with the mfs/N restriction. Figure 13-25 shows the test configuration. It's prudent to use bandpass filters (BPF) to improve the spectral purity of the sinewave generators' outputs, and small-valued fixed attenuators (pads) are used to keep the generators from adversely interacting with each other. (I recommend 3-dB attenuators for this.) The power combiner is typically an analog power splitter driven backward, and the A/D clock generator output is a squarewave. The dashed lines in Figure 13-25 indicate that all three generators are locked to the same frequency reference source.
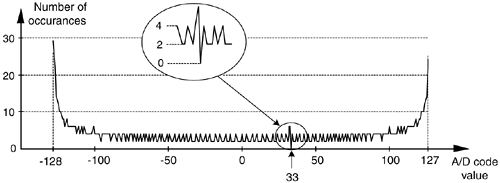
One problem that can plague A/D converters is missing codes. This defect occurs when a converter is incapable of outputting a specific binary word (a code). Think about driving an 8-bit converter with an analog sinusoid and the effect when its output should be the binary word 00100001 (decimal 33); its output is actually the word 00100000 (decimal 32) as shown in Figure 13-26. The binary word representing decimal 33 is a missing code. This subtle nonlinearity is very difficult to detect by examining time-domain samples or performing spectrum analysis. Fortunately there is a simple, reliable way to detect the missing 33 using histogram analysis.
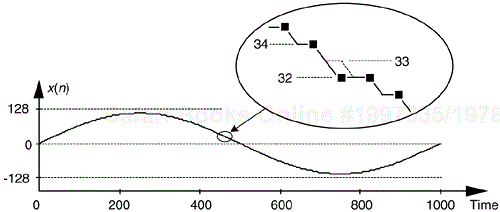
Figure 13-26. Time-domain plot of an 8-bit converter exhibiting a missing code of binary value 0010001, decimal 33.
The histogram testing technique merely involves collecting many A/D converter output samples and plotting the number of occurrences of each sample value versus that sample value as shown in Figure 13-27. Any missing code (like our missing 33) would show up in the histogram as a zero value. That is, there were zero occurrences of the binary code representing a decimal 33.
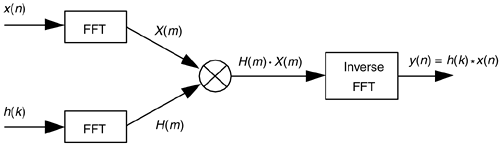
While contemplating the convolution relationships in Eq. (5-31) and Figure 5-41, digital signal processing practitioners realized that convolution could sometimes be performed more efficiently using FFT algorithms than it could be using the direct convolution method. This FFT-based convolution scheme, called fast convolution, is diagrammed in Figure 13-28.
The standard convolution equation for an M-tap nonrecursive FIR filter, given in Eq. (5-6) and repeated here, is
where h(k) is the impulse response sequence (coefficients) of the FIR filter and the * symbol indicates convolution. It has been shown that when the final y(n) output sequence has a length greater than 30, the process in Figure 13-28 requires fewer multiplications than implementing the convolution expression in Eq. (13-67) directly. Consequently, this fast convolution technique is a very powerful signal processing tool, particularly when used for digital filtering. Very efficient FIR filters can be designed using this technique because, if their impulse response h(k) is constant, then we don't have to bother recalculating H(m) each time a new x(n) sequence is filtered. In this case the H(m) sequence can be precalculated and stored in memory.
The necessary forward and inverse FFT sizes must of course be equal, and are dependent upon the length of the original h(k) and x(n) sequences. Recall from Eq. (5-29) that if h(k) is of length P and x(n) is of length Q, the length of the final y(n) sequence will be (P+Q–1). For this fast convolution technique to give valid results, the forward and inverse FFT sizes must be equal and greater than (P+Q–1). This means that h(k) and x(n) must both be padded with zero-valued samples, at the end of their respective sequences, to make their lengths identical and greater than (P+Q–1). This zero padding will not invalidate the fast convolution results. So to use fast convolution, we must choose an N-point FFT size such that N ≥ (P+Q–1) and zero pad h(k) and x(n) so they have new lengths equal to N.
An interesting aspect of fast convolution, from a hardware standpoint, is that the FFT indexing bit-reversal problem discussed in Sections 4.5 and 4.6 is not an issue here. If the identical FFT structures used in Figure 13-28 result in X(m) and H(m) having bit-reversed indices, the multiplication can still be performed directly on the scrambled H(m) and X(m) sequences. Then an appropriate inverse FFT structure can be used that expects bit-reversed input data. That inverse FFT then provides an output y(n) whose data index is in the correct order!
Section D.4 in Appendix D discusses the normal distribution curve as it relates to random data. A problem we may encounter is how actually to generate random data samples whose distribution follows that normal (Gaussian) curve. There's a straightforward way to solve this problem using any software package that can generate uniformly distributed random data, as most of them do[27]. Figure 13-29 shows our situation pictorially where we require random data that's distributed normally with a mean (average) of μ' and a standard deviation of σ', as in Figure 13-29(a), and all we have available is a software routine that generates random data that's uniformly distributed between zero and one as in Figure 13-29(b).
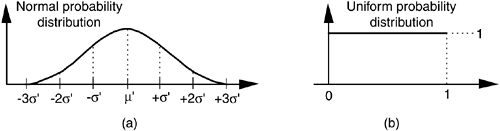
Figure 13-29. Probability distribution functions: (a) Normal distribution with mean = μ', and standard deviation σ'; (b) Uniform distribution between zero and one.
As it turns out, there's a principle in advanced probability theory, known as the Central Limit Theorem, that says when random data from an arbitrary distribution is summed over M samples, the probability distribution of the sum begins to approach a normal distribution as M increases[28–30]. In other words, if we generate a set of N random samples that are uniformly distributed between zero and one, we can begin adding other sets of N samples to the first set. As we continue summing additional sets, the distribution of the N-element set of sums becomes more and more normal. We can sound impressive and state that “the sum becomes asymptotically normal.” Experience has shown that for practical purposes, if we sum M ≥ 30 times, the summed data distribution is essentially normal. With this rule in mind, we're half way to solving our problem.
After summing M sets of uniformly distributed samples, the summed set ysum will have a distribution as shown in Figure 13-30.
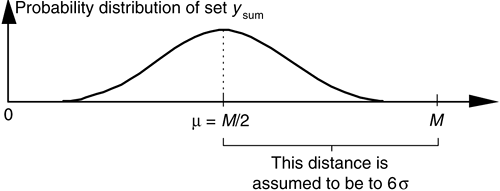
Figure 13-30. Probability distribution of the summed set of random data derived from uniformly distributed data.
Because we've summed M sets, the mean of ysum is μ = M/2. To determine ysum's standard deviation σ, we assume that the six sigma point is equal to M–μ. That is,
That assumption is valid because we know that the probability of an element in ysum being greater that M is zero, and the probability of having a normal data sample at six sigma is one chance in six billion, or essentially zero. Because μ = M/2, from Eq. (13-68), ysum's standard deviation is set to
To convert the ysum data set to our desired data set having a mean of μ' and a standard deviation of σ', we :
subtract M/2 from each element of ysum to shift its mean to zero,
ensure that 6σ' is equal to M/2 by multiplying each element in the shifted data set by 12σ'/M, and
center the new data set about the desired μ' by adding μ' to each element of the new data.
If we call our desired normally distributed random data set ydesired, then the nth element of that set is described mathematically as
Our discussion thus far has had a decidedly software algorithm flavor, but hardware designers also occasionally need to generate normally distributed random data at high speeds in their designs. For you hardware designers, Reference [30] presents an efficient hardware design technique to generate normally distributed random data using fixed-point arithmetic integrated circuits.
The above method for generating normally distributed random numbers works reasonably well, but its results are not perfect because the tails of the probability distribution curve in Figure 13-30 are not perfectly Gaussian.[†] An advanced, and more statistically correct (improved randomness), technique that you may want to explore is called the Ziggurat method[31–33].
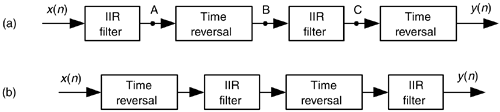
You can cancel the nonlinear phase effects of an IIR filter by following the process shown in Figure 13-31(a). The y(n) output will be a filtered version of x(n) with no filter-induced phase distortion. The same IIR filter is used twice in this scheme, and the time reversal step is a straight left-right flipping of a time-domain sequence. Consider the following. If some spectral component in x(n) has an arbitrary phase of α degrees, and the first filter induces a phase shift of –β degrees, that spectral component's phase at node A will be α–β degrees. The first time reversal step will conjugate that phase and induce an additional phase shift of –θ degrees. (Appendix C explains this effect.) Consequently, the component's phase at node B will be –α+β–θ degrees. The second filter's phase shift of –β degrees yields a phase of –α–θ degrees at node C. The final time reversal step (often omitted in literary descriptions of this zero-phase filtering process) will conjugate that phase and again induce an additional phase shift of –θ degrees. Thankfully, the spectral component's phase in y(n) will be α+θ–θ = α degrees, the same phase as in x(n). This property yields an overall filter whose phase response is zero degrees over the entire frequency range.
An equivalent zero-phase filter is presented in Figure 13-31(b). Of course, these methods of zero-phase filtering cannot be performed in real time because we can't reverse the flow of time (at least not in our universe). This filtering is a block processing, or off-line process, such as filtering an audio sound file on a computer. We must have all the time samples available before we start processing. The initial time reversal in Figure 13-31(b) illustrates this restriction.
There will be filter transient effects at the beginning and end of the filtered sequences. If transient effects are bothersome in a given application, consider discarding L samples from the beginning and end of the final y(n) time sequence, where L is 4 (or 5) times the order of the IIR filter.
By the way, the final peak-to-peak passband ripple (in dB) of this zero-phase filtering process will be twice the peak-to-peak passband ripple of the single IIR filter. The final stopband attenuation will also be double that of the single filter.
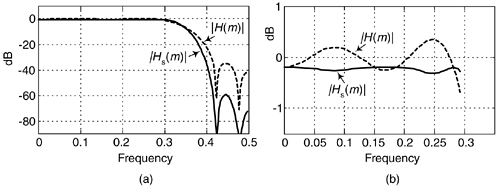
Here's an interesting technique for improving the stopband attenuation of a digital under the condition that we're unable, for whatever reason, to modify that filter's coefficients. Actually, we can a filter's double stopband attenuation by cascading the filter with itself. This works, as shown in Figure 13-32(a), where the frequency magnitude response of a single filter is a dashed curve |H(m)| and the response of the filter cascaded with itself is represented by solid curve |H2(m)|. The problem with this simple cascade idea is that it also doubles the passband peak-to-peak ripple as shown in Figure 13-32(b). The frequency axis in Figure 13-32 is normalized such that a value of 0.5 represents half the signal sample rate.
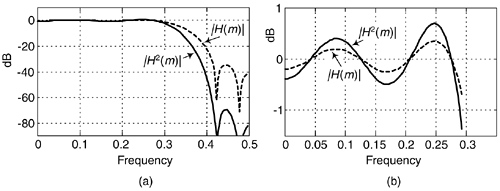
Figure 13-32. Frequency magnitude responses of a single filter and that filter cascaded with itself: (a) full response; (b) passband detail.
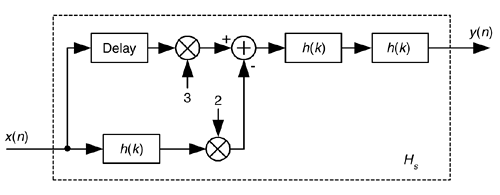
Well, there's a better scheme for improving the stopband attenuation performance of a filter and avoiding passband ripple degradation without actually changing the filter's coefficients. The technique is called filter sharpening[34], and is shown as Hs in Figure 13-33.
The delay element in Figure 13-33 is equal to (N–1)/2 samples where N is the number of h(k) coefficients, the unit-impulse response length, in the original H(m) FIR filter. Using the sharpening process results in the improved |Hs(m)| filter performance shown as the solid curve in Figure 13-34, where we see the increased stopband attenuation and reduced passband ripple beyond that afforded by the original H(m) filter. Because of the delayed time-alignment constraint, filter sharpening is not applicable to filters having non-constant group delay, such as minimum-phase FIR filters or IIR filters.
If perhaps more stopband attenuation is needed then the process shown in Figure 13-35 can be used, where again the delay element is equal to (N–1)/2 samples.
The filter sharpening procedure is straightforward and applicable to lowpass, bandpass, and highpass FIR filters having symmetrical coefficients and an odd number of taps. Filter sharpening can be used whenever a given filter response cannot be modified, such as an unchangeable software subroutine, and can even be applied to cascaded integrator-comb (CIC) filters to flatten their passband responses, as well as FIR fixed-point multiplierless filters where the coefficients are constrained to be powers of two[35,36].
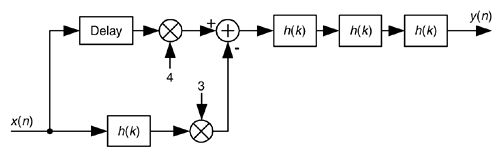
There are many digital communications applications where a real signal is centered at one fourth the sample rate, or fs/4. This condition makes quadrature downconversion particularly simple. (See Sections 8.9 and 13.1.) In the event that you'd like to generate an interpolated (increased sample rate) version of the bandpass signal but maintain its fs/4 center frequency, there's an efficient way to do so[37]. Suppose we want to interpolate by a factor of two so the output sample rate is twice the input sample rate, fs-out = 2fs-in. In this case the process is: quadrature downconversion by fs-in/4, interpolation factor of two, quadrature upconversion by fs-out/4, and then take only the real part of the complex upconverted sequence. The implementation of this scheme is shown at the top of Figure 13-36.
The sequences applied to the first multiplier in the top signal path are the real x(n) input and the repeating mixing sequence 1,0,–1,0. That mixing sequence is the real (or in-phase) part of the complex exponential
needed for quadrature downconversion by fs/4. Likewise, the repeating mixing sequence 0,–1,0,1 applied to the first multiplier in the bottom path is the imaginary (or quadrature phase) part of the complex downconversion exponential ![]() . The ↑2 symbol means insert one zero-valued sample between each signal at the A nodes. The final subtraction to obtain y(n) is how we extract the real part of the complex sequence at Node D. (That is, we're extracting the real part of the product of the complex signal at Node C times ej2π(1/4).) The spectra at various nodes of this process are shown at the bottom of Figure 13-35. The shaded spectra indicate true spectral components, while the white spectra represent spectral replications. Of course, the same lowpass filter must be used in both processing paths to maintain the proper time delay and orthogonal phase relationships.
. The ↑2 symbol means insert one zero-valued sample between each signal at the A nodes. The final subtraction to obtain y(n) is how we extract the real part of the complex sequence at Node D. (That is, we're extracting the real part of the product of the complex signal at Node C times ej2π(1/4).) The spectra at various nodes of this process are shown at the bottom of Figure 13-35. The shaded spectra indicate true spectral components, while the white spectra represent spectral replications. Of course, the same lowpass filter must be used in both processing paths to maintain the proper time delay and orthogonal phase relationships.
There are several additional issues worth considering regarding this interpolation process[38]. If the amplitude loss, inherent in interpolation, of a factor of two is bothersome, we can make the final mixing sequences 2,0,–2,0, and 0,2,0,–2 to compensate for that loss. Because there are so many zeros in the sequences at Node B (three/fourths of the samples), we should consider those efficient polyphase filters for the lowpass filtering. Finally, if it's sensible in your implementation, consider replacing the final adder with a multiplexer (because alternate samples of the sequences at Node D are zeros). In this case, the mixing sequence in the bottom path would be changed to 0,–1,0,1.
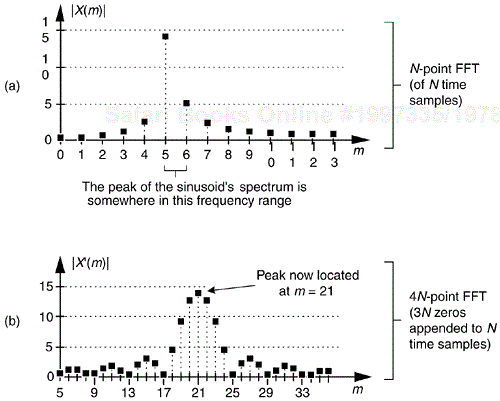
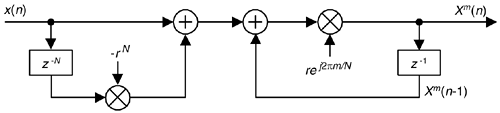
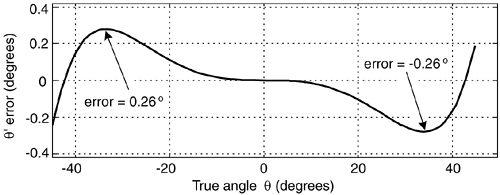
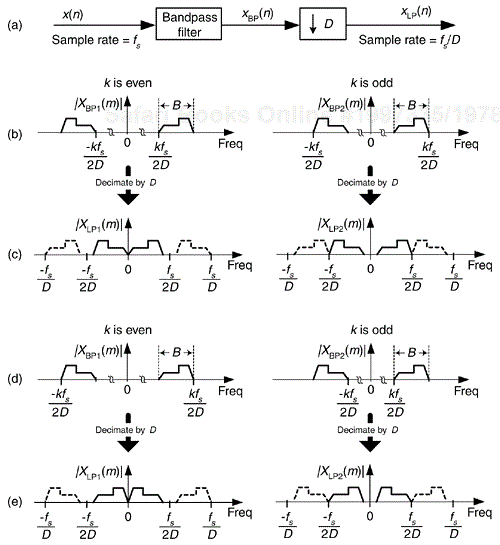
In the practical world of discrete spectrum analysis, we often want to estimate the frequency of a sinusoid (or the center frequency of a very narrowband signal of interest). Upon applying the radix-2 fast Fourier transform (FFT), our narrowband signals of interest rarely reside exactly on an FFT bin center whose frequency is exactly known. As such, due to the FFT's leakage properties, the discrete spectrum of a sinusoid having N time-domain samples may look like the magnitude samples shown in Figure 13-37(a). There we see the sinusoid's spectral peak residing between the FFT's m = 5 and m = 6 bin centers. (Variable m is an N-point FFT's frequency-domain index. The FFT bin spacing is fs/N where, as always, fs is the sample rate.) Close examination of Figure 13-37(a) allows us to say the sinusoid lies in the range of m = 5 and m = 5.5, because we see that the maximum spectral sample is closer to the m = 5 bin center than the m = 6 bin center. The real-valued sinusoidal time signal has, in this example, a frequency of 5.25fs/N Hz. In this situation, our frequency estimation resolution is half the FFT bin spacing. We often need better frequency estimation resolution, and there are indeed several ways to improve that resolution.
We could collect, say, 4N time-domain signal samples and perform a 4N-point FFT yielding a reduced bin spacing of fs/4N. Or we could pad (append to the end of the original time samples) the original N time samples with 3N zero-valued samples and perform a 4N-point FFT on the lengthened time sequence. That would also provide an improved frequency resolution of fs/4N, as shown in Figure 13-37(b). With the spectral peak located at bin mpeak = 21, we estimate the signal's center frequency, in Hz, using
Both schemes, collect more data and zero-padding, are computationally expensive. Many other techniques for enhanced-precision frequency measurement have been described in the scientific literature—from the close-to-home field of geophysics to the lofty studies of astrophysics—but most of those schemes seek precision without regard to computational simplicity. Here we describe a computationally simple frequency estimation scheme[3].
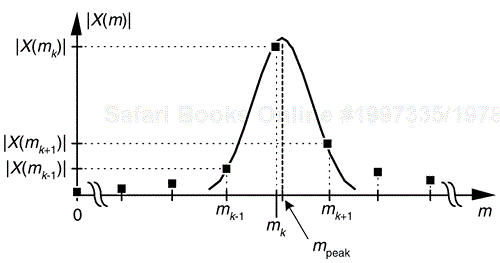
Assume we have FFT spectral samples X(m), of a real-valued narrowband time signal, whose magnitudes are shown in Figure 13-38. The vertical magnitude axis is linear, not logarithmic.
The signal's index-based center frequency, mpeak, can be estimated using
where real(δ) means the real part of the δ correction factor defined as
where mk is the integer index of the largest magnitude sample |X(mk)|. Values X(mk–1) and X(mk+1) are the complex spectral samples on either side of the peak sample as shown in Figure 13-38. Based on the complex spectral values, we compute the signal's index-based frequency mpeak (which may not be an integer), and apply that value to
to provide a frequency estimate in Hz. Equations (13-73) and (13-74) apply only when the majority of the signal's spectral energy lies within a single FFT bin width (fs/N).
This spectral peak location estimation algorithm is quite accurate for its simplicity. Its peak frequency estimation error is roughly 0.06, 0.04, and 0.03 bin widths for signal-to-noise ratios of 3, 6, and 9 dB respectively. Not bad at all! The nice features of the algorithm are that it does not require the original time samples to be windowed, as do some other spectral peak location algorithms, and it uses the raw FFT samples without the need for spectral magnitudes to be computed.
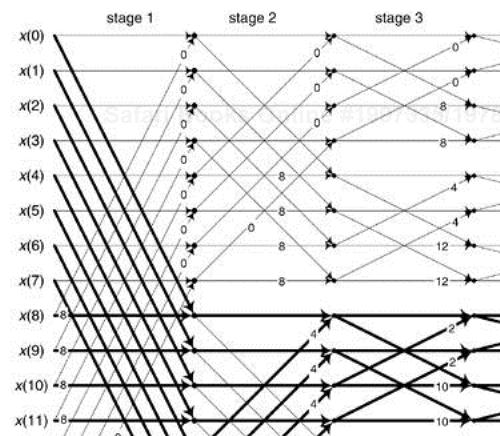
Typical applications using an N-point radix-2 FFT accept N input time samples, x(n), and compute N frequency-domain samples X(m). However, there are non-standard FFT applications (for example, specialized harmonic analysis, or perhaps using an FFT to implement a bank of filters) where only a subset of the X(m) results are required. Consider Figure 13-39 showing a 16-point radix-2 decimation in time FFT, and assume we only need to compute the X(1), X(5), X(9) and X(13) output samples. In this case, rather than compute the entire FFT we only need perform the computations indicated by the heavy lines. Reduced-computation FFTs are often called pruned FFTs[39–42]. (As we did in Chapter 4, for simplicity the butterflies in Figure 13-39 only show the twiddle phase angle factors and not the entire twiddle phase angles.) To implement pruned FFTs, we need to know the twiddle phase angles associated with each necessary butterfly computation as shown in Figure 13-40(a). Here we give an interesting algorithm for computing the 2πA1/N and 2πA2/N twiddle phase angles for an arbitrary-size FFT[43].
The algorithm draws upon the following characteristics of a radix-2 decimation-in-time FFT:
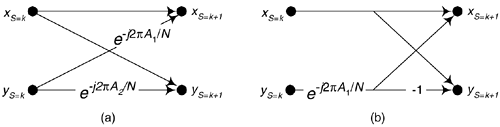
A general FFT butterfly is that shown in Figure 13-40(a).
The A1 and A2 angle factors are the integer values shown in Figure 13-39.
An N-point radix-2 FFT has M stages (shown at the top of Figure 13-39) where M = log2(N).
Each stage comprises N/2 butterflies.
The A1 phase angle factor of an arbitrary butterfly is
where S is the index of the M stages over the range 1 ≤ S ≤ M. Similarly, B serves as the index for the N/2 butterflies in each stage, where 1 ≤ B ≤ N/2. B = 1 means the top butterfly within a stage. The ⌊q⌋ operation is a function that returns the smallest integer ≤ q. Brev[z] represents the three-step operation of: convert decimal integer z to a binary number represented by M–1 binary bits, perform bit reversal on the binary number as discussed in Section 4.5, and convert the bit reversed number back to a decimal integer yielding angle factor A1. Angle factor A2, in Figure 13-40(a), is then computed using
The algorithm can also be used to compute the single twiddle angle factor of the optimized butterfly shown in Figure 13-40(b). Below is a code listing, in MATLAB, implementing our twiddle angle factor computational algorithm.
clear
N = 16; %FFT size
M = log2(N); %Number of stages
Sstart = 1; %First stage to compute
Sstop = M; %Last stage to compute
Bstart = 1; %First butterfly to compute
Bstop = N/2; %Last butterfly to compute
Pointer = 0; %Init Results pointer
for S = Sstart:Sstop
for B = Bstart:Bstop
Z = floor((2^S*(B–1))/N); %Compute integer z
% Compute bit reversal of Z
Zbr = 0;
for I = M–2:–1:0
if Z>=2^I
Zbr = Zbr + 2^(M–I–2);
Z = Z –2^I;
end
end %End bit reversal
A1 = Zbr; %Angle factor A1
A2 = Zbr + N/2; %Angle factor A2
Pointer = Pointer +1;
Results(Pointer,:) = [S,B,A1,A2];
end
end
Results, disp(' Stage B–fly, A1, A2'), disp(' ')
The variables in the code with start and stop in their names allow computation of a subset of the of all the twiddle angle factors in an N-point FFT. For example, to compute the twiddle angle factors for the fifth and sixth butterflies in the third stage of a 32-point FFT, we can assign N = 32, Sstart = 3, Sstop = 3, Bstart = 5, and Bstop = 6, and run the code.
In this section we present an IIR filter structure used to perform spectrum analysis in the detection and measurement of single sinusoidal tones. The standard method for spectral energy is the discrete Fourier transform (DFT), typically implemented using a fast Fourier transform (FFT) algorithm. However, there are applications that require spectrum analysis only over a subset of the N bin-center frequencies of an N-point DFT. A popular, as well as efficient, technique for computing sparse FFT results is the Goertzel algorithm, using an IIR filter implementation to compute a single complex DFT spectral bin value based upon N input time samples. The most common application of this process is to detect the presence of a single continuous-wave sinusoidal tone. With that in mind, let's look briefly at tone detection.
It's certainly possible to use the FFT to detect the presence of a single sinusoidal tone in a time-domain sequence x(n). For example, if we wanted to detect a 30 kHz tone in a time-domain sequence whose sample rate was fs = 128 kHz, we could start by performing a 64-point FFT as shown in Figure 13-41. Then we would examine the magnitude of the X(15) complex sample to see if it exceeds some predefined threshold.
This FFT method is very inefficient. In our example, we'd be performing 192, (64/2)(log264), complex multiplies to obtain the 64-point complex X(m) in order to compute the one X(15) in which we're interested. We discarded 98% of our computations results! We could be more efficient and calculate our desired X(15) using the single-point discrete Fourier transform (DFT) in Eq. (13-77), which requires N = 64 complex multiplies using
That would be an improvement but, happily, there's a better way. It's called the Goertzel algorithm (pronounced: girt'zel).
The Goertzel algorithm is implemented in the form of a second-order IIR filter, with two real feedback coefficients and a single complex feedforward coefficient, as shown in Figure 13-42. (Although we don't use this process as a traditional filter, common terminology refers to the structure as a filter.) This filter computes a single-bin DFT output (the mth bin of an N-point DFT) defined by
The filter's y(n) output is equal to the DFT output frequency coefficient, X(m), at the time index n = N, where the first time index value is n = 0. For emphasis, we remind the reader that the filter's y(n) output is not equal to X(m) at any time index when n ≠ N. To be equivalent to the DFT, the frequency-domain index m must an integer in the range 0 ≤ m ≤ N–1. You're welcome to think of the Goertzel algorithm as a single-bin DFT. The derivation of this filter (this algorithm) structure is readily available in the literature[44–46].
The z-domain transfer function of the Goertzel filter is
with a single z-domain zero located at z = e–j2πm/N and conjugate poles at z = e±j2πm/N as shown in Figure 13-43(a). The pole/zero pair at z = e–j2πm/N cancel each other. Having a filter pole on the unit circle is typically a risky thing to do for stability reasons, but not so with the Goertzel algorithm. Because it processes N+1-length blocks of time samples (where N is usually in the hundreds), the filter remains stable for such short time sequences because its internal data storage registers, w(n–1) and w(n–2), are reset to zero at the beginning of each new block of input data. The filter's frequency magnitude response, provided in Figure 13-43(b), shows resonance centered at a normalized frequency of 2πm/N, corresponding to a cyclic frequency of mfs/N Hz (where fs is the signal sample rate).
The Goertzel algorithm is implemented with a complex resonator having an infinite-length unit impulse response, h(n) = ej2πnm/N, and that's why its frequency magnitude response is so narrow. The time-domain difference equations for the Goertzel filter are
An advantage of the Goertzel filter in computing an N-point X(m) DFT bin value is that Eq. (13-80) is implemented N times while Eq. (13-81), the feed forward path in Figure 13-42, need only be computed once after the arrival of the Nth input sample. Thus for real x(n) inputs the filter requires N+2 real multiplies and 2N+1 real adds to compute an N-point X(m). However, when modeling the Goertzel filter if the time index begins at n = 0, the filter must process N+1 time samples with x(N) = 0 to compute X(m).
In typical applications, to minimize spectral leakage, we choose N so there's an integer number of cycles in our input sequence of the tone we're trying to detect. N can be any integer, and the larger N the better the frequency resolution and noise immunity. However, larger N means more computations.
It's worth noting that while the typical Goertzel algorithm description in the literature specifies the frequency resonance variable m to be an integer (making the Goertzel filter's output equivalent to an N-point DFT bin output), the m in Figure 13-42 and Eq. (13-79) can in fact be any value between 0 and N–1, giving us full flexibility in specifying our filter's resonant frequency.
Let's use Goertzel to calculate the spectral magnitude of that ftone = 30 kHz tone from the Figure 13-41 example. When fs = 128 kHz and N = 64, then our resonant frequency integer m is
The Goertzel filter and the necessary computations for our 30 kHz detection example are provided in Figure 13-44.
It's useful to know that if we want to compute the power of X(15), |X(15)2|, the final feedforward complex calculations can be avoided by computing:
In our example, Eq. (13-83) becomes
Here are some implementation advantages of the Goertzel algorithm over the standard radix-2 FFT for single tone detection:
N does not need to be an integer power of 2.
The resonant frequency can be any value between zero and fs Hz.
The amount of filter coefficient (versus FFT twiddle factor) storage is reduced. If Eq. (13-83) is used, only one coefficient need be stored.
No storing a block of input data is needed before processing can begin (as with the FFT). Processing can begin with first input time sample.
No data bit reversal is needed for Goertzel.
If you implement the Goertzel algorithm M times to detect M different tones, Goertzel is more efficient (fewer multiplies) than the FFT when M < log2N.
Computational requirements to detect a single tone (assuming real-only x(n) input) are given in Table 13-4.
As a final note, although the Goertzel algorithm is implemented with a complex resonating filter structure, it's not used as a typical filter where we retain each output sample. For the Goertzel algorithm we retain only every Nth, or (N+1)th, output sample. As such, the frequency magnitude response of the Goertzel algorithm when treated as a black-box process is equivalent to the |sin(x)/x|-like magnitude response of a single bin of an N-point DFT, a portion of which is shown in Figure 13-45.
The above Goertzel algorithm computes a single complex DFT spectral bin value for every N input time samples. Here we describe a sliding DFT process whose spectral bin output rate is equal to the input data rate, on a sample-by-sample basis, with the advantage that it requires fewer computations than the Goertzel algorithm for real-time spectral analysis. In applications where a new DFT output spectrum is desired every sample, or every few samples, the sliding DFT is computationally simpler than the traditional radix-2 FFT.
Table 13-4. Single-Bin DFT Computational Comparisons
Method | Real multiplies | Real additions |
|---|---|---|
Single-bin DFT | 4N | 2N |
FFT | 2Nlog2N | Nlog2N |
Goertzel | N + 2 | 2N + 1 |
The sliding DFT (SDFT) algorithm computes a single bin result of an N-point DFT on time samples within a sliding-window. That is, for the mth bin of an N-point DFT, the SDFT computes
Let's take care to understand the notation of Xm(q). Typically, as in Chapter 3, the index of a DFT result value was the frequency-domain index m. In Eq. (13-85) the index of the DFT result is a time-domain index q = 0, 1, 2, 3, ... , such that our first mth-bin SDFT is Xm(0), our second SDFT is Xm(1), and so on.
An example SDFT analysis time window is shown in Figure 13-46(a) where Xm(0) is computed for the N = 16 time samples x(0) to x(15). The time window is then advanced one sample, as in Figure 13-46(b), and the new Xm(1) is calculated. The value of this process is that each new DFT result is efficiently computed directly from the result of the previous DFT. The incremental advance of the time window for each output computation leads to the name sliding DFT or sliding-window DFT.
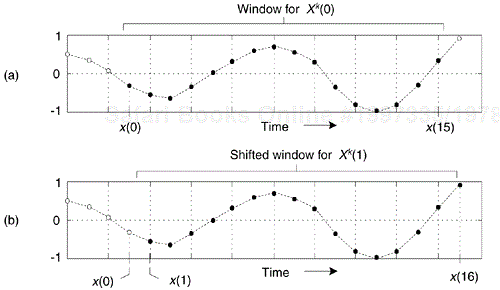
Figure 13-46. Analysis window for two 16-point DFTs: (a) data samples in the first computation; (b) second computation samples.
We can develop the mathematical expression for the SDFT as follows: the standard N-point DFT equation, of the mth DFT bin, for the qth DFT of the time sequence x(q), x(q+1), ..., x(q+N–1) is
(Variable m is the frequency-domain index, where m = 0, 1, 2, ..., N–1.) Likewise, the expression for the next DFT, the (q+1)th DFT performed on time samples x(q+1), x(q+2), ..., x(q+N) , is
Letting p = n+1 in Eq. (13-87), we can write
Shifting the limits of summation in Eq. (13-88), and including the appropriate terms (subtract the p = 0 term and add the p = N term) to compensate for the shifted limits, we write
Factoring the common exponential term (ej2πm/N), we write
Recognizing the summation in the brackets being equal to the previous Xm(q) in Eq. (13-86), and e–j2πm = 1, we write the desired recursive expression for the sliding N-point DFT as
where Xm(q+1) is the new single-bin DFT result and Xm(q) is the previous single-bin DFT value. The superscript m reminds us that the Xm(q) spectral samples are those associated with the mth DFT bin.
Let's plug some numbers into Eq. (13-91) to reveal the nature of its time indexing. If N = 20, then 20 time samples (x(0) to x(19)) are needed to compute the first result Xm(0). The computation of Xm(1) is then
Due to our derivation method's time indexing, Eq. (13-92) appears compelled to look into the future for x(20) to compute Xm(1). With no loss in generality, we can modify Eq. (13-91)'s time indexing so that the x(n) input samples and the Xm(q) output samples use the same time index n. That modification yields our SDFT time-domain difference equation of
Equation (13-93) reveals the value of this process in computing real-time spectra. We compute Xm(n) by subtracting the x(n–N) sample and adding the current x(n) sample to the previous Xm(n–1), and phase shifting the result. Thus the SDFT requires only two real additions and one complex multiply per output sample. Not bad at all! Equation (13-93) leads to the single-bin SDFT filter implementation shown in Figure 13-47.
The single-bin SDFT algorithm is implemented as an IIR filter with a comb filter followed by a complex resonator. (If you need to compute all N DFT spectral components, N resonators with m = 0 to N–1 will be needed, all driven by a single comb filter.) The comb filter delay of N samples forces the SDFT filter's transient response to be N samples in length, so the output will not reach steady state until the Xm(N–1) sample. The output will not be valid, or equivalent to Eq. (13-86)'s Xm(q), until N input samples have been processed. The z-transform of Eq. (13-93) is
where factors of Xm(z) and X(z) are collected yielding the z-domain transfer function for the mth bin of the SDFT filter as
This complex filter has N zeros equally spaced around the z-domain's unit circle, due to the N-delay comb filter, as well as a single pole canceling the zero at z = ej2πm/N. The SDFT filter's complex unit impulse response h(n) and pole/zero locations are shown in Figure 13-48 for the example where m = 2 and N = 20.
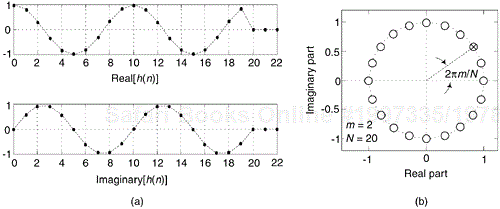
Figure 13-48. Sliding DFT characteristics for m = 2 and N = 20: (a) complex impulse response; (b) pole/zero locations.
Because of the comb subfilter, the SDFT filter's complex sinusoidal unit impulse response is finite in length—truncated in time to N samples—and that property makes the frequency magnitude response of the SDFT filter identical to the sin(Nx)/sin(x) response of a single DFT bin centered at a frequency of 2πm/N.
One of the attributes of the SDFT is that once an Xm(n) is obtained, the number of computations to compute Xm(n+1) is fixed and independent of N. A computational workload comparison between the Goertzel and SDFT filters is provided later in this section. Unlike the radix-2 FFT, the SDFT's N can be any positive integer giving us greater flexibility to tune the SDFT's center frequency by defining integer m such that m = Nfi/fs, when fi is a frequency of interest in Hz and fs is the signal sample rate in Hz. In addition, the SDFT requires no bit-reversal processing as does the FFT. Like the Goertzel algorithm, the SDFT is especially efficient for narrowband spectrum analysis.
For completeness, we mention that a radix-2 sliding FFT technique exists for computing all N bins of Xm(q) in Eq. (13-85)[47,48]. That technique is computationally attractive because it requires only N complex multiplies to update the N-point FFT for all N bins; however, it requires 3N memory locations (2N for data and N for twiddle coefficients). Unlike the SDFT, the radix-2 sliding FFT scheme requires address bit-reversal processing and restricts N to be an integer power of two.
The SDFT filter is only marginally stable because its pole resides on the z-domain's unit circle. If filter coefficient numerical rounding error is not severe, the SDFT is bounded-input-bounded-output stable. Filter instability can be a problem, however, if numerical coefficient rounding causes the filter's pole to move outside the unit circle. We can use a damping factor r to force the pole and zeros in Figure 13-48(b) to be at a radius of r just slightly inside the unit circle and guarantee stability using a transfer function of
with the subscript gs meaning guaranteed-stable. (Section 7.1.3 provides the mathematical details of moving a filter's poles and zeros inside the unit circle.) The stabilized feedforward and feedback coefficients become –rN and rej2πm/N, respectively. The difference equation for the stable SDFT filter becomes
with the stabilized-filter structure shown in Figure 13-49. In this case, we perform five real multiplies and four real additions per output sample.
Using a damping factor as in Figure 13-49 guarantees stability, but the Xm(q) output, defined by
is no longer exactly equal to the mth bin of an N-point DFT in Eq. (13-85). While the error is reduced by making r very close to (but less than) unity, a scheme does exist for eliminating that error completely once every N output samples at the expense of additional conditional logic operations[49]. Determining if the damping factor r is necessary for a particular SDFT application requires careful empirical investigation. As is so often the case in the world of DSP, this means you have test your SDFT implementation very thoroughly and carefully!
Another stabilization method worth consideration is decrementing the largest component (either real or imaginary) of the filter's ej2πm/N feedback coefficient by one least significant bit. This technique can be applied selectively to problematic output bins and is effective in combating instability due to rounding errors which result in finite-precision ej2πm/N coefficients having magnitudes greater than unity. Like the DFT, the SDFT's output is proportional to N, so in fixed-point binary implementations the designer must allocate sufficiently wide registers to hold the computed results.
Being equivalent to the DFT, the SDFT also suffers from spectral leakage effects. As with the DFT, SDFT leakage can be reduced by the standard concept of windowing the x(n) input time samples as discussed in Section 3.9. However, windowing by time-domain multiplication would ruin the real-time computational simplicity of the SDFT. Thanks to the convolution theorem properties of discrete systems, we can implement time-domain windowing by means of frequency-domain convolution, as discussed in Section 13.3.
Spectral leakage reduction performed in the frequency domain is accomplished by convolving adjacent Xm(q) values with the DFT of a window function. For example, the DFT of a Hamming window comprises only three non-zero values, –0.23, 0.54, and –0.23. As such, we can compute a Hamming-windowed Xm(q) with a three-point convolution using
Figure 13-50 shows this process using three resonators, each tuned to adjacent DFT bins (m–1, m, and m+1). The comb filter stage need only be implemented once.
Table 13-5 provides a computational workload comparison of various spectrum analysis schemes in computing an initial Xm(n) value and computing a subsequent Xm(n+1) value.
To compute the initial windowed Xm(n) values in Table 13-5, the three-term frequency-domain convolution need only be performed once, upon arrival of the Nth time sample. However, the convolution needs to be performed for all subsequent computations
We remind the reader that Section 13.3 discusses several implementation issues regarding Hanning windowing in the frequency domain, using binary shifts to eliminate the multiplications in Eq. (13-99), as well as the use of other window functions.
Table 13-5. Single-Bin DFT Computation Comparison
Method | Compute initial Xm(n) | Compute Xm(n+1) | ||
|---|---|---|---|---|
Real multiplies | Real adds | Real multiplies | Real adds | |
DFT | 4N | 2N | 4N | 2N |
Goertzel algorithm | N + 2 | 2N + 1 | N + 2 | 2N + 1 |
Sliding DFT (marginally stable) | 4N | 4N | 4 | 4 |
Sliding DFT (guaranteed stable) | 5N | 4N | 5 | 4 |
Three-term windowed sliding DFT (marginally stable) | 12N + 6 | 10N + 4 | 18 | 14 |
Three-term windowed sliding DFT (guaranteed stable) | 13N + 6 | 10N + 4 | 19 | 14 |
The SDFT has a special property that's not widely known, but is very important. If we change the SDFT's comb filter feedforward coefficient (in Figure 13-47) from a –1 to +1, the comb's zeros will be rotated counterclockwise around the unit circle by an angle of π/N radians. This situation, for N = 8, is shown on the right side of Figure 13-51(a). The zeros are located at angles of 2π(m + 1/2)/N radians. The m = 0 zeros are shown as solid dots. Figure 13-51(b) shows the zeros locations for an N = 9 SDFT under the two conditions of the comb filter's feedforward coefficient being –1 and +1.
This alternate situation is useful: we can now expand our set of spectrum analysis center frequencies to more than just N angular frequency points around the unit circle. The analysis frequencies can be either 2πm/N or 2π(m+1/2)/N, where integer m is in the range 0 ≤ m ≤ N–1. Thus we can build an SDFT analyzer that resonates at any one of 2N frequencies between 0 and fs Hz. Of course, if the comb filter's feedforward coefficient is set to +1, the resonator's feedforward coefficient must be ej2π(m+1/2)/N to achieve pole/zero cancellation.
The Zoom FFT is interesting because it blends complex downconversion, lowpass filtering, and sample rate change through decimation in a spectrum analysis application. The Zoom FFT method of spectrum analysis is used when fine spectral resolution is needed within a small portion of a signal's overall frequency range. This technique is more efficient than the traditional FFT in such a situation.
Think of the spectral analysis situation where we require fine frequency resolution, closely spaced FFT bins, over the frequency range occupied by the signal of interest shown in Figure 13-52(a). (The other signals are of no interest to us.) We could collect many time samples and perform a large-size radix-2 FFT to satisfy our fine spectral resolution requirement. This solution is inefficient because we'd be discarding most of our FFT results. The Zoom FFT can help us improve our computational efficiency through:
frequency translation by means of complex downconversion,
low-pass filtering,
decimation, and finally
performing a smaller size FFT.
The process begins with the continuous x(t) signal being digitized at a sample rate of fs1 by an analog-to-digital (A/D) converter yielding the N-point x(n) time sequence whose spectral magnitude is |X(m)| in Figure 13-52(a). The Zoom FFT technique requires narrowband filtering and decimation in order to reduce the number of time samples prior to the final FFT, as shown in Figure 13-52(b). The downconverted signal's spectrum, centered at zero Hz, is the |Xc(m)| shown in Figure 13-52(c). (The lowpass filter's frequency response is the dashed curve.) After lowpass filtering xc(n), the filter's output is decimated by an integer factor D yielding a time sequence ![]() whose sample rate is fs2 = fs1/D prior to the FFT operation. The key here is that the length of
whose sample rate is fs2 = fs1/D prior to the FFT operation. The key here is that the length of ![]() is N/D, allowing a reduced-size FFT. (N/D must be an integer power of two to enable the use of radix-2 FFTs.) We perform the FFT only over the decimated signal's bandwidth. It's of interest to note that, because its input is complex, the N/D-point FFT has a non-redundant frequency analysis range from –fs2/2 to +fs2/2. (Unlike the case of real inputs, where the positive and negative frequency ranges are redundant.)
is N/D, allowing a reduced-size FFT. (N/D must be an integer power of two to enable the use of radix-2 FFTs.) We perform the FFT only over the decimated signal's bandwidth. It's of interest to note that, because its input is complex, the N/D-point FFT has a non-redundant frequency analysis range from –fs2/2 to +fs2/2. (Unlike the case of real inputs, where the positive and negative frequency ranges are redundant.)
The implementation of the Zoom FFT is given in Figure 13-53, where all discrete sequences are real valued.
Relating the discrete sequences in Figure 13-52(b) and Figure 13-53, the complex time sequence xc(n) is represented mathematically as:
while the complex decimated sequence ![]() is
is
The complex mixing sequence ![]() , where ts1 = 1/fs1, can be represented in the two forms of
, where ts1 = 1/fs1, can be represented in the two forms of
Let's use an example to illustrate the Zoom FFT's ability to reduce standard FFT computational workloads. Say we have a signal sampled at fs1 = 1024 kHz, and we require 2 kHz FFT bin spacing for our spectrum analysis resolution. These conditions require us to collect 512 samples (1024 kHz/2 kHz) and perform a 512-point FFT. If the signal of interest's bandwidth is less than fs1/8, we could lowpass filter, use a decimation factor of D = 8, and only perform a 512/8 = 64-point FFT and still achieve the desired 2 kHz frequency resolution. We've reduced the 512-point FFT (requiring 2304 complex multiplies) to a 64-point FFT (requiring 192 complex multiplies). That's an computational workload reduction of more than 90%!
We're using the following definition for the percent computation reduction in complex multiplies afforded by the (N/D)-point Zoom FFT over the standard N-point FFT,
Plotting Eq. (13-103) for various decimation factors over a range of FFT sizes (all integer powers of two) yields the percent of FFT computational reduction curves in Figure 13-54.
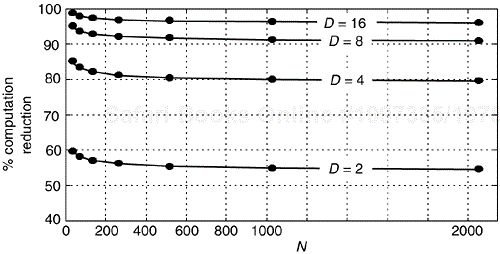
Figure 13-54. Percent computational workload reduction, in complex multiplies, of an (N/D)-point Zoom FFT relative to a standard N-point FFT.
We see that the Zoom FFT affords significant computational saving over a straightforward FFT for spectrum analysis of a narrowband portion of some X(m) spectrum—and the computational savings in complex multiplies improves as the decimation factor D increases. Ah, but here's the rub. As D increases, the Zoom FFT's lowpass filters must become more narrow which increases their computational workload; this is the trade-off. What you have to ask yourself is: “Does the FFT size reduction compensate for the additional quadrature mixing and dual filtering computational workload?” It certainly would if a large-size FFT is impossible with your available FFT hardware or software. If you can arrange for your continuous signal of interest to be centered at fs1/4, then the quadrature mixing can be performed without multiplications. (See Section 13.1.) You may be able to use a simple, efficient, IIR filter if spectral phase is unimportant. If phase distortion is unacceptable, then efficient polyphase and half-band FIR filters are applicable. The computationally efficient frequency sampling and interpolated FIR filters, in Chapter 7, should be considered. If the signal of interest is very narrowband relative to the fs1 sample rate, requiring a large decimation factor and very narrowband computationally expensive filters, perhaps a cascaded integrator-comb (CIC) filter can be used to reduce the filtering computational workload.
Here's a clever trick for implementing a practical spectrum analyzer by modifying the time-domain data before applying a radix-2 FFT algorithm.
Let's say we need to build a spectrum analyzer to display, in some manner, the spectral magnitude of a time-domain sequence. We'd like our spectrum analyzer, a bank of bandpass filters, to have a frequency magnitude response something like that shown in Figure 13-55(a). For spectrum analysis, the radix-2 FFT algorithm comes to mind first, as it should. However, the frequency response of individual FFT bins is that shown in Figure 13-55(b), with their non-flat passbands, unpleasantly high sidelobes due to spectral leakage, and overlapped main lobes. We can reduce the leakage sidelobe levels by windowing the time-domain sequence, but that leads to the increased main lobe overlap shown in Figure 13-55(c) and degraded frequency resolution, and we still have considerable droop in the passband response.
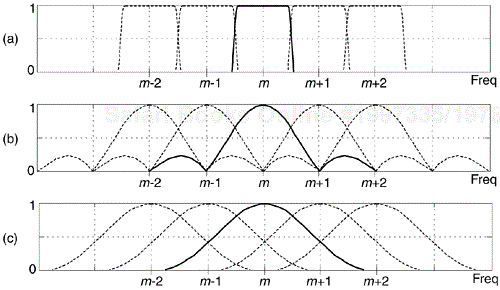
Figure 13-55. Spectrum analyzer: (a) desired frequency response; (b) frequency response of standard FFT bins; (c) windowed-data FFT frequency response.
Here's how we can solve our problem. Consider an x(n) sequence of time samples of length M whose M-point DFT is
Next consider partitioning x(n) into P subsequences, each of length N. Thus PN = M. If we add, element for element, the P subsequences we'll obtain a new y(n) sequence of length N whose N-point DFT is
The good news is that
That is, the DFT magnitudes of sequence y(n) are equal to a subset of the longer DFT magnitudes of x(n). Y(m) is equal to a decimated-by-P version of X(k). The relationship between |Y(m)| and |X(Pm)| doesn't seem too important, but here's how we'll take advantage of that equality. We'll create an M-point window sequence whose single-bin frequency response, of an M-point FFT, is the bold curve in Figure 13-56(a). Instead of computing all M FFT outputs, we'll only compute every Pth output of the M-point FFT, implementing Eq. (13-105), giving us the decimated FFT bins shown in Figure 13-56(b). In that figure P = 5.
That decimation of the frequency-domain |X(k)| spectrum is accomplished in the time domain by a time-aliasing operation as shown in Figure 13-57 where again, for example, P = 5. We partition the M-sample windowed-x(n) time sequence into P = 5 subsequences, sum the subsequences element for element to obtain the time-aliased N-sample y(n) sequence. Next the |Y(m)| spectral magnitudes are computed using the radix-2 FFT. (With the input x(n) sequence being real-valued, with spectral symmetry, only N/2+1 the |Y(m)| magnitude values need be computed for display.)
This process, sweet in its simplicity, is called the weighted overlap-add structure[50,51], and is alternatively referred to as the window-presum FFT[52]. The most difficult part of building this analyzer is designing the M-point window sequence used to window the original x(n) sequence. We do that by specifying the window's frequency domain characteristics just as if it were a digital filter frequency response, and use our favorite filter design software to compute the filter's time-domain impulse response. That impulse response is the window sequence. With the signal sample rate being fs, the window's passband width will be just less than fs/N. This makes the filter's one-sided passband width roughly fs/2N.
Figure 13-58 illustrates an example FFT analyzer with fs = 1 Mhz, N = 64, with P = 5 making M = 320. The FFT bin spacing is 15.63 kHz, so the window design was set for a passband width of 10 kHz (thus the filter's one-sided bandwidth was specified as 5 kHz in a Parks-McClellan design routine). Figure 13-58(a) is the 320-point window sequence, while Figure 13-58(b) shows FFT analyzer's response for the m = 3, 4, and 5 bins, with the |Y(4)| response being the solid curve.
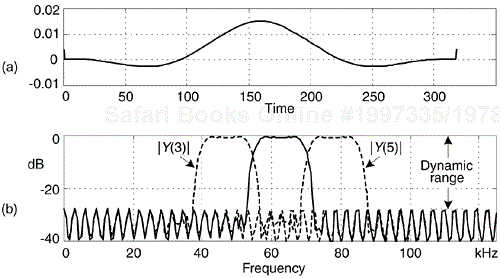
Figure 13-58. FFT analyzer example: (a) window sequence; (b) analyzer response for 64-point FFT bins |Y(3)|, |Y(4)|, and |Y(5)|.
The width of the spectrum analyzer's passbands is primarily controlled by the window's passband width. The center frequencies of the analyzer's individual passbands is defined by fs/N. What this means is that the amount of overlap in the analyzer's passbands depends on both the window's passband width, fs, and N. The dynamic range of the analyzer can be increased by increasing P, which increases M and lengthens the x(n) sequence. As M is increased, the longer window sequence will yield analyzer passbands having a more rectangular shape, lower sidelobes, and reduced passband ripple.
Again, to implement this radix-2 FFT spectrum analyzer, the length of the time-domain sequence (M) must be an integer multiple (P) of an integer power of two (N).
Fast and accurate methods for computing the arctangent of a complex number x = I + jQ have been the subject of extensive study because estimating the angle θ of a complex value has so many applications in the field of signal processing. The angle of x is defined as θ = tan–1(Q/I).
Practitioners interested in computing high speed (minimum computations) arctangents typically use look-up tables where the value Q/I specifies a memory address in programmable read-only memory (PROM) containing an approximation of angle θ. Those folks interested in enhanced precision implement compute-intensive high-order algebraic polynomials, where Chebyshev polynomials seem to be more popular than Taylor series, to approximate angle θ. (Unfortunately, because it is such a non-linear function, the arctangent is resistant to accurate reasonable-length polynomial approximations. So we end up choosing the least undesirable method for computing arctangents.)
Here's another contender in the arctangent approximation race that uses neither look-up tables nor high-order polynomials. We can estimate the angle θ, in radians, of x = I + jQ using the following approximation
where –1 ≤ Q/I ≤ 1. That is, θ is in the range –45° to +45° (–π/4 ≤ θ ≤ +π/4 radians). Equation (13-107) has surprisingly good performance, particularly for a 90° (π/2 radians) angle range. Figure 13-59 shows the maximum error is 0.26° using Eq. (13-107) when the true angle θ is within the angular range of –45° to +45°.
A nice feature of this θ' computation is that it can be written as:
eliminating Eq. (13-107)'s Q/I division operation, at the expense of two additional multiplies. Another attribute of Eq. (13-108) is that a single multiply can be eliminated with binary right shifts. The product 0.28125Q2 is equal to (1/4+1/32)Q2, so we can implement the product by adding Q2 shifted right by two bits to Q2 shifted right by five bits. This arctangent scheme may be useful in a digital receiver application where I2 and Q2 have been previously computed in conjunction with an AM (amplitude modulation) demodulation process or envelope detection associated with automatic gain control (AGC).
We can extend the angle range over which our approximation operates. If we break up a circle into eight 45° octants, with the first octant being 0° -to- 45°, we can compute the arctangent of a complex number residing in any octant. We do this by using the rotational symmetry properties of the arctangent:
Table 13-6. Octant Location versus Arctangent Expressions
Octant | Arctan approximation |
|---|---|
1st, or 8th |
|
2nd, or 3rd |
|
4th, or 5th |
|
6th, or 7th |
|
Those properties allow us to create Table 13-6.
So we have to check the signs of Q and I, and see if |Q| > |I|, to determine the octant location, and then use the appropriate approximation in Table 13-6. The maximum angle approximation error is 0.26° for all octants.
When θ is in the 5th octant, the above algorithm will yield a θ' that's more positive than +π radians. If we need to keep the θ' estimate in the range of –π -to- +π, we can rotate any θ residing in the 5th quadrant +π/4 radians (45°), by multiplying (I +jQ) by (1 +j), placing it in the 6th octant. That multiplication yields new real and imaginary parts defined as
Then the 5th octant θ' is estimated using I' and Q' with
In Section 9.2 we discussed the notion of measuring the instantaneous frequency of a complex sinusoidal signal by computing the derivative of the signal's instantaneous θ(n) phase as shown in Figure 13-60.
This is the traditional discrete signal FM demodulation method, and it works fine. The demodulator's instantaneous output frequency is
where fs is the sample rate in Hz.
Computing instantaneous phase θ(n) requires an arctangent operation, which is difficult to implement accurately without considerable computational resources. Here's a scheme for computing Δθ(n) for use in Eq. (13-111) without the intermediate θ(n) phase computation (and its pesky arctangent)[53,54]. We derive the Δθ(n) computation algorithm as follows, initially using continuous-time variables based on the following definitions:
First, we let r(t) = q(t)/i(t) be the signal for which we're trying to compute the derivative of its arctangent. The time derivative of tan–1[r(t)], a calculus identity, is
Because d[r(t)]/dt = d[q(t)/i(t)]/dt, we use the calculus identity for the derivative of a ratio to write
Plugging Eq. (13-114)'s result into Eq. (13-113), we have
Replacing r(t) in Eq. (13-115) with q(t)/i(t) yields
We're getting there. Next we multiply the numerator and denominator of the first ratio in Eq. (13-116) by i2(t), and replace t with our discrete time variable index n to arrive at our final result of
The implementation of this algorithm, where the derivatives of i(n) and q(n) are i'(n) and q'(n) respectively, is shown in Figure 13-61(a). The Δφ(n) output sequence is used in Eq. (13-111) to compute instantaneous frequency.
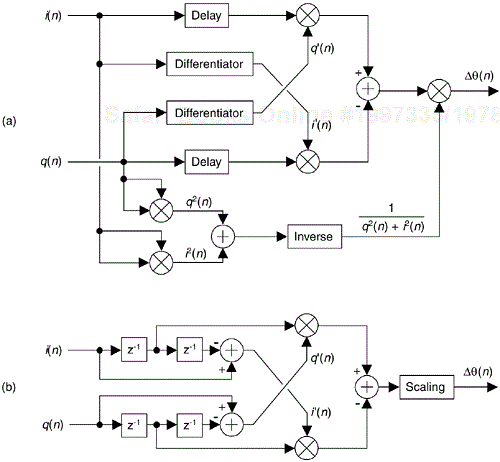
Figure 13-61. Frequency demodulator without arctangent: (a) standard process; (b) simplified process.
The Differentiator is an tapped-delay line FIR differentiating filter with an odd number of taps. Reference [54] reports acceptable results when the differentiator is a FIR filter having 1,0,–1 as coefficients. The Delay elements in Figure 13-61 are used to time-align i(n) and q(n) with the outputs of the differentiators such that the delay is (K–1)/2 samples when a K-tap differentiator is used. In practice, the Delay can be obtained by tapping off the center tap of the differentiating filter.
If the i(n)+jq(n) signal is purely FM and hard limited such that i2(n)+q2(n) = Constant, the denominator computations in Eq. (13-117) need not be performed. In this case, using the 1,0,–1 coefficient differentiators, the FM demodulator is simplified to that shown in Figure 13-61(b) where the Scaling operation is multiplication by the reciprocal of Constant.
When we digitize analog signals using an analog-to-digital (A/D) converter, the converter's output typically contains some small DC bias: that is, the average of the digitized time samples is not zero. That DC bias may have come from the original analog signal or from imperfections within the A/D converter. Another source of DC bias contamination in DSP is when we truncate a discrete sequence from a B-bit representation to word widths less than B bits. Whatever the source, unwanted DC bias on a signal can cause problems. When we're performing spectrum analysis, any DC bias on the signal shows up in the frequency domain as energy at zero Hz, the X(0) spectral sample. For an N-point FFT the X(0) spectral value is proportional to N and becomes inconveniently large for large-sized FFTs. When we plot our spectral magnitudes, the plotting software will accommodate any large X(0) value and squash down the remainder of the spectrum in which we are more interested.
A non-zero DC bias level in audio signals is particularly troublesome because concatenating two audio signals, or switching between two audio signals, results in unpleasant audible clicks. In modern digital communications systems, a DC bias on quadrature signals degrades system performance and increases bit error rates. With that said, it's clear that methods for DC removal are of interest to many DSP practitioners.
If you're processing in non-real-time, and the signal data is acquired in blocks (fixed-length sequences) of block length N, DC removal is straightforward. We merely compute the average of our N time samples, and subtract that average value from each original sample to yield a new time sequence whose DC bias will be extremely small.
This scheme, although very effective, is not compatible with continuous-throughput (real-time) systems. For real-time systems we're forced to use filters for DC removal.
The author has encountered three proposed filters for DC removal[55–57]; their structures are shown in Figure 13-62(a), (b), and (c).
Ignoring the constant gains of those DC-removal filters, all three filters have identical performance with the general DC-removal filter structure in Figure 13-62(d) having a z-domain transfer function of
(It's not immediately obvious that the filters in Figure 13-62(c) and (d) are equivalent. You can verify that equivalency by writing the time-domain difference equations relating the various nodes in the feedback path of Figure 13-62(c)'s filter. Next, convert those equations to z-transform expressions and solve for Y(z)/X(z) to yield Eq. (13-118)).
Because the DC-removal filters can be modeled with the general DC-removal filter in Figure 13-62(d), we provide the general filter's frequency magnitude and phase responses in Figure 13-63(a) and (b) for α = 0.95. The filter's pole/zero locations are given in Figure 13-63(c), where a zero resides at z = 1 providing infinite attenuation at DC (zero Hz) and a pole at z = α making the magnitude notch at DC very sharp. The closer a is to unity, the narrower the frequency magnitude notch centered at zero Hz. Figure 13-63(d) shows the general filter's unit-sample impulse response.
Figure 13-63. DC-removal filter, α = 0.95: (a) magnitude response; (b) phase response; (c) pole/zero locations; (d) impulse response.
Figure 13-64 shows the time-domain input/output performance of the general DC-removal filter (with α = 0.95) when its input is a sinusoid suddenly contaminated with a DC bias of 2 beginning at the 100th time sample and disappearing at the 200th sample. The DC-removal filter works well.
Because the general DC-removal filter has feedback the y(n) output samples may require wider binary word widths than those used for the x(n) input samples. This could result in overflows in fixed-point binary implementations. The scaling factors of (1+α)/2 and K, in Figure 13-62(a) and (b), are less than one to minimize the chance of y(n) binary overflow.
In fixed-point hardware the y(n) samples are often truncated to the same word width as the input x(n). This quantization (by means of truncation) will induce a negative DC bias onto the quantized output samples, degrading our desired DC removal. When we truncate a binary sample value, by discarding some of its least significant bits, we induce a negative error in the truncated sample. Fortunately, that error value is available for us to add to the next unquantized signal sample, increasing its positive DC bias. When that next sample is truncated, the positive error we've added minimizes the negative error induced by truncation of the next sample.
Figure 13-65(a) shows the addition of a quantizing sigma-delta modulator to the feedback path of the DC-removal filter given in Figure 13-62(c). The positive error induced by truncation quantization (the Q block) is delayed by one sample time and fed back to the quantizer input. Because the modulator has a noise shaping property where quantization error noise is shifted up in frequency, away from zero Hz (DC), the overall DC bias at the output of the filter is minimized[56].
An equivalent quantization noise shaping process can be applied to a Direct Form I version of the Figure 13-62(d) general DC-removal filter as shown in Figure 13-65(b). Again, the positive quantization error is delayed by one sample time and added to the quantizer input[58–60]. To reiterate, the DC-removal filters in Figure 13-65 are used to avoid binary data overflow, by means of quantization, without the use of scaling multipliers.
A major design goal for cascaded integrator-comb (CIC) filters, as introduced in Section 10.5 in conjunction with sample rate conversion, is to minimize their hardware power consumption by reducing data word width and reducing data clock rates wherever possible. Here we introduce a clever trick that reduces CIC filter power consumption using nonrecursive structures, by means of polynomial factoring, easing the word width growth problem. These nonrecursive structures require that the sample rate change R be an integer power of two enhancing computational simplicity through polyphase decomposition, transposed structures, simplified multiplication, and substructure sharing[61–63]. (These processes are not complicated; they merely have fancy names.) Next, we'll review a nonrecursive scheme that enables sample rate changes other than powers of two. The following discussion assumes that the reader is familiar with the CIC filter material in Section 10.5.
Recall that the structures of first-order (M = 1) and third-order (M = 3) CIC decimation filters, having a comb delay equal to the sample rate change factor R, are those shown in Figure 13-66. As presented in Section 10.5, the transfer function of an Mth-order decimating CIC filter can be expressed either in a recursive form or a nonrecursive form, as indicated in Eq. (13-119). (You could, if you wish, use the geometric series discussion in Appendix B to show the equality of the two forms of the filter's transfer function.)
Now if the sample rate change factor R is an integer power of two, R = 2K where K is some positive integer, the Eq. (13-119') Mth-order nonrecursive polynomial form of Hcic(z) can be factored as
The reward for this factorization is that the CIC filter can then be implemented with K nonrecursive stages as shown in Figure 13-67. This implementation eliminates filter feedback loops with their unpleasant binary word width growth. The data word width does increase in this nonrecursive structure by M bits for each stage, but the sampling rate is reduced by a factor of two for each stage. This nonrecursive structure has been shown to consume less power than the Figure 13-66(b) recursive implementation for filter orders greater than three and decimation/interpolation factors larger than eight[63]. Thus the power savings from sample rate reduction is greater than the power consumption increase due to data word width growth.
Happily, further improvements are possible with each stage of this nonrecursive structure[62]. For example, assume we desire an M = fifth-order decimating CIC for Stage 1 in Figure 13-67. In that case, the stage's transfer function is
The second step in Eq. (13-121), known as polyphase decomposition[64–68], enables a polyphase implementation having two parallel paths as shown in Figure 13-68. The decimation by two is implemented by routing the odd-index input samples to FA'(z), and the even-index samples to FB'(z). Because we implement decimation by 2 before the filtering, the new polyphase components are FA'(z) = 1 + 10z–1 + 5z–2, and FB'(z) = 5 + 10z–1 + z–2 implemented at half the data rate into the stage. (Reducing data rates as early as possible is a key design goal in the implementation of CIC decimation filters.)
The FA'(z) and FB'(z) polyphase components are implemented in a tapped-delay line fashion and, fortunately, further simplifications are possible. Let's consider the FA'(z) polyphase filter component, in a tapped-delay line configuration, shown in Figure 13-69(a). The transposed version of this filter is presented in Figure 13-69(b) with its flipped coefficient sequence. The adder in the Figure 13-69(a) must perform two additions per input data sample, while in the transposed structure no adder need perform more than one add per data sample. Thus the transposed structure can operate at a higher speed.
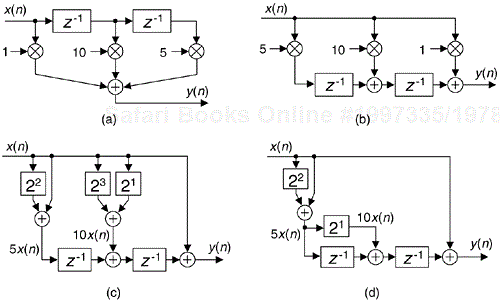
Figure 13-69. Filter component FA'(z): (a) delay line structure; (b) transposed structure; (c) simplified multiplication; (d) substructure sharing.
The next improvement uses simplified multiplication, as shown in Figure 13-69(c), by means of arithmetic shifts and adds. Thus a factor of 5 is implemented as 22 + 1, eliminating all multiplications. Finally, because of the transposed structure, we can use the technique of substructure sharing in Figure 13-69(d) to reduce the hardware component count. Pretty slick! By the way, these nonrecursive filters are still called cascaded integrator-comb filters, even though they have no integrators. Go figure.
Table 13-7 is provided to help the reader avoid computing the polynomial equivalent of several Mth-order nonrecursive stages, as was performed in Eq. (13-121).
The nonrecursive CIC decimation filters described above have the restriction that the R decimation factor must be an integer power of two. That constraint is loosened due to a clever scheme of factoring R into a product of prime numbers[69]. This multiple prime-factor-R technique is based on the process of factoring integer R into the form R = 2p3q5r7s11t ..., where 2, 3, 5, 7, 11 are the prime numbers. (This process is called prime factorization, or prime decomposition, and has been of interest since the days of Euclid.). Then the appropriate number of CIC subfilters are cascaded as shown in Figure 13-70(a). The fortunate condition is that those Mth-order CIC filters are described by
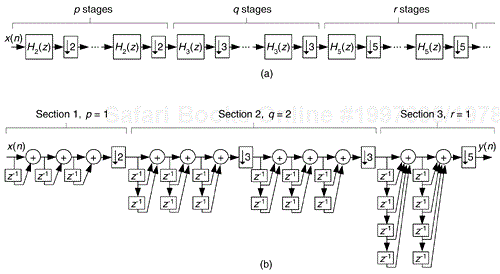
Figure 13-70. Multiple prime-factor nonrecursive CIC example: (a) cascaded-stage structure; (b) third-order, R = 90, nonrecursive CIC example.
Table 13-7. Expansions of (1 + z–1)M.
M | (1 + z–1)M |
|---|---|
2 | (1 + z–1)2 = 1 + 2z–1 + z–2 |
3 | (1 + z–1)3 = 1 + 3z–1 + 3z–2 + z–3 |
4 | (1 + z–1)4 = 1 + 4z–1 + 6z–2 + 4z–3 + z–4 |
5 | (1 + z–1)5 = 1 + 5z–1 + 10z–2 + 10z–3 + 5z–4 + z–5 |
6 | (1 + z–1)6 = 1 + 6z–1 + 15z–2 + 20z–3 + 15z–4 + 6z–5 + z–6 |
7 | (1 + z–1)7 = 1 + 7z–1 + 21z–2 + 35z–3 + 35z–4 + 21z–5 + 7z–6 + z–7 |
8 | (1 + z–1)8 = 1 + 8z–1 + 28z–2 + 56z–3 + 70z–4 + 56z–5 + 28z–6 + 8z–7 + z–8 |
9 | (1 + z–1)9 = 1 + 9z–1 + 36z–2 + 84z–3 + 126z–4 + 126z–5 + 84z–6 + 36z–7 + 9z–8 + z–9 |
and so on, enabling nonrecursive implementations.
Due to space constraints, the elegant and arduous derivation of this technique is not given here; but this process can illustrated with an example. Assume we desire a third-order CIC filter with a decimation factor of R = 90. That decimation rate is factored as 90 = (2)(3)(3)(5). So p = 1, q = 2, and r = 1. Our composite CIC filter is implemented as H2(z)H3(z)H3(z)H5(z) shown in Figure 13-70(b).
At first glance the many additions of the Figure 13-70(b) CIC filter appear to aggravate the power consumption of such a filter, but the reduced sample rates significantly reduce power requirements[69]. If one addition in Section 1 of Figure 13-70(b) consumes P units of power, then Section 1 consumes 3P units of power, and each addition in the first portion of Section 2 consumes P/2 units of power. Each addition in the second portion of Section 2 consumes P/6 of units power, while each addition in Section 3 consumes P/18 units of power.
We have flexibility here because the subfilters in each section of Figure 13-70(b) can be implemented recursively or nonrecursively, as indicated in Eq. (13-122). In nonrecursive implementations the polyphase decomposition, transposed structures, simplified multiplication, and substructure sharing schemes can be applied. CIC filter design certainly has come a long way since its introduction in the early 1980s.
In practice we may be required to make precise measurements in the presence of high noise or interference. Without some sort of analog signal conditioning, or digital signal processing, it can be difficult to obtain stable and repeatable, measurements. This impulsive-noise smoothing trick, originally developed to detect microampere changes in milliampere signals, describes a smoothing algorithm that improves the stability of precision measurements in the presence of impulsive noise[70].
Practical noise reduction methods often involve multiple-sample averaging (block averaging) of a sequence of measured values, x(n), to compute a sequence of N-sample arithmetic means, M(q). As such, the block averaged sequence M(q) is defined by:
where the time index of the averaging process is q = 0, 1, 2, 3, etc. When N = 10 for example, for the first block of data (q = 0), time samples x(0) through x(9) are averaged to compute M(0). For the second block of data (q = 1), time samples x(10) through x(19) are averaged to compute M(1), and so on[71].
The following impulsive-noise smoothing algorithm processes a block of time-domain samples, obtained through periodic sampling, and the number of samples, N, may be varied according to individual needs and processing resources. The processing of a single block of N time samples proceeds as follows: collect N+2 samples of x(n), discard the maximum (most positive) and minimum (most negative) samples to obtain an N-sample block of data, and compute the arithmetic mean, M(q), of the N samples. Each sample in the block is then compared to the mean. The direction of each sample relative to the mean (greater than, or less than) is accumulated, as well as the cumulative magnitude of the deviation of the samples in one direction (which, by definition of the mean, equals that of the other direction). This data is used to compute a correction term that is added to the mean according to the following formula:
where A(q) is the corrected mean, M(q) is the arithmetic mean (average) from Eq. (13-123), Pos is the number of samples greater than M(q), and Neg is the number of samples less than M(q), and Dtotal is the sum of deviations from the mean (absolute values and one direction only). Dtotal, then, is the sum of the differences between the Pos samples and M(q).
For an example, consider a system acquiring 10 measured samples of 10, 10, 11, 9, 10, 10, 13, 10, 10, and 10. The mean is M = 10.3, the total number of samples positive is Pos = 2, and the total number of samples negative is Neg = 8 (so Pos–Neg = –6). The total deviation in either direction from the mean is 3.4 [using the eight samples less than the mean, (10.3–10) times 7 plus (10.3–9); or using the two samples greater than the mean, (13–10.3) plus (11–10.3)]. With Dtotal = 3.4, Eq. (13-124) yields an improved result of A = 10.096.
The smoothing algorithm's performance, relative to traditional block averaging, can be illustrated by example. Figure 13-71(a) shows a measured 300-sample x(n) signal sequence comprising a step signal of amplitude one contaminated with random noise (with a variance of 0.1) and two large impulsive-noise spike samples.
Figure 13-71. Noise smoothing for N = 10: (a) input x(n) signal; (b) block average output (white) and impulsive-noise smoothing algorithm output (solid).
A few meaningful issues regarding this noise smoothing process are:
The block size (N) used in the smoothing algorithm can be any integer, but for real-time fixed binary-point implementations it's beneficial to set N equal to an integer power of two. In that case the compute-intensive division operations in Eq. (13-123) and Eq. (13-124) can be accomplished by binary arithmetic right shifts to reduce the computational workload.
If there's a possibility that more than two large noise spikes are contained in a block of input samples, then we collect more than N+2 samples of x(n) and discard the appropriate number of maximum and minimum samples to eliminate the large impulsive noise samples.
We could forego the Eq. (13-124) processing and merely perform Eq. (13-123) to compute the mean M(q). In that case, for a given N, the standard deviation of M(q) would be roughly 15–20% greater than A(q).
On the off chance that you didn't know, to speed up polynomial evaluations (computations) in software it's smart to use what's known as Horner's rule. An example of polynomial evaluation is, say, using the following expression to compute the arctangent of x:
To see how the computational workload of polynomial evaluations can be reduced, consider the following kth-order polynomial:
It can be rewritten as:
where the H subscript means Horner. Using this method to compute polynomials:
reduces the number of necessary multiply operations, and
is straightforward to implement using programmable DSP chips with their multiply and accumulate (MAC) architectures.
For example, consider the fifth-order polynomial:
Evaluated in the standard way, Eq. (13-128) would require nine multiplies and five additions, whereas the Horner version
requires only five multiplies and five adds when the computations begin with the innermost multiply and add operations (c5x + c4).
Here are a few examples of polynomials in the Horner format:
By the way, the multiplications and additions cannot be performed in parallel. Because Horner's rule is inherently serial, we need the result of the last multiplication before we can start the next addition, and that addition result is needed before the follow-on multiplication.
Horner's rule is another of those handy computer techniques we use whose origins are very old. Chinese mathematicians described it in the 1200s. European mathematicians (including William Horner) rediscovered and publicized it in the early 1800s. It seems Sir Isaac Newton also invented and used it in the 1600s.
There are linear phase filtering applications wherein we're interested in designing very high performance (very narrow passband widths, and/or very high attenuation) nonrecursive FIR filters. Consider the possibility that you've used Eq. (7-39), or some other algorithm, to determine that you need to implement a 2000-tap linear phase FIR filter. Then when you try to design such a filter using your trusty Remez-Exchange-based (Parks-McClellan) filter design software, you obtain unusable design results. It happens that some software incarnations of the Remez-Exchange algorithm have convergence problems (inaccurate results) when the number of filter taps, or filter order, exceeds four to five hundred. There's a slick way around this high-order FIR filter design problem using a frequency-domain zero stuffing technique.[†]
If our FIR filter design software cannot generate FIR coefficient sets whose lengths are in the thousands, then we can design a shorter length set of coefficients and interpolate those coefficients (time-domain impulse response) to whatever length we desire. Rather than use time-domain interpolation schemes and account for their inaccuracies, we can simplify the process by performing time-domain interpolation by means of frequency-domain zero stuffing.
An example of the process is as follows: assume that we have a signal sampled at a rate of fs = 1000 Hz. We want a lowpass filter whose cutoff frequency is 20 Hz with 60 dB of stopband attenuation. Compounding the problem are the requirements for linear phase and removal of any DC (zero Hz) component from the signal. (Those last two requirements preclude using the DC-removal schemes in Section 13.23.) First, we design a prototype nonrecursive FIR filter having, say, N = 168 coefficients whose desired frequency response magnitude is shown in Figure 13-72(a), its hp(k) coefficients are depicted in Figure 13-72(b). Next, we compute a 168-point DFT of the coefficients to obtain the frequency-domain samples Hp(m) whose magnitudes are shown in Figure 13-72(c).
Figure 13-72. Prototype FIR filter: (a) magnitude response; (b) hp(k) coefficients; (c) |Hp(m)| magnitudes of the 168-point DFT of hp(k).
Under the assumption that our final desired filter required roughly 1600 taps, we'll interpolate the hp(k) prototype impulse response by a factor of M = 10. We perform the interpolation by inserting (M–1)N zeros in the center of the Hp(m) frequency-domain samples, yielding a 1680-point H(m) frequency-domain sequence whose magnitudes are shown in Figure 13-73(a). Finally, we perform a 1680-point inverse DFT on H(m) to obtain the interpolated h(k) impulse response (coefficients), shown in Figure 13-73(b), for our desired filter. (The ten-fold compression of the Hp(m) passband samples results in a ten-fold expansion of the hp(k) impulse response samples.) The frequency magnitude response of our final very high-order FIR filter, over the frequency range of –30 -to- 30 Hz, is provided in Figure 13-73(c).
Figure 13-73. Desired FIR filter: (a) magnitude of zero-stuffed Hp(m); (b) interpolated h(k) coefficients; (c) magnitude of desired frequency response.
With this process, the prototype filter's hp(k) coefficients are preserved within the interpolated filter's coefficients if the Hp(N/2) sample (fs/2) is zero. That condition ensures that H(m) exhibits conjugate symmetry and forces the h(k) coefficients to be real-only.
The design steps for this high-order filter design scheme are:
With the desired filter requiring MN taps, set the number of prototype filter coefficients, N, to an integer value small enough so your FIR filter design software provides useable results. The integer interpolation factor M equals the number of desired taps divided by N.
Design the N-tap prototype FIR filter accounting for the M-fold frequency compression in the final filter. (That is, cutoff frequencies for the prototype filter are M times the desired final cutoff frequencies.)
Perform an N-point DFT on the prototype filter's hp(k) coefficients to obtain Hp(m).
Insert M–1 zero-valued samples just before the Hp(N/2) sample of Hp(m) to obtain the new MN-point H(m) frequency response.
Compute the MN-point inverse DFT of H(m) yielding an MN-length interpolated h(k) coefficient set. (Due to computational errors, discard the imaginary part of h(k), making it real-only.)
Multiply h(k) by M to compensate for the 1/M amplitude loss induced by interpolation.
Test the h(k) coefficient set to determine its actual frequency response using standard filter analysis methods. (One method: append thousands of zeros to h(k) and perform a very large FFT on the expanded sequence.)
An example application of this filter design is when you're building a high-performance lowpass polyphase filter, as discussed in Section 10.4. (The structures of the high-performance interpolated FIR and frequency sampling lowpass filters don't permit their decomposition into polyphase sub-filters for such an application.)
The thoughtful reader may have looked at the Section 13.27 FIR filter impulse response interpolation scheme, and wondered, “If we can interpolate time-domain impulse responses, we should be able to interpolate time-domain signals using the same frequency-domain zero stuffing method”. This is true, and the above interpolation-by-M process applied to time signals is sometimes called exact interpolation—because its performance is equivalent to using an ideal, infinite-stopband attenuation, time-domain interpolation filter—and has made its way into DSP textbooks, journal articles, and classroom notes of famous DSP professors.
To establish our notation, lets say we compute the FFT of an N-point x(n) time sequence to produce its X(m) frequency-domain samples. Next, we stuff (M–1)N zeros in the middle of X(m) to yield the MN-length Xint(m) frequency samples, where MN is an integer power of two. Then we perform an MN-point inverse FFT on Xint(m) to obtain the interpolated-by-M xint(n) times samples. Using this frequency-domain zero stuffing to implement time-domain signal interpolation involves two important issues upon which we now focus.
The first issue: to ensure the interpolated xint(n) time sequence is real only, conjugate symmetry must be maintained in the zero-stuffed Xint(m) frequency samples. If the X(m) sequence has a nonzero sample at Xint(N/2), the fs/2 frequency component, we must use the following steps in computing Xint(m) to guarantee conjugate symmetry:
Perform an N-point FFT on an N-point x(n) time sequence, yielding N frequency samples, X(m).
Create an MN-point spectral sequence Xint(m) initially set to all zeros.
Assign Xint(m) = X(m), for 0 ≤ m ≤ (N/2)–1.
Assign both Xint(N/2) and Xint(MN–N/2) equal to X(N/2)/2. (This step, to maintain conjugate symmetry and improve interpolation accuracy, is not so well known[72].)
Assign Xint(m) = X(q), where MN–(N/2)+1 ≤ m ≤ MN–1, and (N/2)+1 ≤ q ≤ N–1.
Compute the MN-point inverse FFT of Xint(m) yielding the desired MN-length interpolated xint(n) sequence.
Finally, if desired, multiply xint(n) by M to compensate for the 1/M amplitude loss induced by interpolation.
Whew! Our mathematical notation makes this signal interpolation scheme look complicated, but it's really not so bad. Table 13-8 shows the frequency-domain Xint(m) sample assignments, where 0 ≤ m ≤ 15, to interpolate an N = 8-point x(n) sequence by a factor of M = 2.
One of the nice properties of the above algorithm is that every Mth xint(n) sample coincides with the original x(n) samples. In practice, due to our finite-precision computing, the imaginary parts of our final xint(n) may have small non-zero values. As such, we take xint(n) to the be real part of the inverse FFT of Xint(m).
Here's the second issue regarding time-domain real signal interpolation, and it's a big deal indeed. This exact interpolation algorithm provides correct results only if the original x(n) sequence is periodic within its full time interval. If X(m) exhibits any spectral leakage, like the signals with which we usually work, the interpolated xint(n) sequence can contain noticeable amplitude errors in its beginning and ending samples, as shown in Figure 13-74(a) where an N = 24 sample x(n) sequence is interpolated by M = 2. In that figure, squares (both white and black) represent the 48-point interpolated xint(n) sequence, white squares are the original x(n) samples, and circles represent the exactly correct interpolated sample values. (In the center portion of the figure, the circles are difficult to see because they're hidden behind the squares.) The interpolation error, the difference between the correct samples and xint(n), is given in Figure 13-74(b).
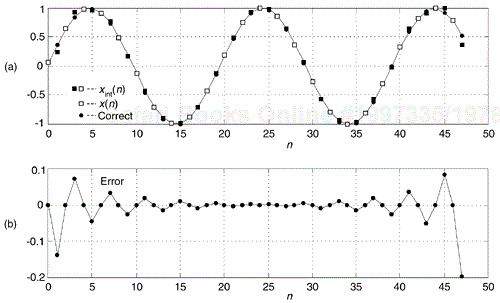
Figure 13-74. Interpolation results, N = 24, M = 2: (a) interpolated xint(n), original x(n), and correct interpolation; (b) interpolation error.
Table 13-8. XINT(m) Assignments for Interpolation by Two
m | Xint(m) | m | Xint(m) |
|---|---|---|---|
0 | X(0) | 8 | 0 |
1 | X(1) | 9 | _ |
2 | X(2) | 10 | 0 |
3 | X(3) | 11 | 0 |
4 | X(4)/2 | 12 | X(4)/2 |
5 | 0 | 13 | X(5) |
6 | 0 | 14 | X(6) |
7 | 0 | 15 | X(7) |
These interpolation errors exist because Xint(m) is not identical to the spectrum obtained had we sampled x(n) at a rate of Mfs and performed an MN-point forward FFT. There's no closed-form mathematical expression enabling us to predict these errors. The error depends on the spectral component magnitudes and phases within x(n), as well as N and M. Reference [72] reports a reduction in interpolation errors for two-dimensional image interpolation when, in an effort to reduce spectral leakage in X(m), simple windowing is applied to the first few and last few samples of x(n).
With the advent of fast hardware DSP chips and pipelined FFT techniques, the above time-domain interpolation algorithm may be viable for a number of applications, such as computing selectable sample rate time sequences of a test signal that has a fixed spectral envelope shape; providing interpolation, by selectable factors, of signals that were filtered in the frequency domain using the fast convolution method (Section 13.10); or digital image resampling. One scenario to consider is using the efficient 2N-Point Real FFT technique, described in Section 13.5.2, to compute the forward FFT of the real-valued x(n). Of course, the prudent engineer would conduct a literature search to see what algorithms are available for efficiently performing inverse FFTs when many of the frequency-domain samples are zeros.
We can use the frequency-domain zero stuffing scheme to generate an interpolated-by-M analytic time signal based upon the real N-point time sequence x(n), if N is even[73]. The process is as follows:
Perform an N-point FFT on an N-point real xr(n) time sequence, yielding N frequency samples, Xr(m).
Create an MN-point spectral sequence Xint(m) initially set to all zeros, where MN is an integer power of two.
Assign Xint(0) = Xr(0), and Xint(N/2) = Xr(N/2).
Assign Xint(m) = 2Xr(m), for 1 ≤ m ≤ = (N/2)–1.
Compute the MN-point inverse FFT of Xint(m) yielding the desired MN-length interpolated analytic (complex) xc,int(n) sequence.
Finally, if desired, multiply xc,int(n) by M to compensate for the 1/M amplitude loss induced by interpolation.
The complex xc,int(n) sequence will also exhibit amplitude errors in its beginning and ending samples.
We can frequency translate a real bandpass signal toward zero Hz, converting it to a lowpass signal, without the need for mixing multipliers using decimation by an integer factor D as shown in Figure 13-75(a). If the bandpass filter provides an output signal of bandwidth B Hz, located as shown in Figure 13-75(b) and Figure 13-75(d) where k is a positive integer, decimation by D will yield lowpass signals whose spectra are shown in Figure 13-75(c) and Figure 13-75(e) depending on whether integer k is odd or even. Please notice the inverted spectra in Figure 13-75(e). To avoid decimated output aliasing errors, we must satisfy the Nyquist criterion and ensure that xBP(n)'s bandwidth B is not greater than fs/2D.
Since the early days of vacuum tube radios, circuits were needed to automatically adjust a receiver's gain, as an input signal varied in amplitude, to maintain a (relatively) constant output signal level. These feedback mechanisms, called automatic gain control (AGC) circuits, are an important component of modern analog and digital communications receivers. Figure 13-76(a) illustrates a simple digital AGC process[74,75]. Its operation is straightforward: the output signal power is sampled and compared to a reference level R (the desired output amplitude rms level). If the output signal level is too high (low), a negative (positive) signal is fed back reducing (increasing) the gain. The control parameter α regulates the amplitude of the feedback signal and is used to control the AGC's time constant (how rapidly gain changes take effect).
Figure 13-76. AGC process: (a) linear AGC circuit; (b) example input x(n) with amplitude fluctuations; (c) y(n) output for α = 0.01 and R = 1.
Given an input signal x(n) in Figure 13-76(b) whose amplitude envelope is fluctuating, the AGC structure provides the relatively constant amplitude y(n) output shown in Figure 13-76(c).
We called Figure 13-76(a) a “simple AGC process,” but AGC is not all that simple. The process is a nonlinear, time-varying, signal-dependent, feedback system. As such it's highly resistant to normal time-domain or z-domain analysis. This is why AGC analysis is empirical rather than mathematical, and explains why there's so little discussion of AGC in the DSP literature.
Depending on the nature of x(n), the feedback signal may fluctuate rapidly and the feedback loop will attempt to adjust the system gain too often. This will cause a mild AM modulation effect inducing low-level harmonics in the y(n) output. That problem can be minimized by inserting a simple lowpass filter in the feedback loop just before, or just after, the R adder. But such filtering does not remedy the circuit's main drawback. The time constant (attack time) of this AGC scheme is input signal level dependent, and is different depending on whether the x(n) is increasing or decreasing. These properties drastically reduce our desired control over the system's time constant. To solve this problem, we follow the lead of venerable radio AGC designs and enter the logarithmic domain.
We can obtain complete control of the AGC's time constant, and increase our AGC's dynamic range, by using logarithms as shown in Figure 13-77(a). As is typical in practice, this log AGC process has a lowpass filter (LPF) to eliminate too-rapid gain changes[76]. That filter can be a simple moving average filter, a cascaded integrator-comb (CIC) filter, or a more traditional lowpass filter having a sin(x)x impulse response.
For the logarithmic AGC scheme, the feedback loop's time constant is dependent solely on α and independent of the input signal level, as can be seen in Figure 13-77(b) when the x(n) input is that in Figure 13-76(b). The Log and Antilog operations can be implemented as log2(x) and 2x, respectively.
In this section, we present a crude (but simple to implement) complex signal envelope detection scheme. By envelope detection, we mean estimating the instantaneous magnitude of a complex signal xc(n). The process is straightforward: we sum the absolute values of a complex signal's real and imaginary parts, and apply that sum to a simple first-order lowpass IIR filter to obtain an envelope signal E(n) as shown in Figure 13-78(a). The filter's feedback coefficient α is in the range of 0 to 1. (That lowpass filter is our exponential averager discussed in Section 11.5, which some DSP folks call a leaky integrator.) The E(n) sequence is proportional to the desired instantaneous magnitude of xc(n), or
Figure 13-78. Envelope detection: (a) block diagram; (b) |xr(n)|+|xi(n)| adder output, and E(n) for α = 0.4; (c) E(n) for α = 0.7 and α = 0.9.
To gauge the envelope detector's performance, consider a sampled version of an amplitude modulated sinusoid such as the xr(n) in Figure 9-7(a) from which a sampled analytic (complex) xc(n) can been generated. If xc(n) is applied to our envelope detection process, the processing results are shown in Figure 13-78(b) and 13-78(c), where the solid curves represent E(n) and the dashed curves are the true magnitude of xc(n). Notice how the amount of smoothing of the E(n) fluctuations depends on the value of α.
Sequence xr(n) must be used to generate a complex analytic xc(n) sequence (using one of the methods discussed in Sections 9.4 and 9.5) upon which this envelope detector scheme can be applied. The advantage of this envelope detection process is that, of course, no squaring or square root computations in Eq. (13-133), nor the |xr(n)| and |xi(n)| comparisons in the vector magnitude approximations in Section 13.2, need be performed.
Whether this envelope approximation technique yields sufficiently accurate results is for the user to decide. Its accuracy may be below the requirements of most AM (amplitude modulation) detection requirements, but the process may well be useful for estimating signal magnitude in automatic gain control (AGC) or energy detection applications.
Here we present a well-behaved digital quadrature oscillator, whose output is yi(n) + jyq(n), having the structure shown in Figure 13-79(a). If you're new to digital oscillators, that structure looks a little complicated but it's really not so bad. If you look carefully, you see the computations are
and
Those computations are merely the rectangular form of multiplying the previous complex output by a complex exponential ejθ as
So the theory of operation is simple. Each new complex output sample is the previous output sample rotated by θ radians, where θ is 2πft/fs with ft and fs being the oscillator tuning frequency and the sample rate, respectively, in Hz.
To start the oscillator, we set the initial conditions of yi(n–1) = 1 and yq(n–1) = 0 and repeatedly compute new outputs, as time index n advances, using Eq. (13-134). This oscillator is called a coupled quadrature oscillator because the both of its previous outputs are used to compute each new in-phase and each new quadrature output. It's a useful oscillator because the full range of tuning frequencies are available (from nearly zero Hz up to roughly fs/2), and its outputs are equal in amplitude unlike some other quadrature oscillator structures[77]. The tough part, however, is making this oscillator stable in fixed-point arithmetic implementations.
Depending on the binary word widths, and the value θ, the output amplitudes can either grow or decay as time increases because it's not possible to represent ejθ having a magnitude of exactly one, over the full range of θ, using fixed-point number formats. The solution to amplitude variations is to compute ![]() and
and ![]() and multiply those samples by an instantaneous gain factor G(n) as shown in Figure 13-79(b). The trick here is how to compute the gain samples G(n).
and multiply those samples by an instantaneous gain factor G(n) as shown in Figure 13-79(b). The trick here is how to compute the gain samples G(n).
We can use a linear automatic gain control (AGC) method, described in Section 13-30, as shown in Figure 13-80(a) where α is a small value, say, α = 0.01. The value R is the desired rms value of the oscillator outputs. This AGC method greatly enhances the stability of our oscillator. However, there's a computationally simpler AGC scheme for our oscillator that can be developed using the Taylor series approximation we learned in school. Here's how.
Using an approach similar to Reference [78], we can define the desired gain as
This is the desired output signal magnitude Mdes over the actual output magnitude Mact. We can also represent the gain using power as
where the constant Pdes is the desired output signal power and Pact is the actual output power. The right side of Eq. (13-137) shows Pact replaced by the desired power Pdes plus an error component E, and that's the ratio we'll compute. To avoid square root computations and, because the error E will be small, we'll approximate that ratio with a two-term Taylor series expansion about E = 0 using
Computing the Taylor series' coefficients to be a0 = 1 and a1 = –1/2Pdes, and recalling that E = Pact–Pdes, we estimate the instantaneous gain as
If we let the quadrature output peak amplitudes equal 1/ ![]() , Pdes equals 1/2 and we eliminate the division in Eq. (13-139) obtaining
, Pdes equals 1/2 and we eliminate the division in Eq. (13-139) obtaining
The simplified structure of the G(n) computation is shown in Figure 13-80(b).
As for practical issues, to avoid gain values greater than one (for those fixed-point fractional number systems that don't allow numbers ≥1), we use the clever recommendation from Reference [77] of multiplying by G(n)/2 and doubling the products in Figure 13-79(b). Reference [78] recommends using rounding, instead of truncation, for all intermediate computations to improve output spectral purity. Rounding also provides a slight improvement in tuning frequency control. Because this oscillator is guaranteed stable, and can be dynamically tuned, it's definitely worth considering for real-valued as well as quadrature oscillator applications[77].
Here's a clever averaging scheme, used for noise reduction, that blends both the quick response of a moving averager and the noise reduction control of an exponential averager.[†] The structure of this dual-mode averager is depicted in Figure 13-81(a). The averager operates as follows: the switch remains open for K input samples after which the y(n) output is equal to the K-point average of the x(n) input. Just prior to the arrival of the K+1 input sample the switch closes converting the moving average filter to an exponential averager, with its (1 – 1/K) feedback, giving us control over the filter's noise reduction properties as described in Section 11.5.
In implementations where the adder's output word-width must be minimized, the second 1/K multiplier can be moved ahead of the adder to reduce the amplitude of the adder's output samples as shown in Figure 13-81(b).
Here's another neat idea. If we can accept K being an integer power of two, the multiply by 1/K computations can be implemented with arithmetic, or hard-wired, binary right shifts giving us a multiplierless noise reduction filter.
[†] A “Max+βMin” algorithm had been in use, but in 1988 this author suggested expanding it to the αMax+βMin form where α could be a value other than unity[6].
[†] This fact is illustrated in Section 3.8 during the discussion of spectral leakage in DFTs.
[†] Remember, when the FFT's input is complex, the FFT outputs may not be conjugate symmetric; that is, we can't assume that F(m) is equal to F*(N–m) when the FFT input sequence's real and imaginary parts are both nonzero.
[†] The complex addition (a+jb) + (c+jd) = (a+c) + j(b+d) requires two real additions. A complex multiplication (a+jb) • (c+jd) = ac–bd + j(ad+bc) requires two real additions and four real multiplications.
[†] The analog sinewave applied to an A/D converter must, of course, be as pure as possible. Any distortion inherent in the analog signal will show up in the final FFT output and could be mistaken for A/D nonlinearity.
[†] I thank my DSP pal Dr. Peter Kootsookos, of The University of Queensland, Australia, for his advice on this issue.
[†] I thank my DSP pal Eric Jacobsen, Minister of Algorithms at Intel Corp., for publicizing this technique.
[†] We thank DSP guru Fred Harris for recommending this dual-mode averager.