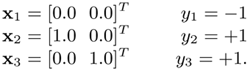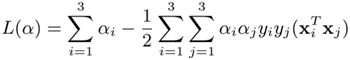4.3. Linear SVMs: Separable Case
The Fisher's criterion aims at maximizing the average class distance, projected onto the direction of discrimination, while having the intraclass variance normalized. While it is a reasonable measurement, for certain critical applications, one may want to remove the influence of patterns that are far from the decision boundary, because their influence on decision accuracy may not be critical. This motivates consideration of learning models (e.g., support vector machines), which, in contrast to Fisher's discriminant, maximize the minimal margin of separation [33, 358]. This notion of separation margin can be further expanded to represent a fuzzy decision region (also called soft-decision region in the literature) under a fuzzy SVM interpretation.
Support vector machines (SVMs) have become popular due to their attractive features and promising performance. Unlike conventional neural networks in which network weights are determined by minimizing the mean-squares error between actual and desired outputs (empirical risk minimization), SVMs optimize their parameters by minimizing classification error (structural risk minimization). Empirical risk minimization relies on the availability of large amounts of training data. In other words, empirical risks will be closed to the true risk when the sample size is large. For problems with a limited amount of training data, even a small empirical risk does not guarantee a low level of true risk. In this circumstance, structural risk minimization, which strikes a balance between empirical risk and complexity of the mapping function (the neural network), is required. Because of this special property of structural risk minimization, SVMs are particularly appropriate for problems in which training data are difficult to obtain. Research has also shown that SVMs possess better generalization capability than conventional neural networks in many application domains, including pattern classification, regression, and density estimation.
To remove the influence of patterns at a distance from the decision boundary, because their influence is usually inconsequential, one might also want to select only a few important data points (known as support vectors) and make the decision exclusively dependent on them. In such cases, an SVM has a decision line as shown in Figure 4.1(d).
For linearly separable problems, such as the one shown in Figure 4.1, support vectors are selected from the training data so that the distance between the two hyperplanes (represented by the dotted lines) passing through the support vectors is at a maximum. Because there is no training data between the two hyperplanes for linearly separable problems, the decision plane, which is midway between the two hyperplanes, should minimize classification error.
4.3.1. Margin of Separation
The SVM approach aims at achieving the largest possible margin of separation. Assume that the decision hyperplane in Figure 4.1(d) can be expressed as
Equation 4.3.1
![]()
Assume also that all training data satisfy the constraints:
Equation 4.3.2
![]()
Equation 4.3.3
![]()
If the equality holds for a data point x, then it is said to be right on the marginal hyperplanes. Mathematically, the marginal hyperplanes are characterized by
Equation 4.3.4
![]()
Note that data points, say x1 and x2, that satisfy
Equation 4.3.5
![]()
Equation 4.3.6
![]()
will, respectively, fall on the two hyperplanes that are parallel to the decision plane and orthogonal to w. These two points, denoted as x1 and x2, are shown in Figure 4.1(d). Subtracting Eq. 4.3.6 from Eq. 4.3.5 results in
Equation 4.3.7
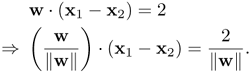
Therefore, the distance between the two hyperplanes is
Equation 4.3.8
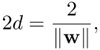
where 2d can be considered as the width of separation, which provides an objective measure on how separable the two classes of training data are. The distance d can be considered as the safety margin of the classifier. In other words, it can be guaranteed that a pattern can still be correctly classified as long as its deviation from the original training pattern is smaller than d. Equivalently, it means that the pattern retains proximity to the corresponding marginal hyperplane within a distance less than d, thus ensuring a correct decision.
4.3.2. Wolfe Dual Optimization
Now, combine the two constraints in Eqs. 4.3.2 and 4.3.3 into a single constraint to get:
Equation 4.3.9
![]()
During the training phase, the objective is to find the support vectors (e.g., x1 and x2) that maximize the margin of separation d. Alternatively, the same goal can be achieved by minimizing ||W||2. Therefore, the objective is to minimize ||W||2 subject to the constraint in Eq. 4.3.9. This is typically solved by introducing Lagrange multipliers αi ≥ 0 and a Lagrangian
Equation 4.3.10
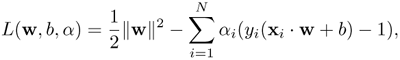
where L(w, b, α) is simultaneously minimized with respect to w and b and maximized with respect to αi. Setting
Equation 4.3.11
![]()
subject to the constraint αi ≥ 0, results in
Equation 4.3.12

Equation 4.3.13

Substituting Eqs. 4.3.12 and 4.3.13 into Eq. 4.3.10, produces
Equation 4.3.14
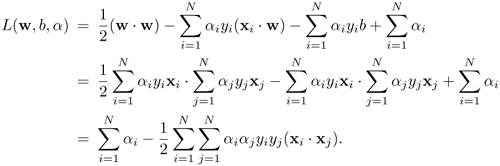
This results in the following Wolfe dual optimization formulation:
Equation 4.3.15
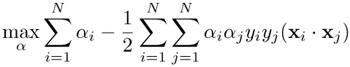
subject to
 and
andαi ≥ 0, i= 1,...,N.
4.3.3. Support Vectors
The solution of the dual optimization problem contains two kinds of Lagrange multipliers αk: (1) one kind with αk = 0 and (2) the other with non-zero αk. Data for which the multipliers αk = 0 are considered to be irrelevant to the classification problem. The data points corresponding to non-zero multipliers (i.e., αk > 0) are deemed to be more critical for the classification problem. These critical data points are called support vectors.
According to the Karush-Kuhn-Tucker conditions of optimization theory [25, 99], the following equality
Equation 4.3.16
![]()
must be satisfied at all of the saddle points. Therefore, only those data points with yi (xi · w + b) -1 = 0 can be support vectors, since they are the only data points that can have a non-zero value of multipliers αi. These vectors lie on the margin of the separable region as shown by the two dashed lines in Figure 4.1(d). In summary, the support vectors satisfy
Equation 4.3.17
![]()
where S is a set containing the indexes to the support vectors.
4.3.4. Decision Boundary
Once the values of ∀i have been found from Eq. 4.3.15, Eq. 4.3.13 can then be used to determine w:
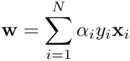
Once w is found, it can in turn be plugged into Eq. 4.3.17 to determine the value of threshold b:
![]()
Ultimately, the decision boundary can be derived as follow:
Equation 4.3.18

Analytical Examples
Example 4.1: 3-point problem
As shown in Figure 4.2(a), there is one data point (0.0, 0.0) for one class and two points in the other: (0.0, 1.0) and (1.0, 0.0). This example presents an analytical method to derive the optimal boundary and find the support vectors for the training data points.[2]
[2] Traditionally, the solution to the SVM optimization problem is found by quadratic programming techniques. For illustration purpose, a short-cut approach in this example is used. Readers should bear in mind that when not all training vectors are also support vectors (as shown in Example 4.3), this short-cut method does not have a solution.
Figure 4.2. Linearly separable problems that can be solved by a linear SVM. (a) A three-point problem in which all data points are SVs. See Example 4.1 in the text for the procedure to find the analytical solutions. (b) A four-point linearly separable problem for Example 4.2; note that this figure only illustrates the case where all four data points are SVs. (c) A four-point linearly separable problem for Example 4.3 in which only three data points are SVs. This figure and others in this chapter were created using the SVM software by Anton Schwaighofer, available from http://www.igi.tugraz.at/aschwaig. Used with permission.
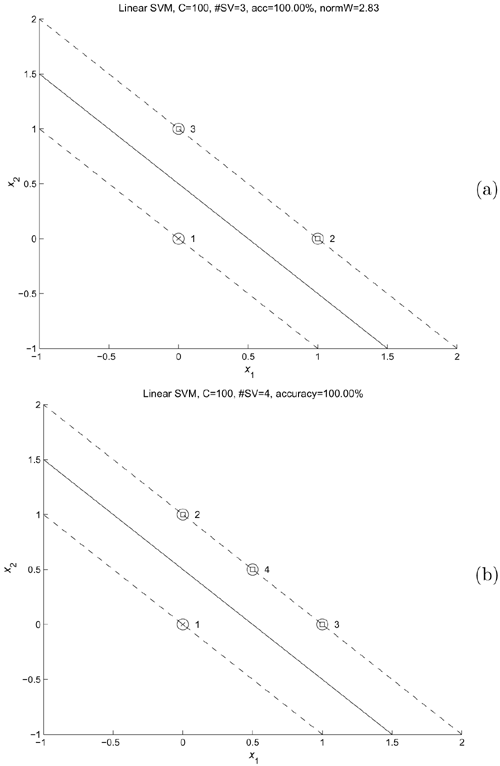
Let the training data points be denoted as
The objective function of interest is now:
Equation 4.3.19
subject to αi ≥ 0 and
.To solve this constraint optimization problem, another Lagrange multiplier, namely A, is introduced so that the resulting
Lagrangian to be maximized is:
Differentiating F(α, λ) with respect to the αi and λ yields the following set of simultaneous equations:
which give α1 = 4, α2 = 2, α3 = 2, and λ = -1. Using these Lagrange multipliers, one can compute the weight vector w and the bias b as follows:
Therefore, the decision plane is defined by the equation:
which is the line x1 + x2 – 0.5 = 0 shown in Figure 4.2(a). The margin of separation is given by 2/||w|| = 0.707.
Example 4.2: 4-point problem with 4 support vectors
In this example, there are three points in one class and one point in the other, as illustrated in Figure 4.2(b). Applying the method shown in Example 4.1 results in the following linear equations:
This set of equations have two solutions for αi (i.e., the solution for the Lagrange multiplier is not unique). One set of solutions can have all of the four points as support vectors:
In another set of solutions, only three points will be support vectors (cf. Problem 5):
Note: both solutions yield the maximum Langrangian (=4) and an identical decision plane (w = [2 2]T and b = -1).
Example 4.3: 4-point problem with 3 support vectors
In this example, there are three points in one class and one point in the other, as illustrated in Figure 4.2(c). Unlike the four-point problem in Example 4.2, the fourth point in this example is [1 1]T. Applying the sample procedure described in the preceding two examples, this is obtained:
Equation 4.3.20
Equation 4.3.21
Equation 4.3.22
Equation 4.3.23
Obviously, Eqs. 4.3.20 and 4.3.21 contradict Eq. 4.3.22. Therefore, there is no solution unless Eq. 4.3.22 is removed from the set of equations. Readers should note that Eq. 4.3.22 is obtained by setting the derivative of the Lagrangian with respective to a4 to 0. However, if the data point corresponding to a4 is not selected as a support vector, the derivative does not have to be 0. Therefore, Eq. 4.3.22 should have been removed from the set of equations. After removing this equation, the solution will be identical to those in Example 4.1. Note that the analytical method requires manual identification of support vectors; this is reasonable because otherwise the more computation intensive quadratic programming technique will not be required for software implementation of SVMs.