6.3. Mixture-of-Experts Modular Networks
An expert-based modular network is built on smaller modules, each representing the behavior of a local or specially tailored pattern space. The most prominent expert-based modular network is the mixture-of-experts (MOE) [162]. The MOE exhibits an explicit relationship with statistical pattern classification methods. Given a pattern, each expert network estimates the pattern's conditional a posteriori probability on the (adaptively tuned or preassigned) feature space. Each local expert network performs multiway classification over K classes by using either K-independent binomial models, each being modeled after one and only one class, or one multinomial model for all classes. The corresponding output of the gating network represents the associated confidence of each expert. The final system output is the weighted sum of the estimated probabilities from all of the expert networks. Another example of the expert-based modular structure is the committee machine [262], which consists of a layer of elementary perceptrons (expert units) followed by a vote-taking perceptron (the gating unit) in the second layer.
6.3.1. Local Experts and Gating Network
With reference to Figure 6.3, the MOE comprises the following subsystems.
Local Experts. The design of modular neural networks hinges on the choice of local experts that serve the following functions:
Extract local features. A local expert is adaptively trained to extract certain local features that are particularly relevant to its local decision. Sometimes, a local expert can be assigned a predetermined feature space.
Conduct local classification and make recommendations. The local experts conduct pattern classification tasks only from the perspective of local regions of the pattern space. In short, based on local features, a local expert produces a local recommendation to the gating network.
Negotiate with the gating network. For competitive learning models, the local expert must coordinate with the gating network to decide how much the local module should be adjusted in reaction to a particular training pattern.
The effectiveness of an expert-based modular network hinges on a proper designation of local experts. For example, one (LBF or RBF) hidden node may be devoted to extract a certain local feature of particular interest to an expert.
Gating Network. The gating network determines the rule that guides how to integrate recommendations collected from various local experts.[3] It estimates the proper weights to be used for the fusion of information, which should reflect the trustworthiness of a local expert's opinion on a given input pattern. A more trustworthy local expert will be assigned a larger (smaller) gating activation and in turn will be allocated a greater (lesser) influence in the final decision-making process. A gating network is often conveniently implemented as a softmax activation function [35, 236], and a probabilistic rule is often adopted to integrate recommendations from local experts. For competitive learning models, the gating network also has a major influence on how much individual modules should be trained in response to a new training pattern.
[3] In this sense, the expert level in neural networks is compatible with the rule level in fuzzy systems.
Figure 6.3. The baseline MOE architecture. An expert network estimates the pattern's conditional a posteriori probability. A baseline MOE comprises two subsystems: local experts and a gating network. The local experts are adaptively trained to extract certain local features, particularly relevant to their own local decisions, while the gating network computes the global weights to be applied to the local decisions. Note: For K-class classification problems, the output P(y|x, ø) is a K-dimensional vector with elements that sum to 1.
The expectation-maximization (EM) algorithm can be adopted to train the local experts and the confidence levels assigned by the gating network. The objective is to estimate the model parameters so as to attain the highest probability of the training set given the estimated parameters. For a given input x, the posterior probability of generating class y given x using K experts can be computed as
Equation 6.3.1
where y is a binary vector, aj(x) is the probability for weighting the expert outputs, and P(y|x, θj) is the output of the j-th expert network. For example, in a two-class classification problem, y is either [1 0] or [0 1], ø is a parameter set comprising of {V, θj}, where V = {Vj, j = 1,..., K} is the parameter set for the gating network, and {θj;,j = 1,..., K} is the parameter set for the j-th expert network. The gating network of MOE can be a linear LBF network (say, a linear perceptron) or a nonlinear RBF network.
6.3.2. LBF MOE Networks
A simple example illustrates how an LBF MOE works. The output of a linear gating network [35, 236] can be expressed as:
Equation 6.3.2
where 
. Now, denote Vj = {vj, dj} as the weight of the j-th neuron of the gating network. Suppose patterns from two classes occupy a two-dimensional space {x=(x1, x2); 0 ≤ x1 ≤ 1, 0 ≤ x2 ≤ 1}. Class 1 patterns occupy the lower quarter of the square in Figure 6.4, and Class 2 patterns take the remaining three quarters of the space. A two-expert MOE classifier with the LBF local experts is used:
Figure 6.4. An example for MOE in which a local expert gets a higher weighting on its proclaimed feature space. In this example, the gating network assigns higher confidence to Expert 1 for region {(x1, x2); 0 ≤ x1 ≤ 0.5, 0 ≤ x2 ≤ 1} and to Expert 2 for the remaining region.
where P(w1|x, θj) is equal to P(y = [1 0] |x, θj) in Eq. 6.3.1. Similarly, P(w2|x, θj) is equal to P(y = [0 1]|x, θj). One solution is
For this solution, Expert 1 creates a decision boundary along the diagonal line from (0,0) to (1,1), and Expert 2 creates a decision boundary along the antidiagonal line from (1,0) to (0,1). The gating network gives Expert 1 higher confidence at region {(x1, x2); 0 ≤ x1 ≤ 0.5, 0 ≤ x2 ≤ 1 } and gives Expert 2 higher confidence at the other half.
6.3.3. RBF MOE Networks
The MOE structure is natural for RBF networks. In an RBF network, each hidden node represents a receptive field with the following normalized Gaussian activation function:
Equation 6.3.3
where
Equation 6.3.4
where x is the D-dimensional input vector and K is the number of hidden nodes. The parameters μk and 
denote the mean and the variance of the k-th Gaussian function. The output y(·) can be computed as the weighted sum of the activation values
Equation 6.3.5
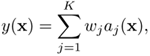
where wj is the weight of the j-th Gaussian kernel.
The RBF network defined in Eq. 6.3.5 can be expressed in terms of the MOE structure. If the gating network output aj(x) in Eq. 6.3.1 is defined as the aj(x) in Eq. 6.3.3, and the P(y|x, θj) is defined to be a constant wj, then the neural network becomes an MOE system with a radial-basis gating function and constant expert output.
The RBF MOE model has been applied to many applications. For example, in an application to sunspot time series, a Bayesian framework for inferring the parameters of an MOE model based on ensemble learning by variational free energy minimization proves to be very effective and performs significantly better than a single network [372]. MOE has also been shown to yield very good performance in automated cytology screening applications [158]. For broader application domains, MOE has also been extended to cope with a multiexpert-level tree structure, known as HME [167].
6.3.4. Comparison of MLP and MOE
The following is a comparison of MLPs and MOE in the context of their architecture, parameter specification, and learning algorithms.
Structural Similarity
As shown in Figures 6.1(a) and (c), MLPs and MOE have a similar structure in that they are both feed-forward networks. In the special case where the local experts of an MOE are single-layer perceptrons and the gating network's outputs are invariant with respect to the input vectors, the MOE is structurally equivalent to an MLP with output weights being equal to the gating network's outputs.
Difference in Parameter Specification
In terms of parameter specification, the output weights, hidden nodes' outputs, and network outputs in an MLP do not need to follow any probabilistic constraint. On the other hand, the training and operation of an MOE network require the gating network's outputs (which can be considered as the output weights of an MLP), experts' outputs, and the MOE's outputs to follow probabilistic constraints. More specifically, referring to Figure 6.3 the following conditions must be satisfied:
Equation 6.3.6
where M denotes the number of experts, K denotes the number of classes, and yk is the k-th component of the vector y. Therefore, given the structural similarity between MOE and MLPs, one should consider the MOE a special type of MLP with some probabilistic constraints.
Algorithmic Comparison
The training algorithms of MLP and MOE have similarities, but they also have important differences. Their training algorithms are similar in that both of them iteratively update the network parameters in order to optimize an objective function. While the MLPs adopt an approximation-based learning scheme (back-propagation) to minimize the sum of squared errors between the actual outputs and desired outputs, the MOE adopts an optimization-based learning scheme (EM algorithm) to maximize the likelihood of model parameters given the training data. To a certain extent, the EM algorithm in MOE can be considered as a probabilistic back-propagation because the posterior probabilities in the E-step can be viewed as a set of optimized learning rates for the iterative M-step.