7.4. Two-Class Probabilistic DBNNs
A probabilistic decision-based neural network (PDBNN) (e.g., described in [208, 210-212]) is a probabilistic variant of its predecessor—the decision-based neural network (DBNN) [192]. This section describes the network structure and learning rules of the PDBNN for binary classification problems. The extension to multiclass pattern classification is presented in Section 7.5.
Consider an the example of binary classification (hypothesis testing) problems based on an independent and identical distributed (i.i.d.) observation sequence:
Hypothesis Ω0: xn is defined by the probability distribution p(x|Ω0) for n= 1,2, ..., N.
Hypothesis Ω1: xn is defined by the probability distribution p(x|Ω1).
A conventional approach to binary classification can be divided into three main steps that: (1) estimate the likelihood densities p(x|Ω0) and p(x|Ω1) by statistical inference methods (parametric or nonparametric [85]); (2) compute the posterior probabilities P(Ω0|x) and P(Ω1|x) by the Bayes rule,
![]()
and (3) form a decision rule based on these posterior probabilities:
Equation 7.4.1
![]()
An equivalent way of forming a decision rule is based on the likelihood ratio:
Equation 7.4.2

where the threshold T is equal to P(Ω0)/P(Ω1). It can be further modified if certain risk factors are taken into consideration. Analogous to Eqs. 7.4.1 and 7.4.2, there are two types of neural network structures for binary classification problems. The first one has two output neurons, with each output designated to approximate the probability distribution of one hypothesis. The second type of structure has only one output neuron, in which the discriminant function computes the likelihood ratio. In general, PDBNNs adopt the first type of network structure; that is, one of the two subnets in the PDBNN is used for estimating the data distribution of one of the two hypotheses.
Two types of binary classification problems exist: balanced and unbalanced.
In a balanced binary classification problem, the distributions of two classes have similar complexities. One example of the balanced type is gender classification based on facial features. For this type of two-class classification problems, it is sensible to consider using two subnets in the classifier, one for each class.
In a unbalanced binary classification problem, the distribution of one class is much more complex than that of the other class. One example of an unbalanced classification problem is face detection. For such kinds of unbalanced two-class problems, it is often more advisable to adopt only one subnet in the PDBNN classifier.
The probability distribution of all nonface patterns in the world is much more complex than the distribution of human face patterns. Estimating the distribution of nonface patterns would exhaust many resources (neurons) but still achieve less than satisfactory results. For this kind of unbalanced problem, PDBNNs emphasize obtaining a good estimate of the likelihood density of the face class only and treating the other hypothesis as the "complement" of the first hypothesis. The decision rule is as follows:
Equation 7.4.3
![]()
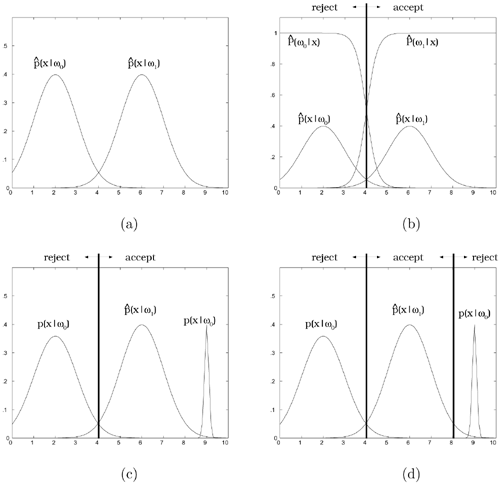
where the hypothesis Ω1 represents the face class and Ω0 represents the non-face class. The threshold T is learned by discriminative learning rules: reinforced/antireinforced rules. If a face pattern falls out of the decision region made by the threshold, the threshold value will be decreased so that the face region can include the pattern. In contrast, if a nonface pattern is found in the face region, the threshold value is increased so that the pattern may be rejected. In order to reduce the effect of outlier patterns, a window function can be applied so that only the neighboring patterns are involved in the threshold adjustment. It has been proven that the discriminant learning rules can achieve a minimum classification error rate [170]. When the window function is present, not all of the nonface patterns are used for training. Only the patterns that "look like face patterns" are included in the training set, thus yielding a more efficient yet accurate learning scheme. One simple example illustrating the power of this one-subnet PDBNN is depicted in Figure 7.7.
Figure 7.7. An example demonstrating the advantage of incorporating an adaptive decision-threshold in a two-class problem. (a) The estimated probability distributions of hypothesis  and hypothesis
and hypothesis  ; here
; here  and
and 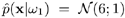 . (b) The decision boundary (thick straight line at x = 4) is generated by estimated posterior probabilities
. (b) The decision boundary (thick straight line at x = 4) is generated by estimated posterior probabilities  . Prior probabilities are assumed to be equal—that is, P(w0) = P(w1); the input pattern is accepted if
. Prior probabilities are assumed to be equal—that is, P(w0) = P(w1); the input pattern is accepted if  , otherwise it is rejected, (c) Decision making based on posterior probabilities may incur an additional misclassification rate in the test phase due to poor density estimation; here the true distribution of hypothesis ωo is
, otherwise it is rejected, (c) Decision making based on posterior probabilities may incur an additional misclassification rate in the test phase due to poor density estimation; here the true distribution of hypothesis ωo is  . (d) The decision boundary is created by
. (d) The decision boundary is created by 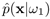 only; here the input pattern is accepted if
only; here the input pattern is accepted if  , otherwise it is rejected. Note that the misclassification rate is reduced.
, otherwise it is rejected. Note that the misclassification rate is reduced.
Similar to DBNNs, PDBNNs use the decision-based learning scheme (see Section 7.3). In the LU phase, PDBNNs use the positive training patterns to adjust the subnet parameters by an unsupervised learning algorithm, and in the GS phase they use only the misclassified patterns for reinforced/antireinforced learning. The negative patterns are used only for the antireinforced training of the subnet. The decision boundaries are determined by a threshold, which can also be trained by reinforced/antireinforced learning. The detailed description of a PDBNN detector (a two-class classifier) follows.
7.4.1. Discriminant Functions of PDBNNs
One major factor differentiating PDBNNs from DBNNs (or other RBF networks) is that PDBNNs must follow probabilistic constraints. That is, the subnet discriminant functions of PDBNNs are designed to model log-likelihood functions. The reinforced and antireinforced learning is applied to all the clusters of the global winner and the correct winner, with a weighting distribution proportional to the degree of possible responsibility (measured by the likelihood) associated with each cluster.
Given a set of identical, independent distributed (i.i.d.) patterns
![]()
the class-likelihood function p(xt|Ω) for class Ω (e.g., face class) is assumed to be a mixture of Gaussian distributions. Define
![]()
as one of the Gaussian distributions that comprise p(xt|Ω); that is,
![]()
where
![]()
P(wr|Ω) is the prior probability of cluster r, and wr denotes the parameters of the r-th cluster in the subnet. By definition
![]()
The discriminant function of a subnet can be expressed in a form of log-likelihood functions:
Equation 7.4.4
![]()
where the classifier is parameterized by
Equation 7.4.5
![]()
In Eq. 7.4.5, T is the threshold of the subnet and is trained in the GS learning phase. The overall system diagram leading to such a form of discriminant function is illustrated in Figure 7.8. Just like the original DBNN, only the teacher's class preference is needed. In other words, no quantitative value is explicitly required from the teacher.
Figure 7.8. Decision-based learning scheme for PDBNNs. Unlike the HME, each subnet in the PDBNN estimates the class-conditional likelihood density function. The neurons estimate the likelihood densities in some local areas, and the subnet output is the weighted sum of the neuron outputs. PDBNN has a two-phase learning scheme. In the first phase, network parameters are trained by the unsupervised learning algorithm (e.g., EM). In the second phase, the obtained decision boundaries are further adjusted by supervised learning rules.

Elliptic Basis Function
In most general formulation, the basis function of a cluster should be able to approximate the Gaussian distribution with a full-rank covariance matrix. However, for those applications that deal with high-dimensional data but provide only a smaller number of training patterns, such a general covariance formulation is often discouraged because it involves training of a large number of covariance parameters using a relatively small database. A natural compromise is to assume that all of the features are uncorrelated but not all features are of equal importance. That is, suppose that p(x|Ω, wr) is a D-dimensional Gaussian distribution with uncorrelated features
![]()
where x = [x1, x2,..., xD]T is the input pattern, μr = [μr1, μr2, , μrD]T is the mean vector, and the diagonal matrix ![]() is the covariance matrix.
is the covariance matrix.
To approximate the density function in Eq. 3.2.16, the elliptic basis function (EBF) serves as the basis function for each cluster:
Equation 7.4.7
![]()
where ![]() . After passing an exponential activation function, exp{ψ(x, Ω, wr)} can be viewed as the same Gaussian distribution described in Eq. 3.2.16, except for a minor notational change:
. After passing an exponential activation function, exp{ψ(x, Ω, wr)} can be viewed as the same Gaussian distribution described in Eq. 3.2.16, except for a minor notational change: ![]() .
.
7. 4.2. Learning Rules for PDBNNs
Recall that the training scheme for PDBNNs follows the LUGS principle. The locally unsupervised phase for the PDBNNs can adopt one of the unsupervised learning schemes (e.g., VQ, K-means, EM, etc.). As for the globally supervised learning, the decision-based learning rule is adopted.
Unsupervised Training for LU Learning
The network parameter values are initialized in the LU learning phase. The following are two unsupervised clustering algorithms, either one of which can be applied to the LU learning.
K-means and vector quantization. The K-means method adjusts the centroid of a cluster based on the distance ||x − μr ||2 of its neighboring patterns x. Basically, the K-means algorithm assumes the covariance matrix of cluster i is
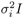 . An iteration of the K-means algorithm in the LU phase contains two steps: (1) All input patterns are examined to determine their closest cluster centers, and (2) each cluster centroid is moved to the mean of its neighboring patterns.
. An iteration of the K-means algorithm in the LU phase contains two steps: (1) All input patterns are examined to determine their closest cluster centers, and (2) each cluster centroid is moved to the mean of its neighboring patterns.Expectation-Maximization (EM). In the LU learning phase of PDBNNs, K-means or VQ are used to determine initial positions of the cluster centroids and EM is used to learn the cluster parameters of each class. Chapter 3 explores the EM algorithm in detail.
One limitation of the K-means algorithm is that the number of clusters needs to be decided before training. An alternative is to use the vector quantization (VQ) algorithm. VQ can adaptively create a new neuron for an incoming input pattern if it is determined (by a vigilance test) to be sufficiently different from the existing clusters. Therefore, the number of clusters may vary from class to class. Notice that one must carefully select the threshold value for the vigilance test so that the clusters are neither too large to incur high reproduction error nor too small to lose generalization accuracy. (Like K-means, the VQ algorithm assumes the covariance matrix of cluster i is ![]() .)
.)
Supervised Training for GS Learning
There is one major difference between PDBNNs and traditional statistical approaches: after maximum-likelihood estimation, the PDBNN has one more learning phase—the GS learning, which minimizes the classification error. The GS learning algorithm is used after the PDBNN finishes the LU training. In the globally supervised training phase, teacher information is used to fine-tune decision boundaries. When a training pattern is misclassified, the LVQ-type reinforced or antireinforced learning technique is applied [184]. The GS training is detailed next.
Assume a set of training patterns X={xt;t = 1, 2, …, M}. Now further divide the data set X into (1) the "positive training set" X+ = {xt; xt ∊ Ω, t = 1, 2, …, N} and (2) the "negative training set" X – = {xt; xt ∉ Ω, t = N + 1, N + 2, …, M}. Define an energy function
Equation 7.4.8

where
Equation 7.4.9
![]()
The discriminant function φ (xt, Θ) is defined in Eq. 7.4.4. T is the threshold value. The penalty function I can be either a piecewise linear function
Equation 7.4.10
![]()
where ζ is a positive constant, or a sigmoidal function
Equation 7.4.11
![]()
Figure 7.9 depicts these two possible penalty functions. The reinforced and antireinforced learning rules for the network are:
Equation 7.4.12
![]()
Figure 7.9. Linear penalty function (solid line) and sigmoidal penalty function (dashed line). From J. S. Taur, "Structural Study on Neural Networks for Pattern Recognition, " Ph.D. Thesis, Princeton University, 1993; used with permission.

If the misclassified training patterns are from the positive training set (e.g., face or eye), reinforced learning will be applied. If the training patterns belong to the negative training (i.e., nonface or noneye) set, then only the antireinforced learning rule will be executed, since there is no "correct" class to be reinforced.
The gradient vectors in Eq. 7.4.12 are computed:
Equation 7.4.13
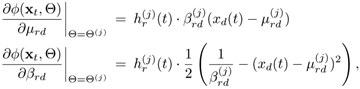
where ![]() is the conditional posterior probability
is the conditional posterior probability
Equation 7.4.14
![]()
and ![]() and
and ![]() are defined in Eqs. 3.2.16 and 7.4.7, respectively. As to the conditional prior probability P(wr|Ω), since the EM algorithm can automatically satisfy the probabilistic constraints Σr P(wr|Ω) = 1 and P(wr|Ω) ≥ 0, it is applied to update P(wr|Ω) in the GS phase so that the influences of different clusters are regulated. Specifically, at the end of the epoch j, one computes
are defined in Eqs. 3.2.16 and 7.4.7, respectively. As to the conditional prior probability P(wr|Ω), since the EM algorithm can automatically satisfy the probabilistic constraints Σr P(wr|Ω) = 1 and P(wr|Ω) ≥ 0, it is applied to update P(wr|Ω) in the GS phase so that the influences of different clusters are regulated. Specifically, at the end of the epoch j, one computes
Equation 7.4.15
![]()
7.4.3. Threshold Updating
The threshold value of PDBNNs can also be learned by reinforced/antireinforced learning rules. Since the increment of the discriminant function φ (xt, Θ) and the decrement of the threshold T have the same effect on the decision-making process, the direction of the reinforced and antireinforced learning for the threshold is the opposite of the one for the discriminant function. For example, given an input xt, if xt ∊ Ω but φ (xt, Θ) < T, then T should reduce its value. On the other hand, if xt ∉ Ω but φ (xt, Θ) > T, then T should increase:
Equation 7.4.16
![]()
