Chapter 16
Thrust
A Productivity-Oriented Library for CUDA
Chapter Outline
16.1 Background
16.2 Motivation
16.3 Basic Thrust Features
16.4 Generic Programming
16.5 Benefits of Abstraction
16.6 Programmer Productivity
16.7 Best Practices
16.8 Exercises
This chapter demonstrates how to leverage the Thrust parallel template library to implement high-performance applications with minimal programming effort. Based on the C++ Standard Template Library (STL), Thrust brings a familiar high-level interface to the realm of GPU computing while remaining fully interoperable with the rest of the CUDA software ecosystem. Thrust provides a set of type-generic parallel algorithms that can be used with user-defined data types. These parallel algorithms can significantly reduce the effort of developing parallel applications. Applications written with Thrust are concise, readable, and efficient.
16.1 Background
C++ provides a way for programmers to define generics. In situations when a programming problem has the same solution for many different data types, the solution can be written once and for all using generics. For example, the two C++ functions shown in the following code sum a float array and an int array. They are defined without using type generics. The only difference between the first and second function is that float is changed to int.
| float sum(int n, float ∗p) { | int sum(int n, int ∗p) { |
| float a = 0; | int a = 0; |
| for (int i = 0; i < n; i++) a += p[i]; | for (int i = 0; i < n; i++) a += p[i]; |
| return a; | return a; |
| } | } |
Instead of writing a different version of sum for each data type, the following generic sum function can be used with any data type. The idea is that the programmer prepares a template of the sum function that can be instantiated on different types of array. The template keyword indicates the beginning of a type-generic definition. From this point on, we will use type-generic and generic interchangeably.
template<typename T>
T sum(int n, T ∗p) {
T a = 0;
for (int i = 0; i < n; i++) a += p[i];
return a;
}
The code uses T as a placeholder where the actual type needs to be. Replacing T by float in the generic code yields one of the two definitions of sum, while replacing T by int yields the other. T could also be replaced by other types, including user-defined types. A C++ compiler will make the appropriate replacement each time the sum function is used. Consequently, sum behaves much like the preceding overloaded C++ function, and it can be used as if it were an overloaded function. The central concept of generic programming is the use of type parameters, like T in this example, that can be replaced by arbitrary types.
Thrust is a library of generic functions. By providing generic functions for each type of computation to be supported, Thrust does not need to have multiple versions of each function replicated for each eligible data type.
In fact, not all data types can be used with a generic function. Because sum uses addition and initializes a to 0, it requires the type T to behave (broadly speaking) like a number. Replacing T by the numeric types int or float produces a valid function definition, but replacing T by void or FILE∗ does not. Such requirements are called concepts, and when a type satisfies a requirement it is said to model a concept. In sum, whatever replaces T must model the “number” concept. That is, sum will compute a sum provided that it’s given a pointer to some type T that acts like a numeric type. Otherwise, it may produce an error or return a meaningless result. Generic libraries like Thrust rely on concepts as part of their interface.
C++ classes can be generic as well. The idea is similar to generic functions, with the extra feature that a class’s fields can depend on type parameters. Generics are commonly used to define reusable container classes, such as those in the STL [HB2011]. Container classes are implementations of data structures, such as queues, linked lists, and hash tables, that can be used to hold arbitrary data types. For instance, a very simple generic array container class could be defined as follows:
template<typename T>
class Array {
T contents[10];
public:
T read(int i) {return contents[i];}
void write(int i, T x} {contents[i] = x;}
};
Containers for different data types can be created using this generic class. Their types are written as the generic class name followed by a type in angle brackets: Array<int> for an array of int, Array<float ∗> for an array of float∗, and so forth. The type given in angle brackets replaces the type parameter in the class definition.
While this is not a complete description of how generics work, it conveys the essential ideas for understanding the use of generics in this chapter.
We will introduce one more background concept: iterators. In the same way that pointers are used to access arrays, iterators are used to access container classes. The term iterator refers to both a C++ concept and a value of which the type is a model of this concept. An iterator represents a position within a container: it can be used to access the element at that position, used to go to a neighboring position, or compared to other positions.
Pointers are a model of the iterator concept, and they can be used to loop over an array as shown in the following:
int a[50];
for (int ∗i = a; i < a + 50; i++) ∗i = 1;
Iterators can be used to loop over an STL vector in a very similar way:
vector<int> a(50);
for (vector<int>:iterator i = a.begin(); i < a.end(); i++) ∗i = 1;
The member functions begin() and end() return iterators referencing the beginning and just past the end of the vector. The ++, <, and ∗ operators are overloaded to act like their pointer counterparts. Because many container classes provide an iterator interface, generic C++ code using iterators can be reused to process different kinds of containers.
16.2 Motivation
CUDA C allows developers to make fine-grained decisions about how computations are decomposed into parallel threads and executed on the device. The level of control offered by CUDA C is an important feature: it facilitates the development of high-performance algorithms for a variety of computationally demanding tasks that (1) merit significant optimization, and (2) profit from low-level control of the mapping onto hardware. For this class of computational tasks CUDA C is an excellent solution.
Thrust [HB2011] solves a complementary set of problems, namely those that are (1) implemented efficiently without a detailed mapping of work onto the target architecture, or those that (2) do not merit or simply will not receive significant optimization effort by the user. With Thrust, developers describe their computation using a collection of high-level algorithms and completely delegate the decision of how to implement the computation to the library. This abstract interface allows programmers to describe what to compute without placing any additional restrictions on how to carry out the computation. By capturing the programmer’s intent at a high level, Thrust has the discretion to make informed decisions on behalf of the programmer and select the most efficient implementation.
The value of high-level libraries is broadly recognized in high-performance computing. For example, the widely used BLAS standard provides an abstract interface to common linear algebra operations. First conceived more than three decades ago, BLAS remains relevant today in large part because it allows valuable, platform-specific optimizations to be introduced behind a uniform interface.
Whereas BLAS is focused on numerical linear algebra, Thrust provides an abstract interface to fundamental parallel algorithms such as scan, sort, and reduction. Thrust leverages the power of C++ templates to make these algorithms generic, enabling them to be used with arbitrary user-defined types and operators. Thrust establishes a durable interface for parallel computing with an eye toward generality, programmer productivity, and real-world performance.
16.3 Basic Thrust Features
Before going into greater detail, let us consider the program in Figure 16.1, which illustrates the salient features of Thrust.

Figure 16.1 A complete Thrust program that sorts data on a GPU.
Thrust provides two vector containers: host_vector and device_vector. As the names suggest, host_vector is stored in the host memory while device_vector lives in the device memory on a GPU. Like the vector container in the C++ STL, host_vector and device_vector are generic containers (i.e., they are able to store any data type) that can be resized dynamically. As the example shows, containers automate the allocation and de-allocation of memory and simplify the process of exchanging data between the host and the device.
The program acts on the vector containers using the generate, sort, and copy algorithms. Here, we adopt the STL convention of specifying ranges using pairs of iterators. In this example, the iterators h_vec.begin() and h_vec.end() point to the first element and the element one past the end of the array, respectively. Together the pair defines a range of integers of size h_vec.end() – h_vec.begin().
Note that even though the computation implied by the call to the sort algorithm suggests one or more CUDA kernel launches, the programmer has not specified a launch configuration. Thrust’s interface abstracts these details. The choice of performance-sensitive variables such as grid and block size of the library, the details of memory management, and even the choice of sorting algorithm are left to the discretion of the implementer.
Iterators and Memory Space
Although vector iterators are similar to pointers, they carry additional information. Notice that we did not have to instruct the sort algorithm that it was operating on the elements of a device_vector or hint that the copy was from the device memory to the host memory. In Thrust the memory spaces of each range are automatically inferred from the iterator arguments and used to dispatch the appropriate implementation.
In addition to memory space, Thrust’s iterators implicitly encode a wealth of information that can guide the dispatch process. For instance, our sort example in Figure 16.1 operates on int, a primitive data type with a fundamental comparison operation. In this case, Thrust dispatches a highly tuned radix sort algorithm [MG2010] that is considerably faster than alternative comparison-based sorting algorithms such as merge sort [SHG2009]. It is important to realize that this dispatch process incurs no performance or storage overhead: metadata encoded by iterators exists only at compile time, and dispatch strategies based on it are selected statically. In general, Thrust’s static dispatch strategies may capitalize on any information that is derivable from the type of an iterator.
Interoperability
Thrust is implemented entirely within CUDA C/C++ and maintains interoperability with the rest of the CUDA ecosystem. Interoperability is an important feature because no single language or library is the best tool for every problem. For example, although Thrust algorithms use CUDA features like shared memory internally, there is no mechanism for users to exploit shared memory directly through Thrust. Therefore, it is sometimes necessary for applications to access CUDA C directly to implement a certain class of specialized algorithms, as illustrated in the software stack of Figure 16.2. Interoperability between Thrust and CUDA C allows the programmer to replace a Thrust kernel with a CUDA kernel and vice versa by making a small number of changes to the surrounding code.
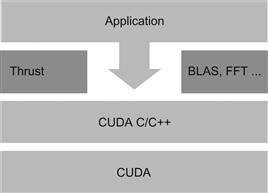
Figure 16.2 Thrust is an abstraction layer on top of CUDA C/C++.
Interfacing Thrust to CUDA C is straightforward and analogous to the use of the C++ STL with standard C code. Data that resides in a Thrust container can be accessed by external libraries by extracting a “raw” pointer from the vector. The code sample in Figure 16.3 illustrates the use of a raw pointer cast to obtain an int point to the contents of a device vector.

Figure 16.3 Thrust interoperates smoothly with CUDA C/C++: (a) interfacing Thrust to CUDA, and (b) interfacing CUDA to Thrust.
In Figure 16.3(a), the function raw_pointer_cast() takes the address of element 0 of a device vector d_vec and returns a raw C pointer raw_ptr. This pointer can then be used to call CUDA C API functions (cudaMemset() in this example) or passed as a parameter to a CUDA C kernel (my_kernel in this example).
Applying Thrust algorithms to raw C pointers is also straightforward. Once the raw pointer has been wrapped by a device_ptr it can be used like an ordinary Thrust iterator. In Figure 16.3(b), the C pointer raw_ptr points to a piece of device memory allocated by cudaMalloc(). It can be converted or wrapped into a device pointer to a device vector by the device_pointer_cast() function. The wrapped pointer provides the memory space information Thrust needs to invoke the appropriate algorithm implementation and also allows a convenient mechanism for accessing device memory from the host. In this case, the information indicates that dev_ptr points to a vector in the device memory and the elements are of type int.
Thrust’s native CUDA C interoperability ensures that Thrust always complements CUDA C and that a Thrust plus CUDA C combination is never worse than either Thrust or CUDA C alone. Indeed, while it may be possible to write whole parallel applications entirely with Thrust functions, it is often valuable to implement domain-specific functionality directly in CUDA C. The level of abstraction targeted by native CUDA C affords programmers fine-grained control over the precise mapping of computational resources to a particular problem. Programming at this level provides developers the flexibility to implement exotic or otherwise specialized algorithms. Interoperability also facilitates an iterative development strategy: (1) quickly prototype a parallel application entirely in Thrust, (2) identify the application’s hot spots, and (3) write more specialized algorithms in CUDA C and optimize as necessary.
16.4 Generic Programming
Thrust presents a style of programming emphasizing code reusability and composability. Indeed, the vast majority of Thrust’s functionality is derived from four fundamental parallel algorithms: for_each, reduce, scan, and sort. For example, the transform algorithm is a derivative of for_each while the inner product is implemented with reduce.
Thrust algorithms are generic in both the type of the data to be processed and the operations to be applied to the data. For instance, the reduce algorithm may be employed to compute the sum of a range of integers (a plus reduction applied to int data) or the maximum of a range of floating-point values (a max reduction applied to float data). This generality is implemented via C++ templates, which allows user-defined types and functions to be used in addition to built-in types such as int or float, or Thrust operators such as plus.
Generic algorithms are extremely valuable because it is impractical to anticipate precisely which particular types and operators a user will require. Indeed, while the computational structure of an algorithm is fixed, the number of instantiations of the algorithm is limitless. However, it is also worth mentioning that while Thrust’s interface is general, the abstraction affords implementors the opportunity to specialize for specific types and operations known to be important use cases. These opportunities may be exploited statically.
In Thrust, user-defined operations take the form of C++ function objects, or functors. Functors allow the programmer to adapt a generic algorithm to perform a specific user-defined operation. For example, the code samples in Figure 16.4 implement SAXPY, the well-known BLAS operation, using CUDA C and Thrust, respectively. The CUDA C code should be very familiar and is provided for comparison.

Figure 16.4 SAXPY implementations in (a) CUDA C and (b) Thrust.
The Trust code has two parts. In the first part, the code sets up a SAXPY functor that receives an input floating value a and maintains it as a state. It can then be called as an operator that performs a∗x +y on two input values x and y. Finally, the generic transform algorithm is called with the user-defined saxpy_functor func. The iterators provided to the transform algorithm will apply func to each pair of the x and y elements and produce the SAXPY results. Note that the operator defined in the saxpy_functor declaration can be overloaded so that different types of a, x, y can be passed into the transform algorithm and the correct operator will be invoked to generate the expected output values for each type of inputs. This makes it possible to create a generic SAXPY function.
C++ Function Objects
A C library developer can set up a generic function by allowing the user to provide a callback function. For example, a sort function can allow the user to pass a function pointer as a parameter to perform the comparison operation for determining the order between two input values. This allows the user to pass any types of input as long as he or she can define a comparison function between two input values.
It is sometimes desirable for a callback function to maintain a state. The C++ function object, or functor, provides a convenient way to do so. A functor is really a function defined on an object that holds a state. The function that is passed as the callback function is just a member function defined in the class declaration of the object. In the case of the saxpy_functor class, a is the class data and operator is the member function defined on the data. When an instance of saxpy_functor func is passed to a generic algorithm function such as transform(), the operator will be called to operate on each pair of x and y elements.
16.5 Benefits of Abstraction
In this section we’ll describe the benefits of Thrust’s abstraction layer with respect to programmer productivity, robustness, and real-world performance.
16.6 Programmer Productivity
Thrust’s high-level algorithms enhance programmer productivity by automating the mapping of computational tasks onto the GPU. Recall the two implementations of SAXPY shown in Figure 16.4. In the CUDA C implementation of SAXPY the programmer has described a specific decomposition of the parallel vector operation into a grid of blocks with 256 threads per block. In contrast, the Thrust implementation does not prescribe a launch configuration. Instead, the only specifications are the input and output ranges and a functor to apply to them. Otherwise, the two codes are roughly the same in terms of length and code complexity.
Delegating the launch configuration to Thrust has a subtle yet profound implication: the launch parameters can be automatically chosen based on a model of machine performance. Currently, Thrust targets maximal occupancy and will compare the resource usage of the kernel (e.g., number of registers, amount of shared memory) with the resources of the target GPU to determine a launch configuration with the highest occupancy. While the maximal occupancy heuristic is not necessarily optimal, it is straightforward to compute and effective in practice. Furthermore, there is nothing to preclude the use of more sophisticated performance models. For instance, a runtime tuning system that examined hardware performance counters could be introduced behind this abstraction without altering client code.
Thrust also boosts programmer productivity by providing a rich set of algorithms for common patterns. For instance, the map-reduce pattern is conveniently implemented with Thrust’s sort by key and reduce by key algorithms, which implement key-value sorting and reduction, respectively.
Robustness
Thrust’s abstraction layer also enhances the robustness of CUDA applications. In the previous section we noted that by delegating the launch configuration details to Thrust we could automatically obtain maximum occupancy during execution. In addition to maximizing occupancy, the abstraction layer also ensures that algorithms “just work,” even in uncommon or pathological use cases. For instance, Thrust automatically handles limits on grid dimensions (no more than 64 K in current devices), works around limitations on the size of global function arguments, and accommodates large user-defined types in most algorithms. To the degree possible, Thrust circumvents such factors and ensures correct program execution across the full spectrum of CUDA-capable devices.
Real-World Performance
In addition to enhancing programmer productivity and improving robustness, the high-level abstractions provided by Thrust improve performance in real-world use cases. In this section we examine two instances where the discretion afforded by Thrust’s high-level interface is exploited for meaningful performance gains.
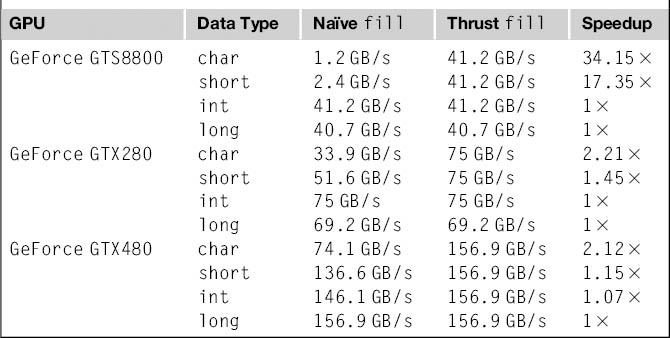
To begin, consider the operation of filling an array with a particular value. In Thrust, this is implemented with the fill algorithm. Unfortunately, a straightforward implementation of this seemingly simple operation is subject to severe performance hazards. Recall that processors based on the G80 architecture (i.e., compute capability 1.0 and 1.1) impose strict conditions on which memory access patterns may benefit from memory coalescing [NVIDIA2010]. In particular, memory accesses of subword granularity (i.e., less than 4 bytes) are not coalesced by these processors. This artifact is detrimental to performance when initializing arrays of char or short types.
Fortunately, the iterators passed to fill implicitly encode all the information necessary to intercept this case and substitute an optimized implementation. Specifically, when fill is dispatched for smaller types, Thrust selects a “wide” version of the algorithm that issues word-sized accesses per thread. While this optimization is straightforward to implement, users are unlikely to invest the effort of making this optimization themselves. Nevertheless, the benefit, shown in Table 16.1, is worthwhile, particularly on earlier architectures. Note that with the relaxed coalescing rules on the more recent processors, the benefit of the optimization has somewhat decreased but is still significant.
Table 16.1 Memory Bandwidth of Two fill Kernels
Like fill, Thrust’s sorting functionality exploits the discretion afforded by the abstract sort and stable sort functions. As long as the algorithm achieves the promised result, we are free to utilize sophisticated static (compile-time) and dynamic (runtime) optimizations to implement the sorting operation in the most efficient manner.
As mentioned in Section 16.3, Thrust statically selects a highly optimized radix sort algorithm [MG2010] for sorting primitive types (e.g., char, int, float, and double) with the standard less and greater comparison operators. For all other types (e.g., user-defined data types) and comparison operators, Thrust uses a general merge sort algorithm. Because sorting primitives with radix sort is considerably faster than merge sort, this static optimization has significant value.
Thrust also applies dynamic optimizations to improve sorting performance. Since the cost of radix sort is proportional to the number of significant key bits, we can exploit unused key bits to reduce the cost of sorting. For instance, when all integer keys are in the range [0, 16), only 4 bits must be sorted, and we observe a 2.71× speedup versus a full 32-bit sort. The relationship between key bits and radix sort performance is plotted in Figure 16.5.
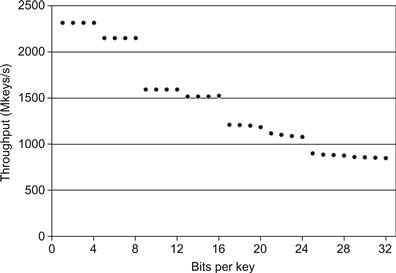
Figure 16.5 Sorting integers on the GeForce GTX480: Thrust’s dynamic sorting optimizations improve performance by a considerable margin in common use cases where keys are less than 32 bits.
16.7 Best Practices
In this section we highlight three high-level optimization techniques that programmers may employ to yield significant performance speedups when using Thrust.
Fusion
The balance of computational resources on modern GPUs implies that algorithms are often bandwidth limited. Specifically, computations with low CGMA (Computation to Global Memory Access) ratio, the ratio of calculations per memory access, are constrained by the available memory bandwidth and do not fully utilize the computational resources of the GPU. One technique for increasing the computational intensity of an algorithm is to fuse multiple pipeline stages together into a single operation. In this section we demonstrate how Thrust enables developers to exploit opportunities for kernel fusion and better utilize GPU memory bandwidth.
The simplest form of kernel fusion is scalar function composition. For example, suppose we have the functions f (x) → y and g(y) → z and would like to compute g(f (x))→ z for a range of scalar values. The most straightforward approach is to read x from memory, compute the value y = f (x), and then write y to memory, and then do the same to compute z = g(y). In Thrust this approach would be implemented with two separate calls to the transform algorithm, one for f and one for g. While this approach is straightforward to understand and implement, it needlessly wastes memory bandwidth, which is a scarce resource.
A better approach is to fuse the functions into a single operation g(f(x)) and halve the number of memory transactions. Unless f and g are computationally expensive operations, the fused implementation will run approximately twice as fast as the first approach. In general, scalar function composition is a profitable optimization and should be applied liberally.
Thrust enables developers to exploit other, less obvious opportunities for fusion. For example, consider the two Thrust implementations of the BLAS function snrm2 shown in Figure 16.6, which computes the Euclidean norm of a float vector.

Figure 16.6 snrm2 has low arithmetic intensity and therefore benefits greatly from fusion.
Note that snrm2 has low arithmetic intensity: each element of the vector participates in only two floating-point operations—one multiply (to square the value) and one addition (to sum values together). Therefore, an implementation of snrm2 using the transform reduce algorithm, which fuses the square transformation with a plus reduction, should be considerably faster. Indeed, this is true and snrm2_fast is fully 3.8 times faster than snr2_slow for a 16 M element vector on a Tesla C1060.
While the previous examples represent some of the more common opportunities for fusion, we have only scratched the surface. As we have seen, fusing a transformation with other algorithms is a worthwhile optimization. However, Thrust would become unwieldy if all algorithms came with a transform variant. For this reason Thrust provides transform iterator, which allows transformations to be fused with any algorithm. Indeed, transform reduce is simply a convenience wrapper for the appropriate combination of transform iterator and reduce. Similarly, Thrust provides permutation iterator, which enables gather and scatter operations to be fused with other algorithms.
Structure of Arrays
In the previous section we examined how fusion minimizes the number of off-chip memory transactions and conserves bandwidth. Another way to improve memory efficiency is to ensure that all memory accesses benefit from coalescing, since coalesced memory access patterns are considerably faster than noncoalesced transactions.
Perhaps the most common violation of the memory coalescing rules arises when using a so-called array of structures (AoS) data layout. Generally speaking, access to the elements of an array filled with C struct or C++ class variables will be uncoalesced. Only explicitly aligned structures such as the uint2 or float4 vector types satisfy the memory coalescing rules.
An alternative to the AoS layout is the structure of arrays (SoA) approach, where the components of each struct are stored in separate arrays. Figure 16.7 illustrates the AoS and SoA methods of representing a range of 3D float vectors. The advantage of the SoA method is that regular access to the x, y, and z components of a given vector is coalesceable (because float satisfies the coalescing rules), while regular access to the float3 structures in the AoS approach is not.

Figure 16.7 Data layouts for 3D float vectors: (a) AoS and (b) SoA.
The problem with SoA is that there is nothing to logically encapsulate the members of each element into a single entity. Whereas we could immediately apply Thrust algorithms to AoS containers like device vector<float3>, we have no direct means of doing the same with three separate device_vector<float> containers. Fortunately, Thrust provides zip iterator, which provides encapsulation of SoA ranges.
The zip iterator [BIL] takes a number of iterators and zips them together into a virtual range of tuples. For instance, binding three device_vector<float> iterators together yields a range of type tuple<float,float,float>, which is analogous to the float3 structure.
Consider the code sample in Figure 16.8 that uses zip iterator to construct a range of 3D float vectors stored in SoA format. Each vector is transformed by a rotation matrix in the rotate tuple functor before being written out again. Note that zip iterator is used for both input and output ranges, transparently packing the underlying scalar ranges into tuples and then unpacking the tuples into the scalar ranges. On a Tesla C1060, SoA implementation is 2.85× faster than the analogous AoS implementation (not shown).

Figure 16.8 The make_zip_iterator facilitates processing of data in structure of arrays format.
Implicit Ranges
In the previous sections we considered ways to efficiently transform ranges of values and ways to construct ad hoc tuples of values from separate ranges. In either case, there was some underlying data stored explicitly in memory. In this section we illustrate the use of implicit ranges, that is, ranges of which the values are defined programmatically and not stored anywhere in memory.
For instance, consider the problem of finding the index of the element with the smallest value in a given range. We could implement a special reduction kernel for this algorithm, which we’ll call min index, but that would be time consuming and unnecessary. A better approach is to implement min_index in terms of existing functionality, such as a specialized reduction over (value, index) tuples, to achieve the desired result. Specifically, we can zip the range of values v[0], v[1], v[2], ::: together with a range of integer indices 0, 1, 2, ::: to form a range of tuples (v[0], 0), (v[1], 1), (v[2],2), ::: and then implement min index with the standard reduce algorithm. Unfortunately, this scheme will be much slower than a customized reduction kernel, since the index range must be created and stored explicitly in memory.
To resolve this issue Thrust provides counting_iterator [BIL], which acts just like the explicit range of values we need to implement min_index, but does not carry any overhead. Specifically, when counting_iterator is dereferenced it generates the appropriate value on-the-fly and yields that value to the caller. An efficient implementation of min_index using counting iterator is shown in Figure 16.9.

Figure 16.9 Implicit ranges improve performance by conserving memory bandwidth.
16.8 Exercises
1. Here counting iterator has allowed us to efficiently implement a special-purpose reduction algorithm without the need to write a new, special-purpose kernel. In addition to counting iterator, Thrust provides constant iterator, which defines an implicit range of constant value. Note that these implicitly defined iterators can be combined with the other iterators to create more complex implicit ranges. For instance, counting iterator can be used in combination with transform iterator to produce a range of indices with nonunit stride.
Read Figure 16.9 and explain the operation of the algorithm using as small example. In practice, there is no need to implement min index since Thrust’s min element algorithm provides the equivalent functionality. Nevertheless the min index example is instructive of best practices. Indeed, Thrust algorithms such as min element, max element, and find if apply the exact same strategy internally.
References
1. Boost Iterator Library. Available at: <www.boost.org/doc/libs/release/libs/iterator/>.
2. Hoberock J, Bell N. Thrust: A Parallel Template Library 2011; [version 1.4.0].
3. Merrill D., & Grimshaw, A., Revisiting sorting for GPGPU stream architectures. Technical Report CS2010-03. University of virginia, department of computer science, Charlottesville. 2010.
4. NVIDIA Corporation. CUDA C best practices guide v3.2. Santa Clara, CA: NVIDIA Corporation. 2010 (Section 3.2.1).
5. Satish, N., Harris, M. & Garland, M. Designing efficient orting algorithms for many-core GPUs. Proceedings twenty third IEEE international parallel and distributed processing symposium, IEEE computer society. Washington, DC: 2009.
