Chapter 13
Merge Sort
In a divide-and-conquer algorithm, either the divide or merge step can sometimes become a bottleneck if done serially. Parallel merge sort demonstrates a case where the merge step can be parallelized to avoid a bottleneck by using divide-and-conquer. The net effect is a divide-and-conquer algorithm running inside a divide-and-conquer algorithm. This illustrates the practical importance of having a parallel framework that supports efficient nested parallelism.
Serial merge sort has two desirable properties:
Weighing against these desirable properties is the disadvantage that merge sort is an out-of-place sort, and thus has a bigger memory and cache footprint than in-place sort algorithms. Conversely, Quicksort is an in-place sort, but lacks the other two properties. In particular, though Quicksort’s expected time is O(N lgN), its worst-case time is O(N2).
Serial merge sort is a divide-and-conquer algorithm where the basic recursive steps are:
The merge step has work Θ(N) to merge N items. If done serially, it can become a bottleneck just as serial partitioning can for Quicksort (Section 8.9.3). Indeed, there is a symmetry to their respective bottlenecks. In Quicksort, a serial divide took time O (N). In merge sort, a serial merge takes time O (N). The effect on the complexity analysis recurrence relations is similar, with similar consequences: The asymptotic speedup for sorting N items is O(lgN). Though efficient for small core counts and big sequences, it is not scalable.
13.1 Parallel Merge
Improving the speedup requires parallelizing the merge step. How to do so is a good lesson in why it is sometimes better to seek a new algorithm than parallelize the obvious serial algorithm. To see this, consider two sorted sequences X and Y that must be merged. The usual serial algorithm inspects the head items of the two sequences and moves the smaller head item to the output sequence. It repeats this incremental inspection until either X or Y becomes empty. Any remaining items are appended to the output. Listing 13.1 shows the code, where X and Y are represented by the half-open intervals [xs, xe) and [ys, ye), respectively.
Listing 13.1 Serial merge. Appendix D.3 explains the meaning of std::move.
A subtle point worth attention is the test in the inner loop. If a key in X and a key in Y are equal, the key in X comes first in the output. This rule for breaking ties ensures that if serial_merge is used for a merge sort then the sort is stable.
Trying to parallelize serial_merge directly is hopeless. The algorithm is inherently serial, because each iteration of the while loop depends upon the previous iteration. However, there is a remarkably simple divide-and-conquer alternative to the usual serial algorithm. Without loss of generality, assume that sequence X is at least as long as sequence Y. The sequences can be merged recursively as follows:
1. Split X into two contiguous subsequences X1 and X2 of approximately equal length. Let K be the first key of X2.
2. Use binary search on Y to find the point where K could be inserted into Y. Split Y at that point into two subsequences Y1 and Y2.
3. Recursively merge X1 and Y1 to form the first part of the output sequence. Recursively merge X2 and Y2 to form the second part of the output sequence.
The two sub-merges are independent and thus can be done in parallel. Listing 13.2 shows a Cilk Plus implementation, using the same argument convention as for serial_merge. A point sometimes overlooked in implementing parallel merge is retaining the stability condition so that if keys in X and Y are equal then X comes first in the output sequence. Doing so requires a slight asymmetry in the binary search:
• If splitting Y at element *ym, then elements of X equal to *ym go in X1.
• If splitting X at element *xm, then elements of Y equal to *xm go in Y2.
The distinction between std::upper_bound and std::lower_bound achieves this asymmetry.
Let N be the total length of the two sequences being merged. The recursion depth never exceeds about 2lg(N/MERGE_CUT_OFF). The qualification “about” is there because when the sequences do not divide evenly at every level of recursion the depth may be one deeper. The depth limit follows from the observation that each two consecutive levels of recursion cut the problem size about in half or better. Here is a sketch of the proof.
Listing 13.2 Parallel merge in Cilk Plus.
Let N be the size of the initial problem and N′ be the size of the biggest subproblem after two levels of recursion. For simplicity of exposition, only cases where sequences split evenly are considered. The point is to prove 
.
Let 
and 
denote the length of X and Y, respectively. Without loss of generality, assume 
. There are two cases:
• The first level of recursion splits X and the second level splits Y. Both sequences have been halved, so 
.
• Both levels split X. This can only happen when 
. Since 
, we know 
. Therefore, 
.
13.1.1 TBB Parallel Merge
The parallel merge code can be translated to Intel® TBB by implementing the parallel fork–join with tbb::parallel_invoke and lambda expressions instead of cilk_spawn. Listing 13.3 shows the rewritten lines.
Listing 13.3 Converting parallel merge from Cilk Plus to TBB. The lines shown are the equivalent of the cilk_spawn/cilk_sync portion of Listing 13.2.
13.1.2 Work and Span of Parallel Merge
The work and span for parallel_merge cannot be found using the recurrence solutions given in Section 8.6, because the recurrences have the wrong form. Instead, other methods have to be used. The span is analyzed first because it is simpler. In the worst case each two levels of recursion halve the problem size. Each level performs a binary search, so there are two binary searches per halving of the problem size. Hence, the span for parallel_merge has the recurrence:
The 2 before the Θ can be immediately eliminated since it is mathematically swallowed by the Θ. Expanding the remaining recurrence and factoring the Θ yields:
which is equivalent to:
The right side is a decreasing arithmetic series starting at lgN and hence has the quadratic sum Θ((lgN2).
The recurrence for work is:
which after expanding the recurrence and factoring the Θ becomes:
Substitute K = lgN to get:
A visual trick to solving this series is to note that the terms are the column sums of the following K × K triangular matrix:
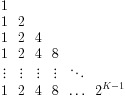
Each row is a geometric series. The sum of the i th row is 2i − 1. Summing all K rows is 
. Thus 
.
Remarkably, both serial and parallel merging have the same asymptotic work! An intuition for this is that the binary search time Θ(lgN) is dominated by the Ω(N) time required to touch each element in the sub-merges, and hence makes no additional contribution to the asymptotic work. However, the constant factors hiding behind Θ deserve some attention. If base case is as small as possible (that is, MERGE_CUT_OFF = 1), then parallel_merge requires about 50% more comparisons than serial_merge. The 50% tax, however, rapidly diminishes if MERGE_CUT_OFF is raised. Raising the latter to 16 reduces the tax to about 6%. In practice, MERGE_CUT_OFF needs to be higher anyway to amortize parallel scheduling overheads, and then the tax practically disappears. Indeed, a more significant concern becomes the less cache-friendly behavior of the search-based merging compared to serial merging, but this too is amortized away by a sufficiently large MERGE_CUT_OFF.
To summarize, the work and span for parallel merge are:
(13.1)
(13.2)
which indicates a theoretical speedup of 
, assuming that memory bandwidth is not a bottleneck.
13.2 Parallel Merge Sort
Turning the sketch (at the chapter opening) of parallel merge sort into code is straightforward. However, merge sort is not an in-place sort because the merge step cannot easily be done in place. Temporary storage is needed. Furthermore, to minimize copying, the merge steps should alternate between merging from the original buffer into the temporary buffer and vice versa. One way to do this is to define parallel merge sort with a flag argument inplace that controls the destination of the sorted sequence:
In both cases, the non-destination buffer is used as scratch space.
Listing 13.4 shows a Cilk implementation. It sorts a sequence defined by the half-open interval [xs,xe). Argument zs should point to a buffer of length xe –xs.
The parallel base case uses a stable sort in order to preserve stability of the overall sort. The flag inplace flipflops at each recursion level. When sorting in place, the subsorts copy into the temporary buffer, and the parallel_merge operation copies the items back into the original buffer. When not sorting in place, the subsorts are done in place, and the parallel_merge copies the items into the destination buffer.
A TBB implementation is similar, except that the fork–join is implemented with parallel_invoke instead of the Cilk keywords, similar as discussed for the TBB implementation of parallel_merge (Section 13.1).
Listing 13.4 Parallel merge sort in Cilk Plus.
13.2.1 Work and Span of Merge Sort
Let N be the length of the input sequence. The recurrences for work and span are:
The recurrence for T1 is case 2 of the Master method (see Section 8.6) and has the closed form solution 
. This is the same as for a serial merge sort, which is not surprising since the constituent components of parallel_merge_sort have the same asymptotic work bounds as their counterparts in the serial algorithm. The solution T∞ can be found by observing that if K = lgN, then the recurrence expands to the series:
which has a cubic sum. Hence, 
.
Thus, the asymptotic speedup for parallel_merge_sort is 
. This suggests that, given about a million keys, on the order of a thousand processors might be used profitably if memory bandwidth does not become a constraint.
13.3 Summary
Merge sort is a classic divide-and-conquer algorithm that lends itself to the parallel fork–join pattern and is easily written in Cilk or TBB. However, for good speedup, the merge step must also be parallelized, because otherwise it takes linear time. The merge step can be parallelized by divide-and-conquer, where the divide step generates two submerges that can be run in parallel.