Chapter 3
Vehicle Longitudinal Dynamics
The longitudinal motions of a vehicle include accelerating, cruising, uphill and downhill motions. The performance and the driveability of a vehicle including accelerations at various loadings and driving conditions are the main topics of this chapter. Vehicle engineers have long realized the importance of driveability in the commercial success of vehicles. Vehicle longitudinal dynamics involves the study of several issues including engine behaviour, tyre tractive force generation, resistive forces acting on the vehicle and the drivers' gearshifting habits.
In this chapter first, simple vehicle models are developed which are useful for the initial estimation of vehicle longitudinal performance. For more detailed analyses and reliable design, however, more elaborate models including the engine characteristics, tyre slips, shifting delays, rotating masses and driveline losses have to be used. Such models with increasing details are being developed and many examples using typical vehicle data are included throughout and MATLAB® codes for vehicle performance calculations are provided in this chapter.
The vehicle is accelerated by a tractive force at the driving wheels which in turn depends on the torque applied at these wheels. In the vehicle longitudinal performance analysis, therefore, the power source which delivers the torque – usually an internal combustion engine (ICE) – plays an important role. Different power sources have different torque generation characteristics. In vehicle performance studies, however, the power source can be regarded as delivering a quasi-steady source of torque (see Section 2.4.3) with predefined characteristics.
Traditionally, IC engines have dominated as power sources in vehicles. However, in spite of all the years of experience using IC engines in vehicles, their torque characteristics and related effects on the vehicle performance still remain an area of discussion. A detailed discussion of the torque generation properties of IC engines was presented in Chapter 2. Electric motors are the main counterparts for engines in hybrid electric vehicles (HEVs) and they have significantly different torque-generating characteristics from engines. In a later section a short review of the performance of electric motors used in vehicle applications will be provided.
3.2.1 Internal Combustion Engines
The torque-speed characteristics of IC engines were discussed in detail in Chapter 2 so only the key features for its application in the current chapter are covered here. The quasi-steady or stationary torque of an ICE is dependent on the speed of rotation ![]() and the amount of throttle opening, θ, i.e.:
and the amount of throttle opening, θ, i.e.:
A typical part throttle engine performance curve representing Equation (3.1) for an SI engine is shown in Figure 3.1. This plot is generated based on engine dynamometer tests.
Figure 3.1 Typical SI engine part-throttle chart

Using the MT engine formula (see Section 2.6) the performance curves can be represented mathematically by a formula of the form:
in which ![]() is the engine full load or wide-open-throttle (WOT) curve and coefficients A, B, C and D are four constants for a specific engine and can be determined from part load tests. For an engine with coefficients given in Table 3.1 and full throttle data of Table 3.2, the part throttle curves are shown in Figure 3.2. In order to produce smooth curves, polynomial curve fitting is applied to the WOT data.
is the engine full load or wide-open-throttle (WOT) curve and coefficients A, B, C and D are four constants for a specific engine and can be determined from part load tests. For an engine with coefficients given in Table 3.1 and full throttle data of Table 3.2, the part throttle curves are shown in Figure 3.2. In order to produce smooth curves, polynomial curve fitting is applied to the WOT data.
Table 3.1 Coefficients of MT formula for a specific engine.

Figure 3.2 Engine part-throttle chart generated by the MT formula

Table 3.2 Engine full throttle data.
![]()
Engines are different in terms of their full load and part load torque-speed characteristics. Diesel engines typically work at larger torques and lower speeds. For diesel engines with common rail fuel injection systems, the WOT torque typically has a flat area of constant torque. Figure 3.3 shows the performance curve of a diesel engine with a common rail system.
Figure 3.3 Performance curves of a diesel engine with a common rail system

3.2.2 Electric Motors
Electric motors play a crucial role in hybrid vehicle powertrain systems (see Chapter 7). Their potential to work as a motor or generator provides opportunities to use them for generation of both traction or braking forces whichever required. There are several types of electric motors suitable for use in hybrid vehicles. Separately excited DC motors are good at speed control and they need relatively simple control electronics. Their brushes need to be changed from time to time and they have high maintenance requirements. Alternating current (AC) motor types include permanent magnet synchronous, induction motors and switched reluctance motors. AC motors are in general less expensive, but require more sophisticated control electronics. Nonetheless, they have higher power density and higher efficiency and in the majority of vehicle applications AC motors are used. The induction AC motors are generally characterized by higher specific powers than permanent magnet motors. One of the inherent properties of electric motors is the production of torque at zero speed. This gives them advantages over IC engines in moving the vehicle from rest without needing a clutch. Power electronics provide the necessary tools for controlling the torque-speed characteristics of the electric motors to suit automotive applications. A constant high torque at low speeds and the retention of maximum power afterwards can be achieved by proper control of the motor voltage, field, flux or frequency depending on the type of the motor. A typical performance curve of an electric motor used in hybrid vehicles is shown in Figure 3.4.
Figure 3.4 Typical performance curves of electric motors used in hybrid vehicles

The vehicle accelerates through the application of tractive forces. The tractive force of a vehicle is produced at the tyre–road interface and it is therefore a function of both tyre and road properties. Different tyres produce different traction forces on a particular road surface, and a particular tyre produces different traction forces over different road surfaces. The tractive force originates from the torque applied on the axle from the torque source. Thus the tractive force is dependent on both the torque source properties as well as the tyre–road properties.
3.3.1 Tyre Force Generation
The tyre produces a tractive force due to the existence of friction at the road interface. The friction force generation by the tyre, however, is quite complicated owing to its rolling motion. In order to examine the difference between a simple sliding friction and that of a rolling tyre, consider a tyre segment cut out from the tyre contact patch as shown in Figure 3.5. A load W equal to a wheel load is considered to act vertically on the tyre segment. When a force F is applied to the segment in order to move it along the road surface, three cases may exist:
a. F is small and no relative motion is produced. In this case, the friction force Ff is simply:
(3.3) ![]()
b. F is large enough to bring the segment to the verge of slip. The friction force in this case is:
(3.4) ![]()
where ![]() is the static coefficient of friction.
is the static coefficient of friction.
c. The segment skids over the surface. In this case all particles on the contact surface will theoretically slide with a similar relative speed to the ground. The friction force can be expressed as:
(3.5) ![]()
where ![]() is the dynamic (or kinematic) coefficient of friction and is usually smaller than
is the dynamic (or kinematic) coefficient of friction and is usually smaller than ![]() . For F larger than Ff, the segment will accelerate. In practice, the friction force varies by increasing the force F in the following range:
. For F larger than Ff, the segment will accelerate. In practice, the friction force varies by increasing the force F in the following range:
(3.6) ![]()
Figure 3.5 A tyre segment on the road surface

Now consider a tyre with the same axle load W standing on the road surface as shown in Figure 3.6. As long as the tyre does not rotate, the friction force Ff will be similar to that of the segment discussed earlier.
Figure 3.6 Skid of a non-rolling tyre

Now if instead of force F, a torque T is applied at the wheel axis as illustrated in Figure 3.7, the direction of friction force at the contact surface will be reversed because the slip direction at the contact surface changes. With the wheel initially at rest, when the torque is applied, the wheel tends to rotate around its axis. This is possible only if the contact patch of the tyre is allowed to slip in reverse direction to the forward motion. The relative motion in the presence of friction at the contact area will result in a friction force opposite to the slip direction. This force will act at the direction of motion of the wheel centre and is called tractive force FT.
Figure 3.7 The tractive force as a result of applying a torque at the wheel axis

One major difference between the simple slip of the tyre segment or the similar case for a non-rolling tyre with the case of a rolling tyre is the slip phenomenon in the contact patch. In the two former cases, the whole contact area slides relative to the ground surface. All contact points, therefore, will experience similar situations. Each point in contact region will generate a share of the total force proportional to the pressure distribution. In the case of the tyre segment, the pressure distribution will be uniform, so any point will have an equal share. For the non-rotating tyre case, the pressure distribution in the contact area is not uniform, but the slip will be uniform, as illustrated in Figure 3.8.
Figure 3.8 Slip distribution for a non-rolling tyre

When the torque is applied at the wheel axis, those elements of the tyre entering the contact region will be forced to stay in contact with the ground and gradually move forward in the direction of the slip. Those close to the leading edge cannot move as fast as those close to the trailing edge. This results in zero slip at leading edge and full slip at the trailing edge. The distribution of slip along the contact length does not have a simple form and an approximation for the slip is illustrated in Figure 3.9. According to this model, a linear slip will exist at the leading region called the ‘adhesion area’ and a uniform slip will exist at the trailing region called the ‘slip area’.
Figure 3.9 Slip distribution for a rolling tyre

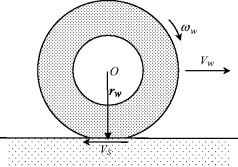
Even this simplified model is difficult to work with, since it needs information regarding the relative width of adhesion and slip lengths, which is dependent on many factors and difficult to determine. In practice, however, a uniform slip is considered in the contact patch of a tyre which means the contact points all have a uniform speed Vs opposite to the direction of wheel travel. If the velocity of wheel centre is denoted by Vw, then the velocity vector, according to Figure 3.10, can be written as:
Figure 3.10 Wheel kinematics during slip
(3.7) ![]()
or in an algebraic form:
(3.8) ![]()
in which ![]() is the effective radius of the tyre. In a pure rolling case, the wheel centre velocity equals
is the effective radius of the tyre. In a pure rolling case, the wheel centre velocity equals ![]() , that means no slip condition with VS = 0. For the slipping case:
, that means no slip condition with VS = 0. For the slipping case:
Longitudinal slip Sx of tyre is defined by dividing the slip speed by the rolling speed ![]() :
:
(3.10) ![]()
From Equation (3.9):
Sx is sometimes expressed as a percentage. The tractive force of the tyre is dependent on the slip within the contact area. However, there are other factors that control the tractive force, e.g. the normal load FZ on the tyre and tyre pressure p. Thus, the tractive force of the tyre can be expressed as a function f of the influencing variables:
(3.12) ![]()
At a certain tyre pressure, the tractive force will be dependent mainly on the longitudinal slip and normal load.
What has been considered so far is the pure slip of the tyre in the longitudinal direction. In practice, the tyre is subjected to slips with components in both the longitudinal and lateral directions. In these combined slip conditions, the slip in the contact region has a complicated nature, since the contact patch is distorted under the application of loads in different directions. For this reason the tyre will produce a force that is acting somewhere other than on the centre of contact patch and in addition to the forces in three directions, moments are also generated.
The tyre force system can be defined in different ways. According to the SAE definition [1], the origin O of the axis system (see Figure 3.11), is taken on the centre of tyre contact (the intersection of wheel plane W and the projection of spin axis onto the road plane R). The ![]() axis is the intersection of the wheel and the road planes. The
axis is the intersection of the wheel and the road planes. The ![]() axis lies in vertical plane V and is perpendicular to the road plane and pointing downward. The
axis lies in vertical plane V and is perpendicular to the road plane and pointing downward. The ![]() axis is therefore in the road plane with positive direction to the right. Only Fx (tractive/brake force) and My (rolling resistance torque) will be needed in this chapter and they are discussed in more detail in the next sections.
axis is therefore in the road plane with positive direction to the right. Only Fx (tractive/brake force) and My (rolling resistance torque) will be needed in this chapter and they are discussed in more detail in the next sections.
Figure 3.11 SAE tyre co-ordinate system [1]

3.3.2 Mathematical Relations for Tractive Force
A large volume of work is available in the literature dealing with the modelling and prediction of the force generating properties of the tyres. In general, tyre modelling is performed in two basic ways: physical and experimental. In physical modelling a simplified model is assumed for the tyre that accounts for the main physical properties affecting the force generation mechanism. By the application of mechanical laws governing the deformation of tyre elements and friction effects at the contact region, mathematical equations are developed. The accuracy of such models depends on the quality of the assumptions made for the physical model. The advantages of these types of models are their simple nature and that the predicted tyre forces do not necessarily require difficult measurements.
There are also software-based physical models involving considerable complexity. These models usually use Finite Elements methods (FEM). Although these sophisticated models are claimed to generate more accurate results than those of simple physical models, they are unnecessarily complicated for vehicle longitudinal performance predictions. Another approach is based on experimental work to measure the force generation properties of the tyres. Experimental results can also help to explain the physics of tyre behaviour when different loading conditions are tested, and hence influence the further developments of tyre models. The normal approach is to fit curves to the measured tyre data.
Finding a general mathematical relationship applicable to all tyres has been a challenge to the automotive industry. The ‘Magic Formula’ tyre model is the result of work carried out at Delft University. The attraction of this approach is its accuracy in fitting the lateral tyre force and aligning moment data in addition to the longitudinal force data of the tyre. The equations of this tyre model are of basic form [2]:
(3.13) ![]()
where:
(3.14) ![]()
(3.15) ![]()
X stands for either longitudinal slip Sx or sideslip angle α (see Figure 3.11). Y stands for either longitudinal force Fx, side force Fy or self-aligning moment Mz. The coefficients B, C, D, E and the horizontal and vertical shifts Sh and Sv are non-linear functions of the vertical tyre load Fz (and camber angle γ for Fy and Mz). For each tyre, a set of tests must be carried out in order that the dependency of the coefficients on the variables (e.g. Fz) is calculated. Typical relations for longitudinal force of a specific tyre are [2]:
(3.16) 
The numerical values for the coefficients a1 to a10 of the same tyre are given in Table 3.3. Fz is in units of N for these values.
Table 3.3 Magic Formula coefficients for a specific tyre [2].

The advantage of the Magic Formula representation is that once the tyre parameters are available, it will be valid for all loading cases with a large range of parameter variations.
Example 3.3.1
Use the Magic Formula with the information in Table 3.3 and plot the variation of tyre longitudinal force for a full range of tyre slips at normal loads of Fz = 1000 to 3500 N.
Solution
The full range of tyre slip is between 0% and 100%. With a simple MATLAB program the plot can be obtained. The MATLAB program is written in two ‘main’ and ‘function’ parts as shown in Figure 3.12. The output result is given in Figure 3.13.
Figure 3.12 MATLAB programs of Example 3.3.1

Figure 3.13 Plot of longitudinal tyre force versus slip at different normal loads

From the results of Example 3.3.1, it can be seen that the overall variation of the tyre longitudinal force with slip can be considered in two linear and non-linear regions as shown in Figure 3.14. The linear region begins from zero slip up to a certain value of 5–10% and the maximum tyre force is developed at slip values around 10–20%. At the full slip (100%) the tyre force is considerably lower than the maximum force. This phenomenon is a typical property of the rolling tyres and if the concept of dry friction is employed, the longitudinal force can be related to the normal load by the coefficient of adhesion:
Figure 3.14 The properties of tyre force

(3.17) ![]()
At a specific normal load, ![]() , the coefficient of adhesion μ is a function only of Fx which is already a function of slip Sx i.e.:
, the coefficient of adhesion μ is a function only of Fx which is already a function of slip Sx i.e.:
(3.18) ![]()
In fact, by dividing the values of Fx by the normal load ![]() , the trend of variation of μ against the slip will be similar to the variation of Fx with Sx.
, the trend of variation of μ against the slip will be similar to the variation of Fx with Sx.
Example 3.3.2
Use the information in Example 3.3.1 and plot the variation of tyre adhesion coefficient versus tyre slip at different normal loads.
Solution
The results shown in Figure 3.15 are obtained by dividing the Fx values by the normal load in the outer loop of Example 3.3.1. Since the curves lie close to each other, only two for = 1000 and 4000 N are presented. It is observed that the dependency of adhesion coefficient on the normal load is very small and in an inverse order.
From the variation of the coefficient of adhesion, two other issues can be noticed. First, the peak of adhesion coefficient ![]() (Figure 3.15) can become even greater than unity at relatively low slips of below 20%. Second, at 100% slip, the value of sliding adhesion coefficient is the lowest value in the non-linear region – in the example tyre in Figure 3.14 it was some 30% lower than
(Figure 3.15) can become even greater than unity at relatively low slips of below 20%. Second, at 100% slip, the value of sliding adhesion coefficient is the lowest value in the non-linear region – in the example tyre in Figure 3.14 it was some 30% lower than ![]() . Thus, the behaviour of coefficient of adhesion in rolling tyres is quite different from the coefficient of friction between the two surfaces. Hence, the following conclusions can be drawn:
. Thus, the behaviour of coefficient of adhesion in rolling tyres is quite different from the coefficient of friction between the two surfaces. Hence, the following conclusions can be drawn:
1. In order that a tractive force is generated by the rolling tyre, a slip must occur in the contact area, otherwise no force will be developed.
2. To obtain the largest tractive force, the tyre slip should be regulated around a specific value, depending on the tyre and road surface. Larger slips will cause the tractive force to reduce considerably.
Figure 3.15 Coefficient of adhesion (Example 3.3.2)

It should be noted that the adhesion coefficient depends not only on the tyre but on the type of road surface as well. On wet surfaces, the values of ![]() will be reduced. Other factors such as tyre treads (shape and depth) will also be influential on the adhesion coefficient. It is worth mentioning that the braking behaviour of the tyre is very similar to its tractive behaviour. Again, to generate braking force at the contact area, slip should take place. This time the rotational speed of tyre is lower than the corresponding straight line speed of the wheel, therefore, the slip will be negative. The braking force can also be determined with the Magic Formula by simply using negative slips. The overall shape of the braking force, therefore, will be similar to that of the tractive force but mirrored relative to the origin.
will be reduced. Other factors such as tyre treads (shape and depth) will also be influential on the adhesion coefficient. It is worth mentioning that the braking behaviour of the tyre is very similar to its tractive behaviour. Again, to generate braking force at the contact area, slip should take place. This time the rotational speed of tyre is lower than the corresponding straight line speed of the wheel, therefore, the slip will be negative. The braking force can also be determined with the Magic Formula by simply using negative slips. The overall shape of the braking force, therefore, will be similar to that of the tractive force but mirrored relative to the origin.
3.3.3 Traction Diagrams
The tractive force is produced at the tyre–road interface provided that two conditions are fulfilled:
1. A torque Tw is applied at the wheel axis.
2. Slip is produced in the contact area.
In a quasi-steady condition, with reference to Figure 3.16:
Figure 3.16 The tractive force in a quasi-steady condition

There is, however, a force limitation in the contact area of the tyre depending on the road conditions. Equation (3.19) is valid up to the limit of tractive force:
(3.20) ![]()
As long as the wheel torque is lower than ![]() , a limited amount of slip will build up, otherwise if a larger torque is applied, the wheel will spin.
, a limited amount of slip will build up, otherwise if a larger torque is applied, the wheel will spin.
Example 3.3.3
A torque of 500 Nm is applied at a wheel axis with effective radius of 35 cm. The weight on the wheel is 360 kg. Use the MF tyre with information given in Table 3.3 and determine:
a. the tractive force available;
b. the maximum possible tractive force and corresponding wheel torque;
c. the value of longitudinal slip (in percentage).
Solution
The load on the wheel in Newton is: Fz = 360 × 9.81 = 3531.6 N.
a. From Equation 16: ![]() (N).
(N).
b. The maximum tractive force must be determined by using the MF tyre at a normal load of 3531.6 N. A relation for the maximum force is not available, so we can use the program in Example 3.3.1 to find the whole force-slip data (no plot is necessary). Then in MATLAB command window we type: ‘Fmax = max(Fx)’ and ‘Enter’. The result is: Fmax = 3774.4 N.
In order that this force is developed at the contact area a torque of ![]() must be applied at wheel axis.
must be applied at wheel axis.
c. Finding a closed form solution for the slip at a specified force is not possible. One way is to plot the variation of the tyre force versus slip and at a specified tyre force, read the slip value. A trial and error solution can also be followed by choosing a value for slip and evaluating the tyre force for it. The slip value must be changed in such a way that the force approximates to the specified value. MATLAB function ‘fsolve’ is also suitable for this work. Issue the following command in MATLAB:
![]()
in which the ‘inline’ function defines our equation to be solved, i.e. ![]() with given values of FT = 1428.6 (N) and Fz = 3531.6 (N). ‘fx’ in the command line is our earlier defined MF tyre function in Example 3.3.1. The value ‘5’ is our initial guess for the Sx. The answer will appear as:
with given values of FT = 1428.6 (N) and Fz = 3531.6 (N). ‘fx’ in the command line is our earlier defined MF tyre function in Example 3.3.1. The value ‘5’ is our initial guess for the Sx. The answer will appear as:
![]()
This means the required tractive force is developed at a very small slip.
Assuming the wheel torque is below the limit, Equation (3.19) means the tractive force is also dependent on the nature of the torque of the wheel. The wheel torque in general is an amplification of the torque of vehicle torque generator (see Section 3.2). Denoting the amplification factor by n (i.e. the overall gear ratio between the torque generator and the wheel):
(3.21) ![]()
and from (3.19):
Thus, the traction force will resemble the torque characteristics of the torque generator (Tg) multiplied by an amplification factor.
Example 3.3.4
An engine torque at wide open throttle (WOT) is approximated by the following equation:
![]()
Plot the variation of the tractive force versus engine rpm for the overall gear ratios of 16.0, 10.5, 7.0, 4.5 and 3.0 respectively, all in a single figure. The wheel effective radius is 30 cm.
Solution
Using Equation (3.22), a simple MATLAB program can be written to plot the required figures. The result is shown in Figure 3.17.
Figure 3.17 Tractive force versus engine rpm of Example 3.3.4

There are resistive forces opposing the motion of the vehicle; some exist from the start of motion and others build up with speed. Resistive forces consume some part of engine power and reduce the speed and acceleration of the vehicle. In order to analyze the straight line performance of the vehicle, it is necessary to characterize the resistive forces acting on the vehicle during the motion. The resistive forces can be categorized into three types: frictional, air resistance and gravitational. The frictional forces are commonly called ‘rolling resistance’ force. Air resistance forces are known as ‘aerodynamic force’ and the gravitational force is called ‘grade force’.
3.4.1 Rolling Resistance
As the name implies, the resistance to motion of rotating parts is summed up together and builds a total resistive force to slow down the vehicle. The rotating parts work under two conditions: with and without the transmission of torque. The former can be excluded from the current discussion since it deals with the driveline power loss during torque transmission and will be treated separately in Section 3.13. The rolling resistance term, therefore, deals only with those resistive torques during vehicle motion with the driveline freely rolling. This includes all the rotating parts in the driveline components. The driving wheels are constantly connected to the driveline and their connection to the engine is controlled by the clutch. Therefore, even when the gearbox is disengaged and left in the neutral position, the driving wheels will rotate the driveline components except for gears inside the gearbox. The total resistive torques of the free rotating parts can be divided into two main categories: due to friction and tyre deformation resistance.
3.4.1.1 Frictional Torques
The frictional torques in the vehicle driveline consist of three parts:
1. bearing torques: the bearing friction terms are usually small compared with other resistive factors and typically increase with load on the bearings.
2. gear teeth friction: friction forces at gear teeth contact points create resistive torques. These are load dependent and thus are relatively small when no load is carried.
3. brake pads: torque resulting from the contact of brake pads with wheel disks or drums is also a resistive factor. Even with no brake activation, there is often a small rubbing effect between the pads and discs that results in a resistive torque. The values of such torques depend on many detailed factors in the design of the brake.
3.4.1.2 Tyre Deformations
For a non-rolling tyre, the load W will cause a symmetrical pressure distribution around the centre of contact area. The resultant reaction load N will act at the centre of contact region as illustrated in Figure 3.18.
Figure 3.18 Pressure distribution for a non-rolling tyre

For a rolling tyre, the tyre elements entering the contact region will experience a compression whereas the trailing materials exiting the contact area will tend to stretch. The pressure on the materials in the contact zone, therefore will tend to increase at the leading edge and decrease at the trailing edge. The pressure distribution will be something similar to that shown in Figure 3.19. The resultant reaction force at the ground will act off-centre closer to the leading edge.
Figure 3.19 Pressure distribution for a rolling tyre

With the resultant reaction force moving forward, it is equivalent to an opposing torque acting around the wheel axis. This torque shown in Figure 3.20a is called rolling resistance torque (TRR). Since the action of the rolling resistance torque is to slow down the wheel (or vehicle), in practice, it is assumed that a resistive force is acting at the ground level with the same effect (see Figure 3.20b). This force is called rolling resistance force (FRR).
Figure 3.20 Rolling resistance (a) torque and (b) force

From an energy point of view, the rolling resistance is caused by the deformations of the tyre. The tyre elements require energy to deform when they enter the contact region. Owing to the visco-elastic properties of rubber, the tyre elements are unable to fully restore this energy when they leave the contact region. This phenomenon is called a hysteresis effect. Therefore a net amount of energy is lost to heat during tyre rolling and is equivalent to the work done by the rolling resistance torque or the work done by the rolling resistance force.
3.4.1.3 Other Factors
There are also other factors besides the rolling frictions and tyre deformation that have small influences on the total resistive force:
- Tyre–road friction loss – due to slipping of the tread compound on the ground surface, heat will be generated.
- Aerodynamic resistance due to wheel spin. The aerodynamic resistance for the whole vehicle usually includes the resistive force for a non-spinning wheel. However, to spin a wheel in the presence of air requires a small amount of energy which will add to the other sources of energy loss.
- Propeller effect of wheel rim during spin. Air passing through the spinning wheel rim also adds a small term to the energy losses.
3.4.1.4 Influencing Parameters
Several parameters influence the rolling resistance force. The main parameters are those which affect the tyre or the contact surface including:
- tyre construction:
 type of tyre (radial or bias ply)
type of tyre (radial or bias ply) tyre materials
tyre materials tread design
tread design tyre diameter
tyre diameter - tyre operating conditions:
 tyre pressure
tyre pressure tyre speed
tyre speed tyre temperature
tyre temperature vertical load
vertical load tyre lateral slip
tyre lateral slip tyre age
tyre age - road surface: it is worth noting that the deformations of the road surface, e.g. on soft deformable ground requires energy and such energy losses are also considered as rolling resistance loss. Some influencing items are:
 road texture
road texture rigidity
rigidity dryness.
dryness.
The extent to which the named parameters influence the rolling resistance has been discussed in specialist references (e.g. [3]). An overview of the influence of various parameters qualitatively is shown in Tables 3.4 and 3.5.
Table 3.4 Effect of increasing tyre parameter values on the rolling resistance force.

Table 3.5 Effect of tyre and road types on the rolling resistance force.

3.4.1.5 Mathematical Representation
A mathematical formula for the rolling resistance force will help in the analysis of vehicle motion. To this end, one can write the rolling resistance force as a function of influencing parameters p1, p2, etc., that is:
(3.23) ![]()
Finding the unknown function f, however, is not a simple task. Of the parameters mentioned earlier, some such as diameter and construction are fixed for an existing tyre, some have little importance such as temperature and some have fixed values, such as pressure. The remaining parameters are speed, load and road type. The type and quality of roads are hard to formulate, thus, for each road type a different formulation is necessary. The dependency of the rolling resistance force on the wheel load is of a linear nature, thus, the ratio of rolling resistance force to the wheel load, fR is called the rolling resistance coefficient and is independent of load:
(3.24) ![]()
The rolling resistance coefficient in general is a function of all the above-mentioned parameters, but according to the justification presented, the only important parameter is the forward speed of the wheel centre, i.e. the vehicle speed:
(3.25) ![]()
The variation of rolling resistance coefficient with speed is reported somewhat differently in various references. The general trend nonetheless shows an increase in the rolling resistance coefficient with speed. From an energy point of view this is acceptable since if a particular amount of energy is lost for one revolution of the tyre, then increasing the revolutions in a time interval will increase the lost energy. The variation of rolling resistance coefficient with speed in general can be approximated in the form of a second order polynomial:
(3.26) ![]()
where the coefficients f0, f1 and f2 are three constants. The quadratic term, however, can be removed since a similar dependency on speed is available through aerodynamic resistance (see Section 3.4.2). In fact, by eliminating this term we are not disregarding this effect, but leaving it included in the aerodynamic force term. With this justification, the rolling resistance coefficient can be simplified to a first order form:
(3.27) ![]()
Often, the dependency of the rolling resistance on speed is also ignored (i.e. f1 = 0) and only a constant coefficient f0 is considered for the rolling resistance coefficient. Typical ranges for the coefficient of rolling resistance f0 can be found in Table 3.6 (additional information may be obtained from [3]).
Table 3.6 Ranges for the rolling resistance coefficient f0 at low speeds.

3.4.2 Vehicle Aerodynamics
The motion of a vehicle is taking place in the air and the forces exerted by air on the vehicle will influence the motion. Aerodynamics is the study of the vehicle motion in air and the effects include:
- internal flows: air flows through the front grills for the purpose of ventilation and cooling. Air flow through windows and sunroof are other examples.
- ground clearance: in ground vehicles, the ground clearance is very low and causes ground effects.
- streamlining: the design of the exterior in accordance with the streamlines of air flow around the body is of great importance in order to reduce the air resistance. For ground vehicles, however, the exterior shape of body is dependent on several factors and streamlining is only one of them (Figure 3.21).
Figure 3.21 Streamlines around the body

3.4.2.1 Aerodynamic Resistance
Aerodynamic resistance forces result from three basic effects:
1.Form resistance: The basis for this resistance force is the pressure difference in front and behind the vehicle due to the separation of the air flow and the vortex creation behind the vehicle. The pressure in front will be higher and a net force opposite to the direction of the air speed will be exerted on the vehicle. The cross-sectional area of vehicle in front of the air flow, therefore, plays an important role in this respect.
2.Skin friction: Air coming into contact with the vehicle surface with a relative speed will apply frictional forces opposite to the direction of motion. The surface roughness of vehicle body is an important factor in this part of the aerodynamic force.
3.Internal flow: Air entering the internal parts of vehicle is slowed down by taking energy from the vehicle and will cause additional resistive force on the vehicle.
The form resistance is responsible for the main part of the aerodynamic force, around 80%, whereas the two others share the remainder at around 10% each.
3.4.2.2 Aerodynamic Forces and Moments
The aerodynamic resistance forces are not in reality discrete forces acting at specific locations, but are actually a summation of infinitesimal forces acting at all points on the vehicle body. The result is a single force RA acting at a point called the centre of aerodynamic force, or centre of pressure CP. In general, the aerodynamic forces are described by a three-dimensional force system with three resolved components at the vehicle body axes. The centre of pressure is also different from the vehicle centre of mass CG and thus the aerodynamic force will have moments around the vehicle axes. Figure 3.22 illustrates the aerodynamic forces and moments.
Figure 3.22 Aerodynamic forces and moments acting on the vehicle

In aircraft aerodynamics, it is a common practice to define other axes systems such as wind axes, separate from the body axes. Aerodynamic forces – drag, lift and sideforce – are defined as components of the aerodynamic force on the wind axes. In ground vehicle applications, due to small aerodynamic angles (in the absence of side wind), the two axes systems are often taken to be coincident. With this assumption, therefore, the components of force in the negative directions of x, y, and z axes are drag, sideforce and lift respectively. As far as the longitudinal motion of the vehicle is concerned, the most important aerodynamic force is the drag force opposing the motion. The lift component can alter the normal loads of the tyres and will therefore also be indirectly influential.
3.4.2.3 Mathematical Representation
It is common practice to express the aerodynamic forces and moments in terms of dimensionless coefficients. In general, any aerodynamic force is written in the basic form:
where CF is aerodynamic force coefficient and stands for drag CD, sideforce CS and lift CL coefficients respectively. ![]() is the characteristic area for the vehicle and it is taken as the frontal area AF (also called the projected area). q is called dynamic pressure and is:
is the characteristic area for the vehicle and it is taken as the frontal area AF (also called the projected area). q is called dynamic pressure and is:
in which ![]() is the air density that is dependent on the ambient conditions. Under the standard conditions of 1 atmosphere (1.013 bar, 10132.5 Pa) at sea level and a temperature of 15 °C (288.15°K), the air density is 1.225 kg/m3. The air density can be approximately calculated from:
is the air density that is dependent on the ambient conditions. Under the standard conditions of 1 atmosphere (1.013 bar, 10132.5 Pa) at sea level and a temperature of 15 °C (288.15°K), the air density is 1.225 kg/m3. The air density can be approximately calculated from:
(3.30) ![]()
with p in Pascal and T in Kelvin (273.15+°C).
The velocity ![]() in Equation (3.29) is called the air speed and is the magnitude of speed of air relative to the vehicle body. In order to calculate the air speed, information on the wind velocity is also necessary. Let us assume a wind speed vW is acting at angle ψW relative to the geographical north (see Figure 3.23). A vehicle is travelling at a speed of vV in the direction of ψV. Vector
in Equation (3.29) is called the air speed and is the magnitude of speed of air relative to the vehicle body. In order to calculate the air speed, information on the wind velocity is also necessary. Let us assume a wind speed vW is acting at angle ψW relative to the geographical north (see Figure 3.23). A vehicle is travelling at a speed of vV in the direction of ψV. Vector ![]() is the air velocity and can be determined as:
is the air velocity and can be determined as:
Figure 3.23 Definition of air velocity vector ![]()

![]() can also be obtained graphically as shown in Figure 3.23.
can also be obtained graphically as shown in Figure 3.23.
The aerodynamic moments are expressed as:
(3.32) ![]()
where l is the characteristic length and for the vehicle usually the wheelbase is considered. CM is the moment coefficient and represents Cl, Cm and Cn for roll, pitch and yaw moments respectively.
Example 3.4.1
A vehicle is travelling with a constant speed of 100 km/h. Determine the air speed for a wind speed of 30 km/h, for: (a) a head wind; and (b) a tail wind.
Solution
It can be assumed that the vehicle velocity vector has a zero angle (ψV = 0), thus for case (a) the head wind, ψW = 180 and from Equation (3.31):
![]()
For the tail wind of case (b) ψW = 0 and similarly:
![]()
Graphical representations are also shown in Figure 3.24.
Figure 3.24 Graphical solutions for Example 3.4.1

Aerodynamic forces are dependent on several parameters, such as the body geometry, ambient conditions and airstream properties. The geometry of the vehicle body includes its shape and dimensions. The latter was already considered as the characteristic area, and the vehicle wheelbase was considered as the characteristic length for the aerodynamic moments. The main influential ambient parameter is the air temperature that influences the air density and directly alters the aerodynamic forces.
The airstream properties include air speed and its direction relative to the body coordinates. When the airstream is at an angle to the vehicle forward axis, this angle is called the angle of attack. This angle also has an influence on the magnitude of the aerodynamic force. In order to account for these influential parameters, the dimensionless parameters Reynolds number (Re) and Mach number (M) are used. In general, the force (or moment) coefficients CF (CM) are a function of these parameters as well as angle of attack α and sideslip β (see Figure 3.22), i.e.:
(3.33) ![]()
In vehicle motion the Mach number is always of a small range of less than 0.2, and the variation of the Reynolds number is also very small. In the case of longitudinal horizontal wind, both angles α and β are small and under these circumstances, the force coefficient is virtually a constant. It is, therefore, practical to consider constant force or moment coefficients for the vehicle.
Example 3.4.2
A vehicle with frontal area of 2.0 square metres has drag coefficient of 0.38. Plot the variation of aerodynamic drag force at the standard ambient condition and in still air up to a speed of 200 km/h.
Solution
The air density at the standard condition is 1.225 kg/m3 and the aerodynamic force is:
![]()
The variation of this force with speed can be plotted easily in MATLAB. The result is given in Figure 3.25.
Figure 3.25 Variation of aerodynamic force for vehicle of Example 3.4.2

Example 3.4.3
For the vehicle in Example 3.4.2, calculate the aerodynamic force at a speed of 100 km/h and examine the changes in the drag force for head and tail winds of 20, 30 and 40 km/h.
Solution
From the equation for the drag force found in the previous example, the force at 100 km/h is 359.2 N.
For the head and tail winds the drag forces simply are ![]() and
and ![]() . The results are compared in Table 3.7.
. The results are compared in Table 3.7.
Table 3.7 Air drag forces (N) for Example 3.4.3.

3.4.3 Slopes
The gravitational force on a slope will act in opposite directions for uphill and downhill motion of the vehicle. With reference to Figure 3.26 for a slope of angle θ relative to horizontal, the gravitational force simply is:
Figure 3.26 Gravitational force
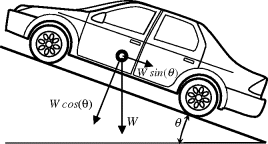
The positive and negative signs are for the downhill and uphill motions respectively. The gravitational force is a constant force as long as the slope is constant.
The slope is often expressed as a percentage rather than an angle. It is the tangent of the angle of the slope multiplied by 100:
(3.35) ![]()
It should be noted that in vehicle motion on a slope, the normal reaction force will also change and the rolling resistance force will be altered accordingly:
3.4.4 Resistance Force Diagrams
The total resistive force is the summation of the rolling resistance, aerodynamic and gravity forces:
Of these forces, the gravity force is constant and the two others are speed-dependent.
Example 3.4.4
Use the information in Example 3.4.2 and for a vehicle of mass 1200 kg, consider a constant rolling resistance coefficient of 0.02.
a. Plot the total resistive force for speeds up to 200 km/h at slope of 10% and specify each component.
b. Plot the total resistive force for slopes of 0, 10, 20, 30, 40 and 50% all in a single figure.
Solution
The results are obtained by making simple use of Equations (3.31), (3.34), (3.36) and (3.37). Plots for (a) and (b) are shown in Figures 3.27 and 3.28.
Figure 3.27 Resistive forces at level road

Figure 3.28 Total resistive force at different slopes

3.4.5 Coast Down Test
A vehicle coast down test is designed to experimentally measure the resistive forces including the rolling resistance (see Section 3.4.1) and aerodynamic drag. In a coast down experiment the vehicle is accelerated up to a high speed and then with the drivetrain disengaged, it is allowed to slow down under the action of the resistive forces. In general, the resistive forces depend on environmental and road conditions (e.g. temperature, wind, road surface and type). Therefore, under standard conditions, usually in still air and on a level road of sufficient length, useful information of vehicle speed variation with elapsed time can be obtained. This information then can be processed in order to estimate the rolling resistance and air resistance forces. Simple methods for the estimation of the resistive forces from speed-time data are discussed in Section 3.12.
3.5 Vehicle Constant Power Performance (CPP)
Modelling the longitudinal performance of a vehicle in general driving conditions is quite complicated when the engine throttle and gearbox ratios vary during motion. Simple models are used in the first instance to facilitate the analysis and understanding of the vehicle performance. One useful approach is to assume that the vehicle uses constant power to accelerate up to its maximum speed, corresponding in practice to full throttle acceleration. Later on it will be revealed that such acceleration is not a constant power motion, nonetheless, the assumption of constant power simplifies the equations of motion initially and provides a simple workable model for rough calculations.
3.5.1 Maximum Power Delivery
There have been arguments about how a power source can deliver maximum power as a function of its rotational speed. We shall examine this by the following mathematical procedure.
Consider a power source with output speed ω that is a function of time t. As shown in Figure 3.29, the output torque T is a function of speed. Therefore:
Figure 3.29 A power source with output torque characteristics

In order to obtain maximum power output, we are interested to find a speed at which the power is at maximum. To this end, Equation (3.38) can simply be differentiated with respect to speed ω:
or:
This is a differential equation that relates the output torque to the speed. Integration of Equation (3.40) results in:
where C is the constant of integration. If C = ln P0 is assumed, then Equation (3.41) can be rewritten as:
(3.42) ![]()
or,
Equation (3.43) apparently implies that to deliver a maximum power from a source, it must be a constant power P0. This statement by itself is false, since the power P0 does not have to be the maximum power and can have different values. So what is wrong with the mathematical approach for the analysis? One must recall that the differentiation as performed in Equation (3.39) was only a necessary condition to obtain the maximum, and to ensure the existence of the maximum, there is also a sufficient condition, namely:
(3.44) ![]()
In the case of our problem, one can simply show by using Equations (3.39) and (3.40) that:
(3.45) ![]()
which means this point is not a maximum, nor a minimum, but a critical point. Thus this analytical approach does not lead to any workable conclusion on the way a power source can deliver maximum power. The discussion of this section is aimed at demonstrating that the idea of a constant power delivery does not relate to the maximum power delivery of a power source as is sometimes claimed. The constant power that is considered in the following sections can be any desired value of power.
3.5.2 Continuous Gear-Ratio Assumption
A geared transmission with clutch shifts causes discontinuous torque flow to the wheels and, in turn, delivers discontinuous tractive forces, and hence acceleration. Figure 3.30 shows a typical acceleration time history of a vehicle equipped with a manual transmission. When first gear is engaged, the vehicle accelerates up to a speed at which the engine rotation speed is too high and a gearshift is necessary. During the gearshift from first to second gear, the clutch is first disengaged, gearshifted, and the clutch re-engaged. This process will take some time during which there will be no tractive force available but the resistive forces are still acting on the vehicle. This situation will result in a temporary negative acceleration, as can be seen from Figure 3.30. During other gearshifts the same phenomena will result in discontinuous vehicle accelerations.
Figure 3.30 Typical time history of vehicle acceleration

We will eventually obtain vehicle performance curves similar to Figure 3.30, but first it is more effective to start with simpler models. The main complexity involved in the general case arises from the gearshift process. One simple and useful assumption is to consider a transmission with continuous gear changing property; in other words, infinite gear ratios and continuous gear ratio changing. This assumption will lead to having a continuous torque flow and corresponding uninterrupted vehicle acceleration.
The constant power assumption may be considered as a single torque-speed point for the engine. In fact, when the power is unchanged, the optimum operating point for the engine can be chosen at this specific power. This means the engine works at a particular torque and speed values denoted by ![]() and
and ![]() . At such a point the engine power Pe is:
. At such a point the engine power Pe is:
(3.46) ![]()
in which ![]() is engine torque in Nm, and Pe and ω* are in Watt and rad/s respectively.
is engine torque in Nm, and Pe and ω* are in Watt and rad/s respectively.
At this engine speed, the vehicle moves ahead with an infinitely variable gear ratio and no shift delays. From a simple kinematic relation one can relate the wheel rotational speed ![]() to the engine rotational speed
to the engine rotational speed ![]() by:
by:
(3.47) ![]()
in which n is the overall vehicle gear ratio, that is the gearbox gear ratio ng times the differential (final drive) gear ratio nf, i.e. (see Figure 3.31):
Figure 3.31 Vehicle transmission and final drive gear ratios

(3.48) ![]()
Now if it is further assumed that there is no slip for the driving wheels when they roll on the road surface, with reference to Figure 3.32 it is clear that the vehicle speed can be written as:
Figure 3.32 The pure rolling of a wheel
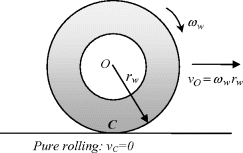
where rw is the effective rolling radius of tyres. Equation (3.55) simply shows that the vehicle speed is inversely proportional to the transmission gear ratio.
It should be noted that the assumption of no slip for the tyre is strictly in conflict with its force-generating mechanism which depends on slip (see Section 3.3.1). Nevertheless, including slip in the analysis will cause difficulties we would like to avoid at this stage.
3.5.3 Governing Equations
The mathematical representation of vehicle motion involves the application of Newton's laws of motion to the vehicle. For our case, the motion of interest involves the longitudinal motion properties including the acceleration, speed and distance travelled. Newton's second law of motion is suitable for this problem of a unidirectional motion of the vehicle centre of mass. In Sections 3.3 and 3.4 the tractive and resistive forces acting on the vehicle were explained. The vehicle motion will be the result of interaction between these forces. The longitudinal vehicle motion involves a multitude of situations with different driving and resistive forces. For a moving vehicle the tractive forces are generated at tyre contact patches. The total tractive force FT is the sum of individual driven tyre forces. The total power consumed due to the forward motion of vehicle with speed v is:
The power available at the driving wheels is:
(3.51) ![]()
Due to driveline losses we must have:
in which Pe is the engine power and it was assumed to remain a constant value P*. Equation (3.52) indicates that the power generated by the engine is not fully utilized and some part is lost due to friction in the vehicle driveline system. To include this effect we must consider the driveline efficiencies in our equations. In order to simplify the equations of motion, we will ignore this effect for the time being and it will be included later on in Section 3.13. For an ideal driveline with 100% efficiency, all three power values are equal:
(3.53) ![]()
Therefore P* is the constant power delivered to the driving wheels and from Equation (3.50):
This equation shows that the traction force depends only on the forward speed in an inversely proportional fashion. The variation of FT versus speed in Equation (3.54) at different power outputs is depicted in Figure 3.33.
Figure 3.33 The variation of total tractive force with vehicle speed
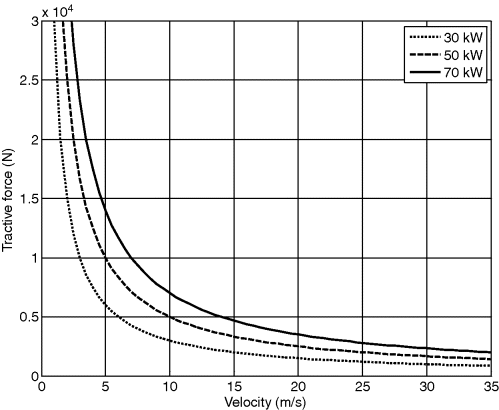
Note that Equation (3.54) implies that at low vehicle speeds, the tractive force mathematically becomes infinite. In practice, however, the tyre force is dependent on the tyre–road friction coefficient and slip ratio and there will be a maximum tractive force available for the tyre. If this limit is imposed, the total tractive force-speed diagram will be similar to Figure 3.34.
Figure 3.34 Tractive force versus speed including tyre traction limit

With this constraint in force, the tractive force will no longer remain uniform and it must be divided into two regions of limit adhesion and constant power. For the sake of simplicity this constraint will also be ignored for the time being and the amount of error induced with this assumption will be examined later in this chapter.
Now Newton's Second Law is applied to the longitudinal motion of vehicle with reference to the free body diagram of the vehicle shown in Figure 3.35. The longitudinal equation of motion simply is:
(3.55) ![]()
Figure 3.35 Free body diagram of a vehicle

with:
(3.56) ![]()
Substituting for the resistive forces FRR (Section 3.4.1), FA (Section 3.4.2) and FG (Section 3.4.3), will lead to:
(3.57) ![]()
In most elementary performance analyses, a constant rolling resistance coefficient is considered and with this assumption and using Equation (3.54), the final form of the longitudinal equation of motion of the vehicle will be:
where c and F0 are two constants defined below:
(3.60) ![]()
It should be noted that in Equation (3.58) the air speed vA is replaced with the vehicle speed v for conditions of still air with no wind.
Equation (3.58) is an ordinary differential equation in terms of the forward speed v of the vehicle. The time history of vehicle velocity will result from the integration of this equation.
It should be noted that Equation (3.58) was obtained under certain assumptions summarized in Table 3.8.
Table 3.8 Assumptions involved in derivation of Equation (3.58).
| There is a constant power demand from the engine during entire motion |
| The vehicle gearbox has infinite gear ratios, changing continuously during vehicle motion |
| The driving wheels roll and there is no slip at road surface |
| There is no power loss in the vehicle driveline |
| Tyres can produce very large tractive forces |
| Rolling resistance force is a constant in all speeds |
| There is no wind during vehicle motion |
3.5.4 Closed Form Solution
Equation (3.58) can be rearranged as:
Then, integration by separation of variables leads to:
(3.62) ![]()
It can be shown that the governing equation of longitudinal vehicle motion will be of the form:
in which vm is the real root of the third order polynomial:
Ct in Equation (3.63) is the constant of integration and must be calculated by introducing an initial condition (e.g. at t = 0, v = 0), and the three constants a, k1 and k2 are given below:
(3.65) ![]()
(3.66) ![]()
(3.67) ![]()
Although Equation (3.63) provides a mathematical solution to the vehicle longitudinal motion, it is in the unusual form of t = f(v) instead of the more useful v = f(t) form. In order to solve for speed vs time, therefore, this non-linear equation must be solved by iteration techniques.
Example 3.5.1
For a vehicle of mass 1000 kg, the rolling resistance coefficient, overall aero-drag coefficient (Equation (3.59)) and engine power are 0.02, 0.4 and 60 kW respectively. On a level road, determine the time history of vehicle speed starting at standstill.
Solution
With the given initial condition of starting from rest, the constant of integration is determined. In order to avoid iteration, instead of evaluating speed for a given value of time, with increasing the speed from zero to the maximum speed, the corresponding times can be calculated. The maximum speed is vm and should be determined by solving Equation (3.64). A MATLAB program is prepared for this example with listing given in Figure 3.36 and several comments included to make it explanatory. The result is depicted in Figure 3.37.
Figure 3.36 MATLAB program listing for Example 3.5.1

Figure 3.37 Variation of speed versus time for Example 3.5.1

3.5.5 Numerical Solutions
In spite of the availability of a closed form solution for the problem, numerical solutions are often advantageous. Nowadays with the widespread availability of computer software, it is not difficult to set up a program and solve the problem numerically. Equation (3.58) for the vehicle acceleration can be written in the form:
which is an ordinary first order differential equation for the velocity v and can be integrated numerically by using well established numerical methods such as the Runge-Kutta method. Different software packages provide this routine for programmers and MATLAB is a good example which has a family of functions called ‘ode’ (standing for Ordinary Differential Equations). One of these functions called ‘ode45’ is a medium order method suitable for solving non-stiff differential equations. Using this routine is quite straightforward and will suffice for our case. In order to become familiar with using this function, Figure 3.38 shows two ‘m’ files, one as the main program and the other as a function to be called within the main program. As shown in Figure 3.38, the main program consists of five parts, whereas the function consists of three parts. The main program introduces values for the main parameters and sets the initial values (e.g. at time t = 0) for the main variables. MATLAB starts integrating the differential equation given in the separate ‘function’, starting from time ‘t0’ and ending at time ‘tf’. An internal MATLAB function ‘ode’ with input arguments will call the differential equation available in ‘function’ and once the integration process is complete, it will return the result. In other words, the user does not have access to the intermediate steps of the integration process.
Figure 3.38 Structure of programming for numerical integration by MATLAB: (a) main program and (b) function

A detailed program listing for the solution of the differential Equation (3.68) is presented in Figure 3.39. It is worth noting that the values for the parameters are also needed in the ‘function’, so one way is to provide the vehicle information inside the ‘function’ itself. Another way is to give the information in the main program and then share them with the ‘function’ by using ‘global’ statement. One more point is to note that the value of dv/dt approaches infinity at v = 0, due to division by zero in p/v term. To avoid this, we can set the initial value of velocity to a very small value close to zero. MATLAB uses a variable called ‘eps’ for this purpose (eps = 2.2204e-016).
Example 3.5.2
For the vehicle of Example 3.5.1, use the program of Figure 3.39 and find the variation of vehicle velocity for the first 80 seconds.
Solution
The solution is found by entering the vehicle data into the MATLAB program. The variation of velocity versus time resulting from this program is shown in Figure 3.40. It can be seen the result is similar to that obtained by the closed form solution given in Figure 3.37.
Figure 3.40 The result of numerical solution to Example 3.5.2 using MATLAB

3.5.6 Power Requirements
The value of the engine power is one of the first requirements in the initial design stages. With a constant power assumption, one can easily evaluate the power necessary for a specific performance requirement. Very rough estimations can be found by using ‘no resistive force’ (NRF) model (see Problem 3.3) or ‘low speed’ (LS) model (see Problem 3.5). For a more accurate power calculation, the general form of the equation of longitudinal motion must be solved.
In the general case, two approaches can be followed; using the closed form equation or numerical integration. In the first approach, Equation (3.63) is used to obtain the power P for given t and v values. Obviously this must be done by applying a trial and error technique. MATLAB's function ‘fsolve’ can be used for this purpose. It finds a solution P* that satisfies Equation (3.63) for given values of t and v. It should be noted that to initiate the ‘fsolve’ function an initial guess is required. A proper initial value must satisfy ![]() (see Equation (3.64)). The following example shows how to use ‘fsolve’ for this problem.
(see Equation (3.64)). The following example shows how to use ‘fsolve’ for this problem.
Example 3.5.3
For a vehicle of 1000 kg mass, total rolling resistance force F0 = 200 N and overall aerodynamic coefficient of 0.4, obtain power necessary to reach a speed of 100 km/h during a 10-second acceleration starting from rest.
Solution
The MATLAB program listings used for the solution of this example are given in Figure 3.41. Figure 3.41a is the main program and Figure 3.41b is the function that includes the equation f (P, t, v) = 0. The result obtained from this program is P_star = 46,097 W.
Alternatively, the equation of motion (Equation (3.68)) can be solved by the numerical integration, but as observed in Section 3.6.5 the solution requires the power as an input. In fact, the process examined earlier was to obtain the speed values from a given power value. Here, the process is reversed as the power P is needed for a required speed v* at a specified time t*. Thus in order to calculate the power, an iteration loop must be performed in the numerical integration process. The result in one iteration process will be a value v1 for speed at time t*; if v1 happens to be equal to the specified speed v*, then the given power P is the answer. Otherwise P must be modified until the speed obtained from iteration process equals v*.
Example 3.5.4
Repeat Example 3.5.3 by using the numerical integration method of Section 3.5.5.
Solution
The MATLAB program of Section 3.5.5 can be modified to include the iteration loop. MATLAB command ‘while’ can be used for this purpose. The program will repeat the instructions inside the loop until the condition in the ‘while’ statement is not satisfied. The modified program is shown in Figure 3.42.
Figure 3.42 MATLAB program for power calculation of Example 3.5.4

The output result of this program is printed as:
![]()
3.5.7 Time of Travel and Distance
Two important parameters in the vehicle motion are the time duration and the distance the vehicle travels during that time. In this section the equations of motion will be used to find these two parameters. The required time to achieve a specified speed can simply be determined by the direct use of the result of the closed form solution given in Equation (3.63). Alternatively, the numerical integration method can also be used to obtain this time value but the process needs a ‘while’ loop. In fact, the travel time was already obtained from the numerical integration of the equation of motion. The integration methods advance the time by small steps to the final integration time tf that is the vehicle's total travel time at the end of the integration process. In other words, in such processes the time is pre-selected and velocity is calculated at the end of that specified period. In the numerical method, therefore, the travel time at a desired speed can be obtained from the time history of motion that is in the form of vehicle speed versus time. Alternatively by using a ‘while’ statement, the time can be obtained directly. For the determination of the travelled distance S, the following relation can be used:
and after substituting from Equation (3.58), one obtains:
(3.70) ![]()
which is similar to Equation (3.61) and can be integrated similarly. The result reads:
with:
(3.72) ![]()
and CS is the constant of integration. Alternatively, to calculate the distance of travel using numerical integration, instead of using the approach of Equation (3.69), it is recalled that velocity is the derivative of travelled distance, that is:
This adds another ordinary differential equation to the one existing before for the velocity (i.e. Equation (3.68)). For the numerical integration, the number of differential equations does not make any difference, in fact, the procedure of numerical solution is similar when a set of differential equations are present. In the MATLAB program of Section 3.5.5, only a few changes listed below are necessary:
a. The two variables must be put together in a single raw matrix (array). Let this array be called x. Then x includes two variables v and S:
(3.74) ![]()
Throughout the program v should be replaced with x.
b. An initial condition must be given for the vector x. For instance, if the motion is started from the rest at origin, then:
(3.75) ![]()
c. In the separate function file, the additional differential equation has to be included (i.e. Equation (3.73)).
d. To plot the results, the command ‘plot(t, x)’ plots both variables in one single figure. In order to separate the two plots one must specify how to plot the results.
Changes necessary to the program of Section 3.5.5 are listed in Figure 3.43.
Figure 3.43 Changes required to the MATLAB program of Figure 3.39

Example 3.5.5
For the vehicle of Example 3.5.1, when starting to accelerate from standstill, find:
a. the time of travel;
b. the distance travelled when the speed is 100 km/h.
Use both closed form and numerical integration methods.
Solution
a. By direct evaluation of Equation (3.63) with the data of Example 3.5.1 the time value of 7.326 s is obtained for the closed form solution. For the numerical method, the result of Example 3.5.2 can be used and at the speed of 27.78 m/s the time can be read from Figure 3.40. In the MATLAB environment by ‘zooming in’ around the specified speed, (or by using the data cursor in the figure window) the value of time is obtained as 7.328 s. For a direct solution using the numerical integration, a ‘while’ statement could be used as was shown in Example 3.5.4 but this time to obtain ‘t’ instead of ‘P’. The ‘check for velocity’ segment in the program is changed to:
if maxv < vd % then increase time of integration to increase velocity
tf=tf*vd/maxv;
else % decrease time (with a different rate) to decrease velocity
tf=0.8*tf*maxv/vd;
end
and the result is obtained as:
![]()
b. A similar approach used in (a) for the time is also applicable for the distance. To obtain the solution by the closed form method for the distance travelled, Equation (3.71) results in 139.02 m.
The numerical solution using program listings of Figure 3.43 produces the time histories of speed and distance depicted in Figure 3.44. At a speed of 100 km/h the travel distance can be read approximately. By zooming in the figure, (or by using the data cursor in the figure window) the value is 139 m. Alternatively, the ‘while’ loop given above can also be used to obtain the distance. In fact, the distance and time are produced simultaneously. The result is 139.01 m.
Figure 3.44 Results obtained from the MATLAB program with changes specified in Figure 3.43

3.5.8 Maximum Speed
The maximum speed of vehicle is one of the important factors in the performance analysis. The acceleration of the vehicle shows the increase of the vehicle speed vs time. The maximum speed will occur when the resistive forces equal the tractive force available. Mathematically this means:
(3.76) ![]()
This also means a steady-state condition for the vehicle motion. From the equation of motion of the vehicle, it is clear for such a condition that:
Since both tractive force FT and resistive force FR are changing by the time, there will be an instant t* in which both forces attain equal values. At this instant the vehicle speed will reach its maximum. If the variation of tractive and resistive forces is drawn in a single figure, the intersection point will indicate the instant t*. The tractive and resistive forces are functions of velocity v, so a diagram can be constructed for the variation of the forces against velocity. The tractive force for CPP was given in Equation (3.54):
(3.78) ![]()
and the resistive force FR(v) depends on the assumptions made for the rolling resistance force. For a constant rolling resistance force f0W (see Section 3.4.1.5), Figure 3.45 shows the variation of the tractive and resistive forces in a single diagram. The maximum speed of the vehicle is reached where the two forces balance each other. This point is the intersection point of FT(v) with FR(v). For the specific condition shown in Figure 3.45, the maximum speed is reached exactly at 50 m/s (180 km/h).
Figure 3.45 The intersection point of tractive and resistive forces gives the maximum speed

To obtain the maximum speed of the vehicle a mathematical solution can also be obtained from Equation (3.77) after substituting the relevant terms for the tractive and resistive forces:
A closed form solution for Equation (3.79) is in the following form:
in which:
(3.81) ![]()
(3.82) ![]()
(3.83) ![]()
(3.84) ![]()
(3.85) ![]()
Alternatively, Equation (3.79) can be solved numerically using MATLAB functions ‘fsolve’ or ‘roots’. The following example will use both methods.
Example 3.5.6
For a vehicle with engine power of 60 kW, constant rolling resistance force of 200 N and overall aerodynamic force coefficient of 0.4, determine the maximum speed:
a. Use Equation (3.80).
b. Use MATLAB's ‘fsolve’ function.
Solution
In a MATLAB program shown in Figure 3.46, both methods are used one after the other. Both will display 50 m/s for the maximum speed.
Figure 3.46 MATLAB program to solve for vehicle maximum speed

3.6 Constant Torque Performance (CTP)
In the previous section we discussed a simplified longitudinal acceleration performance of the vehicle. The major assumption was to consider a constant power demand from the vehicle during the entire motion. This was to simulate a constant load (including the full load) acceleration in which the vehicle is assumed to demand fixed power. In practice, the power demand of the vehicle, however, depends on the torque-speed combination during the acceleration. It is, therefore, necessary to take into the consideration the torque generator's characteristics as well as the vehicle parameters.
There are circumstances in which the torque of the power source is almost constant. Two examples are electric traction motors in their constant torque phase of operation (see Figure 3.4) and modern diesel engines (see Figure 3.3) in their flat torque area. For such cases, the power is not constant and the foregoing discussion cannot be used. Another difference for the constant torque case is the effect of the gearshifts that take place during the acceleration. With a constant torque T from the power source, the tractive force FTi of the vehicle in a specified gear ratio ni is a constant:
(3.86) ![]()
in which ni and rw are the overall gear ratio and the wheel effective radius respectively. At any speed, the resistive force is known and the difference between the tractive and resistive force will generate the acceleration a(v):
The implication from Equation (3.87) is that any gearshift will change FTi and in turn the acceleration.
3.6.1 Closed Form Solution
In order to find the velocity, Equation (3.87) should be integrated with respect to time. In differential equation form:
This is a differential equation that can be integrated by the separation of variables. The closed form solution of Equation (3.88) is of the form:
(3.89) ![]()
where:
(3.91) ![]()
The time to reach a specified speed v can be obtained from following relation:
The travelled distance S, in terms of vehicle speed is given by:
(3.93) ![]()
In order to apply the results to the motion of a vehicle with a number of gears, consider that the torque-speed diagram of the power source is as shown in Figure 3.47. Let us assume that the vehicle accelerates up to the speed of ![]() at each gear. In other words, when in first gear the rotational speed reaches
at each gear. In other words, when in first gear the rotational speed reaches ![]() , the gear is shifted to gear 2. The same applies for the 2–3 gear and so on.
, the gear is shifted to gear 2. The same applies for the 2–3 gear and so on.
Figure 3.47 Torque-speed diagram of a constant torque power source

The maximum speed at each low and middle gear is when the engine rotational speed is ![]() :
:
But this situation for high gears can only happen if the balance of forces is also consistent. The force balance for a high gear nH is:
(3.95) ![]()
which results in:
This result according to Equation (3.90) is simply equal to β and is only valid if the associated engine speed is less than the maximum speed. Therefore the smaller of results obtained from Equation (3.94) and the value of β must be used. The travel time for each gear is calculated from Equation (92), noting that:
(3.97) ![]()
The total travel time at the end of gear number N (to reach ![]() ) is:
) is:
(3.98) ![]()
A similar approach must be used for the vehicle speed and travel distance at the end of gear number N.
The maximum power for each gear is:
(3.99) ![]()
With the assumption of no power loss in the driveline, the maximum power for all gears at the maximum speed will be equal, as the power at the maximum speed points is:
If the maximum speed at a particular gear is less than the maximum speed ![]() , the actual speed must be used in Equation (3.100).
, the actual speed must be used in Equation (3.100).
Example 3.6.1
A diesel engine produces a constant torque of 220 Nm from 1200 to 2800 rpm. A vehicle of mass 2000 kg, with tyre rolling radius of 0.3 m, rolling resistance coefficient 0.02 and overall aero coefficient of 0.5, accelerates on a level road from the rest in its lowest gear with overall ratio of 20 and then shifts successively up to gear 4 with overall ratio of 5. Each successive gear ratio is 0.63 times the previous gear ratio.
In reality, the clutch slip at gear 1 allows the engine speed to differ from corresponding values of the vehicle speed. For the sake of simplicity, however, assume the engine speed at gear 1 can start from zero.
1. Calculate the speeds and travel distances at the end of constant torque curve and the times when these speeds are reached.
2. Plot the variations of engine speed, vehicle acceleration, speed and distance with time.
Solution
A MATLAB program facilitates the solution and with straightforward steps the required outputs can be obtained. The program listing is given in Figure 3.48.
a. Solution to this part is performed in the first loop of program for each gear. At first, the vehicle maximum speed at each gear is calculated as the minimum of kinematic relation (Equation (3.94)) and β. These values are then used to determine the time values and distances travelled at the end of each gear engagement phase. The results for time, velocity and distance at the end of each gear are:
| Time (s): | 0.6164 1.2014 2.7221 6.8327 |
| Velocity (m/s): | 4.3982 6.9813 11.0787 17.5929 |
| Distance (m): | 1.3557 4.6844 18.4198 77.4139 |
b. Once the minimum and maximum of each variable are available, the intermediate points can be determined in a second loop. The loop is designed to calculate 100 points for each variable. The results are plotted in Figures 3.49–3.52.
Figure 3.49 Variation of engine speed
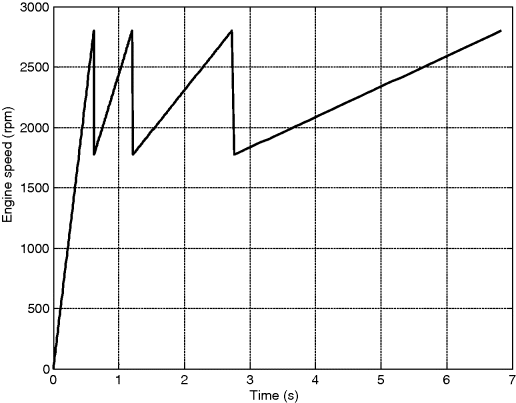
Figure 3.50 Variation of vehicle acceleration

Figure 3.51 Variation of vehicle speed

Figure 3.52 Variation of vehicle travelled distance

From Figure 3.50 it can clearly be seen that the acceleration at each gear is almost constant and the variation of velocity is almost perfectly linear. This is due to the low velocity regime in which the aerodynamic force does not play an important role.
3.6.2 Numerical Solutions
For the constant torque equation of motion 3.87, a closed form solution was presented in the previous section. In order to obtain a numerical solution, the method of Section 3.5.5 can be applied with some modifications. The main difference in this case is that the integration must take place at each gear separately. To this end the process for each gear must be repeated, thus there should be a loop with repetition up to the number of gears. The initial conditions at each gear (except gear 1) will be the final results at the previous gear. Another issue in this case is the need for iteration to find the time at which a gear is engaged. This is because the integration at each gear is taking place between two specified times t0 and tf. However, the final integration time tf is related to the maximum speed of the constant torque phase.
A sample MATLAB program is provided in Figure 3.53 in which a loop is considered for four gears (i = 1: 4), and the iteration loop is done within a ‘while-end’ statement. The function associated with the main program contains the differential equation (3.87). In practice, gearshifts will take some time; nevertheless no delay for gearshifts is included in the program in this case. It would only require a simple modification to include it.
Figure 3.53 MATLAB programs main_t.m and const_trq.m function

Example 3.6.2
For the vehicle of Example 3.6.1, use the numerical integration technique and plot the variation of velocity versus time with successive gearshifts.
Solution
The result of the inclusion of the vehicle data and running the program is illustrated in Figure 3.54. It is identical to Figure 3.51 that was obtained using closed form formulas.
Figure 3.54 The variation of vehicle speed with time

3.7 Fixed Throttle Performance (FTP)
The general longitudinal motion of a vehicle involves the driver's throttle inputs and gearshifts, both of which will have influential effects on the overall performance of the vehicle. Taking into consideration the different inputs from the driver requires a more complicated analysis. One special case in driving already discussed is the full throttle acceleration. In this particular case, the torque-speed characteristics of the engine are usually available and can be used in the analysis. An extension to this case is the fixed throttle acceleration in which instead of 100% throttle input, a fixed part throttle is the input from the driver.
3.7.1 Gearshift and Traction Force
When the throttle is fixed, the quasi-steady engine torque-speed diagram is available and from the MT engine formula (Section 2.6), the part throttle torque-speed relation can be obtained. Full throttle acceleration will be a special case for the analysis and of course, the full throttle curve is usually available for most engines, and analysis can be performed more easily for this case. The engine torque at a constant throttle can be written as:
(3.101) ![]()
Assuming no driveline losses (see Section 3.13), the torque at the driving wheels is:
(3.102) ![]()
where ng and nf are the transmission and final drive gear ratios. According to the free body diagram of the driving wheel shown in Figure 3.55, the tractive force is related to the wheel torque by ignoring the wheel rotational dynamics (Section 3.10):
Figure 3.55 The driving wheel

This tractive force must be produced by the tyre through the generation of slip between the tyre and the road, provided that sufficient friction is present at the surface. For the time being it will be assumed that the tyre is able to generate the necessary tractive force.
In a certain gear, the tractive force will change according to Equation (3.103) with the engine's rotational speed. With the kinematic relation between the engine speed and the wheel rotational speed, the tractive force at each gear can be related to the wheel rotational speed. A no-slip approximation is considered for the tyre rotation in order to directly relate the forward speed of the wheel centre v to its rotational speed by the simple relation:
or,
(3.105) ![]()
Therefore, the tractive force at each gear can be directly related to the forward speed of the wheel that is equal to the forward speed of vehicle when no slip is present. At different gear ratios, by using Equations (3.103) and (3.104), different tractive force-speed diagrams can be constructed.
Example 3.7.1
The gear ratios for a five-speed transmission are 4, 2.6, 1.7, 1.1 and 0.72 and the vehicle final drive ratio is 4. The effective radius of the driving wheels is 27 cm.
The full-throttle engine torque-speed is described by following equation:
![]()
a. Plot the engine torque-speed and power-speed diagrams.
b. At each gear ratio for different engine speeds, find the corresponding values of v and FT and plot FT-v diagram for all gears in a single figure.
Solution
a. It is a simple task to vary the engine speed ωe and determine the corresponding Te values. The result is plotted in Figure 3.56.
b. The tractive force FT(ωe) and vehicle speed v(ωe) can be determined by using Equations (3.103) and (3.104) at any given gear ratio for the different values of engine speed ωe. The variation of FT versus v for each gear can then be plotted. The results for all gears are shown in Figure 3.57. In each gear the tractive force follows the pattern of the engine torque-speed variation, and when the gear is upshifted, the force magnitude reduces sharply and the curve flattens.
Figure 3.56 WOT engine torque and power variation of Example 3.7.1

Figure 3.57 Tractive force versus speed at different gears

3.7.2 Acceleration, Speed and Distance
The difference between the tractive force of the vehicle FTi in a typical gear number i with the resistive force FR at a specific speed v will generate the acceleration:
This equation can be represented by Figure 3.58 for a specific gear ratio. It is clear that the excess force at each gear varies with vehicle speed and the resulting acceleration will also vary with speed. It is also important to note that at low gears the excess force is greater (see Figure 3.57) and produces greater accelerations.
Figure 3.58 The vehicle acceleration is the result of excess force

In order to find the velocity, Equation (3.106) can be integrated with respect to time. In differential form it reads:
Theoretically this is a differential equation that can be integrated by separation of variables. Based on our experience in the previous cases in which the tractive force had simpler forms, and also owing to the fact that the engine torque-speed variation usually takes a complex form, looking for a universal closed form solution is not attractive. Nonetheless, there are cases in which the engine torque-speed variation has a relatively simple form and the integration of Equation (3.107) is possible. In general, however, a numerical solution would be preferred.
In order to solve Equation (3.107) numerically, it can be written as a time-based differential equation of the form:
(3.108) ![]()
Since v(t) is obtained through the numerical integration, FTi(v) and FR(v) of Equation (3.106) are available at each instant. The main MATLAB program for this case is similar to the main program of Section 3.6.2, but its accompanying function will differ to some extent. In the main program a similar inner loop for the acceleration up to a certain engine speed (ωem) will be present. Also, an outer loop for gear selection is present as shown in Figure 3.59. It is assumed that the shifts are performed instantly and no delay is involved.
Figure 3.59 Main MATLAB program for fixed throttle performance

The function for this case must include the instantaneous engine torque and tractive force calculations. For this reason the engine torque-speed formula is needed in the function statements. This information can be shared with the function through the ‘global’ statement. In the program of Figure 3.60a second order polynomial is assumed for the torque-speed of engine (see Example 3.7.1) and its coefficients are given in a vector ‘p’ that is shared between the main program and the function.
Figure 3.60 MATLAB function for fixed throttle performance

Example 3.7.2
For a vehicle with mass of 1000 kg, rolling resistance coefficient of 0.02 and overall aerodynamic force coefficient of 0.35, use the transmission and engine information given in Example 3.7.1.
a. Plot the variation of vehicle speed and distance versus time.
b. Plot the variation of acceleration versus time.
Solution
Enter the necessary information such as p, nf, m, fR, c and rw and the main program will be ready for run. No change is needed to the function. The results obtained for speed and distance are given in Figure 3.61.
Figure 3.61 Results for velocity and distance of Example 3.7.2

It is worth noting that at the highest gear (gear 5), as the resistive forces approach the tractive force value, the acceleration approaches zero. The theoretical final speed is, therefore, attained after a substantial time. For this reason, the integration time ‘tf’ needs be set to large values. This in turn will increase the integration time. Thus, in this example, a tf = 60 seconds is chosen, for which the final speed (a little above 50 m/s) is not actually reached.
The values of vehicle acceleration are calculated inside the ‘function’ and not in the main program. For this reason the data is lost when it returns to the main program. In order to find the acceleration, the best way is to regenerate it within the main program from the values of speed available. A subprogram listing below shows how an inner loop can be constructed at the end of each gear loop to calculate acceleration values:
v=×(:,1);
omega=ni*v*30/rw/pi;
Trq=polyval(p,omega);
Fti=Trq*ni/rw;
acc=(Fti-f0-c*v.^2)/m;
figure(2)
plot(t, acc')
hold on
clear acc
Including the subprogram in the main program will generate the plot of Figure 3.62.
Figure 3.62 Acceleration performance of Example 3.7.2

3.7.3 Shift Times
When a gear should be shifted depends on several factors. In automatic transmissions the decision is made by the controller and in manual transmissions by the driver. In the latter case, the gearshift is performed according to the individual driving style and the engine speed at which the gear is shifted differs for different drivers. In theory, when a new gear is engaged, the vehicle can accelerate up to the limit speed of the engine. In practice, however, this is not the case and every driver changes the gear based on their style of driving at speeds below the maximum. Gearshift issues are discussed in more detail in Chapter 4.
In most transmissions, and especially in manual transmissions, there is an engine torque interruption during a shift. This will eliminate the tractive force and with FT absent, only resistive forces will act on the vehicle during the shifts and negative accelerations will result (see Figure 3.30). This duration is different for different drivers and even for different gears. In the previous analysis, immediate gearshifts with no torque interruption were assumed. In order to consider the torque break involved in the gearshifts, an inner subprogram should be included in the existing MATLAB program. The main idea is to set the tractive force to zero during this ‘tdelay’ time. This is left to the reader as an exercise to apply the necessary changes to the MATLAB program and generate results that are depicted in Figures 3.30 and 3.63 for the vehicle acceleration, speed and distance (see Problem 3.15).
Figure 3.63 Effect of including shift delays

3.7.4 Maximum Speed at Each Gear
The maximum speed at each gear may be reached in two different situations: kinematic limit or dynamic balance point. The kinematic limit is when the tractive force exceeds the resistive force and vehicle can still accelerate but the engine cannot turn faster. A good example is acceleration in low gears at which the tractive force is very high and the resistive forces are very low and the excess force is used to accelerate the vehicle but the engine speed can reach very high values close to its cut-off point. At this point an upshift is needed, as the forward speed is still low but driveline kinematics imposes a constraint on the motion. Upshifts will allow higher kinematic vehicle speeds but at the same time lower tractive forces and reduced accelerations will occur. In high gears, due to high speeds and low traction forces, there are points at which the resistive force can balance the tractive force. These points, called dynamic balance points, represent steady states for the vehicle motion – even though the vehicle may not remain in this steady condition for long.
Figure 3.64 summarizes these issues for an example vehicle on a level road. At low gears (1, 2 and 3) as seen, there are excess tractive forces at the points of engine maximum speeds. These points are kinematic limit points at which the gear must be shifted. At the highest gear (gear 5), the resistive force grows with speed and at a certain point equals the tractive force. At this point, the dynamic balance is met and vehicle attains its final speed. At gear 4, too, it is sometimes possible to have a dynamic balance point, for example on a slight slope. Also in Figure 3.64 an intersection point would be possible for gear 4 if a slightly higher engine speed were attainable.
Figure 3.64 Definitions of kinematic limit and dynamic balance points

At the dynamic balance points where the tractive and resistive forces balance, the equation of motion simply is:
This equation will be satisfied at a certain forward speed v* and a corresponding engine speed of ω*. At each gear ni, Equation (3.109) should be solved for v* where the steady state could be achieved (e.g. high gears), but the speed of engine at v* must be smaller than the engine limit speed ![]() , that is:
, that is:
(3.110) ![]()
This process should usually be performed numerically by modifying the existing MATLAB program. However, for some cases where the engine torque-speed relation at a fixed throttle is available, a mathematical solution can also be obtained. Let the engine torque-speed formula be written in the form:
(3.111) ![]()
Then the solution is obtained from:
Example 3.7.3
For the vehicle in Example 3.7.2, investigate the existence of dynamic balance points on a level road for gears 3 and 5.
Solution
The engine torque-speed formula is:
![]()
In which ![]() is in rpm. This relation in general can be written as (
is in rpm. This relation in general can be written as (![]() in rad/s):
in rad/s):
![]()
Substituting in Equation (3.112) and after some manipulations, one finds:
![]()
in which:
![]()
![]()
t1, t2 and t3 after conversion to rad/s are found to be 4.1 × 10−4, 0.3027 and 55.24 respectively. For gear 3 the overall ratio is n3 = 1.7 × 4 = 6.8 and k1 and k2 are:
![]()
Solving the quadratic equation for ![]() results in:
results in:
![]()
With the positive answer, the engine speed must be checked:
![]()
This is not possible at all! For gear 5, the same procedure will result in:
![]()
which is fine.
3.7.5 Best Acceleration Performance
A question is often raised of how to perform gearshifts to get the best acceleration performance. In practice, achieving higher velocities in less time means higher average accelerations. From a mathematical view point, velocity is the time integral of acceleration:
In a graphical representation, the area under the acceleration curve versus time gives the velocity. For a fixed throttle performance (FTP) (e.g. WOT), the acceleration behaviour of the vehicle is determined with the gearshifts. To see the effect of the choice of the shift point, consider the acceleration performance of a typical vehicle at two different shift speeds shown in Figure 3.65 in an acceleration-speed diagram. Solid lines represent a shift carried out at a certain engine speed where the traction force is equal at two consecutive gears (corresponding to the point of intersection of traction curves of the two gears), whereas the dashed lines belong to a shift at lower engine speeds.
Figure 3.65 Effect of shift rpm on the acceleration performance in a-v plot

It is clear that the area under the solid lines (A1) is larger than the area under the dashed lines (A2). Also if the shift speeds of the dashed lines are further reduced, the area A2 will also be decreased. Therefore, as the maximum area is A1 it can be concluded that the concept of gearshifting at the points of intersection with consecutive traction curves, produces higher accelerations. According to Equation (3.113), the area under the acceleration-time equals the speed of the vehicle at the end of the acceleration phase and thus for the area A1 the speed is maximum.
In the acceleration-time plot, the acceleration curve of each gear will not remain identical when the shift speed varies. This can be seen in the plots of Figure 3.66 for two different shift speeds of 5500 rpm (solid lines) and 4000 rpm (dashed lines). Nonetheless, the area under the acceleration-time curves is still larger overall as the shift rpm is increased. In order to further clarify the effect of the shift rpm, the time to attain a specific speed is a good measure as it indicates the overall acceleration performance. Figure 3.67 shows the velocity-time curves for four different shift rpm 4000, 4500, 5000 and 5500. It is clear that at any speed (a horizontal line), the time to reach that speed is smaller for larger shift speeds. This is shown for speed of 30 m/s (108 km/h). The time to reach the specified speed reduces in a non-linear fashion for example from 4000 to 4500 rpm the time reduces around 3 seconds, whereas from 5000 to 5500 rpm it is reduced around 1 second.
Figure 3.66 Effect of shift rpm on the acceleration performance in a-t plot

Figure 3.67 Effect of shift rpm on reduction of time to attain a certain speed

It should be noted that the overall appearance of the acceleration and speed curves are dependent on the transmission gear ratios as well as the vehicle physical properties. In changing any of the parameters, the details of the figures presented above will change, nevertheless the overall behaviour is similar for different configurations.
3.7.6 Power Consumption
The power requirement during the vehicle motion comprises two parts: power to accelerate; and power to overcome resistive forces. The total power used to move the vehicle at a specified speed v(t) is:
(3.114) ![]()
The tractive force FT can be written as:
(3.115) ![]()
Therefore:
The first term Pa is the power needed for the vehicle acceleration and the second term PR is the power to overcome the resistive forces. Equation (3.116) indicates that the power is an instantaneous quantity that varies during the vehicle motion according to the variations of acceleration or speed. It also signifies that for greater acceleration more power is needed.
During the vehicle motion with a fixed throttle input (e.g. WOT), the variation of power with speed at different gears is shown in Figure 3.68. As the acceleration is higher at lower gears while the speed is low (low resistive forces), the main part of power is used for accelerating and only a small portion is used for resistive forces. Upshifting reduces the acceleration where the speed is high and the resistive forces play an important role; as a result, the share of the power to overcome the resistive forces increases at higher gears. At the final speed (where the acceleration is zero), the total power is devoted to overcoming only the resistive forces.
Figure 3.68 A power-speed diagram for WOT acceleration

The time history of power variation at different gears is shown in Figure 3.69 for a full throttle acceleration with gearshifts at the maximum power point. When a gear is upshifted, the acceleration will drop and as the resistive forces remain unchanged at the specific speed, the power demand will be reduced. In less aggressive driving, the acceleration in low gears often ends in lower engine speeds, and as a result, the power use in low gears is usually much lower than the maximum engine power. It should be noted that the selection of transmission gear ratios can change the results by moving the points in the plots. The effect of gear ratios on the power curves, especially at high gears, will be discussed in Chapter 4.
Figure 3.69 Typical power-time diagram for fixed throttle performance

3.8 Throttle Pedal Cycle Performance (PCP)
In real driving situations, the accelerator pedal is depressed by the driver according to driving requirements. In a vehicle equipped with a manual gearbox, the pedal input even in a high acceleration performance is not kept constant, since at least during gearshifts it is necessary to release the pedal and press it once again. In normal driving conditions, the pedal input varies in different driving situations. Thus in the study of vehicle longitudinal performance, one category of problem is when the input variable is the engine throttle and the output is the resulting vehicle motion.
Drivers' pedal inputs can vary largely owing to diverse driving situations and driving habits. The time history of the pedal variations with time may look like that of Figure 3.70 in which the pedal input varies between 0 (fully closed) to 100 (wide open).
Figure 3.70 A typical time history for accelerator pedal inputs (a pedal cycle)

In order to simulate a driving condition under pedal inputs, the engine torque-speed- throttle characteristics will be necessary. This can be in the form of look-up tables or the MT engine formula introduced in Chapter 2.
Moreover, during driving, the gearshifts are also carried out according to the vehicle and engine speeds and driver's selection. In order to include the pedal inputs in the MATLAB programs, it is necessary to do it inside the ‘function’ and not inside the main program. The reason is that the pedal inputs are time-dependent and when ‘ode’ is called inside the main, all integration steps are performed by the ‘function’ and the final results are returned. The following example is designed to illustrate this concept.
Example 3.8.1
The MT engine formula for a passenger car engine is given in Equation (3.2) together with the information of Tables 3.1 and 3.2. For a throttle pedal cycle shown in Figure 3.71, use the vehicle information of Example 3.7.2 and plot the variation of vehicle speed with time. Ignore time delays during the gearshifts.
Figure 3.71 Pedal cycle of Example 3.8.1

Solution
The programs shown in Figure 3.72 provide the details of instructions for this case. In the main program, inputs are given and information is passed to the ‘function’ by the ‘global’ statement. The tricky part is to specify the gear that is engaged. It is assumed each gear is engaged up to the maximum engine speed and then upshifted. It should be noted that in this program the downshifts are not taken into consideration otherwise another loop should be defined to check for the lower limit of the engine speed and determine the downshifts.
Figure 3.72 MATLAB programs for Example 3.8.1: (a) Main and (b) the function

The output results are shown in Figures 3.73a and 3.73b. From the time history of vehicle acceleration, the gearshift points to gears 2, 3 and 4 are clear. Note that the acceleration calculations are similar to those explained in Example 3.7.2.
Figure 3.73 (a) Time histories of velocity and distance for Example 3.8.1. (b) Time history of acceleration for Example 3.8.1

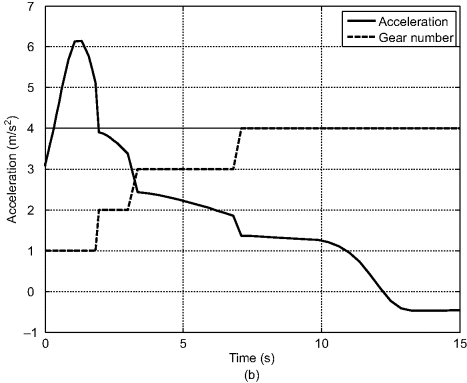
When the vehicle accelerates, the wheels, rotating shafts and even the engine accelerates. In other words, in addition to the vehicle body (mass) which needs tractive force to develop its kinetic energy, the rotating inertias also need torques in order that their corresponding kinetic energy is developed. The demanded power produced by vehicle engine is therefore divided and the part that propels the vehicle body is reduced due to the share taken by rotating masses. This will reduce the vehicle acceleration compared with the case with no rotating masses. Consider the torque balance from the engine to the driving wheels through each of the torque-consuming driveline components as shown in Figure 3.74.
Figure 3.74 Main components of the vehicle driveline
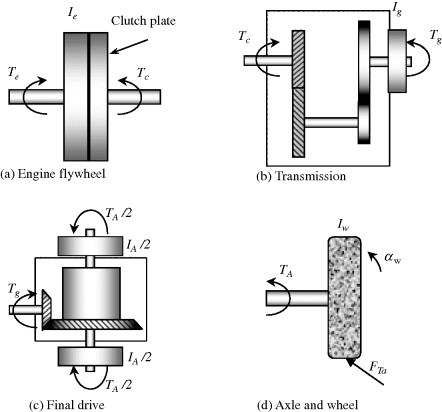
The application of Newton's Second Law to the rotational motion of the engine output with regard to Figure 3.74a reads:
(3.117) ![]()
This means the clutch torque Tc is what is left from the engine output torque Te after accelerating the relevant inertias Ie grouped at the engine output shaft (including the engine rotating masses, flywheel, clutch assembly, etc.) with angular acceleration ![]() . In Figure 3.74b it is assumed that the inertias of all rotating masses related to the gearbox input and output are summed up as a single inertia Ig at the output shaft of gearbox. Before this inertia, the torque on the output shaft simply is the input torque multiplied by the gearbox ratio ng:
. In Figure 3.74b it is assumed that the inertias of all rotating masses related to the gearbox input and output are summed up as a single inertia Ig at the output shaft of gearbox. Before this inertia, the torque on the output shaft simply is the input torque multiplied by the gearbox ratio ng:
(3.118) ![]()
The output torque after the inertia Ig, therefore, is:
(3.119) ![]()
where ![]() is the angular acceleration of the output shaft of gearbox. For the final drive, according to Figure 3.74 it is assumed that there is only a single drive axle and all the rotating inertias related to it are collected as a single inertia IA at the output side of the differential. The governing equation in this case will be:
is the angular acceleration of the output shaft of gearbox. For the final drive, according to Figure 3.74 it is assumed that there is only a single drive axle and all the rotating inertias related to it are collected as a single inertia IA at the output side of the differential. The governing equation in this case will be:
(3.120) ![]()
![]() being the angular acceleration of the final drive output shaft. Finally, the torque output from the final drive reaches the wheel with an overall inertia IW rotating with the wheel speed
being the angular acceleration of the final drive output shaft. Finally, the torque output from the final drive reaches the wheel with an overall inertia IW rotating with the wheel speed ![]() and accelerates it. According to Figure 3.74d, the balance of torques around the wheel centre results in:
and accelerates it. According to Figure 3.74d, the balance of torques around the wheel centre results in:
(3.121) ![]()
where FTa is the tractive force available at the tyre–road interface. Since all the shafts are connected, their rotational speeds (or accelerations) are related to the engine rotational speed (acceleration), i.e.:
(3.122) ![]()
(3.123) ![]()
Combining all equations results in:
This is the force propelling the vehicle, whereas in the previous discussions the tractive force was simplified as:
Now, for the longitudinal motion of the vehicle under the action of tractive and resistive forces, the equation of motion reads:
where a is the longitudinal acceleration of the vehicle. FTa is produced by the tyre through slip generation at contact patch. With slip at the tyre–road interface, the rotational speed of the tyre will differ slightly from the speed of wheel centre divided by the tyre rolling radius (see Section 3.10). Accepting a small error, the no-slip condition for the tyre will be assumed and that allows the rotational acceleration of the wheel ![]() to be directly related to the vehicle acceleration a:
to be directly related to the vehicle acceleration a:
Substituting Equations (3.124), 3.125 and (3.127) into Equation (3.126) yields:
(3.128) ![]()
which can be written as:
with:
From Equation (3.130) it is clear that meq is always larger than m, therefore the vehicle acceleration in the real case will be smaller than that obtained in previous analyses without accounting for the rotating masses. In other words, when the effect of rotating masses is taken into consideration, it is like considering an extra mass for the vehicle. Alternatively, when no rotating masses are considered, a larger tractive force will be available. Figure 3.75 conveys this concept by assuming a single flywheel equivalent to all rotating masses, attached to the driving wheels.
Figure 3.75 Concept of rotating masses

In general, meq can be written as:
(3.131) ![]()
where mr is regarded as the equivalent mass of the rotating inertias:
In Equation (3.132) the inertias are defined as:
![]() is the sum of all inertias rotating with the speed of driving wheels.
is the sum of all inertias rotating with the speed of driving wheels.
![]() is the sum of all inertias rotating with the speed of gearbox output shaft.
is the sum of all inertias rotating with the speed of gearbox output shaft.
![]() is the sum of all inertias rotating with the speed of engine.
is the sum of all inertias rotating with the speed of engine.
It is important to note that the meq has different values at different gears, since ![]() changes with transmission gear ratio ng. Larger transmission ratios will make meq larger (by power 2 of ng). This means in the lowest gear (i.e. gear 1), meq will have the largest value whereas at highest gear (e.g. gear 5) it will have the smallest value. This is working against the requirements of high accelerations at low gears.
changes with transmission gear ratio ng. Larger transmission ratios will make meq larger (by power 2 of ng). This means in the lowest gear (i.e. gear 1), meq will have the largest value whereas at highest gear (e.g. gear 5) it will have the smallest value. This is working against the requirements of high accelerations at low gears.
Example 3.9.1
For a vehicle with information given in Table 3.9 and gear information of Example 3.7.2, compare the terms of Equation (3.132). Also evaluate the ratio meq/m for different gears.
Table 3.9 Data for Example 3.9.1.

Solution
Calculation of the individual terms in Equation (3.132) is straightforward. Let us define the existing terms as:
![]()
The dimensions of each term are kg, thus these terms effectively represent extra masses that are accelerated. The results are summarized in Table 3.10.
Table 3.10 Equivalent masses of Example 3.9.1

As seen from Table 3.10, the effect of terms 1 and 2 altogether is about 6–7% of vehicle mass, whereas the effect of term 3 is something over 70% of the vehicle mass in gear 1 and some 2% in gear 5. The total effect at gear 1 is almost 80% of the vehicle mass. Therefore it is evident that the effect of rotating masses especially at low gears is quite large compared to the vehicle mass itself.
3.9.1 Corrections to Former Analyses
When meq is substituted in the equation of vehicle longitudinal motion it will be of the general form:
(3.133) ![]()
The gear ratio n for a discrete ratio gearbox is a fixed value at a specific gear. For a CVT, however, its value also depends on the speed. Thus, for the two cases of analyses, the following corrections must be made in order that the effect of rotating masses is included.
3.9.1.1 Discrete Gear Ratios
For all cases of constant torque, fixed throttle and throttle pedal cycle, the condition of gear ratio changing during the vehicle motion was discussed. In order to include the effect of rotating masses, the only required change will be the evaluation of the equivalent mass at each engaged gear, as for a particular gear ratio n the equivalent mass ![]() is an unchanging quantity. The method of solution for all cases will be similar once the gear ratio is specified.
is an unchanging quantity. The method of solution for all cases will be similar once the gear ratio is specified.
Example 3.9.2
For the vehicle in Example 3.7.2, investigate the effect of rotating masses on the acceleration of the vehicle. Use the information for rotating masses from Example 3.9.1.
Solution
The inclusion of the equivalent mass in the MATLAB program can be done inside the main loop for the gears in Figure 3.59:
Mr1=Iw/(rw^2);
Mr2=Ig*(nf^2)/(rw^2);
for i=1: length(ng) % Loop for gears
ni=ng(i)*nf; % Overall gear ratio at each gear
Mr3=Ie*(ni/rw)^2;
m=Mr1+Mr2+Mr3+m0;
f0=m0*9.81*fr;
The result is shown in Figure 3.76 for the rotating and non-rotating masses. In gear 1 the difference in acceleration is very large and decreases as the gear number increases. It should be noted that the time of gearshift is also delayed when the rotating masses are included as the engine rpm reaches the shifting rpm later due to lower accelerations.
Figure 3.76 Acceleration results for Example 3.9.2

3.9.1.2 Continuous Gear Ratios
The continuous variation of gear ratio was considered in the Constant Power Performance analysis. The equation of motion for this case when the rotating masses are included reads:
From the kinematic relation (no slip assumption):
but since power is kept constant, there are two different cases:
a. Torque is also constant: for this case, the engine speed must be fixed too, since torque multiplied by speed equals power. If engine speed is a constant ![]() , then for each vehicle speed, say
, then for each vehicle speed, say ![]() :
:
At every instant, the velocity values are determined from the integration of Equation (3.134) and the gear ratio n can be evaluated from Equation (3.135b). It should be noted that this equation will result in large values for n at very low speeds, therefore, an upper limit for n should be imposed in the program.
b. Torque is variable: if the engine torque is variable while the power is constant, it means the engine speed must vary to keep power constant. In this case, Equation (3.135a) is unable to produce a result for n unless the variation of engine speed is known. This will require an additional criterion to change the engine speed in a desired manner (e.g. for fuel economy).
Example 3.9.3
For the vehicle in Example 3.5.4, find the effect of rotating masses on the time history of vehicle speed. Use the information in Example 3.9.1 for the rotating masses. Assume a fixed engine rpm of 500 rad/s and a maximum overall gear ratio of 16.
Solution
The instantaneous value of gear ratio n can be calculated from Equation (3.135b) and equivalent mass calculations from the statements given in Example 3.9.2 can be used in this case too. It should be noted that the described process must be included within the ‘function’ and not inside the main program.
Figure 3.77 compares the effect of including the rotating masses with those of the base case with no rotating masses. It is evident that the vehicle speed is considerably lower when the rotating masses are included.
Figure 3.77 Effect of rotating masses on CPP acceleration performance
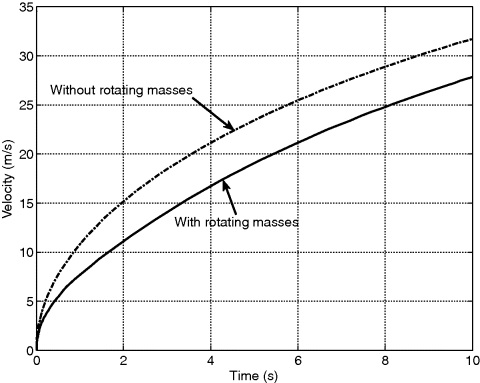
In the foregoing discussions in order to simplify the relation of the vehicle speed to the wheel rotational speed, the driving wheels were assumed to roll without slipping. In reality, however, this is not the case since according to the discussions in Section 3.3, the traction force is produced by the tyre only if longitudinal slip is developed between the tyre and road surface. In fact, in the real driving situation, the process by which the vehicle motion is built up can be described by the flowchart of Figure 3.78. According to this process, the transformation of the wheel torque to the tyre traction force is accomplished through the generation of tyre slip. This process, in addition to the vehicle longitudinal dynamics, involves the wheel rotational dynamics in which the input torque generates the wheel rotational speed. The rotational motion of a driving wheel can be modelled according to the free body diagram of Figure 3.79.
Figure 3.78 The process of the development of vehicle motion from engine torque

Figure 3.79 Free body diagram of a driving wheel

Application of Newton's Second Law to the rotation of a wheel results in:
in which Tw is the wheel torque, ωw is the rotational speed of the wheel and Iw is the polar moment of inertia of the wheel including the other rotating parts (see Section 3.9). From Equation (3.11), the tyre slip is:
Equations (3.136) and (3.137) show the interdependency between the wheel speed ![]() and slip Sx. In fact, Equation (3.136) is a differential equation which, when integrated, leads to values for the wheel rotational speed
and slip Sx. In fact, Equation (3.136) is a differential equation which, when integrated, leads to values for the wheel rotational speed ![]() . To this end, however, Sx must be available beforehand but it is dependent on the wheel rotational speed (Equation (3.137)). With a numerical solution the problem can be resolved by having an initial condition for the vehicle motion, e.g. starting from rest. The wheel rotational speed and vehicle speed are then obtained by simultaneous numerical integration for
. To this end, however, Sx must be available beforehand but it is dependent on the wheel rotational speed (Equation (3.137)). With a numerical solution the problem can be resolved by having an initial condition for the vehicle motion, e.g. starting from rest. The wheel rotational speed and vehicle speed are then obtained by simultaneous numerical integration for ![]() and v of the vehicle. The solution of the differential Equation (3.136) together with Equation (3.137) involves rapid fluctuations in the wheel slip and its rotational speed values. In MATLAB to solve this type of differential equations one must invoke ‘ode15s’ instead of ‘ode45’. There are also other points that must be taken into consideration:
and v of the vehicle. The solution of the differential Equation (3.136) together with Equation (3.137) involves rapid fluctuations in the wheel slip and its rotational speed values. In MATLAB to solve this type of differential equations one must invoke ‘ode15s’ instead of ‘ode45’. There are also other points that must be taken into consideration:
a. In the equation of longitudinal motion, the tractive tyre force Fx is a function of normal load on the tyre and tyre slip Sx (see Section 3.3):
(3.138) ![]()
The Magic Formula could be used for this, for example (see Section 3.3).
b. The problem is sensitive to the wheel speed initial condition and different initial conditions for ωw can lead to different output results for the wheel rotational speed, especially at low speeds. A reliable initial rotational speed assumption for the wheel in a motion starting from rest is 100*eps, which is still a very small value (2.22 × 10−14).
c. In practice, Sx during longitudinal acceleration performance is bounded by the 1 ≥ Sx ≥ 0 range. Mathematically, however, Equation (3.137) can have results outside the range, e.g. Sx > 1 (even very large values) or Sx < 0. In programming, therefore, care must be taken to impose the necessary constraints on Sx to keep it within practical limits.
The programming for this problem is left to the reader and typical speed and acceleration results are given below as a reference. The time history of vehicle speed looks like that shown in Figure 3.80. This figure also shows the equivalent centre of wheel speed that is wheel rotational speed times its radius. It is clear that the equivalent speed must be greater than the vehicle speed due to the wheel slip. The time history of vehicle acceleration is depicted in Figure 3.81 together with the same results for the case with no wheel slip. It is noted that there is a short delay in the response of the vehicle owing to the wheel dynamics. In fact, with the wheel dynamics in effect, the tyre tractive forces build up after the tyre slip is generated.
Figure 3.80 Vehicle and wheel equivalent speeds with wheel dynamics

Figure 3.81 Vehicle acceleration with and without wheel dynamics

So far the vehicle motion was assumed to take place on a level road only for the sake of simplicity. In this section, the effect of motion on a slope will be discussed. It should be noted that the intention is to see what happens to the vehicle performance (e.g. speed or acceleration) when it moves on a sloping road. Another area of interest is to examine the grade capability of a vehicle – which will be discussed in Chapter 4.
The vehicle motion on a slope can be viewed from the following perspectives:
- How will a vehicle accelerate?
- What is the maximum vehicle speed at each gear?
- What is the maximum slope a vehicle can move on at a specified speed?
- What is the vehicle performance on a road of variable slope?
The FBD of a vehicle on a sloping road was shown in Figure 3.36 with all forces acting on it and the governing equation of motion was shown to be of the form:
(3.139) ![]()
Depending on the nature of the tractive force FT the solution method will be different as it was discussed in previous sections.
3.11.1 Constant Power Performance (CPP)
For the constant power case, there is no concern about the gear ratios and with the inclusion of the angle θ in the equation of motion, the performance can be analyzed during vehicle acceleration. The acceleration performance and maximum speed of vehicle on the slope will obviously be reduced due to the increase in resistive forces. The MATLAB program of Figure 3.39 already includes the slope terms and can be used without any change. In order to find the maximum slope on which the vehicle can move with a specified speed, the same MATLAB program for finding maximum speed can be used. In fact, with an iteration procedure the input slope can be varied until the specified maximum speed is reached.
Example 3.11.1
For the vehicle in Example 3.5.2, obtain the time histories of velocity and acceleration for slopes of 0, 10 and 20 degrees.
Solution
Using the MATLAB program of Figure 3.39 for the specified slopes will produce the results shown in Figure 3.82.
Figure 3.82 Results of Example 3.11.1
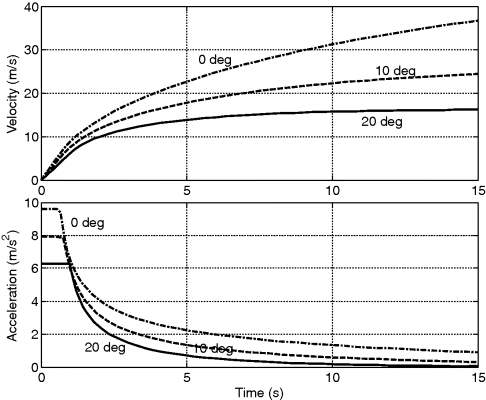
3.11.2 Constant Torque Performance (CTP)
In this case, the gearshifts occur and it is necessary to examine if the vehicle can ascend a slope in a certain gear. In each gear, therefore, there is a certain maximum slope that vehicle can move at a constant speed. In order that the vehicle can maintain the speed in a specific gear ni right after an upshift, the force balance must be positive at the time of gearshift, i.e.:
where:
(3.141) ![]()
and ![]() is the maximum speed of previous gear prior to the gearshift. If Equation (3.140) is not satisfied at gear i, the vehicle cannot keep the final speed of previous gear and either a lower maximum speed is achieved or a downshift to a lower gear is required. The maximum achievable vehicle speed in each gear ni can be written as (Equation (3.96)):
is the maximum speed of previous gear prior to the gearshift. If Equation (3.140) is not satisfied at gear i, the vehicle cannot keep the final speed of previous gear and either a lower maximum speed is achieved or a downshift to a lower gear is required. The maximum achievable vehicle speed in each gear ni can be written as (Equation (3.96)):
provided that the term in the parenthesis is positive – otherwise gear ni cannot be maintained and a downshift would be necessary. In addition, the resulting value from Equation (3.142) must be less than or equal to the kinematic speed limit:
In fact, the minimum of the two results obtained from Equations (3.142) and (3.143) is the maximum speed in that gear. The required changes for the inclusion of slopes in the MATLAB programs are straightforward.
Example 3.11.2
For the vehicle in Example 3.6.2, plot the time variation of velocity for successive gearshifts at slopes 0, 5 and 10 degrees.
Solution
Inclusion of slope in the calculations is simply done by replacing ‘f0’ in Figure 3.53 with:
![]()
The result of running the program is depicted in Figure 3.83. It is clear that the vehicle can accelerate even in gear 4 on the slopes of 0 and 5 degrees, whereas on the 10-degree slope the gearshift from 3 to 4 will result in a negative acceleration that eventually may need a downshift to 3 again. This can be seen by examining Equation (3.140) as the results given in Table 3.11 indicate that on a 10-degree slope, a gearshift to 4 results in a negative force balance which means in this gear the vehicle will decelerate.
Figure 3.83 Results of Example 3.11.2

Table 3.11 Force balance (Equation (3.140)) over slopes (N).

3.11.3 Fixed Throttle (FT)
For this case too, the concept is similar to those discussed in previous sections and the force balance condition for any gear to maintain a positive acceleration after an upshift on a slope is:
where ![]() is the engine torque at a given throttle input θ and at engine rpm ωi immediately after shifting to ni. If this condition is not satisfied for a gear ni, the resultant force in the direction of motion will be negative after an upshift, and a downshift might be necessary if the engine speed is reduced to a low value ωL. A steady state maximum vehicle speed is also attainable for those gears not satisfying Equation (3.144) but at a lower value than that of the previous gear. In any case, the constraint for the engine speed (Equation (3.143)) should not be violated.
is the engine torque at a given throttle input θ and at engine rpm ωi immediately after shifting to ni. If this condition is not satisfied for a gear ni, the resultant force in the direction of motion will be negative after an upshift, and a downshift might be necessary if the engine speed is reduced to a low value ωL. A steady state maximum vehicle speed is also attainable for those gears not satisfying Equation (3.144) but at a lower value than that of the previous gear. In any case, the constraint for the engine speed (Equation (3.143)) should not be violated.
Example 3.11.3
Repeat Example 3.7.2 for slopes of 5 and 10 degrees. Also evaluate the force balance of Equation (3.144) to show which gear can maintain a positive acceleration.
Solution
The inclusion of slopes in the MATLAB program is similar to the previous example and the time histories of velocity and distance for the three cases are presented in Figure 3.84. On the flat road all the gears generate positive accelerations. On the 5-degree slope the fifth gear cannot maintain a positive acceleration and on a 10-degree slope even the fourth gear has similar problems so that gear 5 is not engaged. The results of Equation (3.144), summarized in Table 3.12, are produced at the maximum engine torque and support those of Figure 3.84.
Figure 3.84 Time histories of velocity and distance for Example 3.11.3

Table 3.12 Force balance (Equation (3.144)) over slopes (N).

3.11.4 Variable Slopes
If the vehicle motion involves several piecewise-constant slopes, the solution can be divided into several solutions for each slope. The initial conditions for every slope are the final results of the previous slope. In general, the slope can be expressed as a varying elevation-distance function and it must be defined inside the MATLAB ‘function’.
Example 3.11.4
The vehicle of Example 3.11.3 starts accelerating from rest and just before gearshift to 5 enters a slope of 10 degrees and continues with gear 4. Knowing that a downshift must be carried out when the engine speed reduces to 2000 rpm, determine the distance travelled on the slope before a downshift to gear 3 is necessary.
Solution
This problem can be solved in two parts. In the first part, the vehicle motion on a level road is considered and its speed before upshift to gear 5 can easily be obtained (see Example 3.7.2). The result is 35.343 m/s. The second part is the vehicle motion on a 10-degree slope at gear 4 with this initial speed. The distance up to the point when the engine speed reduces to 2000 rpm is the answer. The MATLAB program of Figure 3.59, modified to include the slope, needs a small change in the integration loop as shown in Figure 3.85. The distance travelled is found to be 1555 m after 70 seconds on the slope, when the speed is 46.3 km/h and the engine speed is 2000 rpm.
Figure 3.85 Changes to the MATLAB program for Example 3.11.4

Vehicle coast down is a condition in which the transmission is disengaged (gear in neutral) and the vehicle is left to roll freely from a particular speed and come to a stop under the action of the resistive forces. A coast down test is very useful when measuring the characteristics of resistive forces acting during vehicle motion. On a level road, the resistive forces comprise the driveline rotational frictions, the rolling resistance and the aerodynamic force. From a coast down test, the time history of vehicle speed can be obtained. In order to exclude the effects of air movements on the results, the tests are usually performed in still, no-wind air conditions. The mathematical modelling of vehicle motion previously developed can be applied to this type of vehicle motion with no motive force from the prime mover and the gradual deceleration of the vehicle under the action of the resistive forces only. The equation of longitudinal motion in a coast down situation will be simpler owing to the absence of the tractive force:
in which FRR is the rolling resistance force and the term cv2 is the aerodynamic force. If the time history of the vehicle speed is available, the two unknowns can be determined. However, the solution depends on the nature of the resistive forces especially the rolling resistance that can be considered a constant or as a function of speed. These will be considered in following sections.
3.12.1 Constant Rolling Resistance
Assuming a constant rolling resistance force is a common practice in many cases, i.e.:
(3.146) ![]()
From the time history of vehicle speed it is possible to determine the rolling resistance coefficient fR and aerodynamic coefficient c.
3.12.1.1 Simple Model
With only a simple test we can estimate the ‘F0’ and ‘c’ values. This test consists of two high speed and low speed parts. Two sets of data are recorded at high speed and low speed cases. Each set consists of an incremental velocity change defined as vH1 and vH2 at high speed and vL1 and vL2 at low speed. The incremental velocity can be as small as 5 km/h. The time increments over which the velocity increments occur are called ![]() and
and ![]() . The mean velocities at each case are defined as:
. The mean velocities at each case are defined as:
(3.147) ![]()
The mean decelerations at each velocity are defined as:
(3.149) ![]()
The equations of motion (Equation (3.145)) for the low and high speeds can be expressed in terms of the above definitions as:
At low speeds it is quite reasonable to ignore aerodynamic force and Equation (c03-mdis-0173) can be simplified to:
This is an equation suitable for calculating the rolling resistance force. Substituting Equation (3.153) into Equation (3.151) and using Equations (3.148) and (3.150) results in:
(3.154) ![]()
If incremental velocities in both low speed and high speed are taken equal, i.e.:
(3.155) ![]()
then the results for F0 and c simplify to:
(3.156) ![]()
(3.157) ![]()
Example 3.12.1
The coast down test result for a vehicle with mass of 1600 kg is given in Table 3.13. Calculate the rolling resistance force F0 and the coefficient of aerodynamic force c.
Table 3.13 Vehicle coast down test results.
| Speed (km/h) | Time (s) | |
| 1 | 110 | 0 |
| 2 | 100 | 4.1 |
| 3 | 30 | 54.5 |
| 4 | 20 | 64.0 |
Solution
The incremental speeds at low and high speeds are both equal to 10 km/h. Calculations are straightforward; convert speeds to m/s and the results are:
![]()
![]()
3.12.1.2 Analytical Model
For the general coast down case, the equation of motion can be integrated analytically. Equation (3.145) can be written as:
in which:
(3.159) ![]()
(3.160) ![]()
Integration of Equation (3.158) results in:
(3.161) ![]()
In general, at time t0 the speed is v0, but is always possible to take t0 = 0, therefore:
(3.162) ![]()
where:
(3.163) ![]()
If test data for two points, say, points 1 and 2, are available, then:
Equations (3.164) and (3.165) constitute a set of two non-linear equations for the two unknowns e and f. With an iteration technique like MATLAB's ‘fsolve’, the equations can be solved and once e and f are obtained, the aerodynamic coefficient c and rolling resistance coefficient fR can simply be calculated from:
(3.166) ![]()
(3.167) ![]()
An interesting result from this method is the evaluation of vehicle mass from a coast down test. Hence, if a further data point is available, then three equations can be solved for three unknowns e, f and m.
Example 3.12.2
A selection of data recorded in the coast down test for a light duty truck is given in Table 3.14. Use four rows of the table to evaluate rolling resistance coefficient fR, aerodynamic force coefficient c and vehicle mass m. If the frontal area is 2.5 square metres and the air density is 1.2 kg/cubic metre, calculate the drag coefficient.
Table 3.14 Vehicle coast down test results.

Solution
A MATLAB program consisting of a main program and a function as shown in Figure 3.86 is suitable to solve the problem. Four sets of data are needed for the calculation of the unknowns. The following sets are chosen:
a. sets: 1, 3, 5 and 6
b. sets: 1, 2, 4 and 6
c. sets: 1, 2, 3 and 5
d. sets: 1, 3, 4 and 5
The results obtained for all cases are summarized in Table 3.15.
Figure 3.86 MATLAB programs (a) main and (b) function for Example 3.12.2

Table 3.15 Results for Example 3.12.2.

3.12.2 Rolling Resistance as a Function of Speed
In general, the resistive force can be written (see Section 3.4.1.5) in the form of:
The two first terms on the right-hand side represent the rolling resistance force which is considered as a linear function of the vehicle speed. It should be noted that the rolling resistance may also involve a speed-squared term, however, that part will be included in the aerodynamic force. In order that the unknowns F0, fv and c are evaluated, the speed-time history obtained from the test must produce the variation of total resistive force versus velocity. To this end, the basic form of the equation of motion in a coast down test reads:
(3.169) ![]()
Thus by differentiating the time history of vehicle velocity with respect to time, the resistive force versus time will be obtained. If a quadratic curve is fitted to the FR-v data, it will have the form:
from which the unknowns F0, fv and c can be evaluated by a simple comparison of Equations (c03-mdis-0191) and (c03-mdis-0193). It is worth noting that this technique can be applied for powers of speed more than 2. For example, it is possible to include an extra term with a power of 3 for speed v and use the same procedure to obtain the unknown coefficients. The drawback of this method is its sensitivity to the accuracy of test data owing to the differentiation involved in the process. In order to avoid such errors, a more sophisticated non-linear curve fitting techniques must be used.
3.12.3 Inertia of Rotating Masses
At the start of a coast down test, the vehicle has a certain initial velocity and all driveline rotating components have their respective rotational speeds. The total mechanical energy E of the system at the starting instant, therefore, consists of kinetic energies of vehicle body together with those of the rotating inertias:
The second term can be written for the rotating components including wheels, axles, propeller shaft and gearbox output shaft (it is assumed that the gear is in neutral and clutch is disengaged, so the input shaft and gears inside the gearbox are not rotating). Thus:
(3.172) ![]()
in which IwA is the sum of all rotating inertias with the wheel speed and Ip is the sum of those rotating inertias with the speed of differential input shaft (or gearbox output shaft):
Assuming no slip for the tyres, one can write:
(3.174) ![]()
Equation (3.171) thus can be simplified to:
(3.175) ![]()
This energy will be dissipated by the work done by resistive forces acting on the vehicle, until the vehicle comes to a complete stop. The work of the resistive forces is:
(3.176) ![]()
where s is the distance travelled. For the case of a constant rolling resistance force, between any two points 1 and 2, it can be written:
The first integral results:
(3.178) ![]()
in which A1 is the area under the v-t diagram:
(3.179) ![]()
and can be determined from summing up the surface between times t1 and t2. The second integral in Equation (3.177) can be changed to a time domain integral:
(3.180) ![]()
This is the area under the v3-t diagram and can be obtained by processing the original data. Thus the total work of Equation (3.177) is:
(3.181) ![]()
The energy change between any two instants is:
(3.182) ![]()
This must be equal to the work done by the resistive forces within this period:
In Equation (3.183) all parameters are known but Ieq, therefore:
For the speed-dependent rolling resistance assumption, too, a similar procedure can be followed. Also it should be noted that the equivalent rotating inertia of Equation (3.173) does not include the rotating masses with engine speed (gearbox input shaft). If a special coast down test is carried out with the gear engaged in an arbitrary gear with only the clutch pedal depressed, then from the test results the full value of rotating masses as seen on the driving wheels can be determined by the method explained in this section.
Example 3.12.3
Use the information of Example 3.12.2 and calculate the equivalent inertia at the driving wheels of the rotating masses. Tyre rolling radius is 38 cm.
Solution
According to Equation (3.184), information for every two points can be used to determine the equivalent inertia for the rotating masses. If data for any two neighbouring points are used, the result will be those listed in Table 3.16. There are negative values for the inertia which is unacceptable and this reflects errors in the data and inaccuracy of calculations between two adjacent points. The average value from the table is some 1.5 kg m2. A close result can also be obtained if A1 and A2 are the sums of all surfaces from t = 0 to t = 28. The results are:
![]()
Table 3.16 Solution with any two adjacent points.

In the preceding discussions the assumption was made that the driveline system is ideal in such a way that all the power transmitted by the driveline will be delivered to the wheels. In practice, however, every component in the driveline will involve losses due to internal friction. The torque necessary to overcome the friction multiplied by speed of rotation of the component results in the power lost to the friction of that component.
3.13.1 Component Efficiencies
Consider a torque-transmitting component shown in Figure 3.87. The input and output powers are:
(3.185) ![]()
Figure 3.87 A torque-carrying component

Due to the rigid connections between the input and the output (flexibilities are ignored), the output rotational speed is related to the input speed by:
(3.186) ![]()
The input energy is:
(3.187) ![]()
The efficiency of the torque transfer is defined as the ratio of the output to the input energies:
(3.188) 
At constant speed and torque inputs, this simplifies to:
(3.189) ![]()
in which ![]() is the output torque at the ideal (no power loss) condition. Thus, it is concluded that when there is energy loss in a component, the output torque will be reduced with respect to the ideal output torque by a factor smaller than 1, defined as the efficiency of that component, i.e.:
is the output torque at the ideal (no power loss) condition. Thus, it is concluded that when there is energy loss in a component, the output torque will be reduced with respect to the ideal output torque by a factor smaller than 1, defined as the efficiency of that component, i.e.:
(3.190) ![]()
which also leads to:
(3.191) ![]()
The torque loss TL and power loss PL for the component are:
Figure 3.88 shows the ratio of torque loss TL to the output torque To with the variation of efficiency. For efficiencies less than 0.5 the output torque is less than the torque loss (see Equation (3.192)).
Figure 3.88 The variation of the ratio of torque loss to output torque with efficiency

In the above discussions, a constant speed was considered at the time of a constant torque delivery and the dependency of the power loss on the speed of rotation or the value of torque was not considered. In fact, friction in the moving parts is of two different natures: dry and/or viscous. The former is independent of relative speed between the moving parts and once the movement starts, it remains proportional to the load (kinetic friction). Viscous friction, however, is speed-dependent and increases as the relative speed of moving parts increase.
The dry friction is often assumed to be linearly dependent on the load (F = μN). Examples of this type of friction in a driveline are contact friction between gear teeth and friction in bearings. When larger torques are transferred, the contact forces on the gear teeth increase and lead to larger friction forces. The same also goes for bearing loads. Speed-dependent friction is typically due to churning and pumping losses of the lubricant which increase with rotational speed. These losses are not usually affected by the amount of torque that is transmitted. There is also another type of loss that is almost constant, regardless of rotational speed or transmitted torque – sliding friction in seals typically behave this way.
In general, the efficiency of a component, therefore, must be considered to depend on speed and load, i.e.:
(3.194) ![]()
In practice, however, it is a common to assume the efficiency is a constant value. In fact, it is an approximation to the real losses in the drivetrain system. This assumption means that increasing the speed of rotation at a specified torque (power increase) will only increase the power loss in the component (Equation (3.193)) and will not influence the torque loss (Equation (3.192)). Conversely at a specified speed, torque increase will increase both the torque and power losses. As Figure 3.89 summarizes, along a line of a certain torque Ti the torque loss is constant but the power loss increases with speed.
Figure 3.89 Power loss changes with speed and torque

For the vehicle driveline with several components, the wheel torque is:
in which ![]() is the overall efficiency and subscripts c, g, j, d, a and w stand for clutch, gearbox, joint (universal or constant velocity), differential, axles and wheels respectively.
is the overall efficiency and subscripts c, g, j, d, a and w stand for clutch, gearbox, joint (universal or constant velocity), differential, axles and wheels respectively. ![]() is the ideal wheel torque:
is the ideal wheel torque:
It should be noted that the clutch efficiency treatment for the transient phase is different from what is considered here, nevertheless the concept will be similar (see Section 4.5.5).
Example 3.13.1
Repeat Example 3.7.2 assuming the efficiencies of the driveline components are 0.97 for the gearbox, 0.94 for the final drive and 0.90 for the rest of components combined.
Solution
The inclusion of Equations (3.195) and (3.196) in the MATLAB program is a simple task. The component efficiencies must be defined in the main program and the overall efficiency (say ‘etov’) must be shared with the ‘function’ in ‘global’ statement. The tractive force is simply modified to Fti=etov*Trq*ni/rw;. The result of the modified program is compared with those of Example 3.7.2 in Figure 3.90.
Figure 3.90 Effect of efficiencies on the vehicle performance of Example 3.7.2

Example 3.13.2
A vehicle test shows that when the engine torque is 100 Nm, at a certain engine speed, a wheel torque of 1200 Nm is produced. With overall gear ratio of 15, calculate the driveline efficiency and the torque loss.
3.13.2 Torque Flow Direction
The driveline efficiency depends on the direction of torque flow. The foregoing discussion applies to the case when the engine torque is transmitted by the driveline to turn the wheels. In the cases when the accelerator pedal is suddenly released during the vehicle motion on a level road or when vehicle is moving downhill, the energy flow is reversed. In the former case, the kinetic energy of vehicle and turning parts is used to overcome the resistive forces and in the latter case the gravitational force is also helping vehicle motion. In both cases, with engaged gears and zero throttle, the engine will run in its braking regions. Thus, in these cases the efficiency equation must be written the other way round, that is:
in which,
(3.198) ![]()
The notation of using primes in Equation (3.197) emphasizes that in the reverse direction the efficiency is not necessarily the same as the other direction. The torque loss in driveline this time will be:
(3.199) ![]()
3.13.3 Effect of Rolling Resistance
In order to move the vehicle from rest, friction in the driveline must be overcome before the vehicle can start to move. Suppose the vehicle is pushed from rest with the gearbox disengaged until it starts to move. The question is whether or not this amount of force is related to the driveline torque or power loss. In fact, this force is just the rolling resistance force that also includes the non-loaded driveline rolling frictions. Therefore, it should not be confused with the driveline losses during the torque delivery.
The objective of the engine torque is to move the vehicle, but throughout the driveline it overcomes friction, and eventually before turning the wheel, it has to overcome the rolling resistance torque. In other words, the total torque loss in the driveline is the summation of component torque losses TCL and rolling resistance torque TRR:
The output torque used for moving the vehicle is:
Since the rolling resistance is already included in the resistive forces against the vehicle motion, substituting Equation (3.200) in 3.201 is not correct and the rolling resistance term must be excluded. Thus the output torque at driving wheels is:
(3.202) ![]()
For a given overall efficiency ![]() the component torque losses can be evaluated as:
the component torque losses can be evaluated as:
(3.202) ![]()
This is what was previously considered as the total torque loss. It should also be noted that the unloaded torque losses of the driveline have already been considered in the rolling resistance, and the efficiency of the wheel ![]() defined earlier represents only those torque losses in the tyre in addition to rolling resistance torque (e.g. tyre slip).
defined earlier represents only those torque losses in the tyre in addition to rolling resistance torque (e.g. tyre slip).
Example 3.13.3
In Example 3.13.2 the effect of rolling resistance was ignored in determining the efficiency of the driveline. For a rolling resistance force of 200 N and tyre rolling radius of 30 cm, determine the true efficiency.
Solution
The component losses should be calculated. The total torque loss is:
![]()
From Equation (3.200):
![]()
From Equation 3.9:
![]()
This is 4% higher than before.
In this chapter, the basics of vehicle longitudinal dynamics studies were discussed and various forms of the vehicle motion were studied. The tractive force generation by the tyres and its dependence on tyre slip were discussed. The natures of resistive forces against vehicle motion were also described and characterized. The equations of vehicle motion in different forms were developed, starting with the simplest forms and gradually adding other terms.
Closed form analytical solutions were presented where such solutions are available. These forms are helpful for quick estimations of the approximate performance. For more detailed studies, numerical integrations are preferred and several examples using MATLAB programs are provided. Several example problems were worked out in order to facilitate the understanding of the physics of vehicle motion in different cases. Students are encouraged to become more familiar with the details by reworking the example problems and writing MATLAB programs. Problems in Section 3.16 will further help students build their knowledge on the subjects.
3.1 Describe the torque-generating properties of engines and motors used in automotive applications.
3.2 Explain the tractive force generation of a tyre with a sliding friction force of rubber on a surface.
3.3 Explain why the Magic Formula representation of the tyre tractive force is different from a simple curve fitting of tyre data.
3.4 Propose a method by which the tractive force of tyre could be maintained at its maximum during the vehicle motion.
3.5 What are the tyre rolling resistance moment and force? How are they related?
3.6 Describe the influencing factors in the tyre rolling resistance generation.
3.7 Explain the main sources of aerodynamic force.
3.8 What are the aerodynamic moments?
3.9 The power delivery from the prime mover to the wheels can be achieved in different ways. Describe the constant power, constant torque and constant throttle cases and how they can be justified.
3.10 List the assumptions involved in the CPP method and explain why they are needed.
3.11 Explain how the final speed of a vehicle is achieved and mathematically how long it takes to attain the maximum speed.
3.12 The maximum speed of a vehicle in each gear is influenced by both kinematic and dynamic factors. Explain how.
3.13 How would you propose to shift the gears in order that a better acceleration performance is achieved?
3.14 Explain why the rotating masses inside the vehicle powertrain would reduce the vehicle acceleration.
3.15 Describe the necessity of having tyre slip for vehicle motion and the cause and effect relationship between the wheel torque and traction force.
3.16 Why is a coast down vehicle test useful? Estimate the length of a road needed for a test speed of 150 km/h.
3.17 What are the basic natures of the torque and power losses of the driveline components? Explain the dependency of the losses on the speed and load.
Problem 3.1
The rolling resistance force is reduced on a slope by a cosine factor (![]() ). On the other hand, on a slope, the gravitational force is added to the resistive forces. Assume a constant rolling resistance force and write the parametric forms of the total resistive force for both cases of level and sloping roads. At a given speed v0:
). On the other hand, on a slope, the gravitational force is added to the resistive forces. Assume a constant rolling resistance force and write the parametric forms of the total resistive force for both cases of level and sloping roads. At a given speed v0:
a. Write an expression that ensures an equal resistive force for both cases.
b. Solve the expression obtained in (a) for the parametric values of corresponding slopes.
c. For the coefficient of rolling resistance equal to 0.02, evaluate the values of the slopes obtained in (b) and discuss the result.
Result:
![]()
Problem 3.2
For the vehicle of Example 3.4.2:
a. Calculate the overall aerodynamic coefficient for the same temperature at altitude of 1000 m.
b. Repeat (a) for the same altitude at temperature 30 °C.
c. At the same altitude of (a), at what temperature does the drag force increase by 20%?
d. At the same temperature of (a), at what altitude does the drag force reduce by 20%?
Problem 3.3
In order to have a rough estimation of the performance of a vehicle, it is proposed to ignore the resistive forces to obtain the No-Resistive-Force (NRF) performance.
a. Derive the governing equations of vehicle longitudinal motion for speed v(t) and distance S(t) by ignoring all resistive forces for the CPP (see Section 3.5).
b. For a vehicle of mass 1.2 ton, determine the required engine power P to achieve an acceleration performance of 0–100 km/h during 10, 8 or 6 seconds.
c. Evaluate the power increase factors from 10 seconds to t* seconds defined as $[P/P_{10} = [P(t*)-P(10)]/P(10)]$, for t* = 8 and 6.
Results:
a. ![]() ,
, ![]() ,
,
b. 46.3, 57.9 and 77.2 kW.
c. 0.25 and 0.67.
Problem 3.4
Use the results of Problem 3.3:
a. Write the expression for the specific power Ps (in W/kg) of a vehicle to reach a certain speed v (km/h) from the rest at a certain acceleration time t.
b. Plot the variation of Ps versus t from 6 to 10 seconds. Repeat the result for three speeds of 80, 90 and 100 km/h.
c. Are the results dependent on the vehicle properties?
Problem 3.5
At very low speeds the aerodynamic force is small and may be ignored. For example, at speeds below 30 km/h, the aerodynamic force is one order of magnitude smaller than the rolling resistance force. For such cases categorized as Low-Speed (LS), ignore the aerodynamic force and for the CPP assume a constant rolling resistance force F0.
a. Integrate the equation of motion (Equation (3.58) with c = 0) and use the initial condition of v = v0 at t = t0 to obtain an expression for the travel time in terms of speed.
b. For a vehicle of 1000 kg mass and total rolling resistance force of 200 N, when starting to move from standstill, plot the variation of vehicle speed against elapsed time up to 10 seconds and compare it with the results of NRF model (Problem 3.3). The engine power is 50 kW.
Results:
![]()
Problem 3.6
For the vehicle of Problem 3.5 and using the LS method, find the required power for the 0–100 km/h acceleration to take place in 7 seconds.
Result: 58,849 W.
Hint: The following statements in MATLAB can be used with a proper initial guess for x0.
fun=inline(`7−1000*×*log(×/(×−(100/3.6/200)))+1000*(100/3.6/200)');
×=fsolve(fun, ×0, optimset(`Display',`off')); (×= P/F0^2)
Problem 3.7
For the vehicle of Problem 3.5 using the LS method determine the power requirements for a performance starting from rest to reach speed v at time t, for three cases of v = 80, 90 and 100 km/h for accelerating times varying from 6 to 10 seconds. Plot the results in a single figure.
Problem 3.8
The power evaluation for the NRF case (Problem 3.3) is a simple closed-form solution but it is not accurate. The LS method (Problems 3.5–3.7) produces more accurate results especially in the low speed ranges. By generating plots similar to those of Problem 3.7 show that an approximate equation of P = PNRF + 0.75F0v can generate results very close to those of LS method.
Problem 3.9
For the LS case, use ![]() that relates the speed to acceleration and distance, substitute for acceleration in terms of speed.
that relates the speed to acceleration and distance, substitute for acceleration in terms of speed.
a. Integrate to obtain an expression for travel distance S in terms of velocity v.
b. Derive the equation for a motion starting at a distance S0 from origin with velocity v0.
c. Simplify the expression for a motion stating from rest at origin.
Results:
![]()
![]()
Problem 3.10
A vehicle of 1200 kg mass starts to accelerate from the rest at origin. If power is constant at 60 kW, for a LS model with F0 = 200 N, determine the travel time and distance when speed is 100 km/h. Compare your results with those of the NRF model.
Results:
![]()
Problem 3.11
In Problem 3.8 a close approximation was used for the power estimation of LS method. For the general case including the aerodynamic force, the approximation given by P = PNRF + 0.5FRv is found to work well.
For the vehicle of Example 3.5.3, plot the variations of power versus acceleration times similar to those of Problem 3.8 and compare the exact solutions with those obtained from the proposed method.
Problem 3.12
According to the solutions obtained for CTP (see Section 3.6) it turned out that at each gear, the acceleration is constant to a good degree of approximation (see Figure 3.50). Thus a simpler solution can be obtained by considering an effective resistive force for each gear that reduces the problem to a Constant Acceleration Approximation (CAA). In each gear assume the resistive force acting on the vehicle is the average of that force at both ends of the constant torque range. Write the expressions for the average speed at each gear vav, the average resistive force Rav.
a. Show that the acceleration, velocity and distance at each gear are ![]() ,
, ![]() and
and ![]() , in which
, in which ![]() and
and ![]() are the initial speed and distance from origin for each gear for i > 1 and v0 and S0 for i = 1.
are the initial speed and distance from origin for each gear for i > 1 and v0 and S0 for i = 1.
b. Repeat Example 3.6.1 by applying the CAA method.
Problem 3.13
A 5th overdrive gear with overall ratio of 3.15 is considered for the vehicle in Problem 3.12, and the torque is extended to 3400 rpm. Obtain the time variations of acceleration, velocity and travel distance for the vehicle by both CAA and numerical methods and plot the results.
Problem 3.14
In Example 3.5.2 impose a limit for the traction force of FT < 0.5 W and compare the results.
Problem 3.15
For a vehicle with transmission and engine information given in Example 3.7.2, include a 1-second torque interruption for each shift and plot similar results. To this end, include a subprogram with listing given below at the end of loop for each gear:
% Inner loop for shifting delay:
if i<5 % No delay after gear 5!
t0=max(t);
tf=t0+tdelay;
×0=[v(end) s(end)];
p=[0 0 0]; % No traction force
[t,×]=ode45(@Fixed_thrt, [t0 tf], ×0);
v=×(:,1);
s=×(:,2);
end
%Now plot the results
p=[p1 p2 p3 p4]; % Set back the engine torque
Problem 3.16
Repeat Problem 3.15 with a different shifting delay for each gear of the form 1.5, 1.25, 1.0 and 0.75 seconds for 1–2, 2–3, 3–4 and 4–5 shifts respectively. (Hint: For this you will need to change the program.)
Problem 3.17
Repeat Example 3.7.2 for a different shifting rpm.
a. Shift all gears at times when the engine speed is 4500 rpm.
b. Shift the gears at 4500, 4000, 3500 and 3000 rpm for shifting 1–2, 2–3, 3–4 and 4–5 respectively. (Hint: For this part you will need to change the program.)
Problem 3.18
In Example 3.7.3, investigate the possibility of having a dynamic balance point in gear 4. If no steady state point is available, find a new gear ratio to achieve a steady state.
Problem 3.19
Repeat Example 3.7.2 with transmission ratios 3.25, 1.772, 1.194, 0.926 and 0.711.
Problem 3.20
In the program listing given for Example 3.7.2, no constraint is imposed for the lower limit of engine speed and at low vehicle speeds the engine rpm will attain values less than its working range of 1000 rpm.
a. For the existing program try to find out at what times and vehicle speeds the engine speed is below 1000 rpm.
b. Modify the program to ensure a speed of at least 1000 rpm for the engine. How are the results affected?
Problem 3.21
In a vehicle roll-out test on a level road, the variation of forward speed with time is found to be of the form:
![]()
where a, b and d are three constants.
a. Assume an aerodynamic resistive force in the form of ![]() and derive an expression for the rolling resistance force FRR.
and derive an expression for the rolling resistance force FRR.
b. Write an expression for the total resistive force acting on the vehicle.
Result:
![]()
Problem 3.22
Two specific tests have been carried out on a vehicle with 1300 kg weight to determine the resistive forces. In the first test on a level road and still air, the vehicle reaches a maximum speed of 195 km/h in gear 5. In the second test on a road with slope of 10%, the vehicle attains a maximum speed of 115 km/h in gear 4. In both tests the engine is working at WOT at 5000 rpm, where the torque is 120 Nm.
a. If the efficiency of the driveline is 90% and 95% at gears 4 and 5 respectively, determine the overall aerodynamic coefficient and the rolling resistance coefficient.
b. If the gearbox ratio at gear 5 is 0.711 and the wheel effective radius is 320 mm, assume a slip of 2.5% at first test and determine the final drive ratio.
c. Calculate the ratio of gear 4 (ignore the wheel slip).
Results:
![]()
Problem 3.23
For a vehicle with specifications given in Table P3.23, engine torque at WOT is of the following form:
![]()
Table P3.23 Vehicle information.
| Vehicle mass | 1200 kg | |
| Rolling Resistance Coefficient | 0.02 | |
| Tyre Rolling Radius | 0.35 m | |
| Final drive Ratio | 3.5 | |
| Transmission Gear Ratio 1 | 4.00 | |
| Gear Ratio 2 | 2.63 | |
| Gear Ratio 3 | 1.73 | |
| Gear Ratio 4 | 1.14 | |
| Gear Ratio 5 | 0.75 | |
| Aerodynamic Coefficient | CD | 0.4 |
| Frontal Area | Af | 2.0 m2 |
| Air density | ρA | 1.2 kg/m3 |
The driveline efficiency is approximated by 0.85+i/100 in which i is the gear number.
a. Determine the maximum engine power.
b. What is the maximum possible speed of the vehicle?
c. Calculate the maximum vehicle speed at gears 4 and 5.
Results:
![]()
Problem 3.24
For the vehicle of Problem 3.23, find the following:
a. For a constant speed of 60 km/h over a slope of 10%, which gears can be engaged?
b. For case (a), in which gear is the input power minimum?
c. On this slope, what would be the maximum vehicle speed in each gear?
Hint: Table P3.24 is useful for solving this problem.

Problem 3.25
The vehicle of Problem 3.23 is moving on a level road at the presence of wind with velocity of 40 km/h. Assume CD = CD0 + 0.1|sin α|, in which α is the wind direction relative to the vehicle direction of travel. Determine the maximum vehicle speed in gear 4 for:
a. a headwind (α = 180)
b. a tailwind (α = 0)
c. a wind with α = 135 degree.
Results:
![]()
Problem 3.26
Two similar vehicles with exactly equal properties are travelling on a level road but in opposite directions. Their limit speeds are measured as v1 and v2 respectively. Engine torque at WOT is approximated by following equation:
![]()
Determine the aerodynamic drag coefficient CD and wind speed in direction of travel vw:
a. By writing a parametric tractive force equation in terms of vehicle speed for both vehicles.
b. Then write a parametric resistive force equation in terms of speed for both vehicles.
c. Equate the two equations for each vehicle and use the numerical values of Problem 3.23 for m, fR, Af, ρA, rW and the additional information given in Table P3.26.
| Transmission Gear Ratio | 0.9 |
| v1 | 180 |
| v2 | 200 |
Results:
![]()
Problem 3.27
While driving uphill in gear 4 on a road with constant slope ![]() , the vehicle of Problem 3.23 reaches its limit speed
, the vehicle of Problem 3.23 reaches its limit speed ![]() at an engine speed of
at an engine speed of ![]() at a still air. The same vehicle is then driven downhill on the same road in gear 5, while keeping the engine speed same as before. Engine powers for uphill and downhill driving are
at a still air. The same vehicle is then driven downhill on the same road in gear 5, while keeping the engine speed same as before. Engine powers for uphill and downhill driving are ![]() and
and ![]() respectively. The tyre slip is roughly estimated from equation Sx = S0 + P × 10−2 (%) where S0 is a constant and P is power in hp.
respectively. The tyre slip is roughly estimated from equation Sx = S0 + P × 10−2 (%) where S0 is a constant and P is power in hp.
Assume a small slope angle and use the additional data given in Table P3.27 to determine:
a. uphill and downhill driving speeds
b. road slope

Results: ![]()
Problem 3.28
For the vehicle of Problem 3.23, find the following:
a. Derive a general parametric expression for the value of speed v* at the maximum attainable acceleration.
b. Use the numerical values and determine the values of v* at each gear.
c. Calculate the maximum accelerations at each gear.
Results:
![]()
![]()
Problem 3.29
In Section 3.9 the effect of rotating masses were discussed and equations for including this effect in the acceleration performance of a vehicle were developed. From an energy consumption point of view, when the vehicle is accelerated to the speed of v, the rotating inertias will be at rotational speeds related to v (ignore the tyre slip).
a. Write the kinetic energies for the vehicle body mass m and rotating masses Ie, Ig and Iw.
b. From the kinematic relations, relate the rotational speeds to the vehicle speed.
c. Write the energy terms in terms of vehicle speed v.
d. Write the total energy of vehicle as: ![]() .
.
e. Determine the equivalent mass meq and compare it with Equation (3.130).
Problem 3.30
For a tyre with the Magic Formula information given in Table 3.3:
a. Plot the longitudinal force (F) against slip (s) for both traction and brake regions at normal load values 1.0, 2.0, 3.0 and 4.0 kN (all in a single figure).
b. Plot coefficients of tyre-road friction for case (a).
c. At slip ratios 5, 10, 20 and 50%, plot the variation of Fx versus Fz (max Fz = 5 kN).
d. Differentiate the Magic Formula with respect to slip to find the value of slip at which the force is maximum. Verify your results by comparing them with those of case (a).
e. In order to have an impression of the influence of different factors in the Magic Formula tyre model, try the following for the above tyre in (a) at a normal load of 3.0 kN:
i. Multiply coefficient B by 0.8, 1.0 and 1.2 while keeping the other coefficients unchanged. Plot all three results in a single figure.
ii. Repeat i for coefficient C.
iii. Repeat i for coefficient D.
iv. Repeat i for coefficient E.
Problem 3.31
The vehicle of Problem 3.23 is moving with a constant speed of 100 km/h. Use the tyre data of Table 3.3 for each of the two driving wheels and for a front/rear weight distribution of 60/40, determine:
a. Longitudinal slip (in percentage) of the tyres for both cases of FWD and RWD.
b. Repeat (a) for a 5-degree grade.
c. Repeat (a) for a level road with adhesion coefficient of 0.4 (ignore the load transfer).
The analysis of the performance of vehicles in the longitudinal direction in terms of accelerations and speeds has been dealt with in many automotive texts. This is not surprising since in practice it has always been one of the most highly debated areas in comparing vehicles – indeed, technical journals and magazines have seemed obsessed with 0 to 60 mile/h times and top speeds even if these aspects of performance cannot actually be used safely on the roads.
A good introduction to the subject which takes a slightly different approach from this book is provided by Gillespie [4]. In Chapter 2, he derives the basic equations and discusses power and traction limited acceleration performance. In Chapter 4, he goes on to discuss in more detail the road loads – both rolling resistance and aerodynamic – which affect longitudinal performance. Gillespie's book, written in the USA in 1992, provides good clear explanations of the fundamentals of vehicle performance – and the only problem for current students is the use of non-SI units which makes the numerical examples somewhat difficult to follow.
Lucas's book, Road Vehicle Performance[5], arose from lecture courses at Loughborough University of Technology. It is interesting because it gives a comprehensive analysis of vehicle performance, and links it to the practical issues of measurements both on the road and on laboratory-based dynamometers. Although it is now rather dated since it was written in 1986, the principles are of course all still relevant and he discusses some useful information on manual vs automatic gearboxes and fuel consumption calculations. It is targeted at undergraduate and graduate students but again has the drawback of using non-SI units.
The text by Guzzella and Sciaretta on vehicle propulsion systems [6] also provides an excellent introduction to vehicle performance in Chapters 2 and 3. It is a modern book, updated in 2007, and based on lectures at the Swiss Federal Institute of Technology (ETH), Zurich. It is useful as a companion to this book because the authors use examples in MATLAB and Simulink, and in particular describe some interesting case studies in the Appendix. They also introduce the QSS toolbox package which was developed at ETH, and which may be downloaded from http://www.idsc.ethz.ch/Downloads/qss.
[1] SAE(1978)Vehicle Dynamics Terminology. SAE J670e, Society of Automotive Engineers.
[2] Bakker, E., Nyborg, L. and Pacejka, H.B. (1987) Tyre Modelling for Use in Vehicle Dynamics Studies, SAE Paper 870421.
[3] Wong, J.Y. (2001)Theory of Ground Vehicles,3rd edn.John Wiley & Sons, Inc., ISBN 0-470-17038-7.
[4] Gillespie, T.D. (1992)Fundamentals of Vehicle Dynamics.SAE, ISBN 1-56091-199-9.
[5] Lucas, G.G. (1986)Road Vehicle Performance.Gordon and Breach, ISBN 0-677-21400-6.
[6] Guzzella, L. and Sciarretta, A. (2005)Vehicle Propulsion Systems: Introduction to Modelling and Optimisation.Springer, ISBN 978-3-549-25195.






