Appendix
An Introduction to Bond Graph Modelling
The basic concept in bond graph analysis is to specify the flow of energy in a system. The energy flow in any system is always governed by simultaneous intervention of two independent parameters. In the bond graph method these two parameters are defined by the general terms of Effort e and Flow f. The power of the instantaneous energy flow is product of these two factors:
Momentum (p) and Displacement (q) are defined as:
(A.3) 
Therefore Energy (E) from Equation A.1 is
(A.4) 
An energy port in a bond graph is the gateway for energy exchange. Should an element exchange energy in a single way (e.g. heat) that element is called a one-port (or single-port) element. A multi-port element, therefore, is an element that exchanges energy in different ways (e.g. heat, electrical, mechanical, etc.).
The elements in a bond graph are models of components in real systems. As far as energy is concerned, an element of a system is either a source of energy or consumes energy. Consuming energy may result in the dissipation of energy (usually as heat), transient storage or transforming it to another useful form. With this brief explanation, the bond graph elements can be categorized as Sources (or Active elements), Passive elements, Converters, and Junctions.
A.2.1 Sources
Energy sources are devices that contain one sort of energy and, when connected to a system, the flow of energy is established. As stated earlier, any sort of energy has both flow and effort components. Sources in a bond graph are distinguished by their dictating component; in other words, an energy source can only dictate either flow or effort factors and cannot control the other factor.
A flow source Sf, therefore, is an energy source that has a specific flow level f* and, when connected to a system, energy will be passed to the system with a flow value of f*. The value of effort of the flow source will depend on the energy demand of the connected system. For an ideal source of flow, the flow level f* is independent of energy demand and always remains unchanged. An example of a flow source in mechanical systems is a large moving body with a constant speed (e.g. the Earth, a train, etc.) and in electrical systems the current source in electrical circuits is an example.
An Effort source Se, is an energy source that has a specific effort level e* and, when connected to a system, energy will be passed to the system with effort value of e*. Again, the value of flow to the system depends on the energy demand of that system and cannot be controlled by the source. For ideal effort sources, the value e*will not be altered by the energy drain from the source. Examples of effort sources in mechanical and electrical systems are a force and a battery respectively. In bond graphs, simple arrows are used to indicate the direction of energy flow. The bond graph graphical symbols for the effort and flow sources are shown in Figure A.1.
Figure A.1 Bond graph graphical symbols for (a) flow source and (b) effort source
Energy sources are single-port elements since they transmit only one sort of energy to the systems.
A.2.2 Passive Elements
There are three types of passive elements in the bond graphs, namely Resistive, Capacitive and Inertia elements. These are all single port elements that receive energy from the system and either dissipate it or increase their energy level.
A Resistive element (R element) is any element that has a static relation between its effort and flow of the form:
The function 
in general is non-linear but for the sake of simplicity a linear function will be assumed hereinafter. Thus Equation A.5a can be simplified to:
(A.5b) 
in which R is the constant slope of e versus f for the linear assumption. According to Equation A.1, power flow from this element is:
(A.6) 
The graphical symbol for the R element is depicted in Figure A.2 and examples of the resistive elements in mechanical and electrical systems are summarized in Table A.1.
Figure A.2 Graphical symbol for Resistive or R element
Table A.1 Examples for R elements.
A Capacitive element (C element) is any element that has a static relation between its effort and displacement, i.e.:
(A.7) 
Again a linear function 
will be assumed here and as a result we will have:
(A.8) 
in which k is the constant slope of e versus q in the linear case. The graphical symbol for the C element is depicted in Figure A.3 and examples of the capacitive elements in electrical and mechanical systems are summarized in Table A.2.
Figure A.3 Graphical symbol for Capacitive or C element
Table A.2 Examples for C elements.
An Inertia element (I element) is any element that has a static relation between its momentum and flow, or:
(A.9) 
Assuming a linear function 
for our case:
in which I is the constant slope of p versus f for the linear relationship. The graphical symbol for the I element is shown in Figure A.4 and examples of the inertia elements in electrical and mechanical systems are summarized in Table A.3.
Figure A.4 Graphical symbol for Inertia or I element
Table A.3 Examples for I elements.
A.2.3 Two Port Elements
Two port elements are basically converters of energy and receive the energy in one port, convert it and transfer it to the output port. Ideal two-port elements do not use or waste energy. The general bond graph representation of a two-port element is shown in Figure A.5.
Figure A.5 Bond graph symbol for a general two-port element
For an ideal 2-port element the energy balance means:
There are two types of two-port elements, namely, transformers and gyrators that will be described below.
A.2.3.1 Transformer
A transformer TF is a two-port element in which the input and output efforts are proportional:
(A.12) 
in which m is proportionally constant and is called the transformer module. In bond graphs m is placed above the transformer as shown in Figure A.6.
Figure A.6 Bond graph representation of transformer element
According to Equation A.11, for a transformer element, the relation between flows is:
(A.13) 
In electrical systems a transformer uses two or more windings wrapped around an iron core and transforms energy from the input winding to the output winding(s). The magnetic field produced by an alternating current in the input coil induces an alternating current in the output coil(s). If the output voltage is greater than the input voltage the transformer is a step-up type, or conversely it can be a step-down transformer. Examples of transformer elements in mechanical systems are a lever, a belt drive and a gear set.
A.2.3.2 Gyrator
A gyrator GY is a two-port element in which the input effort and its output flow are proportional:
in which r is the proportionally constant and is called the gyrator ratio. In bond graphs similar to transformer case, r is placed above the gyrator. According to Equation A.11, for a gyrator element the relation between input flow and output effort is:
A rotating mass in a mechanical system has a gyroscopic property. Figure A.7 shows a simple gyroscope consisting of a spinning rotor with a fixed axis inside a light frame. Applying a torque Tx about the x axis will not turn the frame around the x axis, but it will instead turn it around the y axis due to the gyroscopic effect. The governing relation is:
Figure A.7 A simple gyroscopic
in which J is the mass moment of inertia of the rotor and Ω is the spin speed. Similarly for input torque Ty the rotation is around the x axis (-x strictly speaking)
The two axes x and y can be regarded as input and output axes and since torque and speed are effort and flow, Equations A.16 and A.17 are of the forms of Equations A.14 and A.15 respectively with r being the inverse of 
.
In an electrical system, a DC motor has its output torque proportional to the input current and at the same time its output speed is proportional to the input voltage. With reference to Figure A.8, one can write:
(A.18) 
(A.19) 
Figure A.8 A DC motor
that is, equivalent to a gyrator with its r inverse of the proportionality constant km.
A.2.4 Junctions
Junctions are elements in bond graphs that are responsible for the implementation of the law of conservation of energy. There are two types of junctions: common-effort and common-flow.
A common effort junction also known as 0-node, is a meeting point for several energy bonds with equal efforts. Consider a general case of three bonds meeting at a 0-node shown in Figure A.9.
Figure A.9 A common effort junction (0-node)
With the condition of common efforts, it can be written:
(A.20) 
The application of the law of conservation of energy will result in:
(A.21) 
Similarly a common flow junction, also called 1-node, is a meeting point for several energy bonds with equal flows. Three bonds meeting at a 1-node are illustrated in Figure A.10 and with the condition of common flow, the equations are:
(A.22) 
(A.23) 
Figure A.10 A common flow junction (1-node)
Constructing the bond graph for a physical system is a simple task of putting together the bond graph symbols of individual elements in the system. The best way to learn the construction of bond graphs is to work through several examples as follows.
Example A.3.1
Construct the bond graph for the basic mechanical system of Figure A.11.
Figure A.11 Basic mechanical system of Example A.3.1
Solution
In Figure A.11 one distinguishes four different elements: forcing function F(t), mass element m, spring element k and damper element B. The forcing function is a source of energy and since the dictating component for the source is its effort (force), thus it is a source of effort Se. The three remaining elements are all passive elements or consumers and bond graph symbols for all three were given earlier.
In order to construct the bond graph, one important point is to see how the elements are connected. Note that the system elements can only connect with one another through junctions and two-port elements. Here there is no two-port element so one should look for junctions only. A 0-junction is where elements with equal efforts (forces) are connected and a 1-junction is where elements of equal flow (speed) are connected. It is easy to note that the spring and damper elements have bottom ends fixed and have equal speeds at upper ends. So these two elements have equal speeds and should be connected through a 1-junction.
The mass element is a one-end element and when compared with two-end elements of spring and damper in a mechanical system, it may cause confusion. In order to resolve any confusion of this kind, the mass element can always be replaced with a two-end element that has its second end connected to the ground. Application of this rule to the system of Figure A.11 will result in Figure A.12, from which it can be seen that the mass element is also in the same situation as the two other elements. Since the force also has similar velocity, therefore, all four elements are joined by a common-flow junction as shown in Figure A.13.
Figure A.12 Equivalent sketch for system of Figure A.11
Figure A.13 Bond graph of Example A.3.1
Example A.3.2
Construct the bond graphs of the electrical systems shown in Figure A.14.
Figure A.14 Electrical circuits of Example A.3.2
Solution
In circuit (a) three passive elements are in series, so that an equal current i will pass through them all and also through the voltage source. Thus all four elements are connected through a common flow junction. The result is the bond graph of Figure A.15 a. The same elements are in parallel in the circuit of Figure A.14b. All three passive elements are connected to both ends of the voltage source, so that a common effort junction should connect them all in a bond graph. The result is shown in Figure A.15b.
Figure A.15 Bond graphs of Example A.2.2
Example A.3.3
Construct the bond graph of the electromechanical system of Figure A.16.
Figure A.16 System of Example A.3.3
Solution
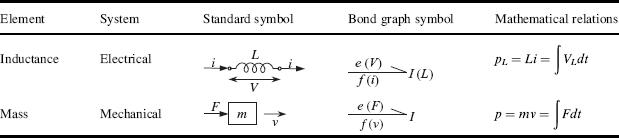
The system consists of a DC motor with its output shaft attached to a gear set. A viscous friction element is also present to model the bearing frictions. The load torque TL is acting on the output shaft.
The main source of energy is electrical voltage source that provides the motor armature current ia. This current also flows through the resistor Ra and the armature produces a shaft torque proportional to the current. In bond graph terms the input source is connected to a 1-node together with the resistor and the armature. The armature is a gyrator that receives electrical energy and produces mechanical torque proportional to its input current. The armature torque drives the damper as well as the small gear with a common speed (these two elements are in a common flow junction). The remaining torque is amplified by the gear set (i.e. a transformer) and drives the larger gear with inertia J2. The load torque acts like a source of effort at the output shaft. The bond graph representation of the system according to the description is shown in Figure A.17.
Figure A.17 Bond graph of system of Example A.3.3
Modelling tools eventually lead to the derivation of governing equations of motion of the systems. For bond graphs, this process starts by specifying the state variables. For this reason, bond graphs use a technique in which Causality Strokes are inserted.
A.4.1 Causality
For I and C elements the relationship between their efforts and flows is governed by integrals. Let us consider the I element, for instance, for which the flow is obtained from integration of its effort (see Equations A.2 and A.10):
Equation A.24 means that in an I element the effort is the cause of energy transfer. In other words, when effort is received by the element, the flow is generated after a delay. An example is the mass in mechanical systems. Applying a force to a mass produces speed. In fact, at time zero there is a force but speed is zero. After some time elapses, speed will result. Thus in I elements the flow always lags the effort. It is said the effort in these elements is the cause and flow is the effect.
In C elements the opposite is true, since the effort and flow change places in Equation A.24:
(A.25) 
Therefore in a C element, flow is the cause and the effort is the effect. Causality plays an important role in determining the system state variables and for this reason the causality must be specified in a bond graph. To this end, a Stroke ‘|’ is used to specify the causality of each element in the bond graph. Table A.4 summarizes the causality strokes of different bond graph elements.
Table A.4 Causality strokes for bond graph elements.
The last column in Table A.4 indicates that there are alternative causality assignments for the bond graph elements. For I and C elements the alternative strokes are at the other ends. In fact, the strokes given to I and C elements shown in Table A.4 are called integral causality since the relation between the flow and effort of these elements is of the integral type. However, in a physical system it is possible that I and C elements can receive alternative causality (called differential causality). It is recommended to avoid this type of causality if possible. For R elements the causality is not important and both forms can be assigned. For the sources, no alternatives for causality assignment is permitted.
Junctions are very important when causality strokes are assigned. The reason is that in every junction there is only one band which controls the property of that junction (i.e. flow or effort) and it is called the Strong band. This means, for instance, in a 1-node, all connected elements that have equal flows, the flow is dictated by only one of the elements. An example is a source of flow connected to a 1-node, obviously all elements will have the flow of the source. Conventionally the strong bond in a common-flow junction receives the causal stroke outside of the junction and the other bonds receive their strokes inside the junction. For a common-effort junction the opposite applies (i.e. the strong bond receives the stroke inside of the junction). Figure A.18 illustrates the causality strokes of both common-flow and common-effort junctions. It is clear that in a 0-junction only one stroke appears inside the junction and in a 1-junction only one stroke appears outside of the junction. The existence of more than one strong bond in a junction indicates a violation of the law of conservation of energy and thus the result is invalid.
Figure A.18 Causal strokes of typical 1-junctions and 0-junctions
A.4.2 Assignment Procedure
Causality assignment procedure in a bond graph is not unique and everyone may use a different way of inserting the strokes. However, there are a few points that are useful to consider before assigning the causal strokes.
- Sources are good starting points since their strokes are definite.
- Try to assign integral causalities for all I and C elements.
- Assign them one by one to avoid mistakes.
- Check the strokes of all junctions and make sure there is only one strong bond in each joint.
Example A.4.1
Assign the causal strokes in the bond graph of Example A.3.3.
Solution
The result is given in Figure A.19. Starting with sources in this case only specifies their own strokes and no further information is obtained. In the second step the I element in the middle 1-junction is given an integral stroke. This specifies the strong bond of the junction and other strokes are inserted inside the junction. The gyrator to the left of the junction and the transformer to the right both receive their appropriate strokes (see Table A.4). The two remaining elements are Ra and I in the first and last 1-junctions and they receive their strokes according to the status of strokes in the junctions where they belong. It is observed that for the I element of the last junction, a differential stroke is assigned. This is acceptable since between the two gears of Figure A.16 no elastic element exists and the speeds of each gear are directly related.
Figure A.19 Causal strokes for the bond graph of system of Example A.4.1
A.4.3 Bond Graph Numbering
Numbering bond graphs is optional but useful since it assigns a number to each element in the bond graph and makes easy to describe a system. The numbering method is also optional and a bond graph can be numbered in different ways. Nevertheless, it is better to number the graph sequentially starting from 0 or 1. A recommended procedure is as follows:
1. Assign number 0 to the source.
2. If there is more than one source, assign 0 to the main source and to the others 00, etc.
3. Assign numbers 1, 2,3, etc. to the integrally stroked I and C elements.
4. Next number the differentially stroked I and C elements.
5. Then number the R elements.
6. Continue numbering the other remaining bonds.
Example A.4.2
Number the bond graph of Example A.3.4.
Solution
The main source is assigned 0 and the other 00. There is only one integrally stroked I element, which receives number 1, and the second I element gets number 2. The two R elements are assigned 3 and 4 and the rest of bonds are numbered from 5 to 8. The result is given in Figure A.20.
Figure A.20 Bond graph numbering for system of Example A.4.2
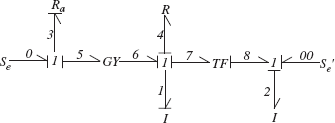
A.4.4 Component Equations
The governing equations of a system are usually obtained by putting together the equations of individual elements of the system. Useful forms of equations for several elements in the bond graph are summarized in Table A.5.
Table A.5 Useful equations for bond graph elements.
A.4.5 Bond Graph Simplifications
Sometimes the nodes and elements in a bond graph are arranged so that some parts of the graph can be simplified. Examples of bond graph modifications will be described below.
- Adjacent 1 or 0 junctions of same type: two adjacent 1 or 0 junctions can be merged to obtain only one node. Figure A.21 illustrates examples of this kind.
- Equivalent I or R: Sometimes at both ends of a transformer there are 1 junctions with I or R elements. This combination can be simplified by taking the elements to either end of the transformer by substituting an equivalent value. Figure A.22 shows the original system and its two alternatives for I elements. The equivalent inertias I′ and I″ are obtained from following equations. For the R elements, the results are exactly similar.
(A.26) 
(A.27) 
Figure A.21 Adjacent node simplifications: (a) 1 junctions and (b) 0 junctions
Figure A.22 Equivalent inertias in a transformer
It should be noted that by using the equivalent inertias, the occurrence of derivative causality for I elements is also prevented.
A.4.6 Derivation of Equations of Motion
Once the bond graph is constructed and causal strokes are assigned, the process for the derivation of equations of motion can be easily followed. The first step in this process is to find the state variables of the system that are the momentum and displacements of those I and C elements of the bond graph with integral causality. This is why care should be taken to assign integral strokes to as many I and C elements as possible in the bond graph, since an inadequate number of state variables cannot explain the system behaviour. In fact, according to the definition, the state variables are the minimum number of variables that fully describe the state of a system at any instant.
Upon identification of the state variables, there will be one differential equation of motion for each state variable. Since the state variables belong to either the I-elements or the C-elements, the differential equations of motion are of the following basic forms:
In which ei (i = 1, 2,...) are the efforts of the I elements with integral causality, and pi are their momentums (that are system state variables). Similarly fj (j = 1, 2,...) are the flows of the C elements with integral causality and qj are their displacements. The task of obtaining the governing equations of motion, therefore, reduces to writing the efforts and flows of the specified I and C elements in terms of state variables (i.e. in terms of p and q). This can be done by making use of equations given in Table A.5. Equations A.28 and A.29 show that the equations of motion of the system are obtained as a set of first order differential equations. This is the advantage of the bond graph method, since the solution of such equations is straightforward by using available software such as MATLAB.
Example A.4.3
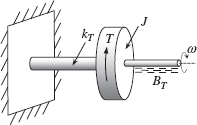
For the torsional vibrating system shown in Figure A.23 derive the equations of motion.
Figure A.23 A torsional vibrating system
Solution
This system is a torsional equivalent of the mass-spring-damper system discussed in Example A.2.1. External torque T, inertia J, torsional spring kT and torsional damper BT replace F, m, k and B of the linear system. The bond graph of the system, therefore, is exactly similar to that depicted in Figure A.13. The result after applying numbering and assigning causality strokes is shown in Figure A.24. As is clear, both I and C elements have received integral strokes and thus the system has two state variables p1 and q2.
Figure A.24 Bond graph of Example A.4.3
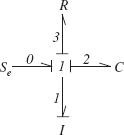
The equations of motion of the system are 
and 
. In order to find the final forms of the equations, parameters e1 and f2 must be written in terms of state variables p1 and q2. From Table A.5, the available equations for the elements are:
These equations do not provide direct solution for the two unknowns. For junction 1 we have:
which is the solution to the second differential equation. To find e1 we have to write the effort summation for the junction (
) from which we have:
that is, only in terms of state variables (and known quantities). Thus the final forms of the equations of motion are:
It might raise a question of how this result is related to a traditional solution of standard mass-spring-damper system of the form 
(or for our case 
), that is a second order differential equation. To answer this question it should be recalled the order reduction process in which a second order differential equation can be broken into two first order equations by change of variable. For instance, by defining 
and 
, the second order equation 
can be reduced to two following first order equations:
Substituting 
(momentum of rotating inertia) and 
(displacement of torsional spring) and making use of 
, I1=J, 
and 
, the bond graph equations of motion will be exactly identical to the two above equations. Hence, the bond graph equations of motions are already in reduced form.
Example A.4.4
Derive the equations of motion for the system of Example A.3.3.
Solution
The numbered and stroked bond graph of the system was given in Figure A.20. Since only one integrally stroked element exists in the system, there would be only 1 state variable p1. Thus the equation of system reads:
e6 can be found from the gyrator relation:
The value in the parenthesis is equal to the adjacent parameter (e.g. f5 = f3) and e3 is obtained from effort balance of the first node:
e4 simply is
In order to determine e7, from the transformer and the effort balance of the last node, we have:
e00 is the effort source at the right (
), but e2 cannot be obtained in usual manner since I2 is differentially stroked. For such cases, a differentiation is necessary.
For I2 we write:
Thus:
After substituting e6, e4 and e7 into the first equation and rearranging, the final result is:
