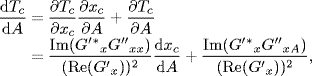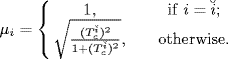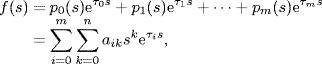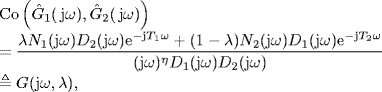Chapter 3

Scalability in the Frequency Domain

Tao generates one, one generates two, two generates three, three generates all things.

—Lao Dan (580–500 BC), Tao Te Ching

This chapter studies the problem of the scalability of the stability results for distributed control systems. The problem is closely related to some differential geometric properties of frequency response plots of local dynamics of agents (nodes) in networks, such as clockwise property, modulus monotonicity, slope monotonicity, phase velocity, critical point of clockwise property, etc. The chapter starts from the clockwise property which plays a key role in scalability analysis. Then, detailed geometric analysis of scalability is conducted for first-order and second-order time-delayed systems which are often encountered in coordinated control systems and end-to-end congestion control systems. Finally, based on the notion of convex directions in the space of stable quasi-polynomials, a frequency sweeping method of scalability test is provided for high-order time-delayed systems.

3.1 How the Scalability Condition is Related with Frequency Responses

Denote by γ the gain margin the transfer function

where W(s) is a rational function of s, and T > 0 is the delay constant. Actually, γ is defined by

(3.1)

where ω_c > 0 is the minimal crossing frequency that satisfies the following equation

(3.2)

Note that the Nyquist plot of γW(jω)e^−jωT crosses the real axis at (− 1, j0) when ω = ω_c. We will call γW(s)e^−Tsthe normalized transfer function of G(s) and denote it as .

Given n transfer functions , denote by the normalized function of G_i(s). Consider a symmetric multi-agent system with G_i(s) as the transfer function of the ith agent. We have shown in the last chapter that the scalability condition for the system is

(3.3)

This condition requires us to check if the point (− 1, j0) is contained in the convex hull of and zero.

The frequency response of the z-transfer function of a discrete-time system can also be denoted as , where the frequency variable ω takes values from the interval [− π, π]. To include the analysis of discrete-time systems in a unified framework, we denote the frequency interval as [ω_a, ω_b], and rewrite the scalability condition as

(3.4)

The following lemma shows that it suffices to check the scalability condition for the boundary of the convex hull involved.

Lemma 3.1 Given normalized transfer functions , assume that

(3.5)

and

(3.6)

Then, the scalability condition (3.4) holds if and only if

(3.7)

for all .

Proof. Note that (3.5) indicates that the condition (3.4) holds for ω = ω₀. By continuity of the set on ω, the point (− 1, j0) enters if and only if the boundary, , or κCo(0, Gⁱ(ω)), passes through (− 1, j0). (3.6) has excluded the possibility that κCo(0, Gⁱ(ω)) passes through (− 1, j0). Therefore, (3.4) holds if and only if (3.7) holds.

Remark. In most cases condition (3.5) can be easily verified. For continuous-time systems, if W_i(s), , are proper, then . Therefore, and hence (3.5) holds. For discrete-time systems, to verify (3.5) we usually choose ω₀ = π because 's are real numbers. Condition (3.6) is ensured by the stability of the individual closed-loop system of each agent. When conditions (3.5) and (3.6) are satisfied, the scalability condition holds if and only if (− 1, j0) is not contained by the Nyquist plot of the convex combination of each pair of agents.

Now, let us consider the following different cases.

Case 1: Homogeneous agents

In this case, the transfer functions of all the agents are assumed to be the same both in the rational part and in the delay unit, i.e.,

Obviously, for such a special case we have

which is a line segment between the origin and any point at for a given frequency ω (see Figure 3.1). Obviously, in this case, the condition(3.4)holds if and only if the Nyquist plot ofdoes not contain the point (− 1, j0).

Figure 3.1 Homogeneous agents with identical delay.

Case 2: Heterogeneous agents with homogeneous frequency response

Let us consider the agents given by

If T_i ≠ T_j, for , the agents generally have different dynamics. However, if there exists a common transfer function such that for any given frequency the following condition holds:

then all the agents have the same Nyquist plot which is delay-independent. For example, take . Then, for a given frequency ω₀, all , , are distributed at different points on the same plot . In this case, we are interested in the geometric property of with which the following inclusion holds

(3.8)

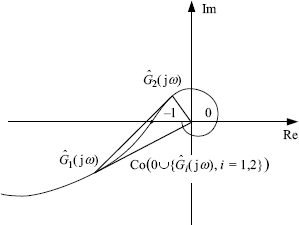
Obviously, if (3.8) holds, then, as shown by Figure 3.2, does not contain the point (− 1, j0) if does not contain (− 1, j0). Intuitively, the inclusion relationship (3.8) implies some “convexity” property of the Nyquist plot . Figure 3.3 gives an illustration that (3.8) may not hold when does not have such convexity. In the next section we will study this property in detail.

Figure 3.2 Delay-independent frequency response: convex case.

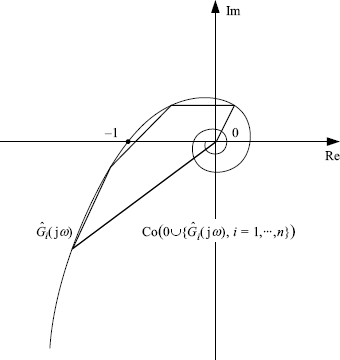
Figure 3.3 Delay-independent frequency response: non-convex case.

Case 3: Heterogeneous agents with heterogeneous frequency response

In this case, the scalability problem becomes much more complicated. Since all the agents have a different frequency response, we can only expect the following inclusion

(3.9)

Obviously, if (3.9) holds, then does not contain the point (− 1, j0) if each does not contain (− 1, j0), . However, even if the convexity is satisfied by each frequency response plot, (3.9) may hold as shown by Figure 3.4(a) or may not hold as shown by Figure 3.4(b).

Figure 3.4 Heterogeneous frequency response.

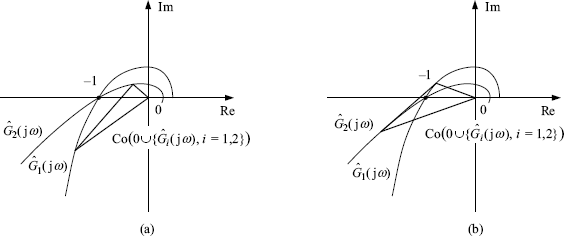
3.2 Clockwise Property of Parameterized Curves

In this section we study the convexity of a smooth curve, which will be defined as a clockwise property. Let us first review some preliminary knowledge on the signed curvature of parameterized curves, which can be found in many textbooks of classic differential geometry such as Guggenheimer (1977).

Let Γ(t) be a curve in defined by two parametric equations:

(3.10)

with X(t), Y(t) C², which denotes the space of functions being two-times differentiable. The curvature of Γ at parameter t is defined as

(3.11)

where a superscript ' represents that a derivative operation is taken and subscripts denote the argument with respect to which derivatives are taken. Assume that exists for all t (t_α, t_β), i.e., the denominator of (3.11) never vanishes in that interval.

Let Γ be an image of the following complex function

(3.12)

in the complex plane. Then, from (3.11) it follows that the curvature of Γ can be also determined by (Gu (1994)

(3.13)

where G ' _ω is the derivative of G(jω) with respect to ω, i.e., G ' _ω = X ' _ω + jY ' _ω, G ” _ωω is the derivative of G ' _ω with respect to ω, and |G ' _ω| are the conjugate and the module of G ' _ω, respectively.

Exercise 3.2 Derive (3.13) based on (3.11).

Now, let us introduce the notion of the clockwise property of a C² curve.

Definition 3.3 The curve is said to be clockwise at t₀ if . Conversely, the curve is anticlockwise at t₀ if . If holds for all t (t_α, t_β) then Γ is said to be a clockwise curve.

Geometrically, condition means that the center of curvature is on the right side of , the tangent vector to Γ at Γ(t₀) = (X(t₀), Y(t₀)), in other words, the vector rotates clockwise (Figure 3.5).

For any ε > 0, denote by the vector from the point Γ(t₀) to the point Γ(t₀ + ε) (Figure 3.5). For convenience of statement we define the positive direction of the tangent line at Γ(t₀) as follows. The tangent vector is said to point to the positive direction if the angle between and goes to zero when ε → 0. Otherwise, is said to point to the negative direction if the angle between and goes to π when ε → 0.

Figure 3.5 Clockwise curve.

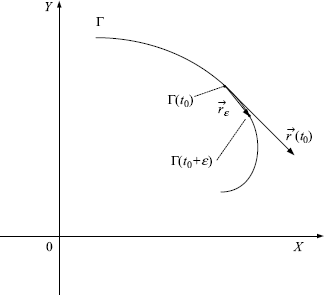
Then, we can split the tangent line r(t₀) at Γ(t₀) as follows:

where r₊(t₀) (r₋(t₀)) denotes the half of the tangent line r(t₀) starting at Γ(t₀) (not including Γ(t₀)) in the positive (negative) direction (Figure 3.6).

Figure 3.6 Partition of a clockwise curve.

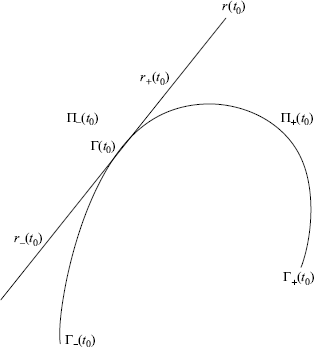
Accordingly, for any given t₀ (t_α, t_β), we can also split the curve Γ as follows (Figure 3.6):

where Γ₊(t₀) (Γ₋(t₀)) denotes the part of the curve parameterized by t (t₀, t_β] (t [t_α, t₀)). Finally, we split the plane as follows

where Π₊(t₀) (Π₋(t₀)) is the open-half plane containing (not containing) the center of curvature of Γ at t₀, assuming that .

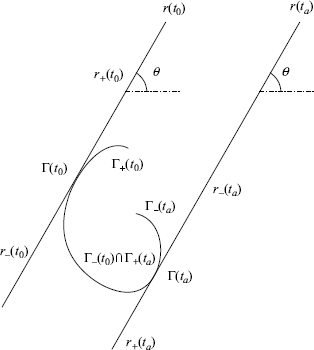
The following lemma states how a clockwise curve enters and leaves the half plane Π₊(t₀).

Lemma 3.4 Suppose that the curve Γ is clockwise and does not admit self-intersections. Then, the following statements are true:

1. If there exists a t < t₀ such that Γ(t) Π₊(t₀), ∀t (t, t₀) and Γ(t) r(t₀), i.e., Γ enters Π₊(t₀) at t, then Γ(t) r₊(t₀).

2. If there exists a t > t₀ such that Γ(t) Π₊(t₀), ∀t (t₀, t) and Γ(t) r(t₀), i.e., Γ leaves Π₊(t₀) at t, then Γ(t) r₋(t₀).

Proof. We only give the proof of statement (1). The proof of statement (2) is similar.

Assume that the phase of the tangent vector of Γ at t₀ is Ψ(t₀) = θ, and assume by contradiction that Γ(t) r₋(t₀). Since Γ is clockwise, the phase, Ψ(t), of is strictly decreasing in t. Therefore, Ψ(t) > θ, ∀t < t₀. So, we have

(3.14)

for some positive integer k. Hence, there exists a t_a (t, t₀) such that Ψ(t_a) = π + θ, i.e., the tangent line r(t_a) is parallel to r(t₀) (see Figure 3.7). Γ₋(t_a) can intersect r₋(t₀) without crossing r₊(t₀) and Γ₋(t₀) ∩ Γ₊(t_a) only if it crosses r₋(t_a) for some t_b < t_a (before crossing r₊(t_a)). By repeating the argument, it can be shown that Ψ(t) > kπ + θ for any finite positive k which can be arbitrarily large. This contradicts (3.14) and hence, Γ(t) r₊(t₀).

Figure 3.7 Illustration of the proof of Lemma 3.4.

By Lemma 3.4, a clockwise curve having no self-intersections lies on one side of its tangent line if it neither crosses the half tangent line r₊(t₀) for t < t₀ nor crosses the half tangent line r₋(t₀) for t > t₀. For a curve lying on one side of its tangent line, the following lemma states that the convex hull of the curve together with the origin lies on one side of the tangent line if and only if the origin and the curve lie on the same side of the tangent line. This lemma addresses the concern of the second case given in the last section.

Lemma 3.5 Given t₀ (t_α, t_β) and , suppose

(3.15)

Then,

(3.16)

holds for all κ [0, 1) if and only if 0 Π₊(t₀).

Proof. Necessity is obvious. We just show sufficiency. Note that = . Since 0 Π₊(t₀) and Γ(t_i) Π₊(t₀) ∪ Γ(t₀), we have κΓ(t_i) Π₊(t₀) for all κ [0, 1). Now, all κΓ(t_i)s, together with the origin are inside Π₊(t₀), by the separation principle of the convex analysis,

for all κ [0, 1).

For the convex combination of two curves we have the following lemma.

Lemma 3.6 Consider two curves Γ₁(t) and Γ₂(t) with t [t_α, t_β]. Suppose Γ₁(t) and Γ₂(t) intersect with each other at the point (− 1, 0) with parameters and , respectively, i.e.,

(3.17)

Then,

(3.18)

holds for all t [t_α, t_β] if

or

for all t [t_α, t_β].

Proof. For any fixed t [t_α, t_β], Γ₁(t) and Γ₂(t) simultaneously lie on the right side of the tangent line or on the right side of . Therefore, for any t [t_α, t_β], we have

or

for 0 ≤ κ < 1, which implies (3.18).

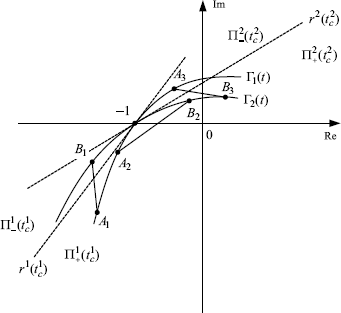
Lemma 3.6 is illustrated by Figure 3.8, where segments A_iB_i, i = 1, 2, 3, represent possible cases of Co(Γ₁(t), Γ₂(t)) for different values of parameter t.

Figure 3.8 Illustration of Lemma 3.6

3.3 Scalability of First-Order Systems

In this section we study some global differential geometric properties of the Nyquist plot of the transfer function of the first-order time-delayed system with a single (open-loop) integrator. Many dynamic nodes in distributed control systems, such as the primal or dual algorithm of the congestion control of communication networks, ideal mobile agents (i.e., mobile agents without inertia), can be modeled by this kind of transfer function.

3.3.1 Continuous-Time System

Consider the transfer function

(3.19)

where T > 0 is the delay constant, and k > 0 is the gain. The frequency response of the system is

(3.20)

(3.21)

(3.22)

Proposition 3.7 The Nyquist plot G(jω) of system (3.19) is clockwise in the parameter interval (0, ∞).

Proof. From (3.20) it is easy to get

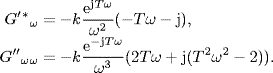
It follows that

Therefore

By Definition 3.3 this implies that G(jω) is clockwise for all ω (0, ∞).

Proposition 3.8 The Nyquist plot G(jω) of system (3.19) has no self-intersection in the parameter interval (0, ∞).

Proof. The proposition is obvious from the fact that the modulus of the frequency response (see (3.20)) is strictly decreasing with respect to ω in the interval (0, ∞).

Let ω_c be the minimal crossing frequency of G(jω), i.e., the Nyquist plot of G(jω) crosses the real axis for the first time at ω = ω_c as ω varies from 0 to ∞. It is easy to get

(3.23)

for system (3.19). According to (3.21), straightforward calculation shows that the slope of r(ω_c), the tangent line to G(jω) at G(jω_c), is

(3.24)

which is independent of the delay constant T. Therefore, the angle Ψ_c between the line r₊(ω_c) and the real axis of the complex plane satisfies

(3.25)

Lemma 3.9 For all ω [0, ∞), the Nyquist plot of system (3.19) lies on the right side of the tangent line to G(jω) at G(jω_c), denoted by r(ω_c), i.e., G(jω) G(jω_c) ∪ Π₊(ω_c), ∀ω [0, ∞).

Proof. Firstly, we prove the lemma for all ω (0, ∞). By Proposition 3.7 and Proposition 3.8, the Nyquist plot of system (3.19) is clockwise and has no self-intersection in the parameter interval (0, ∞). Therefore, by Lemma 3.4, the only way that the curve G₊(jω_c) can leave the half plane Π₊(ω_c) is by crossing the line r₋(ω_c) and the only way that G₋(ω_c) can enter the half plane Π₊(ω_c) is by crossing the line r₊(ω_c). Inequality (3.25) implies that the modulus of any point on r₋(ω_c) is greater than |G(jω_c)|. However, the modulus of the frequency response, , is strictly decreasing in the interval (0, ∞) and hence, |G(jω)| < |G(jω_c)|, ∀ω (ω_c, ∞). Therefore, it is impossible that the curve Γ₊(ω_c) crosses the line r₋(ω_c) for all ω (ω_c, ∞). On the other hand, from (<xreftarget = " c03− mdis − 0033 "/>) we know that for all ω (0, ω_c) the phase of G(jω) is in the interval , i.e., the curve G₋(jω_c) lies inside the third quadrant of the complex plane and hence cannot cross the line r₊(ω_c) which is above the real axis of the complex plane. Hence, we have proved G(jω) G(jω_c) ∪ Π₊(ω_c), for all ω (0, ∞).

When ω → 0, we can write G(jω) as

(3.26)

where ε is an infinitely small positive number and θ [0, π/2]. When θ varies from 0 to π/2, G(jω) draws a clockwise infinitely large quarter-circle with phase angle in [− π/2, 0]. So it is also in Π₊(ω_c).

Now we are ready to prove the following theorem.

Theorem 3.10 For any given natural number n ≥ 2, let

(3.27)

where

(3.28)

and , are divers nonnegative delay constants. Then does not contain the point (− 1, j0) for all κ [0, 1) and all ω (− ∞, ∞).

Proof. By the symmetry property of the frequency response we need only to prove the theorem for all ω [0, ∞).

Let

(3.29)

Obviously, (3.29) forms an onto map from ω [0, ∞) to x_i [0, ∞). We notice that under the given gain condition (3.28), . Therefore, all of the Nyquist plots of , share a common curve, i.e., , on the complex plane. And the curve crosses the real axis for the first time at the point (− 1, j0). By Lemma 3.9 we have G(jx) (− 1, j0) ∪ Π₊(− 1, j0), ∀x [0, ∞). For any given ω [0, ∞) we have x_i = T_iω [0, ∞). So it follows that

(3.30)

By Lemma 3.5 we know that

(3.31)

holds for all κ [0, 1). Therefore does not contain the point (− 1, j0) for all κ [0, 1) and all ω [0, ∞) because (− 1, j0) ∉ Π₊(− 1, j0).

3.3.2 Discrete-Time System

For a discrete-time system the frequency response is the value of its z-transfer function at the unit circle, namely, G(e^jω), ω (− π, π]. For simplicity of notation we will write G(e^jω) as G(ω) for discrete-time systems. Let us study the first-order time-delayed system

(3.32)

where D is a positive integer representing the delay, and k > 0 is the gain. This is a discrete-time analogue of system (3.19). Along the modified unit circle the frequency response of system (3.32) is

(3.33)

(3.34)

(3.35)

(3.36)

Since G(z) has a pole z = 1 on the unit circle, we should modify the unit circle by adding a small half-circle around the pole z = 1 (see Figure 2.13). In this way the pole can be considered as inside the unit circle. The Nyquist plot of G(ω) will go to infinity when ω → 0 and draw a half-circle with an infinite radius clockwise.

Proposition 3.11 The Nyquist plot of system G(ω) (3.32) is clockwise in the parameter interval [0, π].

Proof. Without loss of generality we suppose that k = 1 in (3.32). To prove the proposition we need to consider only the sign of the numerator of the curvature. By (3.13) we have

Straightforward calculating yields

Therefore, we have

which implies

So, the clockwise property of the Nyquist plot of (3.32) is proved.

Proposition 3.12 The Nyquist plot G(ω) of system (3.32) has no self-intersection in the parameter interval (0, π].

Proof. The proposition is obvious from the fact that the modulus of the frequency response (see (3.34)), , is strictly decreasing in the interval (0, π].

Let ω_c be the frequency at which the Nyquist plot Γ(ω) intersects the real axis for the first time as ω varies from 0 to π. It is easy to get

(3.37)

for system (3.32). From (3.35), straightforward calculation shows that the slope of r(ω_c), the tangent line to G(ω) at G(ω_c), is

(3.38)

It is always the case that k_c > 0 as D is a delay constant which is a nonnegative integer for discrete-time systems. Therefore, the angle Ψ_c between the line r₊(ω_c) and the real axis of the complex plane satisfies

(3.39)

Proposition 3.13 For all ω (0, π], the Nyquist plot G(ω) of system (3.19) lies on the right side of r(ω_c), i.e., G(ω) G(ω_c) ∪ Π₊(ω_c), ∀ω (0, π].

Proof. By Proposition 3.11 and Proposition 3.12, the Nyquist plot G(ω) of system (3.32) is clockwise and has no self-intersection in the parameter interval [0, π]. Therefore, by Lemma 3.4, the only way that the curve G₊(ω_c) can leave the half plane Π₊(ω_c) is by crossing the line r₋(ω_c) and the only way that G₋(ω_c) can enter the half plane Π₊(ω_c) is by crossing the line r₊(ω_c) (see Figure 3.9). Equation (3.34) shows that the modulus of the frequency response, , is strictly decreasing in the interval (0, π] and hence, |G(ω)| < |G(ω_c)|, ∀ω (ω_c, π]. But inequality (3.39) implies that the modulus of any point on r₋(ω_c) is greater than |G(ω_c)|. Therefore, it is impossible that the curve G₊(ω_c) crosses the line r₋(ω_c) for all ω (ω_c, π]. On the other hand, from (3.34) we know that for all ω (0, ω_c) the phase of G(ω) is in the interval , i.e., the curve G₋(ω_c) lies inside the third quadrant of the complex plane and hence cannot cross the line r₊(ω_c) which is above the real axis of the complex plane.

Figure 3.9 Proposition 3.13

Now, let us consider the Nyquist plots of two systems of the same form with different delay constants

(3.40)

where

(3.41)

It is not difficult to verify that both of the plots cross the real axis for the first time at the same point (− 1, j0) with the crossing frequencies as

(3.42)

Let and be slopes of tangent lines to G₁(ω) and G₂(ω) at the point (− 1, j0) respectively. It is easy to show that k_c given by (3.38) is strictly decreasing in the delay constant D. Therefore, we have the following proposition.

Proposition 3.14 For frequency responses given by (3.40) and (3.41) the following inequality holds:

(3.43)

Lemma 3.15 Let G_i(ω), i = 1, 2 be given by (3.40) and (3.41). Then,

(3.44)

holds for all ω [− π, π] and 0 ≤ κ < 1.

Proof. First of all, we note that both G₁(ω) and G₂(ω) enjoy the symmetry property with respect to the real axis of the complex plane, i.e.,

Thus, we need only to prove (3.44) for all ω [0, π]. Without loss of generality, we assume that D₂ < D₁. Then we have by (3.42). Now, let us split the frequency interval [0, π] into four parts, namely , and , and consider each case below.

Case 1:

In this case both G₁(ω) and G₂(ω) are in the third quadrant of the complex plane because their phases are between −π and −π/2. In this quadrant, tangent line is on the right side of tangent line because by Proposition 3.14 And the tangent lines meet at the point (− 1, j0) (see Figure 3.10). So, by Proposition 3.13, both curves G₁(ω) and G₂(ω) are on the right side of in this case. Moreover, only G₁(ω) intersects at the point (− 1, j0) when . Therefore, we have .

Case 2:

In this case we claim that both G₁(ω) and G₂(ω) are on the right side of . Noticing Proposition 3.13 and Proposition 3.14, to prove this claim it suffices to show that G₁(ω) never intersects in the third quadrant. This is indeed the case because but any point on has modulus greater than unity (since ). Therefore, we have .

Case 3:

In this case G₂(ω) on the right side of (by Proposition 3.13) and under the real axis of the complex plane (by the same argument given in Case 1), and G₁(ω) is on the right side of (by Proposition 3.13) and never intersects in the third quadrant (by the same argument given in Case 2). Therefore, both G₁(ω) and (G₂(ω) are inside .

Case 4: ω → 0

Figure 3.10 Illustration of proof of Lemma 3.15.

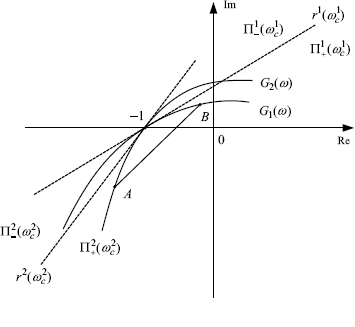
In this case we can write G₁(ω) and G₂(ω) as

where ε is an infinitely small positive number and θ [0, π/2]. So delays play no role when ω → 0. When θ varies from 0 to π/2 Both G₁(ω) and G₂(ω) synchronously draw a clockwise infinitely large quarter-circle with phase angle in [− π/2, 0]. Hence, in this case.

Summarizing all the four cases we know

or

for any ω [0, π]. By Lemma 3.6, we conclude that

holds for all ω [0, π] and 0 ≤ κ < 1.

Now, we are ready to prove the following theorem.

Theorem 3.16 Given any natural number n ≥ 2,

(3.45)

holds for all κ [0, 1) and all ω (− π, π), where

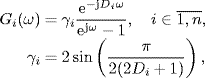
where , are divers nonnegative integers. Consequently, does not contain the point (− 1, j0) for all ω [− π, π] and all κ [0, 1).

Proof. By the symmetry property of the frequency response we need only to prove the lemma for all ω [0, π].

We first note that

(3.46)

holds for all ω [0, π] since both G_i(ω) and the origin of the complex plane lie in . We also note that

holds for ω = π since G_i(π) = − cos (D_iπ)/2 > − 1. Then, by continuity of the set on ω, goes out of the region implies its boundary, , or κCo{0, G_i(ω)}, goes out of the same region. But Lemma 3.15 and (3.46) have excluded this possibility. Therefore, we conclude that

for all ω [− π, π]. Therefore, does not contain the point (− 1, j0) for all ω [− π, π] because .

3.4 Scalability of Second-Order Systems

In this section we study the second-order time-delayed systems of two types. In accordance with textbooks on classic control theory, it will be called a system of type I if its (open-loop) transfer function contains a single integrator, or a system of type II if its transfer function contains double integrators.

3.4.1 System of Type I

Many dynamic nodes of distributed control systems, such as the primal-dual algorithm of the congestion control of communication networks, and position feedback control of a mobile agent with inertia, can be modeled as a second-order system with a single integrator. The time-delayed form of such a system is given by

(3.47)

where k > 0 is the gain, T > 0 is the delay constant, and −α < 0 is the LHP pole of the system.

The frequency response of system (3.47) is given by

(3.48)

Denote by ω_c > 0 the minimal crossing frequency of G(jω), i.e., G(jω) crosses the real axis of the complex plane for the first time when ω = ω_c. Actually, ω_c > 0 is the minimal frequency satisfying the following equation:

(3.49)

Denote by γ the gain margin of G(s), which is defined by

(3.50)

From (3.49) we have

Using this equality, we get

(3.51)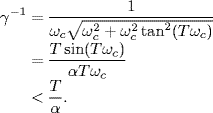

Now, let

(3.52)

(3.53)

Then, G(jω) can be rewritten as

(3.54)

by abusing the notation G(·) just for convenience. Obviously, for a given system G(s), the curve

(3.55)

is just a linear zoom of the Nyquist plot of G(jω) and hence preserves almost all of the geometric properties of G(jω). For example, the Nyquist plot of G(jω) is clockwise in the frequency interval [ω₁, ω₂] if and only if the curve of G(jx) is clockwise in the parameter interval [Tω₁, Tω₂]. Similarly, G(jω) does not admit self-intersection in the interval [ω₁, ω₂] if and only if G(jx) does not admit self-intersections in the interval [Tω₁, Tω₂].

Proposition 3.17 The curve G(jx) does not admit self-intersections for all x ≥ 0.

Proof. The assertion is obvious from the fact that the modulus of G(jx), i.e.,

is strictly decreasing in x in the interval [0, ∞).

Proposition 3.18 The curve G(jx) is clockwise in the parameter interval [0, ∞).

Proof. To prove the proposition, we only need to check the sign of the numerator of the curvature. By (3.13) we know that the curvature of G(jx) is given by

Denote

where

(3.56)

(3.57)

Then, we have

(3.58)

Therefore,

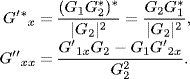
Straightforward calculation yields

(3.59)

Taking (3.58) into account, we get

(3.60)

From (3.56) and (3.57), we get

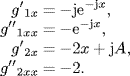
So, we have

where

(3.61)

(3.62)

Therefore,

(3.63)

where

(3.64)

Obviously, Im(QP^*) < 0, for all x > 0 and all A ≥ 0. This implies

Thus, the clockwise property of the curve of G(jx) in the interval [0, ∞) is proved.

Given ω_c the minimal crossing frequency of G(jω), it is obvious that G(jx) crosses the real axis of the complex plane for the first time when

(3.65)

According to (3.49), the minimal crossing parameter x_c satisfies

(3.66)

Differentiating both sides of the above equation with respect to A, we get

which gives

(3.67)

where . So, we have the following proposition.

Proposition 3.19 The minimal crossing point x_c is a strictly monotonically increasing function of parameter A.

Denote by r(x_c) the tangent line of G(jx) at the minimal crossing point x_c. Then, we can prove the following result.

Proposition 3.20 The slope of r(x_c), denoted by T_c, is a strictly monotonically increasing function of parameter A. Moreover, T_c > 0 for all A > 0.

Proof. The slope of the tangent line r(x_c) is given by

(3.68)

Note that

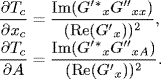
So, we get

(3.69)

where has been obtained in the proof of Proposition 3.18 (see (3.63) and (3.64)), and is given by (3.67). Now, we calculate . Denote

where g₁(x) and g₂(x) are given by (3.56) and (3.57), respectively. Then, we have

(3.70)

Therefore,

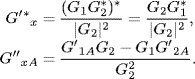
Straightforward calculation yields

Taking (3.70) into account, we get

From (3.56) and (3.57), we get

So, we have

where

and P is given by (3.62). Therefore,

(3.72)

where

(3.73)

Now, substituting (3.67), (3.63), (3.64), (3.72) and (3.73) into (3.69) yields

where

Therefore, T_c(A) is a strictly monotonically increasing function of the parameter A. Finally, we note that T_c = 0 when A = 0. This implies that T_c > 0 for all A > 0. The proposition is thus proved.

Now, using Lemma 3.4, we can prove the following result.

Proposition 3.21 For all x [0, ∞), the curve G(jx) lies on the right side of r(x_c), i.e., G(jx) G(jx_c) ∪ Π₊(x_c), ∀x [0, ∞).

Proof. For simplicity of statement, we denote the curve of G(jx) in the parameter interval [0, ∞) as G[0, ∞). Also, we denote the curve G(jx) in the parameter interval (x_c, ∞) as G₊(x_c) and the curve G(jx) in the parameter interval [0, x_c) as G₋(x_c). By Proposition 3.17 and Proposition 3.18, G[0, ∞) is clockwise and has no self-intersections. Therefore, by Lemma 3.4, the only way that the curve G₊(x_c) can leave the half plane Π₊(x_c) is by crossing the line r₋(x_c) and the only way that G₋(x_c) can enter the half plane Π₊(ω_c) is by crossing the line r₊(ω_c). In the proof of Proposition 3.17, we have mentioned that the modulus |G(jx)| is strictly decreasing in x, and hence, |G(jx)| < |G(jx_c)|, ∀x (x_c, ∞). But, from Proposition 3.20, we know that the slope of the tangent line at x = x_c is greater than zero. This implies that the modulus of any point on r₋(x_c) is greater than |G(jx_c)|. Therefore, it is impossible that the curve G₊(x_c) crosses the line r₋(x_c) for all x (x_c, ∞). On the other hand, for any x [0, x_c), the curve G₋(x_c) lies inside the third quadrant of the complex plane and hence cannot cross the line r₊(x_c), which is located above the real axis of the complex plane. The proposition is thus proved.

Next, let us consider the Nyquist plots of two systems of the same form with different delay constants:

(3.74)

where γ_i is the gain margin of the transfer function

Lemma 3.22 If the following condition

(3.75)

holds for the frequency responses of systems given by (3.74), then

(3.76)

holds for all real numbers κ [0, 1) and all ω [0, ∞).

Proof. First of all, we note that both of the two plots of the functions in the form (3.74) cross the real axis for the first time at the same point (− 1, j0), with minimal crossing frequencies

(3.77)

where is given by (3.66). Without loss of generality, assume that A₁ < A₂, which by (3.75) also implies that

Since when both G₁(jω) and G₂(jω) are in the third quadrant, the conclusion of the lemma obviously holds in the frequency interval . We need to prove the proposition for the frequency interval . To do so, let us split this frequency interval into two parts, namely and . We consider each case below.

Case 1:

In this case, G₂(jω) is on the right side of (by Proposition 3.13) and under the real axis of the complex plane (since ), and G₁(jω) is on the right side of (by Proposition 3.13). Moreover, G₁(jω) never intersects in the third quadrant because , but any point on has modulus greater than unity (since by Proposition 3.20). Therefore, both G₁(jω) and G₂(jω) are inside , which is a convex set (since by Proposition 3.20). Thus, for any given κ [0, 1), we have .

Case 2:

In this case, both G₁(jω) and G₂(jω) have already crossed the real axis for the first time. We claim that both G₁(jω) and G₂(jω) are on the right side of . Noticing Proposition 3.13, to prove this claim it suffices to show that G₁(jω) never intersects in the third quadrant. This is indeed the case as we have shown in Case 1. Therefore, both G₁(jω) and G₂(jω) are inside , which is obviously a convex set. Note that only G₂(jω) intersects at the point (− 1, j0) when . Thus, we have , for any given 0 ≤ κ < 1.

Summarizing the conclusion obtained in the above two cases, we complete the proof of the lemma.

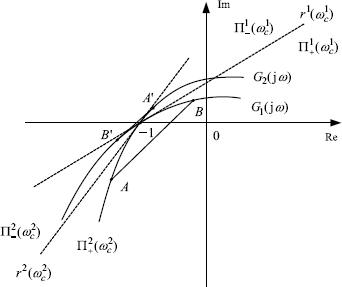
A graphical illustration of Lemma 3.22 is given by Figure 3.11. Note that condition (3.75) is necessary for the conclusion of Lemma 3.22 Otherwise, the less curved G₂(jω) may cross the real axis and enter the second quadrant before the more curved G₁(jω) does. In this case, Co(G₁(jω), G₂(jω)) will be out of the region , as illustrated as A ' B ' in Figure 3.11.

Figure 3.11 Illustration of Lemma 3.22

Now, we are ready to prove the following theorem.

Theorem 3.23 Suppose that the following condition

(3.78)

holds for the frequency response of a family of systems described by

(3.79)

where γ_i is the gain margin of the transfer function

Then, does not contain the point (− 1, j0) for all real numbers κ [0, 1) and all ω [0, ∞).

Proof. By Lemma 3.22, we know that

(3.80)

holds for all . Note that

(3.81)

holds for all ω [0, ∞) since both G_i(jω) and the origin of the complex plane lie in . Also, note that

holds when ω→ ∞ since G_i(j ∞) goes to the origin of the complex plane for all . Therefore, by continuity of the set on ω, if goes out of the region , then its boundary,

or

will go out of the same region at some frequency. But (3.80) and (3.81) have excluded this possibility. Therefore, we conclude that

Since , does not contain the point (− 1, j0) for all ω [0, ∞). The theorem is thus proved.

For the family of systems given by (3.79), denote by the index of the system with minimal value of parameter A_i, i.e.,

(3.82)

Let be the slope of the tangent line to the Nyquist plot of at the intersection point C, as illustrated by Figure 3.12. It is easy to see that . An analytic formula of is given by

(3.83)

Define

(3.84)

Now, we are ready to give an alternative theorem for checking if (− 1, j0) is contained by .

Figure 3.12 Definition of μ_i and illustration of the proof of Theorem 3.24.

Theorem 3.24 Let μ_i be defined by (3.84) and G_i(jω) be defined by (3.79). Then, does not contain the point (− 1, j0) for all real numbers κ [0, 1) and all ω [0, ∞).

Proof. For simplicity, we only show the validity of the theorem for the case of two systems. But the proof can be directly extended to the general case.

Without loss of generality, assume A₁ < A₂, i.e., . Then, we have μ₁ = 1 and

where is the slope of the tangent line (see Figure 3.12). To prove the theorem, it suffices to show that .

Note that G₁(jω) intersects the real axis of the complex plane at (− 1, j0) while μ₂G₂(jω) intersects the real axis at point F with coordinate (μ₂, j0). It is easy to see that |OF| = |OE| = μ₂, where |OE| is the shortest distance to the origin from the tangent line . Since the modulus of μ₂G₂(jω) is strictly monotonically decreasing in ω, we have

which implies that μ₂G₂(jω) never touches for . To show that μ₂G₂(jω) never touches for , we only need to notice the fact that μ₂ < 1 and (by Proposition 3.20), where and are the slopes of the tangent lines and , respectively (see Figure 3.12).

3.4.2 System of Type II

Many dynamic nodes in distributed control systems, such as the second-order active queue management (AQM) algorithm, force-controlled ideal mobile agents with both position and velocity feedback, can be modeled as a second-order system with double integrators, which is referred to as the second-order system of type II in the literature of classic feedback control. In this subsection, we give detailed analysis of the geometric properties of the frequency response of the time-delayed system

(3.85)

where k > 0 is the gain, T > 0 is the delay constant, and −α < 0 is the zero of the system. The frequency response of system (3.85) is

(3.86)

Let x = Tω. Then, G(jω) can be rewritten as

(3.87)

where

(3.88)

is a key parameter in the geometric analysis for this system. (3.87) shows that for a given system G(s), the curve

(3.89)

is just a linear zoom of the Nyquist plot of G(jω). Hence, G(jx) preserves all of the geometric properties of G(jω). For example, the Nyquist plot of G(jω) is clockwise in the frequency interval [ω₁, ω₂] if and only if the curve of G(jx) is clockwise in the parameter interval [Tω₁, Tω₂]. Similarly, G(jω) does not admit self-intersection in the interval [ω₁, ω₂] if and only if G(jx) does not admit self-intersections in the interval [Tω₁, Tω₂]. Therefore, next we will mainly study the geometric property of G(jx) instead of G(jω).

Proposition 3.25 The curve G(jx) does not admit self-intersections for all x ≥ 0.

Proof. The proposition is obvious from the fact that the modulus of G(jx), i.e.,

is strictly decreasing in x in the interval [0, ∞).

Proposition 3.26 If A < 1, then the curve G(jx) is clockwise in the parameter interval [x₀, ∞), where

(3.90)

Proof. To prove the proposition we only need to check the sign of the numerator of the curvature

Straightforward calculating yields

(3.91)

(3.92)

(3.93)

Therefore,

(3.94)

Denote

(3.95)

When 0 ≤ A ≤ 1, it is easy to get the largest root of p(x) as

(3.96)

When x > x₀ we have p(x) > 0. This implies

So, the clockwise property of the curve of G(jx) in the interval [x₀, ∞) is proved.

We call x₀ the maximal critical parameter of G(jx), and correspondingly, ω₀ = x₀/T the maximal critical frequency of G(jω).

Let ω_c be the minimal crossing frequency of G(jω), i.e, the Nyquist plot of G(jω) crosses the real axis for the first time at ω = ω_c as ω varies from 0 to ∞. It is easy to prove that ω_c is the minimal frequency satisfying

(3.97)

Similarly, we have the minimal crossing parameter of G(jx) at

According to (3.97), the minimal crossing point x_c satisfies

(3.98)

Both x₀ and x_c can be regarded as functions of A, an adjustable parameter. The following proposition gives some important properties of x₀(A) and x_c(A) of G(jx).

Proposition 3.27 If A [0, 1), then the following claims are true:

1. The maximal critical parameter x₀(A) is a strictly monotonically increasing function of the parameter A.

2. The minimal crossing point x_c(A) is a strictly monotonically decreasing function of the parameter A.

3. There exists such that x₀(A) ≤ x_c(A) for all , and the equality holds if and only if .

Proof. Denote . Then from (3.90) we have

Thus,

(3.99)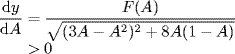

as A [0, 1), where

Therefore, y is a strictly monotonically increasing function of A. Hence, so is x₀(A). Claim (1) of the proposition is proved.

According to the definition of x_c we have

Obviously, the equation has a solution x_c [0, π/2) if A (0, 1]. x_c = 0 if and only if A = 1. By the formula for derivatives of implicit functions, it is easy to get

for x_c (0, π/2). So x_c(A) is a strictly monotonically decreasing function of A. Claim (2) of the proposition is proved.

Notice that x_c = π/2, x₀ = 0 when A = 0 and when A = 1. According to Claim (1) and Claim (2), this fact directly results in Claim (3) of the proposition.

Letting x_c = x₀, we can get the value of . When , the maximal critical point meets the minimal crossing point. Substituting (3.98) into (3.90), we obtain an equation with respect to the parameter A, the solution of which is

(3.100)

So, the following proposition is straightforward from the foregoing discussion.

Proposition 3.28 If , then the curve G(jx) is inside the third quadrant of the complex plane for the parameter interval [0, x₀], and is clockwise for the parameter interval [x₀, ∞), where x₀ is the maximal critical parameter of G(jx).

Denote the tangent line of G(jx) at the minimal crossing point x_c as r(x_c). Then we can prove the following proposition.

Proposition 3.29 The slope, denoted by T_c, of r(x_c) is a strictly monotonically decreasing function of the parameter A, and moreover, T_c > 0 for all .

Proof. The slope of the tangent line r(x_c) is given by

(3.101)

To show T_c > 0 for all it suffices to show

(3.102)

By Proposition 3.27, we know that for all

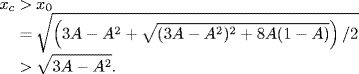
So , and hence, T_c > 0 for all .

Now we show that T_c is a strictly monotonically decreasing function of A. Note that

where G ” _xA represents and all the remaining notations are the same as given in the Proof of Proposition 3.26. So from (3.101) it follows that

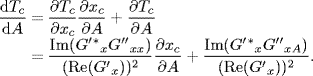
Straightforward computing gives

(3.103)

In Proof of Proposition 3.27 we have shown

(3.104)

So, using (3.91)–(3.94) and (3.103), we get

where the polynomial Π(x_c) is defined by (3.95). Substituting (3.95) and (3.104) into the above equation yields

Therefore, T_c(A) is a strictly monotonically decreasing function of A. The proposition is thus proved.

Now, using Lemma 3.4, we can prove the following proposition.

Proposition 3.30 For all x [x₀, ∞), the curve G(jx) lies on the right side of r(x_c), i.e., G(jx) G(jx_c) ∪ Π₊(x_c), ∀x [x₀, ∞).

Proof. For simplicity of statement we denote the curve of G(jx) in the parameter interval [x₀, ∞) as G[x₀, ∞). Also, we denote the curve G(jx) in the parameter interval (x_c, ∞) as G₊(x_c) and the curve G(jx) in the parameter interval [x₀, x_c) as G₋(x_c). By Proposition 3.17 and Proposition 3.18, G[x₀, ∞) is clockwise and has no self-intersections. Therefore, by Lemma 3.4, the only way that the curve G₊(x_c) can leave the half plane Π₊(x_c) is by crossing the line r₋(x_c) and the only way that G₋(x_c) can enter the half plane Π₊(ω_c) is by crossing the line r₊(ω_c) (see Figure 3.13). In the proof of Proposition 3.25 we have mentioned that the modulus |G(jx)| is strictly decreasing in x, and hence, |G(jx)| < |G(jx_c)|, ∀x (x_c, ∞). But, from Proposition 3.29, we know the slope of the tangent line at x = x_c is greater than zero. This implies that the modulus of any point on r₋(x_c) is greater than |G(jx_c)|. Therefore, it is impossible that the curve G₊(x_c) crosses the line r₋(x_c) for all x (x_c, ∞). On the other hand, from Proposition 3.28 we know that for all x [x₀, x_c) the curve G₋(x_c) lies inside the third quadrant of the complex plane and hence cannot cross the line r₊(x_c) which is above the real axis of the complex plane. The proposition is thus proved.

Figure 3.13 Graphic illustration of Proposition 3.30

Now, let us consider the Nyquist plots of two systems of the same form with different delay constants:

(3.105)

where γ_i is the gain margin of the transfer function

(3.106)

Lemma 3.31 If the frequency responses of systems (3.105) satisfy the following conditions:

1. A_i < 0.4495, ∀i = 1, 2,

2. , ∀i = 1, 2,

where

(3.107)

then

holds for any given real number κ [0, 1) and any .

Proof. First of all, we note that both of the two plots of the functions in the form (3.105) cross the real axis for the first time at the same point (− 1, j0) with the minimal crossing frequencies as

(3.109)

where is given by (3.98). Without loss of generality, we assume that A₂ < A₁. This also implies T₂ < T₁. Then, by Proposition 3.27, we have

which also implies that

since T₂ < T₁.

Now, we consider the lemma in the following two cases separately.

Case 1:

In this case G₁(jω) has crossed the real axis while G₂(jω) is still under the real axis of the complex plane. We note that condition (2) of the lemma implies the maximal critical frequencies of both G₁(jω) and G₂(jω) are less than . Therefore, by Proposition 3.28, the Nyquist plots of G₁(jω) and G₂(jω) are both clockwise for the frequency interval under condition (1) of the lemma. Hence, by Proposition 3.30, G₁(jω) is on the right side of and G₂(jω) is on the right side of . Moreover, G₁(jω) never intersects in the third quadrant because but any point on has modulus greater than unity (since the slope of the tangent line is greater than zero by Proposition 3.29). Now, from Proposition 3.29 we know that under the assumption A₂ < A₁, the slope of the tangent line is less than the slope of the tangent line . This implies that both G₁(jω) and G₂(jω) lie in the intersection of and for each . Hence, by Lemma 3.6, for any given 0 ≤ κ < 1 and for each , the convex combination κCo(G₁(jω), G₂(jω)) lies in .

Case 2:

In this case both G₁(jω) and G₂(jω) have crossed the real axis for the first time. We claim that both G₁(jω) and G₂(jω) are on the right side of . Noticing Proposition 3.28 and Proposition 3.29, to prove this claim it suffices to show that G₁(jω) never intersects in the third quadrant. This is indeed the case as we have shown in Case 1. Therefore, both G₁(jω) and G₂(jω) are inside which is obviously a convex set. Note that only G₂(jω) intersects at the point (− 1, j0) when . Thus, by Lemma 3.6, we have , for any given 0 ≤ κ < 1.

So, we conclude that the lemma is true.

Now, we are ready to prove the following theorem.

Theorem 3.32 Suppose that the frequency responses of a family of systems are described by

(3.110)

where γ_i is the gain margin of the transfer function

If the following conditions hold:

1. A_i < 0.4495, ,

2. , ,

where

(3.111)

then, does not contain the point (− 1, j0) for any given real number κ [0, 1) and any ω [0, ∞).

Proof. Let be the minimal crossing frequency of G_i(jω). By Proposition 3.27, is strictly decreasing in A_i, and hence in T_i. Therefore, we have

where is given by (3.111). Since

we have

Now, we split the frequency interval [0, ∞) into two parts: and , and prove the theorem for the following two cases separately.

Case 1:

In this case, all the plots are in the third quadrant under condition (1) of the theorem. So does not contain the point (− 1, j0).

Case 2:

Note that in this case all the plots have passed their maximal critical frequencies and are thus clockwise because condition (2) of the theorem guarantees that

By Lemma 3.31 we know that

(3.112)

holds for any . Now, we note that

(3.113)

holds for all since both G_i(jω) and the origin of the complex plane lie in . We also note that ⊂ holds when ω→ ∞ since G_i(j ∞) goes to the origin of the complex plane for all . Therefore, by continuity of the set on ω, goes out of the region implies that its boundary, i.e., κCo(G_i(jω), G_k(jω)) or κCo(0, G_i(jω)), will go out of the same region. But (3.112) and (3.113) have excluded this possibility. Therefore, we conclude that

Since , does not contain the point (− 1, j0) for .

Therefore, summarizing the above two cases, the theorem is proved.

3.5 Frequency-Sweeping Condition

Lemma 3.1 shows that the scalability condition for symmetric multi-agent system can be verified by checking if the point (− 1, j0) is touched by the convex combination of Nyquist plots of each pair of agents. In this section we will further convert the latter into the problem of the stability test for a convex combination of two stable quasi-polynomials.

3.5.1 Stable Quasi-Polynomials

First let us recall the concept of stability of a quasi-polynomial.

A quasi-polynomial is an entire function of the form

(3.114)

where p_i(s), i = 0, 1, , m, are polynomials with coefficients and τ₀ < τ₁ < < τ_m are real numbers representing delays.

For n ≥ 0, m > 0 and any real vector τ = [τ₀, τ₁, , τ_m]^T with ordered components τ₀ < τ₁ < < τ_m, let denote the set of all quasi-polynomials defined by (3.114) with coefficients in .

A non-constant quasi-polynomial is called Hurwitz stable or simply stable if all its roots belong to the open left half plane. The set of all Hurwitz stable quasi-polynomials in is denoted by .

Definition 3.33 A quasi-polynomial is called a global convex direction for the set if, for all stable quasi-polynomials , the stability of f(s) + g(s) implies the stability of the whole segment of quasi-polynomials [f, f + g] = {f(s) + μg(s); μ [0, 1]}, i.e., if g(s) satisfies, for all ,

The following lemma due to Kharitonov and Zhabko (1994) shows that the global convex direction can be verified through a frequency-sweeping test of the phase velocity.

Lemma 3.34 A quasi-polynomial is a global convex direction for the set if and only if for all ω {ω > 0 | g(jω) ≠ 0} the following condition is satisfied:

(3.115)

Note that the global convex direction is defined for the set of all Hurwitz stable quasi-polynomials. To check the stability of a convex combination of two specific quasi-polynomials, we need the following definition of local convex direction.

Definition 3.35 A quasi-polynomial is called a local convex direction for a Hurwitz quasi-polynomial f(s) if the stability of f(s) + g(s) implies the stability of the whole segment of quasi-polynomials [f, f + g] = {f(s) + μg(s); μ [0, 1]}, i.e., if g(s) satisfies

By Definition 3.35, the following proposition is true.

Proposition 3.36 Given . Then, the following two statements are equivalent:

1. ;

2. , and f₁(s) − f₀(s) is a local convex direction for f₀(s).

The following lemma gives a sufficient condition for the local convex direction.

Lemma 3.37 A quasi-polynomial is a local convex direction for the quasi-polynomial f(s) if for all ω {ω > 0 : g(jω) ≠ 0} the following condition is satisfied:

(3.116)

Proof. The lemma can be proved based on the fact that the phase of any Hurwitz quasi-polynomial is monotonically increasing when s goes along the imaginary axis from −j∞ to j∞. We leave the completion of the proof to the reader as an exercise.

The following lemma gives a necessary and sufficient condition of the local convex direction. It is directly from the fact that the instability of one of the polynomials , implies that there is a quasi-polynomial , with at least one zero on the imaginary axis (Gu, Kharitonov and Chen 2003).

Lemma 3.38 A quasi-polynomial is a local convex direction for the quasi-polynomial f(s) if and only if the complex curve

does not touch the negative real semi-axis of the complex plane.

3.5.2 Frequency-Sweeping Test

Given the normalized transfer function of time-delayed system as

(3.117)

where η, l, n are non-negative integers satisfying l ≤ n + η; N_i(s) and D_i(s) are l-order and n-order real-coefficient polynomials of s, respectively; D₁(s) and D₂(s) are coprime. Note that D_i(s) can be a constant which can be considered as a zero-order polynomial. Without loss of generality, it is assumed that 0 ≤ T₁ ≤ T₂. Denote

(3.118)

(3.119)

(3.120)

(3.121)

The following lemma relates the stability of a convex hull of two time-delayed systems to the robust stability of a convex combination of two Hurwitz polynomials.

Theorem 3.39 Suppose normalized transfer functions are given by (3.117), and D_i(s), i = 1, 2, are coprime Hurwitz stable polynomials or positive constants. Then, the following conditions are equivalent:

1. ;

2. ;

3. f₀(s) and f₁(s) are stable, g(s) is a local convex direction for f₀(s).

Proof. “(1) (2)”. Write as

(3.122)

where λ [0, 1]. Since D₁(s), D₂(s) are Hurwitz stable polynomials or positive constants, by the Nyquist criterion of stability we know that the system with characteristic equation as

(3.123)

is robustly stable for all λ [0, 1] if and only if

From (3.122) it is easy to see that the characteristic quasi-polynomial associated with (3.123) is given by

(3.124)

Rewrite f_λ(s) as

Then, the equivalence between (1) and (2) is clear.

“(2) (3)”. It follows directly from Proposition 3.36.

Note that if we replace statement (1) in Theorem 3.39 by

(3.125)

then, it is not equivalent to statement (2) or (3) in Theorem 3.39. Actually, straightforward calculation will show that (3.125) is equivalent to saying

(3.126)

is Hurwitz stable. By the Nyquist criterion of stability it is equivalent to say that the system with characteristic equation as

(3.127)

is robustly stable for all λ [0, 1]. Rewrite f_λ,κ(s) as

Note that the Nyquist plots of normalized transfer-functions , i = 1, 2, cross the real axis at the point (− 1, j0). Therefore, , i = 1, 2, do not contain the point (− 1, j0) for any ω [0, ∞) and any κ [0, 1). Since D_i(s), i = 1, 2, are Hurwitz stable polynomials or positive constants, by the Nyquist criterion of stability again, we know the systems with the following characteristic equations

are stable. This implies that quasi-polynomials

are Hurwitz stable. Therefore, by Definition 3.33 we know that f_λ,κ(s) is Hurwitz stable if and only if the quasi-polynomial

is a local convex direction for f_0,κ(s), or simply if it is a convex direction. The following lemma summarizes the above discussion.

Theorem 3.40 Suppose normalized transfer functions are given by (3.117), and D_i(s), i = 1, 2, are coprime Hurwitz stable polynomials or positive constants. Then,

if and only if g(s) = N₂(s)D₁(s)e^−T₂^s − N₁(s)D₂(s)e^−T₁^s is a local convex direction for f_0,κ(s), or simply if g(s) is convex direction.

Now, we can generalize the result of Theorem 3.40 to a family of n normalized systems.

Theorem 3.41 Consider a family of normalized systems described by

(3.128)

Suppose that

(3.129)

Then,

if for any , the quasi-polynomial

is a convex direction.

Proof. Suppose N_k(s)D_i(s)e^−T_k^s − N_i(s)D_k(s)e^−T_i^s is a convex direction. Then, by Theorem 3.40, we know that

(3.130)

holds for any . Note that

(3.131)

also holds for any since does not contain (− 1, j0) and the origin is inside the region enclosed by . Also, note that

holds when ω→ ∞ since . Therefore, by continuity of the set on ω, if intersects the point (− 1, j0) then its boundary, or will definitely intersects the point (− 1, j0) for some ω^* [0, ∞). But (3.130) and (3.131) have excluded the possibility. Therefore, we conclude that

Theorem is thus proved.

3.6 Notes and References

The concept and expression of the signed curvature for parametric equation a curve can be found in many textbooks on classical differential geometry such as Guggenheimer (1977).

The clockwise property of the Nyquist plot of transfer functions attracted attention of control researchers as early as the 1980s (Horowitz and Ben-Adam (1989). It was found useful in the study of absolute stability (Tesi et al. 1992). Lemma 3.5 was initially given in Tesi et al. 1992) and extended to the current version in Tian and Yang (2004a).

In 1990s, convexity, a notion very closely related to the clockwise property, was proved for the frequency response arc of stable polynomials as a by-product of the study of robust stability against parametric uncertainties (Gu 1994; Hamann and Barmish 1993). Rantzer (1992) studied the relationship between the phase velocity of the frequency response plot of polynomials and the robust stability of a convex set of stable polynomials, and proposed the notion of convex direction in the space of stable polynomials. Kharitonov and Zhabko (1994) extended the notion of convex direction to the space of stable quasi-polynomials.

The relationship between the scalability of a distributed congestion control algorithm and differential geometric properties of the frequency response of the control system was uncovered in Tian and Yang (2004a). In this chapter it was shown that the clockwise property of the frequency response curve (Nyquist plot) of a congestion control system plays a key role in the scalability of the stability criterion for a network with diverse round-trip delays. Besides, some other differential geometric properties, such as phase monotonicity and/or modulus monotonicity, critical point of clockwise property, phase velocity, etc., are also shown to be very important in the scalability analysis for distributed congestion control systems (Tian 2005a,b; Tian and Chen 2006). In Tian and Liu (2008) and Tian and Liu (2009) it was revealed that the scalability of consensus criteria for multi-agent systems with diverse input delays are also closely related to differential geometric properties of node dynamics of networks.

The material of Section 3.3 is taken from Tian and Yang (2004a,b). Section 3.4 is based on Tian (2005a); Tian and Chen (2006) while Section 3.5 is based on Kharitonov and Zhabko (1994) and Tian (2005b).

References

Gu K (1994). Comments on “Convexity of frequency response arcs associated with a stable polynomials”. IEEE Transactions on Robotics and Automation, 39, 2262–2265.

Gu K, Kharitonov VL and Chen J (2003). Stability of Time-delayed Systems. Birkhäuser, Boston.

Guggenheimer HW (1977). Differential Geometry. Dover, New York.

Hamann JC and Barmish BR (1993). Convexity of frequency response arcs associated with a stable polynomial. IEEE Transactions on Bobotics and Automation, 38, 904–915.

Horowitz I and Ben-Adam S (1989). Clockwise nature of Nyquist locus of stable transfer functions. International Journal Control, 49, 1433–1436.

Kharitonov VL and Zhabko AP (1994). Robust stability of time-delayed systems. IEEE Transactions on Automatic Control, 39, 2388–2397.

Rantzer A (1992). Stability conditions for polytopes of polynomials. IEEE Transactions on Automatic Control, 37, 79–84.

Tesi A, Vicino A and Zappa G (1992). Clockwise property of the Nyquist plot with implications for absolute stability. Automatica, 28, 71–80.

Tian Y-P and Yang H-Y (2004a). Stability of the Internet congestion control with diverse delays. Automatica, 40, 1533–1541.

Tian Y-P and Yang H-Y (2004b). Stability of distributed congestion control with diverse communication delays. Proceedings of the World Congress on Intelligent Control and Automation 2, 1438–1442.

Tian Y-P (2005a). Stability analysis and design of the second-order congestion control for networks with heterogeneous delays. IEEE/ACM Transactions on Networking, 13, 1082–1093.

Tian Y-P (2005b). A general stability criterion for congestion control with diverse communication delays. Automatica, 41, 1255–1262.

Tian Y-P and Chen G (2006). Stability of the primal-dual algorithm for congestion control. International Journal of Control, 79, 662–676.

Tian Y-P and Liu C-L (2008). Consensus of multi-agent systems with diverse input and communication delays. IEEE Transactions on Automatic Control, 53, 2122–2128.

Tian Y-P and Liu C-L (2009). Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations. Automatica, 45, 1347–1353.