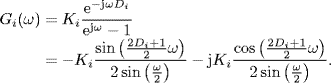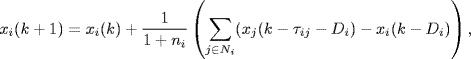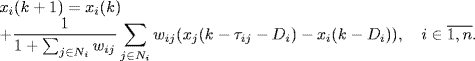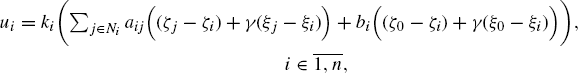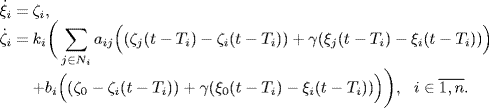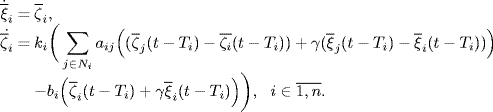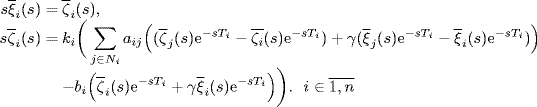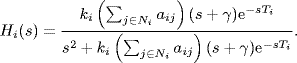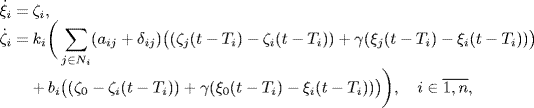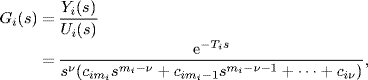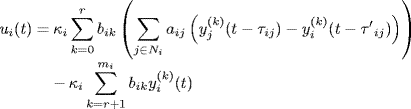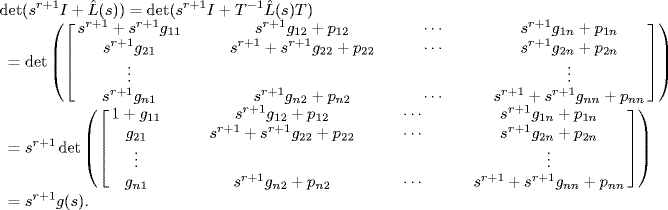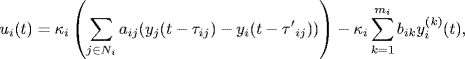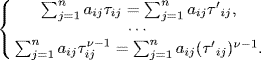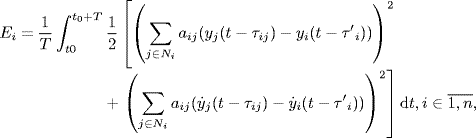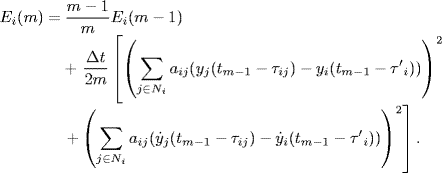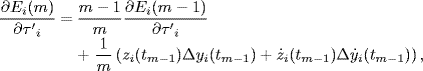Chapter 7
Consensus in Heterogeneous Multi-Agent Systems
Gentlemen can live harmoniously together even though they have heterogeneous characters, but non-gentlemen of the same character live in discord.
Confucius (551–479 BC), Analects of Confucius
Multi-agent systems (MASs) may contain heterogeneous network channels and/or heterogeneous agent dynamics. Even for systems with identical plants in agents, diverse input delays generate heterogeneous agent dynamics, and diverse communication delays result in heterogeneous network channels. Consensus problems in heterogeneous MASs are studied in this chapter. High-order consensus is defined for a class of high-order heterogeneous MASs. A necessary and sufficient condition is given for the existence of high-order consensus solutions to the considered class of systems. The condition shows that for systems with diverse communication delays, high-order consensus does not require that the self-delay of each agent to be equal to the corresponding communication delay. The frequency-domain scalability analysis method developed in Chapter 3 is applied to first-order and second-order MASs with diverse input delays and communication delays.
7.1 Integrator Agent System with Diverse Input and Communication Delays
In this section, we first consider the consensus problem for the integrator agent system with diverse input delays based on undirected graphs. Due to the heterogeneousness caused by the diverse input delays, the consensus problem of such a system can not be converted into an ordinary stability problem by using the technique developed in Chapter 6. However, we will show that it can still be considered as a semi-stability problem if the interconnection topology graph is connected. Therefore, using the frequency-domain analysis theory developed in Chapter 3, we develop various scalable consensus conditions, which uses only local information of each agent. Finally, by considering the consensus problem for digraph-based systems with both diverse communication delays and diverse input delays, we will show that consensus condition is dependent on input delays but independent of communication delays when the digraph contains a globally reachable node.
7.1.1 Consensus in Discrete-Time Systems
Consider a discrete-time multi-agent system with topology graph G = (V, E, A) and integrator agents given by
where ![]() and
and ![]() denote the state and the control input of agent i at time instant k, respectively. The topology graph G = (V, E, A) of the system can be directed or undirected, depending on context. The consensus protocol for the system is given by
denote the state and the control input of agent i at time instant k, respectively. The topology graph G = (V, E, A) of the system can be directed or undirected, depending on context. The consensus protocol for the system is given by
(7.2) ![]()
where Ni denotes the neighbors of agent i, and aij > 0 is the adjacency element of A in the graph G = (V, E, A).
When each agent is subject to an input delay Di, system (7.1) becomes
Under diverse communication delays, the consensus protocol becomes
where τij represents the communication delay from agent j to agent i.
Under protocol (7.4), multi-agent system (7.3) is said to achieve a consensus asymptotically if
![]()
where ![]() is a constant.
is a constant.
The closed-loop system of (7.3) and (7.4) is
Let x(k) = [x1(k), ![]() , xn(k)]T, and
, xn(k)]T, and
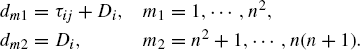
Then, equation (7.5) can be rewritten as a time-delayed system in a vector form
where ![]() , and nd = n(n + 1). Obviously,
, and nd = n(n + 1). Obviously, ![]() , which is the Laplacian matrix of the topology graph.
, which is the Laplacian matrix of the topology graph.
The characteristic equation of system (7.6) is given by
The equilibrium set of system (7.6) is defined by
![]()
When L is singular, Xe is a continuum of equilibrium points. Assume that the interconnection topology of the system is described by a connected undirected graph or a digraph containing a globally reachable node. Then, by Theorem 1.9, the Laplacian matrix L has a simple eigenvalue 0, i.e., det (L) = 0 and rank(L) = n − 1. By the definition of L we also have L1n = 0. So, all the elements in Xe can be represented as c1n where c is any constant. Therefore, system (7.6) achieves a consensus asymptotically, if the solution of the system starting from any given initial states ![]() , asymptotically converges to an element in Xe. According to this analysis the following lemma can be easily proved.
, asymptotically converges to an element in Xe. According to this analysis the following lemma can be easily proved.
Lemma 7.1 If the solutions of equation (7.7) have modulus less than unity except for a root at z = 1, then system (7.6) with a connected undirected graph or a digraph containing a globally reachable node achieves a consensus asymptotically.
This lemma implies that under the assumption that the graph is connected or the digraph contains a globally reachable node the first-order agent system with diverse input delays and communication delays achieves a consensus asymptotically if the closed-loop system is steady semi-stable with z = 1 as a simple pole.
7.1.2 Consensus under Diverse Input Delays
In this subsection we consider the consensus problem for multi-agent systems with input delays only. In this case, the closed-loop form (7.5) of the system reduces to
The following theorem gives a scalable consensus condition for multi-agent systems with diverse input delays
Theorem 7.2 Assume that system (7.8) of n agents is based on an undirected and connected graph G = (V, E, A) with symmetric weights. The system achieves a consensus asymptotically if
Proof. Taking the z-transformation of system (7.8) and writing it in vector form, we get
Note that L in (7.10) is a positively semi-definite matrix since an undirected graph is considered. The characteristic equation is
(7.11) ![]()
Define ![]() . Then, we will prove that all the zeros of p(z) have modulus less than unity except for a zero at z = 1.
. Then, we will prove that all the zeros of p(z) have modulus less than unity except for a zero at z = 1.
Let z = 1, then p(1) = det (L). Since G = (V, E, A) is connected, by Theorem 1.9, zero is a simple eigenvalue of L, i.e., det (L) = 0 and rank(L) = n − 1. Thus, p(z) indeed has a zero at z = 1.
To prove that the system is steady semi-stable with z = 1 as a simple pole it suffices to prove that the zeros of ![]() have modulus less than unity. By the general Nyquist stability criterion for discrete-time systems (Theorem 2.22), this is the case if the eigenloci of
have modulus less than unity. By the general Nyquist stability criterion for discrete-time systems (Theorem 2.22), this is the case if the eigenloci of
![]()
do not enclose the point (− 1, j0) for all ω ![]() [− π, π]. To show this we rewrite F(jω) as
[− π, π]. To show this we rewrite F(jω) as
![]()
where ![]() . Since
. Since
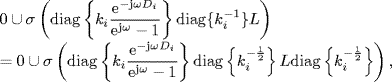
by Lemma 2.34 we have
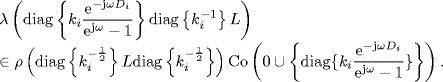
Since the spectral radius of any matrix is bounded by its maximum absolute row sum according to Corollary 2.31 of Gershgorin's disc lemma, it follows from the condition (7.9) that
![]()
Now, from Theorem 3.16 we conclude that eigenloci of F(jω) do not enclose the point (− 1, j0) for all ω ![]() [− π, π], which implies that the zeros of p(z) have modulus less than unity except for a zero at z = 1. Theorem 7.2 is thus proved by Lemma 7.1.
[− π, π], which implies that the zeros of p(z) have modulus less than unity except for a zero at z = 1. Theorem 7.2 is thus proved by Lemma 7.1. ![]()
Remark. By using Corollary 2.32 instead of Corollary 2.31 of Gershgorin's disc lemma in the proof, we know that system (7.8) achieves a consensus asymptotically if there exists ![]() such that
such that
(7.12) ![]()
Of course, this condition can be less conservative than (7.9) and reduces to it if H = I.
Theorem 7.2 gives a scalable delay-dependent consensus condition. This condition suggests that under large input delays, small interconnection weights and small numbers of neighbors increase the possibility of achieving consensus if the interconnection topology graph is connected.
Now, we apply the result of Theorem 7.2 to study the effect of diverse input delays on some important systems that have been extensively investigated in literature.
First, let us consider Vicsek's model, which describes a group of agents moving in the plane with the same line velocity (Vicsek et al. 1995). When the headings of the agents are close to each other, the local updating rule for the headings may be approximated by the following linearized equation (Jadbabaie, Lin and Morse 2003)
(7.13) ![]()
with ![]() and where ni denotes the number of the neighbors of agent i. By applying Theorem 7.2 to this model, it is easy to get its consensus condition as follows:
and where ni denotes the number of the neighbors of agent i. By applying Theorem 7.2 to this model, it is easy to get its consensus condition as follows:
Obviously, when n > 1, condition (7.14) holds only if Di = 0. This implies that Vicsek's model is very sensitive to input delays. To overcome this problem we proposed a modified linearized Vicsek's model with input delays as
where εi > 0 is an adjustable interconnection gain. From Theorem 7.2, we get the following corollary.
Corollary 7.3 Suppose that the interconnection topology graph of system (7.15) is connected. Then, the system achieves a consensus asymptotically if
Remark 1. When Di = 0, from (7.16) it follows that
![]()
which always holds if εi ≤ 1. This implies that the linearized Vicsek's model in its original form (εi = 1) can achieve a consensus asymptotically if and only if the interconnection topology graph of the system is connected. When Di ≥ 1, inequality (7.16) holds only if εi < 1. So, the introduction of small εi is necessary for enhancing the robustness of the linearized Vicsek's model against input delays.
Remark 2. Corollary 7.3 clearly shows the relationship of input delays, interconnection weights and number of neighbors: for large input delays one should use small interconnection weights or have small numbers of neighbors when the graph is kept connected.
Similarly, we can also apply Theorem 7.2 to Moreau's model (Moreau 2005) with input delays
where ![]() denotes the positive weight corresponding to the edge eij in the weighted graph G. The following result is a direct corollary of Theorem 7.2.
denotes the positive weight corresponding to the edge eij in the weighted graph G. The following result is a direct corollary of Theorem 7.2.
Corollary 7.4 Suppose that the interconnection topology graph of system (7.17) is connected and has symmetric weights. Then, the system achieves a consensus asymptotically if
Remark. Obviously, (7.18) always holds if Di = 0. This implies that a symmetric Moreau's model can achieve a consensus asymptotically if and only if the interconnection topology graph of the system is connected. For Di ≥ 1, from (7.18) we get a sufficient consensus condition of Moreau's model as
(7.19) ![]()
7.1.3 Consensus under Diverse Communication Delays and Input Delays
In this subsection, we consider multi-agent systems with both communication delays and input delays. Actually, if the communication delays τij are symmetric, i.e., they satisfy the requirement (2.26), then all the results given in Section 7.1.2 can be extended to systems with both communication delays and input delays without any difficulty.
In general, however, the diversity of communication delays destroys the symmetry of the system even if the graph is undirected with symmetric weights. This implies that the tools used for Theorem 7.2, which are mainly referred to Lemma 2.34 and Theorem 3.16, are no longer applicable. So, in the following analysis we will use Greshgorin's disk theorem (Lemma 2.30) to estimate matrix eigenvalues, which does not require the symmetry. Note that the interconnection topology studied in this subsection can be a digraph with asymmetric weights.
Let us first introduce the following lemma as a preliminary result.
Lemma 7.5 The following inequality
holds for all non-negative integers D and all ω ![]() [− π, π].
[− π, π].
Proof. First of all, we claim that
holds for any non-negative integer D. Indeed, by denoting ![]() , we have x
, we have x ![]() (0, 1] for any non-negative integer D. Thus, inequality (7.21) is equivalent to the well-known inequality
(0, 1] for any non-negative integer D. Thus, inequality (7.21) is equivalent to the well-known inequality ![]() , where x
, where x ![]() (0, 1].
(0, 1].
Now, we note that ![]() We just need to prove (7.20) for all ω
We just need to prove (7.20) for all ω ![]() (0, π] because the left-hand side of (7.20) is an even function for ω
(0, π] because the left-hand side of (7.20) is an even function for ω ![]() [− π, π].
[− π, π].
When ![]() , let
, let ![]() . Calculating the derivative of h(ω) with respect to ω yields
. Calculating the derivative of h(ω) with respect to ω yields ![]() Obviously, we have
Obviously, we have ![]() , i.e., h(ω) is not increasing for all
, i.e., h(ω) is not increasing for all ![]() . Since h(0) = 0, we have h(ω) ≤ 0, i.e.,
. Since h(0) = 0, we have h(ω) ≤ 0, i.e., ![]() for all
for all ![]() . Since
. Since ![]() , we get
, we get ![]() .
.
When ![]() , we have
, we have ![]() for all non-negative integers D. So, from (7.21), we get
for all non-negative integers D. So, from (7.21), we get
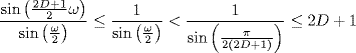
for all ![]() and all non-negative integers D. The lemma is proved.
and all non-negative integers D. The lemma is proved. ![]()
Theorem 7.6 Consider multi-agent system (7.3) with protocol (7.4). Assume that the interconnection topology digraph G = (V, E, A) of the system has a globally reachable node. Then the system achieves a consensus asymptotically if
Proof. The closed-loop system of (7.3) with (7.4) is given by (7.5). Taking the z-transformation of the system (7.5), we get
where Xi(z) is the z-transformation of xi(k). Define an n × n matrix ![]() as follows:
as follows:
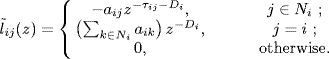
Obviously, ![]() , which is the Laplacian matrix. Then, (7.23) can be written as
, which is the Laplacian matrix. Then, (7.23) can be written as ![]() where X(z) = [X1(z),
where X(z) = [X1(z), ![]() , Xn(z)]T. Define
, Xn(z)]T. Define
![]()
Then, we will prove that all the zeros of p(z) have modulus less than unity except for a zero at z = 1 in the following.
Let z = 1, ![]() . Since G = (V, E, A) has a globally reachable node, by Theorem 1.9, zero is a simple eigenvalue of L, i.e., det (L) = 0 and rank(L) = n − 1. Thus, p(z) indeed has a simple zero at z = 1.
. Since G = (V, E, A) has a globally reachable node, by Theorem 1.9, zero is a simple eigenvalue of L, i.e., det (L) = 0 and rank(L) = n − 1. Thus, p(z) indeed has a simple zero at z = 1.
Now, we prove that the zeros of ![]() have modulus less than unity. Based on the general Nyquist stability criterion (Corollary 2.20), the zeros of f(z) have modulus less than unity, if the eigenloci of
have modulus less than unity. Based on the general Nyquist stability criterion (Corollary 2.20), the zeros of f(z) have modulus less than unity, if the eigenloci of ![]() , i.e.,
, i.e., ![]() , do not enclose the point (− 1, j0) for ω
, do not enclose the point (− 1, j0) for ω ![]() [− π, π]. By Greshgorin's disk lemma (Lemma 2.30), we have
[− π, π]. By Greshgorin's disk lemma (Lemma 2.30), we have ![]() for all ω
for all ω ![]() [− π, π], where
[− π, π], where
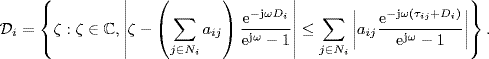
Further, we can show that
![]()
where ![]() . Now, define
. Now, define
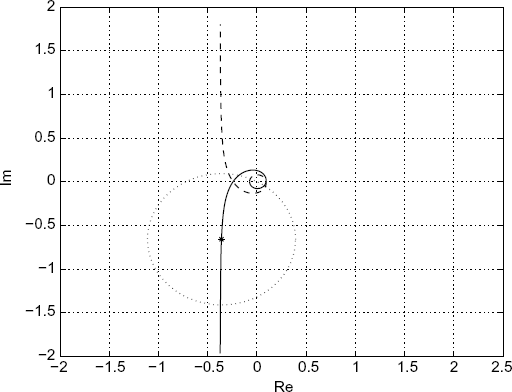
The Nyquist plot of Gi(ω) for ω ![]() [− π, π] is illustrated by Figure 7.1. Note that Gi(ω) is just the center of the disc
[− π, π] is illustrated by Figure 7.1. Note that Gi(ω) is just the center of the disc ![]() . So,
. So, ![]() does not enclose the point (− 1, j0) for all ω
does not enclose the point (− 1, j0) for all ω ![]() [− π, π] as long as the point (− a, j0) with a ≥ 1 is not in the disc
[− π, π] as long as the point (− a, j0) with a ≥ 1 is not in the disc ![]() for all ω
for all ω ![]() [− π, π], i.e.,
[− π, π], i.e., ![]() holds for all ω
holds for all ω ![]() [− π, π] when a ≥ 1.
[− π, π] when a ≥ 1.
Figure 7.1 Nyquist plot of Gi(ω). (Reproduced with permission from Tian Y.-P. and Liu C.-L., “Consensus of multi-agent systems with diverse input and communication delays,” IEEE Transactions on Automatic Control, 53, 9, 2122–2128, 2008. © 2008 IEEE.)
From (7.24), we have
![]()
Because ![]() holds for ω
holds for ω ![]() [− π, π] by Lemma 7.5, it follows from (7.22) that
[− π, π] by Lemma 7.5, it follows from (7.22) that
![]()
Thus,
![]()
i.e.,
![]()
holds for all ω ![]() [− π, π] when a ≥ 1.
[− π, π] when a ≥ 1.
Now, we have proved that the zeros of p(z) have modulus less than unity except for a zero at z = 1. Therefore, Theorem 7.6 is proved by Lemma 7.1. ![]()
Remark 1. Noticing the inequality (7.21), we know that the condition (7.22) is more conservative than the condition (7.9) given by Theorem 7.2, which is even necessary and sufficient for the case of a single-link, two-node network with equal delay. However, it is still scalable, and moreover, it is applicable to the systems based on digraphs with asymmetric weights.
Remark 2. When there are no input delays, i.e., Di = 0, the consensus condition (7.22) reduces to
which implies that the system can achieve a consensus asymptotically if and only the interconnection topology digraph of the system has a globally reachable node and (7.25) holds regardless of the existence of diverse communication delays.
Now, let us apply Theorem 7.6 to study the linearized Vicsek model and Moreau's model.
With communication delays and input delays, the linearized Vicsek model given in Jadbabaie, Lin and Morse (2003) becomes
where ni denotes the number of the neighbors of agent i.
From Theorem 7.6 we get the following corollary for Vicsek's model (7.26).
Corollary 7.7 Assume that the interconnection topology of system (7.26) has a globally reachable node. System (7.26) achieves a consensus asymptotically if
Remark. On the one hand, when Di = 0, inequality (7.27) holds automatically. This implies that the convergence of the consensus protocol given by Vicsek's model is independent of communication delays provided the graph has a globally reachable node. This coincides with the result given in Wang and Slotine (2006). Cao et al. (2006) extended this result to the case when the graph is jointly rooted. On the other hand, inequality (7.27) holds only for Di = 0. This may suggest that Vicsek's model is very sensitive to input delays. To enhance its robustness against input delays, one should introduce small weights as shown in model (7.15).
Similarly, Moreau's model given in (Moreau 2005) with communication delays and input delays can be written as
The following result is a direct corollary of Theorem 7.6.
Corollary 7.8 If the interconnection topology digraph of system (7.28) has a globally reachable node, then the system achieves a consensus asymptotically if
Remark. Obviously, (7.29) can be rewritten as ![]() . So, it always holds if Di = 0. But for Di > 0 it holds only for some appropriately designed weights
. So, it always holds if Di = 0. But for Di > 0 it holds only for some appropriately designed weights ![]() .
.
7.1.4 Continuous-Time System
Consider a continuous-time multi-agent system with diverse input delays and communication delays
It is easy to show that under the assumption that the topology graph is connected or the topology digraph contains a globally reachable node, the system achieves a consensus asymptotically if it is steady semi-stable with s = 0 as a simple pole.
Using the theory developed in Chapter 3 (Theorem 3.10), in a similar way to that shown in the proof of Theorem 7.2 one can get the consensus condition for continuous-time systems with input delays.
Theorem 7.9 Suppose that the topology graph of system (7.30) is connected with symmetric weights. Then, the system achieves a consensus asymptotically if
Remark. It is easy to see that in the case when all the delays Ti are the same for all ![]() , the condition (7.31) reduces to the result given by Olfati-Saber and Murray (2004).
, the condition (7.31) reduces to the result given by Olfati-Saber and Murray (2004).
The continuous-time system with diverse input and communication delays can be written as
Through a similar procedure to that used in the proof of Theorem 7.6, one can get a consensus condition for continuous-time systems with diverse communication and input delays.
Theorem 7.10 If the interconnection topology digraph of system (7.32) has a globally reachable node, then the system achieves a consensus asymptotically if
Remark. When there is no input delays, i.e., Ti = 0, the consensus condition (7.33) always holds, which implies that the system can achieve a consensus asymptotically if and only the interconnection topology digraph of the system has a globally reachable node regardless of the existence of diverse communication delays. This conclusion coincides with existing results in references such as Blondel et al. (2005) and Wang and Slotine (2006).
7.1.5 Simulation Study
Example 7.1 Symmetric system.
Consider a system of eighty agents described by the modified linearized Vicsek model (7.15). The interconnection topology for the agents is a closed ring (Figure 7.2). Note that under non-zero input delays, the linearized Vicsek's model with unity weights (εi = 1) has no consensus. In simulations, we choose the coupling weights as
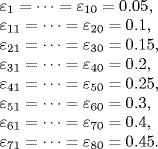
By Corollary 7.3, the admissible values of the input delays are
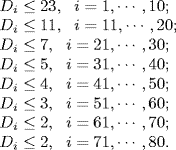
Simulations validate that under the admissible input delays the system achieves consensus asymptotically. We depict the boundary values of the input delay versus the coupling weights in Figure 7.3.
Figure 7.2 Undirected graph: a closed ring. (Reproduced with permission from Tian Y.-P. and Liu C.-L., “Consensus of multi-agent systems with diverse input and communication delays,” IEEE Transactions on Automatic Control, 53, 9, 2122–2128, 2008. © 2008 IEEE.)
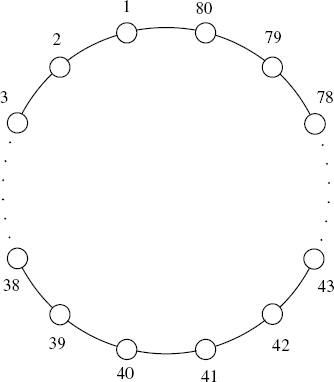
Figure 7.3 Bounds of input delays. (Reproduced with permission from Tian Y.-P. and Liu C.-L., “Consensus of multi-agent systems with diverse input and communication delays,” IEEE Transactions on Automatic Control, 53, 9, 2122–2128, 2008. © 2008 IEEE.)
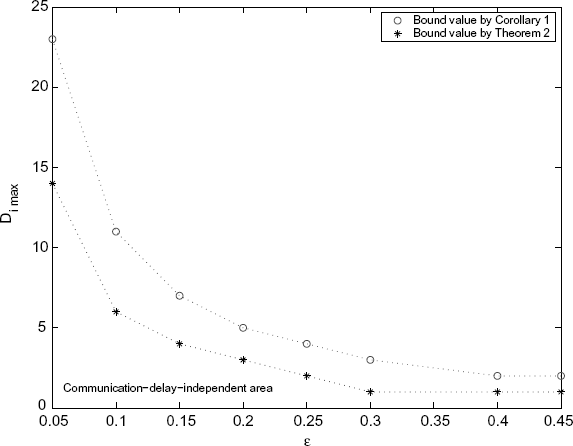
Note that the bound of input delay determined by Corollary 7.3 may not apply to asymmetric systems. For example, with each agent's input delay at boundary, we introduce an identical communication delay, T ≥ 1, which destroys the conjugate symmetry of the system matrix in the frequency domain, between each pair of neighboring agents. Then, the simulation shows that the system has no asymptotic consensus.
Now, we can use Theorem 7.6 to get a consensus condition for the system with both input delays and communication delays. By Theorem 7.6, the admissible values of the input delays are
The boundary values of input delays estimated by Theorem 7.6 are also shown in Figure 7.3. The boundary determined by Theorem 7.6 is lower than the boundary given by Corollary 7.3, which implies that Theorem 7.6 is more conservative than Corollary 7.3 for symmetric systems. However, with input delays in the area determined by Theorem 7.6, the asymptotic consensus of the system is robust to arbitrary communication delays.
Example 7.2 Asymmetric system.
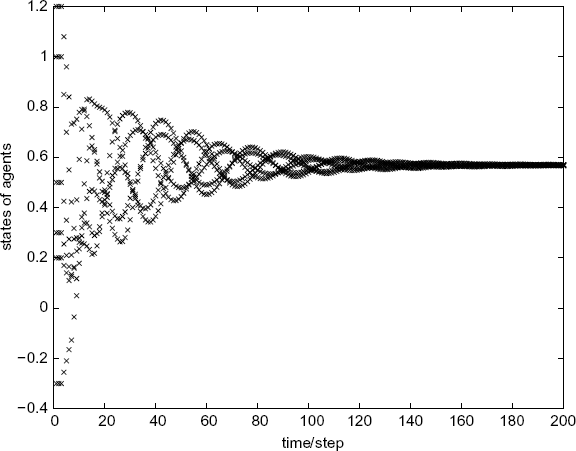
Consider the multi-agent system (7.5) with an interconnection digraph shown by Figure 7.4. The weights of the directed paths are: a12 = 0.1, a16 = 0.05, a23 = 0.15, a36 = 0.1, a43 = 0.05, a45 = 0.1, a56 = 0.15, a62 = 0.15, and the corresponding communication delays are: τ12 = 5, τ16 = 3, τ23 = 4, τ36 = 4, τ43 = 4, τ45 = 6, τ56 = 6, τ62 = 5. Simulation shows that the system is quite sensitive to input delays, and it cannot converge to any consensus when Ti > 3. This is an asymmetric system to which Theorem 7.2 does not apply. Using Theorem 7.6, we get that Ti ≤ 2 is a sufficient consensus condition which is independent of communication delays. We choose Ti = 2, i = 1, 2, 3, 4, 5, 6, in the simulation. The multi-agent system converges to a consensus as shown by Figure 7.5.
Figure 7.4 Digraph of a group of six agents.
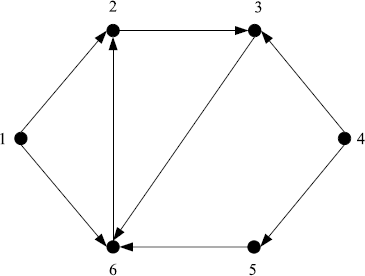
Figure 7.5 Consensus with communication and input delays. (Reproduced with permission from Tian Y.-P. and Liu C.-L., “Consensus of multi-agent systems with diverse input and communication delays,” IEEE Transactions on Automatic Control, 53, 9, 2122–2128, 2008. © 2008 IEEE.)
7.2 Double Integrator System with Diverse Input Delays and Interconnection Uncertainties
7.2.1 Leader-Following Consensus Algorithm
Consider a multi-agent system with interconnection topology graph G = (V, E, A). There are n agents with diverse input delays
where ![]() ,
, ![]() ,
, ![]() , and Ti > 0 are the position, velocity, acceleration and input delay, respectively, of agent i.
, and Ti > 0 are the position, velocity, acceleration and input delay, respectively, of agent i.
For system (7.34), the leader-following coordination control strategy is adopted in this section. Let the dynamics of the leader be determined by
where ![]() is the position of the leader, and
is the position of the leader, and ![]() is a constant which represents the desired velocity for all the agents.
is a constant which represents the desired velocity for all the agents.
Then, the consensus protocol for the first-order multi-agent system (Olfati-Saber and Murray (2004) can be easily extended to the leader-following system as follows
where ki > 0 and γ > 0, Ni denotes the neighbors of agent i, aij > 0 is the adjacency element of A in the digraph G = (V, E, A), and bi is the linking weight from agent i to the leader (7.35). Note that bi > 0 if there is a directed edge from agent i to the leader; otherwise, bi = 0. Let ![]() for notation convenience.
for notation convenience.
Remark. Protocol (7.36) can be used only for following a leader with a constant velocity, or a leader with a velocity which is time-varying but asymptotically approaching to a constant. If the leader's velocity is not converging to any constant, then each agent should estimate its neighbors' accelerations, and the stability analysis of that kind of consensus protocol will be much more complicated.
With consensus protocol (7.36), the closed-loop form of system (7.34) is given by
The following lemma gives some structural property of the leader-following system.
Lemma 7.13 Assume that the interconnection topology graph of n agents together with the leader in system (7.37) has the leader as a globally reachable node. Then, the matrix L + B has no zero eigenvalues, where L is the Laplacian matrix of the interconnection topology of n agents without the leader.
Proof. Consider the interconnection topology graph with n + 1 nodes corresponding to the n agents of system (7.37) and the leader. Obviously the Laplacian matrix of this topology is given by
![]()
where ![]() . Since the leader is a globally reachable node in the graph, we have
. Since the leader is a globally reachable node in the graph, we have ![]() , by Theorem 1.9. Taking elementary column transforms for
, by Theorem 1.9. Taking elementary column transforms for ![]() by adding all the other columns to the first column as follows
by adding all the other columns to the first column as follows
![]()
we get rank(L + B) = n. The lemma is proved. ![]()
7.2.2 Consensus Condition under Symmetric Coupling Weights
Let
![]()
Then, from (7.37) it follows that
Taking the Laplace transform of (7.38), one gets
Denote
Then, using the framework of Lee and Spong (2006) one can get a sufficient condition of consensus as
However, it can be shown that this condition is so conservative that it gives an empty set of available control parameters for the second-order multi-agent system with input delays. Let us rewrite (7.40) as
![]()
where ![]() , and
, and
Then, the condition (7.41) is equivalent to
(7.43) ![]()
Actually, such a condition never holds for any κi > 0 when γ > 0, Ti > 0.
Let us derive a less conservative consensus condition for system (7.37) with symmetric coupling weights.
For all ![]() , we denote
, we denote
![]()
![]()
As shown in Chapter 3 (Proposition 3.26), ω0(i) is the critical point of the frequency response of Wi(s) from clockwise part to anti-clockwise part.
Let ![]() be the agent which has the maximal input delay constant
be the agent which has the maximal input delay constant ![]() , i.e.,
, i.e.,
(7.44) ![]()
Now, we are in a position to present some sufficient consensus conditions for the second-order multi-agent system with input delays.
Theorem 7.14 Assume that system (7.37) is composed of n agents and a leader with a static interconnection topology that has the leader as a globally reachable node, and the topology graph has symmetric weights, i.e., aij = aji. For each agent the following preconditions are assumed:
Then, all the agents in the system asymptotically converge to the leader's state, if
where ![]() is the gain margin of the transfer function Wi(s) defined in (7.42).
is the gain margin of the transfer function Wi(s) defined in (7.42).
Proof. Writing (7.39) in the vector form, we can get the characteristic equation of system (7.38) as
where L is the Laplacian matrix corresponding to the interconnection topology for all the agents without the leader.
Define ![]() . To prove Theorem 7.14 it suffices to prove that all the zeros of F(s) are in the open left half of the complex plane.
. To prove Theorem 7.14 it suffices to prove that all the zeros of F(s) are in the open left half of the complex plane.
Let s = 0. Then F(0) = det (γdiag{ki}(L + B)). Because the interconnection topology composed of the n agents together with the leader has the leader as a globally reachable node, F(0) ≠ 0 by Lemma 7.13.
Now, define ![]() . We will prove that all the zeros of p(s) are inside the LHP. Based on the general Nyquist stability criterion (Corollary 2.20), all the zeros of p(s) lie inside the LHP, if the eigenloci
. We will prove that all the zeros of p(s) are inside the LHP. Based on the general Nyquist stability criterion (Corollary 2.20), all the zeros of p(s) lie inside the LHP, if the eigenloci
![]()
do not enclose the point (− 1, j0) for all ![]() .
.
For the symmetric weights (aij = aji), L + B = (L + B)T. Hence, based on Lemma 2.34, we have
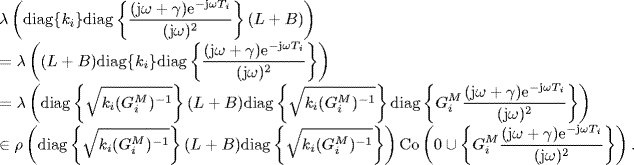
Since the spectral radius of any matrix is bounded by its largest absolute row sum, it follows from the condition (7.47) that
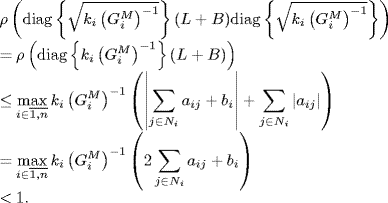
Therefore, from Theorem 3.32 it follows that
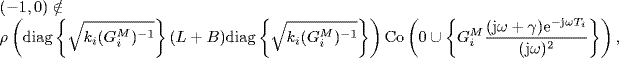
i.e., the eigenloci of ![]() do not enclose the point (− 1, j0) for all
do not enclose the point (− 1, j0) for all ![]() , which implies that the zeros of F(s) are all inside the LHP. Theorem 7.14 is thus proved.
, which implies that the zeros of F(s) are all inside the LHP. Theorem 7.14 is thus proved. ![]()
Remark. The result of Theorem 7.14 can be extended to systems with both communication delays and input delays without any difficulty if the diverse communication delays τij are symmetric, i.e., they satisfy the requirement (2.26).
7.2.3 Robust Consensus under Asymmetric Perturbations
The consensus condition given by Theorem 7.14 depends on the strict symmetry of the Laplacian matrix L. In practice, however, perturbations of coupling weights may occur and destroy the symmetry. In the following, we study the robustness of the consensus protocol against asymmetric perturbations.
Suppose that the symmetric coupling weights of system (7.37) are subject to some asymmetric perturbations, denoted by ![]() for each one. Then the system becomes
for each one. Then the system becomes
where aij = aji, and aij + δij > 0 hold for j ![]() Ni.
Ni.
A robust consensus condition of the perturbed system is given by the following theorem.
Theorem 7.15 Assume that the nominal part of system (7.49), i.e., the system without asymmetric weight perturbations δij, converges to the leader's states asymptotically. Let
where ![]() and
and
![]()
Then, the agents in the perturbed system (7.49) converge to the leader's states asymptotically, if
where ![]() denotes the largest singular value of matrix, and Δ = {Δij} is the asymmetric perturbation matrix, which is defined as follows
denotes the largest singular value of matrix, and Δ = {Δij} is the asymmetric perturbation matrix, which is defined as follows
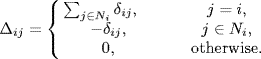
Proof. Under the same variable transformation as used in the previous subsection
![]()
it is easy to get the characteristic equation of system (7.49) as
Since the system (7.49) without asymmetric weight perturbations δij converges to the leader's states asymptotically, the roots of the characteristic equation (7.48) all lie inside the LHP, i.e., the zeros of det (s2I + s2KD(s)(L + B)) lie inside the LHP, and det (L + B) ≠ 0.
In the following, we will prove that the roots of equation (7.52) are all inside the LHP.
First we show that equation (7.52) has no roots at s = 0. Indeed, by setting ω = 0 we get from (7.51) that ![]() . This implies that
. This implies that
![]()
So, it follows that
![]()
or equivalently,
![]()
This proves that equation (7.52) has no roots at s = 0. Therefore, the characteristic equation (7.52) can be equivalently rewritten as
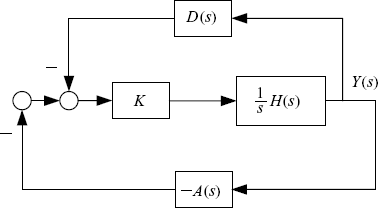
The feedback diagram corresponding to the characteristic equation (7.53) is demonstrated in Figure 7.6.Using the linear fractional transformation, the diagram in Figure 7.6 can be equivalently transformed into the form shown by Figure 7.7, where M(s) is given by equation (7.50).
Figure 7.6 System with asymmetric perturbation.
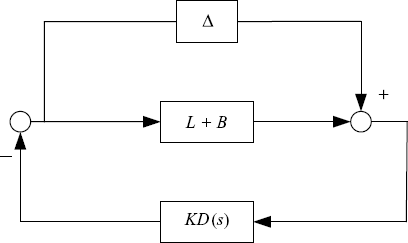
Figure 7.7 Transformed system.
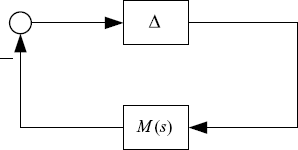
The characteristic equation of the closed-loop system in Figure 7.7 is
Obviously, D(s) has no poles in the open RHP. Thus, ΔM(s) has no poles in the open RHP. According to the general Nyquist stability criterion (Corollary 2.20), the roots of the characteristic equation (7.54) all lie inside the LHP, as long as the eigenloci of ΔM(s), i.e., λ(ΔM(jω)), do not enclose the point (− 1, j0) for ![]() .
.
From condition (7.51) it follows that
(7.55) 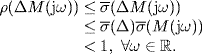
Hence, λ(ΔM(jω)) does not enclose the point (− 1, j0) for all ![]() , i.e., the roots of the characteristic equation (7.54) all lie inside the LHP. Therefore, the closed-loop system in Figure 7.7 is asymptotically stable, and the agents in (7.49) converge to the leader's states asymptotically. Theorem 7.15 is proved.
, i.e., the roots of the characteristic equation (7.54) all lie inside the LHP. Therefore, the closed-loop system in Figure 7.7 is asymptotically stable, and the agents in (7.49) converge to the leader's states asymptotically. Theorem 7.15 is proved. ![]()
7.2.4 Simulation Study
Example 7.16 Design procedure based on Theorem 7.14
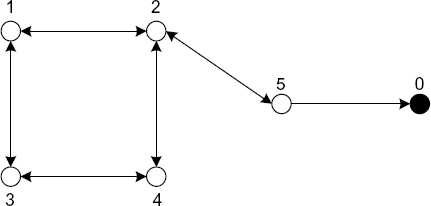
Consider a system (7.37) of five agents and one leader described by (7.35). The interconnection topology is described in Figure 7.8. Obviously, the leader is globally reachable. Assume that the input delays for the agents are: T1 = 0.5(s), T2 = 1.0(s), T3 = 0.7(s), T4 = 0.6(s) and T5 = 0.8(s). The weights of the edges are: a12 = a21 = 0.30, a25 = a52 = 0.70, a13 = a31 = 0.10, a34 = a43 = 1.10, a42 = a24 = 0.50, b5 = 1.50.
In the following, we design parameters γ and ki in the consensus protocol (7.36) so that the agents converge to the leader's state asymptotically.
Figure 7.8 Network of five agents and a leader. (Reprinted from Automatica, 45, 5, Tian Y.-P. and Liu C.-L., “Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations,” 1347–1353, 2009, with permission from Elsevier.)
Step 1: Choosing γ.
The condition (7.45) requires γ ![]() (0, 0.4495/Ti),
(0, 0.4495/Ti), ![]() , which implies that
, which implies that
Since T2 is the maximal input delay, we have ![]() . Denote
. Denote ![]() , and the condition (7.46) can be represented as Ei > 0, i = 1, 2, 3, 4, 5. With the given input delays, Ei is a function of γ. The curves of Ei on γ are shown in Figure 7.9.
, and the condition (7.46) can be represented as Ei > 0, i = 1, 2, 3, 4, 5. With the given input delays, Ei is a function of γ. The curves of Ei on γ are shown in Figure 7.9.
Figure 7.9 Choosing parameter γ. (Reprinted from Automatica, 45, 5, Tian Y.-P. and Liu C.-L., “Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations,” 1347–1353, 2009, with permission from Elsevier.)
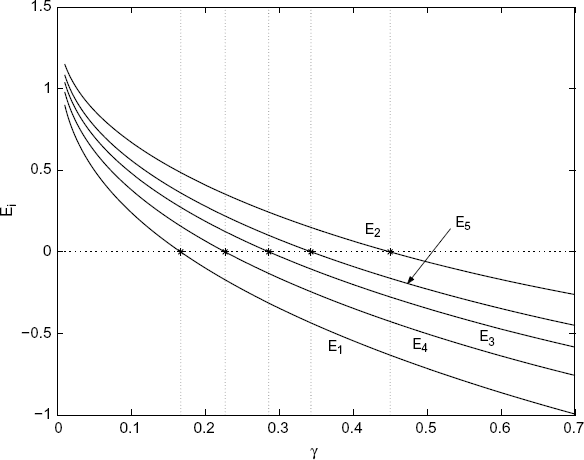
From Figure 7.9 it is clear that the condition Ei > 0, i = 1, 2, 3, 4, 5, holds if
According to (7.56) and (7.57), we can choose γ = 0.10 to guarantee the conditions (7.45) and (7.46).
Step 2: Choosing ki.
For the transfer functions
![]()
using the MATLAB® simulator we obtain the inverses of their gain margins as ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . From the condition (7.47), the constraints on ki can be calculated as k1
. From the condition (7.47), the constraints on ki can be calculated as k1 ![]() (0, 3.788), k2
(0, 3.788), k2 ![]() (0, 0.498), k3
(0, 0.498), k3 ![]() (0, 0.906), k4
(0, 0.906), k4 ![]() (0, 0.801), k5
(0, 0.801), k5 ![]() (0, 0.651), We choose k1 = 3.4, k2 = k3 = k4 = k5 = 0.4 for the simulation.
(0, 0.651), We choose k1 = 3.4, k2 = k3 = k4 = k5 = 0.4 for the simulation.
With the parameters chosen above and the initial states generated randomly, the agents in the system (7.37) asymptotically converge to the leader's state as shown in Figure 7.10.
Figure 7.10 Positions and velocities of the agents under symmetric weights. (Reprinted from Automatica, 45, 5, Tian Y.-P. and Liu C.-L., “Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations,” 1347–1353, 2009, with permission from Elsevier.)
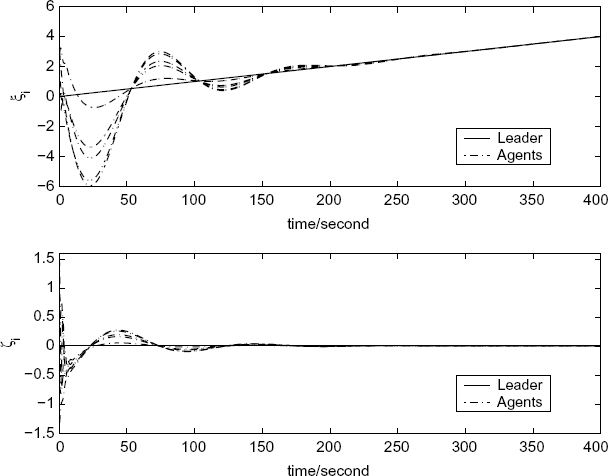
Since there are no other theoretic results to compare with, we test the conservatism of our results by simulation. The procedure is as follows. Setting k2, k3, k4 and k5 at our theoretic boundary values as 0.498, 0.906, 0.801 and 0.651 respectively, we increase k1 from our boundary value 3.788 until the system has no consensus. Then we find the computational margin for k1 is k1m = 7.519. Using similar procedures we can obtain the other marginal gains as k2m = 0.797, k3m = 1.088, k4m = 0.954, k5m = 0.773. Note that unlike our theoretical results, these computational margins cannot be used in the consensus protocol simultaneously.
Example 7.17 System with interconnection uncertainties.
Consider the multi-agent systems (7.49) of five agents and one leader described by (7.35) with the same interconnection topology as Example 7.16 (see Figure 7.8). For simplicity, we choose the same aij, bi, input delays Ti and control parameters γ and ![]() as given in Example 7.16. From Theorem 7.14, the system (7.49) without asymmetric weight perturbations converges to the leader's states asymptotically, and the zeros of det (s2I + s2KD(s)(L + B)) lie inside the LHP. Using the MATLAB® simulator, we obtain that the largest value of
as given in Example 7.16. From Theorem 7.14, the system (7.49) without asymmetric weight perturbations converges to the leader's states asymptotically, and the zeros of det (s2I + s2KD(s)(L + B)) lie inside the LHP. Using the MATLAB® simulator, we obtain that the largest value of ![]() on ω
on ω ![]() (− ∞, ∞) is
(− ∞, ∞) is ![]() . From Theorem 7.15, if the largest singular value of the asymmetric disturbance matrix Δ, i.e.,
. From Theorem 7.15, if the largest singular value of the asymmetric disturbance matrix Δ, i.e., ![]() , satisfies
, satisfies ![]() , the closed system in Figure 7.6 with Δ is asymptotically stable. For example, when
, the closed system in Figure 7.6 with Δ is asymptotically stable. For example, when
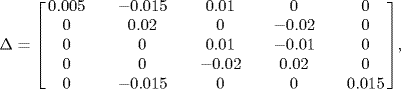
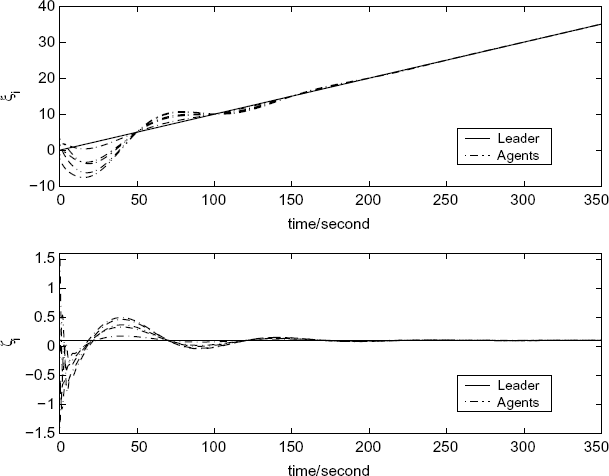
one can check that ![]() , and aij + δij > 0 for j
, and aij + δij > 0 for j ![]() Ni. Therefore, with the Laplacian matrix L + Δ and the initial states generated randomly, the agents in (7.49) converge to the leader's states asymptotically as shown in Figure 7.11.
Ni. Therefore, with the Laplacian matrix L + Δ and the initial states generated randomly, the agents in (7.49) converge to the leader's states asymptotically as shown in Figure 7.11.
Figure 7.11 Positions and velocities of the agents under asymmetric weights. (Reprinted from Automatica, 45, 5, Tian Y.-P. and Liu C.-L., “Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations,” 1347–1353, 2009, with permission from Elsevier.)
7.3 High-Order Consensus in High-Order Systems
7.3.1 System Model
Suppose the interconnection topology of the system is described by a digraph G = (V, E, A) with |V| = n. We assume that the interconnection topology of the system is a connected undirected graph or a digraph containing a globally reachable node. Then, by Theorem 1.9, the Laplacian matrix L has a simple eigenvalue 0, i.e., det (L) = 0 and rank(L) = n − 1. Moreover, the definition of L implies that L · 1n = 0.
Let the model of the ith agent (![]() ) be given by the following transfer function
) be given by the following transfer function
where ![]() and
and ![]() denote the Laplace transformation of the output and input, respectively, of the ith agent; Ti is the input delay; ν and mi are positive integers satisfying mi ≥ ν;
denote the Laplace transformation of the output and input, respectively, of the ith agent; Ti is the input delay; ν and mi are positive integers satisfying mi ≥ ν; ![]() are system parameters. For any non-negative integer k, denotes by
are system parameters. For any non-negative integer k, denotes by ![]() the kth-order derivative of the output yi(t) of the ith agent.
the kth-order derivative of the output yi(t) of the ith agent.
Definition 7.18 Multi-agent system (7.58) is said to reach the rth-order consensus asymptotically if
for system solutions from any admissible initial conditions, and
for system solutions from some admissible initial conditions.
Note that when r = 0, the above definition implies that
![]()
where ![]() is a constant. In this case we say the system achieves a constant consensus. So, constant consensus can be regarded as the zeroth-order consensus by Definition 7.18. We also note by this definition the constant c can not identically be zero for all initial conditions, i.e., it excludes the case of trivial consensus which actually implies that each agent is asymptotically stabilized.
is a constant. In this case we say the system achieves a constant consensus. So, constant consensus can be regarded as the zeroth-order consensus by Definition 7.18. We also note by this definition the constant c can not identically be zero for all initial conditions, i.e., it excludes the case of trivial consensus which actually implies that each agent is asymptotically stabilized.
Let τij be the communication delay from agent j to agent i. Then, at time instance t the information obtained by agent i from agent j is ![]() instead of
instead of ![]() . Let the consensus protocol be
. Let the consensus protocol be
where κi > 0, ![]() are some control parameters, and τ'ij denotes the estimation of communication delay τij used by agent i. Sometimes τ'ij, j
are some control parameters, and τ'ij denotes the estimation of communication delay τij used by agent i. Sometimes τ'ij, j ![]() Ni are also referred to as self-delays of agent i. We will show that the high-order consensus can be achieved even though the self-delays are not equal to the communication delays.
Ni are also referred to as self-delays of agent i. We will show that the high-order consensus can be achieved even though the self-delays are not equal to the communication delays.
7.3.2 Consensus Condition
It is easy to get the closed-loop form of system (7.58) with protocol (7.62) as
(7.63) 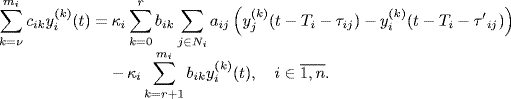
Taking the Laplace transform under zero initial condition for the above equation yields
(7.64) 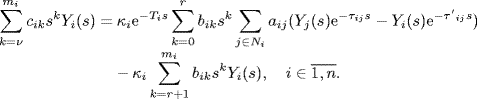
Let
(7.65) ![]()
(7.66) ![]()
(7.67) ![]()
(7.68)–(7.69) ![]()
and
(7.71) ![]()
Then, the closed-loop system can be shown by Figure 7.12.The frequency-domain model of the closed-loop system is given by
and the return difference equation of the system is given by
![]()
According to (2.42), direct use of the equation
(7.74) ![]()
may ignore cancelation between the poles of the closed-loop system and the poles of the open-loop system at s = 0. To avoid these cancelations we consider the following equation
as the characteristic equation of the system. Obviously,
Therefore, all the non-zero solutions of (7.75) are contained in the solutions of (7.76), and vice versa.
Figure 7.12 Interconnected system.
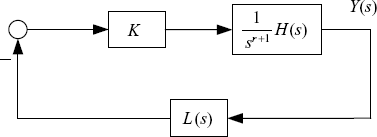
The following proposition gives an obvious condition for justifying if the open-loop poles at s = 0 enter into the set of the closed-loop poles.
Proposition 7.19 Suppose H(s)KL(s) is analytic at s = 0. If rank[H(s)KL(s)] = n − 1, for all ![]() at which H(s)KL(s) is analytic, then
at which H(s)KL(s) is analytic, then
![]()
where g(s) has neither poles nor zeros at s = 0.
Proof. The proposition can be easily proved by converting H(s)KL(s) into a diagonal matrix through a similar transformation. ![]()
Proposition 7.19 shows that s = 0 is a repeated pole with multiplicity r + 1 of the closed-loop system. This also implies that the solution of the closed-loop system can be expressed as
where ![]() are constant vectors,
are constant vectors, ![]() are vectors whose elements are polynomials of t, λk are zeros of g(s), and M is a finite or infinite positive integer. Furthermore, if Reλi < 0, we have
are vectors whose elements are polynomials of t, λk are zeros of g(s), and M is a finite or infinite positive integer. Furthermore, if Reλi < 0, we have ![]() as t→ ∞. We call
as t→ ∞. We call ![]() the steady state of the system.
the steady state of the system.
Lemma 7.20 Assume that det (sr+1I + H(s)KL(s)) = sr+1g(s), where g(s) has neither poles nor zeros at s = 0. Then, for any s ≠ 0, g(s) = 0 if and only if
Proof. The lemma is obvious due to the equation (7.76).![]()
By Definition 2.7, a linear time-invariant system is said to be steady semi-stable if all its characteristic roots are inside the LHP or at the origin of the complex plane. By Lemma 7.20, to verify the steady semi-stability of the system, we just need to check if all the zeros of (7.78) have negative real parts. Note that the generalized Nyquist stability criterion (Theorem 2.19 and Theorem 2.20) can be used for this purpose.
Denote ![]() for convenience, and denote by
for convenience, and denote by ![]() the kth-order derivative of
the kth-order derivative of ![]() .
.
Theorem 7.21 Assume that the multi-agent system (7.58) with consensus protocol (7.62) is steady semi-stable, and the transfer function ![]() is analytic in a neighborhood of s = 0. Then, the rth-order consensus is reached at the steady state if
is analytic in a neighborhood of s = 0. Then, the rth-order consensus is reached at the steady state if ![]() , for all
, for all ![]() , and
, and ![]() for all
for all ![]() at which
at which ![]() is analytic.
is analytic.
Proof. By Proposition 7.19 we know that the system has zeros at s = 0 with multiplicity r + 1, and the system solution can be expressed by (7.77). With the assumption of the steady semi-stability, from (7.77) it is easy to see that
and
when t→ ∞. So, conditions (7.60) and (7.61) in Definition 7.18 are already satisfied. We just need to check (7.59).
Let s be in the neighborhood D of s = 0 in which ![]() is analytic. By the Taylor formula for functions of a complex variable we have
is analytic. By the Taylor formula for functions of a complex variable we have
where
(7.82) ![]()
(7.83) ![]()
Substituting (7.81) into (7.73) yields
![]()
Note that the above equation holds in the neighborhood D of s = 0. When the system is steady semi-stable, Y(s) is analytic for Res > 0. Then, by taking the inverse Laplace transformation of the equation, we have
(7.84) 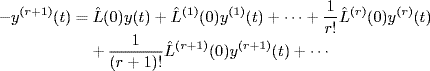
for t→ ∞. Applying (7.79) to the above equation we get
when t→ ∞.
Differentiating (7.80)r times yields
Substituting (7.80) and (7.86) into (7.85) yields
where
(7.88) 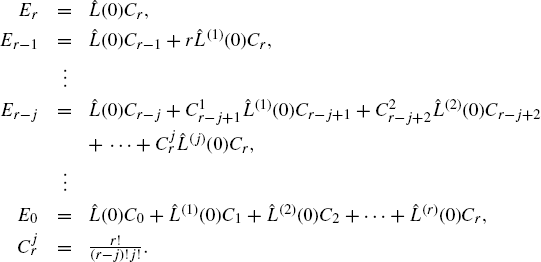
Equation (7.87) holds if and only if ![]() .
.
From Er = 0 we get Cr ![]() span(1n) because
span(1n) because ![]() and
and ![]() . Using the result Cr
. Using the result Cr ![]() span(1n) and the assumption
span(1n) and the assumption ![]() , from Er−1 = 0 it follows that
, from Er−1 = 0 it follows that ![]() which implies Cr−1
which implies Cr−1 ![]() span(1n). Conducting this procedure to the end, i.e., E0 = 0, we get
span(1n). Conducting this procedure to the end, i.e., E0 = 0, we get ![]() . Thus, we have y(t)
. Thus, we have y(t) ![]() span(1n) when t→ ∞, which, by (7.80), also implies that
span(1n) when t→ ∞, which, by (7.80), also implies that ![]() .
. ![]()
7.3.3 Existence of High-Order Consensus Solutions
Theorem 7.21 gives some sufficient consensus conditions for the system. Here we try to find a necessary and sufficient condition of the existence of high-order consensus solutions. First, we show that the condition given by Proposition 7.19 can be further weakened as follows.
Proposition 7.22 Suppose ![]() is analytic in a neighborhood of s = 0. Then,
is analytic in a neighborhood of s = 0. Then,
![]()
with g(s) having neither poles nor zeros at s = 0, if and only if ![]() , and there exists a non-zero constant vector α
, and there exists a non-zero constant vector α ![]() span(1n) such that
span(1n) such that ![]() ,
, ![]() , and
, and ![]() .
.
Proof. Let s be in the neighborhood of s = 0, denoted by D, in which ![]() is analytic. By the Taylor formula for functions of a complex variable, we have
is analytic. By the Taylor formula for functions of a complex variable, we have
(7.89) ![]()
where
(7.90) ![]()
(7.91) ![]()
It is clear that
![]()
if and only if there exists a normalized non-singular matrix ![]() (i.e., det (T) = 1) such that one column (say without loss of generality, the first one) of T−1L1(s)T is zero, i.e., [T−1L1(s)T](:, 1) = 0. Denote by α the first column of T. It is easy to get
(i.e., det (T) = 1) such that one column (say without loss of generality, the first one) of T−1L1(s)T is zero, i.e., [T−1L1(s)T](:, 1) = 0. Denote by α the first column of T. It is easy to get
![]()
Obviously, [T−1L1(s)T](:, 1) = 0, ∀ s ![]() D if and only if
D if and only if ![]() ,
, ![]() .
.
Denoting by pij the (i, j)th elements of T−1L1(s)T for ![]() , we have
, we have
And denoting by gij the (i, j)th elements of T−1L2(s)T, we have
Since H(s)KL(s) is analytic at s = 0, all the elements pij (![]() ) are analytic at s = 0. Hence, g(s) is also analytic at s = 0.
) are analytic at s = 0. Hence, g(s) is also analytic at s = 0.
Now, we prove g(s) has no zeros at s = 0, i.e., g(0) ≠ 0 if and only if ![]() and
and ![]() . Denote
. Denote ![]() . From (7.93) we have
. From (7.93) we have
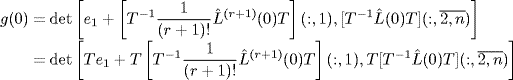
because det (T−1) = 1. Obviously, g(0) ≠ 0 if and only if
![]()
and
![]()
From (7.92) we know that
![]()
and hence ![]() if and only if
if and only if ![]() . Simple calculation shows that
. Simple calculation shows that ![]() . So g(0) ≠ 0 if and only if
. So g(0) ≠ 0 if and only if ![]() , and
, and ![]() . Finally, we note that the non-zero vector α
. Finally, we note that the non-zero vector α ![]() span(1n). This is indeed the case. Since we have proved
span(1n). This is indeed the case. Since we have proved ![]() , the null space of
, the null space of ![]() is one-dimensional. From the property of Laplacian matrix, L(0) · 1n = 0, we get
is one-dimensional. From the property of Laplacian matrix, L(0) · 1n = 0, we get ![]() . So, α
. So, α ![]() span(1n). The proposition is proved.
span(1n). The proposition is proved. ![]()
Remark. When ![]() , a sufficient condition for
, a sufficient condition for ![]() is
is ![]() , where c is a non-zero constant. And a more sufficient condition for is
, where c is a non-zero constant. And a more sufficient condition for is ![]() .
.
Exercises 7.23 Suppose ![]() and
and ![]() . Show α : = c1n with c ≠ 0 is not in
. Show α : = c1n with c ≠ 0 is not in ![]() .
.
When s = 0 is a repeated pole with multiplicity r + 1 of the closed-loop system, the solution of the closed-loop system can be expressed by equation (7.77)
Now, we are ready to present the following theorem.
Theorem 7.24 Assume that the multi-agent system (7.58) with consensus protocol (7.62) is steady semi-stable and the transfer function ![]() is analytic in a neighborhood of s = 0. Then, the rth-order consensus is reached at the steady state if and only if
is analytic in a neighborhood of s = 0. Then, the rth-order consensus is reached at the steady state if and only if ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Proof. (Sufficiency) Suppose ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then, by Proposition 7.22 we know that the system has zeros at s = 0 with multiplicity r + 1, and the system solution can be expressed by (7.77). The rest of the sufficiency part of the this proof is as the same as given in the proof of Theorem 7.21.
. Then, by Proposition 7.22 we know that the system has zeros at s = 0 with multiplicity r + 1, and the system solution can be expressed by (7.77). The rest of the sufficiency part of the this proof is as the same as given in the proof of Theorem 7.21.
(Necessity) Suppose that the system reaches the consensus defined by (7.59), (7.60) and (7.61). Note that (7.60), (7.61) and the steady semi-stability assumption imply that the system has zeros at s = 0 of multiplicity r + 1. So, by Proposition 7.22, the necessity is obvious. ![]()
7.3.4 Constant Consensus
For the case of constant consensus, i.e., the case when r = 0, without loss of generality, we let bi0 = 1 for all ![]() . Then, the protocol (7.62) reduces to the following form
. Then, the protocol (7.62) reduces to the following form
the closed-loop system equation becomes
![]()
and H(s) defined in (7.70) takes the form
![]()
where
(7.95) ![]()
Let us apply Theorem 7.24 to the case of constant consensus. For this case, Theo-rem 7.24 requires: (1) the marginal stability of the closed-loop system, (2) ![]() and
and ![]() . Since κi ≠ 0, requirement (2) implies that rank[L(0)] = n − 1 and L(0) · 1 = 0. It is well known that this is equivalent to the connectivity condition for the interconnection graph, i.e., the digraph has a globally reachable node.
. Since κi ≠ 0, requirement (2) implies that rank[L(0)] = n − 1 and L(0) · 1 = 0. It is well known that this is equivalent to the connectivity condition for the interconnection graph, i.e., the digraph has a globally reachable node.
To check the marginal stability of the closed-loop system, we may make some loop transformation on the system as shown by Figure 2.8. Denote by ![]() the open-loop transfer function matrix after the loop transformation. Then, based on the extended spectral radius theorem for steady semi-stability (Theorem 2.24), we get the following result immediately.
the open-loop transfer function matrix after the loop transformation. Then, based on the extended spectral radius theorem for steady semi-stability (Theorem 2.24), we get the following result immediately.
Theorem 7.26 Consider the multi-agent system (7.58) with the protocol (7.94). Assume the interconnection digraph has a globally reachable node, then, the system achieves a constant consensus, if
(7.96) ![]()
Since L(s) defined in (7.72) can be rewritten as
![]()
where
![]()
and
![]()
the system diagram shown in Figure 7.12 can be equivalently transformed as shown in Figure 7.13. In this case we have
(7.98) ![]()
where
(7.99) ![]()
Straightforward calculation shows that
![]()
So, the requirement (7.97) of Theorem 7.25 is satisfied. Therefore, under the assumption that the interconnection digraph has a globally reachable node, a sufficient condition for achieving a constant consensus is
(7.100) ![]()
By using Corollary 2.31 of Gershgorin's disc lemma, a more conservative but scalable condition is
(7.101) 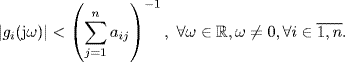
This condition was first given by Lee and Spong (2006).
Figure 7.13 Equivalent diagram for constant consensus.
Similarly, from Theorem 2.27 and Theorem 2.29 we can also get the following two theorems for the constant consensus problem.
Theorem 7.26 Consider the multi-agent system (7.58) with the protocol (7.94). Assume the interconnection digraph has a globally reachable node, then, the system achieves a constant consensus, if
(7.102) ![]()
(7.103) ![]()
Theorem 7.27 Consider the multi-agent system (7.58) with the protocol (7.94). Assume the interconnection digraph has a globally reachable node, then, the system achieves a constant consensus, if
(7.104) ![]()
(7.105) ![]()
7.3.5 Consensus in Ideal Networks
Before applying Theorem 7.24 to ideal networks, i.e., networks with zero communication delays and constant channel dynamics, let us review the following fact from graph theory.
Let G be a digraph having at least one globally reachable node. If we choose only one globally reachable node, say ![]() , of G, and cut off all the edges from
, of G, and cut off all the edges from ![]() , then obviously
, then obviously ![]() is still a globally reachable node of G. But, if we do this operation for a node which is not globally reachable in G, or simultaneously do this operation for two or more globally reachable nodes, then G has no globally reachable node anymore. This is equivalent to saying, if
is still a globally reachable node of G. But, if we do this operation for a node which is not globally reachable in G, or simultaneously do this operation for two or more globally reachable nodes, then G has no globally reachable node anymore. This is equivalent to saying, if ![]() is a Laplacian of a digraph having at least one globally reachable node, then rank[diag{b1, . . . , bn}L] = n − 1 if and only if
is a Laplacian of a digraph having at least one globally reachable node, then rank[diag{b1, . . . , bn}L] = n − 1 if and only if ![]() , or
, or ![]() and
and ![]() is a globally reachable node of G, where
is a globally reachable node of G, where ![]() denotes the set of integers from 1 to n excluding j.
denotes the set of integers from 1 to n excluding j.
Now, let us consider a multi-agent system based on an ideal network. Suppose the topology digraph G contains at least one globally reachable node. Then, we have rank[L] = n − 1 and L · 1n = 0. In this case we have τij = τ'ij = 0 and L(s) = L. From L · 1n = 0 it is easy to get ![]() ,
, ![]() and
and ![]() . Finally, by denoting
. Finally, by denoting ![]() , we know that
, we know that ![]() if and only if gi(0) ≠ 0, or
if and only if gi(0) ≠ 0, or ![]() and
and ![]() is a globally reachable node of digraph G. Thus, we get the following result as a corollary of Theorem 7.24.
is a globally reachable node of digraph G. Thus, we get the following result as a corollary of Theorem 7.24.
Theorem 7.28 In an ideal network with zero communication delays and constant channel dynamics, the rth-order consensus will be achieved for a steady semi-stable system at its steady state if and only if the topology graph contains at least one globally reachable node, and the agents's dynamics and the protocol satisfy gi(0) ≠ 0, or ![]() and
and ![]() is a globally reachable node of digraph G.
is a globally reachable node of digraph G.
7.4 Integrator-Chain Systems with Diverse Communication Delays
7.4.1 Matching Condition for Self-Delay
Consider the multi-agent system, whose agents are chains of integrators, i.e., mi = ν, and hi(s) = 1. In this case gi(s) = bi(s), and thus we have
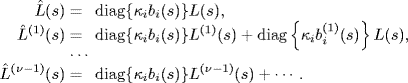
Since κi > 0 and bi0 ≠ 0, we have ![]() when the topology graph contains a globally reachable node. Now, we check the condition
when the topology graph contains a globally reachable node. Now, we check the condition ![]() ,
, ![]() . For the second-order consensus (ν = 2), this condition implies that
. For the second-order consensus (ν = 2), this condition implies that
And generally, the consensus condition for the νth-order consensus can be obtained as
Equation (7.106) or (7.107) uncovers a very interesting fact that the second-order or high-order consensus does not necessarily require τ'ij = τij. We call condition (7.107) the matching condition for self-delays.
7.4.2 Adaptive Adjustment of Self-Delay
Since (7.106) does not require each self-delay to be equal to the communication delay, for the second-order consensus each agent can set an identical self-delay, i.e., τ'ij = τ'i, ∀ j ![]() Ni, and adjust τ'i so that (7.106) is satisfied. In the following, we propose a simple algorithm for the adaptive adjustment of the self-delay.
Ni, and adjust τ'i so that (7.106) is satisfied. In the following, we propose a simple algorithm for the adaptive adjustment of the self-delay.
The performance index can be proposed as
where t0 is an initial time instant from which the adaptive adjustment begins, T > 0 is a large enough constant of time interval.
The algorithm of adaptive adjustment of τ'i is as follows:
(7.112) 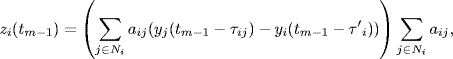
(7.113) ![]()
The proposed algorithm is essentially a gradient algorithm which is usually just locally convergent. To get the equilibria of the algorithm, one can set ![]() . Then, it follows
. Then, it follows
Since yi(t) → C0 + C1t, from (7.114) it follows that
or
Obviously, (7.115) is exactly (7.106) corresponding to the desired equilibrium; (7.116) implies that the velocities of all the agents go to zero, which is the zeroth-order consensus (constant consensus) state for the second-order system.
7.4.3 Simulation Study
In this subsection several simulation experiments are conducted through two numerical examples to verify the obtained theoretical results.
Example 7.29 Consensus of a system of heterogeneous agents.
Consider a system of five agents described by
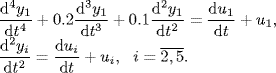
Obviously, agent 1 is absolutely different from the other four agents which are all double-integrators. The agents are interconnected by a digraph shown in Figure 7.14. The weighted adjacency matrix is given as follows
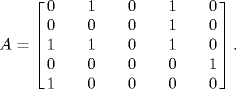
Figure 7.14 Interconnection graph.
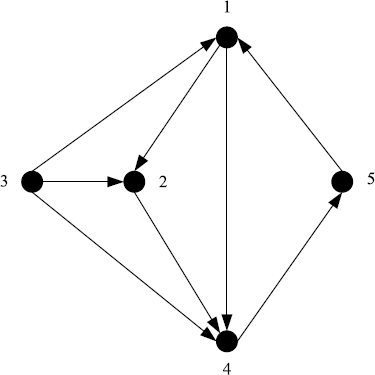
![]()
Figure 7.15 Positions of the agents (without delays).
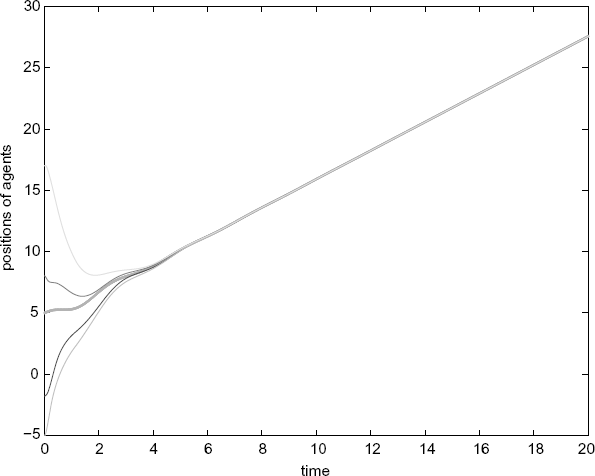
Figure 7.16 Velocities of the agents (without delays).
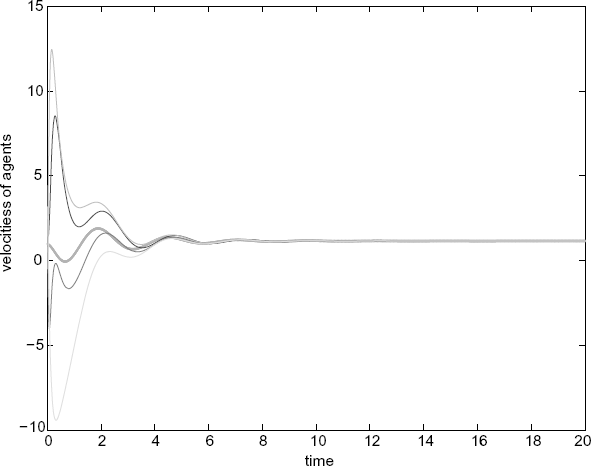
Figure 7.17 Position error between agent 1 and agent 2.
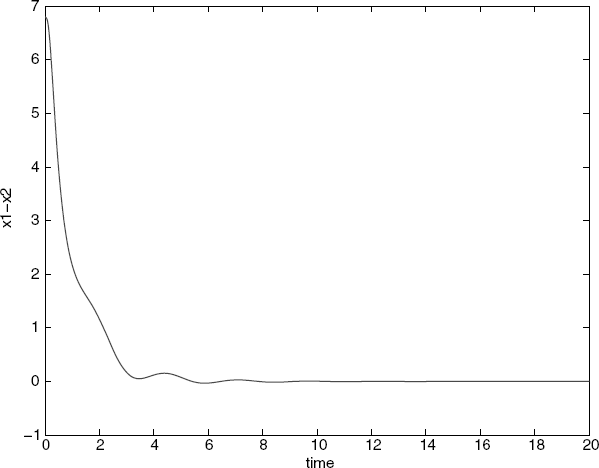
Figure 7.18 Velocity error between agent 1 and agent 2.
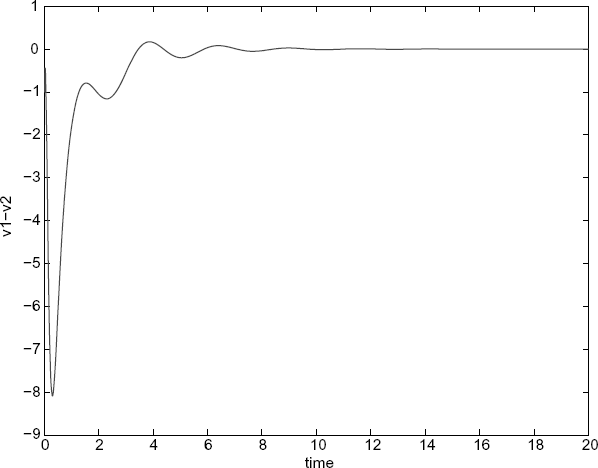
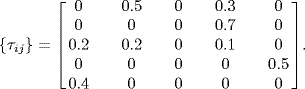
![]()
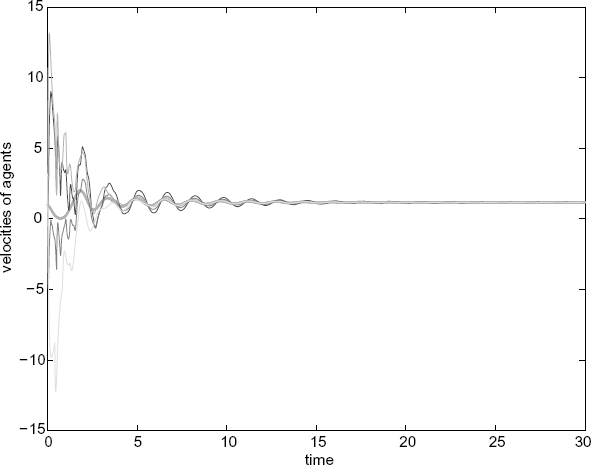
Figure 7.19 Positions of the agents (with diverse delays).
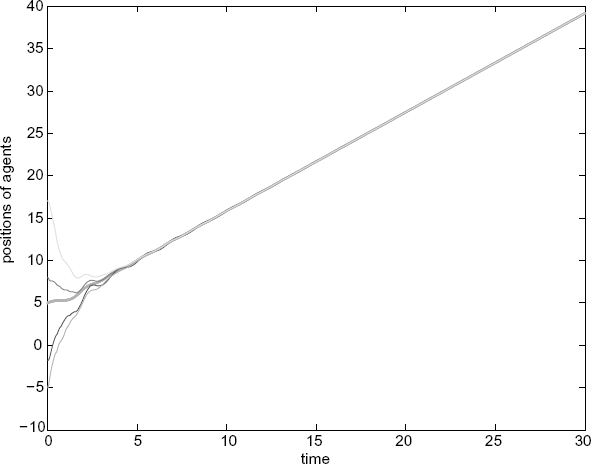
Figure 7.20 Velocities of the agents (with diverse delays).
Example 7.30 Consensus with unknown communication delays.
Now, we study the consensus protocols for unknown communication delays. To show the correctness of the theoretical results, we consider the case of identical double-integrator agents, which are extensively studied in the literature. Let
![]()
The interconnection topology graph is assumed to be the same as Figure 7.14. The adjacency matrix is given by
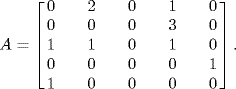
The diverse communication delays are set as
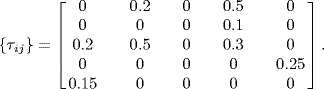
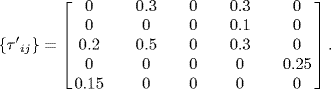
Figure 7.21 Positions and velocities of the agents (with unmatched but constrained delays).
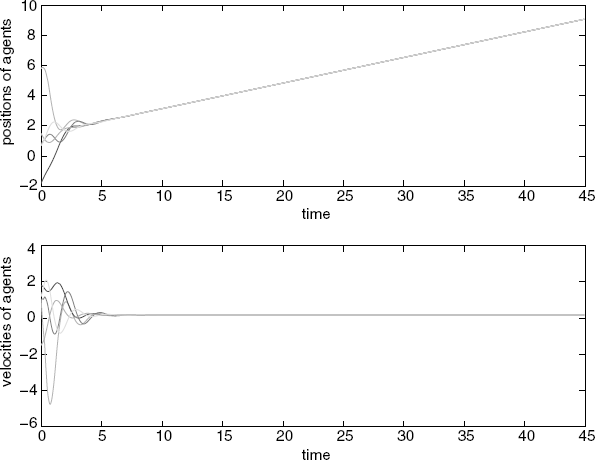
Figure 7.22 Position errors and velocity errors (with unconstrained delays).
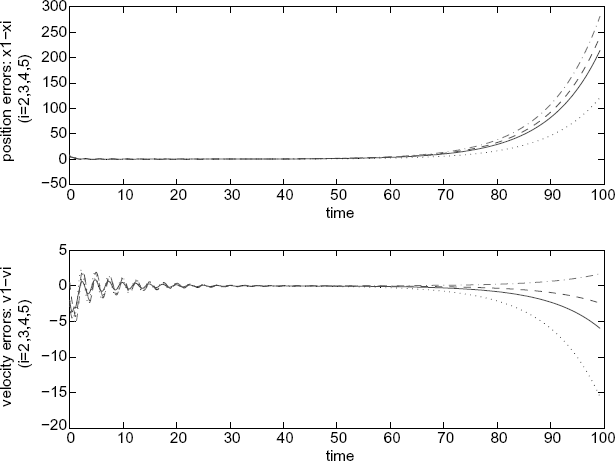
Figure 7.23 Positions of the agents (with an adaptive adjustment of self-delay).
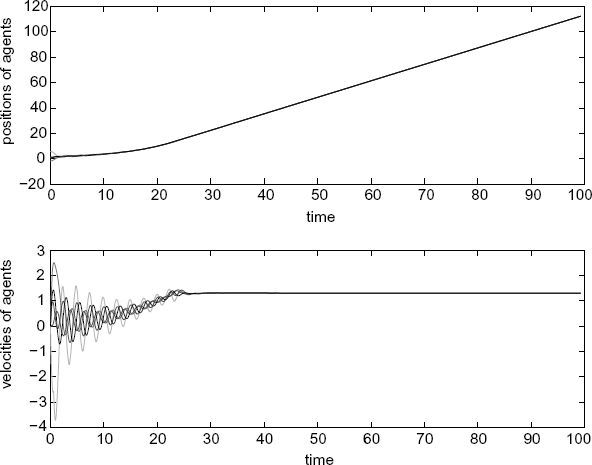
Figure 7.24 Position errors and velocity errors (with an adaptive adjustment of self-delay).
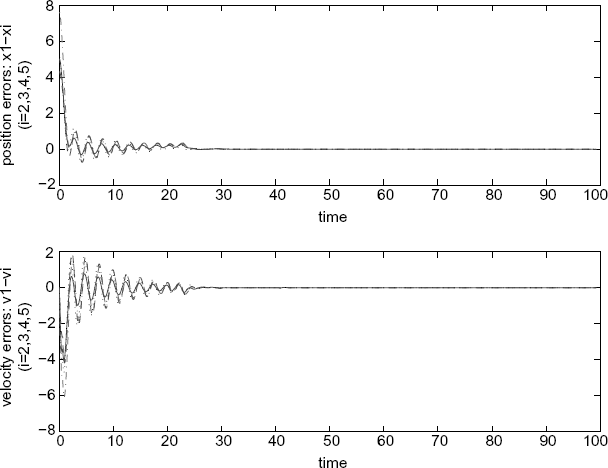
It should be noted that the convergence of both the adaptive algorithm and the stability of the overall system heavily depend on the values of the adaptive gain β and the initial value of the delay estimation τ'1(0). Generally speaking, the larger β is, the smaller the upper bound of admissible initial value of τ'1 is; when the initial value of the delay estimation is sufficiently close to the value satisfying the matching condition, the adaptive gain can be arbitrarily large (see Table 7.1).
Table 7.1 Parameter values under which the adaptive algorithm converges.

7.5 Notes and References
The study on consensus problems with communication delays can be traced in the research of distributed computation algorithms back to as early as the 1980s (Tsitsiklis, Bertsekas and Athans 1986). Similar problems are also studied in the context of synchronization of coupled oscillators (Yeung and Strogatz 1999). Recently, Olfati-Saber and Murray (2004) reviewed the consensus problem of the first-order multi-agent system and proposed a consensus protocol in which each agent delays its own measurement of state by the same value as the communication delay so that it could be matched by the delayed states of its neighbors. Olfati-Saber and Murray (2004) obtained a delay-dependent sufficient condition of constant consensus for the system with a uniform communication delay. Lin et al. (2007) extended the consensus protocol of Olfati-Saber and Murray (2004) to the second-order multi-agent system, and also obtained a delay-dependent sufficient condition of the second-order consensus. However, since each self-delay is equal to the corresponding communication delay in their protocol and only the unified delay bound is considered, the multi-agent systems studied in Olfati-Saber and Murray (2004) and Lin et al. (2007) are essentially homogeneous.
Lee and Spong (2006) considered a consensus protocol without self-delay and obtained a delay-independent sufficient condition of constant consensus for high-order heterogeneous systems with diverse communication delays by using Gershgorin's disc lemma and the small-gain theorem shown in Chapter 2. By using a similar technique, Wang and Elia (2008) also considered the consensus protocol without self-delay and gave a delay-independent sufficient condition of constant consensus for the first-order multi-agent systems with heterogeneous dynamic communication channels. Arcak (2007), Chopra and Spong (2006) studied heterogeneous MASs based on the passivity theory, and developed a general framework for the design of group coordination control of systems with nonlinear dynamical agents, which is applicable to the constant-consensus problem. Lestas and Vinnicombe (2006, 2007, 2010) also considered the constant-consensus problem for heterogeneous systems, and introduced the notion of S-hull, a relaxation of the convex hull of a set in the complex plane, to overcome the conservativeness of small-gain-like or passivity-like stability results. Using the frequency-domain analysis theory developed in Chapter 3, Section 7.1 gives scalable delay-dependent conditions of constant consensus for the first-order multi-agent system with diverse input delays and communication delays while Section 7.2 gives scalable delay-dependent conditions of the second-order consensus for the second-order multi-agent system with diverse input delays and asymmetric perturbations in communication channels. Sections 7.1 and 7.2 are mainly based on the results of Tian and Liu (2008, 2009).
Actually, the existence of constant consensus depends only on the connectivity of the interconnection topology of MASs (Ren and Beard 2005; Wang, Cheng and Hu 2008; Xiao and Wang 2007). The values of self-delays introduced by agents in consensus protocols may lead to instability of the consensus solution (Papachristodoulou, Jadbabaie and Mijünz 2010) but they do not influence the existence of the constant-consensus solution. Therefore, the main focus of the above-mentioned references on high-order heterogeneous MASs is on the stability instead of the existence of the set of consensus solutions.
It can be shown that an inappropriate value of self-delay may lead to the non-existence of high-order consensus solution. To guarantee the existence of high-order consensus solutions, currently existing consensus protocols introduce self-delays which are exactly equal to the corresponding communication delays (see, e.g., Hu and Hong 2007). In practice, however, communication delays can only be estimated approximately. Section 7.3 proposes a high-order consensus protocol based on the estimation of communication delays and investigates the existence of high-order consensus solution of high-order heterogeneous MASs under such a protocol. Section 7.4 presents a simple algorithm for on-line adjusting self-delays to guarantee the existence of high-order consensus solutions. These two sections are mainly taken from Tian and Zhang (2012) except for Section 7.3.4.
Arcak M (2007). Passivity as a design tool for group coordination. IEEE Transactions on Automatic Control, 52, 1380–1390.
Blondel VD, Hendrickx JM, Olshevsky A and Tsitsiklis JN (2005). Convergence in multiagent coordination, consensus, and flocking. Proceeding of the Joint 44th IEEE Conference on Decision and Control and European Control Conference, Seville, Spain, 2996–3000.
Cao M, Morse AS and Anderson BDO (2006). Reaching an agreement using delayed information. IEEE Conference on Decision and Control, San Diego, CA, USA, 3375–3380.
Chopra N and Spong MW (2006). Passivity-based control of multi-agent systems. Advances in Robot Control: From Everyday Physics to Human-like Movements, S. Kawamura and M. Svinin, Editors, 107–134, Spinger-Verlag, Berlin.
Hu J and Hong Y (2007). Leader-following coordination of multi-agent systems with coupling time delays. Physica A, 374, 853–863.
Jadbabaie A, Lin J and Morse AS (2003). Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 48, 988–1001.
Lee D and Spong MW (2006). Agreement with non-uniform information delays. Proceedings of the American Control Conference, Minneapolis, Minnesota, USA, 756–761.
Lestas I and Vinnicombe G (2006). Scalable decentralized robust stability certificates networks of interconnected heterogeneous dynamical systems. IEEE Transactions on Automatic Control, 51, 1613–1625.
Lestas I and Vinnicombe G (2007). The S-hull approach to consensus. Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, USA, 182–187.
Lestas I and Vinnicombe G (2010). Heterogeneity and scalability in group agreement protocols: Beyond small gain and passivity approaches. Automatica, 46, 1141–1151.
Lin P, Jia Y, Du J and Yuan S (2007). Distributed consensus control for second-order agents with fixed topology and time-delay. Proceeding of the 26th Chinese Control Conference, Zhangjiajie, Hunan, China, 577–581.
Moreau L (2005). Stability of multiagent systems with time-dependent communication links. IEEE Transactions on Automatic Control, 50, 169–182.
Olfati-Saber R and Murray RM (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 49, 1520–1533.
Papachristodoulou A, Jadbabaie A and Münz U (2010). Effect of delay in multi-agent consensus and oscillator synchronization. IEEE Transactions on Automatic Control, 55, 1471–1477.
Ren W and Beard RW (2005). Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Transactions on Automatic Control, 50, 655–661.
Tian Y-P and Liu C-L (2008). Consensus of multi-agent systems with diverse input and communication delays. IEEE Transactions on Automatic Control, 53, 2122–2128.
Tian Y-P and Liu C-L (2009). Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations. Automatica, 45, 1347–1353.
Tian Y-P and Zhang Y (2012). High-order consensus of heterogeneous multi-agent systems with unknown communication delays. Automatica, 48, 1205–1212.
Tsitsiklis JN, Bertsekas DP and Athans M (1986). Distributed asynchronous deterministic and stochastic gradient optimisation algorithms. IEEE Transactions on Automatic Control, 31, 803–812.
Vicsek T, Czirok A, Ben Jacob E, et al.(1995). Novel type of phase transitions in a system of self-driven particles. Physical Review Letters, 75, 1226–1229.
Wang J, Cheng D and Hu X (2008). Consensus of multi-agent linear dynamic systems. Asian Journal of Control, 10, 144–155.
Wang J and Elia N (2008). Consensus over network with dynamic channels. Proceeding of the American Control Conference, Seattle, WA, 2637–2642.
Wang W and Slotine JJE (2006). Contraction analysis of time-delayed communications and group cooperation. IEEE Transactions on Automatic Control, 51, 712–717.
Xiao F and Wang L (2007). Consensus problems for high-dimensional multi-agent systems. IET Control Theory and Applications, 1, 830–837.
Yeung MKS and Strogatz SH (1999). Time delay in the Kuramoto model of coupled oscillators. Physical Review Letter, 82, 648–651.