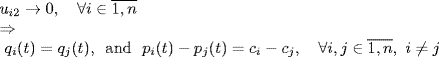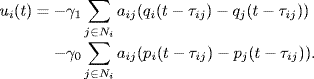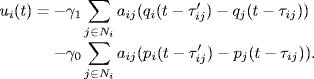Chapter 1
Introduction
Ruling a large country is like cooking a small fish.
—Lao Dan (580–500 BC), Tao Te Ching
This chapter is concerned with some common characteristics of distributed control systems, such as distributive interconnections, local control rules and scalability. Basic notions and results of algebraic graph theory are introduced as a theoretic foundation for modeling interconnections of subsystems (agents) in distributed control systems. Coordination control systems and end-to-end congestion control systems are also introduced as two typical kinds of distributed control systems. The main topics of this book are also highlighted in the introduction of these two kinds of systems.
1.1 Network-Based Distributed Control System
From the “flyball” speed governor of Watt's steam engine to the control of communication systems including the telephone system, cell phones and the Internet, the control mechanism in industrial, social and many other real-world systems has experienced a development process from centralized control to distributed control. In the past decade, this process has been significantly speeded up thanks to rapid advances of communication techniques and their application to control systems.
Recently, workshops, seminars, short courses and even regular courses on distributed control systems emerge in the control society just like bamboo shoots after spring rain. But the following questions, which are often raised in seminars or lectures by post-graduate students, may also puzzle the reader of this book. What kind of control systems can be called distributed control system? Are there any differences between a distributed control system and a so-called large-scale control system or a decentralized control systems? What's the advantage of distributed control over centralized control? etc. We will not attempt to answer all the questions; rather, we will try to grasp some common features of distributed control systems.
Cooperation Among Agents
Cooperation is perhaps the soul of a distributed control system. Since there is no centralized control unit, the only way through which all the agents in the system can work in harmony is to conduct some kind of cooperation.
Ignoring cooperation in biology might be one of a few shortcomings by which one could rebuke the great theory of Darwin (1859). Indeed, cooperation has been observed in many biological colonies, such as in birds, fish, bacilli and so on. Through cooperation they increase the probability of discovering food, get rid of prey and other dangers. Breder (1954) proposed a simple mathematic model to characterize the attracting and excluding actions in schools of fish. To describe the flocks and aggregations of schools more effectively, Reynolds (1987) proposed three simple rules: (1) collision avoidance, (2) agreement on velocity and (3) approaching center, which actually implies approaching any neighbor. He successfully simulated the motion of fish by using these rules. These investigations stimulate researchers to develop artificial systems that make decisions and take actions in distributive but cooperative manners. Nowadays, distributed control mechanisms have been widely used in engineering systems, such as aircraft traffic control (Tomlin, Pappas and Sastry (1998), multi-robot control (Rekleitis, Dudek and Milios (2000), coverage control of sensor networks (Qi, Iyengar and Chakrabarty (2001), formation control of unmanned aerial vehicles (UAVs) (Giulietti, Pollini and Innocenti (2000) etc.
Spatially Distributed Interconnection
In a classic feedback control system, the controller gets the output signal of the plant, compares it with some reference signal and makes decisions on how to act. Such a system also serves as one of basic units (subsystems) in a distributed control system. However, to cooperate with other units in the entire system, it should be equipped with a sensor/communication modular besides the classic decision/action modular (controller), as shown in Figure 1.1. Such a subsystem is sometimes called an agent. In a distributed control system, therefore, each subsystem gets not only the information of the output of itself but also the information of some other subsystems via sensor or/and communication networks (Figure 1.2). A distributed control system interconnected with multiple agents is also called a multi-agent system (MAS).
Figure 1.1 An agent in distributed control system.
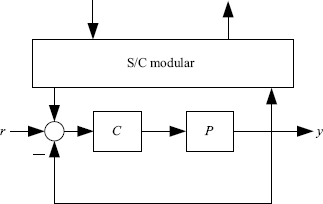
Figure 1.2 A network-based distributed control system.
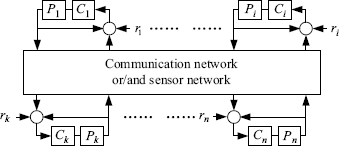
For many distributed control systems such as the Internet, power grids, traffic control systems etc., subsystems (agents) are often distributed across multiple computational units in an immense space and connected through long-distance packet-based communications. In these system packet loss and delay are unavoidable, and hence, computational and communication constraints cannot be ignored. New formalism to ensure stability, performance and robustness is required in the analysis and design of distributed control systems (Murray et al. (2003).
Local Control Rule
A distributed control law should be subject to the local control rule, which implies that in most cases there is no kind of centralized supervision or control unit in the system, and each agent makes decisions based only on the information received by its own sensor or from its neighboring agents through communication. The action rules proposed by Reynolds (1987) are typically local control rules. The local control rule is the most important feature of distributed control systems and makes the distributed control distinguished from the decentralized control of large-scale systems, which were extensively studied in the 1970s and 1980s (see, e.g., Sastry (1999) for a survey on large-scale systems). The decentralized control mechanism allows each agent to communicate perfectly with any other agent in the system, ignoring the computational and communication constraints. Moreover, the plant in decentralized control systems is usually a single tightly connected unit and not a rather loosely interconnected group of complete systems, which is the typical case in distributed control systems. Therefore, cooperation among agents in distributed control systems is much more important than in large-scale systems, and hence the coupling between a pair of subsystems can not be dealt with as a disturbance as in some decentralized control designs.
A remarkable advantage of the local control rule over the non-local control rules is its higher fault-tolerance capability. This is extremely important for many large-scale engineering systems which must operate continuously even when some individual units fail. Therefore, building a very reliable distributed control system with fault-tolerance ability from unreliable parts is a very promising research direction (Murray et al. (2003), although the topic is beyond the scope of this book.
Scalability
Scalability is perhaps another very important reason why distributed control systems prefer the local control rule. In this book the scalability of a distributed control system implies that the controller of the system and its maintenance utilize only local information around each agent and rarely depends on the scale of the system. In other words, by scalability we mean that not only the control law but also most important properties of the system rely on the local information. For example, in checking the stability of the entire distributed control system the scalability requires that the stability criterion does not need to use information about the global interconnection topology of the system because such global information is usually unavailable to individual agents. A scalable system allows new applications to be designed and deployed without requiring changes to the underlying system. The scalability of heterogeneous distributed control systems has drawn much more attention of researchers because most practical networked systems such as the Internet are heterogeneous. Diverse communication and/or input delays, different channel capacities, non-identical agent dynamics and so on, can make a system heterogeneous. Analysis and design of heterogeneous systems are much more difficult in comparison with homogeneous systems. One reason for that is the analysis and/or design of a large but homogenous systems can usually be treated as a task for a small system through diagonalization of the original system. But in most cases such a simplification method is not applicable to heterogeneous systems.
1.2 Graph Theory and Interconnection Topology
1.2.1 Basic Definitions
Graph theory plays a crucial role in describing the interconnection topology of distributed control systems. In this section we only present basic definitions about graph theory. For systematic study of graph theory we refer the reader to, for example, Biggs (1994); Bollobijás (1998); Diestel (1997); Godsil and Royle (2001).
Digraph
A directed graph (in short, digraph) of order n is a pair G= (V, E), where V is a set with n elements called vertices (or nodes) and E is a set of ordered pairs of vertices called edges. In other words, E ⊆ V × V. We denote by V(G) and E(G) the vertex set and edge set of graph G, respectively, and denote by ![]() a finite set for vertex index. For two vertices
a finite set for vertex index. For two vertices ![]() , i.e.,
, i.e., ![]() , the ordered pair
, the ordered pair ![]() represents an edge from
represents an edge from ![]() to
to ![]() and is also simply denoted by eij.
and is also simply denoted by eij.
A digraph G(V ', E ') is said to be a subgraph of a digraph (V, E) if V ' ⊂ V and E ' ⊂ E. In particular, a digraph (V ', E ') is said to be a spanning subgraph of a digraph (V, E) if it is a subgraph and V ' = V. The digraph (V ', E ') is the subgraph of (V, E) induced by V ' ⊂ V if E ' contains all edges in E between two vertices in V '.
Path and Connectivity
A path in a digraph is an ordered sequence of vertices such that any ordered pair of vertices appearing consecutively in the sequence is an edge of the digraph. A path is simple if no vertices appear more than once in it, except possibly for the initial and final vertices. The length of a path is defined as the number of consecutive edges in the path. For a simple path, the path length is less than the number of vertices contained in the path by unity.
A vertex ![]() in digraph G is said to be reachable from another vertex
in digraph G is said to be reachable from another vertex ![]() if there is a path in G from
if there is a path in G from ![]() to
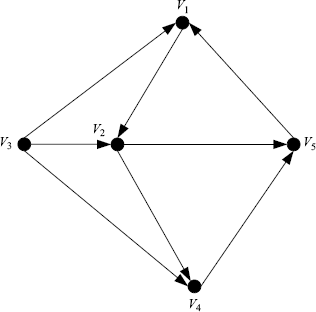
to ![]() . A vertex in the digraph is said to be globally reachable if it is reachable from every other vertex in the digraph. A digraph is strongly connected if every vertex is globally reachable. In Figure 1.3,
. A vertex in the digraph is said to be globally reachable if it is reachable from every other vertex in the digraph. A digraph is strongly connected if every vertex is globally reachable. In Figure 1.3, ![]() are globally reachable vertices. But the digraph is not strongly connected because
are globally reachable vertices. But the digraph is not strongly connected because ![]() is unreachable from the other vertices.
is unreachable from the other vertices.
Figure 1.3 A digraph.
Cycle and Tree
A cycle is a simple path that starts and ends at the same vertex. A cycle containing only one vertex is called a self-cycle (or self-loop). The length of a cycle is defined as the number of edges contained in the cycle. A cycle is odd (even) if it 's length is odd (even). If a vertex in a cycle is globally reachable, then any other vertex in the cycle is also globally reachable. In Figure 1.3, the path ![]() is a cycle. The path
is a cycle. The path ![]() and the path
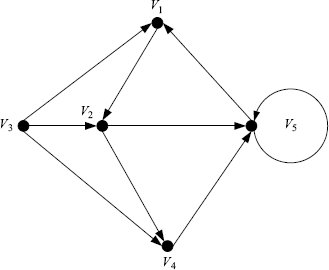
and the path ![]() are also cycles. This digraph has no self-cycle. A digraph with self-cycle is shown in Figure 1.4.
are also cycles. This digraph has no self-cycle. A digraph with self-cycle is shown in Figure 1.4.
Figure 1.4 A digraph with a self-cycle.
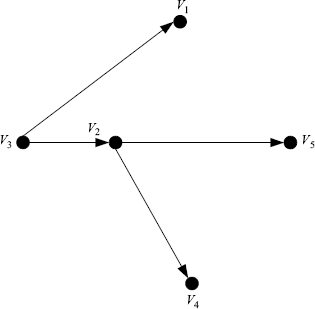
A digraph is acyclic if it contains no cycles. An acyclic digraph is called a directed tree if it satisfies the following property: there exists a vertex, called the root, such that any other vertex of the digraph can be reached by one and only one path starting at the root. A directed spanning tree of a digraph is a spanning subgraph that is a directed tree.
The digraph shown in Figure 1.5 is a directed tree. Obviously, it is a directed spanning tree of both the digraph in Figure 1.3 and the digraph in Figure 1.4.
Figure 1.5 A directed tree.
Neighbor and Degree
If ![]() is an edge of digraph G, then
is an edge of digraph G, then ![]() is an out-neighbor of
is an out-neighbor of ![]() , and
, and ![]() is an in-neighbor of
is an in-neighbor of ![]() . The set of out-neighbors (in-neighbors) of vertex
. The set of out-neighbors (in-neighbors) of vertex ![]() in digraph G(V, E) is denoted by
in digraph G(V, E) is denoted by ![]() (
(![]() ).
).
The out-degree (in-degree) of ![]() is the cardinality of
is the cardinality of ![]() (
(![]() ). A digraph is topologically balanced if each vertex has the same in-and out-degrees. Note that neither
). A digraph is topologically balanced if each vertex has the same in-and out-degrees. Note that neither ![]() nor
nor ![]() contains the vertex i itself even if there is a self-loop at vertex i.
contains the vertex i itself even if there is a self-loop at vertex i.
Let us consider the example of a digraph shown in Figure 1.3. For vertex 1, its out-neighbor set is ![]() , and its in-neighbor set is
, and its in-neighbor set is ![]() . The out-degree and the in-degree of
. The out-degree and the in-degree of ![]() are 1 and 2, respectively.
are 1 and 2, respectively.
In this book, if the superscript is dropped in formulae or the prefix is omitted in texts, it will be referred to as the out-neighbor, i.e., ![]() .
.
Sometimes we may use the term multi-level neighbor. If there is an m-length path in digraph G from vertex i to vertex j, then vertex j is said to be an m-level neighbor of vertex i. Of course, a neighbor in conventional sense is a 1-level neighbor. The set of m-level neighbors of agent i in digraph G is denoted by ![]() . For example, in the digraph shown in Figure 1.3,
. For example, in the digraph shown in Figure 1.3, ![]() .
.
Digraph and Information Flow
In a distributed control system, each agent can be considered as a vertex in a digraph, and the information flow between two agents can be regarded as a directed path between the vertices in the digraph. Thus, the interconnection topology of a distributed control system can be described by a digraph. However, differing from the classic signal-flow graph (Chen (1984), in this book and in many other references on the distributed control system, the direction of an edge in the digraph does not mean the direction of an information flow. Let us consider the digraph shown in Figure 1.3 for an instance. Denote by ![]() , the state of agent i associated with vertex i. The existence of edge eij implies that agent i gets the state information xj from agent j. For example, agent 1 gets information from agent 2.
, the state of agent i associated with vertex i. The existence of edge eij implies that agent i gets the state information xj from agent j. For example, agent 1 gets information from agent 2.
1.2.2 Graph Operations
We shall construct new graphs from old ones by graph operations.
For two digraphs G1 = (V1, E1) and G2 = (V2, E2), the intersection and union of G1 and G2 are defined by
![]()
For a digraph G = (V, E), the reverse digraph of G is a pair rev(G) = (V, rev(E)), where rev(E) consists of all edges in E with reversed directions.
If W ⊂ V(G), then G − W = G[V W] is the subgraph of G obtained by deleting the vertices in W and all edges incident with them. Obviously, G − W is the subgraph of G induced by V W. Similarly, if E ' ⊂ E(G), then G − E ' = (V(G), E(G) E '). If W (or E ') contains a single vertex ![]() (or a single edge xy, respectively), the notion is simplified to
(or a single edge xy, respectively), the notion is simplified to ![]() (or G − xy, respectively). Similarly, if x and y are non-adjacent vertices of G, then G + xy is obtained from G by joining x to y.
(or G − xy, respectively). Similarly, if x and y are non-adjacent vertices of G, then G + xy is obtained from G by joining x to y.
Undirected Graph
An undirected graph (in short, graph) G consists of a vertex set V and a set E of unordered pairs of vertices. If each edge of the graph G is given a particular orientation, then we get an oriented graph of G, denoted by G→, which is a digraph. Denote by G← the reverse of G→. Then, G = G→ ∪ G←.
For an undirected graph G, the in-neighbor set of any vertex is always equal to the out-neighbor set of the same vertex. Therefore, in the undirected case we simply use the terminations neighbor, neighbor set and degree.
For an undirected graph, if it contains a globally reachable node, then any other vertex is also globally reachable. In that case we simply say that the undirected graph is connected.
For an undirected graph, it is said to be a tree if it is connected and acyclic.
Theorem 1.1 G(V, E) is a tree if and only if G is connected and |E| = |V| − 1. Alternatively, G(V, E) is a tree if and only if G is acyclic and |E| = |V| − 1.
Theorem 1.2 A graph is connected if and only if it contains a spanning tree.
Bipartite Graph
A graph G is a bipartite graph with vertex classes V1 and V2 if V(G) is a direct sum of V1 and V2, i.e., V = V1 ⊕ V2, which implies that V = V1 ∪ V2 and V1∩ V2 = , and every edge joins a vertex of V1 to a vertex of V2. It is also said that G has bipartition (V1, V2). Figure 1.6 shows an example of a bipartite graph. For this graph, the vertex set V is a direct sum of ![]() and
and ![]() . Each vertex in V1 has neighbors only in V2, and vice versa.
. Each vertex in V1 has neighbors only in V2, and vice versa.
Figure 1.6 A bipartite graph.
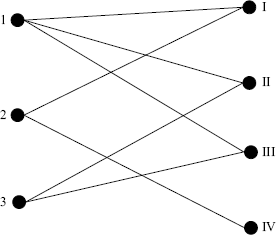
Theorem 1.3 A graph is bipartite if and only if it does not contain an odd cycle.
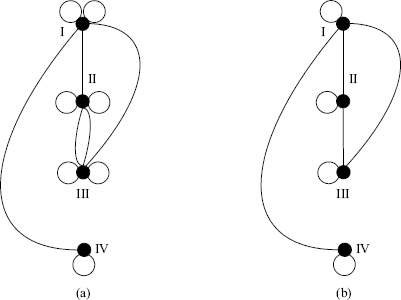
For the bipartite graph G with vertex classes V1 and V2, define
Note that in both (1.1) and (1.2), ![]() and
and ![]() can be the same vertex. In this case,
can be the same vertex. In this case, ![]() is a self-loop. Let
is a self-loop. Let
and
G1 is a new graph obtained from G by deleting all the vertices in V2 and adding the new edges in E ' 12. By definition (1.1), E ' 12 is the set of new edges, each of which adds a self-loop to one vertex or joins two vertices in V1 that are neighbors of a vertex in V2. Similarly, G2 is a new graph obtained from G by deleting all the vertices in V1 and adding the new edges in E ' 21. E ' 21 is the set of new edges, each of which adds a self-loop to one vertex or joins two vertices in V2 that are neighbors of a vertex in V1.
G1 (G2) is said to be the equivalent graph for V1 (V2) deduced from G. Obviously, neither G1 nor G2 is a subgraph of G. But the interconnection topology between any two vertices in one vertex class remains unchanged for G and the equivalent graph G1 (or G2).
The graph operation defined by (1.3) for the bipartite graph shown in Figure 1.6 is illustrated by Figure 1.7(a). Since only one edge is defined between any pair of vertices in graph, the equivalent graph for V1 is given by Figure 1.7(b). Similarly, the graph operation defined by (1.4) for the same bipartite graph is illustrated by Figure 1.8(a). The equivalent graph for V2 is given by Figure 1.8(b).
Figure 1.7 Graph operation and equivalent graph for V1.
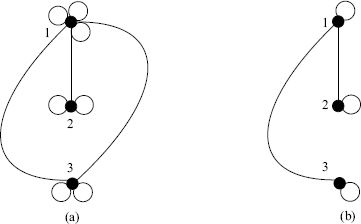
Figure 1.8 Graph operation and equivalent graph for V2.
1.2.3 Algebraic Graph Theory
Algebraic graph theory studies matrices associated with digraphs.
Weighted Digraph and Adjacency Matrix
A weighted digraph of digraph G(V, E) is a triplet G = (V, E, A), where ![]() is an adjacency matrix satisfying
is an adjacency matrix satisfying
We denote by A(G) the adjacency matrix of a weighted digraph G. Figure 1.9 shows an example of a weighted digraph. The adjacency matrix of the weighted digraph is
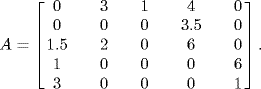
Figure 1.9 A weighted digraph.
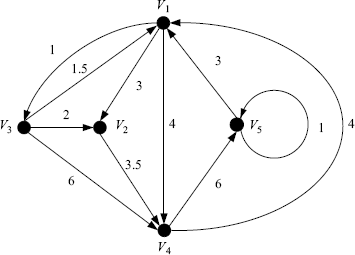
Obviously, a weighted digraph is undirected if and only if aij = aji, that is, A(G) is symmetric.1
If digraph G contains no self-loop, then all the diagonal elements of its adjacency matrix A are zero, i.e., ![]() . However, sometimes we may encounter with graphs with self-loops. In this case, aii may be positive numbers. To avoid confusion in terminology, by adjacency matrix we still mean the matrix A with zero entries in the diagonal. Actually, A(G) is associated with the digraph that is obtained by cutting off all the self-loops in G. We denote by
. However, sometimes we may encounter with graphs with self-loops. In this case, aii may be positive numbers. To avoid confusion in terminology, by adjacency matrix we still mean the matrix A with zero entries in the diagonal. Actually, A(G) is associated with the digraph that is obtained by cutting off all the self-loops in G. We denote by ![]() the matrix that characterizes the existence of all edges including self-loops in G, i.e.,
the matrix that characterizes the existence of all edges including self-loops in G, i.e.,
(1.5) ![]()
and refer to ![]() as the generalized adjacency matrix of G.
as the generalized adjacency matrix of G.
For a weighted digraph ![]() of order n, we use
of order n, we use ![]() to denote its un-weighted adjacency matrix, where
to denote its un-weighted adjacency matrix, where
![]()
Let ![]() be a weighted digraph of G(V, E) of order n. Given a matrix
be a weighted digraph of G(V, E) of order n. Given a matrix ![]() with
with ![]() , if
, if
(1.6) ![]()
then, by the definition of adjacency matrix, ![]() is also a weighted digraph of G(V, E).
is also a weighted digraph of G(V, E).
Naturally, a digraph G = (V, E) can be considered as a weighted digraph with {0, 1}-weights, i.e.,
![]()
The weighted out-degree matrix of digraph G, denoted by Dout(G), is the diagonal matrix with the weighted out-degree of each node along its diagonal, i.e.,
(1.7) ![]()
The weighted in-degree matrix of digraph G, denoted by Din(G), is the diagonal matrix with the weighted in-degree of each node along its diagonal, i.e.,
(1.8) ![]()
While the adjacency matrix characterizes the location of edges among vertices in a digraph, the following result shows that powers of the adjacency matrix characterize the relationship between directed paths and vertices in the digraph.
Lemma 1.4 Let ![]() be a weighted digraph of order n possibly with self-loops.
be a weighted digraph of order n possibly with self-loops. ![]() is its un-weighted adjacency matrix. Then, for all
is its un-weighted adjacency matrix. Then, for all![]() ,
,
Gain, Measurement Matrix and State-Transfer Matrix
Let ![]() , be the state of agent i associated with vertex i, where k represents the time. By our stipulation of the physical meaning of the edge direction in a digraph, the existence of eij implies that agent i gets the state information xj from agent j. Then, the weight aij associated with eij can be regarded as the gain for the information flow. So, for a system with G(V, E, A) as its interconnection topology digraph, the existence of eij implies that the agent i gets the amplified state information aijxj(k) from agent j. Let the measurement yi(k) of agent i be equal to the sum of all the amplified states at the present time received by agent i, i.e.,
, be the state of agent i associated with vertex i, where k represents the time. By our stipulation of the physical meaning of the edge direction in a digraph, the existence of eij implies that agent i gets the state information xj from agent j. Then, the weight aij associated with eij can be regarded as the gain for the information flow. So, for a system with G(V, E, A) as its interconnection topology digraph, the existence of eij implies that the agent i gets the amplified state information aijxj(k) from agent j. Let the measurement yi(k) of agent i be equal to the sum of all the amplified states at the present time received by agent i, i.e.,
Such a measurement will be also referred to as aggregated measurement. Sometimes, each agent can get only some relative measurement which can be expressed as
Denote by x(k) = [x1(k), ![]() , xn(k)]T the state vector and y(k) = [y1(k),
, xn(k)]T the state vector and y(k) = [y1(k), ![]() , yn(k)]T the measurement vector. Then, the matrix form of the aggregated measurement (1.9) is
, yn(k)]T the measurement vector. Then, the matrix form of the aggregated measurement (1.9) is
Equation (1.11) provides an interpretation of the generalized adjacency matrix ![]() from a viewpoint of system theory: it can be considered as a measurement matrix.
from a viewpoint of system theory: it can be considered as a measurement matrix.
Suppose the state formation of each agent is updated by the following local law:
where ![]() Then, we have
Then, we have
(1.13) ![]()
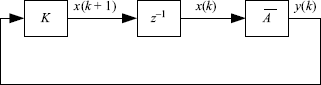
So, with the updating law (1.12), ![]() is a state-transfer matrix of a closed-loop system, as shown in Figure 1.10.
is a state-transfer matrix of a closed-loop system, as shown in Figure 1.10.
Figure 1.10 A closed-loop system.
Weighted Bipartite Graph
Let G(V, E, A) be a weighted bipartite graph with vertex classes ![]() and
and ![]() . Then, by the definition of bipartite graph, the adjacency matrix A(G) can be partitioned as
. Then, by the definition of bipartite graph, the adjacency matrix A(G) can be partitioned as
where ![]() . Hence,
. Hence,
(1.15) ![]()
By Lemma 1.4 we know that any vertex in V1 has two-level neighbors in V1, and any vertex in V2 has two-level neighbors in V2. Furthermore, the existence of paths of length 2 (including self-loops) in G between any pair of vertices in V1 (or V2) is characterized by the sign of entries of ![]() (or
(or ![]() ). So, by the definition of equivalent graph,
). So, by the definition of equivalent graph, ![]() (or
(or ![]() ) can be defined as a weighted adjacency matrix associated with the equivalent graph of the bipartite graph G for V1 (or V2). Summarizing the discussion we have the following proposition.
) can be defined as a weighted adjacency matrix associated with the equivalent graph of the bipartite graph G for V1 (or V2). Summarizing the discussion we have the following proposition.
Proposition 1.5 Let G1(V1, E1) and G2(V2, E2) be the equivalent graphs of the bipartite graph G(A) for V1 and V2, respectively, where A is given by (1.14). Then,
(1.16) ![]()
(1.17) ![]()
are weighted adjacency matrices associated with G1 and G2, respectively.
By the definition of un-weighted adjacency matrix,
(1.18) ![]()
So, we have
![]()
So, by Lemma 1.4, the number of paths of
length 2 (including self-loops) in G from vertex i to vertex j (![]() ) in V1 equals the value of the (i, j) entry of
) in V1 equals the value of the (i, j) entry of ![]() ; and the number of paths of length 2 (including self-loops) in G from vertex i to vertex j (
; and the number of paths of length 2 (including self-loops) in G from vertex i to vertex j (![]() ) in V2 equals the value of the (i, j) entry of
) in V2 equals the value of the (i, j) entry of ![]() ). However, the signs of entries of
). However, the signs of entries of ![]() (or
(or ![]() ) also characterize the existence of paths of length 2 (including self-loops) in G between any pair of vertices in V1 (or V2) (see Exercise 1.7). So, by the definition of equivalent graph, the following proposition is also true.
) also characterize the existence of paths of length 2 (including self-loops) in G between any pair of vertices in V1 (or V2) (see Exercise 1.7). So, by the definition of equivalent graph, the following proposition is also true.
Proposition 1.6 Let G1(V1, E1) and G2(V2, E2) be the equivalent graphs of the bipartite graph G(A) for V1 and V2, respectively, where A is given by (1.14). Denote
(1.19) ![]()
(1.20) ![]()
Then, ![]() and
and ![]() are weighted equivalent graphs of the bipartite graph G for V1 and V2, respectively.
are weighted equivalent graphs of the bipartite graph G for V1 and V2, respectively.
Remark. ![]() (or
(or ![]() ) is not the un-weighted matrix of
) is not the un-weighted matrix of ![]() (or
(or ![]() ), i.e.,
), i.e.,
![]()
Exercises 1.7 show
(1.21) ![]()
(1.22) ![]()
Let ![]() be the state vectors associated with V1 and V2, respectively. Denote
be the state vectors associated with V1 and V2, respectively. Denote ![]() . Then, under the measurement rule (1.11) and the state updated law (1.12), we have
. Then, under the measurement rule (1.11) and the state updated law (1.12), we have
![]()
Partition K as K = diag{K1, K2}, where ![]() ,
, ![]() . Hence,
. Hence,
(1.23) ![]()
which yields
If K2 > 0, we can define a new weight matrix for the bipartite graph G as
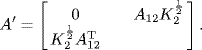
Then, by Proposition 1.5, ![]() is a weighted adjacency matrix of the equivalent graph for vertex class V1 in G. Equation (1.24) links x(k + 1) to x(k − 1) instead of x(k) because any vertex in V1 has no (one-level) neighbors in V1. So,
is a weighted adjacency matrix of the equivalent graph for vertex class V1 in G. Equation (1.24) links x(k + 1) to x(k − 1) instead of x(k) because any vertex in V1 has no (one-level) neighbors in V1. So, ![]() is also the state-transfer matrix for the states associated with the vertices in V1.
is also the state-transfer matrix for the states associated with the vertices in V1.
Laplacian Matrix
Now, we can generalize the notions of in-and out-degree to weighted digraphs. In a weighted digraph G(V, E, A) with ![]() , the weighted out-degree and the weighted in-degree of vertex
, the weighted out-degree and the weighted in-degree of vertex ![]() are defined by, respectively,
are defined by, respectively,
(1.25) ![]()
and
(1.26) ![]()
The weighted digraph G is weight-balanced if ![]() for all
for all ![]() .
.
Definition 1.8 The Laplacian matrix of the weighted digraph G(V, E, A) is defined as
(1.27) ![]()
If we let
![]()
then, the relative measurement (1.10) can be rewritten as
![]()
or in the matrix form
![]()
So, the Laplacian matrix can be interpreted as a kind of relative-measurement matrix.
The following theorems give some useful properties of Laplacian matrices.
Theorem 1.9 Let G be a weighted digraph of order n. The following statements hold:
Theorem 1.10 Digraph G is weight-balanced if and only if one of the following statements holds:
1.3 Distributed Control Systems
In this section we introduce two typical kinds of distributed control systems, which will be studied more carefully in the remaining chapters of this book.
1.3.1 End-to-End Congestion Control Systems
One effective way for agents in a distributed control system to cooperate with each other is to optimize some performance index which concerns all of the agents in the system, such as allocation of limited resources in a communication network (Kelly 1997; Kelly, Maulloo and Tan 1998), coverage of as much as possible an area by a sensing network (Cortés et al. (2004), etc. Congestion control of the Internet is a typical system designed by using a distributed real-time optimization approach, which will be presented in Chapter 4. Here we just introduce some basic models with some necessary notions of end-to-end congestion control systems.
Basic Model
Let us consider an end-to-end congestion control system for a network with a set of L link nodes shared by a set of S source nodes. Denote by ![]() the set of all link nodes and by
the set of all link nodes and by ![]() the set of source nodes. Link node
the set of source nodes. Link node ![]() is used by a set of sources denoted by
is used by a set of sources denoted by ![]() , and source node
, and source node ![]() sends packets to a set of links denoted by
sends packets to a set of links denoted by ![]() . The sets Li define an L × S routing matrix R = {Rli}, where
. The sets Li define an L × S routing matrix R = {Rli}, where
![]()
From a viewpoint of graph theory, each node in ![]() has neighbors only in
has neighbors only in ![]() and each node in
and each node in ![]() has neighbors only in
has neighbors only in ![]() . So, the topology of such a system can be described by a bipartite graph G(V, E), where
. So, the topology of such a system can be described by a bipartite graph G(V, E), where ![]() . A weighted adjacency matrix of the bipartite graph can be given by
. A weighted adjacency matrix of the bipartite graph can be given by
where ![]() ,
, ![]() are two positively definite diagonal matrices. Source
are two positively definite diagonal matrices. Source ![]() transmits packets to all the links used by source i at a rate xi(t); in other words, all the links in Li receive packets at rate xi(t).
transmits packets to all the links used by source i at a rate xi(t); in other words, all the links in Li receive packets at rate xi(t).
The primal algorithm for the congestion-avoidance rate control is given by (Kelly, Maulloo and Tan (1998)
where the control gain ki is a positive constant, and ![]() is some desired value of the rate of marked packets received back at sources i. The first equation describes the time evolution of the transmission rate xi(t) of source i. The second equation describes the generation of congestion signal ql(t) at link l, by means of a congestion indication function pl(y), which is assumed to be monotonically increasing, nonnegative, and not identically zero (a candidate of such a function can be taken as p(y) = 1 − ey(1 − y), which is positive and strictly increasing for all y > 0).
is some desired value of the rate of marked packets received back at sources i. The first equation describes the time evolution of the transmission rate xi(t) of source i. The second equation describes the generation of congestion signal ql(t) at link l, by means of a congestion indication function pl(y), which is assumed to be monotonically increasing, nonnegative, and not identically zero (a candidate of such a function can be taken as p(y) = 1 − ey(1 − y), which is positive and strictly increasing for all y > 0).
Suppose that matrix R is of full row rank. Then, one can get the unique equilibrium point of system (1.29)– (1.30) as ![]() , where
, where ![]() . Define
. Define
![]()
The dynamic property of the system around the equilibrium is determined by the following linearized model:
where p ' l is the derivative of pl evaluated at ![]() , i.e.
, i.e. ![]() . Since pl(y) is assumed to be monotonically increasing,
. Since pl(y) is assumed to be monotonically increasing, ![]() . By defining
. By defining
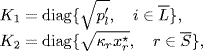
and
![]()
it is easy to verify that the interconnection between yl and yr can be described by a weighted equivalent graph ![]() for vertex class
for vertex class ![]() in the bipartite graph G(V, E, A), where
in the bipartite graph G(V, E, A), where ![]() and A is given by (1.28). Denote
and A is given by (1.28). Denote
![]()
Then, the matrix form of (1.31) is given by
(1.32) ![]()
Model with Delays
When propagation delays are considered, the congestion control algorithms can be modeled by the following delayed differential equations (Johari and Tan (2001)
(1.34) ![]()
where ![]() denotes the forward delay of delivering packets from source i to link l,
denotes the forward delay of delivering packets from source i to link l, ![]() denotes the backward delay of sending the feedback signal from link l to source i, and Di is the round-trip delay associated with source i. In the current Internet, it is assumed that propagation delay is much more significant than queueing delay. Therefore, ignoring the queueing delay, the following relationship holds:
denotes the backward delay of sending the feedback signal from link l to source i, and Di is the round-trip delay associated with source i. In the current Internet, it is assumed that propagation delay is much more significant than queueing delay. Therefore, ignoring the queueing delay, the following relationship holds:
![]()
The linearized model around the equilibrium is given by
(1.35) ![]()
Delay Effects on Stability
Let us use the congestion control system to check the influence of delays. Consider a simple network shown in Figure 1.11. There are two sources transmitting packages and three links through which packages are sent to destinations. Source 1 uses link 1 and link 2, source 2 uses link 2 and link 3. The interconnection topology of sources and links can be represented by a bipartite graph shown in Figure 1.12. According to (1.33) the congestion control algorithm is given by
![]()
where
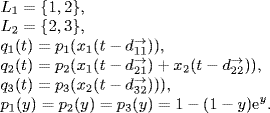
Figure 1.11 Communication network.
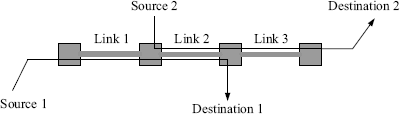
Figure 1.12 Interconnection graph.
The parameters in the simulation are selected as follows: ![]() ,
, ![]() , D1 = 22(s), D2 = 25(s),
, D1 = 22(s), D2 = 25(s), ![]() (s). Under this set of parameters, the system is asymptotically stable. Suppose that the transmission process of the network is influenced by some external factors so that D2 changes from 25(s) to 50(s) when t ≥ 1000(s), and suppose that the increments of both
(s). Under this set of parameters, the system is asymptotically stable. Suppose that the transmission process of the network is influenced by some external factors so that D2 changes from 25(s) to 50(s) when t ≥ 1000(s), and suppose that the increments of both ![]() and
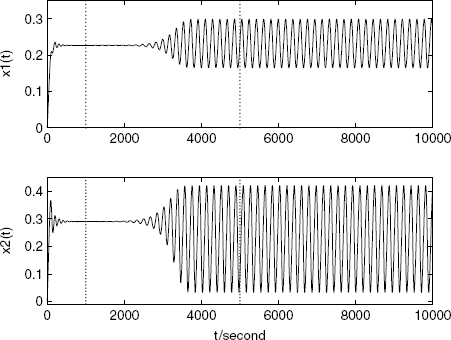
and ![]() are equal to 12.5(s). In this case, the equilibrium point becomes unstable and periodic oscillation takes place. The simulation of this process is shown in Figure 1.13.
are equal to 12.5(s). In this case, the equilibrium point becomes unstable and periodic oscillation takes place. The simulation of this process is shown in Figure 1.13.
Figure 1.13 Periodic oscillations due to communication delays.
The above example shows that the size of delay constant plays a significant role in the stability analysis. The problem of the stability of time-delayed feedback control systems has been extensively studied in recent years (see, e.g., Gu, Kharitonov and Chen (2003) and Niculescu (2001)). In this book we will pay more attention to one specific aspect of the problem: under what condition can one get a scalable stability criterion for a time-delayed distributed control system? Here, under the scalability we mean the criterion checks only dynamics and parameters locally around each individual agent. The stability and scalability of distributed congestion control systems will be studied in Chapter 5.
Stabilization by Time-Delayed Feedback Control
On the one hand, propagation delay may destroy the stability of the congestion system as we have shown by numerical experiments. On the other hand, an appropriately introduced time-delayed feedback controller may serve as a stabilizer. Let us introduce the following time-delayed feedback control (TDFC)
![]()
into the equation of x2(t). Then, the closed-loop system is modified as
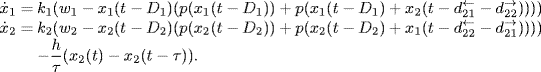
Now, let us conduct numerical experiments again for the foregoing oscillating system. In the simulation, the gain and the delay time are selected as h = 0.8 and τ = 4(s), respectively. For the system, the TDFC is introduced when t ≥ 5000(s). Figure 1.14 shows that the closed-loop system becomes stable again at a steady transmission rate: x![]() = (0.2271, 0.2901). Figure 1.15 shows that the control force returns to zero when the equilibrium is stabilized by the TDFC.
= (0.2271, 0.2901). Figure 1.15 shows that the control force returns to zero when the equilibrium is stabilized by the TDFC.
Figure 1.14 Stabilization of oscillations by TDFC.
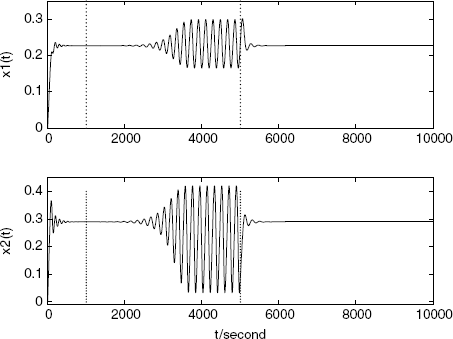
Figure 1.15 Control signal of TDFC.
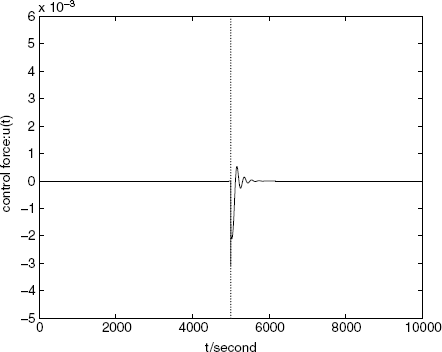
It is natural to guess that the delay constant of the TDFC can not be arbitrarily large. In the simulation, the algorithm becomes unstable again when τ is greater than a certain value. The simulation shown in Figure 1.16 demonstrates that oscillations of the sending rates of the sources come about when τ ≥ 84(s). So, an interesting problem is why the TDFC works and how to select the gains and delay constants of a TDFC. Related problems are also discussed in Chapter 5.
Figure 1.16 Oscillations due to large delay in TDFC.
1.3.2 Consensus-Based Formation Control
Trying to reach some agreement (or consensus) among agents is another effective way to conduct cooperation in a distributed control system. Here we briefly review the consensus-based formation control approach. Formation control is one of the most important and fundamental issues in the coordination control of multi-agent systems, which requires that each agent moves according to the prescribed trajectory, and all the agents keep a particular spatial formation pattern at the same time (Balch and Arkin 1998; Hu 2001).
Consider the multi-agent system modeled as a group of Newtonian particles
where ![]() and
and ![]() denote the position and velocity of agent i, respectively;
denote the position and velocity of agent i, respectively; ![]() denotes its control input.
denotes its control input.
Here we just consider the formation control in the plane. To describe the desired geometric pattern of the multi-agent system, let us introduce vector ![]() to specify the position of agent i in the pattern. Then, the desired formation can be described by a set of vectors,
to specify the position of agent i in the pattern. Then, the desired formation can be described by a set of vectors, ![]() . Figure 1.17 shows a pentagon formation with vertex-position vectors
. Figure 1.17 shows a pentagon formation with vertex-position vectors ![]() . Note that for any
. Note that for any ![]() ,
, ![]() describes the same formation as F. The objective of formation control includes that the agents asymptotically converge to the prescribed geometric pattern F and each agent 's velocity asymptotically approaches to a desired constant
describes the same formation as F. The objective of formation control includes that the agents asymptotically converge to the prescribed geometric pattern F and each agent 's velocity asymptotically approaches to a desired constant ![]() . Suppose the desired velocity
. Suppose the desired velocity ![]() is known by only one or a few agents which are called leaders among the other agents. Let us denote by
is known by only one or a few agents which are called leaders among the other agents. Let us denote by ![]() the index set of leaders.
the index set of leaders.
Figure 1.17 A pentagon formation.
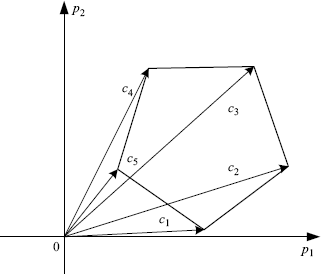
For the system (1.36), a formation control algorithm can be given by
where
(1.38) ![]()
is the velocity tracking part for leader agents, and
(1.39) ![]()
is the coordination control part. In the control law, γi > 0, i = 0, 1, and β > 0 are control parameters, aij > 0 is a weight used by agent i for the information obtained from its neighboring agent j, and Ni is the set of neighbors of agent i. Obviously, the interconnection between the agents in such a system can be described by a digraph G = (V, E, A): each agent can be considered as a vertex in V; the information flow between two agents can be considered as a directed edge in E, i.e., if agent i uses position and velocity information of agent j, then there is an edge from vertex i to vertex j; and the weight aij can be regarded as the entry of the adjacency matrix A. The formation control algorithm (1.37) is indeed a local control law because each agent uses only the information of itself and its neighbors.
For such a distributed control system, of course, the first problem we are interested in is stabilizability and stability, i.e., under what conditions do there exist available control parameters such that the closed-loop system is stable? and how can control parameters be selected in order to ensure the stability? The second problem we are interested in is: can the desired formation indeed be achieved when the system is asymptotically stabilized? In the first problem, the scalability of the stabilizability and/or the stability criteria is the profile to which we will pay more attention due to the possible huge scale of distributed control systems. While the problem of stabilizability and stability is of concern in all feedback control systems, the second problem raised here is a more distinct feature of distributed control systems. Indeed, even if the system is stable, does it imply the conclusion ui1 → 0, ∀ i ![]() L and
L and ![]() ? Even if ui1 → 0, ∀ i
? Even if ui1 → 0, ∀ i ![]() L and
L and ![]() , does it imply that all the agents track the desired velocity
, does it imply that all the agents track the desired velocity ![]() and that the relative displacement of each pair of agents satisfies the formation requirement F? By taking a first look at the questions, we can see that the condition of
and that the relative displacement of each pair of agents satisfies the formation requirement F? By taking a first look at the questions, we can see that the condition of
and the implication
are critical for getting the answer to all the questions.
To consider the problem formulated by (1.40) and (1.41) one can let ![]() . In this case, the formation problem reduces to the so-called rendezvous problem (i.e., position agreement). Actually, the basic algorithm for the rendezvous problem is
. In this case, the formation problem reduces to the so-called rendezvous problem (i.e., position agreement). Actually, the basic algorithm for the rendezvous problem is
This algorithm is also called the consensus (or agreement) algorithm. If the multi-agent system (1.36) is stable under this control, then the states (velocities and positions) of all the agents in the system approach to the same value.
From the above discussion, we see that the stability of the consensus algorithm is at the center of the problem. The problem, in particular, includes the analysis and design of the available values of control parameters γi, β and even adjacent weights aij in the sense of stability. We should note the difference between the stability of the consensus problem and the stability of conventional control systems. In most conventional (linear) feedback control systems, the origin is the only equilibrium and the stability implies that all the eigenvalues of the system matrix of the closed-loop system have positive real parts. But, it is easy to see that the system matrix of the closed-loop system of (1.36) with (1.42) is singular, and thus the system has a continuum of equilibrium points. And therefore, the stability of the consensus algorithm does not imply that all the eigenvalues of the closed-loop have positive real parts. The stability of consensus control systems and other related problems are discussed in Chapter 6.
If the agents are distributed in a huge range of space and connected with the help of a communication network, delay is inevitable in information transmission. At current time t agent i can get only the delayed information pij(t − τij) and qij(t − τij) from its neighboring agent j, where τij > 0 is the communication delay of information flow from agent j to agent i. In this case, if the value of the delay constant is available for agent i, then the consensus algorithm (1.42) can be modified as follows:
Note that when diverse communication delays are involved in the communication network, the stability and scalability analysis of such consensus algorithms will become much more complicated and challenging. Related problems are discussed in Chapter 7.
In the algorithm (1.43) the communication delay τij is assumed to be available for agent i and is used as a “self-delay”. In practice, however, only approximate estimations of communication delays are available. If the self-delay in the (1.43) is replaced by the estimation of the communication delay, then we have to use the following consensus algorithm:
In this case, a new question is raised naturally: does there exists any consensus solution of the closed-loop system (1.36) under feedback control (1.44) when τ ' ij ≠ τij? This question will be also answered in Chapter 7 for this and more generalized systems.
In closing, we would like to note that although the consensus control and the congestion control are designed from quite different principles of cooperation, they share a lot of similarities in system structure, and hence the stability and scalability of the two kinds of systems can be dealt with by using some common tools which are introduced in this chapter and the following two chapters as well.
1.4 Notes and References
1.4.1 Graph Theory and Distributed Control Systems
Graph theory is a fundamental tool in distributed control and distributed computation. The basic definitions of graph theory introduced in this book are quite standard; see, for example, Biggs (1994), Bollobijás (1998), Diestel (1997), Godsil and Royle (2001). For powers of the adjacency matrix the reader is referred to literature on algebraic graph theory (Biggs 1994; Bullo, Cortés and Martiínez 2009; Godsil and Royle 2001). Laplacian matrices have numerous remarkable properties and some of them play a key role in the analysis of consensus problems. The reader is referred to Mohar (1991) and Merris (1994) for elegant surveys of Laplacian matrices. Theorem 1.9 and Theorem 1.10, characterizing the properties of the Laplacian matrix, contain some recent results. A proof of statement (2) of Theorem 1.9 was given in Olfati-Saber and Murray (2004). Statement (3) of Theorem 1.10 was proved by Lin, Francis and Maggiore (2005). An equivalent version of statement (3) was proved in Ren and Beard (2005). Statement (1) of Theorem 1.10 was proved by Olfati-Saber and Murray (2004), and statement (2) of Theorem 1.10 was proved by Moreau (2005).
Two typical kinds of distributed control systems are introduced in this chapter. The first is the end-to-end congestion control and the second is the consensus-based formation control.
The first congestion avoidance control algorithm for the Internet was proposed by Jacobson (1988). Motivated by the theory of economics, Kelly (1997) and Kelly, Maulloo and Tan (1998) introduced the concept of price into the congestion control, and formulated the rate control in communication networks as a problem of optimization of allocation resources (utilization of channel capacities) in networks. For a mathematic treatment of congestion control problems the reader is referred to, for example, Low and Lapsley (1999); Low, Paganini and Doyle (2002); Srikant (2004), but this is the first book to use bipartite graphs to describe the architecture of congestion control systems. It will be shown in the remaining chapters of this book that we benefit from such a treatment in characterizing the symmetry of congestion control systems and relating them to multi-agent systems discussed in consensus problems.
Consensus problems are closely related to many other problems in coordination control, such as formation control (Balch and Arkin 1998; Fax and Murray 2004; Hu 2001; Wang and Hadaegh 1994) and flocking (Olfati-Saber and Murray 2006; Toner and Tu 1998). For a survey on the relationship between consensus problems and coordination control strategies the reader is referred to Olfati-Saber, Fax and Murray (2007).
1.4.2 Delay in Control and Control by Delay
The fact that delay in feedback may cause oscillation and instability was pointed out as early as the 1930s (see, e.g., Wiener (1948)). The delay effects on the stability of feedback control systems have been extensively studied with tools from both classic Lyapunov stability theory and contemporary robust control theory (Gu, Kharitonov and Chen (2003); Niculescu (2001).
Johari and Tan (2001) studied the stability of the primal algorithm of the end-to-end congestion control system with propagation delays. They gave a stability criterion for systems with identical round-trip delay and also proposed a conjecture for systems with diverse round-trip delays. The conjecture was proved in its original version and generalized to a less conservative form by Tian and Yang (2004) via a frequency-domain method. Tian (2005) further showed that such a frequency-domain method was powerful in studying the stability of second-order congestion control systems with diverse propagation delays.
The study on the consensus problem with communication delays started as early as the 1980s in the context of distributed computation (Bertsekas and Tsitsiklis 2007; Tsitsiklis, Bertsekas and Athans 1986). In some other communities such as physics, this problem has also been extensively studied as synchronization of coupled oscillators (see, e.g., Yeung and Strogatz (1999). Recently, these kinds of consensus protocols have been studied for fixed or even switched graphs by using different analysis methods, such as the contraction analysis method (Wang and Slotine (2006), the passivity-based method (Chopra and Spong (2006), the method based on delayed and hierarchical graphs (Cao, Morse and Anderson (2006), among others. Tian and Liu (2008), (2009) noticed the symmetry of multi-agent systems with diverse input delays, and used the frequency-domain method developed initially for congestion control to study the stability of consensus control systems.
The idea of using a time-delayed feedback controller (TDFC) to stabilize unstable periodic orbits of chaotic systems was first proposed by Pyragas (1992). Kokame et al. (2001) illustrated the TDFC as a kind of differential control and applied it to stabilize uncertain steady states. Liu and Tian (2008) noticed the fact that the equilibrium point of the Internet is usually not available for each source node or link node and thus proposed a stabilization scheme for the congestion control system of the Internet by introducing the TDFC into the primal algorithm and proved that the system with any round-trip delay can be locally stabilized by the modified algorithm.
Many other applications of the TDFC method have also been reported in the literature, such as stabilization of coherent models of lasers (Bleich and Socolar 1996; Naumenko et al. 1998) and magneto-elastic systems (Hilkihara, Touno and Kawagoshi 1997), control of cardiac conduction model (Brandt, Shih and Chen 1997), control of stick-slip friction oscillations (Elmer 1998), traffic models (Konishi, Kokame and Hirata 1999) and PWM-controlled buck convertors (Battle, Fossas and Olivar 1999), just to name a few. The reader is referred to Tian, Zhu and Chen (2005) for a recent survey of time-delayed feedback control.
Note
1. If ![]() , under the symmetry, we mean the conjugate symmetry, i.e., A* = A, where A* is the conjugate transpose of A.
, under the symmetry, we mean the conjugate symmetry, i.e., A* = A, where A* is the conjugate transpose of A.
Balch T and Arkin RC (1998). Behavior-based formation control for multirobot terms. IEEE Transanctions on Robotics and Automation, 14, 926–939.
Battle C, Fossas E and Olivar G (1999). Stabilization of periodic orbits of the buck convertor by time-delayed feedback. International Journal of Circuits Theory and Application, 27(6), 617–631.
Bertsekas DP and Tsitsiklis JN (2007). Comments on “Coordination of groups of mobile autonomous agents using nearest neighbor rules”. IEEE Transactions on Automatic Control, 52, 968–969.
Biggs N (1994). Algebraic Graph Theory, second edition. Cambridge University Press, Cambridge.
Bleich ME and Socolar JES (1996). Controlling spatiotemporal dynamics with time-delay feedback. Physics Review E, 54(1), R17–R20.
Bollobás B (1998). Modern Graph Theory. Graduate Text in Mathematics, 184, Sringer, New York.
Brandt MEH, Shih T and Chen G (1997). Linear time-delayed feedback control of a pathological rhythm in a cardiac conduction model. Physics Review E, 56(2), R1334–R1337.
Breder CM (1954). Equations descriptive of fish schools and other animal aggregations. Ecology, 35(3), 361–370.
Bullo F, Cortés J and Martínez (2009). Distributed Control of Robotic Networks. Princeton University Press. available online at http://coordinationbook.info
Cao M, Morse AS and Anderson BDO (2006). Reaching an agreement using delayed information. IEEE Conference on Decision and Control, San Diego, CA, USA, 3375–3380.
Chen CT (1984). Linear System Theory and Design. CBS College Publishing, New Yoyk.
Chopra N and Spong MW (2006). Passivity-based control of multi-agent systems. Advances in Robot Control: From Everyday Physics to Muman-like Movements, S Kawamura and M Svinin, Editors, pp.107–134, Spinger-Verlag, Berlin.
Cortés J, Martinez S, Karatas T, and Bullo F (2004). Coverage control for mobile sensing networks. IEEE Transactions on Robotics and Automation, 20(2), 243–255.
Darwin R (1859). The Origin of Species. Chinese Translation by Qian Xun, Chong Qin Publishing Company, Chong Qin, China.
Diestel R (1997). Graph Theory. Springer-Verlag, New York.
Elmer FJ (1998). Controlling friction. Physics Review E, 57(5), R4903–R4906.
Fax JA and Murray RM (2004). Information flow and cooperative control of vehicle formations. IEEE Transactions on Automatic Control, 49, 1465–1476.
Godsil C and Royle G (2001). Algebraic Graph Theory. Graduate Text in Mathematics, 207, Sringer, New York.
Gu K, Kharitonov VL and Chen J (2003). Stability of Time-delayed Systems. Birkhäuser, Boston.
Giulietti F, Pollini L and Innocenti M (2000). Autonomous formation flight. IEEE Control Systems Magazine, 20(12), 34–44.
Hilkihara T, Touno M and Kawagoshi T (1997). Experiment stabilization of unstable periodic orbit in magneto-elastic chaos by delayed feedback control. International Journal of Bifurcation and Chaos, 7(12), 2837–2846.
Hu X (2001). Formation control with virtual leaders and reduced communications. IEEE Transactions on Robotics and Automation, 17, 947–951.
Jacobson V (1988). Congestion avoidance and control. Proceedings of ACM SIGCOMM’ 88, Stanford, CA, 314–329.
Johari R and Tan D (2001). End to end congestion control for the internet: delays and stability. IEEE/ACM Transactions on Networking, 9, 818–832.
Kelly FP Charging and rate control for elastic traffic. European Transactions on Telecommunication, 8, 33–37.
Kelly FP, Maulloo A and Tan D (1998). Rate control for communication networks: shadow prices proportional fairness and stability. J. Oper. Res. Soc., 49, 237–252.
Kokame H, Hirata K, Konishi K and Mori T (2001). Difference feedback can stabilize uncertain steady states. IEEE Transactions on Automatic Control, 46, 1908–1913.
Konishi K, Kokame H and Hirata K (1999). Coupled map car-following model and its delayed-feedback control. Physics Review E, 60(4), 4000–4007.
Lin Z, Francis B and Maggiore M (2005). Necessary and sufficient graphical conditions for formation control of unicycles. IEEE Transactions on Automatic Control, 50, 121–127.
Liu C-L and Tian Y-P (2008). Eliminating oscillations in the Internet by time-delayed feedback control. Chaos, Solitons and Fractals, 35, 878–887.
Low SH and Lapsley DE (1999). Optimization flow control, I: basic algorithm and convergence. IEEE/ACM Transactions on Networking, 7, 861–874.
Low SH, Paganini F and Doyle JC (2002). Internet congestion control. IEEE Control Systems Magazine, 22, 28–43.
Lunch NA (1997). Distributed Algorithms. Morgan Kaufmann, San Francisco.
Merris R (1994). Laplacian matrices of a graph: a survey. Linear Algebra and its Applications, 197, 143–176.
Mohar B (1991). The Laplacian spectrum of graphs. Graph Theory, Combinatorics, and Applications, Alavi Y, Chartrand G, Oellermann OR, and Schwenk AJ, editors, 2, 871–898, John Wiley.
Moreau L (2005). Stability of multiagent systems with time-dependent communication links. IEEE Transactions on Automatic Control, 50, 169–182.
Murray RM, Åström KJ, Boyd SP, Brockett RW and Stein G (2003). Future directions in control in an information-rich world. IEEE Control Systems Magazine, 23(April), 20–33.
Naumenko AV, Loiko NA, Turovets SI, Spencer PS and Shore KA (1998). Chaos control in external cavity laser diodes using electronic impulsive delayed feedback. International Journal of Bifurcation and Chaos, 8(9), 1791–1799.
Niculescu S-I (2001). Delay effects on stability: a robust control approach. Lecture Notes in Control and Information Sciences, 269, Springer, Berlin.
Olfati-Saber R and Murray RM (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control, 49, 1520–1533.
Olfati-Saber R and Murray RM (2006). Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Transactions on Automatic Control, 51, 401–420.
Olfati-Saber R, Fax JA and Murray RM (2007). Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 95(1), 215–223.
Pyragas K (1992). Continuous control of chaos by self-controlling feedback. Physics Letters A, 170, 421–428.
Qi HR, Iyengar SS and Chakrabarty K (2001). Distributed sensor networks –a review of recent research. Journal of the Franklin Institute, 338(6), 655–668.
Rekleitis IM, Dudek G and Milios EE (2000). Multi-robot collaboration for robust exploration. Proceeding of the IEEE International Conference on Robotics and Automation, 4, 3164–3168.
Ren W and Beard RW (2005). Consensus seeking in multi-agent systems under dynamically changing interaction topologies. IEEE Transactions on Automatic Control, 50, 655–661.
Reynolds CW (1987). Flocks, herds, and schools: a distributed behavioral model. Computer Graphics, 21(4), 25–34.
Sastry SS (1999). Nonlinear Systems: Analysis, Stability, and Control. Interdisciplinary applied mathematics, 10, Springer, New York.
Srikant R (2004). The Mathematics of Internet Congestion Control. Birkhäuser, Boston.
Tian Y-P and Yang H-Y (2004). Stability of the Internet congestion control with diverse delays. Automatica, 40, 1533–1541.
Tian Y-P (2005). Stability analysis and design of the second-order congestion control for networks with heterogeneous delays. IEEE/ACM Transactions on Networking, 13, 1082–1093.
Tian Y-P, Zhu J and Chen G (2005). A survey on delayed feedback control of chaos. Journal of Control Theory and Applications, 3, 311–319.
Tian Y-P and Liu C-L (2008). Consensus of multi-agent systems with diverse input and communication delays. IEEE Transactions on Automatic Control, 53, 2122–2128.
Tian Y-P and Liu C-L (2009). Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations. Automatica, 45, 1347–1353.
Tomlin C, Pappas GJ and Sastry S (1998). Conflict resolution for air traffic management: a study in multiagent hybrid systems. IEEE Transactions on Automatic Control, 43(4), 509–521.
Toner J and Tu Y (1998). Flocks, herds, and schools: A quantitative theory of flocking. Physical Review W, 58, 4828–4858.
Tsitsiklis JN, Bertsekas DP and Athans M (1986). Distributed asynchronous deterministic and stochastic gradient optimisation algorithms. IEEE Transactions on Automatic Control, 31, 803–812.
Ushio T (1996). Limitation of delayed feedback control in nonlinear discrete-time systems. IEEE Transactions on Circuits and Systems, 43, 815–816.
Wang PKC and Hadaegh FY (1994). Coordination and control of multiple microspacecraft moving in formation. J. Astronaut. Sci., 44, 315–355.
Wang W and Slotine JJE (2006). Contraction analysis of time-delayed communications and group co-operation. IEEE Transactions on Automatic Control, 51, 712–717.
Wiener N (1948). Cybernetics: Or Control and Communication in the animal and the machine. Wiley, New York.
Yeung MKS and Strogatz SH (1999). Time delay in the Kuramoto model of coupled oscillators. Physical Review Letter, 82, 648–651.