THE MATHEMAGICIAN

When Persi Diaconis was fourteen years old, he dropped out of high school and ran away from home to travel with Dai Vernon, a world-class magician. Persi became a professional magician, performing all over the world for more than a decade. One of the things he loved about magic was the math behind some of his tricks. Eventually, Persi decided to go back to school and began studying math at City College of New York, where he got his bachelor’s degree. Later, the head of Harvard’s statistics department, who was also a math-emagician (mathematical magician), arranged for Persi to get into Harvard’s PhD program. Persi has been a math and statistics professor at either Harvard or Stanford ever since.

CARD SHUFFLING

Persi’s mathematical interests include randomness and randomization, especially coin flipping and card shuffling. One of his most famous papers investigated how many times a normal fifty-two-card deck needs to be riffle (standard) shuffled to be considered truly randomized. The paper proved that a deck should be shuffled seven times, and that more shuffles wouldn’t introduce much extra randomness. More than a decade after publishing that paper, a company that makes card-shuffling machines used by casinos asked Persi to check whether their machines were randomizing the decks enough. It turned out that the machines weren’t shuffling well enough, so it’s a good thing they asked Persi to check! The mathematics of card shuffling has applications to turbulence, fluid dynamics, and even how long a vat of cookie dough must be blended to make sure the ingredients are mixed enough.

FLIPPING COINS

Persi has also investigated whether a coin flip is as fair as we think. He found out that a flipped coin is more likely to end up on the same side on which it starts. But he is quick to point out that the coin will only land on the same side about 51 percent of the time, so flipping a coin is still pretty close to fair. That said, you should never agree to flip a coin with Persi, as he has practiced so much that he can flip a coin to come up heads ten times in a row!

DIACONIS THE DEBUNKER

Persi is a well-known skeptic. He famously debunked some prominent psychics who claimed to be experts in extrasensory perception (also known as ESP or sixth sense). Persi believes he is in a better position than most to figure out what is really going on when someone is supposedly practicing telepathy or bending spoons with their mind. Magicians, like psychics, use many psychological tricks, so Persi can better spot them in use. Also, his deep understanding of statistics helps him know when someone is using statistics in a sloppy or intentionally deceptive way.

HONORS AND AWARDS

Persi Diaconis won the MacArthur Fellowship (often called the “genius prize”) in 1982. He and Ron Graham (whom you can also read about in this book) wrote a book called Magical Mathematics: The Mathematical Ideas That Animate Great Magic Tricks. The book won the Euler Book Prize for “an outstanding book in mathematics that is likely to improve the public view of the field.” Persi is very proud to be a member of the National Academy of Sciences, American Philosophical Society, and American Academy of Arts and Sciences.

MATHEMATICAL MAGIC

Did you know that many of the magic tricks magicians do are based on math? Here you’ll learn how to amaze your friends with mathematical magic, just like Persi Diaconis does!

MATERIALS

• A full deck of 52 cards

DIRECTIONS

1 Give your audience a pile of nine cards from your deck.

WORKING YOUNG

George Boole grew up in a very loving but poor family. His father, John Boole, was a member of the Lincoln Mechanics’ Institute, a group that helped working men further their education. John passed his love of learning and books on to George, who also joined the group. Unfortunately, because his father wasn’t very successful in his career, George had to start working at age sixteen to help support his parents and siblings. He got a junior teacher job in Doncaster, England.

CREATING A SCHOOL

George’s first job didn’t pay enough for him to provide for his family, so when he was nineteen, he decided to open his own school in Lincoln. George was an excellent head of school with strong leadership and teaching abilities. Four years later, his great reputation placed him in a position to take over a bigger school in Waddington.

BECOMING A MATH PROFESSOR

Even during his early career running schools and teaching, George made time to study math. He could read multiple languages, which allowed him to read many math books and papers. Mathematician Duncan F. Gregory, who had a more intensive math research education and was the editor of the Cambridge Mathematical Journal, became a good friend and mentor to George, despite being only two years older. Duncan taught George how to write a mathematical paper, allowing George to publish his first math paper in 1840. Publishing math papers led to George becoming the first professor of mathematics at Queen’s College, Cork in Ireland in 1849. Finally, George was able to fulfill his dream of studying math full-time while still earning enough money to provide for his family.

MATHEMATICAL FAMILY

While working as a professor, George met Mary Everest (whom you can also read about in this book), the niece of one of his colleagues. The two of them became very close and eventually married. Together they had five daughters. Sadly, George died of pneumonia shortly after the birth of their fifth daughter. Their daughters had amazing careers too, many following in the footsteps of their parents to become academics. One of their children, Alicia Boole Stott, even became a respected mathematician in the field of four-dimensional geometry!

BOOLEAN LOGIC

George is best known for inventing Boolean logic, also known as Boolean algebra. His innovation was to apply methods from the then-new field of symbolic algebra to logic. Over two thousand years earlier, the famous philosopher Aristotle had laid out rules of logic. George wanted to broaden the rules so they would be useful in more situations and give it a solid mathematical foundation. As is often the case in mathematics, George pursued this work because it was interesting, despite the fact that there were no obvious practical applications. Nearly a hundred years later, mathematician Claude Shannon, who is commonly called “the father of information theory,” realized that Boolean algebra could optimize telephone routing switches. Using electrical switches to process logic is the fundamental concept underlying all modern computers!

THE PRINCESS’S PUZZLES

Did you know that puzzles are extremely mathematical? Well, they are, and here we’ll explore a special kind—logic puzzles! They have tricky solutions and are super fun to solve.

MATERIALS

• A piece of paper
• A pencil

DIRECTIONS

PUZZLE 1

The princess’s dog, Fluffy, was kidnapped! Fluffy is a special dog with purple polka dots and golden eyes. The guards have swept the city and found five dogs matching Fluffy’s description. The problem is that each dog has a child claiming the dog is theirs. Each child—Aaliyah, Bo, Imani, Jaiden, and Marissa—has given a statement. The four who actually own a purple polka-dotted dog with golden eyes all told the truth, and the one who kidnapped the princess’s dog lied. If four are telling the truth and one is lying, figure out who kidnapped Fluffy. Here is what each child said:

HOW TO SOLVE

Let’s make a table.

TRAILBLAZER

When Amalie Emmy Noether died, Albert Einstein wrote in the New York Times that she was widely considered to be the greatest female mathematician who had ever lived. Emmy earned her PhD in 1907 from the University of Erlangen in Germany, where she was one of only two women enrolled. After she graduated, Emmy taught at Erlangen for seven years without being paid or having an official title.

CONTROVERSY

In 1915, two famous mathematicians, David Hilbert and Felix Klein, invited Emmy to join the math department at the University of Göttingen, one of the best math and physics research centers in the world at that time. Various nonmath professors objected to a woman joining the faculty, but David famously responded to the controversy by saying, “I do not see that the sex of the candidate is an argument against her [being a professor]. After all, we are a university, not a bath house.” Nevertheless, Emmy was not allowed to officially join the faculty, so she spent four years teaching at the University of Göttingen by pretending to be David’s assistant.

NOETHER’S FIRST FAMOUS THEOREM

In 1918, Emmy proved what remains today one of the most important theorems in physics! The theorem, which is called Noether’s theorem, states, “Wherever a symmetry of nature exists, there is a conservation law attached to it, and vice versa.” Conservation of momentum, also known as Newton’s third law, and general relativity are both examples of Noether’s theorem.

MORE GROUNDBREAKING WORK

Finally, in 1919, Emmy was allowed to teach under her own name. She quickly became one of the leading members of the Göttingen math department. Her students were sometimes called “Noether boys.” In the second phase of her career, her work changed and guided abstract algebra, an important field of mathematics. In the final chapter of her influential career, Emmy united the previously separate mathematical fields of representation theory and the theory of modules and ideals, which allowed both fields to progress further than they had separately.

UNUSUAL TEACHING STYLE

Unlike most professors, Dr. Emmy Noether did not develop lesson plans but used lecture time to discuss important math questions with her students. Some of her students took very careful notes, which ended up being important, as many of Emmy’s most significant ideas were developed during her lectures. A few of her students even turned their detailed notes into influential textbooks. Teaching was so important to Emmy that she sometimes held classes at her home when the university was closed and once took a class to a coffee shop to deliver a lecture on a holiday. Emmy was extremely generous and sometimes allowed her students or colleagues to take credit for her ideas to help their careers.

MOVE TO THE UNITED STATES

In 1933, Germany’s Nazi government fired all Jews from university jobs, forcing Emmy and many other famous scholars to flee. Emmy was so well known that she received a grant to move to Bryn Mawr College in the United States. She also taught at the Institute for Advanced Study at Princeton but didn’t feel welcome at “the men’s university, where nothing female is admitted.” On the other hand, she treasured her time at Bryn Mawr, where she had many enthusiastic female collaborators.

FABULOUS FOLDING FLEXAGONS

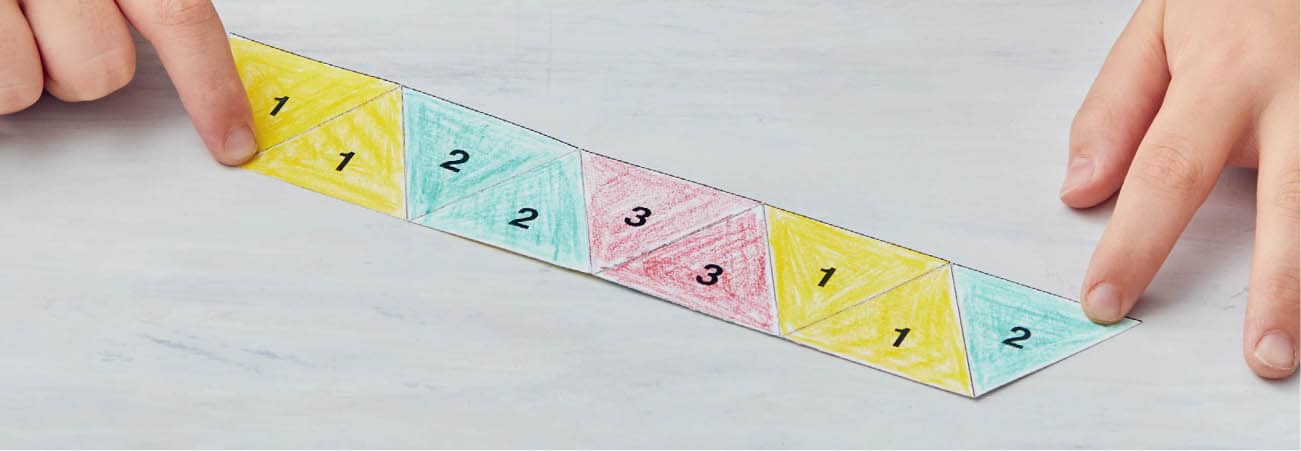
Flexagons are interesting shapes that can be folded and bent to reveal previously hidden aspects. In this activity, we’ll make a trihexaflexagon, which is a shape that looks like a hexagon but has three sides!

MATERIALS

• Trihexaflexagon template from the back of the book (it can also be downloaded from www.mathlabforkids.com and https://quarto.com/files/MathForKids)
• Paper (thicker paper or cardstock works best but any paper will do)
• Craft knife (recommended) or scissors
• Cutting mat and ruler (if using a craft knife)
• Colored pencils or markers (optional)
• Pencil
• Tape

DIRECTIONS

CONSTRUCT A TRIHEXAFLEXAGON

1 Copy the Trihexaflexagon template from the book. You’ll get best results with thicker paper or cardstock. (It can also be downloaded from www.mathlabforkids.com and https://quarto.com/files/MathForKids.)

FLEX YOUR TRIHEXAFLEXAGON

1 Now comes the fun part: flexing! Push the creases between the two 1s you labeled by hand and the other two adjacent 1s all toward each other. Fig. 9 and Fig. 10.

MATH POPULARIZER

Martin Gardner never took a college math class and didn’t consider himself a mathematician. Despite that, mathematicians proudly claim Martin as one of their own because he did more than anyone else in the twentieth century (and maybe ever) to popularize and explain math to nonmathematicians. Persi Diaconis (also featured in this book) joked, “Warning: Martin Gardner has turned dozens of innocent youngsters into math professors and thousands of math professors into innocent youngsters.” Martin hung out with some of the most famous people of the twentieth century—writers, artists, Nobel Prize winners, world-famous magicians, and, of course, mathematicians.

MATHEMATICAL GAMES

Martin started as a writer/editor of children’s magazines and particularly enjoyed paper-folding puzzles. He once wrote a column for Scientific American (SA), a widely read popular science magazine, about hexaflexagons. That column was such a success that the editor asked, “Is there enough similar material . . . to make a regular feature?” The answer was a resounding yes! For twenty-five years, Martin wrote a monthly column in SA called “Mathematical Games.” Many famous scientists, such as Albert Einstein, have written articles for SA, but Martin’s column was the magazine’s most popular section for many years. His column was so widely read that he sometimes made people famous just by writing about them. For example, M. C. Escher, now one of the twentieth century’s most famous artists, was basically unknown until Martin included his work in a column. (You can read more about Escher’s work in the section on Jennifer McLoud-Mann.)

MARTIN THE MAGICIAN

Martin was fascinated by magic. His first publication, when he was only fifteen years old, was a magic trick in the official magazine of the Society of American Magicians. He helped pay his University of Chicago tuition by performing magic tricks at a department store. Martin’s book The Encyclopedia of Impromptu Magic is highly respected among magicians and his book about mathematical magic tricks, Mathematics, Magic, and Mystery, is still a classic. Magic magazine recognized Martin as one of the “100 Most Influential Magicians of the Twentieth Century.” Fittingly, his last published article was also a magic trick.

SKEPTIC

Martin was a famous skeptic of all forms of pseudoscience. He is credited with launching the modern skeptical movement with his book Fads and Fallacies in the Name of Science. The famed evolutionary biologist and history of science writer Stephen Jay Gould called Martin “The Quack Detector” who “expunged nonsense [and was] a priceless national resource.”

OTHER WRITING

Martin wrote or edited more than a hundred books and countless articles, columns, and reviews. In addition to books and articles on math, magic, and skepticism, he wrote two novels. Martin’s most famous and best-selling book, which sold over a million copies, was The Annotated Alice. It included the original illustrations and entire text of Lewis Carroll’s Alice’s Adventures in Wonderland and Through the Looking-Glass, along with extensive commentary explaining mathematical concepts, wordplay, literary references, games, and customs of the time in which Carroll wrote the books. Academics had been writing annotated versions of books meant to be read by other scholars for a long time, but The Annotated Alice was the first annotated book aimed at all readers. It was such a success that it spawned a whole field of annotated books written for the general public. Martin wrote several more, including annotated versions of famous poems “Casey at the Bat” and “The Night Before Christmas.”

A HEAP OF HEXAGONS

We’ll make an object that will look just like the trihexaflexagons we made earlier but it has six sides instead of three!

MATERIALS

• Hexahexaflexagon template from the back of the book (it can also be downloaded from www.mathlabforkids.com and https://quarto.com/files/MathForKids)
• Paper
• Craft knife (recommended) or scissors
• Cutting mat and ruler (if using a craft knife)
• Colored pencils or markers (optional)
• Glue stick

DIRECTIONS

1 Copy the template from the book onto paper. It can also be downloaded from www.mathlabforkids.com and https://quarto.com/files/MathForKids.