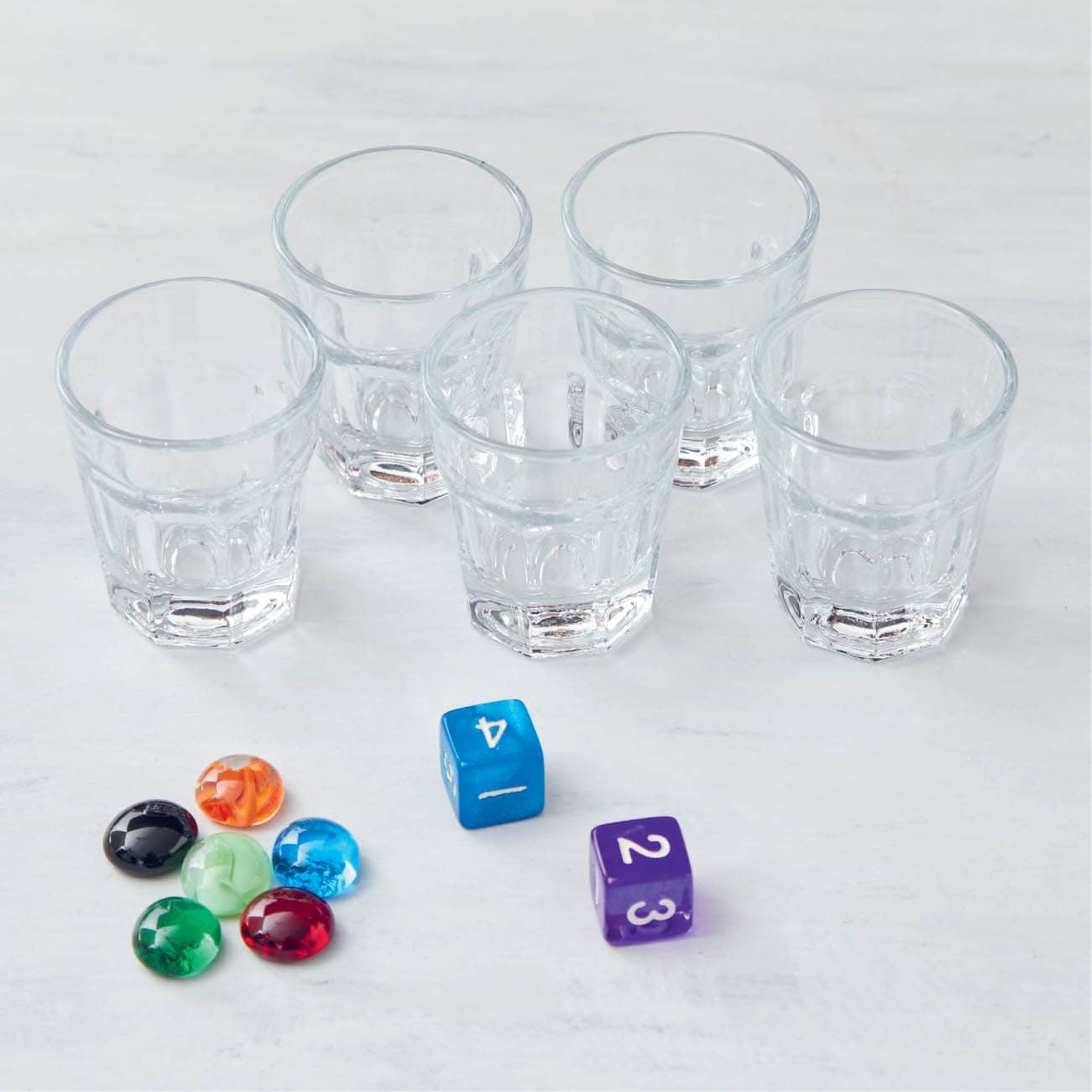John Conway
December 26, 1937 – April 11, 2020
THE GOOFBALL
John Conway was an unpopular kid, so he decided to reinvent himself when he went to King’s College, Cambridge University, in England. He became funny and outgoing, told great stories, and learned to laugh at himself. He succeeded in his goal so effectively that when it came time to apply for a job, the head of the math department at King’s College wrote the letter of application for John. John was such a popular teacher that some students formed the John Conway Appreciation Society. A student described one memorable class where John completed a difficult proof while balancing a broom by its handle on his chin and juggling.
LOVE OF GAMES
While at King’s College, John explored many different areas of math and discovered his love of games. He loved using math to determine the best strategy for games, or even to invent his own.
EARLY CAREER
For a while after John got his PhD, he felt lost, unsure of what to do next. He played a lot of games and worried he wasn’t doing much math. Then someone told him about a twenty-four-dimensional structure called the Leech lattice. He decided he would work hard to learn something new about it. He set aside several days per week for a few months to do his research. But the very first evening, he made a major discovery that is now called the Conway Group. John made a number of discoveries and advanced many different areas of math and physics, including in group theory and knots. However, he is most well known for the Game of Life.
GAME OF LIFE
The Game of Life was one of the first-ever video games, though John described it as a “no-player never-ending” game. This Game of Life, nothing like the board game by the same name, has three rules: one for creating life, one for losing life, and one for survival. The idea of the game is to show how real animals live, die, and evolve. John showed the Game of Life to Martin Gardner (who is profiled on this page), a mathematical journalist who wrote a recreational mathematics column for Scientific American. After Gardner wrote about the Game of Life, it became extremely popular and made John famous, even outside mathematics. The Game of Life has so much potential for discoveries that tons of mathematicians and programmers studied it and continue to do so even today.
OTHER ACCOMPLISHMENTS
In 1985, Dr. John Conway and several coauthors published the ATLAS of Finite Groups, considered by many to be the most important group theory book ever written. John wrote or co-wrote several other books too. His best seller was Winning Ways for Your Mathematical Plays, which is all about the math of various games. John was most proud of his discovery of surreal numbers, which resulted from his study of the game of Go. He was also proud of his work on the free will theorem and its influence on physics. John was a fellow of the American Academy of Arts and Sciences and the Royal Society, and received numerous awards, including being the first winner of the London Pólya Prize.

DOTS AND BOXES
John Conway loved applying math to games to help him win. See if you can do the same with the game Dots and Boxes, which you can play with a friend, sibling, or parent.
MATERIALS
- Dots and Boxes Board
- 2 different colored writing utensils
- 2 players
DIRECTIONS
1 Make a 5 × 5 grid yourself or download and print one from www.mathlabforkids.com. Feel free to play on the boards on this page. Fig. 1.
RULES OF THE GAME
1 Each player picks a different color crayon, pencil, or pen.
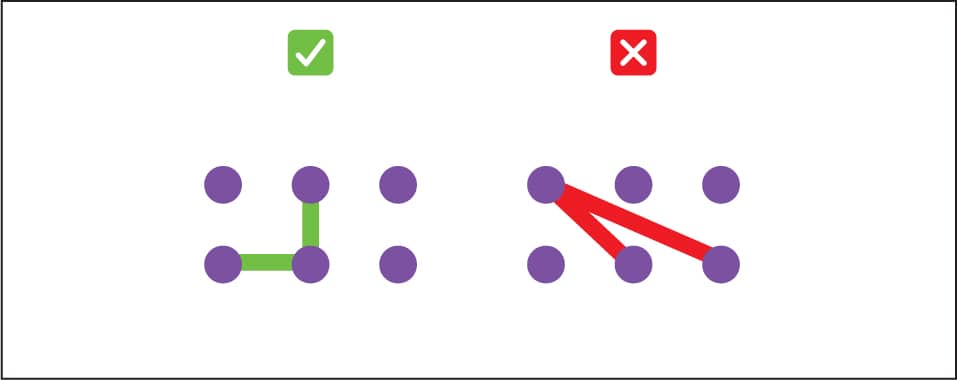
2 Players take turns drawing a line between two dots that are next to each other. You can draw a line vertically or horizontally, but you cannot draw a diagonal line. Fig. 2.
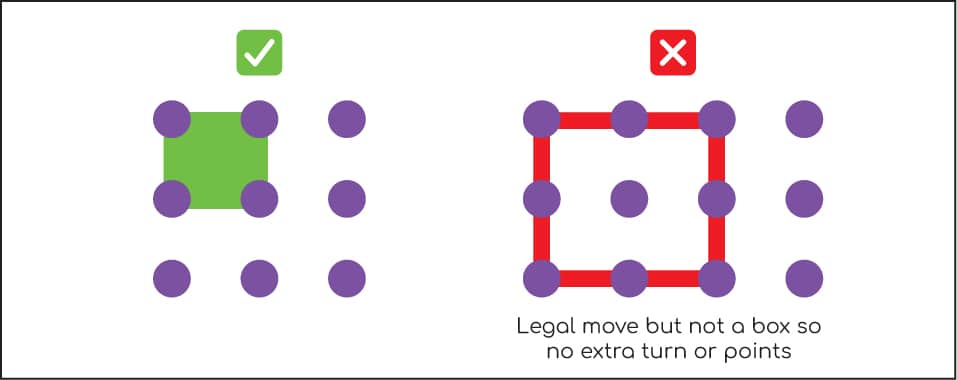
3 If drawing a line lets you complete a box, color in that box with your color and take an extra turn. Fig. 3.
4 Once there are lines between every pair of dots, the game ends.
5 Each player counts the number of boxes of their color. The player with the most boxes of their color wins! Fig. 4.
Born: April 5, 1977 Federico Ardila is a mathematician and a DJ. That’s not as surprising a combination as you might think. To Federico, music is one of the most powerful tools in the world for connecting people. He plays the marimba de chonta, a melodic percussion instrument made from trees from Colombian rainforests. He believes that both math and music can speak to all people, regardless of any differences. Federico uses music to “create an atmosphere where people can build bridges and connect.” He cofounded the Oakland DJ collective La Pelenga to bring people together by introducing them to music from different cultures. As children growing up in Colombia, Federico’s sister and cousin were the math whizzes in the family, not Federico. He didn’t enjoy school, or even math classes, but he still placed first in the national math competition in fourth grade! In high school, he won a bronze medal in the International Math Olympiad in 1993 and a silver medal in 1994. Federico enjoyed the math competition scene, but his sister and cousin felt out of place because they thought that the math community was more welcoming of males. Hoping other girls won’t feel excluded from math, Federico is working hard to make math a friendly and accepting community for all. One story Federico tells often is about how he ended up at MIT, one of the United States’ best technical universities. He applied after a friend told him that MIT was an excellent place to study math and had awesome financial aid. Federico now says he would never have applied if he had known how selective MIT is because he didn’t get good grades in high school. He hopes this story encourages students to reach for seemingly impossible things, as they just might come true. Federico’s mathematical work forges connections between combinatorics (the math of combinations) and other diverse areas of math, including geometry, algebra, topology, and applied math. He spent five years working with another mathematician on unifying the geometric and algebraic sides of combinatorics. One night someone stole the backpack containing all their work. They were able to reconstruct it, but it took several years. Federico’s work to make connections extends to his teaching, where one of his main goals is to make math a place in which his sister, cousin, and everyone else feels like they belong. Dr. Federico Ardila received a National Science Foundation (NSF) CAREER grant that helped his inclusion goals. He created four axioms to promote diversity in mathematics. An axiom is a math statement that is assumed to be true and from which other math ideas follow. Ardila’s axioms are ideas he believes are true, but that the math community doesn’t necessarily treat as fact. For example, his first axiom is that mathematical potential is equally present in different groups, such as different races and economic classes. Unfortunately, the math community doesn’t reflect this ideal, so Federico works really hard to encourage minority students to pursue math. His other axioms are that everyone can have fun with math, that math is powerful and can be used to help people in all kinds of situations, and that every student should be treated well. Federico’s outreach work includes over two hundred hours of free math lecture videos.
There are many really cool and easy-to-understand ideas in math. One of these, from the area of math called combinatorics—which happens to be one of Federico Ardila’s specialties—is called the pigeonhole principle. In this activity we’re going to learn all about it and even play a game. What is the pigeonhole principle? Let’s explore to find out. 1 Take six pigeons and five of your holes. Fig. 1. 2 Place pigeons into the holes according to the rules, with each pigeon being in a hole. 3 Can you make it so that each pigeon has its own hole while still following the rules? The closest you can get is to put one pigeon in four of the holes and two in the fifth. This is the pigeonhole principle: If every pigeon must go into a hole, and there are more pigeons than holes, some pigeons will have to share their holes. Fig. 2. 1 Player 1 rolls their die and places that many pigeons in front of them. Fig. 3. 2 Player 2 rolls their die and places that many holes in front of Player 1. Fig. 4. 3 Player 1 tries to place the pigeons in the holes according to the pigeonhole principle. If they succeed, they get a point. Fig. 5. 4 Repeat steps 1 to 3, this time with Player 2 rolling for pigeons, Player 1 rolling for holes, and Player 2 placing the pigeons in the holes. 5 Take turns back and forth until someone has five points. The first player to have five points wins!Federico Ardila
MATH AND MUSIC
COLOMBIAN CHILDHOOD
APPLYING TO MIT
MAKING CONNECTIONS
ARDILA’S AXIOMS
PIGEONS LOVE HOLES
MATERIALS
DIRECTIONS
RULES OF THE GAME
December 22, 1887 – April 26, 1920 Part of the legend of Srinivasa Ramanujan is his fascinating mathematical partnership with G. H. Hardy. The two accomplished amazing things together. While Hardy was an extremely impressive English mathematician, he famously said that his greatest contribution to mathematics was discovering Srinivasa. Prior to their friendship, Srinivasa grew up as a poor child in India. His family was often sick. His three siblings all sadly passed away when they were very young. Srinivasa was often sick too, which luckily did not prevent him from being a very good student. He got the best scores in his whole district on all his exams when he was only ten years old! Only a year later, he was learning college-level math faster than most college students. When Srinivasa was sixteen years old, he found a book that would change his life: A Synopsis of Elementary Results in Pure and Applied Mathematics. The book contained five thousand mathematical theorems, most with no proof. He became so obsessed with proving some of the theorems that he ignored many of his other classes, ultimately failing college. Nonetheless, he proved amazing mathematical results and published his first paper (on Bernoulli numbers) in the Journal of the Indian Mathematical Society. Srinivasa struggled to find a job that would allow him to focus wholly on math and make a decent wage. He decided to try to get in touch with some mathematicians in England. Most of the mathematicians to whom he sent letters thought he was a fraud. G. H. Hardy initially thought so too after receiving Srinivasa’s long letter that included a ton of theorems. But fortunately, one of them caught his eye! Hardy was impressed by how much Srinivasa was able to accomplish while being completely self-taught. He could only imagine what Srinivasa could accomplish with more training, and the two quickly began sending letters back and forth. Hardy helped Srinivasa get a mathematical research job in India, then later arranged for Srinivasa to come to England. The two worked together in Cambridge for five years. Srinivasa was frequently sick. When he was around two years old, he caught smallpox, which he luckily survived. Later, he became sick again, this time requiring surgery. His family was very poor, but fortunately a doctor volunteered to help for free. When Srinivasa became sick again that same year, he was so afraid he would die that he gave his math notebooks to math professor Singaravelu Mudaliar, in case he didn’t survive. Luckily, Srinivasa lived and was able to take his books back after recovering. However, he became sick once more when he moved to England. His religion’s strict dietary requirements combined with food being rationed in England due to World War I worsened his condition. In 1919, Srinivasa went back to India, hoping that would help him recover. While it did help at first, he became sick again the next year and sadly passed away. Doctors have since studied his medical history and believe he suffered from undiagnosed amoebiasis, a parasitic disease that could have been cured had they known what it was.
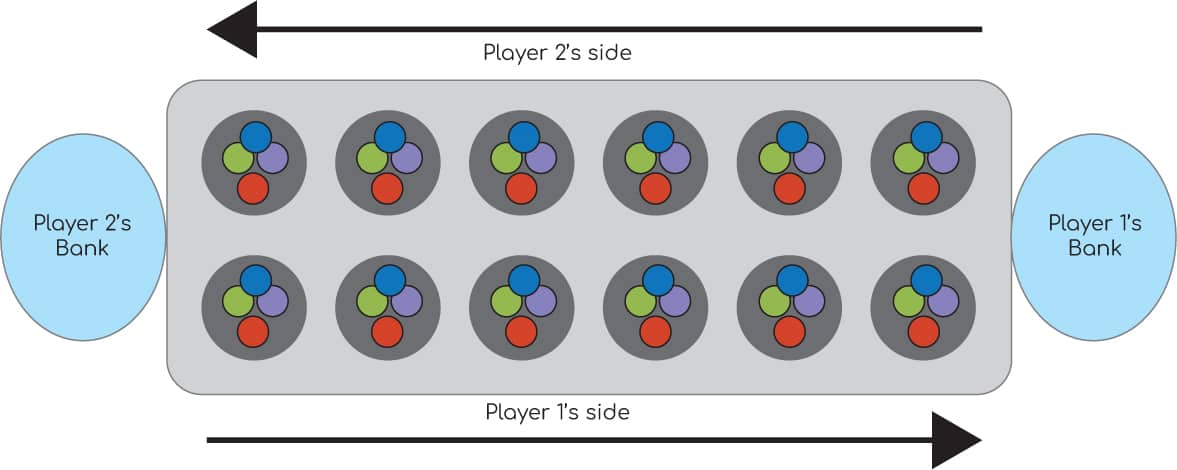
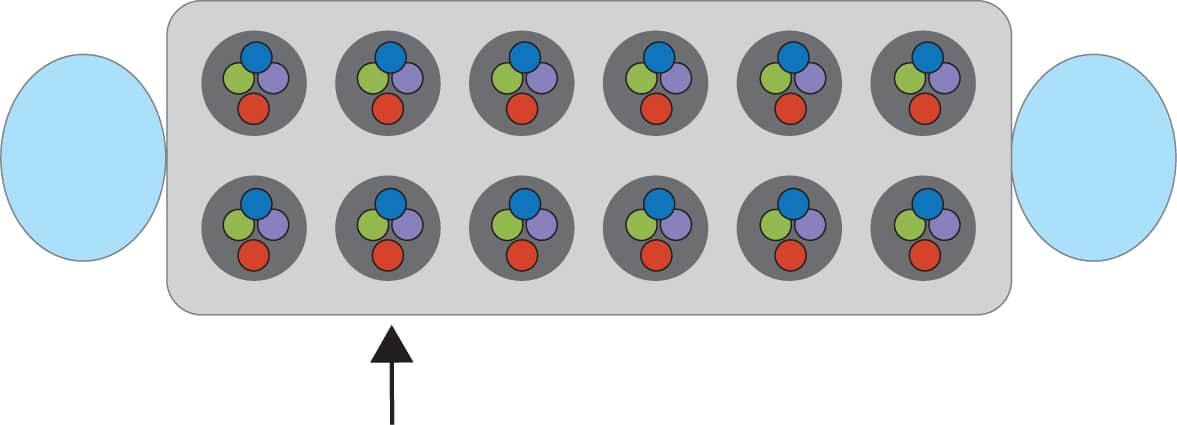
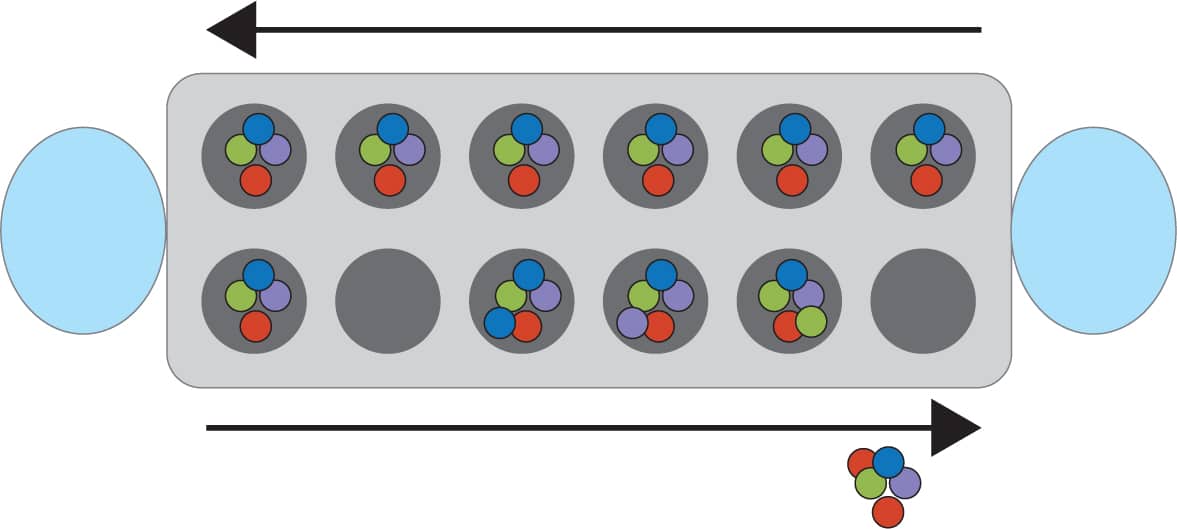
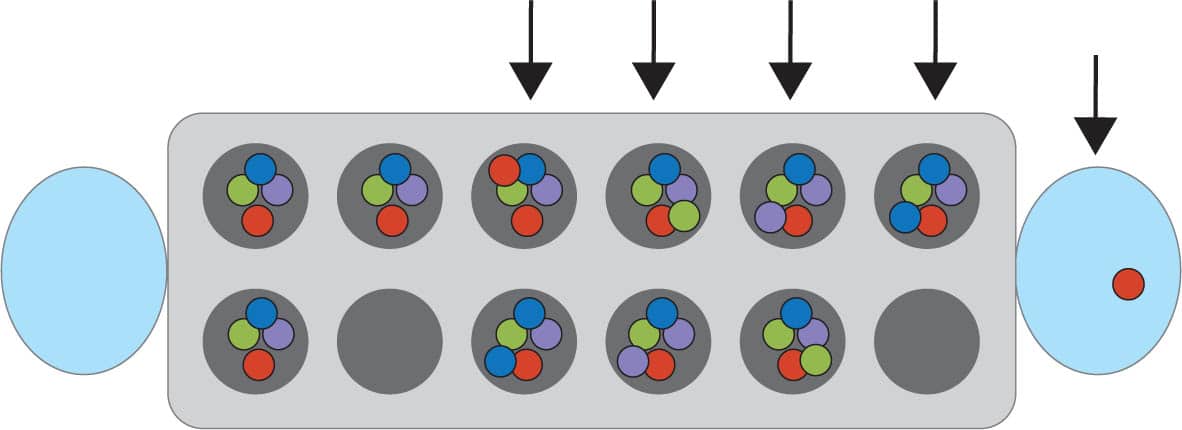
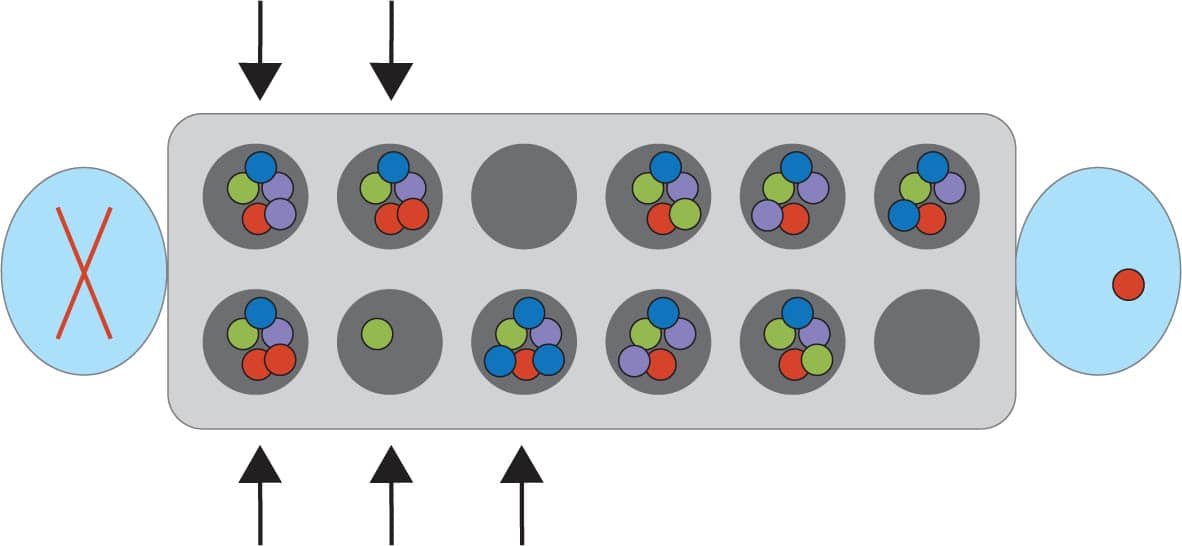
Srinivasa Ramanujan studied number theory extensively. Number theory can help you win Mancala, a classic game where you try to collect as many marbles into your side of the board as you can. We’re going to learn how to play Mancala on a handmade game board! 1 First, we need to create our game board. We only need the bottom half of the egg carton, so cut the top off using scissors. Fig. 1. 2 Next, tape a bowl to each short end of the egg carton. Fig. 2. 3 Finally, set up the game by placing four counters in each pit of the egg carton. Now you’re ready to play! Fig. 3. 1 Players should sit opposite each other, each in front of one of the bowls. The bowl closest to each player is their “bank.” Banks help with scoring at the end of the game. 2 Counters, called “seeds,” move around the board in a counterclockwise direction. The six pockets, or pits, to the left of each player are that player’s “side.” Fig. 4. 3 Player 1 picks one of the pits on their side and picks up all of the seeds from that pit. They then move counterclockwise toward their bank, dropping one seed in each pit they pass on the way to their bank. Fig. 5 and Fig. 6 and Fig. 7. 4 When Player 1 runs out of seeds, they pick up all of the seeds in the pit where they placed their last seed and repeat step 3. Fig. 8. 5 When Player 1 passes their bank, they place one seed into their bank and then continue placing seeds on Player 2’s side. Fig. 9. 6 When Player 1 passes Player 2’s bank, they do not place a seed into Player 2’s bank. Instead, they place seeds on their own side, moving toward their bank. Fig. 10. 7 Repeat steps 3 to 6 until the final seed is dropped into an empty pit or is dropped into the active player’s bank. 8 If the last seed is dropped into the active player’s bank, the active player takes another turn, picking up all the seeds in one of the pits on their side. 9 If the last seed is dropped into an empty pit, the turn passes to Player 2. 10 Player 2 takes their turn in the same way that Player 1 did, but picks a pit on their own side and places seeds into their bank and not in Player 1’s. 11 Continue taking turns until one side is out of seeds. All of the seeds on the nonempty side go into the bank of the player whose side they are on. Fig. 11. 12 Whoever has the most seeds in their bank at the end wins! Fig. 12.Srinivasa Ramanujan
CHILD GENIUS
GETTING DEEPER INTO MATH
MOVE TO ENGLAND
HEALTH ISSUES
MANCALA
MATERIALS
DIRECTIONS
RULES OF THE GAME
c. 780 – 850 CE Muḥammad ibn Mūsā al-Khwārizmī is considered the father of modern algebra, a foundational area of math that most people learn in high school these days. In fact, “algebra” got its name from “al-Jabr” in the title of Muḥammad’s book, al-Kitāb al-Mukhtaṣar fī Ḥisāb al-Jabr wal-Muqābalah, known in English as The Compendious Book on Calculation by Completion and Balancing. The book was translated into Latin in 1145 CE and used as the main math textbook in European universities for the next five hundred years! Muḥammad wrote The Compendious Book on Calculation to simplify and create a system for solving problems merchants commonly faced. The book laid out many of the main concepts of algebra. He was the first to develop the abstract concept of an equation and solving for general “unknowns” or “variables.” He even used the Arabic word for “root,” a term we still use. “Al-jabr,” which means “restoration,” refers to combining similar terms that appear on both sides of an equal sign so they appear on just one side. He also taught various methods to solve linear and quadratic equations. Muḥammad was the first to treat algebra as a separate field of math. Previously, math was thought of in mostly geometric terms due to the huge Greek influence on math’s early development. The important thing about algebra was it allowed math to do math on itself. Given that Muḥammad basically invented a whole new important area of math, it’s no surprise that he is considered the greatest mathematician of his generation and one of the most influential mathematicians of all time! Muḥammad wrote another extremely influential book. The word “algorithm” comes from the version of Muḥammad’s name that appears in the title of the Latin translation of the book, Algoritmi de Numero Indorum. He did not invent the Hindu-Arabic number system that uses the symbols 0, 1, . . . , 9, but he adopted them for his books. As his books were widely published and translated throughout Europe and the rest of the world, the number system spread too. The book also introduced the concepts of place value and using zero as a placeholder. The book also covered algorithms for addition, subtraction, multiplication, division, fractions, and decimals. Muḥammad’s algorithms were adopted throughout Europe. Around 820 CE, Muḥammad ibn Mūsā al-Khwārizmī became the head of the library and the chief astronomer of the House of Wisdom, a major intellectual center of his era. He created astronomical tables, calendars, and astrolabes. He made highly accurate sine and cosine tables that are important in astronomy and the first known table of tangents. He was part of a project to calculate the circumference of the Earth. Muḥammad also refined the theory of how to make sundials, which made them much easier to create and use going forward. After that, it became traditional to include a sundial at mosques to help identify the times to pray.
You may have heard of algebra as being something scary, but it’s actually really easy! In this activity, you’re going to learn how to do algebra all by yourself the way that Muḥammad ibn Mūsā al-Khwārizmī did. NOTE: For this activity, left refers to the reader's left and right refers to the reader's right. 1 In this activity, we will have two sides that we want to make equal. To make the sides clear, place a large stick or string in the middle of your workspace. We’ll refer to the stick as the “divider.” The workspace can be the floor or a table, as long as it is large enough to place counters on both sides. Fig. 1. 2 Place ten counters on the left side of the string and five on the right. Place the bowl on the right too. Fig. 2. 3 Our goal is to figure out how many counters we need to add to the right side to have the same number of counters on both sides of the divider. The bowl represents the answer. 4 Add counters one by one to the bowl until there are the same number of counters on each side. Fig. 3. How many counters did you add? This is the answer. Fig. 4. 5 Congratulations, you just did algebra! Pretty easy, right? Algebra is all about making things equal and using a variable. A variable is something that represents the answer before we know what the answer is. In this case, the bowl is our variable, and when it is filled, that is the answer! Let’s look at another problem. 1 Place five counters on each side of the divider. Leave the bowl out this time. Fig. 5. 2 Five is the same number as five, so if we have five on both sides, the sides are equal. Because our goal is for the sides to be equal, we are done, but let’s explore what happens if we add or subtract counters. 3 Add three counters to the left and put the bowl on the right. Fig. 6. 4 Figure out how many counters need to be added to the bowl to make the sides equal again. 5 The answer is three! You probably knew this ahead of time. Why? Fig. 7. Here’s the answer: If five is the same as five, meaning they are equal, and then we add a number to one side, we need to add the same number to the other side to make them equal again. Similarly, if we take away two from the left side, then we need to take away two from the right to make the sides the same again. This is the most important idea behind algebra, that if you have two equal things and change them in the exact same way, then they will still be equal. Let’s put the two ideas we’ve explored together, but with a special rule: We want to find out how many counters need to go in the bowl without placing any in it. 1 Start with twelve counters on the left, four on the right, and the bowl on the right as well. Fig. 8. 2 We know the number of counters should be equal on both sides. The bowl represents how many counters the right needs to be equal to the left. 3 How can we keep both sides equal without adding to the bowl? Earlier, we were able to add or subtract from two equal things. The sides would be equal if we knew how many were in the bowl, so let’s subtract. 4 Take away four counters from both sides. Now you should have eight counters on the left and just the bowl on the right. Fig. 9. 5 According to our rules, both sides of the divider should be equal, meaning the bowl equals eight counters. 6 Let’s check our work. Set up the problem again, with twelve on the left and four and the bowl on the right. Since the bowl equaled eight, put eight counters into the bowl. Count up the counters on both sides. Twelve on both! Fig. 10.Muḥammad ibn Mūsā al-Khwārizmī
FATHER OF ALGEBRA
DEVELOPMENT OF ALGEBRA
ALGEBRA STANDS ALONE
ARITHMETIC ALGORITHMS
OTHER WORK
AWESOME ALGEBRA
MATERIALS
DIRECTIONS