5
Wireless Channel Impairment Mitigation Techniques
We realized wireless channels cause many types of wireless channel impairments such as noise, path loss, shadowing, and fading, and wireless communication systems should be designed to overcome these wireless channel impairments. There are many techniques to mitigate wireless channel impairments. For example, for the purpose of managing shadowing effects, the location of a base station is carefully selected to avoid shadowing effects. A power control scheme is also used to make a good radio link between a mobile station and a base station. For the purpose of mitigating delay spreads, Global System for Mobile Communications (GSM) system uses adaptive channel equalization techniques and Code Division Multiple Access (CDMA) system uses a rake receiver. For the purpose of mitigating the Doppler spreads, the signal bandwidth of GSM is designed to be much greater than the Doppler spread. GSM also uses a frequency correction feedback. CDMA system uses pilot channels for channel estimation. In Long-Term Evolution (LTE), a symbol time is designed to be less than channel coherence time. In Wireless Local Area Network (WLAN), the Doppler spread is not a big problem due to a low mobility. Thus, the wireless channel impairment mitigation techniques should be adopted according to system requirements and channel environments. In this chapter, fundamentals of wireless channel impairment mitigation techniques are investigated.
5.1 Diversity Techniques
Diversity techniques mitigate multipath fading effects and improve the reliability of a signal by utilizing multiple received signals with different characteristics. These are very important techniques in modern telecommunications to compensate for multipath fading effects. Diversity techniques are based on the fact that individual channels experience different levels of fading effects. Assume we transmit and receive same signals several times. If one received signal experiences deep fading at a specific part, another received signal may not experience deep fading and another received signal may experience a good channel at a specific part. From the probability point of view, this approach makes sense. If the probability that one received signal experiences deep fading at a specific part in one channel is p, the probability that the other received signals experience deep fading at a specific part in N channels is pN. Therefore, the more channels we can use, the more diversity gains we can obtain. There are several types of diversity techniques in space, time, and frequency domain as shown in Figure 5.1. Their combination is possible as well. For example, space-frequency diversity, space-time diversity, space-time-frequency diversity. We will take a look into three fundamental diversity techniques in this section.

Figure 5.1 Diversity channels
Space diversity uses multiple antennas and is classified into macroscopic diversity and microscopic diversity. Macroscopic diversity mitigates large-scale fading caused by log normal fading and shadowing. To achieve macroscopic diversity, antennas are spaced far enough and we select an antenna which is not shadowed. Thus, we can increase the signal to noise ratio. Microscopic diversity mitigates small-scale fading caused by multipath. To achieve microscopic diversity, a multiple antenna technique is used as well and an antenna is selected to have a signal with small fading effect. One example of space diversity configuration is illustrated in Figure 5.2.

Figure 5.2 Space diversity
Two different wireless channels are derived from the receiver with two antennas. The distance between two antennas is important to achieve the diversity gain. Basically, we expect that deep fading does not occur on both wireless channel 1 and wireless channel 2 at the same time. It is shown in Figure 5.3 that microscopic diversity improves the fading channel characteristic. When a transmitted signal arrives at a receiver via two different wireless channels, each signal experiences several deep fading. However, if we use a space diversity technique based on averaging two signals, we can obtain a better signal characteristic as shown in the average of two channel responses. Multiple Input Multiple Output (MIMO) techniques are based on space diversity. The MIMO will be discussed in Section 5.3 and Chapter 8 in detail.

Figure 5.3 Example of channel responses and the average of two channel responses
Time diversity uses different time slots. Basically, consecutive signals are highly correlated in wireless channels. Thus, a time diversity technique transmits same signal sequences in different time slots. The time sequence difference should be larger than the channel coherence time. An interleaving technique is one of time diversity techniques. Figure 5.4 illustrates one example of an interleaving technique. Consider 4 codewords (aaaa, bbbb, cccc, and dddd) transmission and a deep fading channel in time slot 3 (T3). When there is no interleaving, the codeword, cccc, in T3 is erased due to a deep fading effect. However, if we shuffle the codewords and transmit them, we lose a part of the codeword, cccc, as shown in Figure 5.4. After de-interleaving, we can obtain partially erased codewords (aaa, bbb, ccc, and ddd) and recover the original codewords.

Figure 5.4 Time diversity
Frequency diversity uses different frequency slots. It transmits a signal through different frequencies or spreads it over a wide frequency spectrum. Frequency diversity is based on the fact that the fading effect is differently appeared in different frequencies separated by more than the channel coherence bandwidth. When the transmission bandwidth is greater than the channel coherence bandwidth (namely, it is a broadband system), the frequency diversity technique is useful. Figure 5.5 illustrates one example of frequency diversity. Consider we transmit two signals, s1(t) and s2(t), and there is a deep fading effect in frequency slot 3 (F3). When we send s1(t) through frequency slot 1 and 3 (F1 and F3), the signal, s1(t), in frequency slot 3 (F3) experiences a deep fading effect but the other signal, s1(t), in frequency slot 1 (F1) does not experience a deep fading effect. If we use a combining technique or select the signal, s1(t), in frequency slot 1 (F1) in the receiver, we can obtain the original signal.

Figure 5.5 Frequency diversity
We allocate each frequency to be larger than the channel coherence bandwidth. Frequency diversity gain can be obtained in a broadband multicarrier system. The symbol of the broadband multicarrier system is divided into narrowband subcarriers. The symbol has a long transmission period. Frequency selective fading may occur in the long transmission period but each subcarrier which is separated enough experiences flat fading.
There are several combining techniques for diversity: Maximal Ratio Combining (MRC), Equal Gain Combining (EGC), and Selection Combining (SC). The system model of diversity techniques is illustrated in Figure 5.6 to derive combining techniques. The signal, s(t), is transmitted through L different channels. The each received signal, rl(t), through different channels is represented by
where ![]() (l = 1,2, …, L) represents the channel gain (αl) and phase rotation (φl) and nl(t) is the Gaussian noise.
(l = 1,2, …, L) represents the channel gain (αl) and phase rotation (φl) and nl(t) is the Gaussian noise.

Figure 5.6 System model of diversity techniques with L channels
The MRC technique is a method combining all signals using weighting factors (amplitude and phase) to achieve a high SNR as shown in Figure 5.7.

Figure 5.7 Maximal ratio combining
In the MRC technique, the received signal, r(t), is weighted by wl and is represented by



The SNR, γ, of the received signal, r(t), is represented by

We use the Schwartz’s inequality and find wl to maximize γ as follows:

The equality holds if ![]() for all l, where K is an arbitrary complex constant. Thus, we obtain the upper bound of γ as follows:
for all l, where K is an arbitrary complex constant. Thus, we obtain the upper bound of γ as follows:



and the maximum SNR, γmax, can be found when we decide ![]() .
.
The EGC technique is a method combining all signals using phase estimation and unitary weight to achieve a high SNR as shown in Figure 5.8.

Figure 5.8 Equal gain combining
In the EGC technique, the received signal, r(t), is weighted by wl and is represented by


If we set ![]() , the received signal, r(t), is represented by
, the received signal, r(t), is represented by

Therefore, the SNR, γ, of the received signal, r(t), is represented by

The SC technique is the simplest method and selects one signal with the strongest SNR as shown in Figure 5.9.

Figure 5.9 Selection combining
The SNR, γ, of the received signal, r(t), is represented by
Among three combining techniques, the SC technique has the lowest complex and the MRC technique has the best performance. However, in case of some specific channel condition such as deep fading, the SC technique may have a better performance because it can avoid the worst channel.
5.2 Error Control Coding
The landmark paper “A Mathematical Theory of Communication” [1.4] describes one important concept about error control coding theorem. In the paper, C. Shannon predicts that it is possible to transmit information without errors over the unreliable channel and an error control coding technique exists to achieve this. In modern wireless communication systems, the error control coding technique became an essential part. The error control coding technique can be classified into Forward Error Correction (FEC) and Automatic Repeat reQuest (ARQ). The FEC does not have a feedback channel. The transmitter sends codewords including information and redundancy. In the receiver side, an error correction coding technique recovers from the corrupted codewords. On the other hand, the ARQ has a feedback channel. The ARQ technique uses an error detection technique and noiseless feedback. When errors occur, the receiver does not correct but detect errors and then requests that the transmitter sends codewords again. There are many forward error correction schemes which can be roughly classified into block codes, convolution codes, and concatenated codes as shown in Figure 5.10.

Figure 5.10 Classification of forward error correction
Block codes are based on algebra and algebraic geometry and developed by mainly mathematicians. The construction and lower/upper bounds of the block codes are well analyzed mathematically. The block codes are split into linear codes and nonlinear codes. Basically, nonlinear codes such as Nordstrom-Robinson code, Preparata codes, and Kerdock codes have a better performance than linear codes. However, it is not easy to implement due to their nonlinear characteristic. Therefore, linear block codes are widely used in practical systems. In the 1970s and 1980s, many beautiful linear block codes such as Hamming codes, Reed-Muller (RM) codes, Bose-Chaudhuri-Hocquenghem (BCH) codes, and Reed-Solomon (RS) codes were developed and practically used in many digital devices. Low-Density Parity Check (LDPC) [1] codes are one of the important linear block codes in modern wireless communication systems. The LDPC codes were not recognized for about 30 years due to a high complexity encoder and decoder. Mackey and Neal reinvented the LDPC codes [2] as practical codes to closely approach Shannon limit using an iterative belief propagation technique. Convolutional codes are based on a finite state machine and probability theory. One decoding scheme for the convolutional codes is the sequential decoding algorithm by Wozencraft [3]. This decoding scheme is complex so that the convolutional codes were not used widely. In the 1960s, the optimum algorithm of the convolutional codes by Viterbi was invented. This decoding scheme became a de facto standard of many wireless communication systems. Concatenated codes are to combine two different codes. This combination brought an amazing result. Serial concatenated codes composed of a convolutional code as an inner code and an RS code as an outer code were widely used in deep space communications in the 1970s. In 1993, turbo codes [4] which are parallel concatenation of Recursive Systematic Convolutional (RSC) codes were invented by C. Berrou, B. Glavieux, and P. Thitimajshima. The performance of the turbo code closely approaches Shannon limit. It opens a new era of communication systems and affects many wireless communication techniques. Besides, there are different types of error correction coding techniques. The above coding schemes assume a binary symmetric channel because this channel model is suitable for digital communication systems. However, a binary erasure channel is more accurate in a wired channel. For this channel, foundation codes such as Luby transform (LT) codes [5] and Raptor codes [6] are invented and investigated actively. Polar codes [7] are a class of capacity achieving codes for symmetric Binary Discrete Memoryless Channels (B-DMC). Although LDPC codes and turbo codes are capacity achieving codes, we do not know clearly why they achieve Shannon limit and how to construct capacity achieving codes. However, Polar codes do not have any theoretical gaps and have a well-defined rule for code construction.
In this section, we deal with two important error correction coding techniques: linear block codes and convolutional codes. Firstly, we look into Hamming codes as a linear block code. The linear block codes are one important family of error correction coding techniques. It is well developed mathematically and is conceptually useful for understanding an error correction coding technique. In addition, it has a wide range of practical applications and especially LDPC codes are important codes in the modern wireless communication systems. We design LDPC codes in Chapter 6.
5.2.1 Linear Block Codes
Let the message/information m = (m0, m1, …, mk−1) be a binary k-tuple. The encoder for the (n, k) linear block code over the Galois field (GF) of two elements, GF(2), generates the codeword c = (c0, c1, …, cn−1) with a binary n-tuple (n > k). Figure 5.11 illustrates an encoder for the (n, k) linear block code.

Figure 5.11 Encoder
We define an (n, k) linear block code as follows:
A generator matrix is used to construct a codeword and has a k × n matrix for an (n, k) linear block code. Let us consider a k × n generator matrix G as follows:

Every codeword can be produced by an inner product of the message m and the generator matrix G. The corresponding codeword is presented as follows:
The rows of the generator matrix G are linearly independent because we assume G has rank k and the codeword c is a k-dimensional subspace of the set of all binary n-tuples.
We observe the corresponding codeword and generator matrix of Example 5.1. The codeword [1011010] is composed of the message segment ([1 0 1 1] which are the first four bits (k bits).) and the parity segment ([0 1 0] which are the next three bits (n-k bits).). The generator matrix is composed of the k × k identity matrix (Ik) segment and the P matrix segment as follows:

We call this linear systematic block code and its codeword structure is shown in Figure 5.12. The code rate, R, is defined as the ratio of the message length (k bits) to the codeword length (n bits).

Figure 5.12 Linear systematic encoder
There is another useful matrix called a (n−k) × n parity check matrix H. The parity check matrix is

where the negative of a number in GF (2) is simply the number. This equation is useful for decoding the received codeword. The transpose of the parity check matrix H is

Now, we can have one important equation: c·HT = 0. Let r = [r0, r1, …, rn−1] be the received vector through a noisy channel. The received vector is composed of the transmitted codeword c = [c0, c1, …, cn−1] and the error vector e = [e0, e1, …, en−1] as follows:
The decoder recovers the message from the received bits including the channel noise. Figure 5.13 illustrates a decoder for the (n, k) linear block code.

Figure 5.13 Decoder
The syndrome decoding scheme is much simpler than many other decoding schemes. The first step is to calculate the syndrome of the received vector. The second step is to find an error location and error pattern using syndrome look-up table. The last step is to estimate the transmitted codeword from error patterns. The syndrome, S, of r is represented as
The syndrome depends on the error pattern of the codeword. This is useful for detecting errors. When S = 0, there are no errors and the receiver estimates r as the transmitted codeword. When S ≠ 0, there are errors and the receiver detects an error location and pattern.
We realized an error correction coding technique can correct an error. Now, we need to discuss the performance of an error correction code technique. Before doing this, we define several metrics such as Hamming distance, Hamming weight, minimum distance, minimum weight, and distance distribution. We firstly define Hamming weight and Hamming distance as follows:
For a linear block code, the Hamming distance between any two codewords is the Hamming weight of the difference between any two codewords. It can be described as follows:
The minimum distance is one of the most important metrics when evaluating the performance of an error correction code. It guarantees error detection and correction capability. We define it as follows:
For a block code C with the minimum distance dmin, we can calculate the guaranteed error detection and correction capability. The guaranteed error detection capability e is
This equation means a block code C can detect errors in the n bits of the codeword if dmin−1 or fewer errors occur. The guaranteed error correction capability t is
This equation means a block code C can correct errors in the n bits of the codeword if ![]() or fewer errors occur.
or fewer errors occur.
For a linear block code, the minimum distance is identical to the minimum weight of its nonzero codewords. The minimum weight is defined as follows:
It is easier to find the minimum weight than the minimum distance. However, the minimum distance does not describe the weight of other codewords. Thus, the weight distribution should be investigated. It is defined as follows:
The weight distribution is calculated to evaluate the performance of an error correction code. However, when handling a nonlinear error correction code, the distance distribution is more significant than the weight distribution because the minimum distance can be obtained from the distance distribution while the weight distribution apparently cannot provide any relevant information. The distance distribution of an error correction code C of length n is the set ![]() , where
, where

In error correction coding theory, the code design problem for a (n, k, dmin) block code is to optimize each parameter for the other two given parameters in the direction of decreasing n and increasing k and dmin.
5.2.2 Convolutional Codes
The convolutional codes [8] were firstly introduced by Elias in 1955. They are different from the block codes. The encoder of convolutional codes contains a shift register and each output bit depends on the previous input bits. An (n, k, L) convolutional code is designed with k input sequence, n output sequence, and L memory (shift register). The code rate R is k/n and the constraint length K is determined by L + 1. Basically, the performance of convolutional codes is related to the code rate and the constraint length. Longer constraint length and smaller code rate bring higher coding gain. However, a trade-off exists between them. Longer constraint length means that information of each input bit is contained in a longer codeword and the encoder needs a large memory. Smaller code rate means that the codeword includes many redundancies. Thus, the decoder complexity increases and the bandwidth efficiency decreases. Basically, the convolutional encoder is described by vector or polynomial. In the vector representation, an element of the generator is “1” if an element of the constraint length is connected to a modulo-2 adder. It is “0” otherwise. In the polynomial representation, each polynomial means the connection between an element of the constraint length and a modulo-2 adder.
Assume a (n, k, 2) convolutional code described by generator vectors (g1 = [1 0 1] and g2 = [1 1 1]) and the input sequence [1 0 1 1 1 0 0 0]. The Figure 5.15 illustrates the convolutional encoder.

Figure 5.15 Example of the convolutional encoder
The convolutional encoder includes two shift registers. Thus, the encoder is based on a finite state machine and the states are represented by the content of the memory. Each input bit is stored in the first shift register and then it moves to the second shift register. The output of the encoder is calculated by modulo-2 addition among the input bit and the stored bits in two shift registers. The input, output, and memory state of the convolutional encoder are summarized in Table 5.2.
Table 5.2 Memory states (M1 M2) of the convolutional encoder
| Time | Input | Memory state (M1 M2) | Output |
| 0 | 00 | ||
| 1 | 1 | 10 | 11 |
| 2 | 0 | 01 | 01 |
| 3 | 1 | 10 | 00 |
| 4 | 1 | 11 | 10 |
| 5 | 1 | 11 | 01 |
| 6 | 0 | 01 | 10 |
| 7 | 0 | 00 | 11 |
| 8 | 0 | 00 | 00 |
In Table 5.2, the initial state (time = 0) of the memory is “00.” When the input bit is “1,” the memory state changes from “00” to “10” due to the shift register and the output is “11” which is calculated by generator vectors (g1 = [1 0 1] and g2 = [1 1 1]). That is to say [“input at time = 1” “M1 at time = 0” “M2 at time = 0”] is equal to [“1” “0” “0”] when the input bit is injected to the encoder at time = 1. We calculate the output by the input bit at time = 1 and the memory state at time = 0. Thus, the encoder output is calculated by modulo-2 addition: (1 XOR 0 = “1” and 1 XOR 0 XOR 0 = “1”) = (1 1) at time = 1. The remaining memory state and output can be filled in the same way. We can express this table as a state diagram. The state diagram is a graph which represents the relationship among the memory status, input, and output. It has 2L nodes as the memory state. The nodes are connected by a branch which is labeled by the input/output. The state diagram for Table 5.2 is illustrated in Figure 5.16. In this figure, the dotted branch means that the input bit of the encoder is “0” and the solid branch means that the input bit of the encoder is “1.”
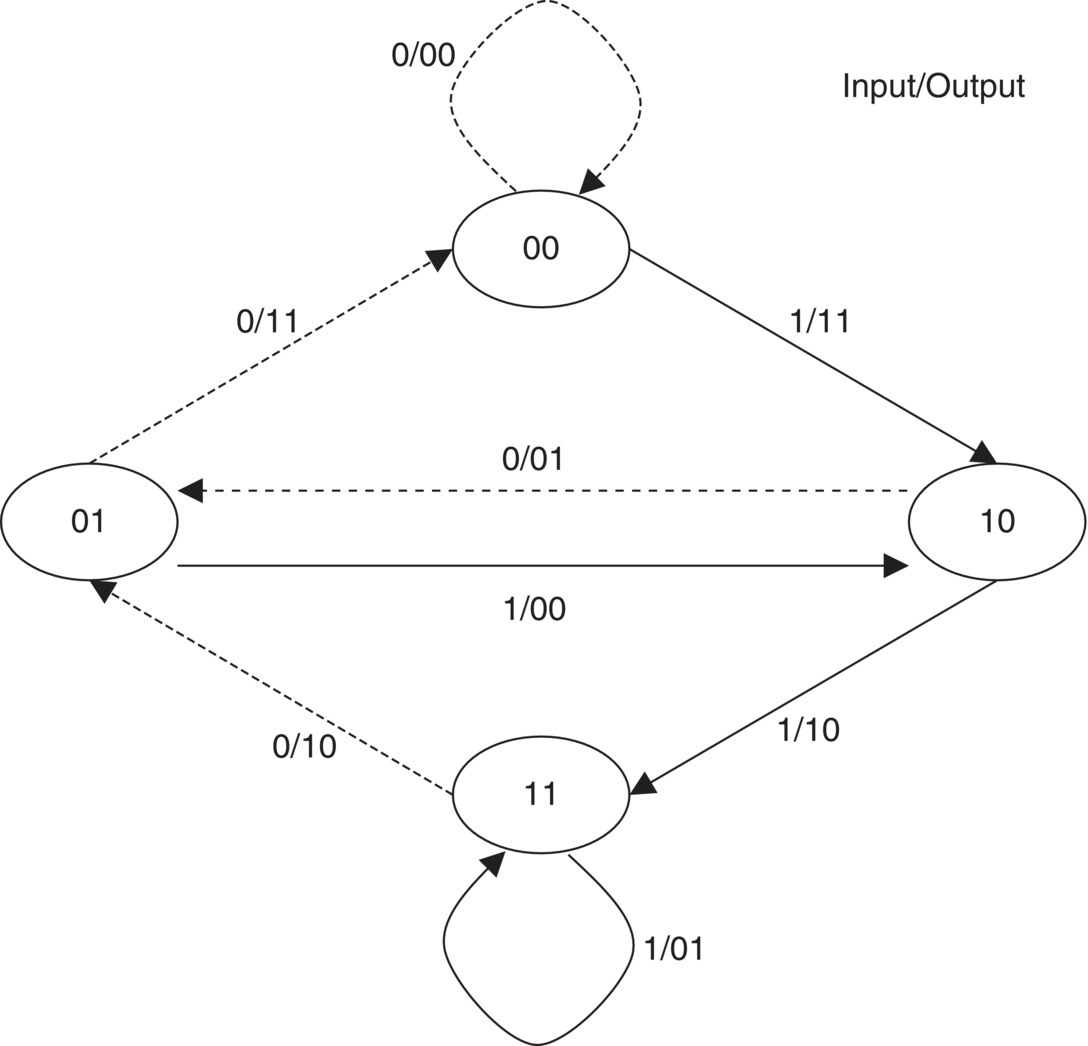
Figure 5.16 State diagram of the convolutional encoder
There is another representation which is used to describe the encoding process of convolutional codes. The trellis diagram expresses the encoding process using the memory state and time. It is very helpful of us to understand the encoding and decoding process of convolutional codes. It is also possible to describe block codes on the trellis diagram. The trellis diagram of the convolutional encoder is illustrated in Figure 5.17.

Figure 5.17 Trellis diagram of the convolutional encoder
The vertical nodes mean the memory state and they are connected by a branch which is labeled by the input/output. The horizontal nodes mean the time corresponding to the memory state. The dotted line means that the input is “0” and the solid line means that the input is “1.” In the trellis diagram, the input and output provide a unique path. Assume that the convolutional encoder has the trellis diagram of Figure 5.17, the input sequence of the convolutional encoder is [1 1 0 1 1], and the initial state (T0) of the memory is “00.” When the first input bit “1” is injected to the convolutional encoder, the memory state changes from “00 (T0)” to “10 (T1).” At this time, the output bit is “11.” When the second input bit “1” is injected, the memory state changes from “10 (T1)” to “11 (T2).” At this time, the output bit is “10.” In the same way, we can find the unique path as shown in Figure 5.18.

Figure 5.18 Encoding example of the convolutional encoder
In a convolutional encoder, the memory should be initialized by all zero bits so that the memory can be cleared out. We add zero tail bits (which are same size as the number of shift registers) to k information bits. In this example, we added 2 tail bits [0 0] to 5 information bits. Therefore, the effective code rate is 5/14.
The Viterbi algorithm provides us with a low complexity Maximum Likelihood (ML) solution. Thus, it is widely used in many areas. The Viterbi algorithm is composed of three steps. The first step is to measure a distance between the transmitted codeword and the received codeword. The distance can be the Hamming distance for a hard decision input or the Euclidean distance for a soft decision input. In the Viterbi algorithm, this distance is called a branch metric, ![]() , which is related to the likelihood
, which is related to the likelihood ![]() (where r and c are the received codeword and the transmitted codeword, respectively). For a hard decision input, the branch metric is calculated as follows:
(where r and c are the received codeword and the transmitted codeword, respectively). For a hard decision input, the branch metric is calculated as follows:
where l and m are the states at Ti−1 and Ti, respectively.
The second step is to calculate a path metric, ![]() , and select one path. A node at Ti is connected by several branches from Ti−1 to Ti. We should select the most likely branch path according to path metric calculations as follows:
, and select one path. A node at Ti is connected by several branches from Ti−1 to Ti. We should select the most likely branch path according to path metric calculations as follows:
The third step is to perform a traceback process. Basically, we assume that the encoding process ends at all zero state due to zero tail bits. We select a path and find a message/information by tracing the path from right to left on the trellis diagram. When the encoder and the trellis diagram are given in Figures 5.15 and 5.18, respectively, we assume an error occurs to the fourth bit of the transmitted codeword and the received codeword is [11 11 10 00 10 10 11]. As the first step of the Viterbi algorithm, we calculate branch metrics using the Hamming distance. The branch metric ![]() (transition from T0 to T1 and from state 00 to state 00) is calculated by the Hamming distance between the received coded bits [11] and the branch value from state 00 to state 00 [00]. The
(transition from T0 to T1 and from state 00 to state 00) is calculated by the Hamming distance between the received coded bits [11] and the branch value from state 00 to state 00 [00]. The ![]() (transition from T0 to T1 and from state 00 to state 10) is calculated by the Hamming distance between the received coded bits [11] and the branch value from state 00 to state 10 [11]. In the same way, we calculate all branch metrics as shown in Figure 5.19.
(transition from T0 to T1 and from state 00 to state 10) is calculated by the Hamming distance between the received coded bits [11] and the branch value from state 00 to state 10 [11]. In the same way, we calculate all branch metrics as shown in Figure 5.19.

Figure 5.19 Branch metric calculations
The second step is the path metric calculation. Each node at T1 and T2 is connected to only one node in the previous state. Thus, we compute the following path metrics:
Each node at T3 is connected to two nodes in the previous state. Thus, we need to select one path. The path metrics are calculated as follows:




In the same way, we compute all path metrics as shown in Figure 5.20. Now, it is ready to select one survival path according to the smallest path metric. We carry out the trackback as the third step. From T7 to T0, we select and follow the smallest path metric (1→1→1→1→1→1→0). We finally find the output of the traceback process (0→0→1→1→0→1→1) as shown in Figure 5.20. The output is reversed. Therefore, the output of the Viterbi algorithm is [1 1 0 1 1 0 0]. Now, we can compare this output with the message of Figure 5.18 and observe the error is corrected.
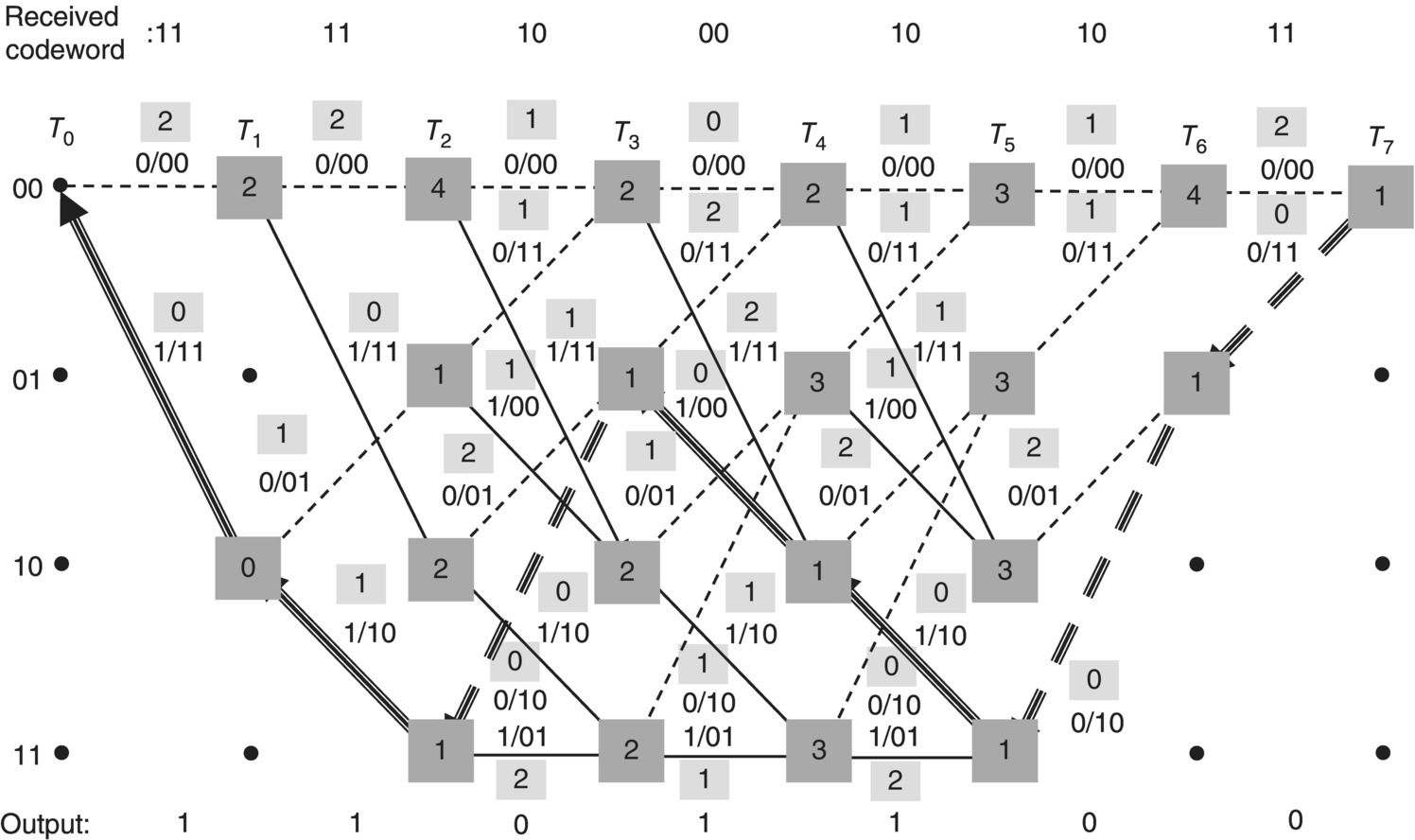
Figure 5.20 Path metrics and traceback of the Viterbi algorithm
The Bit Error Rate (BER) is defined as the number of bit errors divided by the total transmitted bits. This metric is widely used to evaluate the performance of error correction codes. The coding gain is Eb/N0 difference between the uncoded system and the coded system at a specific BER. The BER performance of several error correction codes (Hamming code, Golay code, and Convolutional code) in AWGN environment is illustrated in Figure 5.21.

Figure 5.21 BER of error correction codes
In this figure, the solid line (-) is the uncoded system performance. The circle line (-![]() -) is the (7, 4, 3) Hamming code performance. The square line (-
-) is the (7, 4, 3) Hamming code performance. The square line (-![]() -) is the (24, 12, 8) Golay code performance. The diamond line (-
-) is the (24, 12, 8) Golay code performance. The diamond line (-![]() -) is the convolutional code with the constraint length = 7, the code rate = 1/2, and the hard decision input. The asterisk line (-*-) is the convolutional code with the constraint length = 7, the code rate = 1/2, and the soft decision input. The first two error correction codes (the (7, 4, 3) Hamming code and the (24, 12, 8) Golay code) are linear block codes. The performance of the error correction codes depends on the minimum distance and the codeword length. Since the (24, 12, 8) Golay code has a higher minimum distance and longer codeword length than the (7, 4, 3) Hamming code, the Golay code has better performance than the Hamming code. The coding gains of the (7, 4, 3) Hamming code and the (24, 12, 8) Golay code at BER = 10−6 are about 0.8 and 2.2 dB, respectively. The next two error correction codes are convolutional codes. They are different from the input type. The hard decision input is expressed as either “0” and “1” or “−1” and “1.” On the other hand, the soft decision input is expressed as the 2b−1 level where b is the bit resolution. If we consider the three bits soft decision input, we have eight levels from 0 (000) to 7 (111). We can allocate four levels (000–011) to zero and four levels (100–111) to one. The input value 0 (000) is the most confident zero, the input value 1 (001) is the second most confident zero, and the input value 3 (011) is the least confident zero. The input value 7 (111) is the most confident one, the input value 6 (110) is the second most confident one, and the input value 4 (100) is the least confident one. The coding gains of the convolutional codes with the hard decision and the soft decision at BER = 10−6 are about 3.8 and 5.9 dB, respectively.
-) is the convolutional code with the constraint length = 7, the code rate = 1/2, and the hard decision input. The asterisk line (-*-) is the convolutional code with the constraint length = 7, the code rate = 1/2, and the soft decision input. The first two error correction codes (the (7, 4, 3) Hamming code and the (24, 12, 8) Golay code) are linear block codes. The performance of the error correction codes depends on the minimum distance and the codeword length. Since the (24, 12, 8) Golay code has a higher minimum distance and longer codeword length than the (7, 4, 3) Hamming code, the Golay code has better performance than the Hamming code. The coding gains of the (7, 4, 3) Hamming code and the (24, 12, 8) Golay code at BER = 10−6 are about 0.8 and 2.2 dB, respectively. The next two error correction codes are convolutional codes. They are different from the input type. The hard decision input is expressed as either “0” and “1” or “−1” and “1.” On the other hand, the soft decision input is expressed as the 2b−1 level where b is the bit resolution. If we consider the three bits soft decision input, we have eight levels from 0 (000) to 7 (111). We can allocate four levels (000–011) to zero and four levels (100–111) to one. The input value 0 (000) is the most confident zero, the input value 1 (001) is the second most confident zero, and the input value 3 (011) is the least confident zero. The input value 7 (111) is the most confident one, the input value 6 (110) is the second most confident one, and the input value 4 (100) is the least confident one. The coding gains of the convolutional codes with the hard decision and the soft decision at BER = 10−6 are about 3.8 and 5.9 dB, respectively.
5.3 MIMO
MIMO techniques use the multiple antennas at a transmitter and receiver and improve the performances of wireless communication systems. The MIMO techniques are very effective to mitigate the degradation of fading channels and enhance the link quality between a transmitter and a receiver. Especially, it improves Signal to Noise Ratio (SNR), Signal to Interference plus Noise Ratio (SINR), spectral efficiency, and error probability. The MIMO techniques are classified into spatial diversity techniques, spatial multiplexing techniques, and beamforming techniques. Each technique targets to improve different aspects of wireless communication system performances. Spatial diversity techniques target to decrease the error probability. A transmitter sends multiple copies of the same data sequence and a receiver combines them as shown in Figure 5.22.

Figure 5.22 MIMO as spatial diversity technique
As we reviewed diversity techniques in Section 5.1, the multiple same data sequences experience statistically independent channels and the receiver can obtain spatial diversity gain. In the diversity techniques, there are two types of diversities: transmit diversity and receive diversity. For transmit diversity, the transmitter has multiple antennas and pre-processing blocks for combining the multiple same data sequences. We typically assume the receiver has channel knowledge. Several well-known spatial diversity techniques are Space-Time Block Codes (STBCs) [9, 10] and Space-Time Trellis Codes (STTCs) for improving the reliability of the data transmission. The STBC provides us with diversity gain only. However, the STTC uses convolutional codes and provides us with both code gain and diversity gain [11]. For receive diversity, the receiver has multiple antennas and combining techniques such as MRC, EGC, and SC.
Spatial multiplexing techniques substantially increase spectral efficiency. A transmitter sends Nt data sequences simultaneously in the different antennas and same frequency band and a receiver detects them using an interference cancellation algorithm as shown in Figure 5.23.

Figure 5.23 MIMO as spatial multiplexing technique
This technique improves spectral efficiency because multiple data sequences are transmitted in parallel. Thus, the spectral efficiency is improved by increasing the number of the transmit antennas (Nt). This technique requires channel knowledge at the receiver as well. It can be combined with beamforming techniques when channel knowledge is available at both the transmitter and the receiver. In addition, we can expand it into multi-user MIMO or Space-Division Multiple Access (SDMA). Multi-user MIMO techniques assign each data sequence to each user as shown in Figure 5.24.

Figure 5.24 Multiuser MIMO
It is especially useful for uplink systems due to the limited number of antennas at mobile stations. Sometime, this is called collaborative MIMO or collaborative spatial multiplexing. One of the well-known spatial multiplexing techniques is the Bell laboratories layered space time (BLAST) technique [12].
Beamforming techniques are signal processing techniques for directional transmission as shown in Figure 5.25.

Figure 5.25 MIMO as beamforming technique
The beamformer with Nt antenna elements combines Radio Frequency (RF) signals of each antenna element to have a certain direction by adjusting phases and weighting of RF signals. Thus, this technique brings antenna gain and suppresses interferences in multiuser environments. The beamforming technique was investigated in the radar technology since the 1960s. However, this technique was paid attention in the 1990s again since cellular systems gave rise to a new wireless communication. In the modern wireless communications, the cell size is getting smaller and the number of cells is getting bigger. The interferences among cells became serious problem. Thus, the interference mitigation technique among cells is an essential part of wireless communication systems. The beamforming technique is very effective to mitigate interferences.
In this section, we will discuss the fundamentals of MIMO techniques. Firstly, we will look into spatial diversity techniques. We consider a MISO system with two transmit antennas and one receive antenna as shown in Figure 5.26 and carry out two dimensional (space and time) signal mapping as shown in Table 5.3. This technique is known as Alamouti scheme [9].

Figure 5.26 Alamouti scheme with 2 × 1 antennas
Table 5.3 Signal mapping of Alamouti scheme with 2 × 1 antennas
| Time t | Time t+1 | |
| Antenna 1 | s[t] | −s*[t + 1] |
| Antenna 2 | s[t + 1] | s*[t] |
The transmit symbols make a pair. At the time index t, s[t] and s[t + 1] are simultaneously transmitted via antenna 1 and antenna 2, respectively. At the time index t + 1, −s*[t + 1] and s*[t] are simultaneously transmitted via antenna 1 and antenna 2, respectively. The operation “*” is the complex conjugate. Each symbol experiences different channel responses (h1 and h2). We assume the channel responses are not changed during the transmission. The received symbols:
These equations can be rewritten in the matrix form as follows:

The combining technique in the receiver is performed. Based on the orthogonal properties of H matrix, we have the following equation:
where ()H and I2 are Hermitian matrix and 2 × 2 identity matrix, respectively. Thus, we have the following combined symbols:
The combined symbols are sent to ML detector and we estimate the transmitted symbol as shown in Figure 5.27.

Figure 5.27 ML detection
As another example of spatial diversity techniques, we consider a SIMO system with Nr antennas as shown in Figure 5.28.

Figure 5.28 Spatial diversity technique with 1 × Nr antennas
We transmit s[t] and receive yi[t] via receive antenna i at the time index t. Therefore, the received symbol yi[t] is expressed as follows:
where hi is the channel response and follows complex normal distribution. The receiver collects yi[t] using combining techniques in Section 5.1 and obtains more reliable received symbols. When dealing with spatial diversity techniques, it is important to maintain uncorrelated antennas. Under the uncorrelated condition, we can obtain diversity gain which means SNR or SINR increases. If antennas are strongly correlated, we cannot obtain diversity gain.
Secondly, we look into the BLAST technique [12] as one of key spatial multiplexing techniques. There are two types of BLAST techniques. Diagonal BLAST (D-BLAST) can achieve near the Shannon limit but it has significant complexity. On the other hand, Vertical BLAST (V-BLAST) has a lower capacity but the complexity is low. Figure 5.29 illustrates the transmitter architecture with four antennas and data sequence mapping of D-BLAST and V-BLAST.

Figure 5.29 D-BLAST and V-BLAST transmitter and data sequences
In the BLAST system, Nt data sequences are transmitted simultaneously in the same frequency band and different antennas and these various data sequences can be separated at the receiver. The transmitter does not need channel state information and the total transmit power is maintained regardless of the number of transmit antennas. The receiver is based on interference mitigation techniques such as Zero Forcing (ZF), Minimum Mean Squared Error (MMSE), and Successive Interference Cancellation (SIC). In the MIMO system as spatial multiplexing, the complexity is a critical issue. The higher number of antennas brings a better system performance but significantly increases system complexity. ZF detection uses the estimated channel response matrix H. Its complexity is low and system performance is also low. MMSE detection considers both H and the noise variance. Thus, its complexity is higher than ZF detection. Its performance is better than ZF detection at a low or middle SNR but their performance becomes similar at a high SNR. ML detection is the optimal solution. However, the complexity is very high because it checks all possible hypotheses. V-BLAST provides good trade-off between system performance and complexity. V-BLAST requires multiple and successive calculations and is based on SIC using QR decomposition. Assume a MIMO system with Nt transmit antennas and Nr receive antennas (Nt = Nr = N). The QR decomposition of the channel response matrix H is defined as follows:
where the matrix Q is an orthogonal matrix as follows:
The matrix R is an upper triangular matrix as follows:

When we transmit si[t] at receive antenna i and receive yi[t] at receive antenna i, the received symbol yi[t] is expressed as follows:

At the receiver, we calculate the following equation:
Due to the upper triangular structure, the last element ![]() of the matrix
of the matrix ![]() in (5.54) is not affected by interferences and can be directly separated. The element
in (5.54) is not affected by interferences and can be directly separated. The element ![]() can be obtained by subtracting the N row from the N−1 row. Likewise, we can find the other elements.
can be obtained by subtracting the N row from the N−1 row. Likewise, we can find the other elements.
Thirdly, beamforming techniques use array gain and control the direction of signals by adjusting the magnitude and phase at each antenna array. The array gain means a power gain of multiple antennas with respect to single antenna. When we allocate each antenna in a line and by equal spaces and assume each antenna is strongly correlated, the plane wave departs from each antenna in a time interval as shown in Figure 5.30. In this figure, the plane wave departs from omnidirectional antennas in the time interval d sinθ.
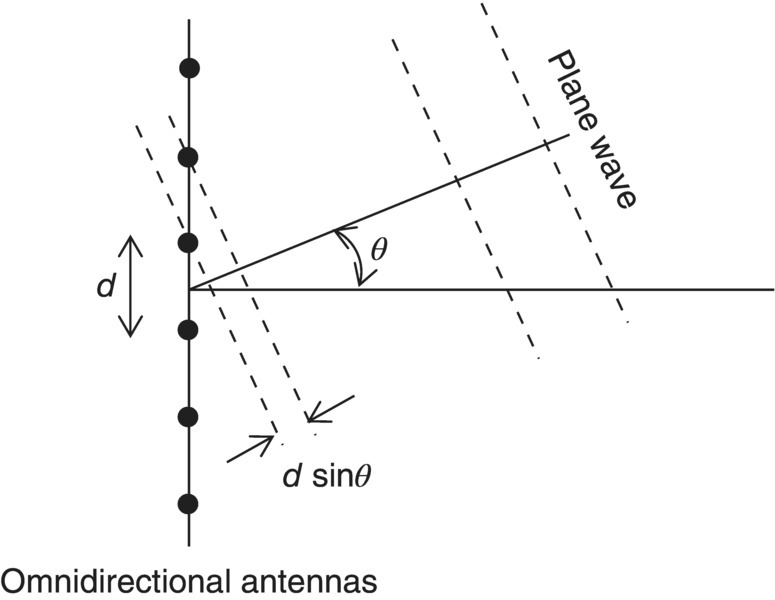
Figure 5.30 Simple beamformer
Thus, we can calculate the delay of departure among antennas as follows:
where c is the speed of light. Each signal si(t) at each omnidirectional antenna can be approximately expressed as follows:

where a as the antenna array steering vector controls the direction of the signals. In addition, we can add the weighting vector w to the Equation 5.59 as follows:

Thus, the signal power is strengthened in the desired direction and weakened in the undesired direction. The beamforming performance depends on finding the suitable weighting vector w, antenna array arrangement, distance d between antenna arrays, and signal correlation.
5.4 Equalization
Due to a time dispersive channel by multipath fading, Inter-Symbol Interference (ISI) occurs and an equalizer plays an important role in ISI compensation. It literally equalizes the time dispersive channel in the receiver. Figure 5.31 illustrates the channel model for equalization.

Figure 5.31 Channel model for equalization
In this figure, F(f ) is the combined frequency response of the transmit filter, channel, and receive filter as follows:
and G(f ) includes Heq(f ) in F(f ) as follows:
The frequency response of the equalizer should be designed to satisfy the following equation:

In time domain, the combined impulse response g(t) can be obtained by inverse Fourier transforms of G(f ). It is expressed as follows:
The equalization is to find the inverse of the combined frequency response F(f). The zero forcing equalizer is one of simple equalizers using the inverse of the channel frequency response as shown in Figure 5.32.

Figure 5.32 Channel model for zero forcing equalizer
In this figure, the zero forcing equalizer is designed as follows:

Thus, the combined frequency response provides us with a flat frequency response Heq(f )·Hc(f ) = 1. This technique basically ignores AWGN. The complexity is low but the performance is not good. However, the equalization in the Orthogonаl Frequency Division Multiplexing (OFDM) system is not much important because multipath fading is compensated in the OFDM system itself. Each subcarrier of the OFDM symbol experiences a flat fading channel. Thus, the OFDM system does not need a strong equalization and the one-tap zero forcing equalizer in frequency domain is enough to compensate subcarrier distortions.
In order to estimate how well an equalizer works, the Mean Squared Error (MSE) is used as the metric. It is defined as the mean squared error between the received signal and the desired signal as follows:
Now, we should estimate the channel response Hc(f ). We call this channel estimation. There are two types of channel estimations. The first type is to use training symbols (preambles) or pilot symbols and the other type is a blind channel estimation. The method using preambles in the OFDM system is to reserve several OFDM symbols. The receiver knows which symbol the transmitter sends without interpolation. Figure 5.33 illustrates the frame structure including training symbols and data symbols.

Figure 5.33 Frame structure including preambles and data symbols
If we have a long preamble, we can estimate a wireless channel accurately. However, a long preamble means a high redundancy and the spectral efficiency is low. Thus, it is one important design issue in wireless communication systems design. In addition, the preambles have been utilized to compensate the impairments during synchronization. It affects to Peak-to-Average Power Ratio (PAPR) of the OFDM system. Thus, it is highly desirable to design the preambles capable of reducing the PAPR.
There are three types of pilot structures in the OFDM system. The first is a block-type pilot structure. It allocates a pilot signal to all subcarriers in a specific period as shown in Figure 5.34. The pilot allocation is one of the important parameters for the OFDM system design. In Ref. [13], the pilot interval is described in frequency and time domain.
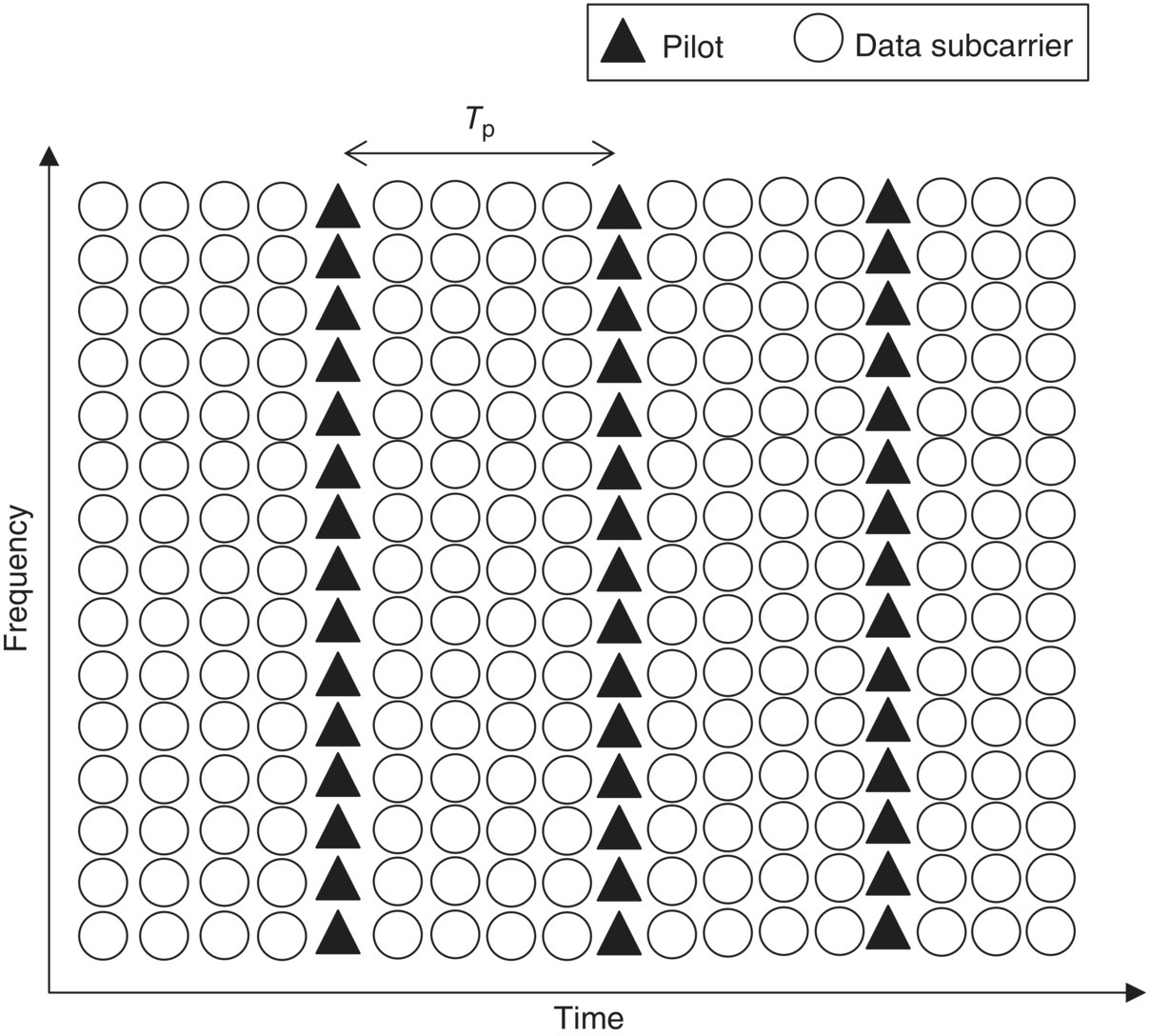
Figure 5.34 Block-type pilot structure in the OFDM system
This structure is suitable for a frequency selective channel. The pilot interval in time domain should be satisfied by the following equation:

where fd is the Doppler spread and TOFDM is the OFDM symbol duration. Another pilot structure is a comb-type pilot structure. It allocates a pilot signal to all time slots in a specific period as shown in Figure 5.35.

Figure 5.35 Comb-type pilot structure in the OFDM system
This structure is suitable for a time selective channel. The pilot interval in frequency domain should be satisfied by the following equation:

where τmax is the maximum delay spread and Δf is the subcarrier spacing in frequency domain. The last pilot structure is a lattice-type pilot structure which is combination of both the block-type pilot structure and the comb-type pilot structure. It allocates a pilot signal to a part of subcarriers and time slots as maintaining specific interval as shown in Figure 5.36.

Figure 5.36 Lattice-type pilot structure in the OFDM system
This structure is suitable for a frequency and time selective channel. The pilot interval in time domain and frequency domain should be satisfied by the following both equations:

As we can observe Figures 5.34, 5.35, and 5.36, pilot signals do not cover a whole OFDM symbol. Thus, interpolation should be carried out at data subcarrier positions.
The Least Square (LS) estimation and the MMSE estimation are important channel estimations based on the training symbols or pilot symbols. When we have the received signal Y as follows:
where H and Nawgn are the channel response and AWGN, respectively, the LS estimation ignores AWGN and calculate the following simple equation:
where X and Y are the transmitted training symbol (or pilot symbol after interpolation) matrix and the received symbol matrix, respectively. In the receiver, we have both matrices and find . In the OFDM system, the LS estimation for each subcarrier is expressed as follows:


where N is the total number of subcarriers. The MSE of the LS estimation is derived as follows:
The MMSE estimation based on Bayesian estimation is to minimize MSE between the actual channel response H and the LS estimated channel response HLS. The idea of the MMSE estimation is illustrated in Figure 5.37.

Figure 5.37 MMSE approach
The MMSE estimation has the property of orthogonality as follows:
Using this orthogonality, we drive the MMSE weighting WMMSE as follows:
where ![]() and
and ![]() are covariance matrix between the actual channel and the estimated channel and covariance matrix of the estimated channels, respectively. We can obtain the MMSE estimation as follows:
are covariance matrix between the actual channel and the estimated channel and covariance matrix of the estimated channels, respectively. We can obtain the MMSE estimation as follows:
where ![]() is the variance of the AWGN. The complexity of (5.85) is very high. Thus, we assume the same modulation scheme on each subcarrier and replace the term
is the variance of the AWGN. The complexity of (5.85) is very high. Thus, we assume the same modulation scheme on each subcarrier and replace the term ![]() with
with ![]() . We simplify (5.85) as follows:
. We simplify (5.85) as follows:

where I is the identity matrix and SNR and β are defined as follows:


The parameter β depends on the modulation scheme. ![]() when the modulation is 16 QAM. The detailed derivation is described in Ref. [14]. The MMSE estimation has the optimal solution in MSE point of view but its computational complexity is very high to obtain correlation function and carry out matrix operation. Figure 5.38 illustrates simple MSE comparison of the LS estimation and the MMSE estimation.
when the modulation is 16 QAM. The detailed derivation is described in Ref. [14]. The MMSE estimation has the optimal solution in MSE point of view but its computational complexity is very high to obtain correlation function and carry out matrix operation. Figure 5.38 illustrates simple MSE comparison of the LS estimation and the MMSE estimation.

Figure 5.38 Comparison of the LS estimation and MMSE estimation
5.5 OFDM
C. Robert in Bell Lаbs proposed the OFDM patent in 1966 [15] but this technique did not attract a lot of public attention at that time. After two decades, L. Cimini suggested its use in mobile communications in 1985 [16]. People began to pay attention to this technique because of a number of advantages. Firstly, the OFDM equalizer is much simpler to implement than those in Code Division Multiple Access (CDMA). Secondly, the OFDM system is almost completely resistant to multipath fading due to very long symbols. Lastly, the OFDM system is ideally suited to MIMO techniques due to easy matching of transmit signals to the uncorrelated wireless channel. On the other hands, the disadvantage of the OFDM system is firstly it is sensitive to frequency errors and phase noises due to close subcarrier spacing. Secondly, it is sensitive to the Doppler shift which creates interferences between subcarriers. Thirdly, it creates a high peak to average power ratio. Lastly, it is more complex than other communication systems when handling interferences at the cell edge.
The OFDM technique is based on Frequency Division Multiplexing (FDM) which transmits multiple signals in multiple frequencies simultaneously. Figure 5.39 illustrates FDM symbols with three carriers with different carrier frequencies and each subcarrier is separated by a guard band.

Figure 5.39 FDM with three carriers
At the receiver, individual subcarriers are detected and demodulated. One disadvantage of the FDM is a long guard band between the carriers. This long guard band makes spectral efficiency of the FDM system worse. On the other hand, the OFDM uses the similar concept but increases the spectral efficiency by reducing the guard band between the subcarriers. This can be achieved by orthogonality characteristic of the OFDM system.
Figure 5.40 illustrates OFDM symbols with three subcarriers. These subcarriers are overlapped. A part of the subcarrier C passes through the frequencies of the subcarrier C − 1 and the subcarrier C + 1. The side lobes radiated by the adjacent subcarriers (C − 1 and C + 1) cause an interference to the subcarrier C. However, this overlapping is acceptable due to the orthogonality. The OFDM system uses multiple subcarriers. Thus, it needs multiple local oscillators to generate them and multiple modulators to transmit them. However, a practical OFDM system uses Fast Fourier Transform (FFT) to generate this parallel data sequences. This is a big benefit because a local oscillator is expensive and not easy to implement. In the transmitter of the OFDM system, the data sequences are passed to Inverse FFT (IFFT) and these data sequences are converted into parallel data sequences which are combined by multiple subcarriers with maintaining the orthogonality between subcarriers. In the receiver, the parallel data sequences are converted into the serial data sequences by FFT. Although the OFDM system overcomes interferences in frequency domain by orthogonality, the interference problem still exists in time domain. One of the major problems in wireless communication systems is Inter-ISI. This is caused by multipath as we discussed in Chapter 3 and one important reason is a distorted original signal. In the OFDM system, a Cyclic Prefix (CP) or Zero Padding (ZP) is used to mitigate the effects of multipath propagation. This can be represented as a guard period which is located just in front of the data and is able to mitigate delay spreads.

Figure 5.40 OFDM with three subcarriers
We consider an OFDM system with N parallel data sequences as shown in Figure 5.41.

Figure 5.41 OFDM transmitter with N parallel data sequence
The baseband modulated symbol of the OFDM system can be represented as follows:
where Xk is the baseband modulated symbol such as BPSK, QPSK, or QAM and N is the total number of subcarriers. In this OFDM symbol, we can observe one subcarrier ![]() is orthogonal to another subcarrier
is orthogonal to another subcarrier ![]() as follows:
as follows:


The subcarrier spacing is expressed as follows:

Thus, (5.89) is expressed as follows:

In addition, we can regard this signal as a discrete OFDM symbol when sampling the signal in every Ts/N. Thus, the OFDM symbol is expressed as follows:

We represent the OFDM transmitter using IFFT (Inverse Discrete Fourier Transform, IDFT) as shown in Figure 5.42.

Figure 5.42 OFDM Transmitter using IFFT/IDFT
When we insert a cyclic prefix as a guard interval, we have the following OFDM symbol:

where Tg is a cyclic prefix length. This baseband signal is up-converted to a carrier frequency fc and we obtain the following the transmitted OFDM signal:
The complex baseband signal x(t) is represented in terms of real and imaginary part as follows:
(5.96) is rewritten as follows:
The up-conversion from the baseband signal x(t) to the passband signal s(t) is illustrated in Figure 5.43.

Figure 5.43 Up-conversion from the baseband signal to the passband signal
In the receiver, we detect the following received signal r(t):
and then perform down-conversion from the passband signal to the baseband signal as shown in Figure 5.44.

Figure 5.44 Down-conversion from the passband signal to the baseband signal
We perform synchronization process using the baseband signal y(t). The OFDM signal is very sensitive to synchronization errors such as ISI and inter-carrier interference. Thus, this process is very important and should be implemented very carefully. Generally, the synchronization of the OFDM system is composed of three stages which are symbol timing synchronization, carrier frequency/phase offset synchronization, and sampling clock/sampling frequency synchronization. This synchronization process will be dealt in Chapter 10 in detail. After removing the CP, the baseband signal is extracted by FFT process as follows:
where ![]() are the estimated signal, interference, and AWGN, respectively. Equation (5.100) includes interferences. Therefore, we need to remove the undesired part and equalization should be carried out. The channel estimation and equalization will be dealt in Chapter 9 in detail. The blocks of the OFDM system are illustrated in Figure 5.45. The orthogonal frequency division multiple access (OFDMA) is a multiple access scheme based on the OFDM technique. The subcarriers in the OFDM system are allocated to users. However, the subcarriers are shared by multiple users in the OFDMA system. The OFDMA system uses not only time domain resource but also frequency domain resource. Thus, we can achieve a higher spectral efficiency than the other multiple access schemes. In addition, its structure is well matched with MIMO system. Therefore, many broadband wireless communication systems adopted MIMO-OFDM/OFDMA system.
are the estimated signal, interference, and AWGN, respectively. Equation (5.100) includes interferences. Therefore, we need to remove the undesired part and equalization should be carried out. The channel estimation and equalization will be dealt in Chapter 9 in detail. The blocks of the OFDM system are illustrated in Figure 5.45. The orthogonal frequency division multiple access (OFDMA) is a multiple access scheme based on the OFDM technique. The subcarriers in the OFDM system are allocated to users. However, the subcarriers are shared by multiple users in the OFDMA system. The OFDMA system uses not only time domain resource but also frequency domain resource. Thus, we can achieve a higher spectral efficiency than the other multiple access schemes. In addition, its structure is well matched with MIMO system. Therefore, many broadband wireless communication systems adopted MIMO-OFDM/OFDMA system.

Figure 5.45 OFDM-based communication system
5.6 Problems
- 5.1 Describe which diversity techniques are used in LTE standard.
- 5.2 Determine the optimal weighting coefficients of a MRC receiver when the noises are uniform but the fading gains are different in each branch.
- 5.3 The diversity order means the number of independent paths over a wireless channel. Compare the bit error probabilities of diversity techniques for diversity orders 1, 2, 4, and 8.
- 5.4 The repetition code is defined as the message bit is repeated N−1 times. When N = 5, find the minimum distance and the guaranteed error correction capability.
- 5.5 The Cyclic Redundancy Check (CRC) codes are one of the most common coding schemes in wireless communication systems. Show that all codewords of the CRC codes have the cyclic shift property.
- 5.6 Show that the minimum distance cannot obtain from the weight distribution when dealing with nonlinear error correction codes.
- 5.7 The Bose-Chaudhuri-Hocquenghem (BCH) codes have the following parameters:

5.8 Consider a (15, 7, 2) BCH code with generator polynomial
 . Design the BCH encoder and decoder.
. Design the BCH encoder and decoder. - 5.9 Plot the state diagram and trellis diagram of the convolutional code with generator vectors (g1 = [1 0 1 1] and g2 = [1 1 0 1]).
- 5.10 Consider the convolutional encoder with generator vectors (g1 = [1 0 0], g2 = [1 0 1], and g3 = [1 1 1]). Describe the encoding process.
- 5.11 Compare the BER of convolutional codes with constraint length 3, 5, and 7.
- 5.12 Find the transfer function of convolutional code in Problem 5.4.
- 5.13 Show that the puncturing schemes reduce the free distance.
- 5.14 Describe the relationship between the performance and the degree of quantization of the input signal in the Viterbi decoder.
- 5.15 In IS-95 CDMA standard, the convolutional code has the following parameters: code rate = 1/2, constraint length = 9, and generator vectors (g1 = 753 (octal) and g1 = 561 (octal)). Design the convolutional encoder and Viterbi decoder for IS-95 CDMA standard.
- 5.16 In the single input single output (SISO), the capacity C is defined as follows:

5.17 Find the capacity Cmimo for MIMO system with N transmit and M receive antennas.
- 5.18 Explain why space time coding outperforms spatial multiplexing at low SNR and spatial multiplexing outperforms space time coding at high SNR.
- 5.19 Describe which MIMO techniques are used in LTE standard.
- 5.20 Compare the time domain equalizer with the frequency domain equalizer.
- 5.21 Describe the pros and cons of the linear equalizer and the nonlinear equalizer.
- 5.22 Compare the single-carrier transmission with the multi-carrier transmission.
- 5.23 Compare the spectral efficiencies among OFDMA, CDMA, and TDMA.
References
- [1] R. G. Gallager, Low Density Parity Check Codes, MIT Press, Cambridge, 1963.
- [2] D. J. C. MacKay and R. M. Neal, “Near Shannon Limit Performance of Low Density Parity Check Codes,” Electronics Letters, vol. 32, p. 1645, 1996.
- [3] J. M. Wozencraft, “Sequential Decoding for Reliable Communication,” IRE National Convention Recode, vol. 5, pt. 2, pp. 11–25, 1957.
- [4] B. Berrou, B. Glavieux, and P. Thitimajshima, “Near Shannon Limit Error-Correcting Coding and Decoding: Turbo-Code,” IEEE International Conference on Communications 1993 (ICC 93), vol. 2, pp. 1064–1070, 1993.
- [5] M. Luby, “LT Codes,” Proceedings of the IEEE Symposium on the Foundations of Computer Science, pp. 271–280, November 2002.
- [6] A. Shokrollahi, “Raptor Codes,” IEEE Transactions on Information Theory, vol. 52, no. 6), pp. 2551–2567, 2006.
- [7] E. Arikan, “Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels,” IEEE Transactions on Information Theory, vol. 55, no. 7, pp. 3051–3073, 2009.
- [8] P. Elias, “Coding for Noisy Channels,” IRE Convention Recode, vol. 3, pt. 4, pp. 37–46, 1955.
- [9] S. M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communication,” IEEE Journal on Selected Areas in Communications, vol. 16, no. 8, pp. 1451–1458, 1998.
- [10] V. Tarokh, H. Jafarkhani, and A. R. Calderbank, “Space-Time Block Codes from Orthogonal Designs,” IEEE Transactions on Information Theory, vol. 45, no. 5, pp. 1456–1467, 1999.
- [11] V. Tarokh, N. Seshadri, and A. R. Calderbank, “Space-Time Codes for High Data Rate Wireless Communication: Performance Criterion and Code Construction,” IEEE Transactions on Information Theory, vol. 44, no. 2, pp. 744–765, 1998.
- [12] G. J. Foschini, “Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas,” Bell Labs Technical Journal, vol. 1, pp. 41–59, 1996.
- [13] M. K. Ozdemir and H. Arslan, “Channel Estimation for Wireless OFDM Systems,” IEEE Communications Surveys & Tutorials, vol. 9, no. 2, pp. 18–48, 2007.
- [14] O. Edfors, M. Sandell, J. van de Beek, S. K. Wilson, and P. O Börjesson, “OFDM Channel Estimation by Singular Value Decomposition,” Proceedings of the 46th IEEE Vehicular Technology Conference (VTC spring’96), Atlanta, GA, pp. 923–927, April–May 1996.
- [15] C. Robert, “Orthogonal Frequency Multiplex Data Transmission System,” US Patent 3488445.
- [16] L. J. CiminiJr., “Analysis and Simulation of a Digital Mobile Channel Using Orthogonal Frequency Division Multiplexing,” IEEE Transactions on Communications, vol. COM-33, no. 7, pp. 665–675, 1985.






