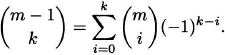CHAPTER 1
BASIC COUNTING METHODS
We begin our tour of combinatorics by investigating elementary methods for counting finite sets. How many ways are there to choose a subset of a set? How many permutations of a set are there? We will explore these and other such questions.
1.1 The multiplication principle
We start with the simplest counting problems. Many of these problems are concerned with the number of ways in which certain choices can occur.
Here is a useful counting principle: If one choice can be made in x ways and another choice in y ways, and the two choices are independent, then the two choices together can be made in xy ways. This rule is called the “multiplication principle.”
 EXAMPLE 1.1
EXAMPLE 1.1
Suppose that you have three hats and four scarves. How many different hat and scarf outfits can you choose?
Solution: By the multiplication principle, there are 3 · 4 = 12 different outfits. Let’s call the hats h1, h2, and h3 and the scarves s1, s2, s3, and s4. Then we can list the different outfits as follows:
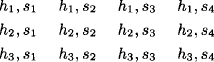
 EXAMPLE 1.2
EXAMPLE 1.2
At the French restaurant Chacun à Son Go![]() t, there are three choices for the appetizer, four choices for the entrée, and five choices for the dessert. How many different dinner orders (consisting of appetizer, entrée, and dessert) can we make?
t, there are three choices for the appetizer, four choices for the entrée, and five choices for the dessert. How many different dinner orders (consisting of appetizer, entrée, and dessert) can we make?
Solution: The answer is 3 · 4 · 5 = 60, and it isn’t difficult to list all the possibilities. Let’s call the appetizers a1, a2, and a3, the entrées e1, e2, e3, and e4, and the desserts d1, d2, d3, d4, and d5. Then the different possible dinners are as follows:
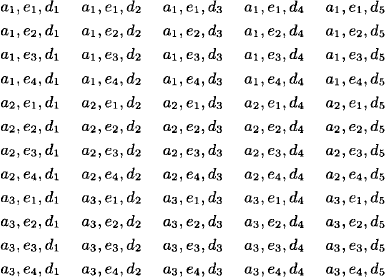
 EXAMPLE 1.3
EXAMPLE 1.3
A variable name in a certain computer programming language consists of a letter (A through Z), a letter followed by another letter, or a letter followed by a digit (0 through 9). How many different variable names are possible?
Solution: There are 26 variable names consisting of a single letter, 262 variable names consisting of two letters, and 26 · 10 variable names consisting of a letter followed by a digit. Altogether, there are
![]()
variable names.
 EXAMPLE 1.4 Number of binary strings
EXAMPLE 1.4 Number of binary strings
How many binary strings of length n are there?
Solution: There are two choices (0 or 1) for each element in the string. Hence, there are 2n possible strings.
For instance, there are 23 = 8 binary strings of lenght 3:
![]()
 EXAMPLE 1.5 Number of subsets of a set
EXAMPLE 1.5 Number of subsets of a set
Let S be a set of n elements. How many subsets does S have?
Solution: There are two choices for each element of S; it can be in the subset or not in the subset. This means that there are 2n subsets altogether.
For instance, let S = {a, b, c}, so that n = 3. Then S has 23 = 8 subsets:
![]()
EXERCISES
1.2 Permutations
One of the fundamental concepts of counting is that of a permutation. A permutation of a set is an ordering of the elements of the set.
 EXAMPLE 1.6
EXAMPLE 1.6
List the permutations of the set {a, b, c}.
Solution: There are six permutations:
![]()
We set
(1.1) ![]()
The expression n! is called n factorial.
We see in the above example that the number of permutations is 6 = 3!.
There are n! permutations of an n-element set. The reason is there are n choices for the first element in the permutation. Once that choice is made, there are n – 1 choices for the second element, and then n – 2 choices for the third element, and so on. Altogether, there are
![]()
choices, which is n!
 EXAMPLE 1.7
EXAMPLE 1.7
In how many ways can the letters of the word MISSISSIPPI be arranged?
Solution: This is an example of a permutation of a set with repeated elements. There are 11! permutations of the 11 letters of MISSISSIPPI, but there is much duplication.
We need to divide by the number of permutations of the four I’s, the four S’s, the two P’s, and the one M. Thus, the number of different arrangements of the letters is
![]()
Let S be an n-element set, where n ≥ 0. How many permutations of k elements of S are there, where 1 ≤ k ≤ n? There are n choices for the first element, n − 1 choices for the second element,…,n – k + 1 choices for the kth element. Hence, there are
![]()
choices altogether. This expression, denoted P(n, k), may be written as
(1.2) ![]()
(Notice that we now allow k = 0, which gives P(n, 0) = 1.) We can interpret this formula as a MISSISSIPPI-type problem. The selected elements may be denoted X1,…,Xk, and the nonselected elements all denoted with the letter N (for nonselected).
 EXAMPLE 1.8
EXAMPLE 1.8
An organization has 100 members. How many ways may they select a president, a vice-president, a secretary, and a treasurer?
Solution: The number of ways to select a permutation of four people from a group of 100 is
![]()
EXERCISES
1.3 Combinations
Another fundamental concept of counting is that of a combination. A combination from a set is an unordered subset (of a given size) of the set.
For convenience, we sometimes refer to an n-element set as an n-set and a k-element subset as a k-subset. Also, we use the notation N = {1, 2, 3,…,} and Nm = {1, 2, 3,…,m}.
Let S be an n-set, where n ≥ 0. How many k-subsets of S are there, where 0 ≤ k ≤ n? We can regard this as a MISSISSIPPI-type problem, i.e., a problem of permutations with repeated elements. Let X denote selected elements and N denote nonselected elements. Then the number of combinations is the number of arrangements of k X’s and n – k N’s, since each such arrangement specifies a combination.
Hence, the number of combinations, denoted C(n, k), is given by
(1.3) ![]()
We call this expression “n choose k.” We set C(n, k) = 0 for k < 0 and k > n.
For example, with n = 5 and k = 3, we have C(5, 3) = 5!/(3!2!) = 10 combinations of three elements from the set S = {a, b, c, d, e}, as shown below with the corresponding arrangements of X’s and N’s:
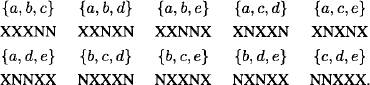
The values of C(n, k) are given by a famous array of numbers known as Pascal’s triangle. See Figure 1.1. The triangle is created by starting with a 1 in the top row, placing 1′s at the ends of each successive row, and adding two consecutive entries in a row to produce the entry beneath and between these entries. Thus, we can generate Pascal’s triangle from the initial values
Figure 1.1 Pascal’s triangle.

(1.4) ![]()
and the relation
(1.5) ![]()
The rows of Pascal’s triangle arc numbered 0, 1, 2, etc. (from top to bottom), and the columns are numbered 0, 1, 2, etc. (from left to right). The entry in row n, column k of Pascal’s triangle is C(n, k).
 EXAMPLE 1.9
EXAMPLE 1.9
Evaluate C(10, 5).
Solution: We see that the 5th entry of the 10th row of Pascal’s triangle is 252. Hence C(10, 5) = 252. This means that there are 252 combinations of five objects from a set of 10 objects.
Pascal’s triangle gives the coefficients of the expansion of a binomial, such as a + b, raised to a power. For example,
![]()
and we see that the coefficients 1, 3, 3, 1 constitute the third row of Pascal’s triangle. For this reason, the entries of Pascal’s triangle are called binomial coefficients.
We often use the notation (nk) for C(n, k). We may also write this binomial coefficient as (nk,n–k). Thus, we know
and
We also have the formula
(1.8) ![]()
Binomial theorem. For any numbers a and b (real or complex) and any nonnegative integer n, we have
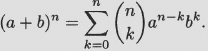
Proof. We give a combinatorial proof showing that, for each k, where 0 ≤ k ≤ n, the coefficients of an–kbk on the two sides of the equation are equal. The coefficient an–kbk on the left side is the number of ways of selecting n – k factors a + b that contribute a′s to the expansion of (a + b)n (the other factors contribute b′s). Such selections are choices of k unordered objects from a set of n objects; hence there are ![]() of them. This number is the coefficient of an–kbk on the right side.
of them. This number is the coefficient of an–kbk on the right side.
We could also have proved the binomial theorem by mathematical induction using (1.6) and (1.7).
 EXAMPLE 1.10
EXAMPLE 1.10
What is the coefficient of a12b8 in the expansion of (a + b)20?
Solution: By the binomial theorem, the coefficient is
![]()
How can we find the expansion of a multinomial expression raised to a power, such as (a + b + c)10? The answer is given by the multinomial theorem.
From the solution to the MISSISSIPPI problem, we know that the number of ways that n objects can be divided into groups of sizes k1, k2,…,km, such that k1 + k2 + · · · + km = n, where order among and within groups is unimportant, is
![]()
This expression, called a multinomial coefficient, is denoted by
![]()
Multinomial theorem. In the expansion of (x1 + x2 + · · · + xm)n, the coefficient of ![]() , where the ki are nonnegative integers such that k1 + k2+· · ·+km = n, is the multinomial coefficient
, where the ki are nonnegative integers such that k1 + k2+· · ·+km = n, is the multinomial coefficient
![]()
 EXAMPLE 1.11
EXAMPLE 1.11
Give the expansion of (a + b + c)3.
Solution: By the multinomial theorem,
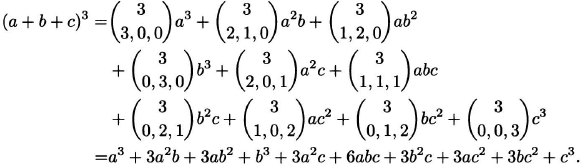
We can also think of a multinomial coefficient as an “ordered partition.” For instance, the multinomial coefficient ![]() is the number of partitions of the set {1, 2, 3,…,23} into three subsets, A, B, and C, where A has seven elements, B has ten elements, and C has six elements.
is the number of partitions of the set {1, 2, 3,…,23} into three subsets, A, B, and C, where A has seven elements, B has ten elements, and C has six elements.
EXERCISES
![]()
![]()
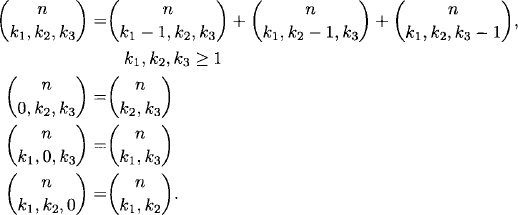
(b) How many paths in R3 start at the origin (0, 0, 0), move in steps of (1, 0, 0), (0, 1, 0), or (0, 0, 1), and end at (10, 15, 20)?
1.4 Binomial coefficient identities
Looking at Pascal’s triangle (Figure 1.1), we see quite a few patterns. Notice that the triangle is symmetric about a vertical line down the middle. To prove this, let X be an n-set. Then a natural bijection between the collection of k-subsets of X and the collection of (n – k)-subsets of X (simply pair each subset with its complement) shows that the two binomial coefficients in question are equal:
(1.9) ![]()
This identity also follows instantly from the formulas for ![]() and
and ![]() .
.
Many identities can be proved both algebraically and combinatorially. Often, the combinatorial proof is more transparent.
The rule that generates Pascal’s triangle (together with the values ![]() is known as Pascal’s identity.
is known as Pascal’s identity.
Pascal’s identity.
![]()
Pascal’s identity has a simple combinatorial proof. The binomial coefficient ![]() is the number of k-subsets of the set {1,…,n}. Each such subset either contains the element 1 or does not contain 1. The number of k-subsets that contain 1 is
is the number of k-subsets of the set {1,…,n}. Each such subset either contains the element 1 or does not contain 1. The number of k-subsets that contain 1 is ![]() . The number of k-subsets that do not contain 1 is
. The number of k-subsets that do not contain 1 is ![]() . The identity follows from this observation.
. The identity follows from this observation.
The combinatorial proof of Pascal’s identity is more enlightening than the following algebraic derivation:
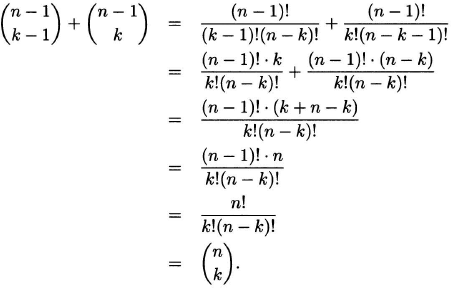
 EXAMPLE 1.12 Sum of a row of Pascal’s triangle
EXAMPLE 1.12 Sum of a row of Pascal’s triangle
The sum of the entries of the nth row of Pascal’s triangle is 2n.
(1.10) ![]()
Combinatorially, this identity says that the number of subsets of an n-set is equal to the number of k-subsets of the n-set, summed over all k = 0,…n. The identity also follows by putting a = b = 1 in the binomial theorem.
 EXAMPLE 1.13 Alternating sum of a row of Pascal’s triangle
EXAMPLE 1.13 Alternating sum of a row of Pascal’s triangle
Evaluate ![]() .
.
Solution: We give three solutions. (1) Letting a = −1 and b = 1 in the binomial theorem, we obtain
(1.11) 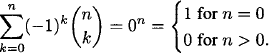
(2) Here is a combinatorial proof. Consider the equivalent formulation
![]()
This relation says that, for any n > 0, the number of subsets of X = {1,…,n} with an odd number of elements is equal to the number of subsets with an even number of elements. For n odd, this assertion follows trivially from the symmetry of the binomial coefficients. We give a combinatorial argument valid for any n > 0. Let
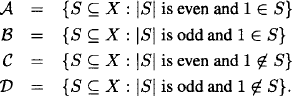
The obvious bijections between ![]() and
and ![]() and between
and between ![]() and
and ![]() establish that |
establish that |![]() | = |
| = |![]() | and |
| and |![]() | = |
| = |![]() |, and hence
|, and hence
![]()
The identity follows immediately.
(3) The identity can be turned into a telescoping series. For n > 0, we have
![]()
 EXAMPLE 1.14 Sum of squares of a row of Pascal’s triangle
EXAMPLE 1.14 Sum of squares of a row of Pascal’s triangle
What is the sum ![]() ?
?
Solution: Let’s work out some instances of the sum using Pascal’s triangle:
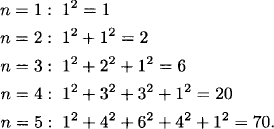
We recognize these sums as central binomial coefficients and conjecture that
(1.12) 
Typically, the mathematical process consists of working example, looking for patterns, making conjectures, and proving the conjectures. Let’s try to prove our conjecture.
We rewrite our conjecture as follows:
![]()
We know that the right side counts the ways of selecting n numbers from the set {1,2,3,…,2n}. Why is this counted by the left side? Rewrite just a little, using Symmetry:
![]()
Now the truth of the identity is clear. The right side counts the number of n-subsets of {1,2,3,…,2n}. The left side counts the same thing, according to the number of elements that are chosen from the subset {1,2,3,…,n}.
This identity has an interesting combinatorial interpretation. The binomial coefficient ![]() is the number of northeast paths which start at the southwest corner of an n × n grid and stop at the northeast corner. Such paths are of length 2n and are determined by a sequence of n “easts” and n “norths” in some order. The summation
is the number of northeast paths which start at the southwest corner of an n × n grid and stop at the northeast corner. Such paths are of length 2n and are determined by a sequence of n “easts” and n “norths” in some order. The summation ![]() counts the paths according to their intersection with the main diagonal of the grid. The number of paths that cross the diagonal at the points i units east of the starting point is
counts the paths according to their intersection with the main diagonal of the grid. The number of paths that cross the diagonal at the points i units east of the starting point is ![]() , where 0 ≤ i ≤ n.
, where 0 ≤ i ≤ n.
Other binomial coefficient identities may be obtained by comparing like powers of x in certain algebraic identities. For example, comparing coefficients of xk in the polynomial identity
![]()
we obtain Vandermonde’s identity.
Vandermonde’s identity.
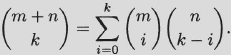
Vandermonde’s identity has a combinatorial interpretation. The binomial coefficient ![]() is the number of k-subsets of the (m + n)-set A ∪ B, where A = {1,…,m} and B ={m + 1,…,m + n}. The number of such subsets that contain i elements of A (and k – i elements of B) is
is the number of k-subsets of the (m + n)-set A ∪ B, where A = {1,…,m} and B ={m + 1,…,m + n}. The number of such subsets that contain i elements of A (and k – i elements of B) is ![]() , and the summation
, and the summation ![]() counts these subsets for i = 1,…,k.
counts these subsets for i = 1,…,k.
Letting m = 1, and changing n to n – 1, the relation becomes Pascal’s identity. Putting k = m = n, we obtain a previously seen identity:
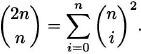
Here is another algebraic identity:
![]()
The coefficient of xn+1 on the left side is ![]() . On the right side, there is a contribution to xn+1 whenever we multiply x′s from n + 1 of the factors. Suppose that the rightmost factor which contributes an x is the (n + i + 1)st factor, where 0 ≤ i ≤ m. This leaves us free to choose n other x′s from a set of n + i factors. Hence the coefficient of xn+1 on the right side is
. On the right side, there is a contribution to xn+1 whenever we multiply x′s from n + 1 of the factors. Suppose that the rightmost factor which contributes an x is the (n + i + 1)st factor, where 0 ≤ i ≤ m. This leaves us free to choose n other x′s from a set of n + i factors. Hence the coefficient of xn+1 on the right side is ![]() . This proves the identity
. This proves the identity
(1.13) 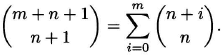
The identity has a combinatorial interpretation. The binomial coefficient ![]() is the number of (n+1)-subsets of the (m+n+1)-set {1,…,m+n+1}. Suppose that the largest element in such a subset is n + i + 1, where 0 ≤ i ≤ m. The number of such subsets is
is the number of (n+1)-subsets of the (m+n+1)-set {1,…,m+n+1}. Suppose that the largest element in such a subset is n + i + 1, where 0 ≤ i ≤ m. The number of such subsets is ![]() , and the summation
, and the summation ![]() counts them all.
counts them all.
Subcommittee identity. For 0 ≤ j ≤ k ≤ n, we have
![]()
Proof. Both expressions count the number of ways to choose, from n people, a committee of size k and a subcommittee of size j.
 EXAMPLE 1.15
EXAMPLE 1.15
Prove the identity:
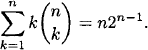
Solution: We will give four proofs.
(1) The first proof is algebraic. We can “pull an n out” of each term in the sum to obtain
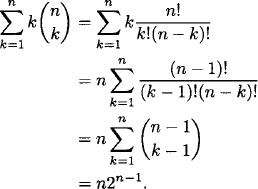
(2) The second proof is by counting. Consider all possible ways of choosing a team and a team leader from a set of n people. The left side clearly counts this, according to the size k of the team. The right side counts the same thing, as we have n choices for the leader and each other person can be on or off the team.
(3) The third proof uses calculus. From the binomial theorem, we have
![]()
Taking a derivative “brings a k down,” so
![]()
Evaluating both sides of the last relation at x = 1 gives our desired identity.
(4) Let’s also do a proof via probability. Upon division by 2n, our identity becomes
![]()
Here is a probabilistic interpretation. Let X be a set of n elements. For each element of X, flip a fair coin and if the coin comes up heads put the element in a subset S. What is the expected size of S? Both sides of the identity give the answer!
 EXAMPLE 1.16
EXAMPLE 1.16
Prove the identity
![]()
Solution: We give a counting proof of the equivalent identity
![]()
The right side of this relation is the number of binary strings of length 2n + 1. We must show that the left side counts the same strings. Every binary string of length 2n + 1 contains at least n + 1 0′s or at least n+ 1 1′s(but not both). Counting from the left, let n+ k+1, where 0 ≤ k ≤ < n, be the position of the (n +1)st 0 or (n +1)st 1. There are two possibilities for this element (0 or 1); there are ![]() binary strings of length n + k that contain n of one symbol and k of the other; and there are 2n-k choices for the remaining n − k elements. This establishes the identity.
binary strings of length n + k that contain n of one symbol and k of the other; and there are 2n-k choices for the remaining n − k elements. This establishes the identity.
 EXAMPLE 1.17 An object moving in the plane
EXAMPLE 1.17 An object moving in the plane
An object travels along the integer points of the plane, starting at the point (0, 0). At each step, the object moves one unit to the right or one unit up (with equal probability). The object stops when it reaches the line x = n or the line y = n. Show that the expected length of the object’s path is ![]() .
.
Solution: Assume that the object hits the line x = n at the point (n, k) or the line y = n at the point (k, n), where 0 ≤ k ≤ n − 1. Then the expected path length is given by
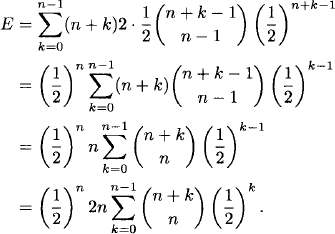
By the result of Example 1.16, this simplifies to
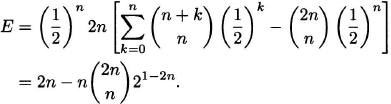
The binomial theorem extends to arbitrary exponents. For any real number α and k a positive integer, define
(1.14) ![]()
Also, define ![]() = 1.
= 1.
 EXAMPLE 1.18
EXAMPLE 1.18
![]()
Binomial series. Let α be a real number and |x| < 1. Then
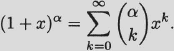
 EXAMPLE 1.19
EXAMPLE 1.19
Let n be an integer greater than or equal to 1. Prove the formula
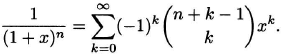
Solution: By the binomial series theorem,
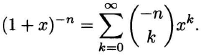
The result now follows from the identity (see Exercises)
(1.15) ![]()
Pascal’s triangle extends upward, as in Figure 1.2. (In the figure, the triangle is left-justified.) Pascal’s identity, together with the initial values ![]() = 1 for all integers n, is used to calculate entries
= 1 for all integers n, is used to calculate entries ![]() , where n is a positive integer. The entries are the numbers (–1)k
, where n is a positive integer. The entries are the numbers (–1)k ![]() given by the binomial series theorem as the coefficients of x in the power series expansion of (1 + x)−n.
given by the binomial series theorem as the coefficients of x in the power series expansion of (1 + x)−n.
Figure 1.2 The extended Pascal’s triangle.

 EXAMPLE 1.20
EXAMPLE 1.20
Give the first several terms of the expansion of (1 + x)−4 in powers of x.
Solution: We can see the coefficients in row −4 of the extended Pascal’s triangle. Thus
![]()
EXERCISES
![]()
![]()
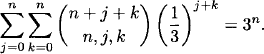
![]()
![]()
1.5 Distributions
Problems in which elements of a set are divided into categories are called distribution problems. Let’s consider a simple scenario. Suppose that five $1 bills are to be distributed among three people. In how many ways can this be done? The answer depends on whether the people are to be considered as identifiable in some way, and the same goes for the dollar bills. For instance, suppose that the people are named Amy, Bobby, and Carly, and the dollar bills have serial numbers so they are identifiable. Then there are three choices for who gets the first dollar bill, three choices for who gets the second dollar bill, and so on. Altogether, there are 35 ways to distribute the five dollars to the three people.
If the dollar bills are interchangeable, then we have a so-called “stars and bars” situation. The number of distributions is the number of ways to arrange five dollar signs (or stars) and two vertical lines (or bars) partitioning the three people along a line. The number of ways is C(7, 2).
If the three people are anonymous but the five bills are numbered, then the number of distributions is given by the Stirling numbers of the second kind. We will see more about this later in this section.
If the people are anonymous and the bills are interchangeable, then we have what are called partition numbers. We will sec mom about this later, too.
 EXAMPLE 1.21
EXAMPLE 1.21
How many solutions in nonnegative integers are there to the equation
![]()
Solution: We can think of the 10 on the right side of the equation as representing 10 units that can be distributed to the three variables, x1, x2, and x3. Such a distribution can be pictured with a linear ordering of 10 *’s (to represent the units) and two vertical lines (to indicate the partitioning of the units among the variables). For instance, the solution 3 + 2 + 5 = 10 is shown as
![]()
Thus, finding the number of distributions is a MISSISSIPPI-type problem. As there are 12 symbols altogether (10 *’s and two vertical lines), the number of solutions is
![]()
Distribution of identical objects into distinguishable classes. The number of ways to distribute k identical objects among n distinguishable classes is ![]() . This is the same as the number of nonnegative integer solutions to
. This is the same as the number of nonnegative integer solutions to
![]()
By contrast, the number of ways to distribute k distinguishable objects into n distinguishable classes is nk.
A partition of X is a collection C of nonempty pairwise-disjoint subsets of X whose union equals X. The members of C are called the parts of the partition.
An equivalence relation on X is a relation on X that is reflexive, symmetric, and transitive. If R is an equivalence relation on X, then, for each a ![]() X, the set [a] = {b
X, the set [a] = {b ![]() , X : (a, b)
, X : (a, b) ![]() R} is the equivalence class of a.
R} is the equivalence class of a.
Equivalence of equivalence relations and partitions. Let X be a nonempty set. The equivalence classes of an equivalence relation on X are the parts of a partition of X. Conversely, the parts of a partition of X are the equivalence classes of an equivalence relation on X.
Proof. Given an equivalence relation R on X, we will show that C = {[x] : x ![]() X} is a partition of X. First, each member [x] of C is nonempty (it contains x). Second, the union of the members of C is all of X, since each element x
X} is a partition of X. First, each member [x] of C is nonempty (it contains x). Second, the union of the members of C is all of X, since each element x ![]() X is contained in a member of C, namely, [x]. Third, the members of C are disjoint. For suppose that [x] ∩ [y] is nonempty for some x, y
X is contained in a member of C, namely, [x]. Third, the members of C are disjoint. For suppose that [x] ∩ [y] is nonempty for some x, y ![]() X; assume that z
X; assume that z ![]() [x] ∩ (y). Then, since (x, z)
[x] ∩ (y). Then, since (x, z) ![]() R and (y, z)
R and (y, z) ![]() R, it follows by symmetry and transitivity that (y, x)
R, it follows by symmetry and transitivity that (y, x) ![]() R. Let x′ be an arbitrary element of [x]. Then, since (x, x′)
R. Let x′ be an arbitrary element of [x]. Then, since (x, x′) ![]() R, it follows by symmetry and transitivity that (y, x′)
R, it follows by symmetry and transitivity that (y, x′) ![]() R, and hence x′
R, and hence x′ ![]() [y]. Since x′ is an arbitrary element of [x], we conclude that [x]
[y]. Since x′ is an arbitrary element of [x], we conclude that [x] ![]() [y]. A similar argument shows that [y]
[y]. A similar argument shows that [y] ![]() [x] and therefore [x] = [y].
[x] and therefore [x] = [y].
Now suppose that ![]() is a partition of X, and define a relation R on X so that (x, y)
is a partition of X, and define a relation R on X so that (x, y) ![]() R if x, y
R if x, y ![]() C for some C
C for some C ![]()
![]() . We will show that R is an equivalence relation on X. Since C is a partition of X, each x
. We will show that R is an equivalence relation on X. Since C is a partition of X, each x ![]() X is an element of some member of
X is an element of some member of ![]() ; hence R is reflexive. If x and y are both elements of some member C of
; hence R is reflexive. If x and y are both elements of some member C of ![]() , then the same can be said of y and x; hence R is symmetric. As for transitivity, if x and y are both elements of C for some C
, then the same can be said of y and x; hence R is symmetric. As for transitivity, if x and y are both elements of C for some C ![]()
![]() , and y and z are both elements of D for some D
, and y and z are both elements of D for some D ![]()
![]() , then C =D (since the parts of a partition are disjoint). Hence, x and z are both elements of the same member of
, then C =D (since the parts of a partition are disjoint). Hence, x and z are both elements of the same member of ![]() .
.
 EXAMPLE 1.22
EXAMPLE 1.22
How many partitions of the set {1, 2, 3, 4} are there?
Solution: In a partition of a set of four elements, the sizes of the equivalence classes sum to 4. There are five possibilities for these sizes:
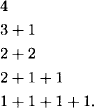
For example, the partition
![]()
is of type 2 + 1 + 1. It is an easy matter to count the partitions of each type, obtaining, respectively, 1, 4, 3, 6, and 1, for a total of 15.
The nth Bell number, denoted B(n), is the total number of partitions of the set (1, 2, 3,…,n). The Stirling number of the second kind ![]() is the number of partitions of {1, 2, 3,…,n} into k equivalence classes. The partition number p(n) is the total number of partitions of a set of n indistinguishable elements. These are also called partitions of an integer.
is the number of partitions of {1, 2, 3,…,n} into k equivalence classes. The partition number p(n) is the total number of partitions of a set of n indistinguishable elements. These are also called partitions of an integer.
According to the above example, ![]() = 1, and p(4) = 5.
= 1, and p(4) = 5.
We also define p(n, k) to be the number of partitions of n indistinguishable objects into k parts. From the above example, p(4, 1) = 1, p(4, 2) = 2, p(4, 3) = 1, and p(4, 4) = 1.
EXERCISES
![]()
1.6 The principle of inclusion and exclusion
The inclusion–exclusion principle is a generalization of the familiar Venn diagram rule.
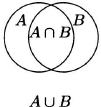
Venn diagram rule. If A and B are finite sets, then
Proof. See Figure 1.3, which shows two sets, A and B, and their union and intersection. The sum |A| + |B| counts all the elements of A ∪ B, but the elements of A ∩ B are counted twice and therefore must be removed as on the right side of (1.16).
Figure 1.3 A Venn diagram for two sets.
Inclusion–exclusion principle. If A1,…,An are subsets of a finite set S, then
where the second sum is over all i-tuples (k1,…,ki) with 1 ≤ k1 < · · · < ki ≤ n.
Proof. Let s ![]() S and assume that s is contained in exactly m of the Ai. The contribution of s to the right side of (1.17) is 0 if m = 0. If m ≥ 1, then the contribution is
S and assume that s is contained in exactly m of the Ai. The contribution of s to the right side of (1.17) is 0 if m = 0. If m ≥ 1, then the contribution is
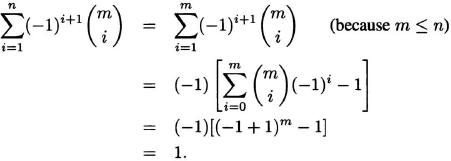
Therefore, each s ![]() S not in the union of the Ai contributes zero to both sides of (1.17), while each s
S not in the union of the Ai contributes zero to both sides of (1.17), while each s ![]() S in the union contributes 1. This means that each element of S contributes an equal amount to both sides of (1.17); hence, (1.17) is a valid relation.
S in the union contributes 1. This means that each element of S contributes an equal amount to both sides of (1.17); hence, (1.17) is a valid relation.
 EXAMPLE 1.23 Derangements
EXAMPLE 1.23 Derangements
A permutation with no fixed points is called a derangement. Let dn be the number of derangements of n elements. Find a formula for dn.
Solution: For 1 ≤ j ≤ n, let Aj be the set of permutations of {1, 2, 3,…,n} such that j is a fixed point. Then the intersection of any i of the Aj, for 1 ≤ i ≤ n, has (n — i)! elements, for the n — i not necessarily fixed elements may be permuted arbitrarily. Since there are ![]() choices for the Aj that make up the intersection, by the principle of inclusion and exclusion we have
choices for the Aj that make up the intersection, by the principle of inclusion and exclusion we have
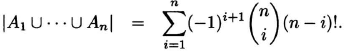
We conclude that
(1.18) 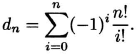
Inclusion—exclusion principle (probability version). Let E1,…, En be events in a finite sample space. Then
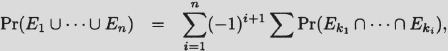
where the second sum is over all i-tuples (k1…,ki) with 1 ≤ k1 < · · · < ki ≤ n.
 EXAMPLE 1.24 Stirling numbers of the second kind
EXAMPLE 1.24 Stirling numbers of the second kind
Find a formula for the Stirling number of the second kind ![]() .
.
Solution: Using the principle of inclusion and exclusion (see Exercises), we can obtain
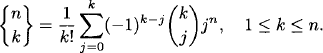
 EXAMPLE 1.25 Cards
EXAMPLE 1.25 Cards
All 52 playing cards arc dealt randomly to four players, 13 cards per player. What is the probability that at least one person has all cards of the same suit?
Solution: For 1 ≤ i ≤ 4, let Ei be the event that player i has all cards of the same suit. By the principle of inclusion and exclusion, the desired probability, Pr (∪ Ei), is
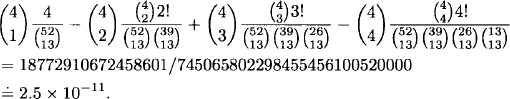
Make sure you understand how the four terms in the first line are obtained.
 EXAMPLE 1.26 “The problem of derangements”
EXAMPLE 1.26 “The problem of derangements”
What is the probability Pn that a random permutation of n elements is a derangement?
Solution: We found in Example 1.23 that
![]()
Therefore
(1.19) ![]()
It may seem strange that a fixed point is less likely to occur when n is 52 than when n is 51 or 53. It is interesting to note that
![]()
Students of probability should not be surprised to see the appearance of the number e in a probability calculation.
 EXAMPLE 1.27 Average number of fixed points of a permutation
EXAMPLE 1.27 Average number of fixed points of a permutation
Fine the average number of fixed points of a permutation of n elements.
Solution: We illustrate the result in the case n = 3. Below are the permutations of {1, 2, 3} and the number of fixed points of each.
| permutation | number of fixed points |
| (1)(2)(3) | 3 |
| (1)(2 3) | 1 |
| (2)(1 3) | 1 |
| (3)(1 2) | 1 |
| (1 2 3) | 0 |
| (1 3 2) | 0 |
The permutations an written in cycle form. For instance, the permutation (2)(13) is the one that maps 2 → 2, 1 → 3, and 3 → 1. The total number of fixed points is 6, and the average number is 6/6 = 1.
Randomly choose a permutation of {1, 2, 3,…,n}. For 1 ≤ i ≤ n, define Xi = 1 if i is fixed and 0 otherwise. Then the number of fixed points is Y = X1 + X2 + · · · + Xn. The expected value of each Xi is (n – 1)!/n! = 1/n. Hence, the expected number of fixed points is
![]()
 EXAMPLE 1.28 Bell numbers
EXAMPLE 1.28 Bell numbers
Find a formula for the Bell number B(n).
Solution: Using the result of Example 1.24, we obtain
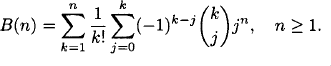
The formula can be simplified considerably:
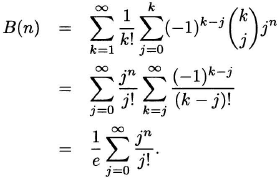
This formula is interesting from a number-theoretic point of view, as it is not at all clear a priori that (1/e) ![]() is an integer.
is an integer.
The inclusion–exclusion principle can be generalized to the Bonferroni inequalities of probability theory. We start with the algebraic identity
![]()
Equating coefficients of xk on both sides of this identity yields
The above identity can also be proved by applying Pascal’s identity to the binomial coefficient ![]() and collapsing the resulting telescoping sum.
and collapsing the resulting telescoping sum.
For each 1 ≤ i ≤ n, let
(1.21) ![]()
where the sum is over all i-tuples (k1,…,ki) with 1 ≤ k1 < · · · < ki ≤ n.
Bonferroni inequalities. Let A1,…,An be subsets of a finite set S. If t is an odd number, then
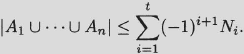
If t is even, then the inequality is reversed.
Proof. Let s ![]() S and assume that s is contained in exactly m of the Ai. If m = 0, then the contribution to both sides of the inequality is 0. For m > 0, the result follows easily from (1.20).
S and assume that s is contained in exactly m of the Ai. If m = 0, then the contribution to both sides of the inequality is 0. For m > 0, the result follows easily from (1.20).
 EXAMPLE 1.29
EXAMPLE 1.29
If k is even, we have
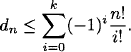
If k is odd, then the inequality is reversed.
Here is a neat technique that everyone should learn. Suppose that the sequence
![]()
represents the values of a polynomial p(n), where n = 0, 1, 2,…. What is the polynomial?
We take differences of consecutive terms, creating a new sequence:
![]()
We repeat this process, creating a sequence of sequences:

Having obtained a constant sequence, we stop.
Now, we find the polynomial by multiplying the first column of our difference array by successive binomial coefficients and adding:
![]()
This polynomial gives the original sequence, starting at p(0).
Why does this work? Suppose that the polynomial is
![]()
where the ai are real numbers. A little reflection shows that we can really write an arbitrary polynomial in this way.
Suppose that the values of the polynomial are
![]()
Letting n = 0, we find that a0 = p(0) (since all the other terms in the polynomial are equal to 0).
The sequence of differences is
![]()
Letting n = 1, we find that
![]()
and hence
![]()
The next sequence of differences is
![]()
Letting n = 2, we obtain
![]()
and hence
![]()
This pattern continues, so that the sequence a0, a1, a2,… is the first column of our difference array. In order to establish this, we introduce a little notation. Define
![]()
We call Δ the difference operator. We define Δ2p(n) = Δ(Δp(n)), Δ3p(n) = Δ(Δ2p(n)), and so on. We have
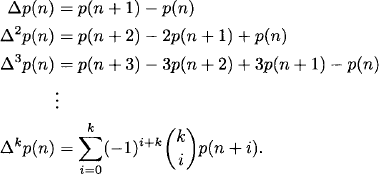
The array of differences looks like
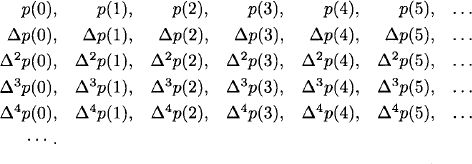
So our claim is that
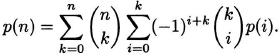
For a fixed i, the coefficient of p(i) is
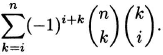
From the subcommittee identity, we obtain
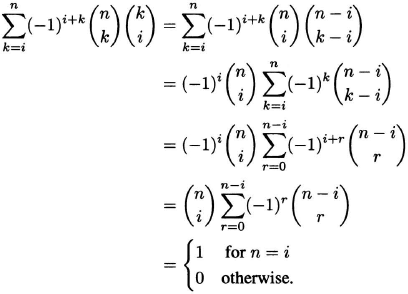
This completes the argument
Theorem. For any n and k, we have
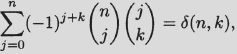
where δ(n, k) = 1 if n = k and δ(n, k) = 0 if n ≠ k.
EXERCISES
![]()
![]()
![]()
![]()
![]()
1.7 Fibonacci numbers
Let’s discuss one of the most famous sequences of numbers, the Fibonacci sequence. The Fibonacci sequence {F0, F1, F2,…} is defined recursively by the initial values
(1.22) ![]()
and the recurrence relation
(1.23) ![]()
Thus, the Fibonacci numbers are
![]()
Fibonacci numbers count many things. For example:
- Fn+1, is the number of ways that an n × 1 box may be packed with 2 × 1 and 1 × 1 boxes.
- Fn+2 is the number of binary strings of length n that do not contain the substring 00.
- Fn+2 is the number of subsets of Nn that contain no two consecutive integers.
- Fn–1 is the number of compositions of n that do not contain 1′s (see Exercise 1.54).
Let’s prove the second of these formulas.
Let sn be the number of binary strings of length n that contain no 00. We will prove that sn = Fn+2 for n ≥ 1. Observe that s1 = 2 = F3 and s2 = 3 = F4. We will show that sn = sn–1 + sn–2 for n ≥ 3 (the same recurrence relation satisfied by the Fibonacci numbers). Notice that each binary string of length n that does not contain 00 ends in either 1 or 10. The number of such strings of the first type is sn–1 and the number of such strings of the second type is sn–2. Hence sn = sn–1 + sn–2 for n ≥ 3. Now, since {sn} satisfies the same recurrence relation as the Fibonacci numbers, and s1 = F3 and s2 = F4, it follows by mathematical induction that sn = Fn+2 for all n ≥ 1.
 EXAMPLE 1.30 Cassini’s identity
EXAMPLE 1.30 Cassini’s identity
Prove that F2n – Fn–1 Fn+1 = (—1)n+1 for n ≥ 1.
Solution: We will prove the result by mathematical induction. The identity holds for n = 1, since F21 — F0F2 = 1 — 0 = 1 = (—1)2. Assume that it holds for n. Then
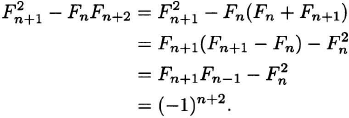
Hence, the formula holds for n + 1 and by induction for all n ≥ 1.
Here is a delight from Pascal’s triangle.
Singmaster’s theorem (1975). There are infinitely many numbers that occur at least six times in Pascal’s triangle.
Proof. Suppose that we have a solution to
![]()
given by
![]()
The number r in such a solution occurs (at least) six times in Pascal’s triangle:
![]()
The following relations are equivalent:
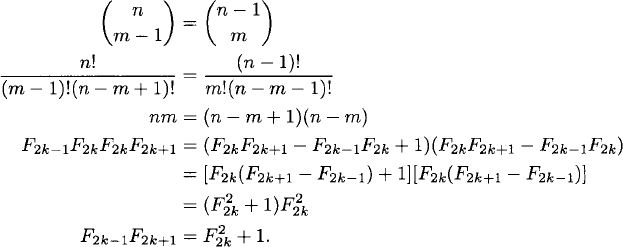
The last relation is true by Cassini’s identity.
The smallest such number given by our proof (when k = 2) is 3003.
EXERCISES
![]()
![]()
![]()
![]()
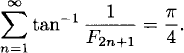
1.8 Linear recurrence relations
A sequence {an} satisfies a linear homogeneous recurrence relation with constant coefficients (of order k) if
(1.24) 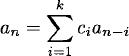
for constants c1,…,ck and all n ≥ k.
The Fibonacci sequence {Fn} satisfies a linear homogeneous recurrence relation with constant coefficients (of order 2).
How fast do the Fibonacci numbers grow? One might guess that they grow exponentially and they do. In order to find the exact rate of growth, we first find an explicit formula for Fn.
We will show how to guess and construct a solution. Assume that xn, where n ≥ 0, is the general term of a sequence that satisfies the Fibonacci recurrence relation (but not necessarily the same initial conditions). Then
![]()
Assuming that x ≠ 0, we divide through by xn and obtain the equation
(1.25) ![]()
This polynomial x2 — x — 1 is called the characteristic polynomial of the sequence. We use the quadratic formula to find the two roots of the characteristic polynomial:
(1.26) ![]()
We call ϕ the “golden ratio.” Note that ϕ ![]() 1.6 and
1.6 and ![]() .
.
So we know that ϕn and ![]() both satisfy the Fibonacci recurrence relation. Any linear combination Aϕn +
both satisfy the Fibonacci recurrence relation. Any linear combination Aϕn + ![]() , with A, B
, with A, B ![]() R, also satisfies the recurrence relation. For
R, also satisfies the recurrence relation. For
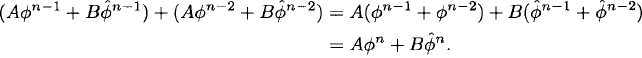
We use the initial conditions to solve for the coefficients A and B. Recalling that F0 = 1 and F1 = 1, we obtain two linear equations to solve simultaneously:
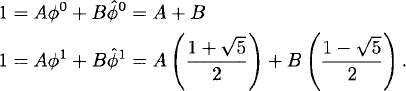
We find that
![]()
Thus, a formula for the Fibonacci numbers is
(1.27) ![]()
The above function satisfies the recurrence relation and initial conditions of the Fibonacci sequence, and hence is a formula for the Fibonacci sequence (since the sequence is well-defined). But the derivation of the formula was based on the assumption that some basic solutions to the recurrence relation were exponential. How did we know this in advance and would it be true for other linear recurrence relations? A more direct way to solve these problems is via generating functions, which we address in Chapter 2.
Now, how do we evaluate the growth rate of Fn? We say that a positive-valued function f(n) is asymptotic to another such function g(n), and we write f(n) ~ g(n), if limn→∞ f(n)/g(n) = 1. Since ![]() → 0 as n → ∞, we conclude that
→ 0 as n → ∞, we conclude that
(1.28) ![]()
 EXAMPLE 1.31
EXAMPLE 1.31
Find an explicit formula for the sequence {an} defined by the recurrence formula
![]()
Solution: The characteristic polynomial of the sequence is
![]()
which has 3 as a double root. Hence, 3n is a solution to the recurrence relation. However, we need a second solution in order to make the formula satisfy the initial conditions. A guess for a second solution is n3n. Let’s verify that this solution satisfies the recurrence relation:
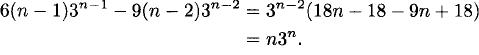
Any linear combination of our two solutions also satisfies the recurrence relation:
![]()
In order to satisfy the initial values, a0 = 1 and a1 = 1, we require that
![]()
and hence A = 1 and B = −2/3. Therefore, an explicit formula for the sequence is
![]()
The next example illustrates the technique of adding a particular solution and a homogeneous solution.
 EXAMPLE 1.32
EXAMPLE 1.32
Find an explicit formula for the sequence {an} defined by the recurrence formula
![]()
Solution: We find a particular solution to the recurrence relation. Assume the existence of a solution of the form an = αn + β, where α and β are constants. Thus
![]()
In order for this identity to hold for all n, we must have α = 1/4 and hence β = 3/4.
Therefore
![]()
satisfies the recurrence relation.
We solved the homogeneous version of this recurrence relation in the previous example. Thus, the general solution to the recurrence relation is of the form
![]()
The initial values, a0 = 1 and a1 = 1, determine the values A = 1/4 and B = −1/4.
Therefore, an explicit formula is
![]()
The Lucas numbers are defined as
(1.29) ![]()
Thus, the Lucas numbers are
![]()
Since the Lucas numbers satisfy the same recurrence relation as the Fibonacci numbers, they have the same characteristic polynomial, x2 − x − 1. Taking into account the initial values L0 = 2 and L1 = 1, we obtain a formula for the Lucas numbers:
(1.30) ![]()
The simplicity of this formula is one of the nice properties of the Lucas sequence. A consequence is that the Lucas numbers are given by the elegant formula Ln = {ϕn} for n ≥ 2, where {x} is the nearest integer to x.
 EXAMPLE 1.33 Squares of Fibonacci numbers
EXAMPLE 1.33 Squares of Fibonacci numbers
Let {F2n} be the sequence of squares of the Fibonacci numbers. Find a linear recurrence relation with constant coefficients for this sequence.
Solution: Start with the relations
![]()
Square both relations and add:
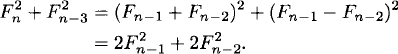
We obtain the recurrence relation
![]()
 EXAMPLE 1.34 Powers of Fibonacci numbers
EXAMPLE 1.34 Powers of Fibonacci numbers
Find a linear recurrence relation with constant coefficients for the sequence {Fkn} of kth powers of the Fibonacci numbers, where k is a positive integer.
Solution: The method is to use characteristic polynomials. Let’s work out the k = 2 case first (this will reproduce the recurrence relation found in the previous example). We know a direct formula for the Fibonacci numbers:
![]()
where A and B are constants (we know the constants but don’t need them). It follows that
![]()
and since ![]() = −1, the roots of the characteristic polynomial for the sequence
= −1, the roots of the characteristic polynomial for the sequence ![]() are
are ![]() , and −1. Hence, the characteristic polynomial for this sequence is
, and −1. Hence, the characteristic polynomial for this sequence is
![]()
To simplify further, recall that the Lucas numbers Ln are given by the formula
![]()
Using this formula, the characteristic polynomial in the case k = 2 simplifies to
![]()
This confirms the recurrence relation found in the previous example:
![]()
The case k = 3 is similar. By the binomial theorem, the formula for F3n contains powers of ![]() , and
, and ![]() . Therefore, the characteristic polynomial of the sequence
. Therefore, the characteristic polynomial of the sequence ![]() is
is
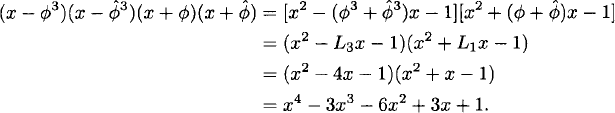
This gives us a recurrence relation for the cubes of the Fibonacci numbers:
![]()
For k ≥ 1, the characteristic polynomial for the sequence of kth powers of the Fibonacci numbers is
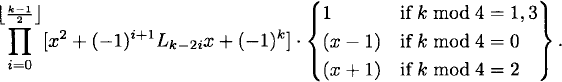
This formula, found by John Riordan, means that the sequence {Fkn} of kth powers of the Fibonacci numbers satisfies a linear recurrence relation of order k + 1 with integer coefficients.
EXERCISES
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1.9 Special recurrence relations
Recall that a derangement is a permutation with no fixed points. Let dn denote the number of derangements of the set {1, 2, 3,…,n}. We know that d1 = 0 and d2 = 1. We claim that {dn} satisfies the linear recurrence relation
(1.31) ![]()
In a derangement of {1, 2, 3,…,n}, the element n must occur in a cycle of length 2 or a cycle of greater length. There are n − 1 choices for the other element in a cycle of length 2, and the remaining elements constitute a derangement of n − 2 elements. In a cycle of length greater than 2, there are n − 1 choices for the element which maps to n, and the elements other than n constitute a derangement of n −1 elements.
We defined the Stirling number of the second kind ![]() , for 1 ≤ k ≤ n, to be the number of partitions of the set {1, 2, 3,…,n} into k parts. We will now find a recurrence formula for these numbers. Note that
, for 1 ≤ k ≤ n, to be the number of partitions of the set {1, 2, 3,…,n} into k parts. We will now find a recurrence formula for these numbers. Note that ![]() = 1 for all n, as there is only one way to partition {1, 2, 3,…,n} into one subset. Also, {nn} = 1 for all n, as {1, 2, 3,…,n} may be partitioned into n subsets in only one way. Now let us find a way to compute {nk} from previous values. In a partition of {1, 2, 3,…,n} into k parts, the element n can be alone in a part of the partition or it can be in a part with other elements. If it is alone, then there are {k−1n−1} ways to partition {1, 2,…,n − 1} into the other k − 1 parts. However, if n is in a part with other elements, then there are k choices for which part contains n and {n−1k} ways to partition {1, 2,…,n − 1} into k parts. Therefore
= 1 for all n, as there is only one way to partition {1, 2, 3,…,n} into one subset. Also, {nn} = 1 for all n, as {1, 2, 3,…,n} may be partitioned into n subsets in only one way. Now let us find a way to compute {nk} from previous values. In a partition of {1, 2, 3,…,n} into k parts, the element n can be alone in a part of the partition or it can be in a part with other elements. If it is alone, then there are {k−1n−1} ways to partition {1, 2,…,n − 1} into the other k − 1 parts. However, if n is in a part with other elements, then there are k choices for which part contains n and {n−1k} ways to partition {1, 2,…,n − 1} into k parts. Therefore
(1.32) 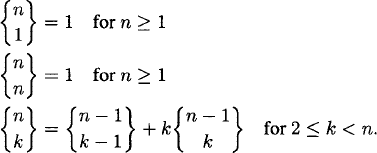
From the recurrence formula, we obtain a table (Table 1.1) of values of {nk} for small n and k. The row sums of this table are the Bell numbers.
Table 1.1 Stirling numbers of the second kind {nk} and Bell numbers B(n).
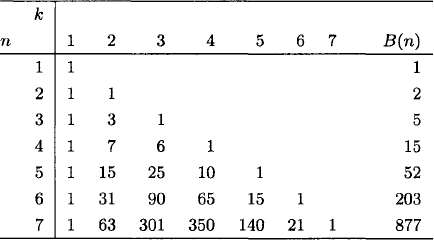
Let us verify an entry of the table, say {43} = 6. There are six ways to partition the set {1, 2, 3, 4} into three subsets: {12, 3, 4}, {1, 3, 24}, {1, 2, 34}, {13, 2, 4}, {1, 4, 23}, {14, 2, 3} (suppressing commas and one level of set notation).
The Stirling number of the first kind ![]() , for 1 ≤ k ≤ n, is defined to be the number of permutations of { 1, 2, 3,…,n} that have k cycles. For example,
, for 1 ≤ k ≤ n, is defined to be the number of permutations of { 1, 2, 3,…,n} that have k cycles. For example, ![]() = 3, as there are three permutations of {1, 2, 3} with two cycles: (1 2)(3), (1 3)(2), and (2 3)(1).
= 3, as there are three permutations of {1, 2, 3} with two cycles: (1 2)(3), (1 3)(2), and (2 3)(1).
Observe that ![]() = 1 (there is only one identity permutation) and
= 1 (there is only one identity permutation) and ![]() ! (there are (n − 1)! ways to seat n guests at a circular table). In a permutation of {1,…,n}, the element n can constitute a cycle by itself or it can follow one of the other n − 1 elements in one of k cycles. In the first case, there are
! (there are (n − 1)! ways to seat n guests at a circular table). In a permutation of {1,…,n}, the element n can constitute a cycle by itself or it can follow one of the other n − 1 elements in one of k cycles. In the first case, there are ![]() choices for dividing the other n − 1 elements into k − 1 cycles. In the second case, there are n − 1 choices for which element n follows and
choices for dividing the other n − 1 elements into k − 1 cycles. In the second case, there are n − 1 choices for which element n follows and ![]() ways to divide n − 1 elements into k cycles. Therefore
ways to divide n − 1 elements into k cycles. Therefore
(1.33) 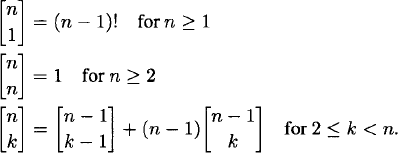
From this recurrence formula, we obtain a table (Table 1.2) of the values of ![]() for small n and k. Note that the sum of the entries of the nth row of the table is n!, which is correct because each permutation of {1, 2, 3,…,n} is counted.
for small n and k. Note that the sum of the entries of the nth row of the table is n!, which is correct because each permutation of {1, 2, 3,…,n} is counted.
Table 1.2 Stirling numbers of the first kind [nk].

We set ![]() . Stirling numbers of the first and second kinds are linked by a simple identity:
. Stirling numbers of the first and second kinds are linked by a simple identity:
(1.34) ![]()
This means that the Stirling numbers are represented in dovetailing arrays (Table 1.3).
Table 1.3 Stirling numbers of the first and second kinds.

Recall that p(n) is the number of partitions of n units into an arbitrary number of parts, while p(n, k) is the number of partitions of n units into k parts. Clearly, p(n) = ![]() .
.
A recurrence relation formula calculates p(n, k):
(1.35) 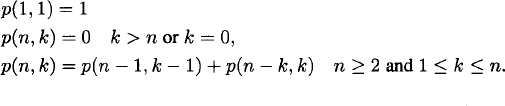
The value p(1, 1) = 1 is obvious. Since there are no partitions of n into more than n parts or into 0 parts, we have p(n, k) = 0 for k > n or k = 0. In a partition of n into k parts, the smallest part is either 1 or greater than 1. In the former case, there are p(n − 1, k − 1) partitions of the remaining number n − 1 into k − 1 parts. In the latter case, the partitions of n into k parts are equinumerous with the partitions of n – k into k parts (just subtract 1 from each part in the partition of n). This proves the formula p(n, k) = p(n – 1, k – 1) + p(n – k, k) for n ≥ 2 and 1 ≤ k ≤ n.
Tables 1.4 and 1.5 show values of p(n, k) and p(n) for small n and k.
Table 1.4 Partition numbers p(n, k).
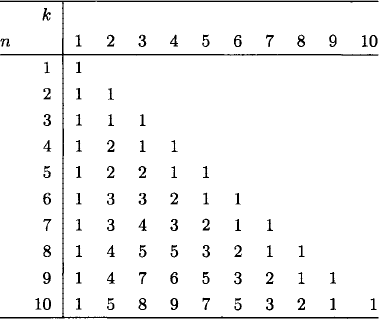
Table 1.5 Partition numbers p(n).

EXERCISES
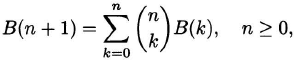
1.10 Counting and number theory
In this section, we investigate divisibility properties of factorials, binomial coefficients, and Fibonacci numbers.
 EXAMPLE 1.35
EXAMPLE 1.35
How many 0′s occur at the right of 40!?
Solution: The 0′s at the right of 40! occur because of factors of 2 and 5 among the numbers 1. 2,…,40. Since there are more 2′s than 5′s, the number of 0′s is determined by the exponent of 5 that divides 40!. This number is
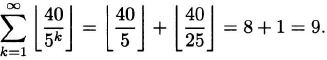
In the following discussion, let p be a prime.
De Polignac’s formula. The exponent to which p divides n! is given by
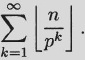
Let db(n) be the sum of the “digits” in the base b representation of n. For instance, if the base 3 representation of n is 1020120, then d3(n) = 6.
Theorem. The exponent of 2 that divides n! is n – d2(n).
Proof. Let the base 2 representation of n be
![]()
Then n = Σki=0bi2i and the exponent of 2 that divides n! is
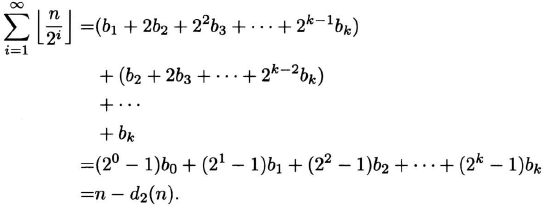
Here is the general version of the theorem.
Legendre’s formula (1808). The exponent of p that divides n! is
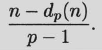
Next we will look at divisibility of binomial coefficients.
Theorem. If 1 ≤ k ≤ p – 1, then (pk) is divisible by p.
Proof. The numerator of p!/(k!(p – k)!) is a multiple of p and p does not divide the denominator.
Kummer’s theorem (1852). The exponent to which p divides the binomial coefficient (nk) is equal to the number of carries when k and n – k are added in base p.
Proof. We will show the proof in the base 2 case. Let j = n – k. The exponent to which 2 divides (nk) is
![]()
Assume that the binary representation of n requires l binary digits. For 1 ≤ i ≤ l, let ni, ji and ki be the ith binary digit of the expansion of n, j, and k, respectively; let ci = 1 if there is a carry in the ith place when j and k are added (in binary) and ci = 0 if there is no carry. Also, define c−1 = 0. We see that ni = ji + ki + ci–1 –2ci for 1 ≤ i ≤ l. Hence, the exponent to which 2 divides ![]() is
is
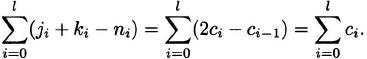
Corollary. For e ≥ 1 and 1 ≤ x < pe, we have
![]()
The next theorem gives a practical method for calculating binomial coefficients modulo p.
Lucas’ theorem (1878). Suppose that 0 ≤ ai, bi < p for 1 ≤ i ≤ k. Then
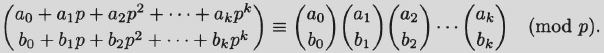
Proof. The left side counts the ways of choosing b0 + b1p + b2p2 + · · · + bkpk balls from a set of a0 + a1p + a2p2 + · · · + akpk balls. Suppose that the balls to be selected are in boxes, with b0 boxes containing a single ball each, b1 boxes containing p balls each, b2 boxes containing p2 balls each,…,and bk boxes containing pk balls each. In selecting the balls from the boxes, any choice of only some balls from a box leads to a contribution of 0 (mod p), since (pex) ![]() 0 (mod p) for 1 ≤ x < pe. Hence, the only selections that matter (modulo p) are those that take none or all the balls from a particular box. This means that we need to select bi boxes from a set of ai boxes from which to take all the balls, for 0 ≤ i ≤ k. The number of ways to do this is
0 (mod p) for 1 ≤ x < pe. Hence, the only selections that matter (modulo p) are those that take none or all the balls from a particular box. This means that we need to select bi boxes from a set of ai boxes from which to take all the balls, for 0 ≤ i ≤ k. The number of ways to do this is
![]()
Say that the base b representation of m dominates the base b representation of n if the former is greater than the latter in each place.
Corollary. The binomial coefficient ![]() is divisible by p if and only if the base p representation of n does not dominate the base p representation of k.
is divisible by p if and only if the base p representation of n does not dominate the base p representation of k.
 EXAMPLE 1.36
EXAMPLE 1.36
Is ![]() divisible by 7?
divisible by 7?
Solution: We have 59 = 1 · 72 + 1 > + 3 and 12 = 1 · 7 + 5. Since the base 7 representation of 59 does not dominate the base 7 representation of 12, we conclude that ![]() is divisible by 7.
is divisible by 7.
Here is a charming result about numbers in a row of Pascal’s triangle.
Erd![]() s and Szekeres theorem (1978). In a row of Pascal’s triangle, any two numbers other than the l’s have a common factor.
s and Szekeres theorem (1978). In a row of Pascal’s triangle, any two numbers other than the l’s have a common factor.
Proof. Suppose that the numbers are ![]() and
and ![]() , with 0 < j < k < n. Then, by the subcommittee identity.
, with 0 < j < k < n. Then, by the subcommittee identity.
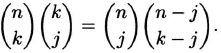
Obviously, ![]() divides the right side of this relation, so it also divides the left side.
divides the right side of this relation, so it also divides the left side.
However, if ![]() and
and ![]() were coprime, then
were coprime, then ![]() would divide
would divide ![]() , but this is impossible since
, but this is impossible since ![]() .
.
It is not known whether there are infinitely many Fibonacci numbers that are primes. There are infinitely many composite Fibonacci numbers, since every third Fibonacci number is even. We will show that there exist relatively prime positive integers a and b such that the Fibonacci-like sequence defined by the Fibonacci recurrence relation and the initial values a and b contains no prime numbers. Our sequence {an} is defined by
![]()
It follows by mathematical induction that
![]()
We define 17 quadruples of integers (pi, mi, ri, ci), where 1 ≤ i ≤ 17. These quadruples satisfy the following properties:
(1) each pi is prime;
(2)pi|Fmi;
(3) the congruences x ![]() ri (mod mi) cover all the integers, that is, given any integer n, one of the congruences is satisfied by n.
ri (mod mi) cover all the integers, that is, given any integer n, one of the congruences is satisfied by n.
The purpose of the ci is to control the size of a and b.
We define
![]()
Such a and b exist by the Chinese remainder theorem.
Chinese Remainder Theorem. If n1, n2,…,nk are pairwise relatively prime numbers, and r1, r2,…,rk are any integers, then there exists an integer x satisfying the simultaneous congruences

Furthermore, x is unique modulo n1n2 … nk.
It follows that
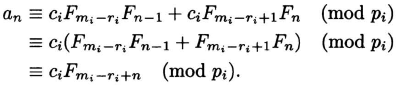
Since Fm | Fmn, we have pi | an.
The following collection of 17 quadruples was found by Maxim Vsemirnov:

Using the Chinese remainder theorem, we find
![]()
These are composite numbers with no common factor.
EXERCISES
![]()
Notes
Pascal’s triangle is named after the French mathematician Blaise Pascal (1623–1662), who introduced it in his work Trait du triangle arithmétique (Treatise on arithmetical triangle), in which he used the triangle to solve problems in probability. However, the triangle was known much earlier in various places around the world. The Indian mathematician Bhattotpala (c. 1068) gave the first sixteen rows of the triangle. In China, the triangle is called “Yanghui’s triangle,” named after the mathematician Yang Hui (1238–1298).
The inclusion–exclusion principle was first studied by D. A. da Silva in 1854. It was studied by James Sylvester (1814–1897) in 1883 and is sometimes referred to as Sylvester’s cross-classification principle.
Fibonacci (Leonardo of Pisa) introduced and discussed the Fibonacci numbers in his Liber Abaci (“Book of Calculations”) in 1202. Abraham de Moivre gave the explicit formula for the Fibonacci numbers in 1730.
Lucas numbers were first investigated by François Édouard Anatole Lucas (1842–1891).