CHAPTER 4
RAMSEY THEORY
The Erdös–Szekeres theorem and Dilworth’s lemma guarantee the existence of particular substructures of certain combinatorial configurations. Large disordered structures contain ordered substructures. We continue this theme by presenting two cornerstones of Ramsey theory: Ramsey’s theorem on graphs and van der Waerden’s theorem on arithmetic progressions. In the process we discuss related results, including Schur’s theorem on equations. We also investigate bounds and asymptotics of Ramsey numbers using techniques from number theory and probability. The central pursuit is always to find ordered substructures of large disordered structures. We want to find order in randomness.
4.1 Ramsey’s theorem
The following problem appeared in the 1953 William Lowell Putnam Mathematical Competition:
Six points are in general position in space (no three in a line, no four in a plane). The fifteen line segments joining them in pairs are drawn and then painted, some segments red, some blue. Prove that some triangle has all its sides the same color.
The description of the six points in general position and the segments joining them in pairs is just another way of defining the graph K6. We introduce a few more graph theory terms. A coloring of the set of edges of a graph G is a function f : E(G) → S, where S is a set of colors. A coloring partitions E(G) into color classes. If f is constant, then G is monochromatic.
Now we may rephrase the Putnam question as follows: If each edge of K6 is colored either red or blue, then there is a monochromatic subgraph K3 (a triangle). We note that the coloring may be done in an arbitrary manner. In fact, because K6 has ![]() = 15 edges, there are 215 possible red–blue colorings of the edges of K6. The claim is that every one of these 32,768 colorings yields a monochromatic K3. (We assume that the vertices of K6 are labeled, so we can distinguish between differently labeled isomorphic graphs, and that all 15 edges can be the same color, a possibility disallowed in the Putnam problem as stated.)
= 15 edges, there are 215 possible red–blue colorings of the edges of K6. The claim is that every one of these 32,768 colorings yields a monochromatic K3. (We assume that the vertices of K6 are labeled, so we can distinguish between differently labeled isomorphic graphs, and that all 15 edges can be the same color, a possibility disallowed in the Putnam problem as stated.)
Here is a simple solution to the problem using the pigeonhole principle. Choose any vertex v of K6. By the pigeonhole principle, some three of the five edges emanating from v are the same color. Without loss of generality, suppose v is joined by red edges to vertices x, y, z. If any of the edges xy, yz, or xz is red, then there is a red triangle (vxy, vyz, or vxz). However, if each of these edges is blue, then xyz is a blue triangle.
A special notation has been introduced to state results of this type. We write
(4.1) ![]()
to indicate that every 2-coloring of the edges of K6 yields a monochromatic K3. This relation may also be written
(4.2) ![]()
Similarly, we write
(4.3) ![]()
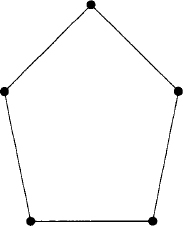
to say that there is a 2-coloring of K5 with no monochromatic K3. It is equivalent to say that there is a graph G on five vertices such that neither G nor ![]() contains a K3. Such a graph is exhibited in Figure 4.1.
contains a K3. Such a graph is exhibited in Figure 4.1.
Figure 4.1 A graph G such that neither G nor ![]() contains K3.
contains K3.
In general, we write
(4.4) ![]()
to indicate that every 2-coloring of the edges of Kn, yields a monochromatic Km. In 1930 F. Ramsey established the existence of such a Kn, for each m. Unlike the authors of the Putnam problem, we prefer green–red colorings to red–blue colorings.
Ramsey’s theorem (1930). Given a, b ≥ 2, there exists a least integer R(a,b) with the property that every green–red coloring of the edges of the complete graph on R(a,b) vertices yields a green Ka or a red Kb. Furthermore,
(4.5) ![]()
for all a, b ≥ 3.
Proof. We employ induction on a and b. The basis of the induction consists of the statements R(a, 2) = a and R(2, b) = b. These are trivial. In the first assertion, if we 2-color Ka and any edge is red, then we obtain a red K2, while if no edge is red, then we obtain a green Ka. Thus R(a, 2) ≤ a. Equality follows from the fact that an all-green-colored Ka−1 contains neither a green Ka nor a red K2. The second assertion is proved similarly. Now, assuming the existence of R(a – 1, b) and R(a, b – 1), we will show that R(a, b) exists. Let G be the complete graph on R(a – 1, b) + R(a, b – 1) vertices, and let v be an arbitrary vertex of G. By the pigeonhole principle, at least R(a – 1, b) green edges or at least R(a,b–1) red edges emanate from v. Without loss of generality, suppose that v is joined by green edges to a complete subgraph on R(a – 1, b) vertices. By definition of R(a – 1, b), this subgraph must contain a red Kb or a green Ka−1. In the latter case, the green Ka−1 and v, and all the edges between the two, constitute a green Ka. We have shown that G contains a green Ka or a red Kb. Therefore, R(a, b) exists and satisfies
![]()
The values of R(a, b) are called Ramsey numbers. Very few nontrivial Ramsey numbers (with a or b greater than 2) have been determined. The fact that we have proved that the Ramsey numbers exist but we do not know their values illustrates one disadvantage of existential proofs.
By definition, R(m, m) is the least positive integer n for which Kn → (Km)2. The values R(m, m) are called diagonal Ramsey numbers because they appear on the main diagonal of a table of Ramsey numbers. We know one diagonal Ramsey number already: R(3, 3) = 6.
We note that R(a, b) = R(b, a) for all a, b ≥ 2, as the roles of the two variables a and b are symmetric. Furthermore, we have noted that R(a, 2) = a for all a. We have already proved that R(3, 3) = 6, but a second proof is furnished by the two observations just made and the inequality R(a, b) ≤ R(a – 1, b) + R(a, b – 1). Thus, R(3, 3) ≤ R(3, 2) + R(2, 3) = 3 + 3 = 6. The lower bound R(3, 3) > 5 is verified by construction as before.
 EXAMPLE 4.1 Confusion graph
EXAMPLE 4.1 Confusion graph
The confusion graph is defined as follows. Suppose that the vertices of the 5-cycle C5 are a, b, c, d, e (in cyclic order) and these vertices represent symbols transmitted over a noisy channel. Adjacent symbols are said to be confusable; each is easily mistaken for the other. Nonadjacent symbols are not confusable. Thus, c and d are confusable while c and e are not. The independence number α(G) is the maximum number of nonconfusable symbols in V(G). It is easy to see that α(C5) = 2, as illustrated by the pair a, d. For two finite graphs G and H, we define a new graph called the strong product G ![]() H as the set V(G) × V(H), with (g, h) adjacent to (g’, h’) if and only if g is adjacent to or equal to g’ and h is adjacent to or equal to h’. We think of α(G
H as the set V(G) × V(H), with (g, h) adjacent to (g’, h’) if and only if g is adjacent to or equal to g’ and h is adjacent to or equal to h’. We think of α(G ![]() H) as the maximum number of nonconfusable ordered pairs in the set V (G) × V (H), where nonconfusability means nonconfusability in at least one coordinate. (We are assuming that a symbol is confusable with itself.)
H) as the maximum number of nonconfusable ordered pairs in the set V (G) × V (H), where nonconfusability means nonconfusability in at least one coordinate. (We are assuming that a symbol is confusable with itself.)
If A is a nonconfusable subset of V(G) and B is a nonconfusable subset of V(H), then A × B is a nonconfusable subset of V(G) × V (H). Therefore α(G)α(H) ≤ α(G ![]() H). Ramsey’s theorem furnishes a strict upper bound: α(G
H). Ramsey’s theorem furnishes a strict upper bound: α(G ![]() H) < R(α(G) + 1, α(H) + 1). For suppose the upper bound is attained by a subset A × B of V(G) × V(H). Color an edge green if there is nonconfusability in the first coordinate and red if there is nonconfusability in the second coordinate. (If nonconfusability holds in both coordinates, then we color the edge green.) Ramsey’s theorem guarantees that A has at least α (G) + 1 points or that B has at least α(H) + 1 points—both contradictions. Putting our lower and upper bounds together we obtain 4 = α(C5)2 ≤ α(C5)
H) < R(α(G) + 1, α(H) + 1). For suppose the upper bound is attained by a subset A × B of V(G) × V(H). Color an edge green if there is nonconfusability in the first coordinate and red if there is nonconfusability in the second coordinate. (If nonconfusability holds in both coordinates, then we color the edge green.) Ramsey’s theorem guarantees that A has at least α (G) + 1 points or that B has at least α(H) + 1 points—both contradictions. Putting our lower and upper bounds together we obtain 4 = α(C5)2 ≤ α(C5) ![]() C5) < R(α(C5) + 1, α(C5) + 1) = R(3, 3) = 6. Is the value of α(C5
C5) < R(α(C5) + 1, α(C5) + 1) = R(3, 3) = 6. Is the value of α(C5 ![]() C5) 4 or 5?
C5) 4 or 5?
EXERCISES
4.2 Generalizations of Ramsey’s theorem
What we can do with two colors, we can do with an arbitrary number, as the following generalization of Ramsey’s theorem shows. All the theorems of this section were proved by Frank Ramsey in the original 1930 paper. See Notes.
Ramsey’s theorem for multiple colors. For any c ≥ 2 and a1,…,ac ≥ 2, there exists a least integer R(a1,…,ac) with the following property: If the edges of the complete graph on R(a1,…,ac) vertices are partitioned into color classes A1,…,Ac, then for some i there exists a complete graph on ai, vertices all of whose edges are color Ai.
Proof. The case c = 2 is covered by our previous version of Ramsey’s theorem. Suppose R(a1,…,ac−1) exists for all a1,…,ac−1 ≥ 2. We claim R(a1,…,ac) exists and satisfies R(a1,…,ac) ≤ R(R(a1,…,ac−1), ac). A c-coloring of the complete graph on R(R(a1,…,ac−1, ac) vertices may be regarded as a 2-coloring with colors {A1,…,Ac−1} and Ac. Such a coloring contains a complete graph on ac vertices colored Ac or a (c – 1)-colored complete graph on R(a1,…,ac−1) vertices, in which case the induction hypothesis holds. In either case, we obtain a complete subgraph on the required number of vertices.?
 EXAMPLE 4.2
EXAMPLE 4.2
We use the c-color Ramsey theorem to prove a weak version of Dilworth’s lemma. Recall that Dilworth’s lemma states that every partial order on mn + 1 elements contains a chain of length m + 1 or an antichain of size n + 1. For k sufficiently large, we define a coloring of the complete graph on the vertex set X – {x1,…,xk} as follows: Assuming i < j, color edge xixj blue if xi and xj are incomparable; green if xi ≤ xj; and red if xi ≥ xj. (Some edges may be colored in two ways, but it won’t matter.) Now if k = R(n + 1, m + 1, m + 1), then we are guaranteed a blue Kn+1 (corresponding to an antichain of size n + 1), a green Km+1 (corresponding to a chain of xi with increasing subscripts), or a red Km+1 (corresponding to a chain of xi, with decreasing subscripts). Thus we have a weak version of Dilworth’s lemma. It is true that the best possible value mn + 1 has been replaced by the presumably much larger value R(n + 1, m + 1, m + 1). However, we have gained information about the increasing or decreasing nature of the subscripts of the xi. It would be unreasonable to expect that the best possible value mn + 1 would be obtained by this proof, because Dilworth’s lemma assumes a transitive relation while Ramsey’s theorem does not. Thus Ramsey’s theorem is more general than Dilworth’s lemma.
We write
(4.6) ![]()
to indicate that every c-coloring of Kn, yields a monochromatic Km. The c-color Ramsey numbers R(a1,…,ac) satisfy certain trivial relations, e.g., they are symmetric in the c variables. Furthermore, R(a1,…,ac−1, 2) = R(a1,…,ac−1) for all ai, because either there is an edge colored Ac, or else all edges are colored from the set {A1,…,Ac−1}.
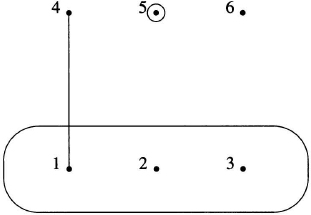
A hypergraph H of order n is a collection of nonempty subsets of an n-set S of vertices. The elements of H are called edges, corresponding to the graphical case in which edges are two-element subsets. A hypergraph is t-uniform if all edges have cardinality t. The complete t-uniform hypergraph of order n is the collection [S]t of all t-subsets of S. One may visualize and draw hypergraphs with edges represented by ovals (cardinality > 2), lines (cardinality = 2), and circles (cardinality = 1), as in Figure 4.2.
Figure 4.2 A hypergraph with edges {1,2,3}, {1,4}, and {5}.
It is now possible to state the most general version of Ramsey’s theorem in its natural hypergraph setting. We sometimes write [Nn]t as [n]t.
Ramsey’s theorem for hypergraphs. Let c ≥ 2 and a1,…,ac ≥ t ≥ 2. There exists a least integer R(a1,…,ac; t) with the following property: Every c-coloring of the complete t-uniform hypergraph [R(a1,…,ac;t)]t with colors A1,…,Ac yields a complete t-uniform hypergraph on ai vertices in color Ai, for some i.
Proof The generalization from 2-colorings to c-colorings works as it did in the generalization from the two-color to the c-color Ramsey theorem. We leave the argument as an exercise. We know that R(a1, a2; 2) exists for all a1, a2 ≥ 2. Let us assume that R(a1, a2; t – 1) exists for all a1, a2 ≥ 2 and that R(a1 – 1, a2; t) and R(a1, a2 – 1; t) exist. We claim that R(a1, a2; t) exists and satisfies R(a1, a2; t) ≤ n, where
![]()
Suppose [Nn]t has been green–red colored, and let v be one of its vertices. We generate an induced 2-coloring of [Nn – {v}]t–1 by assigning to each (t – 1)-set A of Nn – {v} the color which has been assigned to the t-set A ∪ {v}. By definition of n, we know that [Nn – {v}]t−1 contains a green ![]() or a red
or a red ![]() . Without loss of generality, suppose there is a green
. Without loss of generality, suppose there is a green ![]() on vertex set A. By definition, [A]t contains a red [a2]t or a green [a1 – 1]t. In the latter case, [A ∪ {v}]t contains a green [a1]t. We have shown that [Nn]t contains a green [a1]t or a red [a2]t, as required.
on vertex set A. By definition, [A]t contains a red [a2]t or a green [a1 – 1]t. In the latter case, [A ∪ {v}]t contains a green [a1]t. We have shown that [Nn]t contains a green [a1]t or a red [a2]t, as required.
An application of the theorem to convex sets occurs in the exercises. Now we discuss infinitary versions of the Ramsey theorems. We write
(4.7) ![]()
to indicate that every c-coloring of the complete countably infinite graph yields a monochromatic complete countably infinite subgraph. Similarly, in the hypergraph setting, the infinite t-uniform complete graph K.∞(t) consists of a countably infinite set and all possible t-element subsets. We write
(4.8) ![]()
to indicate that every c-coloring of the t-uniform complete infinite graph yields a monochromatic t-uniform complete infinite subgraph.
Ramsey’s theorem for infinite graphs. For every c ≥ 2, we have
![]()
Proof. Define f : N → {1,…,c} as follows. Let n = 1 and Xn, = V (K∞). Choose xn ![]() Xn, and let Ai = {v
Xn, and let Ai = {v ![]() Xn : edge vxn is color i}. By the infinitary pigeonhole principle, some Ai is infinite. Let Xn+1 = Ai, and define f(n) = i accordingly. Replace n by n + 1 and repeat this process.
Xn : edge vxn is color i}. By the infinitary pigeonhole principle, some Ai is infinite. Let Xn+1 = Ai, and define f(n) = i accordingly. Replace n by n + 1 and repeat this process.
This recursive procedure defines the function f. Some f−1 (j) is infinite and the complete graph on vertex set {xn : n ![]() f−1(j)} is monochromatic.
f−1(j)} is monochromatic.
Ramsey’s theorem for infinite hypergraphs. For every t ≥ 2, c ≥ 2, we have
![]()
The infinite hypergraph Ramsey theorem includes the infinite graph Ramsey theorem as a special case (when t = 2). The proof of the infinite hypergraph Ramsey theorem is left as an exercise.
We close this section by indicating how Ramsey’s theorem for infinite graphs implies Ramsey’s theorem for finite graphs. The technique for doing this, the “compactness principle,” is used throughout combinatorics. Assuming the truth of the infinite graph Ramsey theorem, we prove the finite graph Ramsey theorem by contradiction. Suppose that there exists a k for which R(k, k) does not exist. For each i ≥ k, let fi be a 2-coloring of Ki without a monochromatic Kk. We assume the Ki, are nested: Kk ![]() Kk+1
Kk+1 ![]() Kk+2
Kk+2 ![]() · · ·. By the infinitary pigeonhole principle, there exists an infinite subset of functions {fik}
· · ·. By the infinitary pigeonhole principle, there exists an infinite subset of functions {fik} ![]() (fi} which agree on Kk. Similarly, there is an infinite subset of functions {fik+1}
(fi} which agree on Kk. Similarly, there is an infinite subset of functions {fik+1} ![]() {fik} agreeing on Kk+i, etc. This process yields an infinite 2-coloring of K∞ without a monochromatic Kk, contradicting the infinite graph Ramsey theorem. Therefore, R(k, k) exists for each k, which implies that R(a1, a2) exists, since it must satisfy the inequality R(a1, a2) ≤ R(max{a1, a2}, max{a1, a2}). In the same manner, the finite hypergraph Ramsey theorem for an arbitrary number of colors is proven from the infinite hypergraph Ramsey theorem for an arbitrary number of colors.
{fik} agreeing on Kk+i, etc. This process yields an infinite 2-coloring of K∞ without a monochromatic Kk, contradicting the infinite graph Ramsey theorem. Therefore, R(k, k) exists for each k, which implies that R(a1, a2) exists, since it must satisfy the inequality R(a1, a2) ≤ R(max{a1, a2}, max{a1, a2}). In the same manner, the finite hypergraph Ramsey theorem for an arbitrary number of colors is proven from the infinite hypergraph Ramsey theorem for an arbitrary number of colors.
EXERCISES
4.3 Ramsey numbers, bounds, and asymptotics
Until now our results have been purely existential. We have shown that sufficiently large structures contain desired nonrandom substructures. But how large is sufficiently large? In general, this quantification question is extremely difficult, and unsolved problems abound. We present a few calculations and proofs in this section and summarize the scant amount of information known about Ramsey numbers.
We have already shown that R(3, 3) = 6. Let us try to evaluate the next more complicated Ramsey number, R(3, 4). To obtain an upper bound, we use the inequality R(a, b) ≤ R(a – 1, b) + R(a, b – 1). Thus R(3, 4) ≤ R(3, 3) + R(2, 4) = G + 4 = 10. However, R(3, 4) turns out to be 9, not 10. For suppose there is a green–red coloring of K9 which has no green K3 and no red K4. Because R(2, 4) = 4 and R(3, 3) = 6, each vertex must be incident with exactly three green edges and five red edges. But this means that the sum of the degrees of the vertices of the green subgraph is 9 · 3 = 27, contradicting the fact that the sum of degrees is always even (the Handshake Theorem). Hence R(3, 4) ≤ 9. In the exercises, the reader is asked to furnish a 2-coloring of K8 containing no green K3 and no red K4, thereby proving R(3, 4) = 9.
The Ramsey number R(3, 5) is evaluated easily: R(3, 5) ≤ R(3, 4) + R(2, 5) = 9 + 5 = 14. In the exercises, the reader is asked to find a 2-coloring of K13 that shows R(3, 5) > 13, thus establishing R(3, 5) = 14.
Next we determine R(4, 4). We have the upper bound R(4, 4) ≤ R(4, 3) + R(3, 4) = 9 + 9 = 18, and 18 turns out to be the value of R(4, 4). To prove this, we need a green-red coloring of K17 containing no monochromatic K4. In general, colorings which establish lower bounds tend to look locally random. However, they must contain quite a bit of structure so that they can be manipulated and analyzed. Such pseudorandom constructions are employed throughout combinatorics.
Let us assume that the vertices of K17 are labeled with the residue classes modulo 17: 0, 1, 2,…,16. An edge ij is colored green or red according to the quadratic character of i–j modulo 17. The 16 nonzero residues fall into two classes, quadratic residues and quadratic nonresidues. The set of quadratic residues modulo 17 is
![]()
the set of quadratic nonresidues is
![]()
Note that R17 is the range of the homomorphism f : Z*17 → Z*17, x ![]() x2. Both R17 and N17 are closed under multiplication by –1 (because –1 = 16
x2. Both R17 and N17 are closed under multiplication by –1 (because –1 = 16 ![]() R17), so i – j has the same quadratic character as j – i. Edge ij is colored green if i – j
R17), so i – j has the same quadratic character as j – i. Edge ij is colored green if i – j ![]() R17 and red if i – j
R17 and red if i – j ![]() N17. Suppose that there is a monochromatic K4 on vertices a, b, c, d. Note that the coloring is translation invariant: (i + k) – (j + k) = i – j. Therefore we may assume that a = 0. Multiply each vertex by b−1 (the multiplicative inverse of b), and note that either no edge changes color (if b
N17. Suppose that there is a monochromatic K4 on vertices a, b, c, d. Note that the coloring is translation invariant: (i + k) – (j + k) = i – j. Therefore we may assume that a = 0. Multiply each vertex by b−1 (the multiplicative inverse of b), and note that either no edge changes color (if b ![]() R17) or else every edge changes color (if b
R17) or else every edge changes color (if b ![]() N17). The reason for this is that b−1i–b−1j = b−1(i – j). In either case, we now have a monochromatic K4 on vertices 0, 1, cb−1, db−1. Now, because 1 is a quadratic residue, the other differences cb−1 db−1, cb−1 –1, db−1 –1, db−1 – cb−1 must be quadratic residues. Upon inspection of the elements of R17, we see that this is impossible. Therefore R(4, 4) > 17, and we conclude that R(4, 4) = 18.
N17). The reason for this is that b−1i–b−1j = b−1(i – j). In either case, we now have a monochromatic K4 on vertices 0, 1, cb−1, db−1. Now, because 1 is a quadratic residue, the other differences cb−1 db−1, cb−1 –1, db−1 –1, db−1 – cb−1 must be quadratic residues. Upon inspection of the elements of R17, we see that this is impossible. Therefore R(4, 4) > 17, and we conclude that R(4, 4) = 18.
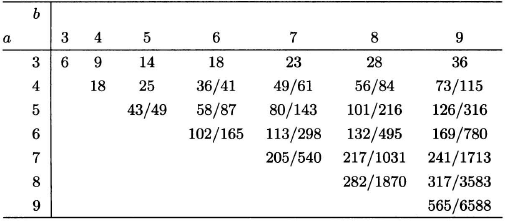
The other two-color Ramsey numbers R(a, b) are considerably more difficult to evaluate. The above construction involving quadratic residues was discovered in 1955 by R. E. Greenwood and A. M. Gleason. Although it gives the exact Ramsey number in the case of R(4, 4), the method gives only bounds for higher numbers. For example, using this technique one can show that 38 ≤ R(5, 5), but in fact other techniques have shown that 43 ≤ R(5, 5). We present all of the known nontrivial Ramsey numbers in Table 4.1. The notation l/u means that l and u are the best known lower and upper bounds for that particular Ramsey number. We refer readers to [11] and to the dynamic survey by S. Radziszowski found in the Electronic Journal of Combinatorics at http://www.combinatorics.org.
Table 4.1 Ramsey numbers R(a, b).
Open problem. Determine R(5, 5).
Open problem. Determine a formula for R(n, n).
We know that R(5, 5) ≤ R(4, 5) + R(5, 4) = 50. Unfortunately, this still leaves an enormous computation problem in evaluating R(5, 5). The naive approach, examining all 2![]() labeled graphs on 49 vertices, is intractable.
labeled graphs on 49 vertices, is intractable.
When we consider more than two colors, the only known nontrivial Ramsey number is R(3, 3, 3) = 17, whose proof we leave as an exercise. The only known nontrivial t-uniform hypergraph Ramsey number with t ≥ 3 is R(4, 4; 3) = 13. This state of limited knowledge is exasperating because Ramsey numbers are intimately connected with other numbers and functions, as we shall see later in this chapter. Any new Ramsey number would be very valuable.
Let us now consider lower and upper bounds for the diagonal Ramsey numbers R(a, a). The trivial lower bound R(a, a) > (a – 1)2 is immediate: join with green edges a – 1 disjoint copies of a red Ka−1; this coloring has no monochromatic Ka. A more sophisticated lower bound is obtained by the probabilistic method in the next section.
To find an upper bound we use Pascal’s identity. We recall that R(a, 2) = a for a ≥ 2 and R(a, b) ≤ R(a – 1, b) + R(a, b – 1) for a, b ≥ 3.
Upper bound for Ramsey numbers. For all a, b ≥ 2, we have R(a, b) ≤ ![]() .
.
Proof We use induction on a and b, noting that R(a, 2) = a = ![]() and R(2, b) = b =
and R(2, b) = b = ![]() , so the inequality holds when b = 2 or a = 2. Suppose that the inequality holds for R(a – 1, b) and R(a, b – 1) for a, b ≥ 3. Then
, so the inequality holds when b = 2 or a = 2. Suppose that the inequality holds for R(a – 1, b) and R(a, b – 1) for a, b ≥ 3. Then
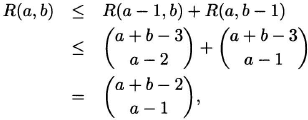
and the inequality is established.?
For diagonal Ramsey numbers, the upper bound becomes R(a, a) ≤ ![]() , and we can determine a asymptotic estimate. One of the great open problems of Ramsey theory is to calculate lima→∞ R(a, a)1/a (if it exists).
, and we can determine a asymptotic estimate. One of the great open problems of Ramsey theory is to calculate lima→∞ R(a, a)1/a (if it exists).
It follows that
(4.9) 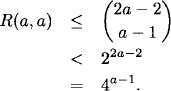
Thus, we obtain an asymptotic upper bound for R(a, a)1/a:
(4.10) ![]()
Using Stirling’s asymptotic approximation to the factorial function,
(4.11) ![]()
we can improve the upper bound a little. Since ![]() , and
, and
(4.12) ![]()
it follows that
![]()
where o(1) is a function of a which tends to 0 as a tends to ∞.
A lower bound for lim inf R(a, a)1/a is determined in the next section.
EXERCISES
4.4 The probabilistic method
To obtain a good lower bound for R(a, a), we turn to the probabilistic method, a technique used widely throughout existential combinatorics. See [2]. The idea is to turn the objects in question (green–red colorings of a graph) into events in a probability space and demonstrate that a desired event (a coloring containing no monochromatic subgraph of specified size) occurs with positive probability. If D is a set of desired objects in a sample space S, then the probability that a random object is desired equals Pr(D) = |D|/|S|. If we can show that Pr(D) is positive, then D is nonempty and there exists a desired object. Usually, probabilistic arguments can be framed directly in terms of the cardinalities |D| and |S|. However, the probabilistic language has undisputed bookkeeping and conceptual advantages in proving complex theorems. To illustrate the distinction and parallelism between the two points of view, we present two proofs of the following lower bound for R(a, a), one in terms of cardinality and the other in terms of probability.
Lower bound for Ramsey numbers. If ![]() < 1, then R(a, a) > n.
< 1, then R(a, a) > n.
Proof 1 (Cardinality). Because each of the ![]() edges of Kn may be colored independently, the number of green–red colorings is 2
edges of Kn may be colored independently, the number of green–red colorings is 2![]() . The number of green–red colorings of Kn, with a monochromatic Ka is |∪ AS|, where AS is the collection of green–red colorings in which the subgraph S is monochromatic and S ranges over all possible subgraphs of Kn isomorphic to Ka. We bound |∪AS| as follows:
. The number of green–red colorings of Kn, with a monochromatic Ka is |∪ AS|, where AS is the collection of green–red colorings in which the subgraph S is monochromatic and S ranges over all possible subgraphs of Kn isomorphic to Ka. We bound |∪AS| as follows:
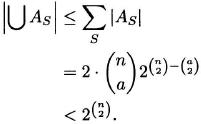
The first inequality is an enumeration estimate proved by induction on the number of terms in the union; it also follows from the inclusion–exclusion principle. The equality follows from the observation that there are ![]() copies of Ka inside Kn. Since each Ka is monochromatic, there are two choices for the color of its edges. The remaining
copies of Ka inside Kn. Since each Ka is monochromatic, there are two choices for the color of its edges. The remaining ![]() edges of Kn are colored green or red arbitrarily.
edges of Kn are colored green or red arbitrarily.
Now, because |∪AS| is less than the total number of green–red colorings of Kn, there is a coloring which does not contain a monochromatic Ka. Therefore R(a, a) > n.
Proof 2 (Probability). Suppose the edges of Kn, are randomly and independently colored green or red. Think of flipping a coin for each edge. If the coin lands heads, then the edge is colored green; if it lands tails, then red. For each subgraph S of Kn isomorphic to Ka, let AS be the event that S is monochromatic. We have
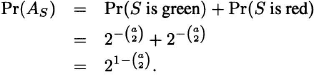
Therefore
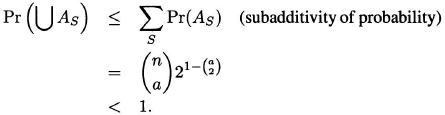
The complement of the event ∪ AS occurs with positive probability; hence there exists a desired configuration–a 2-coloring of Kn, with no monochromatic Ka. Again, R(a, a) > n.
The theorem contains an implicit lower bound for R(a, a), if we can untangle it. Fix a and let N be the minimum value of n satisfying ![]() 21–
21–![]() ≥ 1. Then
≥ 1. Then
(4.13) 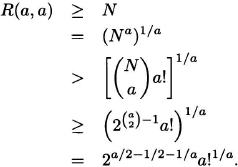
From Stirling’s asymptotic formula for the factorial function, it follows that
(4.14) ![]()
Finally, we have
(4.15) 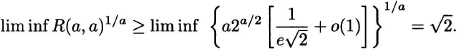
Combining this lower bound with our previously obtained upper bound, we obtain bounds on lima→∞ R(a, a)1/a (if it exists):
(4.16) ![]()
These are the best bounds known at present.
Open problem Determine whether lima→∞ R(a, a)1/a exists and find its value.
In 1995 J. H. Kim proved the first conclusive result about the growth of R(n, k) for fixed k. He showed that the order of magnitude of R(n, 3) is n2/logn. See [6].
Open problem. Determine the asymptotic behavior of R(n, 4).
EXERCISES
4.5 Schur’s theorem
In this section, we prove a proposition about equations as a corollary of Ramsey’s theorem, and in the next section we prove van der Waerden’s theorem, an elegant statement about arithmetic progressions. The theme is that of finding order in disorder.
Given c, n ≥ 1, we consider functions f : Nn → {A1,…,Ac}. As usual, we think of the Ai, as colors and f as assigning a color to each integer, thereby partitioning Nn into color classes. If S is a set of positive integers and f restricted to S is a constant function, then S is monochromatic. What kinds of monochromatic sets can we find given that n is large enough compared to c? One answer to this question was provided by Issai Schur (1875–1941) in 1916.
Schur’s theorem. For each c ≥ 1, there exists a least integer n = S(c) with the following property: For any function f : Nn → {A1,…,Ac}, there exists an Ai, containing x, y, z (with x = y allowed) such that x + y = z. In other words, there is a monochromatic solution to the equation x + y = z.
Proof. Let m = R(3,…,3) – 1, where R(3,…,3) is the c-color Ramsey number that guarantees a monochromatic triangle. We claim that m has the desired property, and hence S(c) exists and satisfies S(c) ≤ m. The function f : Nm → {A1,…,Ac} generates a c-coloring of the complete graph on vertices 1, 2,…,m + 1 by assigning to edge ij the color that has been assigned to the integer |i – j|. The presence of a monochromatic triangle on, say, vertices a, b, c (a < b < c) implies that the equation x + y = z has the monochromatic solution (b – a) + (c – b) = (c – a).
Although it is considered an important part of Ramsey theory, Schur’s theorem was introduced by Schur in an attempt to prove Fermat’s last theorem. See Notes.
The integers S(c) are called c-color Schur numbers. It is trivial to observe that S(1) = 2 (1 + 1 = 2). We leave it to the reader to check that S(2) = 5 and S(3) = 14. The only other known Schur number is S(4) = 45. Thus there is a general state of ignorance about Schur numbers, although they are linked to the equally mysterious Ramsey numbers by the inequality
(4.17) ![]()
Open problem. Find the value of S(5).
EXERCISES
4.6 Van der Waerden’s theorem
Schur’s theorem states that any coloring function f : Nn → {A1,…,Ac} forces a monochromatic solution to the equation x + y = z (whenever n is sufficiently large compared to c). What other monochromatic structures are forced? One direction for generalization is provided by Rado’s theorem, which asserts the existence of a monochromatic solution to the equation
![]()
as long as some nonempty subset of the αi, sums to 0. If this condition is met, we say that the equation is regular. For example, the equation 2x1 – 7x2 + 3x3 + 4x4 – 6x5 = 0 is regular (–7 + 3 + 4 = 0). Another direction is provided by B. L. van der Waerden’s 1927 theorem concerning arithmetic progressions. An arithmetic progression of length l (or l-AP) is a sequence
![]()
of l numbers (integers, say), where each consecutive pair differ by a constant number d ≥ 1. For example, the sequence 20, 30, 40, 50, 60, 70 is a 6-AP. Van der Waerden’s theorem asserts the existence of a monochromatic l-AP when Nn, is partitioned into c classes (and n is sufficiently large with respect to c and l).
Van der Waerden’s theorem (1927). Given c ≥ 1 and l ≥ 1, there exists a least integer W = W (c, l) with the following property: If Nw is partitioned into c classes A1,…,Ac, then one of the classes Ai contains a monochromatic l-AP.
Proof. The proof is by induction on c and l. In this proof, we use the notation [n] for Nn. The theorem is trivially true for some ordered pairs c, l, and in these cases we can actually determine the values of W(c, l): W (1, l) = l, W(c, 1) = 1, W (c, 2) = c+ 1. The first and third of these statements are the basis of the induction. We shall assume the existence of W(d, l) for every d and prove the existence of W(c, l + 1). The reader is encouraged to envision a table of c and l, and judge whether this plan would really cover all ordered pairs c, l. We claim that W(c, l + 1) exists and satisfies W(c, l + 1) ≤ f (c), where f is defined recursively:
(4.18) ![]()
As in the proof of Ramsey’s theorem, we are establishing an existence result by constructing an upper bound. However, the formulas in the upper bound grow too rapidly to furnish much insight into the exact values of W(c, l).
Suppose that [f (c)], which we call a c-block, is c-colored without a monochromatic l + 1-AP, and [f(c)] is partitioned into f(c)/f(c – 1) blocks of f (c – 1) consecutive integers, which we call (c – 1)-blocks. Likewise, each (c – 1)-block is partitioned into f (c – 1)/f(c – 2) blocks of f(c – 2) consecutive integers, which we call (c – 2)-blocks. This partitioning happens at each of the c levels, until, at last, each 1-block is partitioned into 2W (c, l) 0-blocks (which are just integers).
By definition of W(c, l), the first half of each 1-block contains a monochromatic l-AR Here occurs the first leap of inspiration in the proof. The coloring of the elements of a 1-block induces a coloring of the 1-block itself. That is, we assign one of cf(1) colors to the 1-block according to the way its elements are c-colored. Because f(2) = 2W(cf(1), l)f(1), each 2-block contains 2W(cf(1), l) 1-blocks, so that, by definition of W(cf(1), l), the first half of each 2-block contains a monochromatic l-AP of 1-blocks. Similarly, the first half of each 3-block contains a monochromatic l-AP of 2-blocks. This construction happens at each level, so that the first half of [f (c + 1)] contains a monochromatic l-AP of c-blocks. Let us consider only those integers which lie in l-APs at all c levels of blocks. We coordinatize each integer as
![]()
with 1 ≤ xi ≤ l, where xi is the position of x in the monochromatic l-AP of the i-block in which it resides. All coordinatized integers have the same color, say A1. Within each 1-block, the 1 integers
![]()
constitute a monochromatic l-AP. Therefore, the integer (l + 1, x2,…,xc) has a color other than A1, say A2. Furthermore, the factor 2 in the definition of f(1) implies that (l + 1, x2,…,xc) occurs within the 1-block. (The 2 is a convenient constant used to stretch the block enough to accommodate the (l + 1)st term of an AP.) Here occurs the second leap of inspiration: the idea of focusing. Within a 2-block, the l integers
![]()
are a monochromatic l-AP of color A2. This forces (l + 1,l + 1, x3,…,xc) to be a color other than A2. However, we can focus a second l-AP on this integer, namely,
![]()
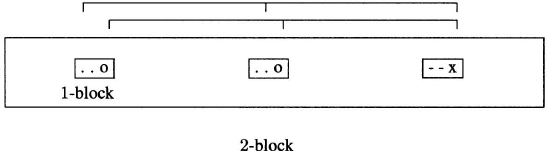
Thus, (l + 1,l + 1, x3,…,xc) cannot be color A1 or A2; say it is colored A3. Figure 4.3 illustrates the two focused progressions, representing colors A1, A2, A3 by dots, circles, and an x, respectively. (The dashes represent numbers with undetermined colors.) Continuing this focusing process at each of the c levels, we conclude that (l + 1,l + 1,…,l + 1) can be none of the colors A1,…,Ac, a contradiction. Therefore, there exists a monochromatic (l + 1)-AP.
Figure 4.3 Two 3-APs focusing on an integer.
The values of W(c, l) are called Van der Waerden numbers. As we remarked in the proof, the inequality W(c, l + 1) ≤ f (c) does little to establish good estimates for them. In fact, the state of knowledge is even worse for van der Waerden numbers than for Ramsey numbers. The seven known nontrivial van der Waerden numbers are listed in Table 4.2. The proof of one of these values, W(2, 3) = 9, is called for in the exercises.
Table 4.2 The known van der Waerden numbers W(c, l) with c ≥ 2, l ≥ 3.
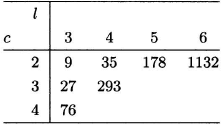
Open problem. Find W(5, 3).
Although van der Waerden’s theorem asserts the existence of a monochromatic l-AP, it does not tell us which color it is. The following theorem, whose proof is beyond the scope of this book, guarantees the existence of a monochromatic l-AP in any color that occurs “with positive density.” We define the density function of a set S of positive integers to be
(4.19) ![]()
The density function measures the fraction of the first n integers which occur in S. Clearly, 0 ≤ d(S, n) ≤ 1 for all S and n.
Szemerédi’s theorem. For all real numbers d > 0 and all l ≥ 1, there is a positive integer N(d, l) with the following property: If n ≥ N(d, l) and S ![]() {1,…,n} with d(S, n) ≥ d, then S contains an l-AP.
{1,…,n} with d(S, n) ≥ d, then S contains an l-AP.
Paul Erd![]() s (1913–1996) conjectured the above result in 1935, but it was not proved until 1975 by Endre Szemerédi. In 1977 Hillel Furstenberg gave a proof using ergodic theory.
s (1913–1996) conjectured the above result in 1935, but it was not proved until 1975 by Endre Szemerédi. In 1977 Hillel Furstenberg gave a proof using ergodic theory.
Conjecture. (Erd![]() s) If {ai}
s) If {ai} ![]() N and
N and ![]() is a divergent series, then {ai} contains arbitrarily long arithmetic progressions.
is a divergent series, then {ai} contains arbitrarily long arithmetic progressions.
It is well known that Σ 1/pi diverges if {pi} is the set of primes (see [15]), and in 2006 Ben Green and Terence Tao proved that there exist arbitrarily long arithmetic progressions of primes. Erdős’ conjecture is still open. In 2010 a 26-AP of primes was found:
![]()
EXERCISES
![]()
![]()
![]()
![]()
Notes
For original papers of Frank Ramsey, Paul Erd![]() s and George Szekeres, and R. P. Dilworth, see [9].
s and George Szekeres, and R. P. Dilworth, see [9].
Ramsey numbers have been generalized in many ways. For example, in 1972 Václav Chvátal and Frank Harary defined the graph Ramsey number r(G, H) to be the minimum number of vertices in a complete graph which, when 2-colored, yields a green subgraph G or a red subgraph H. They showed that
![]()
where χ(G) is the chromatic number of G and p(H) is the number of vertices of H. They used this inequality to prove r(Tm, Kn) = (m – 1)(n – 1) + 1, where Tm is a tree with m vertices. See [11].
Schur’s theorem was proven by Issai Schur in an attempt to prove Fermat’s last theorem (FLT). Although Schur didn’t prove FLT, he did prove that, for all n, if p is prime and sufficiently large, then the congruence xn + yn ![]() zn has a nonzero solution modulo p. Briefly, the argument is to suppose that p is prime and greater than S(n). Thus if { 1,…,p – 1} is n-colored, there exists a monochromatic subset {a, b, c} with a + b = c. Let H = {xn : x
zn has a nonzero solution modulo p. Briefly, the argument is to suppose that p is prime and greater than S(n). Thus if { 1,…,p – 1} is n-colored, there exists a monochromatic subset {a, b, c} with a + b = c. Let H = {xn : x ![]() Z*p}, a subgroup of Z*p of index gcd(n, p – 1) ≤ n. The cosets of Z*p define an n-coloring f of Z*p such that f (a) = f (b) = f (c) and a + b = c. This implies that 1 + a−1b = a−1c = (in Zp), and in fact 1, a−1b, and a−1c are all nth powers in Zp.
Z*p}, a subgroup of Z*p of index gcd(n, p – 1) ≤ n. The cosets of Z*p define an n-coloring f of Z*p such that f (a) = f (b) = f (c) and a + b = c. This implies that 1 + a−1b = a−1c = (in Zp), and in fact 1, a−1b, and a−1c are all nth powers in Zp.
B. L. van der Waerden (1903–1996) proved his 1927 theorem as a generalization of the following conjecture of Schur: If N is partitioned into two classes, then one of the classes contains arbitrarily long arithmetic progressions.
Ramsey’s theorem (in its various formulations) and van der Waerden’s theorem are usually thought of as the two cornerstone theorems of Ramsey theory. See [11] for a further discussion of these theorems and other theorems of Ramsey theory, including Gallai’s theorem, Rado’s theorem, Folkman’s theorem, and the Hales–Jewett theorem.
