EXERCISE SOLUTIONS
SOLUTIONS FOR CHAPTER 1
1.5 There are 299 binary strings of length 99. Half of these, 298, have an odd number of 1′s. The reason is that, regardless of the first 98 bits, the last bit may be chosen to make the total number of 1′s even or odd.
1.7 There are nn such functions.
1.17 There are 2n2 different binary relations on an n-set.
1.20 Since the tenth row of Pascal’s triangle is 1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1, we have (a + b)10 = a10 + 10a9b + 45a8b2 + 120a7b3+210a6b4 + 252a5b5 + 210a4b6 + 120a3b7 + 45a2b8 + 10ab9 + b10.
1.21 By the binomial theorem, the coefficient is 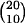 = 184,756.
= 184,756.
1.25 By the multinomial theorem, (a + b + c)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 + 4a3c 12a2bc + 12ab2c + 4b3c + 6a2c2 + 12abc2 + 6b2c2 + 4ac3 + 4bc3 + c4.
1.26 By the multinomial theorem, the coefficient is 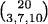 = 22,170,720.
= 22,170,720.
1.27 By simplifying, we see that
1.30 (a) The number of paths is 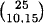 = 3,268,760.
= 3,268,760.
(b) The number of paths is 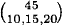 = 10,361,546,974,682,663,760.
= 10,361,546,974,682,663,760.
1.32 The identity to prove is equivalent to
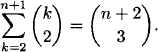
The right side is the number of selections of three distinct elements from the set {1,…,n + 2}. Let the largest such element be k + 1, where 2 ≤ k ≤ n + 1. Then, for each k, the other two elements must be selected from the set {1,…,k}, and the number of ways to do this is  . The left side counts these selections for all k.
. The left side counts these selections for all k.
1.45 Clearly, S0(n) = n. The formula for S1 (n) can be obtained by noting that 2S1(n) = (n + 1)n and hence S1 (n) = n(n + 1)/2. To find S2(n) and S3(n), we use the following technique. The sum Σni=1[(i + 1)k+1 – ik+1] is a telescoping series. Hence
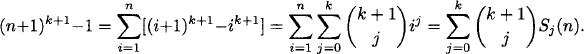
Therefore
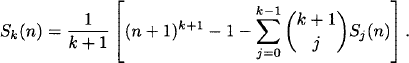
Now we find
![]()
and
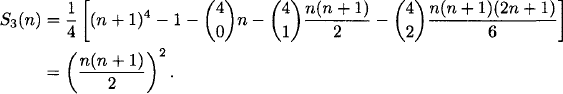
The fact that Sk(n) is a monic polynomial in n of degree k + 1 is clear from our method.
1.46 A k-dimensional face of an n-dimensional hypercube is a subset of the 2n vertices of the cube isomorphic to a k-dimensional hypercube. There are 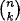 choices for the coordinates on which to base the face. The other coordinates can be 0 or 1.
choices for the coordinates on which to base the face. The other coordinates can be 0 or 1.
1.47 The total number of pizzas is
![]()
1.49 (a) The number of such functions is  .
.
(b) The number of such functions is 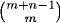 .
.
1.50 We have 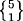 = 1, =
= 1, = 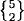 = 15,
= 15, 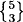 = 25,
= 25, 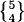 = 10,
= 10, 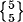 = 1, and B(5) = 52.
= 1, and B(5) = 52.
1.52 The formula 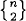 = 2n−1 – 1 holds since any subset of {1, 2, 3,…,n – 1}, except the set itself, together with n, constitutes a part in a partition of {1, 2, 3,…,n} into two subsets. The formula
= 2n−1 – 1 holds since any subset of {1, 2, 3,…,n – 1}, except the set itself, together with n, constitutes a part in a partition of {1, 2, 3,…,n} into two subsets. The formula 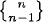 =
= 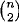 for n ≥ 2 holds since in a partition of {1, 2, 3,…,n} into n – 1 parts, the element n is in any one of n – 1 parts and there are
for n ≥ 2 holds since in a partition of {1, 2, 3,…,n} into n – 1 parts, the element n is in any one of n – 1 parts and there are 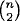 choices for which part it is in.
choices for which part it is in.
1.53 There are 1030/4 + 1 choices for z, namely, all the integers from 0 to 1030/4. Among these choices, the average value of 4z is 1030/2. Hence, on average, x+2y = 1030/2. There are 1030/4 + 1 values of y that satisfy this equation, namely, the integers from 0 to 1030/2. Once z and y are chosen, the value of x is determined. Therefore, the total number of nonnegative integer solutions is
![]()
1.56 (a) Let S be the set of functions from {1, 2, 3,…,m} to {1, 2, 3,…,n}. Then S has cardinality nm. We wish to find the cardinality of the subset of S consisting of all onto functions. For 1 ≤ i ≤ n, let Ai be the collection of functions whose range does not contain i. Then the intersection of j of the Ai has cardinality (n – j)m, the number of unrestricted functions from {1, 2, 3,…,m} to the n – j nonexcluded elements of {1, 2, 3,…,n}. Applying the inclusion–exclusion principle, we obtain
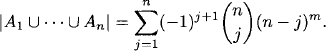
The number of onto functions is the complement of this union:
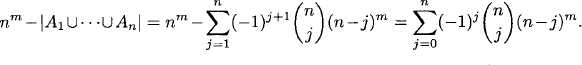
(b) From (a), we obtain
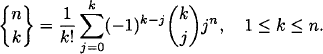
1.60 We take successive differences:
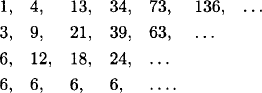
Having obtained a constant sequence, we stop. We find that the polynomial is
![]()
1.61 We can think of a pair of linked sets (A, B) as an onto function from S to the set {A, B, A ∩ B} or to the set 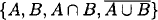 . So the total number of pairs of linked sets is T(n, 3) + T(n, 4).
. So the total number of pairs of linked sets is T(n, 3) + T(n, 4).
1.65 The Fibonacci numbers are sums of “shallow triangles” of Pascal’s triangle:
![]()
We prove the identity by induction. For n = 0, we have
![]()
Assume that the identity holds for n and n – 1. Then
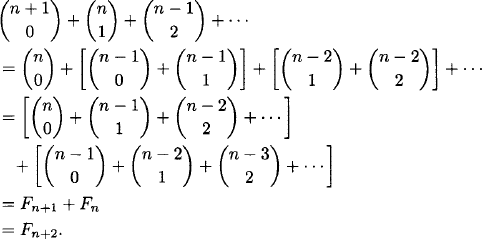
Hence, the identity holds for n + 1 and by induction for all n.
1.68 The number 210 occurs six times in Pascal’s triangle:
![]()
1.74 A particular solution to the recurrence relation is an = -n –3. Hence, the general solution is of the form
![]()
We need to choose A and B so that the initial values are satisfied. Thus
![]()
We find that A = (15 + 7√5)/10 and B = (15 – 7√5)/10.
1.86 We have 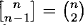 , as this counts the ways of choosing two elements to be in the same cycle.
, as this counts the ways of choosing two elements to be in the same cycle.
1.88 In a partition of n + 1 elements, the (n + 1)st element is together with n – k other elements for some k with 0 ≤ k ≤ n. There are 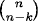 choices for these n – k elements. Hence
choices for these n – k elements. Hence
![]()
1.89 From the recurrence relation for Stirling numbers of the second kind,
![]()
and hence
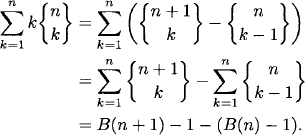
Therefore, the expected number of parts is
![]()
1.90 Upon the substitutions k → –n + 1 and n → –k + 1, the recurrence relation (1.32) becomes the recurrence relation (1.33).
1.91 The relation follows by subtracting 1 from each part in the partition of n into k parts.
1.107 Obviously, Fm|Fm. Applying the identity
![]()
(Exercise 1.64 with n = m), we obtain
![]()
and hence Fm|F2m. Similarly, with n = 2m, we obtain
![]()
and hence Fm |F3m. Continuing in this manner, we find that Fm | Fkm for all k ≥ 1.
Now suppose that n = mk + r, with 0 ≤ r < m. Then, applying the identity again, we obtain
![]()
If Fm | Fn, then, since Fm | Fmk, it follows that Fm | Fmk-+1 Fr. But consecutive Fibonacci numbers are coprime, and so Fm and Fmk+1 are coprime. Hence Fm | Fr, but this is possible only if r = 0 (since Fm > Fr). Therefore m | n.
1.108 Since gcd(a, b) | a, it follows from the previous exercise that Fgcd(a,b) | Fa. Likewise, Fgcd(a,b) | Fb. Hence Fgcd(a,b) | gcd(Fa, Fb).
There exist integers x and y such that gcd(a, b) = ax + by. Without loss of generality, assume that x is negative and y is positive (they cannot both be positive). Hence
![]()
By the identity of the previous exercise,
![]()
Thus, Fgcd(a,b)Fa(–x)+1 is a linear combination of Fa and Fb and hence divisible by gcd(Fa, Fb). Since Fa and Fa(–x)+1 are relatively prime, it follows that gcd(Fa, Fb) | Fgcd(a,b).
Therefore Fgcd(a,b) = gcd(Fa, Fb).
SOLUTIONS FOR CHAPTER 2
2.1 The sum is
![]()
2.4 The generating function is x(x((1 – x)−1)’)’ = x(x + 1)(1 – x)−3.
2.12 A recurrence formula is a0 = 1, a1 = –3, and an = –3an−1 – an–2 for n ≥ 2. Notice that an = (–1)nF2n+2.
2.14 The identity follows upon summing f(x), with x replaced by ωjx and weighted by ω−jp for 0 ≤ j ≤ q – 1, using the relation 1 + ω + ω2 + · · · + ωq – 1 = 0.
2.17 We can find a simple formula for t(n) where n has any given remainder upon division by 12. Thus
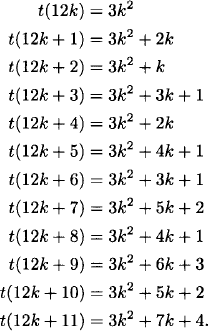
Since these formula are all quadratic polynomials, t(n) satisfies the recurrence relation
![]()
The desired recurrence relation follows immediately.
2.19 First, we prove that the period of {t(n) mod m} is at most 12m. If n is even, we may write n = 12m + 2r and we have
![]()
Here, {x} denotes the nearest integer to x. The odd case is similar; it follows that t(12m+u)  t(u) mod m for all u. Hence, the period of {t(n) mod m} is a divisor of 12m (and therefore at most 12m).
t(u) mod m for all u. Hence, the period of {t(n) mod m} is a divisor of 12m (and therefore at most 12m).
Second, we show that the period of {t(n) mod m} is at most 12m.
Suppose that the period is p, and let k = p or p – 1 so that k is even. We then have {k2/48} = 0 (mod m) and {(k + 2)2/48} = 0 (mod m) since t(–1) = t(0) = t(1) = t(2) = 0. Thus m divides {(k + 2)2/48} – {k2/48} which is nonzero because p > 12. This difference is less than (k + 2)2/48k2/48 + 1, which implies that 12m < k + 13 ≤ p + 13, thus completing the proof since 12m is a multiple of p and p > 12.
2.21 We will prove the result by induction on n. The claim is true for n = 0 since C0 = 1 and 0 = 21 – 1. Assume that the claim holds for all Catalan numbers up to Cn. Now consider Cn+1. If n + 1 is even, then
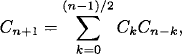
which is even. If n + 1 is odd, then
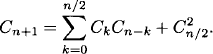
So Cm+1 is odd if and only if Cn/2 is odd. By the induction hypothesis, this means that n/2 = 2k – 1, for some integer k. Thus, Cn is odd if and only if
![]()
By mathematical induction, the claim holds for all nonnegative integers n.
2.22 From the recurrence relation Cn = 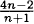 Cn–1, we have
Cn–1, we have
![]()
If n  2 (mod 3), then Cn
2 (mod 3), then Cn  Cn–1 (mod 3). Letting n = 3k, we have C3k
Cn–1 (mod 3). Letting n = 3k, we have C3k  C3k−1 (mod 3). Letting n = 3k + 1, we have C3k+1
C3k−1 (mod 3). Letting n = 3k + 1, we have C3k+1 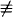 C3k (mod 3). Therefore
C3k (mod 3). Therefore
![]()
2.27 Clearly, the formula holds for n = 0 and n = 1. Assume that it holds for n. Then
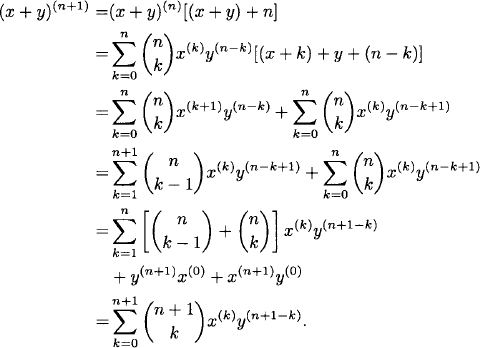
Thus, the formula holds for n + 1 and hence for all n by induction.
The proof of the formula for (x + y)(n) is similar.
2.31 There are 48,639 such walks. It is easy to generate an 8 × 8 table by starting with 1 at a1 and at each cell adding the left, lower, and lower-left neighbors. This produces the Delannoy numbers. The main diagonal Delannoy numbers are 1, 3, 13, 63, 321, 1683, 8989, 48639.
2.32 A recurrence relation is
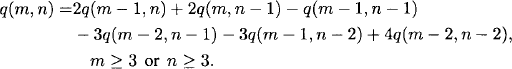
The initial values are
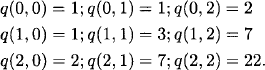
The corresponding generating function is
![]()
2.43 For x 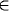 X, let Nx (neighborhood) be the intersection of all sets in S that contain x. Since S is closed under unions and complements, it is closed under intersections. Hence Nx
X, let Nx (neighborhood) be the intersection of all sets in S that contain x. Since S is closed under unions and complements, it is closed under intersections. Hence Nx 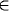 S. The sets Nx partition X. Therefore, the number of algebras is equal to the number of partitions of X. (a) If X is labeled, then the number is B(n). (b) If X is unlabeled, then the number is p(n).
S. The sets Nx partition X. Therefore, the number of algebras is equal to the number of partitions of X. (a) If X is labeled, then the number is B(n). (b) If X is unlabeled, then the number is p(n).
2.44 The number of functions is nn. Given any element x 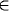 {1,…,n}, there are (n–1)n functions that do not include x in their range. Altogether, there are n(n–1)n of these elements x (with multiplicity). Hence
{1,…,n}, there are (n–1)n functions that do not include x in their range. Altogether, there are n(n–1)n of these elements x (with multiplicity). Hence
![]()
and so
![]()
2.52 There are 3210 such necklaces.
2.56 From the generating function in Example 2.22, we see that there are 16 circular necklaces with five white beads and five black beads.
2.63 There are 34 nonisomorphic graphs of order 5.
2.69 (a) We will show that the coefficients of 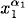 · · ·
· · · 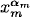 in both expressions are equal. Let k = 1α1 + · · · + mαm and αm+1 = · · · = αk = 0. In the expression on the left, the contribution to
in both expressions are equal. Let k = 1α1 + · · · + mαm and αm+1 = · · · = αk = 0. In the expression on the left, the contribution to 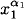 · · ·
· · · 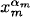 comes from the n = k term, which is
comes from the n = k term, which is
![]()
In the expression on the right, the factor 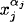 comes from the
comes from the 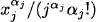 term in the jth factor of exp
term in the jth factor of exp 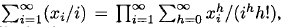 for j = 1, · · · m. Hence, the overall contribution is
for j = 1, · · · m. Hence, the overall contribution is
![]()
2.70 There are two such graphs of order 5 and none of order 6. A self-complementary graph of order n > 1 has n(n – 1)/4 edges. For this to be an integer, n must be of the form 4k or k + 1.
2.74 It is approximately 1.3 × 101332.
SOLUTIONS FOR CHAPTER 3
3.1 By the pigeonhole principle, there exist m and n, with m < n, such that 17m 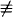 17n (mod 104). Since gcd(17, 104) = 1, we have 17n–m
17n (mod 104). Since gcd(17, 104) = 1, we have 17n–m 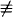 1 (mod 104).
1 (mod 104).
We can actually find such an exponent using Euler’s theorem: aϕ(m) 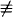 1 (mod m) if gcd(a, m) = 1. The furnished exponent is ϕ(104) = 4000.
1 (mod m) if gcd(a, m) = 1. The furnished exponent is ϕ(104) = 4000.
3.3 To show that this result is the best possible, let S = {1,…,100} and take A1 to be any subset of S with 67 elements. Let the other Ai be cyclic shifts of A1. In this system of sets, each x 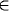 S is contained in exactly 67 of the Ai.
S is contained in exactly 67 of the Ai.
3.23 Let G1 consist of three disjoint copies of K4 and G2 be G with one edge added.
3.24 If α(G) and χ(G) were both finite, then the number of vertices in G would be bounded by their product (a finite number). Since the number of vertices is infinite, at least one of α(G) and χ(G) is infinite.
3.25 Given any two vertices x and y of G, the degree conditions imply that x and y have a common neighbor z, and hence there is a path from x to y. Therefore G is connected.
3.26 Suppose that the longest path contained in G had fewer than n vertices. Then, choosing any two consecutive vertices in the path, say, x and y, the degree condition implies that x and y have a common neighbor z. Using z, we can make a longer path. Hence, the longest path in G has n vertices. The same type of argument allows us to close the path to make a cycle of length n.
3.27 The result follows by mathematical induction. Removing an end vertex and its incident edge from the graph amounts to subtracting 1 from both sides of the relation p = q+1. Continue this process until the graph contains only one vertex; the relation certainly holds for this graph.
3.33 Take n disjoint copies of a total order on m elements.
SOLUTIONS FOR CHAPTER 4
4.2 We can take f(n) = R(n, n). Number the vertices 1, 2,…,f(n), and color the edge {i, j}, where i < j, green if i is directed to j, and red otherwise. Ramsey’s theorem guarantees a monochromatic subgraph Kn. The corresponding directed subgraph is a transitive subtournament.
4.10 Take G = K∞, ∞ ∞. Call the parts of the tripartite graph A, B, and C. Color all edges between A and B green and all other edges red.
4.11 Let the graph be the cycle C8 together with all four diagonals.
4.13 Given a 3-coloring of K17, let v be any vertex. There are 16 edges incident with v. By the pigeonhole principle, at least six of these edges are the same color, say, green. Suppose that v is incident to vertices x1, x2, x3, x4, x5, x6 by green edges. If any edge {xi, xj} is green, then we have a green K3. If not, then we have a red K3 or a blue K3 (since R(3, 3) = 6). To finish the argument, show a 3-coloring of K16 with no monochromatic triangle.
4.15 From the probabilistic method, we obtain the lower bound 3.0038 × 1016.
4.23 False. Take one part to be the union of {1}, {3, 4}, {7, 8, 9}, {13, 14, 15, 16}, etc.
4.26 An example of a 6-AP of primes is 7, 37, 67, 97, 127, 157.
SOLUTIONS FOR CHAPTER 5
5.1 The contribution from each component to both sides of the identity is 0 if xi = yi and 1 if xi ≠ yi.
5.4 0000, 0011, 0101, 0110, 1001, 1010, 1100, 1111 The code detects one error.
5.6 Such a code would require that
![]()
a contradiction.
5.11 The probability that the Hamming code corrects one error is
![]()
If no code is used, then the probability that the message is transmitted correctly is
![]()
5.12 Append an eighth component to the Hamming code such that the entry makes the total number of 1′s even. This ensures that the distance of the code is 4.
5.25 The group is GL(3, 2).
SOLUTIONS FOR CHAPTER 6
6.2 A projective place of order 4 is a 2-(21, 5, 1) design.
6.7 Let the first row of the matrix be [1 1 0 1 0 0 0] and take cyclic shifts.
6.11 If |Ci| = λ for some i, then every other Cj contains Ci, so m ≤ n + 1 – λ ≤ n.
Suppose not. Let γi = |Ci| – λ > 0 for 1 ≤ i ≤ m. For the incidence matrix A, we have
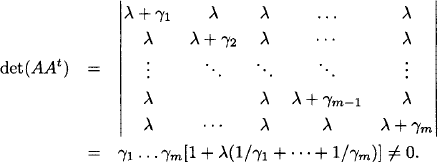
6.20 The result follows from the observation that, for any given α and β modulo n, there exist unique (mod n) i and j such that i + j  α and i – j
α and i – j  β. For 2i
β. For 2i  α + β and 2j
α + β and 2j  α – β, this determines unique i and j since n is odd.
α – β, this determines unique i and j since n is odd.
6.21

6.33 Each lattice point has all n integer coordinates. Its lattice neighbors are those points with the same coordinates save for one change to an integer one greater or one lesser. Hence, each lattice point has 2n neighbors.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
