Chapter 6
Advanced Fault Analysis with Techniques from Cryptanalysis
As introduced in Chapter 5, fault analysis causes a faulty computation during the encryption process. The basic differential fault analysis (DFA) exploits the difference of the correct computation and the faulty computation and recovers the key using the principle of differential cryptanalysis. Once the desired fault is injected to the middle of the computation, the remaining analysis is basically the same as the theoretical cryptanalysis. In fact, many of the techniques developed for the theoretical cryptanalysis can also be used in fault analysis.
On the contrary, fault analysis requires to deal with several problems that do not appear in the theoretical cryptanalysis. For example, in the theoretical differential cryptanalysis, the value of input difference can be chosen by the attacker because the input difference is the one between two plaintexts that are chosen by the attacker in the chosen plaintext attack model. On the other hand, in the DFA, the value of input difference cannot be chosen by the attacker because the fault injection cannot be controlled by the attacker in the random fault model.
The purpose of this chapter is applying the techniques for the theoretical cryptanalysis to fault analysis in order to optimize the attack. There are two approaches of optimizing fault analysis.
- Relaxing the fault model: This is very important for fault analysis. To recover the key in practice, the fault model must match the effect that can actually be caused by physical fault injections. In general, the more expensive devices are used, the more accurate and complicated faults can be injected. Relaxing the fault model is meaningful in the sense that fault analysis becomes more feasible.
- Reducing the cost to recover the key: Different from theoretical cryptanalysis, the goal of the fault analysis is recovering the key in practice, rather than finding a shortcut attack, which is infeasible but theoretically faster than the brute force attack. For example, for AES with a 128-bit key, the attack with a computational cost of
AES operations is regarded as a vulnerability of the AES algorithm in the sense of theoretical cryptanalysis, whereas operating 
AES encryptions are computationally infeasible withthe current computation resources, and thus is not important in the sense of fault analysis. There seems to exist a consensus in the current cryptographic community that performing 
operations is hard or at least too expensive for fault analysis. In another aspect, a small number of fault injections is very important for fault analysis. This is because fault analysis is an active attack, that is, it actually gives unusual physical impact to the device. The device can be broken by such a physical impact, and then the attacker faces two problems:
- 1. The attacker cannot continue the key recovery procedure.
- 2. The attacker may be detected by the owner of the device that the device is being attacked.
6.1 Optimized Differential Fault Analysis
The basic DFA in Chapter 5 only introduced the basic concept, but did not explain the full description of the attack or advanced techniques for optimization. This section aims to optimize DFA.
6.1.1 Relaxing Fault Model
Recall Figure 5.75 in Chapter 5, which is a differential propagation in basic DFA. The assumed fault model in this attack is as follows:
1 byte of fault is injected at the beginning of the 8th round of AES-128. The faulty byte position is known to attackers, while the faulty value is not known to attackers.
As mentioned before, relaxing the fault model is important for fault analysis, hence optimized DFA relaxes it as follows:
1 byte of fault is injected at the beginning of the 8th round of AES-128. The faulty byte position is unknown to attackers. The faulty value, either.
The assumption is relaxed in optimized DFA, that is, the faulty byte position becomes unknown to the attackers. This is very meaningful for applications in practice. The attacker indeed cannot detect the faulty byte position after some physical impact is added to the device. Several experimental reports also indicate that causing the fault on a fixed target byte position with probability 1 is infeasible. Hence, DFA that can deal with unknown faulty byte position is practically meaningful.
6.1.1.1 Obtaining 
The generation of correct and faulty ciphertexts is basically the same as basic DFA. The attacker assumes that a plaintext P is encrypted twice. For the first time, the attacker observes the corresponding ciphertext C without injecting fault, and achieves a pair of 
. For the second time, the attacker injects a 1-byte fault at the beginning of round 8, and obtains the corresponding faulty ciphertext 
. Note that the timing of the fault injection (the beginning of round 8) should be measured before the analysis. It is widely known that the timing can be measured quite accurately. In summary, the attacker obtains a pair of 
and the faulty ciphertexts 
generated by the fault satisfying the fault model.
6.1.2 Four Classes of Faulty Byte Positions
On the basis of this fault model, the differential propagation in Figure 5.75 is reviewed. The new differential propagation is depicted in Figure 6.1. From the new fault model, the 1-byte fault is injected at state 
but its position is unknown. The straightforward method for the attacker is guessing the faulty byte position exhaustively, and performing the basic DFA for all the guesses. Because the state consists of 16 bytes, the number of guesses is at most 16, which roughly concludes that DFA with the new fault model can finish with 16 times as much cost as basic DFA.
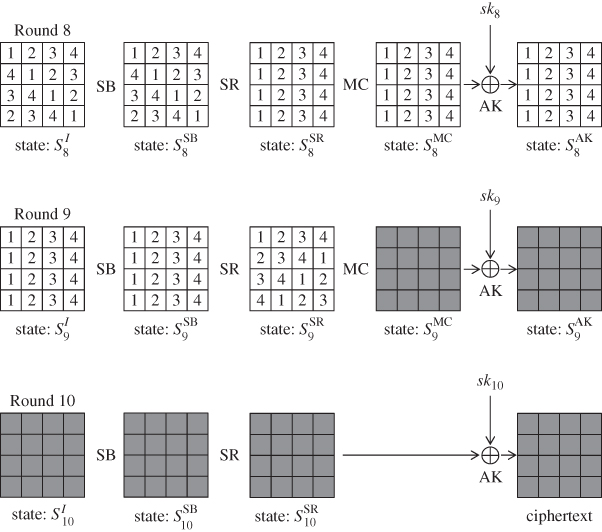
Figure 6.1 Differential propagation for four classes of faulty byte position at 
The attack cost can be improved more. The 16 candidates of the faulty byte position are divided into the following four classes:
- Class 1: byte positions 0, 5, 10, and 15.
- Class 2: byte positions 3, 4, 9, and 14.
- Class 3: byte positions 2, 7, 8, and 13.
- Class 4: byte positions 1, 6, 11, and 12.
The numbers in each state in Figure 6.1 show the differential propagation for each class.
Four positions in each class can be analyzed with exactly the same procedure. Therefore, the attack cost can be at most four times as much as basic DFA. Suppose that the fault is injected to any 1 byte of 
. The corresponding active byte position after the 
operation is 1 byte of 
, and the corresponding active byte position after the 
operation is 1 byte of 
. The important fact is that in any of the four cases, the input state to the 
operation, 
, contains 1 active byte in the left most column. The MDS property of the 
operation guarantees that the number of active bytes in the input and the output columns is greater than or equal to 5. Therefore, in any of the four cases, all the 4 bytes in the left most column (labeled as “1”) of 
are active. In the remaining part of the attack, only the information of 4 active byte positions in 
is used. Thus, 4 faulty byte positions in class 1 are equivalent for the analysis. Similarly, 4 faulty byte positions in each of the other classes can be shown to be equivalent for the analysis. Classes 2, 3, and 4 contain 4 active bytes labeled as “2,” “3,” and “4” at 
, respectively.
6.1.3 Recovering Subkey Candidates of 
The key recovery procedure is iterated four times by exhaustively guessing the class of the faulty byte position. In the following, the analysis for class 1 is explained.
DFA first aims to recover the last subkey 
. The overall picture for this process is shown in Figure 6.2.
Figure 6.2 Recovery of 4 bytes of 
for class 1
The attacker analyzes the difference of two encryption processes, one is for computing C and the other is for computing 
. When the faulty byte position at 
belongs to class 1, 4 bytes of 
have nonzero difference. From the MDS property of the 
operation, all bytes of 
have nonzero difference. The number of possible differences for each input column is 
, thus the number of possible differences for each output column is also 
. Because the 
operation does not affect the difference, the same difference is preserved until 
, which is equivalent to 
. From the analysis so far, the input difference to the S-box in round 10, 
, is determined uniquely for each possibility of 
.
The output difference from the S-box in round 10, 
, can be computed from the ciphertext pair 
. C and 
are known values to the attacker, thus its difference 
can be computed. During the backward computation, the values are soon hidden by the last subkey XOR with 
, however, the difference can still be traced. In fact 
can be computed by 
.
As explained in differential cryptanalysis in Section 4.2, for a pair of input and output differences for S-box, the paired values can be obtained using the differential distribution table (DDT) of the AES S-box. The idea was introduced in Figure 4.22 as a technique for driving key suggestions without guess. For DFA, subkey candidates for 
are derived with this technique, and the analysis is processed column by column. The analysis for the left most column is stressed by bold line in Figure 6.2.
How to derive the paired values of the left most column of 
is explained below. The 4-byte output difference is uniquely fixed by 
, and there are about 
choices for the 4-byte input difference of 
. According to the DDT of the AES S-box, a pair of randomly determined input and output differences of the S-box has
- two solutions with probability 126/256,
- four solutions with probability 1/256, and
- no solution with probability 129/256.
For the sake of simplicity, the above can be roughly approximated such that a pair of randomly determined input and output differences of the S-box has two solutions with probability 1/2, otherwise, the pair does not have a solution. A pair of input and output differences is called “matched” when they have solutions to satisfy its propagation. For each of the 
choices of 
, the existence of the solution to achieve 
is checked with DDT. Because the matchis examined for 4 bytes, the probability that there exist solutions for all bytes is 
. Once the match is verified for 4 bytes, 4 byte values can be fixed to any of the solutions. The number of solution for each byte is 2, and any combination of the solutions of 4 bytes can make a valid value of 
. Thus, 
solutions of 
are obtained from each match. In total, 
choices of the input difference can match in all of the 4 bytes, and 
solutions are obtained, which yields 
values of the left most column of 
.
values 
will move to 
by the subsequent 
operation. Finally, 
candidates of 
can be computed as
6.1.3.1 Obtaining Subkey Candidates for Entire 
After obtaining 
candidates of 
, the analysis is performed for the other columns independently. The analysis is almost the same. The only difference is that the input difference comes from a different byte position of 
, which does not give significant impact to the attack procedure. Thus, 
candidates of 
, 
candidates of 
, and 
candidates of 
are obtained by iterating the same procedure for the second, third, and the fourth column of the 
operation in the last round.
6.1.3.2 Recovery of the Original Key 
The correct value of 
is now limited to 
candidates per diagonal, which makes 
candidates of the entire 
. The correctness of those 
candidates can be verified by the exhaustive search. The attacker uses the pair of 
. For each of the 
candidates of 
, the attacker computes the corresponding 
by inverting the key schedule function. The correctness of the candidate can be checked by matching 
and C, where 
represents that plaintext P is processed by AES under the key 
. This is a match of 128-bit values. With 
matching trials, only the correct key value can result in the match, and thus the correct key is recovered.
6.1.3.3 Remarks
The analysis of the subkey or key recovery is performed for each guess of the class of the faulty byte position. Hence, the procedure is iterated four times. If the guess of the class is wrong, the attacker fails the validity check for all of 
candidates of 
. Only if the guess of the class is correct, the attacker obtains the correct suggestion of 
.
6.1.4 Attack Procedure
The attack procedure in an algorithmic form is described in Algorithm 6.1.
6.1.4.1 Complexity Evaluation
In Algorithm 6.1, the computational complexity inside the loop of step 4 is 
column operations, which would require about 1/4 cost of the round function. Then, owing to the loop in step 3, the column-wise operations are iterated four times, which makes the cost inside the loop of step 3 
round function operations. The computational cost for the loop of step 15 is 
AES computations. Finally, the computational cost for the loop of step 2 becomes 
AES computations.
The data complexity is a valid pair of plaintext P and its correct ciphertext C and the faulty ciphertext 
. The number of fault injection is only 1. The required memory amount is storing 
32-bit values for 
, which is about 
AES state values.
The attack complexity is summarized as follows:
The attack complexity is feasible, which meets the requirement for side-channel analysis and fault analysis.
6.1.5 Probabilistic Fault Injection
In a real environment, injecting the fault in the byte position with probability 1 is hard. For example,
- The fault may be injected in a different timing.
- The fault may be injected in several bytes nearby the target byte position.
If the desired fault is not guaranteed with probability 1, the attack requires more fault injections and its complexity increases. Fault injection that can succeed only probabilistically is called noisy fault injection, meaning that the intended fault only occurs with probability p, and the useless fault (noise) is obtained with probability 
.
Optimized DFA has a good characteristic against noisy fault injection. Namely, it still can recover the key practically. The attacker performs 
fault injections and collects 
tuples of 
. Because the impact of the fault at state 
propagates to all bytes at the ciphertext, there is no method to efficiently detect the desired or undesired fault injection. Thus, the attacker analyzes all the tuples by assuming that each tuple is obtained by the desired fault injection. Note that if the pair is the wrong pair, the key recovery procedure does not return anything, and thus the attacker eventually finds the right tuple caused by the desired fault injection.
This increases the attack cost only linearly to the number of pairs analyzed. In summary, the key is recovered with the following cost:
According to the experiment of the fault injection, p is not so small. Assuming 
is sufficient. Then, the attack complexity is only 10 times of the original optimized DFA, which is still feasible.
6.1.6 Optimized DFA with the 
Operation in the Last Round 
It is often misunderstood that the absence of the 
operation in the last round enables optimized DFA to recover the last round key efficiently. In other words, it is often misunderstood that, if the AES encryption algorithm computed the 
operation in the last round, efficient DFA could be prevented.
This section explains that, even with the 
operation in the last round, optimized DFA can recover the key with exactly the same cost as the case of the original AES. Note that the modified AES is inconsistent with the original AES, namely, they do not return the same ciphertext for the same pair of plaintext and key. The purpose of this discussion is understanding the impact of the last 
operation.
For clarity, the structure of the modified AES along with the differential characteristic for DFA is described in Figure 6.3.
Figure 6.3 Differential propagation against modified AES
6.1.6.1 Hardness of Straightforward Application to Modified AES
What does cause the misunderstanding? In order to explain it, Figure 6.2 and Algorithm 6.1 are reviewed. Optimized DFA for the original AES analyzes the internal state value column by column over the 
operation in round 10, and then the corresponding 4-byte subkey candidates of 
are obtained. This corresponds to step 9 of Algorithm 6.1, and is depicted in Figure 6.2.
In the original AES, computing 4 bytes of 
in the byte position 
can be trivially done. However, if the 
operation is used in round 10, the computation becomes as depicted in Figure 6.4. Namely, the 4 bytes in a column obtained at state 
will move to four different columns with the subsequent 
operation. Then, the attacker cannot compute the subsequent 
operation without knowing the values of other bytes. This prevents the attacker from obtaining 4 byte values of 
.
Figure 6.4 Impossibility of straightforward recovery of 
for class 1
Although optimized DFA on the original AES cannot be applied to the modified AES in a straightforward manner, the attack procedure can be modified so that the key is recovered with the same efficiency. There are two approaches of modifying the attack procedure.
6.1.6.2 Storing Internal State Values
The idea is very simple. To recover the key, storing 4 bytes of 
after the analysis of each column over the 
operation in the last round is not necessary.
In the original AES, if the internal state value of 
is recovered, the corresponding 
is obtained accordingly using the ciphertext. In other words, the internal state value of 
can be converted into the 
by 1-to-1 mapping. With this property, the core idea of optimized DFA for the original AES can be summarized in Algorithm 6.2.
Considering that the conversion from the internal state value of 
to 
can be applied at any timing, the pseudocode can be changed as shown in Algorithm 6.3.
Nothing is changed but for the timing of the conversion from 
to 
. The important learning from those two algorithms is that the mechanism of reducing the candidates in optimized DFA is obtaining only 
candidates of 
using differential cryptanalysis. It is easy to see that storing 4 bytes of 
for each diagonal is not the main mechanism.
With this observation, DFA for the modified AES with the 
operation in the last round is constructed. Adding the 
operation in the last round does not affect the core mechanism of DFA, that is, reducing the internal state values during the 
operation in the last round. Hence, the key should be recovered as efficiently as the original AES. Actually, the procedure in Algorithm 6.2 can be applied to the modified AES quite simply. After 
internal state values are obtained as a solution of the differential transition through the S-box for each column, the attacker stores the corresponding 4 bytes in the diagonal of state 
. After obtaining 
candidates for each diagonal of 
, the attacker generates the exhaustive combinations of four diagonals, which generates 
candidates of the entire 
. For each of the 
values of 
, the last subkey 
is recovered as
Then, the corresponding secret key 
can be computed by inverting the key schedule function, and its correctness can be verified by checking if C matches 
with a pair of plaintext and ciphertext 
. The attack is depicted in Figure 6.5.
Figure 6.5 Storing 
internal state values for each diagonal against modified AES
The procedure of DFA against the modified AES with the 
operation in the last round is given in Algorithm 6.4.
Owing to the similarity of the procedure, the detailed complexity evaluation is omitted. The correct 
can be recovered with the same complexity as Algorithm 6.1.
6.1.6.3 Equivalent Transformation of Subkey Addition
The first approach with storing the internal state values illustrated the core mechanism of DFA very well. The second approach does not mention the core mechanism but seems to be much simpler.
In the second approach, the technique of the equivalent transformation of subkey addition is used. This technique was used for the impossible differential cryptanalysis in Section 4.3, which represents the computations of the AES round function in an alternative method. In particular, the order of two linear computations 
and 
is exchanged.
By taking 
and 
as input, the computation for round 10 can be written as follows:
Let 
be 
. Then, the above-mentioned equation can be converted as follows:
Namely, the order of the 
and 
operations is exchanged. The computation structure along with the differential propagation for DFA is described in Figure 6.6.
Figure 6.6 DFA against modified AES with equivalent transformation of subkey addition
For each of the obtained ciphertexts C and 
, the corresponding state 
is easily computed by the inverse 
operation. Because the order of the 
and 
operations is exchanged, 
can be computed without the knowledge of the key.
Then, the remaining structure is almost the same as the DFA against the original AES, which is drawn in Figure 6.1. The only difference is that the recovered subkey is 
, instead of 
. However, when 
candidates of 
are exhaustively examined in the original AES, the attacker can first apply the 
operation to 
, and then invert it with the key schedule function. Finally, the correct 
can be recovered with the same complexity as DFA against the original AES.
6.1.7 Countermeasures against DFA and Motivation of Advanced DFA
As explained in this section, DFA is a strong attack, and thus the countermeasures are often implemented. The details will be explained in Chapter 7. An example is that the system computes the same plaintext twice and checks if the results of the two computations are always the same. If the computation results do not match, the system halts the computation immediately, and never outputs the faulty ciphertext 
. While this countermeasure can detect DFA, the efficiency loss is not small. The overhead is 100%, which is not acceptable for some environment.
In order to minimize the overhead, the number of rounds computed twice can be minimized. If the fault injection can be prevented for the last three rounds, the DFA cannot recover the key efficiently. Considering DFA against the AES decryption algorithm, protecting the first three rounds and the last three rounds, in total protecting six rounds, is enough to prevent DFA, which reduces the overhead to 60%.
Given the situation, cryptographers have developed other types of DFA in order to recover the key even if the first and last three rounds are protected. In the remaining sections, such advanced DFA will be explained.
6.2 Impossible Differential Fault Analysis
As long as the fault is injected during the last three rounds under the random byte-fault model, the optimized DFA is highly efficient to be practical, and thus the motivation of developing other types of fault analysis is weak. It is assumed that the last three rounds of the AES encryption are protected against the fault injection. The fault can be injected only in the 7th round or earlier during the encryption process. This section explains that the impossible differential cryptanalysis enables the attacker to recover the key with byte fault injected at the beginning of the seventh round. Hereafter, the combination of DFA with impossible differential cryptanalysis is called impossible DFA.
6.2.1 Fault Model
Because the last three rounds are protected, the attacker injects the fault at the beginning of the 7th round 
. Two types of fault model can be considered, and the attack cost depends on the strength of the fault model assumed. The first fault model is as follows:
1 byte of fault is injected at the beginning of the 7th round of AES-128. The faulty byte position is unknown to attackers. The faulty value, either. Every time the fault is injected, the faulty byte position may change, and the (unknown) fault value is assumed to be determined accordingly to the uniform distribution for 1-byte values.
The second fault model is as follows:
1 byte of fault is injected at the beginning of the 7th round of AES-128. The faulty byte position is unknown to attackers. The faulty value, either. Every time the fault is injected, the attacker can cause the fault in the same but unknown byte position. Every time the fault is injected, the (unknown) fault value is assumed to be determined accordingly to the uniform distribution for 1-byte values.
Compared with DFA, impossible DFA requires more fault injections. Thus, the assumption for multiple fault injections is added in the fault model. The second fault model assumes stronger property than the first one. Indeed, owing to the assumed ability, that is, the ability of targeting an identical faulty byte position, the attack cost can be smaller than the one in the first model. In the following, impossible DFA with the first assumption is explained. Then, impossible DFA with the second assumption is explained.
6.2.2 Impossible DFA with Unknown Faulty Byte Positions
Similarly to impossible differential cryptanalysis in Section 4.3, impossible DFA requires to collect several pairs. The attack assumes that several plaintexts 
for some i are available, and each of them is encrypted twice. For each plaintext, for the first time, the attacker observes the corresponding ciphertext C without injecting fault, and achieves a pair of 
. For the second time, the attacker injects 1-byte fault at the beginning of round 7, and obtains the corresponding faulty ciphertext 
. In summary, the attacker obtains a tuple of 
for some i generated by the fault satisfying the first fault model (faulty byte position is unknown and may change every time).
6.2.2.1 Differential Characteristic
On the basis of the fault model, the differential propagation during the last four rounds of AES is shown in Figure 6.7.
Figure 6.7 Differential propagation for impossible DFA
The differential propagation starts from the 1-byte fault injected at state 
, but its position is unknown. An important property is that for any active byte position at state 
, all bytes become active, that is, fully active, after two rounds. (The detailed analysis was given in Section 4.3, and thus omitted here.) Such a probability 1 property is important for impossible differential cryptanalysis. In Figure 6.7, the fully active states are marked by dark gray. The fully active state will be broken after the 
operation in round 9 with a relatively low probability. The probability that a byte becomes inactive is about 
for each byte. Hence, the ciphertext may not be fully active. In Figure 6.7, the bytes that can be either active or inactive are marked by light gray.
6.2.2.2 Mechanism of Reducing Subkey Space
The mechanism of reducing the subkey space of the last subkey 
is principally the same as impossible differential cryptanalysis for theoretical cryptanalysis. The attacker applies the partial decryption for the ciphertext pair by guessing the last subkey 
, and obtains the corresponding difference at state 
. For wrong guesses, the result of the partial decryption behaves randomly, and thus some bytes at 
will have no difference. This contradicts the differential propagation depicted in Figure 6.7. Hence, the guess is detected to be wrong and can be discarded from the subkey space. With several pairs of ciphertexts 
, the attacker iterates the analysis until only one value remains in the subkey space. The mechanism of impossible DFA is described in Figure 6.8.
Figure 6.8 Key recovery mechanism of impossible DFA
6.2.2.3 Key Recovery Procedure
As depicted in Figure 6.8, the subkey value of 
is recovered for each of the diagonally located 4 bytes. The same procedure to recover 4 bytes can be applied in parallel to recover the other 12 bytes. In the following, to be consistent with Figure 6.8, the procedure to recover 
is explained.
In a simple method, the attacker first collects several pairs of correct and faulty ciphertexts. Let N be the number of collected pairs. Then, the ciphertext pairs are denoted by 
.
- Subkey space
for 
is initialized to all the possible 
values. - For each of
, the attacker exhaustively guesses the subkey value of 
and computes the corresponding difference at state 
.
- If all bytes are active, do nothing (keep the guess in
). - If at least one byte is inactive, discard the guess from
.
- If all bytes are active, do nothing (keep the guess in
- Repeat the above until the subkey space
becomes 1.
The above-mentioned procedure requires the computational cost of 
inverse round function computations. The attack works, but has a room to be improved owing to step 2a, which does nothing as a result of some computation. This part can be optimized so that ineffective computations can be avoided. In short, the attacker chooses contradictory difference at state 
without guessing the subkey values, and then derive the corresponding internal state values through the 
computation in round 10 to derive the corresponding wrong subkey.
In the optimized procedure, the attacker first prepares the look-up table T of 
target differences for 
. The construction of T starts from choosing 
impossible difference at 
. Namely, all the differences with at least one inactive byte are collected. When the byte position 
is chosen to be inactive and the other three bytes are active, there are 
ways to choose the active 3-byte differences. Similarly, roughly 
differences are obtained for the cases that the inactive-byte position is set to byte positions 1, 2, and 3. In total, 
impossible differences are chosen. Actually, there are 
differences for two inactive-byte patterns and 
differences for three inactive-byte patterns. Because they only have a small factor, those differential patterns are ignored here for simplifying the description. For the 
impossible differences for 
, the corresponding difference at 
can uniquely be computed by linearly propagating the differences. Those are stored in the look-up table T. In detail, T is constructed by Algorithm 6.5.
Using the 
target differences in the look-up table T, only the wrong subkey guesses are obtained for each correct and faulty ciphertexts pair 
. From the 
, the corresponding 
can be uniquely computed owing to the linearityof the operations. Then, for each of the target difference in T, the corresponding internal state values are obtained by looking up the DDT of the S-box. Each S-box has about two solutions satisfying the given input and output differences with probability about 
. After trying 
target difference for 
, 
target differences have solutions for all the 4 bytes, and the number of obtained solutions is 
. In the end, 
wrong key suggestions are obtained for each pair of 
.
Let N be the number of collected ciphertext pairs, which are determined later. The optimized attack procedure is summarized in Algorithm 6.6.
6.2.2.4 Evaluation of the Number of Ciphertext Pairs
In the following, the number of ciphertext pairs necessary to reduce the subkey space to 1 is evaluated. Because each pair generates 
wrong subkey suggestions, by analyzing 
pairs, 
wrong subkey suggestions are obtained. However, different ciphertext pairs may derive identical wrong key suggestions. Considering the overlap, more than 
ciphertext pairs are necessary. The analysis of the number of the necessary pairs is the same as impossible differential cryptanalysis in Section 4.3.
At the initial stage, the size of the remaining subkey space is 
. By deriving one wrong key suggestion, the size of the remaining subkey space becomes
After discarding r wrong key suggestions, the size of the remaining subkey space becomes
When the number of wrong key suggestions is 
, the size of the remaining subkey space becomes
For 
, Equation (6.9) becomes 
. Therefore, the size of the subkey space is reduced to 1 by obtaining 
wrong key suggestions. The suitable choice of the number of ciphertexts pairs, N, can be obtained by the following inequation:
which concludes that 
is the necessary number of correct and faulty ciphertext pairs.
6.2.2.5 Complexity Evaluation
Algorithm 6.5 firstly runs before the attack starts. Its computational cost is 
round function computations and its memory requirement is 
4-byte values. Because it is performed offline, the data complexity is 0 and the number of fault injection is 0 at this stage. In any type of the attack complexity, Algorithm 6.5 requires much smaller cost than Algorithm 6.6.
In Algorithm 6.6, initializing the subkey space 
requires a memory to store 
4-byte values. The computational complexity inside the loop of step 4 is 
one-round operations for a single column, which would require about 1/4 cost of the round function. Then, the column-wise operations of Algorithm 6.6 are iterated four times for all the columns, which makes the entire computational cost 
round function operations.
different plaintexts 
must be processed twice to obtain the corresponding 
and 
. Thus, the data complexity is 
plaintexts. The number of fault injection is 
.
The attack complexity is summarized as follows:
The attack complexity is feasible, which meets the requirement for side-channel analysis and fault analysis.
6.2.2.6 Memory-Efficient Attack Variant
The impossible DFA starts with preparing the subkey space 
containing 
values. It seems to indicate that the attack cannot work without a memory to store 
4-byte values. However, the impossible DFA can recover the subkey with a much less memory requirement. This variant of the attack requires a memory only for collecting correct and faulty ciphertext pairs. Hence, it only requires 
ciphertexts, which is equivalent to 
bytes, although it requires a little bit more computational cost than Algorithm 6.6.
The attack procedure is simple. Suppose that the attacker collects 
correct and faulty ciphertext pairs 
for 
. The attacker guesses the 4 bytes of 
exhaustively, and then computes the corresponding difference at 
for each ciphertext pair. If the guess is wrong, the result will have inactive bytes for at least a pair. If the guess is correct, the result is always fully active for all the 
pairs. Thus, the correct subkey values are obtained. The attack procedure for the memory-efficient attack variant is given in Algorithm 6.7.
Algorithm 6.7 requires the same data complexity as Algorithm 6.6. The memory requirement is reduced to 
for storing correct and faulty ciphertext pairs. The computational cost increases to 
round function computations. Note that Algorithm 6.5 cannot be performed with the limited memory requirement. In summary, the attack complexity of the memory-efficient attack variant is as follows:
6.2.3 Impossible DFA with Fixed Faulty Byte Position
Suppose that the attacker can target an identical byte position for every fault injection trials. The assumption of such a stronger attacker's ability enables to improve impossible DFA.
The attack assumes that an identical plaintext P is encrypted many times. For the first time, the attacker observes the corresponding ciphertext without injecting fault. Let 
be the correct ciphertext. For the second time or later, the attacker injects 1-byte fault at the beginning of round 7 in the same byte position. The faulty byte position is not necessarily to be known to the attacker as long as the position is fixed. It is assumed that the injected fault value is determined accordingly to the uniform distribution. Let 
be the obtained faulty ciphertext with the ith fault injection. In summary, after the encryption of the plaintext i times and fault injection 
times, the attacker obtains i ciphertexts 
. Note that the attack in this fault model does not distinguish whether the obtain ciphertext is correct or faulty. The differential propagation in this fault model is described in Figure 6.9.
Figure 6.9 Differential propagation for impossible DFA with fixed faulty byte position. The figure describes the case in which the byte 
has a fault. The attack can work for any byte position as long as the faulty byte position is fixed. Moreover, the attacker does not have to know the faulty byte position as long as it is fixed.
6.2.3.1 Reducing Data Complexity
The core mechanism and the subkey recovery procedure of this attack is exactly the same as the one in the previous fault model. The main improvement that can be utilized in this fault model is that any of the two ciphertexts among 
can be used to derive wrong subkey suggestions. To be more precise, from i distinct ciphertexts,
ciphertext pairs are constructed, and all of the 
pairs can suggest the wrong subkey suggestions.
Recall that impossible DFA requires to collect 
ciphertext pairs in the previous fault model in Equation (6.10). The data complexity i and the number of fault injections 
in this model can be computed as
By setting 
, 
. In the end, the attack complexity can be reduced as follows:
6.3 Integral Differential Fault Analysis
Similarly to impossible DFA, the motivation is to attack the AES implementation in which the last three rounds of the AES encryption are protected against the fault injection. Thus, the fault can be injected only in the 7th round or earlier during the encryption process. This section explains that the integral cryptanalysis enables the attacker to recover the key with fault injected at the beginning of the 7th round. Hereafter, the combination of DFA with integral cryptanalysis is called integral DFA.
Integral DFA has been improved several times. The first integral DFA assumes the bit-fault model, in which the attacker can flip any bit of the internal state with probability 1. The fault model is very strong if the real environment is considered. Then, the bit-fault model was relaxed to the random byte model with more sophisticated analysis of the key recovery mechanism. Finally, the fault model in integral DFA was further relaxed to accept the noise during fault injection trials. Integral DFA can recover the key even if the fault injection can succeed only probabilistically.
6.3.1 Fault Model
Because the last three rounds are protected, the attacker injects the fault at the beginning of the 7th round 
. Three types of fault model have been considered depending on the progress of the attack theory. The first fault model is the so-called bit-fault model, explained as follows:
1 bit of fault is injected at the beginning of the 7th round of AES-128. The attacker can choose the target bit and the value of the faulty bit is flipped owing to the fault.
The second fault model is a random byte-fault model on the fixed unknown byte position, which is the same as the second fault model in impossible DFA:
1 byte of fault is injected at the beginning of the 7th round of AES-128. The faulty byte position is unknown to attackers. The faulty value, either. Every time the fault is injected, the attacker can cause the fault in the same but unknown byte position. Everytime the fault is injected, the (unknown) fault value is assumed to be determined accordingly to the uniform distribution for 1-byte values.
The third fault model is a noisy random byte-fault model on the fixed unknown byte position, explained as follows:
1 byte of fault is intended to be injected at the beginning of the 7th round of AES-128. The attacker intends to target an identical byte position for every fault injection trials. The faulty byte position is unknown to attackers. The faulty value, either. The fault injecting attempt may fail with some probability. The attacker cannot know whether or not the intended fault is injected. Every time the intended fault is injected, the (unknown) fault value is assumed to be determined accordingly to the uniform distribution for 1-byte values.
The assumption for the attacker's ability is getting more and more relaxed. In the noisy random fault model, the attacker obtains a set of ciphertexts, in which some of them are derived by the intended fault and the others are completely random noise. The attacker cannot distinguish which of the collected ciphertexts are the intended ones, but still needs to recover the key.
6.3.2 Integral DFA with Bit-Fault Model
Recall integral cryptanalysis in Section 4.4, in particular a set of 256 plaintexts in Equation (4.160). The attack requires to collect a set of 256 intermediate values in which only 1 byte of the state takes all the 256 possible values and the other 15 bytes are fixed to the unique value among 256 intermediate values.
The attack assumes that an identical plaintext P is encrypted at least 256 times under the fixed key. For the first time, the attacker observes the corresponding ciphertext 
without injecting fault. For the second time, the attacker injects 1-bit fault to the least significant bit of the target byte so that the second state value has difference 1 compared to the original state value. The attacker obtains the corresponding ciphertext 
. For the third time, the attacker injects 1-bit fault to the second least significant bit of the target byte so that the third state value has difference 2 compared to the original state value. The attacker obtains the corresponding ciphertext 
. For the fourth time, the attacker injects 1-bit faultto the least significant bit and the second least significant bit of the target byte simultaneously so that the second state value has difference 3 compared to the original state value. The attacker obtains the corresponding ciphertext 
. This procedure is iterated 255 times to collect 256 internal state values containing 256 different values on the target byte of the state at the beginning of round 7. In summary, the attacker obtains a tuple of 
. The attacker does not have to know the faulty byte position as long as the target faulty bit is located in the same byte position. Note that the attack in this fault model does not distinguish whether the obtain ciphertext is correct or faulty.
6.3.2.1 Integral Property
The collected 256 intermediate state values are propagated toward the ciphertext. With the same notations as Section 4.4, the 2.5-round integral property from round 7 is shown in Figure 6.10.
Figure 6.10 Integral property for integral DFA in bit fault model
The propagation of the property up to state 
is exactly the same as the theoretical cryptanalysis in Section 4.4. Namely, all bytes have the “all” property at 
. In round 9, the order of the 
and 
operations is exchanged by linearly transforming 
. Because the subkey XOR does not affect the integral property, the all property is maintained in all bytes at state 
.
In Figure 6.10, the propagation of the integral property finishes at state 
, while the theoretical cryptanalysis in Section 4.4 propagates over one more 
operation. Recall Figure 4.41. After the subsequent 
operation, all bytes still hold the “balanced” property. Actually, the same analysis can be applied about the propagation in integral DFA. Namely, all bytes at state 
in Figure 6.10 satisfy the balanced property.
Why such a property is not considered in integral DFA? The problem here is that the balanced property occurs even for wrong guesses with a relatively high probability. For a wrong guess, the sum of the decryption results among 256 texts can be 0 in each byte with probability 
, which may not be enough to reduce the subkey space. In theoretical cryptanalysis, the goal of the attacker is recovering the key faster than the exhaustive search. The feasibility of the attack in practice is not an important issue. However, in side-channel analysis, the goal is recovering the key in practice, which may prefer a much stronger property than the one used in theoretical cryptanalysis.
6.3.2.2 Key Recovery Procedure
The mechanism of reducing the subkey space of the last subkey 
is similar to the theoretical integral cryptanalysis, but the subkey space can be reduced much faster. The attacker first collects 256 ciphertexts 
, in which the corresponding internal state at 1 byte of 
takes all 256 values owing to the bit fault.
In order to simplify the attack evaluation as much as possible, the order of the 
operation and 
is exchanged by applying the linear transformation 
to subkey 
. Then, the partial decryption from the ciphertext to state 
becomes as Figure 6.11.
Figure 6.11 Key recovery procedure for integral DFA
is converted to 
by the inverse of the 
operation. Hereafter, integral DFA first aims to recover the value of 
. Note that if 
is recovered, the corresponding 
can be computed easily, and eventually the original key 
is recovered by computing the inverse of the key schedule function. Not only 
, but also each ciphertext is converted by the inverse of 
operation. Hereafter, the converted ciphertexts are renamed as 
. During the key recovery procedure, the converted ciphertexts are used instead of the real ciphertexts.
Because the 
operation in round 10 is ignored now, the partial decryption from converted ciphertexts to 
is done column by column. The related bytes to the analysis of the first column are stressed by bold line in Figure 6.11.
The attacker exhaustively guesses the first column of 
, and performs the partial decryption for 256 converted ciphertexts. Let 
be the 4 byte values of 
corresponding to 
. For each guess, the attacker computes 
for 
and stores the results. Then, the attacker checks if 
for 
covers all the 256 possibilities. Similarly, the occurrence of the same event is checked for byte positions 
, and 
. Because the bit-fault model can inject the fault on a target bit with probability 1, the 256 texts in the set always satisfy the “all” property in state 
. Therefore, if the guess is correct, the results of the partial decryption up to 
for 256 ciphertexts will contain all the 256 values in each byte. If the guess is wrong, the results of the partial decryption show a random behavior. The probability that 256 texts will result in 256 different state values is very low (later evaluated in details). From this reason, the attack can recover the correct value of 
.
6.3.2.3 Evaluation of the Remaining Subkey Space
In integral DFA, if the guess of 
is correct, the results of the partial decryption always satisfy the “all” property at state 
. Hence, false negatives never occur. On the other hand, the “all” property at state 
may happen to be satisfied with a low probability for wrong guesses. Thus, it is necessary to evaluate the probability of the false positive.
Assume that the partial decryption of 
with a wrong guess of 
behaves randomly and independently for different i. Then, the occurrence of false positives in a single byte of 
is equivalent to the occurrence of the following event.
Let
be a byte value space, that is,
. Let “random pick up” be a procedure to randomly choose 1 element from
according to the uniform distribution. The false positive in a single byte is equivalent to the event that after doing the random pick up 256 times, all of the 256 elements are chosen once.
The random pick up trial corresponds to obtaining a result of the partial decryption in one byte for one ciphertext. The evaluation of the occurrence of this event is widely known. In the first pick up, any value can be chosen. Thus, the success probability of the first pick up is 
. In the second pick up, any value but for the already appeared one can be chosen. Thus, the success probability of the second pick up is 
. Similarly, the success probability for the 
th pick up is 
. In the end, the probability of the event is evaluated as
This test is applied to 4 bytes in a column simultaneously. Thus, the probability of the false positive of this attack is
The probability of the false positive is negligible, which indicates that only the correct guess can satisfy the “all” property at 4 bytes of state 
.
6.3.2.4 Attack Procedure
The attack procedure of integral DFA in the bit-fault model is described in an algorithmic form in Algorithm 6.8.
After the fist column of 
is recovered, the same procedure is iterated three times in order to recover the second, the third, and the fourth column of 
. Then, 
is computed by 
, and eventually 
is recovered by computing the inverse of the key schedule function.
6.3.2.5 Complexity Evaluation
Owing to the exhaustive guess of 
at step 4 and 256 converted ciphertexts at step 5, the computational cost of this attack is about 
round function computations for one column. After iterating Algorithm 6.8 four times, the computational cost becomes 
round function computations, which is equivalent to 
AES computations. The memory complexity is only 256 state values. Regarding the data complexity, the same plaintext must be encrypted 256 times. The attacker needs to cause intended bit faults for 255 times out of 256 opportunities. In the end, the attack complexity is summarized as follows:
The attack complexity is feasible, which meets the requirement for side-channel analysis and fault analysis.
6.3.3 Integral DFA with Random Byte-Fault Model
Similarly to the bit-fault model, the attack in the random byte-fault model injects many faults in a fixed byte at the beginning of round 7 (state 
), while the same plaintext is encrypted under the same key many times. The main difference from the bit-fault model is that the attacker cannot collect all the 256 values at a fixed byte of 
because the attacker does not have an ability to control the fault bit by bit.
To solve this problem, integral DFA in a random byte-fault model introduces a similar, but different, integral property from Figure 6.10. Here, the attacker does not collect 256 texts containing all the 256 values in a target byte. Instead, the attacker collects only d texts containing distinct d values in the target byte, where 
. Note that when 
, the property becomes the same as Figure 6.10.
6.3.3.1 “Distinct” Property D
Consider a set of d byte values 
satisfying 
such that 
. Such a set of byte values is defined to have distinct property, or in short D. The attacker tries to make d distinct state values at state 
in which only one byte satisfies the “distinct” property and all the other bytes satisfy the constant property. The intuition behind is that, for a relatively small d, d distinct fault values can be caused efficiently even with the random byte-fault model. After those d texts are obtained, the corresponding properties in several AES operations are considered.
- Suppose that d distinct byte values are processed by the S-box transformation. Because S-box is a bijective mapping, d distinct input values always result in d distinct output values. Therefore, the D property never be broken by the S-box transformation.
- The
operation only changes the byte positions in a state. It does not affect the value inside each byte. Therefore, the 
operation never breaks the D property. - Suppose that d distinct 4-byte values consisting of 1 byte with the D property (in any position) and 3 bytes with the C property are input to the
operation. Then, all of the 4 output bytes from the 
operation will have the d property. Note that this holds only when the number of byte with the d property is 1. If more than 1 byte with the d property are input to the 
operation, no property can be exploited. - Suppose that d distinct byte values are XORed with some constant byte values. Obviously, the output-byte values take d distinct byte values. Therefore, the D property is never broken by the constant addition.
Those properties are summarized in Figure 6.12. With the distinct property, the previous integral property from 
in Figure 6.10 is updated for the random byte-fault model. The updated property is shown in Figure 6.13.
Figure 6.12 Propagation of distinct property
Figure 6.13 Integral property for integral DFA in random byte fault model
6.3.3.2 Key Recovery Procedure and the Number of Distinct Fault Values
The key recovery procedure basically follows the one in the bit-fault model. The attacker exhaustively guesses 
column by column and decrypts the collected ciphertexts up to state 
. For the right guess, d distinct values appear for each of 4 bytes of 
in the target column. The main difference is that only d ciphertexts are obtained instead of 256 ciphertexts. The key recovery procedure is shown in Figure 6.14. The smaller number of ciphertexts decreases the attack complexity, while the effect of reducing the key space is reduced as well. For wrong guesses, the event now occurs with a higher probability than the bit-fault model.
Figure 6.14 Integral property for integral DFA in random byte fault model
The probability that d distinct values can be obtained after the partial decryption of d ciphertexts for a wrong guess can be evaluated easily with Equation (6.15). Considering that the property is examined for 4 bytes in parallel, the probability of this event denoted by 
for each of the subkey guess is
If this event is sufficiently small to discard all the 
wrong guesses, the right key can be identified. Hence, the condition for the number of d that the attack requires is written as
For 
, 
in Equation (6.17) becomes smaller than 
, and thus only one correct subkey can be expected.
The detailed attack procedure is almost the same as Algorithm 6.8, thus omitted here. In precise, the loops in steps 1 and 5 of Algorithm 6.8 are iterated 
times. Then, from steps 12 to 15 check if d distinct values are obtained.
6.3.3.3 Complexity Evaluation
Owing to the column-wise exhaustive guesses of 
at step 4 and 44 converted ciphertexts at step 5, the computational cost of this attack is 
, which is less than 
round function computations for one column. After iterating the attack four times, the computational cost becomes 
round function computations, which is equivalent to 
AES computations. The memory complexity is only 44 state values. Regarding the data complexity, the same plaintext must be encrypted 44 times. The attacker needs to cause intended byte faults for 43 times out of 44 opportunities. In the end, the attack complexity is summarized as follows:
It clearly shows that the fault model is relaxed, and the attack complexity is reduced compared to the one in the bit-fault model.
6.3.3.4 Remarks
The “distinct” property is interesting in the sense that it is particular to fault analysis. In the theoretical cryptanalysis in Section 4.4, the attacker can choose any number of plaintexts in the chosen plaintext attack model, and thus it does not have any motivation to investigate “distinct” property.
Moreover, the theoretical cryptanalysis prefers to use the “all” property because the number of distinguished rounds can be extended by introducing the “balanced” property. The “balanced” property is not suitable for integral DFA because it can be satisfied with a relatively high probability for wrong guesses, whereas the goal of the theoretical cryptanalysis is finding shortcut attacks that can be infeasible as long as the attack cost is faster than the generic attack, or exhaustive search of the key.
Integral DFA in a random byte-fault model uses a lot of features particular to the practical analysis. In the next topic, more features particular to the practical analysis will be discussed.
6.3.4 Integral DFA with Noisy Random Byte-Fault Model 
Finally, the fault model is relaxed so that the fault injection succeeds only probabilistically, with some probability p. The fault injecting setting is exactly the same as the previous ones in the bit-fault model and the random byte-fault model. While the same plaintext is encrypted under the same key many times, the attacker tries to inject the fault to a fixed byte at the beginning of round 7, or state 
. Let n be the number of fault injection trials. The attacker obtains 
intended faults and 
unintended faults. Hereafter, unintended faults are called noise. In this attack, noise is regarded as a completely random value. Thus, after a noisy fault injection, the whole state value will become completely random at state 
. As indicated by Figure 6.10 or Figure 6.13, the impact of the fault at state 
will expand to the entire state until the computation reaches ciphertext. The attacker cannot detect if each obtained ciphertext is an intended one or noise. The attacker's goal is recovering the key when a set of n ciphertexts are given, in which 
ciphertexts are the intended ones.
The success probability of the attack and its efficiency depends on the success probability of the fault injection, or the ratio of n and 
. Hereafter, let 
be the number of intended ciphertexts, that is, 
.
6.3.4.1 Key Recovery Mechanism Based on Coupon Collector's Problem
Remember the key recovery mechanism in the bit-fault model. With the right guess, the attacker obtains 256 distinct values only with 256 trials, while with wrong guesses, the probability of this event is too low.
Then, let us consider a slightly different situation:
The attacker obtains 256 ciphertexts and 1 noise ciphertext. Among those 257 ciphertexts, the attacker does not know which ciphertext is noise.
To recover the key, the attacker anyway partially decrypts 257 ciphertexts under the guessed subkey 
. Owing to the 256 intended ciphertexts, the results of the partial decryption cover all the 256 possibilities, and then 1 overlap owing to the noise. If the probability of this event is sufficiently low for wrong guesses, the attacker can recover the correct subkey value. Actually, this probability is very low. There are
ways to choose 256 ciphertexts from a set of 257 ciphertexts, and for each of the 256 choices, Equation (6.15) is evaluated. Therefore, the probability of covering all the 256 values in the 4 bytes at 
is 
, which is small enough to filter out all the 
wrong guesses.
This probabilistic event is equivalent to the widely known problem called Coupon Collector's Problem.
The coupon collector's problem is also illustrated in Figure 6.15.
Figure 6.15 Illustration of coupon collector's problem
Considering the application to integral DFA, the parameters in the coupon collector's problem correspond to integral DFA as follows:
- The number of coupon-drawing events correspond to the number of ciphertexts (sum of the numbers of partial decryption for intended and noisy ciphertexts). When the probability of obtaining an intended fault is p,
ciphertexts must be collected to obtain the 256 intended faults. The number of coupon-drawing events is 
. 
corresponds to 256, which is the possible number of values that each byte can take.
Integral DFA checks the occurrence of this event for 4 bytes at the same time. Thus, by denoting the success probability of the coupon collector's problem by 
, the probability that each subkey candidate is regarded as the right guess is written by 
. If 
is smaller than 
, all the wrong guesses will be discarded with a good probability, and thus integral DFA can recover the key. In other words, the condition to be a valid integral DFA is that the success probability of the coupon collector's problem with 
events should be lower than 
.
It is also widely known that, when there are 
coupons, the coupon collector's problem requires about
Coupon-drawing events to complete all the 
coupons. When 
, 
. The corresponding p is evaluated as
which indicates that the coupon collector's problem will succeed with a reasonably high probability when integral DFA can inject intended faults with 
. In other words, in order to recover the key with integral DFA, the probability of the fault injection should be higher than 
.
In general, to evaluate the number of acceptable noisy fault injections in integral DFA, a success probability of the coupon collector's problem with a given number of coupon-drawing event is needed. Before going into theevaluation, a generalization of the coupon collector's problem is considered below.
Generalized Coupon Collector's Problem
The discussion in the previous section is the probabilistic fault injection for the bit-fault model, that is, the discussion for the noisy bit-fault model. In order to relax the strong assumption of the bit-fault model, the probabilistic fault injection for the random byte-fault model is needed.
The major issue here is that the attacker cannot expect to collect all the 256 values in the fixed byte at state 
. The integral property is based on the “distinct” property rather than the “all” property. Remember that, in the random byte-fault model, the key recovery mechanism is based on the low probability of the event that d distinct byte values are obtained by decrypting d different ciphertexts. In the noisy fault model, the attacker obtains n texts in total, and 
of them are intended ciphertexts. Thus, to recover the key, the probability of the event that at least 
distinct byte values are obtained by decrypting n different ciphertexts must be sufficiently small so that all the wrong guesses are filtered out. In the context of the coupon collector's problem, the new event is defined as follows.
Note that the coupon collector's problem is a subset of the generalized coupon collector's problem. Indeed, the coupon collector's problem is a special case of the generalized version when 
.
6.3.4.2 Probability Evaluation of Generalized Coupon Collector's Problem
The answer for the above-mentioned generalized coupon collector's problem is given as a relation between the number of coupon-drawing events and the success probability. Suppose that the number of coupon-drawing events is represented as a variable n. Then, the success probability should be calculated as a function of 
, 
, and n, in which 
and 
are the number of coupons to be collected and the number ofall coupons, respectively. As long as the application to integral DFA on AES is discussed, 
is fixed to 
. Here, for the sake of generality, 
is treated as a variable. In the following, the probability that at least 
distinct coupons are collected after n coupon-drawing events is evaluated.
The proof is omitted in this book. Using Lemma 6.3.3, the success probability of the generalized coupon collector's problem for given parameters 
, 
, and n can be written in a form of the recursive equation as follows.
The evaluation results of 
for various 
and n are given in Figure 6.16. Considering the application to integral DFA on AES, 
is fixed to 256. The parameter with a low probability indicates that wrong key values can be discarded efficiently with integral DFA. For example, for 
, even if the attack requires 1500 fault injections (a relatively large number of noise), the key space can be reduced by 1 bit for each byte. On the other hand, when only 
distinct values can be obtained from the fault injection, only a few number of noisy fault injections spoil the attack.
Figure 6.16 Probability evaluation of generalized coupon collector's problem
6.3.4.3 Subkey Recovery Procedure
How the key space of AES-128 is reduced with the noisy random byte-fault model is explained here. 
is fixed to 
. Then, the attack depends on the parameters 
. In practice, the suitable choice of 
should be determined depending on the attacker's ability. For example, if the attack can spend a lot of cost for the fault injection, the attacker may be able to inject various fault values in the target byte at the beginning of round 7, and the success probability of injecting the intended fault can be high. Namely, 
can be big and p is close to 1.
In the following explanation, the parameters are set to 
, which indicates that the corresponding probability of obtaining the intended fault, p, is 0.18 as evaluated in Equation (6.22). From Equation (6.24), the corresponding probability is calculated as 
. In this parameter, the key space is gradually reduced by analyzing eight data sets, and thus the behavior of the attack can be explained clearly. Note that the attack can work for various parameters in general.
Collecting Ciphertexts
- The attacker obtains a pair of plaintext and ciphertext denoted by
without injecting the fault, and stores it in a list. - While the same plaintext
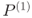is processed, the attacker tries to inject a fault in the target fixed byte position at the beginning of round 7. If the obtained ciphertext does not overlap with the already stored ciphertexts in a table, add it to the table. - Repeat the second step until n ciphertexts
are obtained.
For one plaintext, a set of n ciphertexts is constructed. The same procedure is iterated eight times to collect eight sets of n ciphertexts by changing the plaintext to 
. Remember that the attacker does not have to distinguish the intended ciphertexts from noisy ones.
Detecting Correct Subkeys
In each set of 
ciphertexts 
, 
values are included in the target fixed byte at 
. The detailed procedure of the key recovery phase is as follows.
- Compute
for 
. - For each column, exhaustively guess the value for
and compute the corresponding value of 
. - If only less than
distinct values are observed in at least one byte of each column of 
, discard the guessed 
from the key candidates. - Repeat the above three steps by
times by changing the text set for 
.
Because 
, the probability that a wrong guess happens to collect 
values for 4 bytes in a column is 
. Hence, the subkey space is reduced by 4 bits per set of 1440 ciphertexts. After iterating the analysis eight times, 
subkey space is expected to be reduced to 1, that is, only the correct guess will remain. Note that the subkey space does not have to be reduced to exactly 1. By combining the exhaustive search, reducing the subkey space to a sufficiently small size is sufficient.
Complexity Evaluation
In order to collect the data, eight sets of 1440 ciphertexts are generated. Hence, the data complexity is 
chosen plaintexts, and the number of fault injection is 
. The computational cost is 
AES round function computations, which is approximately 
AES computations. The attack requires the memory to store less than 
AES states to count the remaining key space.
The small optimization of the computational cost can be applied. Once a subkey candidate is identified to be wrong, it does not have to be examined again for different sets of ciphertexts. Therefore, the complexity becomes
AES computations. In summary, the attack complexity of the integral DFA in this fault model is as follows:
6.4 Meet-in-the-Middle Fault Analysis
The meet-in-the-middle differential fault analysis (MitM DFA) is another fault analysis that injects faults at the beginning of the seventh round. In short, MitM DFA recovers the last subkey 
with about 10 plaintexts, 
computational cost, 
amount of memory, and 10 fault injections. In particular, the MitM DFA has an advantage for a small data complexity and the number of fault injections.
In this section, the concept of the MitM attack against block cipher is first introduced. Then, its application in DFA is explained.
6.4.1 Meet-in-the-Middle Attack on Block Ciphers
6.4.1.1 Introduction of Meet-in-the-Middle Attack
The MitM attack is a classical cryptanalytic technique against block ciphers. Let 
be an encryption algorithm under the key K. The MitM attack can be applied efficiently when 
can be represented as a sequence of two subencryption functions 
and 
, namely
where 
and 
are two independent subkeys, that is, 
and 
. An encryption algorithm satisfying this condition is described in Figure 6.17.
Figure 6.17 Target structure of meet-in-the-middle attacks
6.4.1.2 Meet-in-the-Middle Attack Procedure
Suppose that the block size, b, is bigger than the key size, k. In addition, suppose that the sizes of 
and 
are identical, which is 
bits. Then, the MitM attack can recover the correct k-bit key K only with one plaintext and ciphertext pair, 
computational cost, and 
memory requirement. This is significantly faster than the exhaustive search for the k-bit key.
The attack idea is simple. The attacker first obtains a pair of plaintext and ciphertext 
from the oracle in the known plaintext setting. Then, the analysis is processed as follows, which is also illustrated in Figure 6.18.
- Exhaustively guess
values of 
. For each guess, compute 
and store the result along with 
in a list 
. Sort the list 
with respect to the value of 
. - Exhaustively guess
values of 
. For each guess, compute 
and store the result along with 
in a list 
, where 
is the decryption algorithm. Sort the list 
with respect to the value of 
. - Find a match between
elements in 
and 
elements in 
. For a matched pair, the corresponding 
and 
are the correct subkey values. Thus, 
is recovered.
Figure 6.18 Key recovery procedure of meet-in-the-middle attacks
6.4.1.3 Mechanism of Key Recovery
For the right guesses of 
and 
, the b-bit intermediate state values will match with probability 1. Thus, the false negative never occurs in the MitM attack. For wrong pairs of 
and 
, the b-bit intermediate state values in 
and 
will match only probabilistically, that is, 
. The number of elements in both of 
and 
is 
, and thus the number of matched pairs is 
. When 
, an event with a probability of 
is unlikely to occur only with 
trials.
Note that the essence of the MitM attack is the independence of 
and 
, which allows the attacker to compute 
and 
completely independently.
If the assumption 
does not hold, the MitM attack cannot recover the correct key only with one pair of plaintext and ciphertext. Each pair provides the b-bit filtering, and thus the key space is reduced by b bits per pair. Therefore, to reduce the key space to 1, the number of necessary pairs is written as
The attack procedure is shown in Algorithm 6.9.
6.4.1.4 Complexity Evaluation
Let us first evaluate the attack complexity of the simple case with 
in Figure 6.18. The data complexity is one known plaintext. The time complexity of the first step is 
evaluations of 
. The time complexity of the second step is 
evaluations of 
. In total, 
evaluations of 
and 
, which is equivalent to 
evaluation of E. Note that the cost of sorting 
data is usually assumed to be negligible compared to 
computations of the encryption algorithm. The memory complexity is 
b-bit internal state values for 
and 
, in total 
state values. Here, the memory complexity for 
can be omitted by performing the match as soon as each element for 
is obtained. If thematch is not found, that element can be discarded immediately without being stored in 
. This reduces the memory complexity to 
state values.
In summary, the complexity of the MitM attack for the simple case with 
is
For the case with 
, the data complexity increases to 
known plaintexts. The time and data complexities also increase by a factor of 
for handling multiple pairs. In summary, the complexity of the MitM attack with 
is
where 
.
6.4.2 Meet-in-the-Middle Attack for Differential Fault Analysis
Remember that the essence of the MitM attack is the independence of 
and 
, which allows the attacker to compute 
and 
completely independently. Unfortunately, such a strong independence of subkeys is unusual forstandard block ciphers. For example, any three versions of AES generate 
from 
. Thus, there is no independent subkey. However, the idea of the MitM attack can be useful when a part of the subkeys is guessed during the attack, or an attack against a small number of rounds is considered. Indeed, fault attacks meet those conditions, and thus the mechanism of the MitM attack can be exploited.
MitM DFA is essentially the same as DFA. The efficient key recovery mechanism of the MitM attack is exploited when subkeys are guessed during DFA. The straightforward differential attack requires to guess 10 subkey bytes (
guesses), which is infeasible. MitM DFA separates the guess of 10 subkey bytes to two independent procedures with five subkey-byte guess. This enables to recover the last subkey 
with about 10 plaintexts, 
computational cost, 
amount of memory, and 10 fault injections.
6.4.2.1 Fault Model
The assumed fault model in MitM DFA is exactly the same as standard DFA but for the fault injection round. The simple attack assumes as follows:
1 byte of fault is injected at the beginning of the 7th round of AES-128. The faulty byte position is known to attackers, while the faulty value is not known to attackers.
The assumption of the knowledge of the faulty byte position can be relaxed as follows:
1 byte of fault is injected at the beginning of the 7th round of AES-128. The faulty byte position is unknown to attackers. The faulty value, either.
6.4.2.2 Differential Characteristic
For simplicity, the attack is first explained in the fault model with the knowledge of the faulty byte position. Let the faulty byte position at the beginning of the seventh round be 6. The attacker obtains a pair of plaintext and ciphertext denoted by 
. Then, the attacker makes a query of 
to the encryption oracle in the chosen plaintext model, and injects a fault in the known and fixed byte position at the beginning of round 7. The differential propagation in the subsequent rounds is described in Figure 6.19.
Figure 6.19 Differential propagation in MitM DFA
The fault injecting timing and the fault model are exactly the same as the ones in impossible DFA discussed at Section 6.2. Thus, the resulting differential propagation is also the same as the one in Figure 6.9. However, MitM DFA exploits a different feature from impossible DFA. Namely, the property of having 16 active bytes at state 
is no longer used. The new property exploited is the ratio of the byte differences in each column at state 
, in which 
. Remember that the input difference to the 
operation in round 8 is unknown to the attacker, while the attacker still can compute the ratio of 4 output-byte differences.
How to compute the ratio of 4 output-byte differences is depicted in Figure 6.20. Suppose that the input column to the 
operation, 
, only has 1 active byte in the top byte as shown in Figure 6.20. Let U be a nonzero difference in 
, which is unknown to the attacker. According to the specification of the 
operation, the difference of the output column, 
, is computed as
Although the value of U is unknown, the attacker knows that
In particular, the relation 
allows the direct application of the MitM attack. That is, the attacker independently computes 
and 
with guessing subkeys, and stores those values. The correct guesses of subkeys always yield thematch of 
and 
, and this much can be found efficiently in the MitM attack.
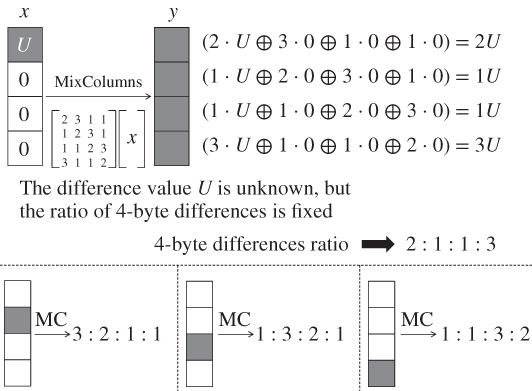
Figure 6.20 Ratio of 4-byte differences in a column
The same property can be obtained for different input active byte positions.
6.4.2.3 Collecting Pairs
The attacker obtains a pair of plaintext and ciphertext denoted by 
. While the same plaintext 
is processed, the attacker injects a fault in the known and fixed byte position at the beginning of round 7 to obtain the faulty ciphertext 
. In Figure 6.19, this position is fixed to the byte position 6. The same procedure is iterated 10 times to collect 
. In the end, the attacker obtains 10 pairs of correct and faulty ciphertexts that follow the differential propagation in Figure 6.19.
6.4.2.4 Key Recovery Procedure
The attacker guesses 4 bytes of the last subkey 
and 1 byte of the converted subkey 
to perform the partial decryption from ciphertext to any 1 byte of 
. Figure 6.21 describes the partial decryption from ciphertext to 1 byte of 
and 1 byte of 
. Note that the order of 
and 
operations is exchanged in round 9.
Figure 6.21 Independent partial decryption with 5-byte guess
From the analysis of the differential ratio, 
holds as long as the fault is injected at 
or the other 3 bytes in the same inverse diagonal, that is, 
, 
and 
. Hereafter, the attacker aims to compute 
and 
independently. As shown in Figure 6.21, subkeys guessed in the partial decryption for 
and for 
do not have any overlap. Thus, subkey guesses and partial decryptions can be performed independently.
- The computation for
requires 5-byte subkey guess, 
and 
. The guessed bytes are marked by filled circles in Figure 6.21. For each 
possibilities of the 5 subkey bytes, compute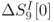 
for all the 10 pairs of 
, where 
. Store the sequence of 10 bytes (
for 10 pairs) in a list 
. Then, sort the list 
. - The computation for
requires 5-byte subkey guess, 
and 
. The guessed bytes are marked by bold line in Figure 6.21. For each 
possibilities of the 5 subkey bytes, compute 
for all the 10 pairs of 
, where 
. Store the sequence of 10 bytes (
for 10 pairs) in a list 
. Then, sort the list 
. - Find the match of 10-byte elements in
and 
.
The attack procedure is also illustrated in Figure 6.22.
Figure 6.22 Key recovery procedure of MitM DFA
6.4.2.5 Evaluation
Step 1 generates 8-bit value of 
for 10 pairs, which yields 80-bit sequences to match. After the exhaustive guess of 5 subkey bytes, 
80-bit sequences are stored in 
. Similarly after step 2, 
80-bit sequences are stored in 
. In step 3, 
pairs are examined for matching 80-bit values. Only one value is expected to match. Thus, the correct 10 subkey bytes are recovered.
By iterating the same attack procedure for different columns, the remaining 8 subkey bytes of 
can be recovered. Thus, all the subkey bytes in 
are recovered.
The data complexity of this attack is 20 chosen plaintexts. It requires 10 fault injections. In step 1, the computational cost is 
AES round functions, which is equivalent to 
AES computations. The memory requirement is storing 
80-bit sequence along with 5 subkey bytes, which is less than 
16-byte values, thus less than 
AES states. In summary, the attack complexity of the MitM DFA in this fault model is as follows:
6.4.2.6 MitM DFA with Unknown Faulty Byte Position
The feasibility of the attack with unknown faulty byte position depends on the assumption whether the unknown faulty byte position at the beginning of round 7 can be fixed or not.
If the faulty byte position can be fixed (but unknown), what the attacker needs is guessing the diagonal position with the faulty byte. The guess is chosen from at most four patterns. Thus, the computational cost of the attack becomes 
rather than 
, but it is still feasible.
If the faulty byte position cannot be fixed, there is no method to efficiently match the 80-bit sequences. Thus, the attack can no longer recover the key.
Further Reading
- Derbez P, Fouque P and Leresteux D 2011 Meet-in-the-middle and impossible differential fault analysis on AES In Cryptographic Hardware and Embedded Systems - CHES 2011 - 13th International Workshop, Nara, Japan, September 28 - October 1, 2011. Proceedings (ed. Preneel B and Takagi T), vol. 6917 of Lecture Notes in Computer Science, pp. 274–291. Springer-Verlag.
- Kim CH 2011 Efficient methods for exploiting faults induced at AES middle rounds Cryptology ePrint Archive, Report 2011/349. International Association for Cryptologic Research.
- Mukhopadhyay D 2009 An improved fault based attack of the advanced encryption standard In Progress in Cryptology - AFRICACRYPT 2009, Second International Conference on Cryptology in Africa, Gammarth, Tunisia, June 21-25, 2009. Proceedings (ed. Preneel B), vol. 5580 of Lecture Notes in Computer Science, pp. 421–434. Springer-Verlag.
- Phan RC and Yen S 2006 Amplifying side-channel attacks with techniques from block cipher cryptanalysis In Smart Card Research and Advanced Applications, 7th IFIP WG 8.8/11.2 International Conference, CARDIS 2006, Tarragona, Spain, April 19-21, 2006, Proceedings (ed. Domingo-Ferrer J, Posegga J and Schreckling D), vol. 3928 of Lecture Notes in Computer Science, pp. 135–150. Springer-Verlag.
- Piret G and Quisquater J 2003 A differential fault attack technique against SPN structures, with application to the AES and KHAZAD In Cryptographic Hardware and Embedded Systems - CHES 2003, 5th International Workshop, Cologne, Germany, September 8-10, 2003, Proceedings (ed. Walter CD, Koç ÇK and Paar C), vol. 2779 of Lecture Notes in Computer Science, pp. 77–88. Springer-Verlag.
- Sasaki Y, Li Y, Sakamoto H and Sakiyama K 2013 Coupon collector's problem for fault analysis against AES - high tolerance for noisy fault injections In Financial Cryptography and Data Security - 17th International Conference, FC 2013, Okinawa, Japan, April 1-5, 2013, Revised Selected Papers (ed. Sadeghi A), vol. 7859 of Lecture Notes in Computer Science, pp. 213–220. Springer-Verlag.
- Tunstall M, Mukhopadhyay D and Ali S 2011 Differential fault analysis of the advanced encryption standard using a single fault In Information Security Theory and Practice. Security and Privacy of Mobile Devices in Wireless Communication - 5th IFIP WG 11.2 International Workshop, WISTP 2011, Heraklion, Crete, Greece, June 1-3, 2011. Proceedings (ed. Ardagna CA and Zhou J), vol. 6633 of Lecture Notes in Computer Science, pp. 224–233. Springer-Verlag.