Chapter 4
Cryptanalysis on Block Ciphers
In this chapter, several cryptanalyses against block ciphers are introduced. The discussion is mainly focused on AES-128, which is the AES with a 128-bit key, although many of the discussions can also be applied to other block ciphers in general.
The ideal security of block ciphers and the goal of the cryptanalysis are firstly defined. Then, many techniques in several cryptanalytic approaches are introduced. The first topic is the differential cryptanalysis, which provides the basic concepts of cryptanalysis. The second topic is the impossible differential cryptanalysis. Finally, the last topic is the integral cryptanalysis. Key recovery attacks against reduced-round versions of AES-128 are demonstrated for each approach.
4.1 Basics of Cryptanalysis
4.1.1 Block Ciphers
Block cipher E takes as input a key K of a fixed bit-length, and produces a one-to-one map (permutation) from b-bit plaintext to b-bit ciphertext, where b is a bit-length of the fixed block size. Let k be a bit-length of the fixed key size. Then, block ciphers are described as follows:
The permutation ![]() is required to behave completely independent for different choices of K. The model of block cipher is depicted in Figure 4.1.
is required to behave completely independent for different choices of K. The model of block cipher is depicted in Figure 4.1.

Figure 4.1 Model of block cipher
On the one hand, from mathematical perspective, any key size and any block size are acceptable. On the other hand, from engineering perspective, suitable choices of those sizes are limited.
The key size is often determined by a cost of managing keys and required security for the block cipher. Long keys have higher security than short keys, while the managing cost for long keys is more expensive than the one for short keys.
The block size is often determined by the processor size of the target platform. For example, if block ciphers are designed to be used in a high-end software with a 64-bit processor, typical choices of the block size are a multiple of 64 bits such as 128 bits or 256 bits. If they are designed to be suitable for resource-restricted environment such as an RFID tag, a smaller block size is chosen. Several examples of the key size and block size of widely used block ciphers are summarized in Table 4.1.
Table 4.1 Key size and block size of widely used block ciphers
| Algorithm | Key size, k | Block size, b |
| AES-128 | 128 | 128 |
| AES-192 | 192 | 128 |
| AES-256 | 256 | 128 |
| Camellia-128 | 128 | 128 |
| Camellia-192 | 192 | 128 |
| Camellia-256 | 256 | 128 |
| Triple-DES | 168 | 64 |
| PRESENT | 80 | 64 |
| PRESENT | 128 | 64 |
| HIGHT | 128 | 64 |
4.1.2 Security of Block Ciphers
Block ciphers are required to provide some robustness against cryptanalysis. To measure the security of block ciphers, security notions must be defined. There are several classes of security notions. Three major notions are key recovery resistance, plaintext recovery resistance, and indistinguishability from a random permutation.
- Key recovery resistance: For any choice of the key K, the block cipher must resist the attack that efficiently recovers the value of K.
- Plaintext recovery resistance: For any choice of the key K, and for any choice of the ciphertext C, the block cipher must resist the attack that efficiently recovers the corresponding plaintext value P such that
 .
. - Indistinguishability: For any choice of the key K, the permutation
 must be indistinguishable from a random permutation. This notion is often referred as pseudo-random permutation. In detail, under a fixed key, a block cipher becomes a b-bit permutation. Without the knowledge of the key K, nobody can compute a valid pair of plaintext and ciphertext. Then, another b-bit permutation is chosen randomly from all the possible b-bit permutations, which is called a random permutation. Suppose that there is a b-bit permutation in which either of a block cipher with an unknown fixed key or a random permutation is implemented. An observer aims to distinguish which of the block cipher or the random permutation is implemented without the knowledge of the key. The indistinguishability is depicted in Figure 4.2.
must be indistinguishable from a random permutation. This notion is often referred as pseudo-random permutation. In detail, under a fixed key, a block cipher becomes a b-bit permutation. Without the knowledge of the key K, nobody can compute a valid pair of plaintext and ciphertext. Then, another b-bit permutation is chosen randomly from all the possible b-bit permutations, which is called a random permutation. Suppose that there is a b-bit permutation in which either of a block cipher with an unknown fixed key or a random permutation is implemented. An observer aims to distinguish which of the block cipher or the random permutation is implemented without the knowledge of the key. The indistinguishability is depicted in Figure 4.2.
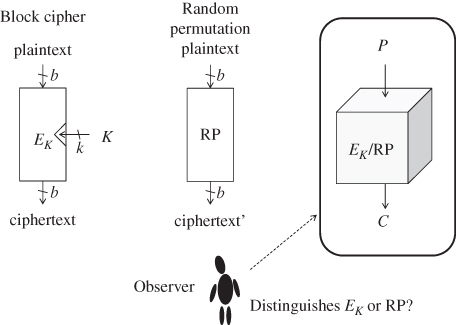
Figure 4.2 Indistinguishability
Here, the term “efficiently” in the security notions leaves ambiguity. More details are explained in a later section explaining generic attacks.
If the key recovery resistance is broken on a block cipher, the other two notions are broken automatically. Therefore, the key recovery resistance is the weakest security notion among the above three. That is to say, from a designer's point of view, the key recovery resistance is the easiest security notion to satisfy, while from an attacker's point of view, it is the hardest security notion to break. The definition of “success of the attack” depends on which class of security notions is expected on that cipher. In general, block ciphers are expected to have ideal security. Thus, efficiently breaking indistinguishability is considered to be a significant vulnerability for block ciphers.
4.1.3 Attack Models
To measure the security of block ciphers, not only the security notion but also the attacker's ability must be defined. The assumed attacker's ability is often referred as the attack model, which is mainly classified by the information that attackers can obtain.
- Ciphertext only attack: The attacker can only observe ciphertexts produced by the encryption system. As long as plaintexts are chosen accordingly to the uniform distribution, the corresponding ciphertexts also follow the uniform distribution. Therefore, in the ciphertext only attack, the attacker must suppose the bias of the plaintexts such as the bias in natural languages or ASCII codes. It is rare to see that modern symmetric-key ciphers are broken by the ciphertext only attack.
- Known plaintext attack: The attacker can observe pairs of plaintext and the corresponding ciphertext. Owing to the knowledge of plaintexts, the known plaintext attack is stronger than the ciphertext only attack. The known plaintext attack, in practice, simulates the attacker who eavesdrops the communication between two players. The attacker does not have any control of the plaintext to be encrypted.
- Chosen plaintext attack: The attacker has an ability to make the system encrypt any plaintext of the attacker's choice. The attacker can observe the corresponding ciphertext. Owing to the ability of choosing plaintexts, the chosen plaintext attack is stronger than the known plaintext attack. The chosen plaintext attack, in practice, simulates the attacker who impersonates a valid communication player. In the chosen plaintext attack, the plaintexts to be encrypted must be chosen before the attack. Once one of the chosen plaintexts is encrypted, the attacker loses the ability to choose new plaintexts.
- Adaptively chosen plaintext attack: The attacker has an ability to choose plaintexts to be encrypted even after chosen messages are encrypted by the system. The adaptively chosen plaintext attack, in practice, simulates the online active attackers who change the attack strategy depending on the behavior of the system.
- Chosen ciphertext attack: Chosen ciphertext attack is a similar model as the chosen plaintext attack. The attacker has an ability to make the system decrypt any ciphertext of the attacker's choice. From mathematical perspective, the ability of choosing plaintexts is as strong as the ability of choosing ciphertexts. However, considering the usage in practice, the latter model is often regarded to be stronger than the former model.
- Adaptively chosen ciphertext attack: Adaptively chosen ciphertext attack is a similar model as the adaptively chosen plaintext attack. The attacker has an ability to choose ciphertexts to be decrypted even after chosen ciphertexts are decrypted by the system.
It is possible to combine models for the plaintext and the ciphertext. Thus, the strongest attack model that can be directly obtained from the above classification is the adaptively chosen plaintext and ciphertext attack.
Block ciphers are usually required to have ideal security. Thus, the indistinguishability must be ensured against the adaptively chosen plaintext and ciphertext attack.
Note that the attackers cannot compute the correspondence between plaintexts and ciphertexts by themselves because the key value is unknown. In any of the above-mentioned attack models, the corresponding ciphertext (resp. plaintext) of known or chosen plaintext (resp. ciphertext) can be obtained only by forcing the system to output the result. Those requests to the system are called queries. A system that returns results from queries is called an oracle. In particular, an oracle that accepts plaintexts as queries and returns the corresponding ciphertexts is called an encryption oracle. Similarly, an oracle that accepts ciphertexts as queries and returns the corresponding plaintexts is called a decryption oracle. As an example, the chosen ciphertext attack is described in Figure 4.3.

Figure 4.3 Chosen ciphertext attack accessing decryption oracle
Other than the above-mentioned models, cryptographers developed various types of attack models. Some of them were introduced only for an academic interest. Two examples of those complicated models are introduced below, however, those are not discussed more in this book.
- Multikey model: There are several users with their own keys in the system. The attacker, under some plaintext or ciphertext model, can access any user. For example, if the attack model is the known plaintext attack in the multikey model, the attacker can eavesdrop pairs of plaintext and ciphertext from multiple users.
- Related-key model: The related-key model is a variant of the multikey model, in which the attacker has more knowledge about the users' keys. Suppose that there are i users,
 in the system, and they use the key labeled as
in the system, and they use the key labeled as  , respectively. The assumption in the related-key model is that the attacker does not know the value of
, respectively. The assumption in the related-key model is that the attacker does not know the value of  , however, the relation of each key pair is known. The bit-wise XOR is a typical example of the relation in the related-key model. Namely, for two indices
, however, the relation of each key pair is known. The bit-wise XOR is a typical example of the relation in the related-key model. Namely, for two indices  , the values of
, the values of  and
and  are unknown, but their relation
are unknown, but their relation  is known.
is known.
4.1.4 Complexity of Cryptanalysis
The efficiency of the cryptanalysis is usually measured by three types of quantity: data, time, and memory.
- Data: The data quantity is measured by the number of queries.
- Time: The time quantity is measured by computational cost executed by an attacker offline. The unit of the computational cost is usually the cost of one execution of the encryption algorithm
 or the decryption algorithm
or the decryption algorithm  . The computational cost for the oracle is not counted as the computational cost of the attack.
. The computational cost for the oracle is not counted as the computational cost of the attack. - Memory: An attacker often needs to store queried plaintexts (resp. ciphertexts) and returned ciphertexts (resp. plaintexts) from the oracle. The attacker may need to store intermediate values generated during the attack. To store such data, a certain amount of memory is required. The memory quantity is measured by memory requirement. In many cases, the unit of the memory requirement is one value of the block size (b bits), or a byte (8 bits).
A triplet of those three types of quantity is called attack complexity. Let ![]() be the data, time, and memory quantity of an attack against some security notion under some attack model. This indicates that if
be the data, time, and memory quantity of an attack against some security notion under some attack model. This indicates that if
- the attacker can ask D queries to the oracle under the assumed attack model,
- the attacker can spend the cost of executing the encryption or decryption algorithm T times, and
- the attacker has enough memory to store M data of the size b bits,
the attacker succeeds in attacking the target cipher with respect to the target security notion in the target attack model.
4.1.5 Generic Attacks
Because block ciphers use a fixed size key, it is information-theoretically impossible to keep the key secret permanently. There always exists an attack that recovers the key in a finite time. This principle is applied to any block cipher even if it is ideally designed. Such attacks are called generic attacks. In the following, two generic attacks against block ciphers are explained.
4.1.5.1 Brute Force Attack (Exhaustive Search)
In the brute force attack, the attacker tries to recover the k-bit correct key value by simply examining all the ![]() possibilities. The attack is often called an exhaustive search. The brute force attack starts by obtaining pairs of plaintext and ciphertext. The number of necessary pairs depends on the key size (k bits) and the block size (b bits). For simplicity, suppose that the block size is bigger than the key size, that is,
possibilities. The attack is often called an exhaustive search. The brute force attack starts by obtaining pairs of plaintext and ciphertext. The number of necessary pairs depends on the key size (k bits) and the block size (b bits). For simplicity, suppose that the block size is bigger than the key size, that is, ![]() . In this case, the attack requires only one pair of a plaintext and the corresponding ciphertext. The attack consists of the online phase for collecting a pair of plaintext and ciphertext in the known plaintext attack and the offline phase for recovering the correct key value.
. In this case, the attack requires only one pair of a plaintext and the corresponding ciphertext. The attack consists of the online phase for collecting a pair of plaintext and ciphertext in the known plaintext attack and the offline phase for recovering the correct key value.
In the online phase, the attacker makes one query of a known plaintext ![]() to the encryption oracle, and receives the corresponding ciphertext
to the encryption oracle, and receives the corresponding ciphertext ![]() . Then, with the knowledge of a valid pair
. Then, with the knowledge of a valid pair ![]() , the attacker aims to recover the correct key in the offline phase. Let G be a k-bit variable representing the key guess. The brute force attack computes the value of
, the attacker aims to recover the correct key in the offline phase. Let G be a k-bit variable representing the key guess. The brute force attack computes the value of ![]() for all the
for all the ![]() possibilities of G, and checks the match of the computedresults and
possibilities of G, and checks the match of the computedresults and ![]() . The detailed process of the brute force attack is shown in Algorithm 4.1.
. The detailed process of the brute force attack is shown in Algorithm 4.1.
If G is the correct guess, the equation ![]() is satisfied with probability 1. If G is not the correct guess,
is satisfied with probability 1. If G is not the correct guess, ![]() occurs with probability
occurs with probability ![]() . When b is bigger than k, the event of the probability
. When b is bigger than k, the event of the probability ![]() is unlikely to occur by
is unlikely to occur by ![]() trials. Thus, Algorithm 4.1 can successfully return the correct key K. The brute force attack is illustrated in Figure 4.4. Because it works in the known plaintext attack, the attack can also work in the stronger attack models.
trials. Thus, Algorithm 4.1 can successfully return the correct key K. The brute force attack is illustrated in Figure 4.4. Because it works in the known plaintext attack, the attack can also work in the stronger attack models.

Figure 4.4 Brute force attack for 
When ![]() , the data complexity of the brute force attack is one known plaintext. The time complexity of the brute force attack is
, the data complexity of the brute force attack is one known plaintext. The time complexity of the brute force attack is ![]() encryption operations. The brute force attack does not need to store any intermediate value during the attack but for a pair of a plaintext and a ciphertext
encryption operations. The brute force attack does not need to store any intermediate value during the attack but for a pair of a plaintext and a ciphertext ![]() . Thus, the memory requirement of the brute force attack is negligible.
. Thus, the memory requirement of the brute force attack is negligible.
Let us consider the case when the key size is equal to the block size, that is, ![]() . The attack algorithm basically follows Algorithm 4.1. However, the probability that a wrong guess satisfies
. The attack algorithm basically follows Algorithm 4.1. However, the probability that a wrong guess satisfies ![]() is not negligible. Owing to the assumption
is not negligible. Owing to the assumption ![]() wrong keys are examined. Then, an event with probability
wrong keys are examined. Then, an event with probability ![]() is satisfied after
is satisfied after ![]() trials with the following number:
trials with the following number:
By assuming that the block size, b, is big enough,
Therefore, besides the correct key K, one false positive (a value wrongly judged to be the correct key) is expected. If more than one key candidates remain, it is impossible to determine the correct key value only with one pair of ![]() . Then, the attack needs to obtain another pair
. Then, the attack needs to obtain another pair ![]() , and also examines the match of
, and also examines the match of ![]() and
and ![]() for the remaining key candidates. The correct key guess can also satisfy the match of those two values, while the wrong key guess succeeds the test only with probability
for the remaining key candidates. The correct key guess can also satisfy the match of those two values, while the wrong key guess succeeds the test only with probability ![]() . In the end, the brute force attack successfully recovers the correct key K with at most two pairs of plaintexts and ciphertexts.
. In the end, the brute force attack successfully recovers the correct key K with at most two pairs of plaintexts and ciphertexts.
Finally, let us consider the case when the key size is much bigger than the block size, that is, ![]() . The attack procedure is basically the same as the other cases but for the number of necessary pairs to detect the correct key K. Each pair of plaintext and ciphertext
. The attack procedure is basically the same as the other cases but for the number of necessary pairs to detect the correct key K. Each pair of plaintext and ciphertext ![]() yields a b-bit relation
yields a b-bit relation ![]() . This can be regarded as a b-bit filter for the key K, that is, the k-bit key space can be reduced to
. This can be regarded as a b-bit filter for the key K, that is, the k-bit key space can be reduced to ![]() bits by checking the match of a b-bit relation. Therefore, to reduce the key space to 1, the number of necessary pairs is described by
bits by checking the match of a b-bit relation. Therefore, to reduce the key space to 1, the number of necessary pairs is described by
The attack procedure is shown in Algorithm 4.2.
The procedure in Algorithm 4.2 first checks the match of ![]() and
and ![]() , and then checks the match of the other pairs. By processing the attack in this order, the computational cost can be optimized to
, and then checks the match of the other pairs. By processing the attack in this order, the computational cost can be optimized to ![]() encryption operations compared to the case that the match of all pairs is checked simultaneously.
encryption operations compared to the case that the match of all pairs is checked simultaneously.
4.1.5.2 Codebook Attack (Dictionary Attack)
Codebook means the set of all plaintexts and the corresponding ciphertexts. For any newly given ciphertext, the attacker can obtain the corresponding plaintext by looking up the codebook. Thus, the plaintext recovery resistance is broken. The attack is also called a dictionary attack. The codebook attack is illustrated in Figure 4.5. The codebook attack breaks the plaintext recovery resistance irrespective of the key size. Note that even with the codebook, the attacker cannot obtain any information of the key K only by observing the correspondence of plaintexts and ciphertexts even if the key size k is smaller than the block size b.

Figure 4.5 Codebook attack
The codebook attack requires to obtain all the ![]() plaintext–ciphertext pairs. The attack can work under the known plaintext model. The data complexity of the codebook attack is
plaintext–ciphertext pairs. The attack can work under the known plaintext model. The data complexity of the codebook attack is ![]() pairs of plaintexts and ciphertexts. The time complexity of the codebook attack is one access of look-up table, which is negligible. The attack requires to store all
pairs of plaintexts and ciphertexts. The time complexity of the codebook attack is one access of look-up table, which is negligible. The attack requires to store all ![]() plaintext–ciphertext pairs in a local memory as the look-up table. Thus, the memory requirement is
plaintext–ciphertext pairs in a local memory as the look-up table. Thus, the memory requirement is ![]() -bit values.
-bit values.
4.1.6 Goal of Shortcut Attacks (Cryptanalysis)
For any block cipher, being attacked by generic attacks is not regarded to be a flaw of the design because it is theoretically impossible to prevent. The purpose of discussing generic attacks is that they can be used to know the goal of the design. That is to say, for secure block ciphers, any attack with a less cost than the one in the generic attack must be prevented.
Such attacks are called shortcut attacks. For a block cipher, allowing a shortcut attack is usually considered to be a significant vulnerability. In other words, the goal of the cryptanalysis is finding a shortcut attack, while the goal of the cipher's designer is preventing any shortcut attack.
Recall the two generic attacks explained earlier. The brute force attack indicates that with the attack complexity (Data, Time, Memory) ![]() , the key is recovered in any block cipher, where
, the key is recovered in any block cipher, where ![]() represents “negligibly small.” The codebook attack indicates that with the attack complexity (Data, Time, Memory)
represents “negligibly small.” The codebook attack indicates that with the attack complexity (Data, Time, Memory) ![]() , the plaintext is recovered in any block cipher. Considering those facts, the number of queries for any shortcut attack must be smaller than
, the plaintext is recovered in any block cipher. Considering those facts, the number of queries for any shortcut attack must be smaller than ![]() , and the computational cost for any shortcut attack must be smaller than
, and the computational cost for any shortcut attack must be smaller than ![]() . The memory requirement of a valid shortcut attack is often bounded by
. The memory requirement of a valid shortcut attack is often bounded by ![]() . In summary, the following lemma is obtained for a shortcut attack.
. In summary, the following lemma is obtained for a shortcut attack.
In some cases, the attack with a complexity of ![]() , and
, and ![]() is discussed. This is because there is no generic method to recover the key faster than the brute force attack even with the full codebook. This motivation is theoretically true, but in practice, the cipher's security has already been broken. The key recovery attack with the full codebook is less interesting than the key recovery attack without the full codebook.
is discussed. This is because there is no generic method to recover the key faster than the brute force attack even with the full codebook. This motivation is theoretically true, but in practice, the cipher's security has already been broken. The key recovery attack with the full codebook is less interesting than the key recovery attack without the full codebook.
From the next section, several popular approaches of the cryptanalysis against block ciphers are introduced.
4.2 Differential Cryptanalysis
4.2.1 Basic Concept and Definition
Differential cryptanalysis was established by Biham and Shamir. Suppose that two input messages M and ![]() are processed by the same function F. Namely,
are processed by the same function F. Namely, ![]() and
and ![]() are computed. The differential cryptanalysis focuses on the difference of two computations.
are computed. The differential cryptanalysis focuses on the difference of two computations.
Suppose that two values x and ![]() with a difference
with a difference ![]() are processed by the function F, and let
are processed by the function F, and let ![]() be the output difference. Then,
be the output difference. Then, ![]() is computed as follows:
is computed as follows:
The concept of the difference is illustrated in Figure 4.6. The fact that the difference ![]() becomes
becomes ![]() after some operation is called “
after some operation is called “![]() is propagated to
is propagated to ![]() (with some operation).”
(with some operation).”
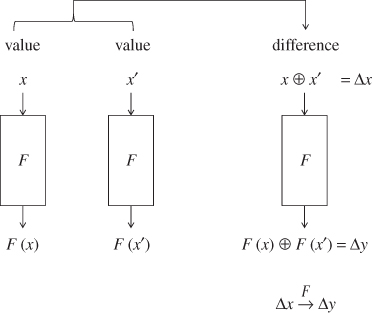
Figure 4.6 Illustration of difference
4.2.2 Motivation of Differential Cryptanalysis
What for the differential cryptanalysis focuses on the difference of two computations rather than the result for each value? The reason is that, in many computations widely adopted in current block cipher algorithms, deterministic (probability 1) differential propagation can be constructed even without knowing the key value. This fact makes the cryptanalysis easy.
In many block ciphers, the key or values derived by the key is mixed to the plaintext or values derived by the plaintext with the XOR operation. Recall the specification of AES in Section 1.5. As the first operation, XOR of the plaintext and the key is taken, and the updated state ![]() is computed. The operation is depicted in Figure 4.7.
is computed. The operation is depicted in Figure 4.7.

Figure 4.7 Mixing key and plaintext in AES
Let us check how the differential cryptanalysis impact the block cipher analysis, by comparing it with the analysis focusing on a single value.
4.2.2.1 Analysis with a Single Value
Suppose that the attacker obtains a single plaintext P in the known plaintext attack model. The attacker does not know the key value K. In AES, the plaintext is XORed with the key K, and the value of the state ![]() is represented as
is represented as ![]() . Because K is unknown to the attacker, the value of
. Because K is unknown to the attacker, the value of ![]() is unknown to the attacker. Thus, the attacker loses all information about the computation, and cannot continue the attack for the subsequent computations.
is unknown to the attacker. Thus, the attacker loses all information about the computation, and cannot continue the attack for the subsequent computations.
4.2.2.2 Analysis with Difference of Two Values
Suppose that the attacker obtains two plaintexts P and ![]() in the known plaintext attack model. Then, the difference of the two plaintexts is represented as
in the known plaintext attack model. Then, the difference of the two plaintexts is represented as ![]() . The attacker does not know the key value K. After taking XOR of the plaintext and the key, the state value
. The attacker does not know the key value K. After taking XOR of the plaintext and the key, the state value ![]() for the two plaintexts is represented by
for the two plaintexts is represented by ![]() and
and ![]() . Then, the difference of the values of
. Then, the difference of the values of ![]() for the two plaintexts is represented as
for the two plaintexts is represented as
Although each of the value of ![]() and
and ![]() is unknown, the attacker still knows their difference irrespective of the key value K. The above-mentioned two cases are depicted in Figure 4.8.
is unknown, the attacker still knows their difference irrespective of the key value K. The above-mentioned two cases are depicted in Figure 4.8.
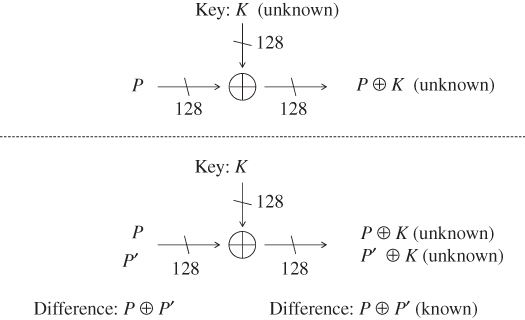
Figure 4.8 Comparison of analysis with value and with difference
4.2.3 Probability of Differential Propagation
For a given pair of values x and ![]() and a function F without any secret value, the corresponding difference after processing F can be computed deterministically, or the difference of
and a function F without any secret value, the corresponding difference after processing F can be computed deterministically, or the difference of ![]() and
and ![]() can be computed without any error probability.
can be computed without any error probability.
The goal of the differential cryptanalysis is recovering the secret key K of a target block cipher ![]() . The attacker usually cannot compute the difference of
. The attacker usually cannot compute the difference of ![]() and
and ![]() without knowing K.
without knowing K.
To solve the issue, the differential cryptanalysis often specifies the difference of input values to a function ![]() , input difference, and the difference of output values from
, input difference, and the difference of output values from ![]() , output difference, without specifying the exact input value of x, and then evaluates the probability that the event
, output difference, without specifying the exact input value of x, and then evaluates the probability that the event ![]() is satisfied when x is randomly chosen according to the uniform distribution. This probability is represented by
is satisfied when x is randomly chosen according to the uniform distribution. This probability is represented by
As a case study, consider the differential propagation of a 4-bit to 4-bit function ![]() , which is defined in Table 4.2. Note that
, which is defined in Table 4.2. Note that ![]() is the S-box computation adopted in a lightweight block cipher TWINE.
is the S-box computation adopted in a lightweight block cipher TWINE.
Table 4.2 A 4-bit to 4-bit function ![]()
| Input | x | 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
| Output | C |
0 |
F |
A |
2 |
B |
9 |
5 |
8 |
3 |
D |
7 |
1 |
E |
6 |
4 |
All values are described in the hexadecimal format.
Consider calculating the probability that the input difference 5 changes into the output difference A, after the computation of ![]() , that is,
, that is, ![]() . To calculate the probability, for all possible input values
. To calculate the probability, for all possible input values ![]() , another input value is obtained by XORing the input difference,
, another input value is obtained by XORing the input difference, ![]() , and the difference of
, and the difference of ![]() and
and ![]() is computed. Then, the probability that the output difference is
is computed. Then, the probability that the output difference is A is calculated. For ![]() , two input values are
, two input values are 0 and ![]() . The output difference is
. The output difference is ![]() . The same evaluation is done for all
. The same evaluation is done for all ![]() . The result is summarized in Table 4.3.
. The result is summarized in Table 4.3.
Table 4.3 Output difference of ![]() when input difference is
when input difference is 5
| x | ||||
0 |
5 |
C |
B |
7 |
1 |
4 |
0 |
2 |
2 |
2 |
7 |
F |
5 |
A |
3 |
6 |
A |
9 |
3 |
4 |
1 |
2 |
0 |
2 |
5 |
0 |
B |
C |
7 |
6 |
3 |
9 |
A |
3 |
7 |
2 |
5 |
F |
A |
8 |
D |
8 |
E |
6 |
9 |
C |
3 |
1 |
2 |
A |
F |
D |
4 |
9 |
B |
E |
7 |
6 |
1 |
C |
9 |
1 |
3 |
2 |
D |
8 |
E |
8 |
6 |
E |
B |
6 |
7 |
1 |
F |
A |
4 |
D |
9 |
From Table 4.3, 2 out of 16 possibilities will result in the output difference A. Therefore,
Similarly, the probability of the differential propagation from 5 to other output differences can be obtained from Table 4.3.
The probability of the differential propagation is formally defined as follows.
4.2.4 Deterministic Differential Propagation in Linear Computations
The case study in Figure 4.8 can be generalized more. Let ![]() be a function that returns XOR of two n-bit input values. Then, XOR of a plaintext and the fixed key K can be represented as
be a function that returns XOR of two n-bit input values. Then, XOR of a plaintext and the fixed key K can be represented as ![]() . As shown in Equation (4.14), for any value of P and
. As shown in Equation (4.14), for any value of P and ![]() , the input difference to
, the input difference to ![]() and the output difference from
and the output difference from ![]() become identical. That is to say, the following lemma holds for
become identical. That is to say, the following lemma holds for ![]() .
.
Moreover, the probability that a difference other than ![]() is output is 0. Namely, the following lemma holds.
is output is 0. Namely, the following lemma holds.
More generally, suppose that two values for the first input variable to ![]() have a difference
have a difference ![]() and two values for the second input variable have a difference
and two values for the second input variable have a difference ![]() . Then, the following lemma holds for
. Then, the following lemma holds for ![]() .
.
Note that Lemma 4.2.4 is the special case of Lemma 4.2.6, in which the difference of the second input variable is 0.
An interesting observation in Equation (4.36) is that
That is to say, the output difference can be computed as if the difference were the input value to the function ![]() . In the differential cryptanalysis, an attacker aims to obtain a high probability differential propagation only with determining differences without determining the paired values. The approach is useful for block cipher analysis because the plaintext values become unknown quickly owing to the key.
. In the differential cryptanalysis, an attacker aims to obtain a high probability differential propagation only with determining differences without determining the paired values. The approach is useful for block cipher analysis because the plaintext values become unknown quickly owing to the key.
Not only for the XOR operation but also for any type of linear computations, the differential propagation can be computed deterministically without determining the exact paired values. A linear function L satisfies the following property:
Therefore, the difference of two values a and b after a linear computationL can be computed by taking their difference as input to L. Namely, the following lemma holds, which is illustrated in Figure 4.9.

Figure 4.9 Computing output difference in a linear computation L
Other two examples of the computation that are widely adopted in current block cipher algorithms are the rotation operation and the multiplication over a finite field.
- Rotation: Let “
 ” be the left rotation by r-bits. Then, for any input difference
” be the left rotation by r-bits. Then, for any input difference  ,
4.41
,
4.41
The differential propagation of the 3-bit rotation for 8-bit values is depicted in Figure 4.10.
 holds for any choices of x and
holds for any choices of x and  .
. - Multiplication over a finite field: Let “
 ” be the multiplication with a constant t over a finite field. Then, for any input difference
” be the multiplication with a constant t over a finite field. Then, for any input difference  ,
4.42
,
4.42

Figure 4.10 Differential propagation over a rotation operation
A composition of more than one linear computations are also linear. Hence, for any composition of linear computations, the output difference can be computed deterministically from the input difference. An example is the ![]() operation in AES. The
operation in AES. The ![]() operation linearly maps a 32-bit value to another 32-bit value, whose computation consists of the multiplications over a finite field and XOR of several values. Thus, if the input difference to the
operation linearly maps a 32-bit value to another 32-bit value, whose computation consists of the multiplications over a finite field and XOR of several values. Thus, if the input difference to the ![]() operation is determined, the corresponding output difference can be deterministically computed without determining the exact values.
operation is determined, the corresponding output difference can be deterministically computed without determining the exact values.
As an application to AES, the deterministic differential propagation for the linear computation part of the AES round function is explained below, which is described in Figure 4.11.

Figure 4.11 Differential propagation for linear operations of AES round function
The linear operation part of the AES round function in round i is ![]() , and
, and ![]() . Suppose that difference of the input state to the
. Suppose that difference of the input state to the ![]() operation
operation ![]() has a nonzero byte difference
has a nonzero byte difference ![]() in the third row of the second column. Hereafter, a sequence of 16-byte values is used to represent a 128-bit value of the state. More precisely, the state whose jth byte value is
in the third row of the second column. Hereafter, a sequence of 16-byte values is used to represent a 128-bit value of the state. More precisely, the state whose jth byte value is ![]() for
for ![]() is denoted by
is denoted by
With this notation, the above ![]() is represented as
is represented as
After the ![]() operation, each byte in the third row is rotated by 2 bytes to left. Thus, in the difference of the state
operation, each byte in the third row is rotated by 2 bytes to left. Thus, in the difference of the state ![]() , a nonzero byte difference
, a nonzero byte difference ![]() moves to the third row in the fourth column, that is,
moves to the third row in the fourth column, that is,
Then, the ![]() operation is applied. Regarding the first, second, and third columns, the output difference is computed as
operation is applied. Regarding the first, second, and third columns, the output difference is computed as

Therefore, the differences for those columns are ![]() . Regarding the fourth column, the output difference is computed as
. Regarding the fourth column, the output difference is computed as

In the end, after the ![]() operation, the difference of the state value
operation, the difference of the state value ![]() becomes as follows:
becomes as follows:
Finally, the ![]() operation is applied, which computes XOR of the state and the subkey. From Lemma 4.2.4, the output difference of the XOR operation is the same as the input difference. Thus, the difference after the
operation is applied, which computes XOR of the state and the subkey. From Lemma 4.2.4, the output difference of the XOR operation is the same as the input difference. Thus, the difference after the ![]() operation is represented as follows:
operation is represented as follows:
which concludes the differential propagation for the linear computation part of the AES round function.
4.2.5 Probabilistic Differential Propagation in Nonlinear Computations
When a function F does not satisfy the definition of linear operation, that is,
no efficient method is known to derive a high probability differential propagation. Hence, all the possibilities must be taken into consideration according to Equation (4.33) in the definition of the probability of differential propagation.
AES adopts a single nonlinear operation in a round function, which is the ![]() operation.
operation. ![]() applies an S-box to each byte of the state in order to substitute a byte (8-bit) value into another one according to a prespecified conversion table. Analyzing 8-bit to 8-bit S-box is complicated. Hence, in this section, the 4-bit to 4-bit S-box
applies an S-box to each byte of the state in order to substitute a byte (8-bit) value into another one according to a prespecified conversion table. Analyzing 8-bit to 8-bit S-box is complicated. Hence, in this section, the 4-bit to 4-bit S-box ![]() defined in Table 4.2 is mainly analyzed as a small example, and the extension to the 8-bit to 8-bit S-box is explained later.
defined in Table 4.2 is mainly analyzed as a small example, and the extension to the 8-bit to 8-bit S-box is explained later.
For a nonlinear function, the attacker aims to obtain the probability of the differential propagation for all possible patterns. Most of the block ciphers adopt a small size S-box, for example, a 4-bit S-box or an 8-bit S-box, in order to avoid inefficiency when it is implemented. Hence, computing all the possibilities is usually feasible. In detail, the attacker computes Equation (4.33) for all the choices of the input difference ![]() and the output difference
and the output difference ![]() . Equations (4.17)–(4.32) show the probabilities of the differential propagation when
. Equations (4.17)–(4.32) show the probabilities of the differential propagation when ![]() is fixed to
is fixed to 5 and ![]() is unfixed. To complete it, the analysis is iterated by changing
is unfixed. To complete it, the analysis is iterated by changing ![]() for all the possibilities.
for all the possibilities.
Owing to the redundancy, the detailed analysis is omitted. The result is shown in Table 4.4. The row with ![]() corresponds to Equations (4.17)–(4.32). Table 4.4 is called a differential distribution table. Hereafter, the differential distribution table is denoted by DDT. Each entry of the DDT represents the number of values that satisfies
corresponds to Equations (4.17)–(4.32). Table 4.4 is called a differential distribution table. Hereafter, the differential distribution table is denoted by DDT. Each entry of the DDT represents the number of values that satisfies
of the corresponding ![]() and
and ![]() . The probability of the differential propagation is obtained by dividing the number in each entry with the number of possible values of x, that is,
. The probability of the differential propagation is obtained by dividing the number in each entry with the number of possible values of x, that is, ![]() . This indicates that the differential propagation whose entry is 4 occurs with a higher probability than the others.
. This indicates that the differential propagation whose entry is 4 occurs with a higher probability than the others.
Table 4.4 Differential distribution table of ![]()
| Output difference | |||||||||||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
||
0 |
16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1 |
0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | 4 | 0 | 0 | 2 | |
2 |
0 | 0 | 0 | 2 | 2 | 2 | 0 | 2 | 0 | 0 | 4 | 2 | 0 | 0 | 2 | 0 | |
3 |
0 | 0 | 2 | 0 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | |
4 |
0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 4 | 0 | 2 | 2 | 2 | |
5 |
0 | 2 | 4 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | |
6 |
0 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 2 | 0 | 0 | 2 | 2 | 2 | 0 | |
| Input | 7 |
0 | 0 | 0 | 2 | 2 | 2 | 2 | 0 | 2 | 4 | 0 | 0 | 2 | 0 | 0 | 0 |
| difference | 8 |
0 | 2 | 2 | 4 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 |
9 |
0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 4 | 0 | 2 | 0 | 2 | 2 | 0 | 2 | |
A |
0 | 2 | 0 | 0 | 2 | 0 | 0 | 4 | 2 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | |
B |
0 | 0 | 2 | 0 | 2 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | 4 | 0 | 0 | |
C |
0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 2 | 4 | 0 | |
D |
0 | 4 | 2 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | 0 | |
E |
0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 2 | 2 | |
F |
0 | 2 | 0 | 0 | 0 | 2 | 4 | 0 | 2 | 0 | 2 | 2 | 0 | 2 | 0 | 0 | |
The DDT of ![]() has several properties.
has several properties.
- Each entry is even: When
 , where
, where  , satisfies the differential propagation in Equation (4.51),
, satisfies the differential propagation in Equation (4.51),  ) always satisfies Equation (4.51). Hence, each entry of DDT is always an even number.
) always satisfies Equation (4.51). Hence, each entry of DDT is always an even number. - Deterministic propagation for zero difference:
 means that the pair has an identical value. Thus, the output value is also identical. When
means that the pair has an identical value. Thus, the output value is also identical. When  is
is  with probability 1.
with probability 1. - Minimizing differential probability: To avoid a high probability differential propagation, each entry of DDT should be as small as possible. Combining the above-mentioned two properties, the best design strategy of
 against the differential cryptanalysis is having one entry with 4 and six entries with 2 in all the rows and columns.
against the differential cryptanalysis is having one entry with 4 and six entries with 2 in all the rows and columns.
The S-box used in AES has the similar property to ![]() . Because the input and the output size of the AES S-box is 8 bits, or 256, the DDT of the AES S-box has 256 rows and 256 columns. Owing to its large size, the exact DDT is omitted in this book. Two important properties are summarized as follows.
. Because the input and the output size of the AES S-box is 8 bits, or 256, the DDT of the AES S-box has 256 rows and 256 columns. Owing to its large size, the exact DDT is omitted in this book. Two important properties are summarized as follows.
As an application to AES, the probability of the differential propagation for one round is explained below, which is described in Figure 4.12.
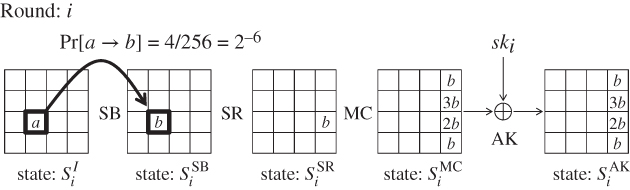
Figure 4.12 Differential propagation for AES one round
The analysis starts from two input values to the ![]() operation in round i denoted by state
operation in round i denoted by state ![]() . The input difference
. The input difference ![]() is set to have a nonzero byte difference a in the third row of the second column, that is,
is set to have a nonzero byte difference a in the third row of the second column, that is,
Then, the S-box is applied to all bytes in the state by the ![]() operation. From Lemma 4.2.8, for any nonzero input difference, there exists one output difference that will be produced with probability
operation. From Lemma 4.2.8, for any nonzero input difference, there exists one output difference that will be produced with probability ![]() . Denote the output difference by b. Thus, the difference of the output state
. Denote the output difference by b. Thus, the difference of the output state ![]() is
is
and the probability of the differential propagation is as follows:
The propagation from ![]() to
to ![]() is the same as the one in Figure 4.11. Then, with probability 1, the difference of the state
is the same as the one in Figure 4.11. Then, with probability 1, the difference of the state ![]() becomes as follows:
becomes as follows:
In the end, the following differential propagation with probability ![]() is obtained for AES one round.
is obtained for AES one round.
4.2.6 Probability of Differential Propagation for Multiple Rounds
Equation (4.33) in the definition of the probability of the differential propagation can be computed only if the computation size is small, that is, the value of z in Equation (4.33) is small. Namely, it can be evaluated for the 4-bit to 4-bit mapping ![]() or the 8-bit to 8-bit mapping of the AES S-box S, while it cannot be evaluated for a 128-bit to 128-bit mapping of the entire AES operation. The goal of the attacker is attacking as many rounds as possible, thus the analysis for a larger map is necessary.
or the 8-bit to 8-bit mapping of the AES S-box S, while it cannot be evaluated for a 128-bit to 128-bit mapping of the entire AES operation. The goal of the attacker is attacking as many rounds as possible, thus the analysis for a larger map is necessary.
When a differential propagation for multiple rounds is evaluated, the differential cryptanalysis iteratively applies the analysis for a single round by assuming that the probability of the differential propagation can be evaluated independently for each round. The validity of this assumption comes from the fact that the internal state value is XORed by an unknown subkey in every round. Suppose that all subkeys are chosen accordingly to the uniform distribution. Then, between two ![]() operations, the internal state value becomes uniformly random owing to the subkey XOR, which makes the probability evaluation of the two
operations, the internal state value becomes uniformly random owing to the subkey XOR, which makes the probability evaluation of the two ![]() operations independent. Note that the key schedule function of AES is not so strong that
operations independent. Note that the key schedule function of AES is not so strong that ![]() and
and ![]() can be completely random. In this sense, the assumption of the independent probability evaluation in different rounds is not true. However, to make the discussion simple, it is usually assumed that each subkey is chosen uniformly randomly. Hereafter, the same assumption is applied in thisbook.
can be completely random. In this sense, the assumption of the independent probability evaluation in different rounds is not true. However, to make the discussion simple, it is usually assumed that each subkey is chosen uniformly randomly. Hereafter, the same assumption is applied in thisbook.
An example analysis for AES reduced to two rounds (for round i and round ![]() ) is illustrated in Figure 4.13. The analysis for round i is the same as Figure 4.12, and another round is appended after the last state in round i.
) is illustrated in Figure 4.13. The analysis for round i is the same as Figure 4.12, and another round is appended after the last state in round i.

Figure 4.13 Differential propagation for AES two rounds
By following the assumption of the independence in different rounds, the probability of the differential propagation in round ![]() is evaluated independently from the one in round i. For each nonzero input difference to the S-box,
is evaluated independently from the one in round i. For each nonzero input difference to the S-box, ![]() , and
, and ![]() , Lemma 4.2.8 ensures that there exists one output difference that will be produced with probability
, Lemma 4.2.8 ensures that there exists one output difference that will be produced with probability ![]() . Let
. Let ![]() , and e be those output differences from the S-box. There are 4 bytes with a nonzero difference, and the probability that the propagation is achieved in all bytes simultaneously is obtained by multiplying the probability of each event. Thus,
, and e be those output differences from the S-box. There are 4 bytes with a nonzero difference, and the probability that the propagation is achieved in all bytes simultaneously is obtained by multiplying the probability of each event. Thus,
After the ![]() operation, the remaining is the linear computation, and thus the differential propagation is determined with probability 1. The probability of the differential propagation in round
operation, the remaining is the linear computation, and thus the differential propagation is determined with probability 1. The probability of the differential propagation in round ![]() shown in Figure 4.13 is concluded as:
shown in Figure 4.13 is concluded as:
Finally, the probability of the differential propagation for two rounds is obtained by multiplying the probability for round i and for round ![]() . Thus,
. Thus,
If the assumption of independence between different rounds is not used, the probability for round ![]() must be a conditional probability that the input value is the output of round i, that is,
must be a conditional probability that the input value is the output of round i, that is,
Evaluating the conditional probability especially for many rounds is hard (computationally infeasible). To make the analysis simple and effective, the differential cryptanalysis usually assumes the independence of differential propagations in different rounds.
4.2.7 Differential Characteristic for AES Reduced to Three Rounds
In the differential cryptanalysis, the attacker first chooses a pair of an input difference and an output difference that will be propagated with a high probability. How the difference will propagate in the attack between the chosen differences is called differential characteristic.
As explained so far, the probability of the differential characteristic decreases only by the ![]() operation. A byte with nonzero difference through the
operation. A byte with nonzero difference through the ![]() operation is called an active byte with respect to the difference, or simply an active byte. The attack strategy is choosing active-byte positions so that the number of active bytes is minimized.
operation is called an active byte with respect to the difference, or simply an active byte. The attack strategy is choosing active-byte positions so that the number of active bytes is minimized.
Regarding AES, a differential characteristic with a relatively high probability, ![]() , can be constructed up to three rounds, which is described in Figure 4.14. Its details are explained below. AES adopts different round functions for the middle rounds and the last round. In the differential cryptanalysis, the attacker later appends several rounds after the differential characteristic in order to recover the key. When the differential characteristic is constructed, only the round function for the middle rounds is considered.
, can be constructed up to three rounds, which is described in Figure 4.14. Its details are explained below. AES adopts different round functions for the middle rounds and the last round. In the differential cryptanalysis, the attacker later appends several rounds after the differential characteristic in order to recover the key. When the differential characteristic is constructed, only the round function for the middle rounds is considered.

Figure 4.14 Differential characteristic for AES three rounds with probability 
The last two rounds of the differential characteristic in Figure 4.14 are the same as the ones in Figure 4.13. The analysis starts from the single active byte at state ![]() whose difference is denoted by a. This is propagated to b after the
whose difference is denoted by a. This is propagated to b after the ![]() operation with a probability
operation with a probability ![]() . After the
. After the ![]() operation in round 2, a single active byte expands to 4 active bytes, and then those derive four differential propagation with probability
operation in round 2, a single active byte expands to 4 active bytes, and then those derive four differential propagation with probability ![]() for the
for the ![]() operation in round 3. The remaining computations in round 3 are linear computations, and thus the attacker obtains the corresponding difference at state
operation in round 3. The remaining computations in round 3 are linear computations, and thus the attacker obtains the corresponding difference at state ![]() with probability 1.
with probability 1.
Then, another round is appended to those two rounds. If one more round is appended in the end of the two rounds, that is, as round 4, the number of active bytes will increase by 16 bytes, which is inefficient. Therefore, another round is appended to the beginning of those two rounds, that is, as round 1. The attacker computes the propagation of the difference ![]() in the backward direction. The
in the backward direction. The ![]() operation simply computes XOR of the subkey
operation simply computes XOR of the subkey ![]() and the state value
and the state value ![]() . As shown in Lemma 4.2.4, the difference never changes with the constant XOR, which derives the following difference in state
. As shown in Lemma 4.2.4, the difference never changes with the constant XOR, which derives the following difference in state ![]() .
.
The inverse ![]() operation is then applied. No difference exists for the first, second, and the third columns. Thus, the difference after the inverse
operation is then applied. No difference exists for the first, second, and the third columns. Thus, the difference after the inverse ![]() operation is also 0. For the fourth column, the difference is computed as follows.
operation is also 0. For the fourth column, the difference is computed as follows.

As a result, the difference of the state ![]() becomes as
becomes as
In the inverse ![]() operation, each byte in row j, where
operation, each byte in row j, where ![]() , is rotated by j bytes to the right. This makes the difference of the state
, is rotated by j bytes to the right. This makes the difference of the state ![]() as
as
From Lemma 4.2.9, for any nonzero output difference of the S-box, there exists one input difference that is achieved with probability ![]() . Let
. Let ![]() , and i be the input differences to the S-box such that
, and i be the input differences to the S-box such that
This makes the difference of the state ![]() as
as
Finally, another ![]() operation is inverted, which does not affect the differential propagation. The plaintext difference
operation is inverted, which does not affect the differential propagation. The plaintext difference ![]() is the same as
is the same as ![]() , that is,
, that is,
As explained in the previous section, the total probability of the three-round differential characteristic in Figure 4.14 is the multiplication of the probability of each round evaluated independently, which is
4.2.8 Distinguishing Attack with Differential Characteristic
The three-round differential characteristic in Figure 4.14 can directly be used to attack the security notion of indistinguishability against AES reduced to three rounds. The attack is called a distinguishing attack. For simplicity, suppose that the attack model is the chosen plaintext attack, in which the attacker can query the plaintext of his choice to observe the corresponding ciphertext.
Recall Figure 4.2 that shows the indistinguishability framework. The attacker (observer) interacts with a 128-bit permutation that is either AES reduced to three rounds with an unknown key or a 128-bit random permutation. By observing plaintexts and ciphertexts, the attacker aims to distinguish which is implemented in the oracle. The output of the distinguisher is a single bit called a determining bit. If the attacker finds that AES reduced to three rounds is implemented, the distinguishing attack outputs a single bit 0 as the determining bit. If the attacker finds that a random permutation is implemented, the distinguishing attack outputs a single bit 1 as the determining bit.
In the attack procedure, the attacker queries ![]() plaintext pairs with a difference
plaintext pairs with a difference ![]() in Figure 4.14, and then checks whether or not one of the corresponding ciphertext pairs has a difference
in Figure 4.14, and then checks whether or not one of the corresponding ciphertext pairs has a difference ![]() in Figure 4.14.
in Figure 4.14.
- If the oracle implements AES reduced to three rounds, one of the pairs is expected to satisfy the differential characteristic with probability
 .
. - If the oracle implements a random permutation, the probability that the ciphertext difference becomes
 is
is  per pair. With a negligible probability, an event with probability
per pair. With a negligible probability, an event with probability  is satisfied by examining
is satisfied by examining  pairs.
pairs.
Therefore, if one of the ciphertext pairs has the difference ![]() , the attack returns 0 as the determining bit. Otherwise, it returns 1 as the determining bit. In Algorithm 4.4, the attack procedure is given in an algorithmic format.
, the attack returns 0 as the determining bit. Otherwise, it returns 1 as the determining bit. In Algorithm 4.4, the attack procedure is given in an algorithmic format.
The attack complexity of the distinguishing attack is evaluated as follows.
- The data complexity is
 chosen plaintexts.
chosen plaintexts. - The time complexity is
 XOR computational cost.
XOR computational cost. - The attack does not need to store intermediate values during the attack but for 1 ciphertext
 . Thus, the memory complexity is 1, or negligible.
. Thus, the memory complexity is 1, or negligible.
Note that when the event with probability ![]() is examined by
is examined by ![]() trials, the expectation number of the success is 1, but it does not ensure the success with probability 1. The success probability of the distinguishing attack can increase by spending more data and time complexities.
trials, the expectation number of the success is 1, but it does not ensure the success with probability 1. The success probability of the distinguishing attack can increase by spending more data and time complexities.
4.2.9 Key Recovery Attack after Differential Characteristic
Although the security of block cipher can be broken by the distinguishing attack, the attacker cannot recover the key value with the distinguishing attack. The differential cryptanalysis can also be used to recover the key. In general, compared to distinguishing attacks, key recovery attacks can attack more rounds while the attack complexity is higher.
The attacker appends a few more rounds to the end of the distinguisher, and the attacker aims to recover the last subkey value. The framework of the key recovery attack is illustrated in Figure 4.15. The key recovery attack starts from collecting several pairs of plaintexts satisfying the differential characteristic. Because a few more rounds are appended to the end of the distinguisher, the attacker cannot identify the pairs satisfying the differential characteristic. Hence, all the pairs are analyzed to recover the key. The pairs satisfying the differential characteristic are called right pairs, while the pairs not satisfying the differential characteristic are called wrong pairs. At the end of the differential characteristic, right pairs have the prespecified difference denoted by ![]() . The attacker exhaustively guesses the last subkey value and performs the partial decryption until the output state of the differential characteristic. The attacker then checks whether or not the difference of the intermediate state values is
. The attacker exhaustively guesses the last subkey value and performs the partial decryption until the output state of the differential characteristic. The attacker then checks whether or not the difference of the intermediate state values is ![]() .
.
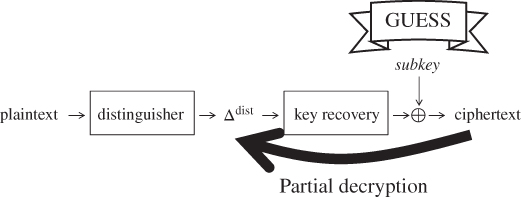
Figure 4.15 Framework of the key recovery attack
Here, the analytic results behave differently for right pairs and wrong pairs. If the pair is the right one and the subkey guess is right, the results of the state difference are always ![]() . In any other combination of right/wrong pair and right/wrong guess, such a deterministic event does not occur. The result of the partial decryption happens to be
. In any other combination of right/wrong pair and right/wrong guess, such a deterministic event does not occur. The result of the partial decryption happens to be ![]() probabilistically, which is much lower probability than 1. Therefore, by analyzing many pairs including right pairs and wrong pairs, the right guess reaches
probabilistically, which is much lower probability than 1. Therefore, by analyzing many pairs including right pairs and wrong pairs, the right guess reaches ![]() more than any other wrong guess, which allows the attacker to detect the right subkey value. The analysis is summarized below.
more than any other wrong guess, which allows the attacker to detect the right subkey value. The analysis is summarized below.
- Right pair with
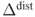 :
:
- Right guess always reaches
 .
. - Wrong guess reaches
 only probabilistically.
only probabilistically.
- Right guess always reaches
- Wrong pair:
- Right guess reaches
 only probabilistically.
only probabilistically. - Wrong guess reaches
 only probabilistically.
only probabilistically.
- Right guess reaches
As an exact procedure to recover the last subkey, the attacker draws the histogram describing how many times each key guess reaches ![]() after the partial decryption. The histogram is illustrated in Figure 4.16. Because the right guess reaches
after the partial decryption. The histogram is illustrated in Figure 4.16. Because the right guess reaches ![]() more than any other wrong guess, it makes the peak in the histogram, which shows the subkey value to the attacker.
more than any other wrong guess, it makes the peak in the histogram, which shows the subkey value to the attacker.

Figure 4.16 Histogram of subkey guess reaching 
Note that as shown in Figure 4.16, there might exist wrong key guesses that are close to the peak value. Moreover, the right guess might not be the peak value. However, this is not a big issue for the attack. The attacker can test several key candidates that are in a high position in the histogram. This method is called the ranking test. By using the ranking test, identifying several key candidates that are likely to be a correct key is sufficient.
From the recovered last subkey, the attacker recovers the original key K. AES uses the original key K as the first subkey ![]() . Because the key schedule function, KSF, is easily invertible, the attacker can compute the corresponding value of
. Because the key schedule function, KSF, is easily invertible, the attacker can compute the corresponding value of ![]() from any subkey by computing the inverse of the key schedule function as illustrated in Figure 4.17. Note that in many block ciphers, the key schedule function is designed in order to avoid the loss of the computation efficiency. Thus, the key schedule function is usually invertible, and recovering a subkey is sufficient to recover the original key K in many block ciphers including AES.
from any subkey by computing the inverse of the key schedule function as illustrated in Figure 4.17. Note that in many block ciphers, the key schedule function is designed in order to avoid the loss of the computation efficiency. Thus, the key schedule function is usually invertible, and recovering a subkey is sufficient to recover the original key K in many block ciphers including AES.

Figure 4.17 Converting subkey value to original key value
4.2.10 Basic Differential Cryptanalysis for Four-Round AES 
This section explains the key recovery attack against AES reduced to four rounds. One round is appended to the end of the three-round differential characteristic in Figure 4.14. The key recovery part of this attack is depicted in Figure 4.18. Note that to describe the subkey byte positions in detail, the figure of the round function changes from Figure 4.14. In addition, note that the last round function does not compute the ![]() operation.
operation.

Figure 4.18 Key recovery attack against four-round AES
All bytes in the ![]() operation in round 4 are active. After the
operation in round 4 are active. After the ![]() operation in round 4, the output difference is nonzero. The attacker does not know the exact difference but only knows that those bytes are active. In Figure 4.18, these type of bytes are filled in gray.
operation in round 4, the output difference is nonzero. The attacker does not know the exact difference but only knows that those bytes are active. In Figure 4.18, these type of bytes are filled in gray.
4.2.10.1 Filtering for Collecting Pairs
The first phase of the attack is collecting plaintext pairs that may follow the three-round differential characteristic in Figure 4.14. Because the probability of the three-round differential characteristic is ![]() , making at least
, making at least ![]() pairs of queries is necessary.
pairs of queries is necessary.
Here, the technique called filtering is introduced in order to maximize the attack efficiency. The purpose of filtering is to remove the pairs that cannot satisfy the differential characteristic with probability 1, which contributes to reducing the number of wrong pairs. To apply the filtering technique, more detailed properties of the S-box need to be considered.
Lemma 4.2.8 in Section 4.2.5 shows that for any fixed input difference, 129 output differences are never produced. In other words, only 127 output differences can be produced. As shown in Figure 4.18, the output difference of the ![]() operation in round 4, that is,
operation in round 4, that is, ![]() can be obtained directly from the ciphertext difference. Then, with the property of the S-box, the attacker can check whether or not the ciphertext difference in each byte is included in the 127 possible output differences from the S-box. The probability that each byte difference is included in the 127 possible output differences is
can be obtained directly from the ciphertext difference. Then, with the property of the S-box, the attacker can check whether or not the ciphertext difference in each byte is included in the 127 possible output differences from the S-box. The probability that each byte difference is included in the 127 possible output differences is ![]() . Thus, with 16 bytes, the probability is
. Thus, with 16 bytes, the probability is
The probability that a randomly generated ciphertext pair is a candidate of the one satisfying the differential characteristic is called filtering power, which is often denoted by a variable ![]() . As discussed earlier, the filtering power
. As discussed earlier, the filtering power ![]() of this attack is
of this attack is
4.2.10.2 Signal-to-Noise Ratio
The number of necessary right pairs to recover the key depends on the value called signal-to-noise ratio, which is often denoted by ![]() .1 In the histogram of the key suggestion in Figure 4.16, regarding the correct key, the number of key suggestions consists of two contributions. One is suggestion from the right pairs, which is called signal, and the other is suggestion from the wrong pairs, which is called noise. When the ratio of the signal to noise is big enough, the key is recovered. The concept of the signal-to-noise ratio is depicted in Figure 4.19.
.1 In the histogram of the key suggestion in Figure 4.16, regarding the correct key, the number of key suggestions consists of two contributions. One is suggestion from the right pairs, which is called signal, and the other is suggestion from the wrong pairs, which is called noise. When the ratio of the signal to noise is big enough, the key is recovered. The concept of the signal-to-noise ratio is depicted in Figure 4.19.

Figure 4.19 Signal-to-noise ratio
Suppose that the attacker queries N chosen plaintext pairs, and the probability of the characteristic is p. In addition, suppose that the bit size of the subkey guess is k and the filtering power of the attack is ![]() . In the following, the amount of signal and noise is evaluated and their ratio is calculated. Note that the numbers for the attack in Figure 4.18 are
. In the following, the amount of signal and noise is evaluated and their ratio is calculated. Note that the numbers for the attack in Figure 4.18 are ![]() , and
, and ![]() .
.
- Signal: Signal is the right key suggestion from right pairs. For each right pair, the partial decryption with the right guess is performed once. Hence, the amount of signal is equal to the amount of the right pair. Because N pairs are queried and the probability of the characteristic is p, the amount of signal is
4.74

- Noise: Noise is the right key suggestion from wrong pairs. (In the attack in Figure 4.18, the combination of the right pair and the wrong guess never suggests the right key.) The number of wrong pairs is
4.75

for small p. After the filtering technique is applied,
4.76
wrong pairs remain. Then, the number of key suggestions (including both right and wrong ones) from each remaining wrong pair is counted. By following the convention, let
 be this number. The total number of key suggestions from all wrong pairs can be evaluated as4.77
be this number. The total number of key suggestions from all wrong pairs can be evaluated as4.77
When it comes to the attack in Figure 4.18, the evaluation of
 is done in each byte. From Lemma 4.2.8 in Section 4.2.5, for 126 difference values, two key values are suggested, and for one difference value, four key values are suggested. Roughly speaking, two keys are suggested for each byte. In the attack in Figure 4.18, 8 subkey bytes are guessed. Thus,
is done in each byte. From Lemma 4.2.8 in Section 4.2.5, for 126 difference values, two key values are suggested, and for one difference value, four key values are suggested. Roughly speaking, two keys are suggested for each byte. In the attack in Figure 4.18, 8 subkey bytes are guessed. Thus,  is the number of all the combinations of two suggestions for each of the 8 bytes, that is,4.78
is the number of all the combinations of two suggestions for each of the 8 bytes, that is,4.78
Finally, the amount of the right key suggestions out of
 wrong suggestions is counted. It is assumed that wrong suggestions are generated according to the uniform distribution. Because the bit size of guessed subkeys is k, the probability that a randomly generated wrong suggestion is for the right key is
wrong suggestions is counted. It is assumed that wrong suggestions are generated according to the uniform distribution. Because the bit size of guessed subkeys is k, the probability that a randomly generated wrong suggestion is for the right key is  . All in all, the amount of noise is represented by4.79
. All in all, the amount of noise is represented by4.79
 : By calculating the ratio of the signal to noise,
: By calculating the ratio of the signal to noise,  is represented as follows:
4.80
is represented as follows:
4.80 4.81
4.81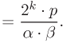
It is known that when
 is bigger than 1, collecting two right pairs is enough to identify the right key by using the ranking test.
is bigger than 1, collecting two right pairs is enough to identify the right key by using the ranking test.
4.2.10.3 Collecting Pairs
The signal-to-noise ratio of the attack in Figure 4.18 is as follows:
Because ![]() is big enough, two right pairs are enough to recover the key. From the condition
is big enough, two right pairs are enough to recover the key. From the condition ![]() , the number of queried messages is
, the number of queried messages is ![]() pairs, which is
pairs, which is ![]() encryption oracle calls.
encryption oracle calls.
For the obtained ciphertext pairs, the filtering technique is applied, that is, the attacker confirms that the ciphertext difference in each byte can be produced from ![]() . The pairs that do not satisfy the filtering are immediately discarded. The filtering power
. The pairs that do not satisfy the filtering are immediately discarded. The filtering power ![]() is
is ![]() . After the filtering, the number of remaining pairs becomes
. After the filtering, the number of remaining pairs becomes
4.2.10.4 Recovering the Last Subkey
Let ![]() for
for ![]() be the obtained ciphertext pairs. The attacker exhaustively guesses the left two columns of the last subkey value
be the obtained ciphertext pairs. The attacker exhaustively guesses the left two columns of the last subkey value ![]() , and partially decrypts each ciphertext pair up to state
, and partially decrypts each ciphertext pair up to state ![]() . With the guessed value of 8 bytes of
. With the guessed value of 8 bytes of ![]() , 8 bytes of
, 8 bytes of ![]() can be computed by taking XOR with the ciphertext pair. The
can be computed by taking XOR with the ciphertext pair. The ![]() operation can be easily inverted because it only changes the byte positions. For the 8 computed bytes in
operation can be easily inverted because it only changes the byte positions. For the 8 computed bytes in ![]() , the
, the ![]() operation can be inverted by looking up the inverse S-box. As a result, 8 bytes of
operation can be inverted by looking up the inverse S-box. As a result, 8 bytes of ![]() can be computed. The computed byte positions are stressed by bold line in Figure 4.18.
can be computed. The computed byte positions are stressed by bold line in Figure 4.18.
To generate a histogram of the key suggestion, the attacker prepares a memory to store counter values for all the ![]() 8-byte values of
8-byte values of ![]() . All the counter values are initialized to 0 at the beginning. If the difference of the partially decrypted 8 bytes in
. All the counter values are initialized to 0 at the beginning. If the difference of the partially decrypted 8 bytes in ![]() matches the output difference from the differential characteristic, the attacker increases the counter for the corresponding 8-byte value of
matches the output difference from the differential characteristic, the attacker increases the counter for the corresponding 8-byte value of ![]() . After the analysis for all the pairs and all the 8-byte guesses of
. After the analysis for all the pairs and all the 8-byte guesses of ![]() , the guess of
, the guess of ![]() with the highest counter value is the right value. Hence, 8 bytes of
with the highest counter value is the right value. Hence, 8 bytes of ![]() are successfully recovered.
are successfully recovered.
4.2.10.5 Recovery of the Key
Independently, the attack applies the last subkey recovery procedure for the right two columns of ![]() , that is,
, that is, ![]() . The correspondence of the guessed byte positions and the ones in
. The correspondence of the guessed byte positions and the ones in ![]() is shown in Figure 4.20. The pair collection part can be shared with the analysis for the left half of
is shown in Figure 4.20. The pair collection part can be shared with the analysis for the left half of ![]() . Only the subkey recovery part is independently processed of the left half.
. Only the subkey recovery part is independently processed of the left half.

Figure 4.20 Recovery of the right half of 
By combining the recovered values of the left half and the right half, ![]() is fully recovered. Then, by computing
is fully recovered. Then, by computing ![]() from
from ![]() with the inverse of the key schedule function as illustrated in Figure 4.17, the original key K is successfully recovered.
with the inverse of the key schedule function as illustrated in Figure 4.17, the original key K is successfully recovered.
4.2.10.6 Attack Procedure
The entire attack procedure is described in Algorithm 4.5. Here, ![]() and
and ![]() are variables to denote 8-byte guesses for the left half of
are variables to denote 8-byte guesses for the left half of ![]() and the right half of
and the right half of ![]() , respectively.
, respectively.
4.2.10.7 Complexity Evaluation
In Algorithm 4.5, queries are made only in step 4, which is ![]() pairs of
pairs of ![]() . Thus, the number of query is
. Thus, the number of query is ![]() chosen plaintexts.
chosen plaintexts.
Regarding the pair collection phase, the computational cost is ![]() XOR computations. The memory requirement is storing
XOR computations. The memory requirement is storing ![]() pairs of
pairs of ![]() , which is
, which is ![]() AES state values. The computational cost and the memory requirement are negligibly small compared to the subkey recovery part.
AES state values. The computational cost and the memory requirement are negligibly small compared to the subkey recovery part.
Regarding the left half of the ![]() recovery phase, the computational cost is
recovery phase, the computational cost is ![]() AES round function computations. The memory requirement is storing counter values for
AES round function computations. The memory requirement is storing counter values for ![]() subkey candidates. The same computational cost is required for the recovery of the right half of
subkey candidates. The same computational cost is required for the recovery of the right half of ![]() . No additional memory is required for the right half of
. No additional memory is required for the right half of ![]() because the memory used for the analysis on the left half can be overwritten.
because the memory used for the analysis on the left half can be overwritten.
Recovering K only requires a negligible cost compared to the other steps. In the end, the computational cost for the entire attack is ![]() AES round function computations for the left half of
AES round function computations for the left half of ![]() and
and ![]() AES roundfunction computations for the right half of
AES roundfunction computations for the right half of ![]() , which is
, which is ![]() AES round function computations. The computational cost is often measured by how many times the entire encryption algorithm is computed. Because the entire structure consists of four rounds, the cost of one round is
AES round function computations. The computational cost is often measured by how many times the entire encryption algorithm is computed. Because the entire structure consists of four rounds, the cost of one round is ![]() of the entire structure. The attack complexity is
of the entire structure. The attack complexity is ![]() computations of AES reduced to four rounds.
computations of AES reduced to four rounds.
In summary, the attack complexity is as follows.
This is significantly smaller than the generic attack complexity in Equation (4.6), that is, ![]() . Therefore, AES reduced to four rounds are vulnerable against the differential cryptanalysis.
. Therefore, AES reduced to four rounds are vulnerable against the differential cryptanalysis.
4.2.11 Advanced Differential Cryptanalysis for Four-Round AES 
The above simple differential cryptanalysis can be improved so that the attack requires a much smaller cost. The bottleneck of the attack complexity lies in recovering ![]() . Two techniques to improve this part are introduced in this section.
. Two techniques to improve this part are introduced in this section.
4.2.11.1 Minimizing Guessed Subkey Size
To recover the key in the differential cryptanalysis, keeping the signal-to-noise ratio, ![]() , high enough is important. The number of the guessed subkey bytes is heavily related to the derivation of
, high enough is important. The number of the guessed subkey bytes is heavily related to the derivation of ![]() . Recall Equations (4.82) and (4.83).
. Recall Equations (4.82) and (4.83). ![]() is enough to make the attack efficient, while the current
is enough to make the attack efficient, while the current ![]() ratio is too high. Hence, the number of the guessed subkey bytes can be reduced, which contributes to reducing the attack complexity. In Figure 4.18, 8 bytes of
ratio is too high. Hence, the number of the guessed subkey bytes can be reduced, which contributes to reducing the attack complexity. In Figure 4.18, 8 bytes of ![]() are guessed, that is,
are guessed, that is, ![]() . Here, the new attack guesses only 6 bytes of
. Here, the new attack guesses only 6 bytes of ![]() . The guessed subkey byte positions and the partial decryption up to
. The guessed subkey byte positions and the partial decryption up to ![]() are shown in Figure 4.21.
are shown in Figure 4.21.

Figure 4.21 Key recovery with 6-byte guess of 
The new ![]() ratio becomes
ratio becomes
which is bigger than 1.
Another improvement is that after the 6 bytes of ![]() are recovered, the attack does not have to iterate the same procedure for the other 10 bytes. The recovered 6 bytes of
are recovered, the attack does not have to iterate the same procedure for the other 10 bytes. The recovered 6 bytes of ![]() can be used to filter out wrong pairs. Given the fixed subkey value
can be used to filter out wrong pairs. Given the fixed subkey value ![]() , the probability that
, the probability that ![]() becomes the target byte difference at
becomes the target byte difference at ![]() is
is ![]() . Thus, the number of wrong pairs after the filtering with recovered 6 subkey bytes is
. Thus, the number of wrong pairs after the filtering with recovered 6 subkey bytes is
which indicates that only two right pairs will survive after the filtering. Therefore, once 6 bytes of ![]() are recovered, the other 10 bytes of
are recovered, the other 10 bytes of ![]() can be recovered trivially, and its complexity can be ignored.
can be recovered trivially, and its complexity can be ignored.
4.2.11.2 Deriving Key Suggestions without Guess
In the basic attack, 8 bytes of ![]() are exhaustively guessed, and then the corresponding differences at
are exhaustively guessed, and then the corresponding differences at ![]() are computed. If the computed differences at
are computed. If the computed differences at ![]() do not match the target, no key suggestion can be obtained. In other words, this is a waste of the computation power.
do not match the target, no key suggestion can be obtained. In other words, this is a waste of the computation power.
This procedure can be modified so that only computations contributing to the key suggestion are performed.
The procedure is the same until ![]() wrong pairs are obtained after the filtering technique. Recall the procedure of applying the filtering technique. For each ciphertext pair, the attacker computes the corresponding difference at state
wrong pairs are obtained after the filtering technique. Recall the procedure of applying the filtering technique. For each ciphertext pair, the attacker computes the corresponding difference at state ![]() and checks if all byte differences can be produced by
and checks if all byte differences can be produced by ![]() specified by the differential characteristic. An important fact here is that both of the input and output difference for S-boxes in round 4 are determined without determining the subkey values
specified by the differential characteristic. An important fact here is that both of the input and output difference for S-boxes in round 4 are determined without determining the subkey values ![]() .
.
Recall Lemmas 4.2.8 and 4.2.9, which specify the property of the AES S-box. When an input difference ![]() and an output difference
and an output difference ![]() for the S-box with nonzero probability are given, they have two solutions (values satisfying the differential propagation of the S-box) with probability
for the S-box with nonzero probability are given, they have two solutions (values satisfying the differential propagation of the S-box) with probability ![]() and four solutions with probability
and four solutions with probability ![]() . Here, the new strategy is preparing the look-up table
. Here, the new strategy is preparing the look-up table ![]() that takes a pair of
that takes a pair of ![]() as input and returns all values x such that
as input and returns all values x such that ![]() as shown in Figure 4.22.
as shown in Figure 4.22.

Figure 4.22 Look-up table returning all solutions for S-box
The procedure to obtain key suggestions for a pair of ciphertexts ![]() is explained below.
is explained below.
- The difference is computed from
 to
to  , and the filtering technique is applied to eliminate wrong pairs.
, and the filtering technique is applied to eliminate wrong pairs. - With the look-up table
 , obtain all combinations of solutions for each S-box. Because each byte has about two solutions, the attacker obtains about
, obtain all combinations of solutions for each S-box. Because each byte has about two solutions, the attacker obtains about  combinations of the solutions for each byte.
combinations of the solutions for each byte. - For each of the
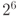 combined solutions, the values of the 6 bytes of
combined solutions, the values of the 6 bytes of  are fixed. The key suggestions for 6 bytes of
are fixed. The key suggestions for 6 bytes of  are obtained by computing
4.91
are obtained by computing
4.91
Note that
 suggests the same key value, thus does not have to be computed.
suggests the same key value, thus does not have to be computed.
The procedure is illustrated in Figure 4.23.

Figure 4.23 Efficient key suggestions derivation
4.2.11.3 Attack Procedure
The updated attack procedure is described in Algorithm 4.6. The pair collection phase is not included in Algorithm 4.6. Instead, the attacker derives the suggestions as soon as each pair satisfying the filtering condition is obtained. This is another optimization of the attack. Unfortunately, because the pair collection phase is not the bottleneck of the attack complexity, this optimization does not contribute to reducing the entire attack complexity. However, the technique is useful when the fault analysis is improved with theoretical cryptanalytic techniques in Chapter 6.
4.2.11.4 Complexity Evaluation
In Algorithm 4.6, queries are made in the same manner as Algorithm 4.5. Thus, the number of queries is the same as Algorithm 4.5, which is ![]() chosen plaintexts.
chosen plaintexts.
Regarding the procedure for recovering the first 6 bytes of ![]() , the computational cost is
, the computational cost is ![]() XOR computations in step 5. After the filtering technique is applied in step 6, only
XOR computations in step 5. After the filtering technique is applied in step 6, only ![]() pairs are examined. Therefore, step 10 requires
pairs are examined. Therefore, step 10 requires ![]() AES one-round computation. The memory requirement is for storing
AES one-round computation. The memory requirement is for storing ![]() counter values and
counter values and ![]() pairs of
pairs of ![]() .
.
The procedure after recovering ![]() is at most
is at most ![]() , which is much smaller than the other part. Thus, the computational cost for the entire attack is
, which is much smaller than the other part. Thus, the computational cost for the entire attack is ![]() XOR computations.
XOR computations.
In summary, the attack complexity is as follows.
Compared to the attack complexity for the basic attack in Equation (4.86), the complexity of the advanced attack is improved significantly.
4.2.12 Preventing Differential Cryptanalysis 
The essence of the differential cryptanalysis is a differential characteristic satisfied with a high probability. In other words, by avoiding a high probability differential characteristic, the differential cryptanalysis can be prevented. As explained so far, the probability of the differential characteristic decreases only when a difference goes through the S-box. Let ![]() be the maximum probability of the differential propagation in a single S-box. Let
be the maximum probability of the differential propagation in a single S-box. Let ![]() be the total number of active S-boxes in a characteristic. Then, the maximum probability of the differential characteristic is bounded by
be the total number of active S-boxes in a characteristic. Then, the maximum probability of the differential characteristic is bounded by
In AES, from Lemma 4.2.8, the maximum probability of the differential propagation in a single S-box is ![]() . Thus, the entire probability of the differential characteristic is bounded by
. Thus, the entire probability of the differential characteristic is bounded by
On the one hand, the differential cryptanalysis needs to collect at least one pair of plaintext to satisfy the differential characteristic. Thus, the attack on AES needs to query at least ![]() pairs. On the other hand, the number of texts that the attack can query is upper-bounded by
pairs. On the other hand, the number of texts that the attack can query is upper-bounded by ![]() , where b is the bit-length of the block size. For AES, b is 128. Therefore, satisfying the differential characteristic of AES becomes impossible if the number of active S-boxes,
, where b is the bit-length of the block size. For AES, b is 128. Therefore, satisfying the differential characteristic of AES becomes impossible if the number of active S-boxes, ![]() , satisfies the following condition:
, satisfies the following condition:
AES was designed so that
is guaranteed for four rounds. Therefore, the full-round (10-round) AES is expected to resist the differential cryptanalysis even if a few rounds are appended for the key recovery part around the differential characteristic. The strategy of proving the number of minimum active S-boxes in AES is called a wide trail strategy.
4.2.12.1 Wide Trail Strategy for Four-Round AES
The rough sketch of the wide trail strategy is introduced below. A differential propagation for four rounds, from round i to round ![]() , is considered. Those four rounds are illustrated in Figure 4.24. As long as two different plaintexts are encrypted under the same key, each internal state has nonzero difference in at least 1 byte.
, is considered. Those four rounds are illustrated in Figure 4.24. As long as two different plaintexts are encrypted under the same key, each internal state has nonzero difference in at least 1 byte.

Figure 4.24 Proof of minimum number of active S-boxes for AES four rounds. Gray byte shows an example of the differential propagation for  and
and 
The analysis starts from 1 active column for the ![]() operation in round
operation in round ![]() . To complete the proof, four cases starting from 1 to 4 active columns must be evaluated. In this book, only the case with one active column is explained. The analysis is irrespective of the position of the one active column. In Figure 4.24, the second column is chosen as an example.
. To complete the proof, four cases starting from 1 to 4 active columns must be evaluated. In this book, only the case with one active column is explained. The analysis is irrespective of the position of the one active column. In Figure 4.24, the second column is chosen as an example.
From the property of the MDS matrix in the ![]() operation, the sum of the number of active bytes before and after the
operation, the sum of the number of active bytes before and after the ![]() operation is at least 5. Let
operation is at least 5. Let ![]() and
and ![]() be the number of active bytes before the
be the number of active bytes before the ![]() operation,
operation, ![]() , and after the
, and after the ![]() operation,
operation, ![]() , respectively. Then, the following condition is obtained.
, respectively. Then, the following condition is obtained.
Those derive ![]() active S-boxes for the
active S-boxes for the ![]() operation in round
operation in round ![]() and
and ![]() active S-boxes for the
active S-boxes for the ![]() operation in round
operation in round ![]() . At this stage, together with Equation (4.98),
. At this stage, together with Equation (4.98),
is proven for AES reduced to two rounds.
Consider propagating the difference at ![]() in the forward direction.
in the forward direction. ![]() active bytes in
active bytes in ![]() are located in one column. Those move to different columns by the next
are located in one column. Those move to different columns by the next ![]() operation in round
operation in round ![]() . In other words, the probability that several active bytes move to the same column is ensured to be 0. Therefore, at state
. In other words, the probability that several active bytes move to the same column is ensured to be 0. Therefore, at state ![]() , there are
, there are ![]() active columns with 1 active byte. After the subsequent
active columns with 1 active byte. After the subsequent ![]() operation, those make 4 bytes active in
operation, those make 4 bytes active in ![]() columns. Finally,
columns. Finally, ![]() active bytes are ensured for the
active bytes are ensured for the ![]() operation in round
operation in round ![]() .
.
Consider propagating the difference at ![]() in the backward direction.
in the backward direction. ![]() active bytes in
active bytes in ![]() are located in one column. Those move to different columns by the next inverse
are located in one column. Those move to different columns by the next inverse ![]() operation in round
operation in round ![]() . Therefore, at state
. Therefore, at state ![]() , there are
, there are ![]() active columns with 1 active byte. After the next inverse
active columns with 1 active byte. After the next inverse ![]() operation, those make 4 bytes active in
operation, those make 4 bytes active in ![]() columns. Finally,
columns. Finally, ![]() active columns are ensured for the
active columns are ensured for the ![]() operation in round i.
operation in round i.
As a result, the number of active S-boxes, ![]() , for AES reduced to four rounds is at least
, for AES reduced to four rounds is at least
From Equation (4.98), the following result is obtained.
As explained before, it ensures that the maximum number of rounds of the differential characteristic for AES that can be used for the attack is 3. The differential characteristic in Figure 4.14 is an example of this case. It also indicates that breaking full-round AES with the differential cryptanalysis is almost impossible.
4.2.12.2 Recent Design Trend and Role of Differential Cryptanalysis
Most of the recent block cipher designs have some security proof so that the cipher can resist the basic differential cryptanalysis. Hence, the theoretical attack with the differential cryptanalysis is impossible for those designs.
The differential cryptanalysis is a base of many other advanced cryptanalytic techniques. Thus, learning its mechanism is useful to learn other attacks. Moreover, when the attacker can exploit the fault injections, the differential cryptanalysis becomes one of the most powerful approaches owing to its simplicity. Differential cryptanalysis combined with fault analysis will be explained in Chapter 6.
4.3 Impossible Differential Cryptanalysis
4.3.1 Basic Concept and Definition
There are several cryptanalyses using an impossible event of the encryption or decryption algorithm. Cryptanalysis with impossible differential propagation was independently found by Knudsen and Biham and Shamir. It exploits a differential propagation that is never satisfied.
An example of impossible differential characteristic is zero input difference and nonzero output difference, that is,
Similarly, when F is a bijective function, the differential propagation from nonzero input difference to zero output difference is impossible, that is,
The basic idea to utilize an impossible differential characteristic in order to recover the key is as follows, which is also illustrated in Figure 4.25. Suppose that there is a plaintext pair ![]() and the corresponding ciphertext pair
and the corresponding ciphertext pair ![]() . In addition, suppose that
. In addition, suppose that ![]() , that is,
, that is, ![]() is an impossible differential characteristic with respect to F. To recover the key, the attacker exhaustively guesses the last subkey value and partially decrypts C and
is an impossible differential characteristic with respect to F. To recover the key, the attacker exhaustively guesses the last subkey value and partially decrypts C and ![]() until the output state of F. If the difference of the partially decrypted results becomes
until the output state of F. If the difference of the partially decrypted results becomes ![]() , the subkey guess is wrong, and it can be removed from subkey candidates. The attack recovers the right key by eliminating all wrong subkey guesses.
, the subkey guess is wrong, and it can be removed from subkey candidates. The attack recovers the right key by eliminating all wrong subkey guesses.

Figure 4.25 Mechanism of impossible differential cryptanalysis
A comparison of the differential cryptanalysis and the cryptanalysis with impossible differential characteristic is given below.
- In the differential cryptanalysis, the attacker aims to construct a differential characteristic that is satisfied with a high probability, and aims to detect the right key from the obtained key suggestions.
- In the cryptanalysis with impossible differential propagation, the attacker aims to construct a differential characteristic that is satisfied with probability 0, and aims to discard all the wrong guesses from the obtained key suggestions.
The analysis is often termed impossible differential cryptanalysis. In this book, the term impossible differential cryptanalysis is used by following the convention of the cryptographic community.
As shown in Figure 4.25, the attack consists of two parts:
- constructing impossible differential characteristic, and
- appending several rounds for recovering subkey value.
4.3.2 Impossible Differential Characteristic for 3.5-round AES
Impossible differential characteristics can be constructed for 3.5 rounds of AES. Here, 0.5 round represents a composition of the ![]() and
and ![]() operations. 3.5 rounds cover from state
operations. 3.5 rounds cover from state ![]() to
to ![]() as shown in Figure 4.26.
as shown in Figure 4.26.

Figure 4.26 Impossible differential characteristic for 3.5-round AES. Gray bytes denote active bytes. During the differential trace in forwards, active bytes are colored in light gray. During the differential trace in backwards, active bytes are colored in dark gray
The input difference ![]() to 3.5 rounds has nonzero difference only in 1 byte. The active byte can be located in any position. In Figure 4.26, the byte position
to 3.5 rounds has nonzero difference only in 1 byte. The active byte can be located in any position. In Figure 4.26, the byte position ![]() is chosen as an example. The input difference
is chosen as an example. The input difference ![]() is described as follows:
is described as follows:
where ![]() represents a nonzero difference, that is,
represents a nonzero difference, that is, ![]() . Similarly to the differential cryptanalysis, a byte with nonzero difference is called active.
. Similarly to the differential cryptanalysis, a byte with nonzero difference is called active.
The output difference ![]() from 3.5 rounds also has nonzero difference only in 1 byte. The active byte can be located in any position. In Figure 4.26, the byte position
from 3.5 rounds also has nonzero difference only in 1 byte. The active byte can be located in any position. In Figure 4.26, the byte position ![]() is chosen as an example. The output difference
is chosen as an example. The output difference ![]() is described as follows.
is described as follows.
where ![]() represents a nonzero difference independent of
represents a nonzero difference independent of ![]() .
.
The impossible differential characteristic in Figure 4.26 can be formally summarized in the following lemma.
4.3.2.1 Another Impossible Differential Characteristic for 3.5-Round AES
The form of the output difference of the 3.5-round impossible differential characteristic ![]() can be chosen from many other choices. For example, the number of active bytes can be increased up to 12 bytes:
can be chosen from many other choices. For example, the number of active bytes can be increased up to 12 bytes:
The characteristic is described in Figure 4.27. Owing to the similarity to the previous 3.5-round impossible differential characteristic, the detailed proof is omitted. In short, the 1.5-round computation in the backward direction from ![]() always makes 4 bytes inactive, which contradicts to the result of the two-round computation in the forward direction from state
always makes 4 bytes inactive, which contradicts to the result of the two-round computation in the forward direction from state ![]() .
.

Figure 4.27 Another impossible differential characteristic for 3.5-round AES
It is hard to conclude which of the 3.5-round impossible differential characteristics is stronger. The attacker needs to carefully choose which 3.5-round impossible differential characteristic is used to optimize the entire attack.
4.3.3 Key Recovery Attacks for Five-Round AES
To demonstrate how the key recovery part works, the simple attack for AES reduced to five rounds is explained. In this attack, one round is added as the key recovery part before the 3.5-round impossible differential characteristic in Figure 4.27. The attack supposes that the AES last round function is used in the last round of the reduced-round variant. The attack structure is described in Figure 4.28. The attack first aims to recover 4 bytes of the first subkey ![]() .
.

Figure 4.28 Key recovery attack for five-round AES
In Figure 4.28, the ![]() operation is added to the end of the 3.5-round distinguisher. Because the
operation is added to the end of the 3.5-round distinguisher. Because the ![]() operation does not change the difference, the 3.5-round impossible differential characteristic can be extended to include the ciphertext difference of the form
operation does not change the difference, the 3.5-round impossible differential characteristic can be extended to include the ciphertext difference of the form
The input difference to the 3.5-round impossible differential characteristic is propagated in the backward direction by one round. It determines the active-byte positions of the plaintext, which are represented as
The exact value of ![]() can be any nonzero value, and can be determined independently for 4 bytes. For simplicity, the following discussion assumes that
can be any nonzero value, and can be determined independently for 4 bytes. For simplicity, the following discussion assumes that ![]() is fixed to one choice of the above form, and the attack is later optimized by relaxing this assumption.
is fixed to one choice of the above form, and the attack is later optimized by relaxing this assumption.
4.3.3.1 Collecting Pairs
The first phase of the attack is collecting many pairs of plaintexts whose corresponding ciphertext difference satisfies the form of ![]() . For simplicity, the attack assumes the chosen plaintext attack model so that the attacker can always choose the pair of plaintexts with the specified difference
. For simplicity, the attack assumes the chosen plaintext attack model so that the attacker can always choose the pair of plaintexts with the specified difference ![]() . Let
. Let ![]() be the number of plaintext pairs queried to the encryption oracle. The probability that a randomly chosen pair has the difference
be the number of plaintext pairs queried to the encryption oracle. The probability that a randomly chosen pair has the difference ![]() at the ciphertext is
at the ciphertext is ![]() because inactive 4 bytes (32 bits) must have difference zero. Thus, the number of pairs satisfying
because inactive 4 bytes (32 bits) must have difference zero. Thus, the number of pairs satisfying ![]() is
is
4.3.3.2 Recovery of Subkey 
The attacker aims to derive wrong key suggestions that generate ![]() at the input state to the 3.5-round impossible differential characteristic. Because the
at the input state to the 3.5-round impossible differential characteristic. Because the ![]() operation does not change the difference, computing
operation does not change the difference, computing ![]() is sufficient, which avoids guessing the subkey value
is sufficient, which avoids guessing the subkey value ![]() .
.
The simple method is guessing the 4 bytes of ![]() , and applying the partial encryption from
, and applying the partial encryption from ![]() to
to ![]() . However, as explained in the advanced differential cryptanalysis, wrong key suggestions can be derived more efficiently. Because the
. However, as explained in the advanced differential cryptanalysis, wrong key suggestions can be derived more efficiently. Because the ![]() operation with
operation with ![]() does not change the difference,
does not change the difference, ![]() .
. ![]() is chosen by the attacker, thus
is chosen by the attacker, thus ![]() is known to the attacker for each pair.
is known to the attacker for each pair.
The attacker then chooses the difference of the active byte at state ![]() . It can be any value but for 0, thus chosen from 255 choices. For each of the 255 choices of
. It can be any value but for 0, thus chosen from 255 choices. For each of the 255 choices of ![]() , the corresponding difference
, the corresponding difference ![]() is uniquely computed by applying the inverse
is uniquely computed by applying the inverse ![]() and the inverse
and the inverse ![]() operations. The 255 results of
operations. The 255 results of ![]() are stored in a look-up table
are stored in a look-up table ![]() , where
, where ![]() . More precisely,
. More precisely, ![]() contains a 4-byte difference of
contains a 4-byte difference of ![]() , which is derived from
, which is derived from ![]() with active-byte difference value i.
with active-byte difference value i.
The values of the pair that maps the fixed ![]() to each of the 255
to each of the 255 ![]() stored in
stored in ![]() can be easily obtained by exploiting the property of the AES S-box. From Lemmas 4.2.8 and 4.2.9, for a randomly fixed input difference and an output difference of the S-box, the number of paired values that can achieve this propagation is as follows.
can be easily obtained by exploiting the property of the AES S-box. From Lemmas 4.2.8 and 4.2.9, for a randomly fixed input difference and an output difference of the S-box, the number of paired values that can achieve this propagation is as follows.
- two paired values with probability
 ,
, - four paired values with probability
 , and
, and - the propagation is impossible (0 paired value) with probability
 .
.
For each plaintext pair with a fixed ![]() , the match with
, the match with ![]() is examined for
is examined for ![]() with respect to four active S-boxes. The expected number of solutions for one pair is
with respect to four active S-boxes. The expected number of solutions for one pair is
By examining 255 ![]() , 255 paired values that map the fixed
, 255 paired values that map the fixed ![]() to the desired
to the desired ![]() are expected.
are expected.
With the plaintext pair ![]() and the state value pair
and the state value pair ![]() , the corresponding subkey value
, the corresponding subkey value ![]() can be computed by simply XORing those values, that is,
can be computed by simply XORing those values, that is,
Those two values lead to the impossible differential characteristic, and thus known to be wrong. The attacker can discard those two values from candidate values for ![]() . Note that the above-mentioned procedure derives
. Note that the above-mentioned procedure derives ![]() values of
values of ![]() . However, each value is counted twice. Thus, the number of distinct values of
. However, each value is counted twice. Thus, the number of distinct values of ![]() is 255. By using 255 paired values of the internal state
is 255. By using 255 paired values of the internal state ![]() , 255 wrong key values are discarded. The idea of the efficient key derivation is summarized in Figure 4.29.
, 255 wrong key values are discarded. The idea of the efficient key derivation is summarized in Figure 4.29.
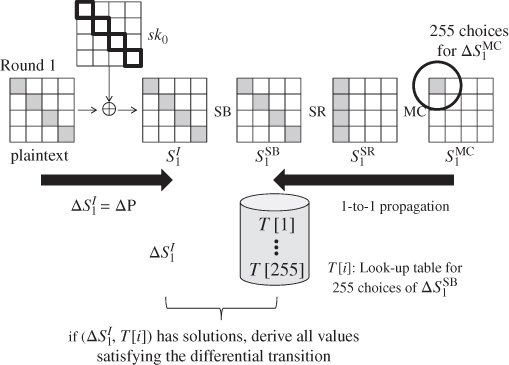
Figure 4.29 Efficient derivation of wrong subkey suggestions
4.3.3.3 The Number of Plaintext Pairs
After the pair collection phase, the attacker obtains ![]() pairs that also satisfy the output difference
pairs that also satisfy the output difference ![]() . Because each pair can derive 255 wrong key suggestions of
. Because each pair can derive 255 wrong key suggestions of ![]() ,
,
wrong key suggestions are obtained in total.
What is the minimum value of N to identify the right value of 32-bit subkey ![]() ? Obtaining
? Obtaining ![]() wrong key suggestions, that is,
wrong key suggestions, that is, ![]() , is not sufficient because the same wrong key can be suggested more than once. More detailed analysis is necessary.
, is not sufficient because the same wrong key can be suggested more than once. More detailed analysis is necessary.
In the impossible differential attack, the attacker first prepares a set of all candidate values for the target subkey. In this attack, the attacker prepares a memory ![]() of
of ![]() entries for 32-bit subkey
entries for 32-bit subkey ![]() , which is used to record the correctness and incorrectness of each subkey value.
, which is used to record the correctness and incorrectness of each subkey value. ![]() is often called key space or subkey space depending on which is the target of the impossible differential attack.
is often called key space or subkey space depending on which is the target of the impossible differential attack. ![]() is first initialized so that all
is first initialized so that all ![]() values of
values of ![]() can be right values. If the attacker obtains wrong key suggestions, the corresponding values are removed from the key space
can be right values. If the attacker obtains wrong key suggestions, the corresponding values are removed from the key space ![]() . The analysis is iterated until the size of the key space
. The analysis is iterated until the size of the key space ![]() becomes 1.
becomes 1.
The procedure of reducing the key space is illustrated in Figure 4.30. At first, all entries of ![]() are initialized to a single bit “1,” which represents that the value can be a right key. If the attacker obtains wrong key suggestions, the corresponding bit is replaced with “0,” which represents that the value is not a right key.
are initialized to a single bit “1,” which represents that the value can be a right key. If the attacker obtains wrong key suggestions, the corresponding bit is replaced with “0,” which represents that the value is not a right key.

Figure 4.30 Reducing key space
At the initial stage, the size of the remaining key space is ![]() . By deriving one wrong key suggestion, the size of the remaining key space becomes
. By deriving one wrong key suggestion, the size of the remaining key space becomes
This is a precise evaluation, however, using this metric (with subtraction) for counting the remaining subkey space is hard to deal with the event in which the same wrong key value is suggested more than once. To solve this issue, the impossible differential cryptanalysis often regards that obtaining one wrong key suggestion reduces the subkey space by a factor of
With this metric, the size of the remaining key space after deriving 1 wrong key suggestion is represented as
After discarding r wrong key suggestions, the size of the remaining key space becomes
With ![]() wrong key suggestions, the size of the remaining key space is not sufficiently reduced as shown below:
wrong key suggestions, the size of the remaining key space is not sufficiently reduced as shown below:
When the number of wrong key suggestions is ![]() , the size of the remaining key space becomes
, the size of the remaining key space becomes
Equation (4.134) takes ![]() for
for ![]() and
and ![]() for
for ![]() . Therefore, the size of the key space is reduced to 1 by obtaining
. Therefore, the size of the key space is reduced to 1 by obtaining ![]() wrong key suggestions. The suitable choice of the number of plaintexts pairs, N, can be obtained by the following inequation:
wrong key suggestions. The suitable choice of the number of plaintexts pairs, N, can be obtained by the following inequation:
which concludes that ![]() is sufficient, namely, that the number of plaintext pairs should be
is sufficient, namely, that the number of plaintext pairs should be ![]() .
.
4.3.3.4 Attack Procedure for Recovering 
The description of the attack in an algorithmic form is given in Algorithm 4.7.
4.3.3.5 Complexity Evaluation
In Algorithm 4.7, queries are made only in step 8, which makes queries of ![]() pairs of chosen plaintexts. The time complexity for the initialization part is at most
pairs of chosen plaintexts. The time complexity for the initialization part is at most ![]() , for collecting pairs is
, for collecting pairs is ![]() XOR operations, and for recovery of
XOR operations, and for recovery of ![]() is at most
is at most ![]() . Hence, the entire time complexity is
. Hence, the entire time complexity is ![]() XOR computations, which is less than
XOR computations, which is less than ![]() five-round AES computations. The memory complexity is
five-round AES computations. The memory complexity is ![]() 32-bit values for
32-bit values for ![]() 32-bit values for
32-bit values for ![]() , and
, and ![]() pairs of plaintexts for L. Therefore, the entire memory complexity is less than
pairs of plaintexts for L. Therefore, the entire memory complexity is less than ![]() 128-bit values. In summary, the attack complexity for recovering
128-bit values. In summary, the attack complexity for recovering ![]() is as follows:
is as follows:
4.3.3.6 Recovering Other Bytes of 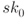
After 4 bytes of ![]() are recovered, the attacker needs to recover the other 12 bytes, or 96 bits. The straightforward method is performing the exhaustive search on the unknown 96 bits. However, this requires
are recovered, the attacker needs to recover the other 12 bytes, or 96 bits. The straightforward method is performing the exhaustive search on the unknown 96 bits. However, this requires ![]() computations, which is much higher than the complexity of the recovery of
computations, which is much higher than the complexity of the recovery of ![]() . Although it is already faster than the original exhaustive search on 128 bits, the attack complexity can be further optimized.
. Although it is already faster than the original exhaustive search on 128 bits, the attack complexity can be further optimized.
The strategy is to change the 3.5-round impossible differential characteristic so that the other 4 bytes of subkey ![]() can be recovered. Recall Figure 4.26. For the input difference of the 3.5-round impossible differential characteristic, the attacker can choose any active-byte position. Then, the attacker chooses the byte position 4 as the active-byte position, that is,
can be recovered. Recall Figure 4.26. For the input difference of the 3.5-round impossible differential characteristic, the attacker can choose any active-byte position. Then, the attacker chooses the byte position 4 as the active-byte position, that is,
This modification impacts the five-round key recovery attack. In detail, the active-byte positions of the plaintext become ![]() as depicted in Figure 4.31.
as depicted in Figure 4.31.
Figure 4.31 Key recovery attack for five-round AES with different active-byte positions
Consider applying the same attack as the subkey recovery for ![]() with slightly modifying the active-byte positions of the plaintext according to the 4 bytes in Figure 4.31. The attack procedure is almost the same as the one for
with slightly modifying the active-byte positions of the plaintext according to the 4 bytes in Figure 4.31. The attack procedure is almost the same as the one for ![]() , and thus the details are omitted. However, in this time, 4 bytes of
, and thus the details are omitted. However, in this time, 4 bytes of ![]() are recovered instead of
are recovered instead of ![]() . The attack complexity to recover 4 bytes of
. The attack complexity to recover 4 bytes of ![]() is also the same as the one for
is also the same as the one for ![]() , which is
, which is ![]() .
.
By applying the same discussion, using the following ![]() , the other 4 bytes of
, the other 4 bytes of ![]() can be recovered with the same complexity.
can be recovered with the same complexity.
After 12 bytes of ![]() are recovered, the remaining 4 bytes of
are recovered, the remaining 4 bytes of ![]() can also be recovered by changing the active-byte position of
can also be recovered by changing the active-byte position of ![]() to the first low of the last column. However, applying the exhaustive search on the remaining 4 bytes is faster than iterating the same analysis one more time. In the end, the last 4 bytes can be recovered only with
to the first low of the last column. However, applying the exhaustive search on the remaining 4 bytes is faster than iterating the same analysis one more time. In the end, the last 4 bytes can be recovered only with ![]() computations without any additional data and memory complexities.
computations without any additional data and memory complexities.
In summary, 12 bytes of ![]() are recovered by iterating the analysis on 4 bytes three times. This increases the data and time complexities three times compared to the 4-byte recovery. The required memory amount does not change because the memory used to recovery the first 4 bytes can be reused during the analysis on the other 4 bytes. After the 12 bytes are recovered, the cost of the exhaustive search on the remaining 4 bytes is negligibly smaller compared to the 12-byte recovery. The entire attack complexity becomes as follows:
are recovered by iterating the analysis on 4 bytes three times. This increases the data and time complexities three times compared to the 4-byte recovery. The required memory amount does not change because the memory used to recovery the first 4 bytes can be reused during the analysis on the other 4 bytes. After the 12 bytes are recovered, the cost of the exhaustive search on the remaining 4 bytes is negligibly smaller compared to the 12-byte recovery. The entire attack complexity becomes as follows:
4.3.3.7 Structure Technique to Reduce the Number of Queries
Let us go back to the 4-byte subkey recovery of ![]() described in Figure 4.28. The attack was first explained under the assumption that the plaintext difference in the 4-byte positions
described in Figure 4.28. The attack was first explained under the assumption that the plaintext difference in the 4-byte positions ![]() was fixed to a single choice. Under this assumption, the attack requires to query
was fixed to a single choice. Under this assumption, the attack requires to query ![]() chosen plaintext pairs.
chosen plaintext pairs.
There is a widely known technique called structure to reduce the data complexity by relaxing this assumption. Remember that the attack principally can work for any differences in the active 4-byte positions ![]() , that is, the differential form is as follows:
, that is, the differential form is as follows:
The idea of the structure technique is using a set of plaintexts that is closed with respect to the XOR operation. More precisely, the following set ![]() consisting of
consisting of ![]() plaintexts is considered:
plaintexts is considered:
where 12 bytes, denoted by “C” (for constant), are fixed to a prespecified value, say 0, and 4 bytes, denoted by “A” (for active), take all the ![]() possibilities. Suppose that all the
possibilities. Suppose that all the ![]() plaintexts included in the set
plaintexts included in the set ![]() are queried to the encryption oracle. Then, how many plaintext pairs following the differential form of Equation (4.140) are generated? The difference of any two plaintexts can satisfy the differential form of Equation (4.140) but for the small probability that the difference of at least 1 active byte happens to 0. Here, for the sake of simplicity, such a small probability event is ignored. The number of plaintext pairs generated from
are queried to the encryption oracle. Then, how many plaintext pairs following the differential form of Equation (4.140) are generated? The difference of any two plaintexts can satisfy the differential form of Equation (4.140) but for the small probability that the difference of at least 1 active byte happens to 0. Here, for the sake of simplicity, such a small probability event is ignored. The number of plaintext pairs generated from ![]() plaintexts is
plaintexts is
Hence, up to ![]() pairs can be generated only with
pairs can be generated only with ![]() queries. This is much better than the single difference case that requires
queries. This is much better than the single difference case that requires ![]() queries to obtain
queries to obtain ![]() pairs.
pairs.
In the case of ![]() recovery attack,
recovery attack, ![]() plaintext pairs are required. Taking
plaintext pairs are required. Taking ![]() plaintexts from the set
plaintexts from the set ![]() and making
and making ![]() queries is sufficient. This reduces the data complexity of the
queries is sufficient. This reduces the data complexity of the ![]() in Equation (4.136) from
in Equation (4.136) from ![]() to
to ![]() . Moreover, the time complexity of the collecting pair part becomes at most
. Moreover, the time complexity of the collecting pair part becomes at most ![]() , which is no longer a bottleneck of the attack. The bottleneck is
, which is no longer a bottleneck of the attack. The bottleneck is ![]() complexity for obtaining the wrong key suggestions. In summary, the attack complexity in Equation (4.136) is updated as follows:
complexity for obtaining the wrong key suggestions. In summary, the attack complexity in Equation (4.136) is updated as follows:
Similarly, the attack complexity for recovering all the 16 bytes is improved as follows:
4.3.4 Key Recovery Attacks for Seven-Round AES 
The impossible differential cryptanalysis can be extended to seven rounds. The essential difference from the five-round attack is that the 3.5-round impossible differential characteristic is carefully chosen so that the attack complexity can be below ![]() . Compared to the five-round attack, more optimization techniques are introduced. In particular, several input and output differences are considered simultaneously to minimize the data complexity, and the round function for the key recovery is equivalently transformed into another representation to minimize the time complexity.
. Compared to the five-round attack, more optimization techniques are introduced. In particular, several input and output differences are considered simultaneously to minimize the data complexity, and the round function for the key recovery is equivalently transformed into another representation to minimize the time complexity.
4.3.4.1 Base of Impossible Differential Characteristics
Several 3.5-round impossible differential characteristics are used for the seven-round attack. One of the choices is shown in Figure 4.32. This is useful to understand the concept of the multiple impossible differential characteristics that will be explained later. Hereafter, the impossible differential characteristic in Figure 4.32 is called basic impossible characteristic.

Figure 4.32 3.5-Round basic impossible differential characteristic for seven-round attack
The input difference ![]() to the basic impossible characteristic is the same as the previously used ones, that is, it has nonzero difference only in 1 byte. In Figure 4.32, the byte position
to the basic impossible characteristic is the same as the previously used ones, that is, it has nonzero difference only in 1 byte. In Figure 4.32, the byte position ![]() is chosen. The input difference
is chosen. The input difference ![]() is described as follows:
is described as follows:
The output difference ![]() from the basic impossible characteristic has nonzero difference in 3 bytes of a single column. The active column can be located in any column position, and 3 active bytes can be located in any byte position inside the selected column. In Figure 4.32, the rightmost column is selected and the first 3 bytes are active. The output difference
from the basic impossible characteristic has nonzero difference in 3 bytes of a single column. The active column can be located in any column position, and 3 active bytes can be located in any byte position inside the selected column. In Figure 4.32, the rightmost column is selected and the first 3 bytes are active. The output difference ![]() is described as follows.
is described as follows.
where ![]() represents a nonzero difference independent of
represents a nonzero difference independent of ![]() .
.
The detailed proof of the impossibility of the differential propagation ![]() is omitted. In short,
is omitted. In short, ![]() makes all bytes active in two rounds, while 4 bytes are ensured to be inactive after 1.5-round decryption from
makes all bytes active in two rounds, while 4 bytes are ensured to be inactive after 1.5-round decryption from ![]() .
.
4.3.4.2 Multiple Impossible Differential Characteristics
The concept of the multiple impossible differential characteristics considers a set of input difference ![]() -set and a set of output difference
-set and a set of output difference ![]() -set such that the differential propagation from any element in the
-set such that the differential propagation from any element in the ![]() -set to any element in the
-set to any element in the ![]() -set is impossible.
-set is impossible.
In the impossible differential cryptanalysis, key guesses generating input and output differences for the impossible differential characteristic are discarded. Hence, by considering multiple input and output differences, wrong key values can be discarded more quickly than the single difference case.
In the basic impossible differential characteristic, the active-byte position of ![]() is fixed to the byte position 0. Here, even if the active-byte position of
is fixed to the byte position 0. Here, even if the active-byte position of ![]() is modified, the modified
is modified, the modified ![]() and
and ![]() are impossible differential transition. This property allows the attacker to consider the
are impossible differential transition. This property allows the attacker to consider the ![]() -set consisting of the 16 differences. It does not mean that all of the 16 elements in the
-set consisting of the 16 differences. It does not mean that all of the 16 elements in the ![]() -set can contribute to reducing the data complexity. Each element can reduce the data complexity only when they can speed up wrong key suggestions in the subkey recovery part. The seven-round attack uses the following
-set can contribute to reducing the data complexity. Each element can reduce the data complexity only when they can speed up wrong key suggestions in the subkey recovery part. The seven-round attack uses the following ![]() -set consisting of four input differences:
-set consisting of four input differences:

The active-byte positions of ![]() can also be modified. As long as 1 byte is inactive in
can also be modified. As long as 1 byte is inactive in ![]() , it forms the impossible differential propagation against any element in the
, it forms the impossible differential propagation against any element in the ![]() -set. The seven-round attack uses the following
-set. The seven-round attack uses the following ![]() -set consisting of four output differences:
-set consisting of four output differences:

4.3.4.3 Appending Subkey Recovery Part
To attack seven rounds, one round and two rounds are added before and after the 3.5-round characteristic, respectively. This locates the 3.5-round characteristic from state ![]() to state
to state ![]() . The entire structure is shown in Figure 4.33. It assumes the basic impossible differential characteristic in the middle 3.5 rounds. The added rounds can be used for any choice of the input and output differences in the
. The entire structure is shown in Figure 4.33. It assumes the basic impossible differential characteristic in the middle 3.5 rounds. The added rounds can be used for any choice of the input and output differences in the ![]() -set and
-set and ![]() -set.
-set.

Figure 4.33 Key recovery attack for seven-round AES
The backward extension by one round is straightforward and the same as the one in the five-round attack shown in Figure 4.28. It derives 4 active bytes in the plaintext, and 4 bytes of subkey ![]() are related to the formulation of the impossible differential characteristic from the plaintext difference. The forward extension by two rounds is more complicated. Given the difference
are related to the formulation of the impossible differential characteristic from the plaintext difference. The forward extension by two rounds is more complicated. Given the difference ![]() , the difference
, the difference ![]() after the next
after the next ![]() operation can take the following three possibilities.
operation can take the following three possibilities.
- The number of active bytes in the active column of
 is 2.
is 2. - The number of active bytes in the active column of
 is 3.
is 3. - The number of active bytes in the active column of
 is 4.
is 4.
The seven-round attack restricts the form of ![]() to the case 1 for minimizing the number of involved subkey bytes to be recovered. Indeed by allowing more than 2 active bytes for
to the case 1 for minimizing the number of involved subkey bytes to be recovered. Indeed by allowing more than 2 active bytes for ![]() , the attack complexity exceeds
, the attack complexity exceeds ![]() , and thus cannot be faster than the exhaustive search for the original 128-bit key. In Figure 4.33, the active-byte positions are the first 2 bytes of the active column.
, and thus cannot be faster than the exhaustive search for the original 128-bit key. In Figure 4.33, the active-byte positions are the first 2 bytes of the active column.
After ![]() is set to case 1, the remaining differential propagation until the ciphertext is straightforward. It derives two fully active columns after the
is set to case 1, the remaining differential propagation until the ciphertext is straightforward. It derives two fully active columns after the ![]() operation in round 6 and then two fully active diagonals at the ciphertext. In the end, the byte positions
operation in round 6 and then two fully active diagonals at the ciphertext. In the end, the byte positions ![]() of the ciphertext are active.
of the ciphertext are active.
How many subkey bytes are related to the formulation of the multiple impossible differential characteristics from the ciphertext difference? To minimize the attack complexity, the number of related subkey bytes needs to be minimized as much as possible. The seven-round attack requires to introduce another technique for this purpose, which is an equivalent transformation of the subkey addition. Note that the seven-round structure in Figure 4.33 has already applied the technique in round 6.
4.3.4.4 Equivalent Transformation of Subkey Addition
This technique represents the computations of the AES round function in an alternative method. In particular, the order of the linear computations (ShiftRows, MixColumns, AddRoundKey) is exchanged.
To understand the motivation of introducing this technique, it is useful to check a simple extension of two rounds to the end of the 3.5-round distinguisher, and simulate how the subkey recovery part would work. The computation structure is depicted in Figure 4.34. To derive wrong key suggestions, the attacker guesses part of subkeys ![]() and
and ![]() , and checks if the difference after the partial decryption up to
, and checks if the difference after the partial decryption up to ![]() satisfies any of the output difference in the
satisfies any of the output difference in the ![]() -set. If the number of guessed subkey bytes is large, the attack complexity is also large. Thus, keeping the number of guessed subkey bytes low is important for the attacker.
-set. If the number of guessed subkey bytes is large, the attack complexity is also large. Thus, keeping the number of guessed subkey bytes low is important for the attacker.

Figure 4.34 Two-round simple extension after the distinguisher
Owing to the linearity of the ![]() and
and ![]() operations,
operations, ![]() can be computed by
can be computed by ![]() , which implies that any value of
, which implies that any value of ![]() is not related to the partial decryption up to
is not related to the partial decryption up to ![]() , thus the attacker does not have to guess the value of
, thus the attacker does not have to guess the value of ![]() . Here, how many subkey bytes need to be guessed to compute
. Here, how many subkey bytes need to be guessed to compute ![]() from the ciphertext difference
from the ciphertext difference ![]() ? In a simple method, 8 bytes of
? In a simple method, 8 bytes of ![]() and 8 bytes of
and 8 bytes of ![]() , in total 16 bytes, need to be guessed as stressed in Figure 4.34. However, guessing 16 bytes requires
, in total 16 bytes, need to be guessed as stressed in Figure 4.34. However, guessing 16 bytes requires ![]() trials, which is the same cost as the exhaustive search of the original 128-bit key. The motivation of the equivalent transformation is to avoid guessing 8 bytes of
trials, which is the same cost as the exhaustive search of the original 128-bit key. The motivation of the equivalent transformation is to avoid guessing 8 bytes of ![]() . Indeed, the number of guessed subkey bytes can be reduced to 2 by guessing linearly converted value of
. Indeed, the number of guessed subkey bytes can be reduced to 2 by guessing linearly converted value of ![]() as implied in Figure 4.33.
as implied in Figure 4.33.
The idea to reduce the number of guessed subkey bytes is changing the place of the ![]() operation. More precisely, the attacker exchanges the order of the
operation. More precisely, the attacker exchanges the order of the ![]() and
and ![]() operations so that the subkey addition is performed before the number of active bytes increases with the
operations so that the subkey addition is performed before the number of active bytes increases with the ![]() operation. Because both operations are linear, such a transformation is possible. In Figure 4.35, the transformation is detailed. The top figure describes that the
operation. Because both operations are linear, such a transformation is possible. In Figure 4.35, the transformation is detailed. The top figure describes that the ![]() operation is applied to state
operation is applied to state ![]() , and then the subkey
, and then the subkey ![]() is XORed to the state. The bottom figure applies a slightly different operation, in which the inverse
is XORed to the state. The bottom figure applies a slightly different operation, in which the inverse ![]() operation is applied to the subkey, and the transformed subkey is XORed to the state before the
operation is applied to the subkey, and the transformed subkey is XORed to the state before the ![]() operation. Both computations result in the same state
operation. Both computations result in the same state ![]() .
.

Figure 4.35 Equivalent transformation of subkey addition. The order of  and
and  is exchanged
is exchanged
To verify the equivalence of two computations, converting the bottom computation to the top one is easier. The bottom computation in Figure 4.35 is represented as follows:
For any linear function ![]() and two input values
and two input values ![]() , the value of
, the value of ![]() is equal to the value of
is equal to the value of ![]() . Therefore,
. Therefore,
which is equivalent to the top computation in Figure 4.35. As shown in Figure 4.35, hereafter the internal state after XOR of ![]() and before the
and before the ![]() operation is denoted by
operation is denoted by ![]() .
.
Finally, the last 1.5 rounds of the seven-round attack become as shown in Figure 4.33. By guessing the 8 bytes of ![]() and 2 bytes of
and 2 bytes of ![]() , the corresponding difference at
, the corresponding difference at ![]() can be computed from each ciphertext pair.
can be computed from each ciphertext pair.
4.3.4.5 Attack Procedure for Recovering Subkey
Collecting Plaintext Pairs
The attack first collects many pairs of plaintexts and the corresponding ciphertexts whose differences satisfy the form of ![]() and
and ![]() in Figure 4.33 by using the structure technique. As previously explained, a structure
in Figure 4.33 by using the structure technique. As previously explained, a structure ![]() that consists of
that consists of ![]() plaintexts is generated for a fixed 12-byte constant C:
plaintexts is generated for a fixed 12-byte constant C:
Then, ![]() plaintext pairs are generated per structure.
plaintext pairs are generated per structure.
Up to ![]() structures can be constructed by changing the value of 12-byte constant C. Let
structures can be constructed by changing the value of 12-byte constant C. Let ![]() be the number of generated structures. Then,
be the number of generated structures. Then, ![]() plaintext pairs are generated with
plaintext pairs are generated with ![]() queries. The exact value of N is later determined so that the entire attack complexity is optimized.
queries. The exact value of N is later determined so that the entire attack complexity is optimized.
The probability that a randomly chosen pair has the difference ![]() at the ciphertext is
at the ciphertext is ![]() because inactive 8 bytes (64 bits) must have difference zero. Thus, the number of pairs satisfying
because inactive 8 bytes (64 bits) must have difference zero. Thus, the number of pairs satisfying ![]() is
is
Deriving Wrong Key Suggestions by Constructing Look-Up Table
From each of the ![]() obtained pairs, the attacker derives wrong key suggestions about the following 14 subkey bytes
obtained pairs, the attacker derives wrong key suggestions about the following 14 subkey bytes ![]() . Wrong key suggestions are efficiently derived by generating the look-up table T.
. Wrong key suggestions are efficiently derived by generating the look-up table T.
As explained in Figure 4.29, a wrong key suggestion for ![]() is obtained for each 1 active-byte difference of
is obtained for each 1 active-byte difference of ![]() by checking the solutions of the differential propagation
by checking the solutions of the differential propagation ![]() . For each element in the
. For each element in the ![]() -set, there are 255 choices of
-set, there are 255 choices of ![]() . Because the
. Because the ![]() -set includes 4 elements, there are
-set includes 4 elements, there are ![]() choices of
choices of ![]() in this attack.
in this attack.
With the same reason, a wrong key suggestion for ![]() is obtained for each 2 active-byte difference of
is obtained for each 2 active-byte difference of ![]() . The attacker, without the knowledge of the key, can compute the difference
. The attacker, without the knowledge of the key, can compute the difference ![]() from ciphertext difference for each pair. For each 2 active-byte difference of
from ciphertext difference for each pair. For each 2 active-byte difference of ![]() , the corresponding
, the corresponding ![]() is computed. By checking the solutions of the differential propagation
is computed. By checking the solutions of the differential propagation ![]() , the value of the 8 active bytes is fixed, and thus the corresponding 8-byte value of
, the value of the 8 active bytes is fixed, and thus the corresponding 8-byte value of ![]() is obtained. After 8 bytes of
is obtained. After 8 bytes of ![]() are recovered, each ciphertext pair can be decrypted until 2 bytes of
are recovered, each ciphertext pair can be decrypted until 2 bytes of ![]() .
.
Similarly, a wrong key suggestion for ![]() can be efficiently derived from the 2-byte difference
can be efficiently derived from the 2-byte difference ![]() and 2 byte values and their difference of
and 2 byte values and their difference of ![]() . Here, 2-byte difference
. Here, 2-byte difference ![]() cannot be chosen from all the
cannot be chosen from all the ![]() possibilities. The 2-byte difference
possibilities. The 2-byte difference ![]() must be chosen so that
must be chosen so that ![]() is included in the
is included in the ![]() -set, that is, the result has zero difference in 1 byte position. The explanation for the basic impossible differential characteristic is given below, in which the inactive byte is located in
-set, that is, the result has zero difference in 1 byte position. The explanation for the basic impossible differential characteristic is given below, in which the inactive byte is located in ![]() . By looking inside the inverse
. By looking inside the inverse ![]() operation, the difference of
operation, the difference of ![]() is computed as follows:
is computed as follows:
For each ![]() choice of
choice of ![]() , there is only one choice of
, there is only one choice of ![]() to satisfy
to satisfy ![]() . Therefore, the number of 2-byte difference
. Therefore, the number of 2-byte difference ![]() satisfying
satisfying ![]() is only
is only ![]() . Because the
. Because the ![]() -set contains four elements, the same discussion can be applied to the other three elements. In the end, the number of valid choices of
-set contains four elements, the same discussion can be applied to the other three elements. In the end, the number of valid choices of ![]() is
is ![]() . Once
. Once ![]() is fixed from those
is fixed from those ![]() choices, the corresponding difference
choices, the corresponding difference ![]() is also fixed. By checking the solutions of the differential propagation
is also fixed. By checking the solutions of the differential propagation ![]() , the value of the 2 active bytes is fixed, and thus the corresponding 2-byte value of
, the value of the 2 active bytes is fixed, and thus the corresponding 2-byte value of ![]() is obtained.
is obtained.
In summary, the attacker first prepares the look-up table T consisting of ![]() elements, which contains the information of 14-byte difference of
elements, which contains the information of 14-byte difference of ![]() ,
, ![]() , and
, and ![]() for
for ![]() choices of
choices of ![]() choices of
choices of ![]() , and
, and ![]() choices of
choices of ![]() .
.
Evaluation of the Number of Structures
From each of the ![]() obtained pairs and each of the
obtained pairs and each of the ![]() choices in the look-up table T, a wrong key suggestion for the target 14 bytes is obtained. Therefore,
choices in the look-up table T, a wrong key suggestion for the target 14 bytes is obtained. Therefore, ![]() wrong key suggestions are obtained. If
wrong key suggestions are obtained. If ![]() suggestions are enough to reduce the 14-byte (112-bit) subkey space, the target 14 subkey bytes are recovered.
suggestions are enough to reduce the 14-byte (112-bit) subkey space, the target 14 subkey bytes are recovered.
The proper choice of N is now evaluated. From Equation (4.134), with ![]() wrong key suggestions, the size of the remaining key space for the 112-bit subkey bytes becomes
wrong key suggestions, the size of the remaining key space for the 112-bit subkey bytes becomes
Equation (4.157) takes ![]() for
for ![]() and
and ![]() for
for ![]() . Therefore, the 112-bit subkey space is reduced to 1 by obtaining all wrong key suggestions for
. Therefore, the 112-bit subkey space is reduced to 1 by obtaining all wrong key suggestions for ![]() structures.
structures.
4.3.4.6 Complexity Evaluation
The attack generates ![]() structures, in which each structure requires queries of
structures, in which each structure requires queries of ![]() chosen plaintexts. Therefore, the data complexity of the attack is
chosen plaintexts. Therefore, the data complexity of the attack is ![]() chosen plaintexts.
chosen plaintexts.
Regarding the computational cost, the attack needs to deal with ![]() ciphertexts received by the encryption oracle for collecting pairs. The cost for generating look-up table T is around
ciphertexts received by the encryption oracle for collecting pairs. The cost for generating look-up table T is around ![]() computations, which is negligibly small compared to the other part. The attack derives
computations, which is negligibly small compared to the other part. The attack derives ![]() wrong key suggestions. The cost for deriving one suggestion is about one-round encryption and two round decryptions, which is about
wrong key suggestions. The cost for deriving one suggestion is about one-round encryption and two round decryptions, which is about ![]() seven-round AES computations. Therefore, the cost for deriving
seven-round AES computations. Therefore, the cost for deriving ![]() wrong key suggestions is less than
wrong key suggestions is less than ![]() seven-round AES computations, which is the bottleneck of the computational cost.
seven-round AES computations, which is the bottleneck of the computational cost.
The largest memory amount is for recording the validity/invalidity of each subkey value in the 112-bit subkey space, which is less than ![]() 128-bit state values.
128-bit state values.
In summary, the attack complexity for recovering 112-bit subkey value is as follows:
4.3.4.7 Recovering Original Secret Key
The procedure for recovering the original 128-bit key is very simple. After the above subkey recovery, 64 bits of ![]() are recovered. The number of remaining unknown key bits of
are recovered. The number of remaining unknown key bits of ![]() is 64 bits. The attacker can perform the exhaustive search on those 64 bits of
is 64 bits. The attacker can perform the exhaustive search on those 64 bits of ![]() . For each guess, the original 128-bit secret key
. For each guess, the original 128-bit secret key ![]() can be computed with the inverse of the key schedule function, and the correctness of the guess can be confirmed with a pair of plaintext and ciphertext. The cost for the exhaustive search on the 64 bits of
can be computed with the inverse of the key schedule function, and the correctness of the guess can be confirmed with a pair of plaintext and ciphertext. The cost for the exhaustive search on the 64 bits of ![]() is around
is around ![]() seven-round AES computations, which is negligibly small compared to the 112-bit subkey recovery attack.
seven-round AES computations, which is negligibly small compared to the 112-bit subkey recovery attack.
4.4 Integral Cryptanalysis
The origin of the integral cryptanalysis was the one proposed by Daemen et al. against Square block cipher. The design of AES is similar to the one for the Square block cipher. In this section, the integral cryptanalysis against AES is explained.
4.4.1 Basic Concept
Remember that the differential cryptanalysis is motivated by the property that the difference of two values never changes by XORing an identical unknown secret value, and the propagation of the difference through the linear computations can be simulated with probability 1. Those properties allow a particular difference to appear with higher probability than other differences.
The motivation of the integral cryptanalysis is exploiting different properties that can hold with a high probability with respect to the frequently used computations in block ciphers.
AES is a byte-oriented cipher, which means that the computation inside the round function is defined bytewise. On the basis of this fact, the integral analysis considers processing a set of 256 plaintexts in which 1 byte takes all possibilities among 256 plaintexts, and all the other bytes are fixed to an identical value among 256 plaintexts. First of all, a set ![]() consisting of 256 plaintexts are defined as follows:
consisting of 256 plaintexts are defined as follows:
where each of ![]() is a constant value fixed before the analysis. The set
is a constant value fixed before the analysis. The set ![]() is also depicted in Figure 4.36. The set
is also depicted in Figure 4.36. The set ![]() is an unordered set, that is, the order of each element in the set is not distinguished. For example, the sets
is an unordered set, that is, the order of each element in the set is not distinguished. For example, the sets ![]() and
and ![]() are regarded to be the same. The only important point is that each of
are regarded to be the same. The only important point is that each of ![]() is included in the set
is included in the set ![]() exactly once.
exactly once.

Figure 4.36 Basic set of plaintexts for integral cryptanalysis
In the integral cryptanalysis, the byte in which all values appear exactly once among all the texts in the set is called the all property, and is often denoted by ![]() . Similarly, the byte in which all texts in the set have an identical value is called the constant property, and is often denoted by
. Similarly, the byte in which all texts in the set have an identical value is called the constant property, and is often denoted by ![]() . With those notations, the property of the set
. With those notations, the property of the set ![]() is written as
is written as ![]() .
.
The set ![]() shows several interesting properties when it is processed by the computations adopted in AES under the same key, which will be detailed below.
shows several interesting properties when it is processed by the computations adopted in AES under the same key, which will be detailed below.
4.4.2 Processing  through Subkey XOR
through Subkey XOR
Because the first operation of AES is an XOR of the plaintext and the first subkey, the status of the set ![]() after the subkey XOR is firstly analyzed. Namely, the subkey
after the subkey XOR is firstly analyzed. Namely, the subkey ![]() is XORed to each of the 256 plaintexts in the set
is XORed to each of the 256 plaintexts in the set ![]() . Here, it is assumed that the key value does not change for encrypting 256 plaintexts in the set. This updates the set
. Here, it is assumed that the key value does not change for encrypting 256 plaintexts in the set. This updates the set ![]() to
to ![]() .
. ![]() is also described in Figure 4.37.
is also described in Figure 4.37.

Figure 4.37 Plaintexts set after XORing subkey 
Regarding the byte position j, where ![]() , the 256 plaintexts originally have the same value
, the 256 plaintexts originally have the same value ![]() . Now the value is updated to
. Now the value is updated to ![]() . The important property is that
. The important property is that ![]() is a fixed value, although its value is unknown to the attacker because of
is a fixed value, although its value is unknown to the attacker because of ![]() . For example, the value of
. For example, the value of ![]() can be represented by another constant
can be represented by another constant ![]() . Clearly, all the jth byte positions (
. Clearly, all the jth byte positions (![]() ) in the updated state satisfy the constant property.
) in the updated state satisfy the constant property.
Regarding the byte position ![]() , the 256 plaintexts originally vary to take all the 256 values (all property). By XORing an unknown constant
, the 256 plaintexts originally vary to take all the 256 values (all property). By XORing an unknown constant ![]() to all of the 256 texts, the property that all the 256 values appear among 256 texts still holds with probability 1. Remember that the set considered in the integral analysis is an unordered set. Thus, changing the order of elements inside the set does not affect the analysis. It is concluded that the byte position 0 in the update state satisfies the all property.
to all of the 256 texts, the property that all the 256 values appear among 256 texts still holds with probability 1. Remember that the set considered in the integral analysis is an unordered set. Thus, changing the order of elements inside the set does not affect the analysis. It is concluded that the byte position 0 in the update state satisfies the all property.
4.4.3 Processing  through
through  Operation
Operation
The next operation of AES is the ![]() operation, which applies the 8-bit to 8-bit S-box to each byte of the state. Here, the status of the set
operation, which applies the 8-bit to 8-bit S-box to each byte of the state. Here, the status of the set ![]() after the
after the ![]() operation is analyzed. This updates the set
operation is analyzed. This updates the set ![]() to
to ![]() .
. ![]() is also described in Figure 4.38.
is also described in Figure 4.38.

Figure 4.38 Plaintexts set after the  operation
operation
Two properties of the S-box are related to the analysis.
- S-box is a bijective mapping from
 to
to  .
. - S-box is a deterministic mapping. It always maps the same input value to the same output value.
Regarding the byte positions j, where ![]() , the 256 plaintexts originally have the same value
, the 256 plaintexts originally have the same value ![]() . Now the value is updated to
. Now the value is updated to ![]() . Because the S-box is a deterministic mapping,
. Because the S-box is a deterministic mapping, ![]() is a fixed value among all the 256 texts in the set. All the jth byte positions (
is a fixed value among all the 256 texts in the set. All the jth byte positions (![]() ) in the updated state satisfy the constant property.
) in the updated state satisfy the constant property.
Regarding the byte position ![]() , the 256 plaintexts originally vary to take all the 256 values (all property). Owing to the bijective property of the S-box, the output of the S-box also varies to take all the 256 values, although the order of the values is changed. It is concluded that the byte position 0 in the update state satisfies the all property.
, the 256 plaintexts originally vary to take all the 256 values (all property). Owing to the bijective property of the S-box, the output of the S-box also varies to take all the 256 values, although the order of the values is changed. It is concluded that the byte position 0 in the update state satisfies the all property.
4.4.4 Processing  through
through  Operation
Operation
The ![]() operation of AES only exchanges the byte positions. It does not operate the data inside each byte. Because the integral analysis only exploits the property inside each byte, the
operation of AES only exchanges the byte positions. It does not operate the data inside each byte. Because the integral analysis only exploits the property inside each byte, the ![]() operation never affects the property used in the integral cryptanalysis.
operation never affects the property used in the integral cryptanalysis.
4.4.5 Processing  through
through  Operation
Operation
Because the ![]() operations is not closed in each byte, that is, it mixes the values of 4 bytes, the analysis is not simple in general. If there is at most 1 byte with the all property in each column, the analysis is simple. Here, the status of the set
operations is not closed in each byte, that is, it mixes the values of 4 bytes, the analysis is not simple in general. If there is at most 1 byte with the all property in each column, the analysis is simple. Here, the status of the set ![]() after the
after the ![]() operation is first analyzed. This updatesthe set
operation is first analyzed. This updatesthe set ![]() to
to ![]() .
. ![]() is also described in Figure 4.39.
is also described in Figure 4.39.

Figure 4.39 Plaintexts set  after the
after the  operation
operation
Regarding the second, third, and the fourth columns, the input value to the ![]() operation is a fixed value among all the 256 texts. Therefore, the output of the
operation is a fixed value among all the 256 texts. Therefore, the output of the ![]() operation is also a fixed value among all the 256 texts. For all bytes in the second, third, and the fourth columns, the updated state satisfies the constant property.
operation is also a fixed value among all the 256 texts. For all bytes in the second, third, and the fourth columns, the updated state satisfies the constant property.
Regarding the first column, according to the specification of the ![]() operation, the 4 output bytes are computed as follows:
operation, the 4 output bytes are computed as follows:
The 4 output bytes are composed of the impact from i and the impact from the other three constant values ![]() . Among the 256 texts, the impact from the constant values, which is the second term on the right-hand side of Equation (4.160), is a fixed value. As summarized in Lemma 4.4.2, XORing the constant does not change the all property and constant property. Hence, the property of the output value only depends on the impact from i (the first term on the right-hand side of Equation (4.160). In the input 256 texts, the value of i varies to take all the 256 values (all property). This makes the values of
. Among the 256 texts, the impact from the constant values, which is the second term on the right-hand side of Equation (4.160), is a fixed value. As summarized in Lemma 4.4.2, XORing the constant does not change the all property and constant property. Hence, the property of the output value only depends on the impact from i (the first term on the right-hand side of Equation (4.160). In the input 256 texts, the value of i varies to take all the 256 values (all property). This makes the values of ![]() , and
, and ![]() vary to take all the 256 values, although the order of the values changes. It is concluded that the 4 output bytes from the first column will have the all property.
vary to take all the 256 values, although the order of the values changes. It is concluded that the 4 output bytes from the first column will have the all property.
The analysis cannot be simple when the number of bytes with the all property is more than 1. The analysis will be explained later when the integral property of AES three rounds is explained.
4.4.6 Integral Property of AES Reduced to 2.5 Rounds
By using the earlier discussions, a certain property can be constructed until 2.5 rounds. The overall structure is given in Figure 4.40. In the following, the transition of the property is explained state by state.

Figure 4.40 Integral property for 2.5-round AES
- Round 1
- Plaintexts: The analysis starts from the set of plaintexts
 , which is defined in Equation (4.159).
, which is defined in Equation (4.159). - State
 : From Lemma 4.4.1, the subkey XOR maintains the all and constant properties.
: From Lemma 4.4.1, the subkey XOR maintains the all and constant properties. - State
 : From Lemma 4.4.2, the
: From Lemma 4.4.2, the  operation maintains the all and constant properties.
operation maintains the all and constant properties. - State
 : The byte positions are moved according to the
: The byte positions are moved according to the  operation (no movement in the first row).
operation (no movement in the first row). - State
 : As shown in Figure 4.39, all bytes in the right three columns maintain the constant property and a single byte with the all property in the input state expands to 4 bytes in the first column.
: As shown in Figure 4.39, all bytes in the right three columns maintain the constant property and a single byte with the all property in the input state expands to 4 bytes in the first column. - State
 : From Lemma 4.4.1, the subkey XOR maintains the all and constant properties.
: From Lemma 4.4.1, the subkey XOR maintains the all and constant properties. - Round 2
- State
 : From Lemma 4.4.2, the
: From Lemma 4.4.2, the  operation maintains the all and constant properties.
operation maintains the all and constant properties. - State
 : The byte positions are moved according to the
: The byte positions are moved according to the  operation. All columns come to contain a byte with the all property.
operation. All columns come to contain a byte with the all property. - State
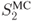 : As the same principle of the first column in Figure 4.39, for all columns, a single byte with the all property in the input state expands to 4 bytes in the first column. As a result, bytes with the constant property disappear and all bytes will show the all property.
: As the same principle of the first column in Figure 4.39, for all columns, a single byte with the all property in the input state expands to 4 bytes in the first column. As a result, bytes with the constant property disappear and all bytes will show the all property. - State
 : From Lemma 4.4.1, the subkey XOR maintains the all property.
: From Lemma 4.4.1, the subkey XOR maintains the all property. - Round 2.5
- State
 : From Lemma 4.4.2, the
: From Lemma 4.4.2, the 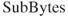 operation maintains the all property.
operation maintains the all property. - State
 : The byte positions are moved according to the
: The byte positions are moved according to the  operation.
operation.
Finally, it was shown that the set of plaintexts ![]() will provide the all property in all 16 bytes after 2.5 rounds.
will provide the all property in all 16 bytes after 2.5 rounds.
4.4.7 Balanced Property
In Figure 4.40, the following question naturally rises.
Does any property remain after the
operation is applied to state
in Figure 4.40?
Actually, the answer is “Yes.” However it is no longer the all property or the constant property. The computation from the state ![]() to
to ![]() is identical for all columns, thus analyzing that a single column is enough. Moreover, the analysis is almost the same among all the 4 output bytes of the column. Here, the property of the first output byte is analyzed in detail. According to the specification of the
is identical for all columns, thus analyzing that a single column is enough. Moreover, the analysis is almost the same among all the 4 output bytes of the column. Here, the property of the first output byte is analyzed in detail. According to the specification of the ![]() operation,
operation, ![]() is computed by the following equation:
is computed by the following equation:
Remember that the analysis initially starts from a set of 256 plaintexts ![]() , where
, where ![]() . Let
. Let ![]() be 4 input bytes to the
be 4 input bytes to the ![]() operation corresponding to
operation corresponding to ![]() . Owing to the 2.5-round integral property, it is ensured that all of the 4 bytes
. Owing to the 2.5-round integral property, it is ensured that all of the 4 bytes ![]() show the all property, that is, the value of
show the all property, that is, the value of ![]() takes all possibilities by collecting all
takes all possibilities by collecting all ![]() , and the same is applied to
, and the same is applied to ![]() , and
, and ![]() . The important fact here is that the all property for each of 4 bytes was derived independently from each other. In other words, no relation is guaranteed among the values of different byte positions in the same text.
. The important fact here is that the all property for each of 4 bytes was derived independently from each other. In other words, no relation is guaranteed among the values of different byte positions in the same text.
There is some probability that 4 independent input bytes for different texts ![]() and
and ![]() will result in the same output value. Hence, the “all” property cannot be ensured for
will result in the same output value. Hence, the “all” property cannot be ensured for ![]() . It is also easy to see that the constant property cannot be ensured for
. It is also easy to see that the constant property cannot be ensured for ![]() .
.
The idea of the new property is computing the XOR sum of all the 256 texts, that is, ![]() . The details of this computation are as follows:
. The details of this computation are as follows:


In the third equality of the above transformation, the fact that each byte satisfies the all property and the fact that ![]() are used.
are used.
In summary, ![]() satisfies the property that the XOR sum of all the 256 texts is 0, that is,
satisfies the property that the XOR sum of all the 256 texts is 0, that is, ![]() . This property is called balanced property, and often denoted by
. This property is called balanced property, and often denoted by ![]() . The same discussion can be applied to the other bytes of
. The same discussion can be applied to the other bytes of ![]() . Thus, all the bytes of
. Thus, all the bytes of ![]() satisfy the balanced property.
satisfy the balanced property.
4.4.8 Integral Property of AES Reduced to Three Rounds and Distinguishing Attack
By using the balanced property, the integral property for three-round AES can be constructed, which is shown in Figure 4.41.

Figure 4.41 Integral property for three-round AES
From Figure 4.40, the ![]() operation is applied to
operation is applied to ![]() , making all the bytes of
, making all the bytes of ![]() balanced. With the last
balanced. With the last ![]() operation for
operation for ![]() , the XOR sum of each byte is further XORed by
, the XOR sum of each byte is further XORed by ![]() 256 times. As long as the number of texts in the original set is an even number, the effect of XORing the same constant is canceled out. In the end, the last
256 times. As long as the number of texts in the original set is an even number, the effect of XORing the same constant is canceled out. In the end, the last ![]() operation does not break the balanced property, making all bytes of the ciphertext balanced.
operation does not break the balanced property, making all bytes of the ciphertext balanced.
The distinguishing attack is now easily constructed for AES three rounds in the chosen plaintext model. The goal of the attacker is identifying which of the AES three rounds or a random permutation is implemented by the oracle. The attacker prepares the set of 256 plaintexts ![]() , and queries all of the 256 plaintexts to the oracle. The attacker then computes the XOR sum of each byte of the received ciphertexts and checks whether the sum is 0 or not. If all the bytes satisfy the balanced property, the oracle implements the AES reduced to three rounds. Otherwise, it implements the random permutation.
, and queries all of the 256 plaintexts to the oracle. The attacker then computes the XOR sum of each byte of the received ciphertexts and checks whether the sum is 0 or not. If all the bytes satisfy the balanced property, the oracle implements the AES reduced to three rounds. Otherwise, it implements the random permutation.
Attack Procedure
The attack procedure in the algorithmic form is described in Algorithm 4.8.
Complexity Evaluation
The attack makes 256 queries. Thus, the data complexity of this attack is 256 chosen plaintexts. The computational cost is updating ![]() value 256 times, which is 256 XOR operations. The required memory is only for storing
value 256 times, which is 256 XOR operations. The required memory is only for storing ![]() value, which is negligibly small. In summary, the complexity of this attack is
value, which is negligibly small. In summary, the complexity of this attack is ![]() , where “
, where “![]() ” stands for negligible.
” stands for negligible.
Success Probability
As long as the oracle implements the AES three rounds, the attack successfully returns the determining bit 0 with probability 1.
When the oracle implements a random permutation, the XOR sum of each byte may happen to be 1 with a low probability. The probability that the XOR sum of randomly generated 256 byte values happens to be 0 is ![]() . The probability that this event happens for all the 16 bytes at the same time is
. The probability that this event happens for all the 16 bytes at the same time is ![]() , which is negligibly small.
, which is negligibly small.
Hence, the distinguishing attack successfully distinguishes the AES three rounds from a random permutation.
4.4.9 Key Recovery Attack with Integral Cryptanalysis for Five Rounds
On the basis of the three-round integral property, a key recovery attack can be mounted against AES reduced to five rounds. The attack appends two rounds after the three-round integral property, which makes the structure shown in Figure 4.42. The attacker guesses the part of the last two subkeys ![]() and
and ![]() and performs the partial decryption up to
and performs the partial decryption up to ![]() . The correct guess always achieves the balanced property in all bytes of
. The correct guess always achieves the balanced property in all bytes of ![]() , which enables the attacker to reduce the key space.
, which enables the attacker to reduce the key space.

Figure 4.42 Key recovery attack against five-round AES. Guessed 4 bytes of  and 4 bytes of
and 4 bytes of  are stressed by bold lines. With those guesses, several bytes of the internal state marked by light gray color can be computed
are stressed by bold lines. With those guesses, several bytes of the internal state marked by light gray color can be computed
Collecting Plaintexts
The attacker prepares sets of 256 plaintexts ![]() . As explained later, the analysis guesses 64 bits of subkeys, and each set of 256 plaintexts
. As explained later, the analysis guesses 64 bits of subkeys, and each set of 256 plaintexts ![]() can reduce the subkey space by a factor of
can reduce the subkey space by a factor of ![]() . In order to reduce the subkey space to 1, two sets of 256 plaintexts
. In order to reduce the subkey space to 1, two sets of 256 plaintexts ![]() are required. Those
are required. Those ![]() plaintexts are passed to the encryption oracle, and the attacker obtains the corresponding two sets of
plaintexts are passed to the encryption oracle, and the attacker obtains the corresponding two sets of ![]() ciphertexts.
ciphertexts.
Recovery of  and
and 
With the obtained two sets of ![]() ciphertexts, the attacker recovers the values of
ciphertexts, the attacker recovers the values of ![]() and
and ![]() . The 4 bytes of
. The 4 bytes of ![]() and the 4 bytes of
and the 4 bytes of ![]() , in total 64-bit subkey space, are reduced to 32 bits with the analysis of the first set of
, in total 64-bit subkey space, are reduced to 32 bits with the analysis of the first set of ![]() plaintexts. Then, the subkey space is further reduced to 1 by using the second set of
plaintexts. Then, the subkey space is further reduced to 1 by using the second set of ![]() plaintexts. The guessed subkey bytes are marked by bold line in Figure 4.42.
plaintexts. The guessed subkey bytes are marked by bold line in Figure 4.42.
With a guess of ![]() and
and ![]() , the attacker can compute the corresponding 4 bytes of
, the attacker can compute the corresponding 4 bytes of ![]() by taking XOR of the ciphertext and the guess of
by taking XOR of the ciphertext and the guess of ![]() for all the 256 ciphertexts in the first set. The inverse of the
for all the 256 ciphertexts in the first set. The inverse of the ![]() operation moves the computed byte positions into
operation moves the computed byte positions into ![]() , and the corresponding 4 bytes of
, and the corresponding 4 bytes of ![]() can be computed with the inverse of the S-box. The guessed
can be computed with the inverse of the S-box. The guessed ![]() allows the attacker to compute the corresponding 4 bytes of
allows the attacker to compute the corresponding 4 bytes of ![]() . Because all values in a column are computed, the corresponding 4 bytes of
. Because all values in a column are computed, the corresponding 4 bytes of ![]() are computed with the inverse of the
are computed with the inverse of the ![]() operation. The next inverse of the
operation. The next inverse of the ![]() operation moves the computed byte positions into
operation moves the computed byte positions into ![]() , and the corresponding 4 bytes of
, and the corresponding 4 bytes of ![]() can be computed with the inverse of the S-box.
can be computed with the inverse of the S-box.
The value of ![]() is computed for all the
is computed for all the ![]() texts in the first set. To check if the balanced property is satisfied, the XOR sum of all the
texts in the first set. To check if the balanced property is satisfied, the XOR sum of all the ![]() texts is computed for 4 bytes of
texts is computed for 4 bytes of ![]() . If the results are 0 in all bytes, that is,
. If the results are 0 in all bytes, that is,
the subkey guess of ![]() is a correct subkey candidate. For this case, the guess is stored in a list
is a correct subkey candidate. For this case, the guess is stored in a list ![]() . If at least 1 byte of
. If at least 1 byte of ![]() does not satisfy the balanced property, the subkey guess is wrong. For this case, the subkey guess is not stored and is discarded immediately.
does not satisfy the balanced property, the subkey guess is wrong. For this case, the subkey guess is not stored and is discarded immediately.
The correct guess always satisfies Equation (4.165). Besides the correct guess, several wrong guesses happen to satisfy Equation (4.165) probabilistically. The probability that randomly chosen 4 byte values become 0 is ![]() . Therefore, with trying
. Therefore, with trying ![]() guesses,
guesses, ![]() wrong guesses are stored in the correct subkey candidates list
wrong guesses are stored in the correct subkey candidates list ![]() , In other words, with the analysis of the first set, the subkey space is reduced from
, In other words, with the analysis of the first set, the subkey space is reduced from ![]() to
to ![]() , by 32 bits.
, by 32 bits.
The same analysis is iterated again by using the ![]() ciphertexts in the second set. This time, the subkey guess of
ciphertexts in the second set. This time, the subkey guess of ![]() is chosen from the list
is chosen from the list ![]() , thus the number of guesses is
, thus the number of guesses is ![]() rather than
rather than ![]() in the analysis for the first set. The subkey space is reduced by another 32 bits, which makes the number of subkey candidates about 1.
in the analysis for the first set. The subkey space is reduced by another 32 bits, which makes the number of subkey candidates about 1.
Recovery of Original Key
The same analysis can be performed to recover other subkey bytes of ![]() and
and ![]() . With iterating the analysis twice,
. With iterating the analysis twice,
- 8 bytes of
 and
and - 8 bytes of

are recovered. As explained in the previous section, the original key ![]() can be recovered with any other subkey. The remaining unknown bytes of
can be recovered with any other subkey. The remaining unknown bytes of ![]() are the 4 bytes of
are the 4 bytes of ![]() . The attacker recovers those 4 bytes with the exhaustive search. Note that, if the subkey candidates for
. The attacker recovers those 4 bytes with the exhaustive search. Note that, if the subkey candidates for ![]() , and
, and ![]() were not reduced to 1, but several candidates are remaining, the correct candidates can be guessed together with the exhaustive search of
were not reduced to 1, but several candidates are remaining, the correct candidates can be guessed together with the exhaustive search of ![]() .
.
Attack Summary
The attack is a chosen plaintext attack. The data complexity of this attack is ![]() chosen plaintexts. The computational cost for constructing two sets of
chosen plaintexts. The computational cost for constructing two sets of ![]() plaintexts is
plaintexts is ![]() computations, which is negligible compared to the key recovery part. For recovering
computations, which is negligible compared to the key recovery part. For recovering ![]() , in the analysis of the first set, the two-round decryption is performed for each of the
, in the analysis of the first set, the two-round decryption is performed for each of the ![]() subkey guesses and
subkey guesses and ![]() ciphertexts in the set. Hence, the computational cost for analyzing the first set is
ciphertexts in the set. Hence, the computational cost for analyzing the first set is ![]() round function computations, which corresponds to
round function computations, which corresponds to ![]() five-round AES computations. The computational cost for the second set is cheaper than the one for the first set by a factor of
five-round AES computations. The computational cost for the second set is cheaper than the one for the first set by a factor of ![]() because only about
because only about ![]() candidates remain in
candidates remain in ![]() . The computational cost for the recovery of
. The computational cost for the recovery of ![]() is two more iterations of the analysis for different columns and the exhaustive search on 32 bits and several remaining candidates. The exhaustive search on 32 bits is much cheaper than the cost for the other part. As a result, the time complexity of this attack is
is two more iterations of the analysis for different columns and the exhaustive search on 32 bits and several remaining candidates. The exhaustive search on 32 bits is much cheaper than the cost for the other part. As a result, the time complexity of this attack is ![]() five-round AES computations.
five-round AES computations.
The reduced subkey space ![]() requires to store
requires to store ![]() 8-byte information, which is equivalent to
8-byte information, which is equivalent to ![]() AES states. The other part is negligibly small. As a result, the memory complexity of this attack is
AES states. The other part is negligibly small. As a result, the memory complexity of this attack is ![]() AES states.
AES states.
In summary, the complexity of this attack is ![]() .
.
4.4.10 Higher-Order Integral Property 
The integral property for three rounds only uses 256 plaintexts. A natural approach to improve the attack is increasing the number of plaintexts to attack more rounds. The approach is called higher-order integral cryptanalysis.
Remember that the values of the 15 bytes with the constant property in the set of plaintexts ![]() in Figure 4.36 can be fixed to any value. The higher-order integral cryptanalysis generates several sets of plaintexts by chaining the values of bytes with the constant property. Suppose that two sets of 256 plaintexts
in Figure 4.36 can be fixed to any value. The higher-order integral cryptanalysis generates several sets of plaintexts by chaining the values of bytes with the constant property. Suppose that two sets of 256 plaintexts ![]() and
and ![]() are generated. For the first set
are generated. For the first set ![]() , the byte position 1 is fixed to 0. For the second set
, the byte position 1 is fixed to 0. For the second set ![]() , the byte position 2 is fixed to 0. Then, those 512 plaintexts are queried to the oracle with AES reduced to three rounds, and the attacker obtains the corresponding 512 ciphertexts.
, the byte position 2 is fixed to 0. Then, those 512 plaintexts are queried to the oracle with AES reduced to three rounds, and the attacker obtains the corresponding 512 ciphertexts.
Suppose that the order of the 512 ciphertexts is mixed in an unknown manner to the attacker, that is, the attacker does not know which of the first or second set each ciphertext belongs to. What property can be ensured for 512 ciphertexts in this situation?
The higher-order integral property computes the XOR sum of those 512 ciphertexts. As discussed in the previous section, 256 ciphertexts belonging to the first set make the balanced property after AES three rounds that is, the XOR sum for those 256 ciphertexts is 0. Similarly, the XOR sum for the 256 ciphertexts belonging to the second set is 0. Thus, the XOR sum of the 512 ciphertexts always becomes 0 even without knowing which sets each ciphertext belongs to. The analysis is shown in Figure 4.43.

Figure 4.43 Idea of the higher-order (second-order) integral property
4.4.10.1 Higher-Order Integral Property of AES Reduced to Four Rounds
To extend the number of attacked rounds by one round, ![]() sets of 256 plaintexts
sets of 256 plaintexts ![]() are generated by changing the values of
are generated by changing the values of ![]() . To make it precise, for
. To make it precise, for ![]() , the values of
, the values of ![]() are fixed to 0 and the byte position 0 takes all the 256 possibilities. For
are fixed to 0 and the byte position 0 takes all the 256 possibilities. For ![]() , the values of
, the values of ![]() are fixed to 1 and the byte position 0 takes all the 256 possibilities. For
are fixed to 1 and the byte position 0 takes all the 256 possibilities. For ![]() , the values of
, the values of ![]() are fixed to
are fixed to ![]() and the byte position 0 takes all the 256 possibilities.
and the byte position 0 takes all the 256 possibilities. ![]() texts are required to construct
texts are required to construct ![]() . Owing to the same discussion as the two sets case, all
. Owing to the same discussion as the two sets case, all ![]() ciphertexts after three rounds satisfy the balanced property, that is, the XOR sum of all
ciphertexts after three rounds satisfy the balanced property, that is, the XOR sum of all ![]() ciphertexts is always 0. Then, those
ciphertexts is always 0. Then, those ![]() texts are computed in the backward direction by one round. The analysis is shown in Figure 4.44.
texts are computed in the backward direction by one round. The analysis is shown in Figure 4.44.

Figure 4.44 Higher-order integral property for four-round AES  sets of 256 plaintexts are generated with
sets of 256 plaintexts are generated with  values of
values of  at state
at state  . This involves all the
. This involves all the  values for the first column at state
values for the first column at state 
The ![]() texts are involving all the
texts are involving all the ![]() values for the first column at the state
values for the first column at the state ![]() . In Figure 4.44, 4 gray bytes in the state represent that all
. In Figure 4.44, 4 gray bytes in the state represent that all ![]() possible values are included in the set of
possible values are included in the set of ![]() plaintexts. The same text structure is preserved at the state
plaintexts. The same text structure is preserved at the state ![]() after the inverse of the
after the inverse of the ![]() operation. The
operation. The ![]() operation is a bijective mapping from 32 bits to 32 bits. Hence, the state
operation is a bijective mapping from 32 bits to 32 bits. Hence, the state ![]() after the inverse of the
after the inverse of the ![]() operation has the same property, that is, all the
operation has the same property, that is, all the ![]() values appear in the first column of
values appear in the first column of ![]() . The byte positions are moved at the state
. The byte positions are moved at the state ![]() owing to the inverse of the
owing to the inverse of the ![]() operation. From Lemmas 4.4.1 and 4.4.2, the same property is preserved until the plaintext. In summary, the following property can be obtained for four-round AES.
operation. From Lemmas 4.4.1 and 4.4.2, the same property is preserved until the plaintext. In summary, the following property can be obtained for four-round AES.
4.4.11 Key Recovery Attack with Integral Cryptanalysis for Six Rounds 
On the basis of the four-round higher-order integral property, a key recovery attack can be mounted against AES reduced to six rounds. The attack appends two rounds after the four-round higher-order integral property, which makes the structure shown in Figure 4.45. As explained in Figure 4.44, ![]() plaintexts that take all
plaintexts that take all ![]() possibilities of the byte position
possibilities of the byte position ![]() will make all bytes at state
will make all bytes at state ![]() satisfy the balanced property after four rounds. The attacker guesses the part of the last two subkeys
satisfy the balanced property after four rounds. The attacker guesses the part of the last two subkeys ![]() and
and ![]() and performs the partial decryption up to
and performs the partial decryption up to ![]() . The correct guess always achieves the balanced property in all bytes of
. The correct guess always achieves the balanced property in all bytes of ![]() , which enables the attacker to reduce the key space.
, which enables the attacker to reduce the key space.

Figure 4.45 Key recovery attack against six-round AES. Guessed 4 bytes of  and 4 bytes of
and 4 bytes of  are stressed by bold lines. With those guesses, several bytes of the internal state marked by light gray color can be computed
are stressed by bold lines. With those guesses, several bytes of the internal state marked by light gray color can be computed
Collecting Plaintexts
The attacker chooses fixed values for 12 bytes of the plaintext in the byte positions ![]() . The attacker then chooses
. The attacker then chooses ![]() plaintexts in which the 4 bytes in
plaintexts in which the 4 bytes in ![]() take all possibilities, and the other bytes are fixed to the chosen values. Those
take all possibilities, and the other bytes are fixed to the chosen values. Those ![]() plaintexts are passed to the encryption oracle and the attacker obtains the corresponding
plaintexts are passed to the encryption oracle and the attacker obtains the corresponding ![]() ciphertexts.
ciphertexts.
For the key recovery phase, the attacker prepares another set of ![]() plaintexts by choosing different fixed values of the plaintext in the byte positions
plaintexts by choosing different fixed values of the plaintext in the byte positions ![]() . Those
. Those ![]() plaintexts are also passed to the encryption oracle and the attacker obtains the corresponding
plaintexts are also passed to the encryption oracle and the attacker obtains the corresponding ![]() ciphertexts. In total, the attacker has two sets of
ciphertexts. In total, the attacker has two sets of ![]() ciphertexts in the key recovery phase.
ciphertexts in the key recovery phase.
Recovery of  and
and 
With the obtained two sets of ![]() ciphertexts, the attacker recovers the value of
ciphertexts, the attacker recovers the value of ![]() and
and ![]() . The 4 bytes of
. The 4 bytes of ![]() and 4 bytes of
and 4 bytes of ![]() , in total 64-bit subkey space, are reduced to 32 bits with the analysis of the first set of
, in total 64-bit subkey space, are reduced to 32 bits with the analysis of the first set of ![]() plaintexts. Then, the subkey space is further reduced to 1 by using the second set of
plaintexts. Then, the subkey space is further reduced to 1 by using the second set of ![]() plaintexts. The guessed subkey bytes are marked by bold line in Figure 4.45.
plaintexts. The guessed subkey bytes are marked by bold line in Figure 4.45.
With a guess of ![]() and
and ![]() , the attacker can compute the corresponding 4 bytes of
, the attacker can compute the corresponding 4 bytes of ![]() by taking XOR of the ciphertext and the guess of
by taking XOR of the ciphertext and the guess of ![]() for all of
for all of ![]() ciphertexts in the first set. The inverse of the
ciphertexts in the first set. The inverse of the ![]() operation moves the computed byte positions into
operation moves the computed byte positions into ![]() , and the corresponding 4 bytes of
, and the corresponding 4 bytes of ![]() can be computed with the inverse of the S-box. The guessed
can be computed with the inverse of the S-box. The guessed ![]() allows the attacker to compute the corresponding 4 bytes of
allows the attacker to compute the corresponding 4 bytes of ![]() . Because all values in a column are computed, the corresponding 4 bytes of
. Because all values in a column are computed, the corresponding 4 bytes of ![]() are computed with the inverse of the
are computed with the inverse of the ![]() operation. The next inverse of the
operation. The next inverse of the ![]() operation moves the computed byte positions into
operation moves the computed byte positions into ![]() , and the corresponding 4 bytes of
, and the corresponding 4 bytes of ![]() can be computed with the inverse of the S-box.
can be computed with the inverse of the S-box.
The value of ![]() is computed for all the
is computed for all the ![]() texts in the first set. To check if the balanced property is satisfied, the XOR sum of all the
texts in the first set. To check if the balanced property is satisfied, the XOR sum of all the ![]() texts is computed for 4 bytes of
texts is computed for 4 bytes of ![]() . If the results are 0 in all bytes, that is,
. If the results are 0 in all bytes, that is,
the subkey guess of ![]() can be correct. Then, the guess is stored in a list
can be correct. Then, the guess is stored in a list ![]() . If at least 1 byte of
. If at least 1 byte of ![]() does not satisfy the balanced property, the subkey guess is wrong. The subkey guess is not stored and discarded immediately.
does not satisfy the balanced property, the subkey guess is wrong. The subkey guess is not stored and discarded immediately.
The correct guess always satisfies Equation (167). Besides the correct guess, several wrong guesses happen to satisfy Equation (167) probabilistically. The probability that randomly chosen 4 byte values become 0 is ![]() . Therefore, with trying
. Therefore, with trying ![]() guesses,
guesses, ![]() wrong guesses are stored in the correct subkey candidates list
wrong guesses are stored in the correct subkey candidates list ![]() , In other words, with the analysis of the first set, the subkey space is reduced from
, In other words, with the analysis of the first set, the subkey space is reduced from ![]() to
to ![]() , by 32 bits.
, by 32 bits.
The same analysis is iterated again by using the ![]() ciphertexts in the second set. This time, the subkey guess of
ciphertexts in the second set. This time, the subkey guess of ![]() is chosen from the list
is chosen from the list ![]() , thus the number of guesses is
, thus the number of guesses is ![]() rather than
rather than ![]() in the analysis for the first set. The subkey space is reduced by another 32 bits, which makes the number of subkey candidates about 1.
in the analysis for the first set. The subkey space is reduced by another 32 bits, which makes the number of subkey candidates about 1.
Recovery of Original Key
The same analysis can be performed to recover other subkey bytes of ![]() and
and ![]() . With iterating the analysis twice,
. With iterating the analysis twice,
- 8 bytes of

- 8 bytes of

are recovered. As explained in the previous section, the original key ![]() can be recovered with any other subkey. The remaining unknown bytes of
can be recovered with any other subkey. The remaining unknown bytes of ![]() are the 4 bytes of
are the 4 bytes of ![]() . The attacker recovers those 4 bytes with the exhaustive search. Note that, if the subkey candidates for
. The attacker recovers those 4 bytes with the exhaustive search. Note that, if the subkey candidates for ![]() , and
, and ![]() were not reduced to 1, but several candidates are remaining, the correct candidates can be guessed together with the exhaustive search of
were not reduced to 1, but several candidates are remaining, the correct candidates can be guessed together with the exhaustive search of ![]() .
.
Attack Procedure
The attack procedure is described in an algorithmic form in Algorithm 4.9.
Attack Evaluation
The attack is a chosen plaintext attack. Queries are made in steps 5 and 7, which requires ![]() queries for each. Hence, the data complexity of this attack is
queries for each. Hence, the data complexity of this attack is ![]() chosen plaintexts.
chosen plaintexts.
The computational cost for constructing two sets of ![]() plaintexts is
plaintexts is ![]() computations, which is negligible compared to the key recovery part. For recovering
computations, which is negligible compared to the key recovery part. For recovering ![]() , in the analysis of the first set, the two-round decryption is performed for each of the
, in the analysis of the first set, the two-round decryption is performed for each of the ![]() subkey guesses and
subkey guesses and ![]() ciphertexts in the set. Hence, the computational cost for analyzing the first set (from step 9 to step 17) is
ciphertexts in the set. Hence, the computational cost for analyzing the first set (from step 9 to step 17) is ![]() round function computations, which is
round function computations, which is ![]() six-round AES computations. The computational cost for the second set is cheaper than the one for the first set by a factor of
six-round AES computations. The computational cost for the second set is cheaper than the one for the first set by a factor of ![]() because only about
because only about ![]() candidates remain in
candidates remain in ![]() . The computational cost for the recovery of
. The computational cost for the recovery of ![]() is two more iterations of the 8-byte subkey recovery in different byte positions and the exhaustive search on 32 bits and several remaining candidates in
is two more iterations of the 8-byte subkey recovery in different byte positions and the exhaustive search on 32 bits and several remaining candidates in ![]() .
.
The exhaustive search on 32 bits is much cheaper than the cost for the other part. As a result, the time complexity of this attack is ![]() six-round AES computations.
six-round AES computations.
Both the sets, ![]() and
and ![]() , require a memory to store
, require a memory to store ![]() AES states. The reduced subkey space
AES states. The reduced subkey space ![]() also requires to store
also requires to store ![]() 8-byte information, which is equivalent to
8-byte information, which is equivalent to ![]() AES states. The other parts are negligibly small. As a result, the memory complexity of this attack is
AES states. The other parts are negligibly small. As a result, the memory complexity of this attack is ![]() AES states.
AES states.
In summary, the complexity of this attack is ![]() .
.
Further Reading
- Bahrak B and Aref MR 2008 Impossible differential attack on seven-round AES-128. IET Information Security 2(2), 28–32.
- Biham E, Biryukov A, Dunkelman O, Richardson E and Shamir A 1999 Initial observations on Skipjack: cryptanalysis of Skipjack-3XOR In Selected Areas in Cryptography 1998 (ed. Tavares S and Meijer H), vol. 1556 of Lecture Notes in Computer Science, pp. 362–375. Springer-Verlag.
- Biham E and Keller N 1999 Cryptanalysis of Reduced Variants of Rijndael. The Second AES (Advanced Encryption Standard) Conference.
- Biham E and Shamir A 1993 Differential Cryptanalysis of the Data Encryption Standard. Springer-Verlag.
- Daemen J, Knudsen LR and Rijmen V 1997 The block cipher Square In Fast Software Encryption 1997 (ed. Biham E), vol. 1267 of Lecture Notes in Computer Science, pp. 149–165. Springer-Verlag.
- Knudsen LR 1998 DEAL – A 128-bit cipher. Technical Report, Department of Informatics, University of Bergen, Norway.
- Knudsen LR and Wagner D 2002 Integral cryptanalysis In Fast Software Encryption 2002 (ed. Daemen J and Rijmen V), vol. 2365 of Lecture Notes in Computer Science, pp. 112–127. Springer-Verlag.
- Suzaki T, Minematsu K, Morioka S and Kobayashi E 2013
 : a lightweight block cipher for multiple platforms In Selected Areas in Cryptography, 19th International Conference, SAC 2012, Windsor, ON, Canada, August 15-16, 2012, Revised Selected Papers (ed. Knudsen LR and Wu H), vol. 7707 of Lecture Notes in Computer Science, pp. 339–354. Springer-Verlag.
: a lightweight block cipher for multiple platforms In Selected Areas in Cryptography, 19th International Conference, SAC 2012, Windsor, ON, Canada, August 15-16, 2012, Revised Selected Papers (ed. Knudsen LR and Wu H), vol. 7707 of Lecture Notes in Computer Science, pp. 339–354. Springer-Verlag.


