7
Fuzzy Logics
Logic is about the process of reaching an answer by thinking about known facts. And logic in general can be divided into formal logic, informal logic, symbolic logic, and mathematical logic. We know that in mathematical reasoning, a statement is either true (e.g. “3 is an odd number”) or false (e.g. “4 is greater than 5”), since nothing else is meaningful. However, outside mathematics, there are statements that are neither true or false. For example, the statement “Brazil will win the next world cup in football” is such a statement. Put simply, fuzzy logic is a mathematical logic to reason about statements that are true, false, or something in between. The discussion that follows is based mainly on [157, 217, 218].
7.1 Mathematical Logic
The word “logic” derives from the Greek word λόγος (logos), which means reason. In fact, logic is yet another ancient Greek invention. In particular, as was noted in Section 2.1, Aristotle is credited with the invention of logic. Logic was born when he begun to study the structure of arguments. Aristotle called syllogisms all these structures. An example of a syllogism is the following: John goes to the movies on Wednesday; today is Wednesday; therefore, John will go to the movies. This deduction is an instance of the general inference rule:
Assume that “
” and “if
then
” are true. Then, “
” is also true.
Aristotle invented logic, but it took more than two millennia to have a mathematical description of logic and its rules (see Ref. [207] for a comprehensive presentation of the history of logic).
In (formal) logic, we are concerned about statements, their properties, and proofs. In addition, we do care about form and not about matter or “content,” if you prefer this expression. In essence this means that in formal logic, we are concerned about rules as the inference rule above, but we are not concerned about the nature of ![]() and
and ![]() . For instance, consider the following syllogism:
. For instance, consider the following syllogism:
- If you have a valid password, then you can log on to your Facebook account.
- You have a valid password.
Therefore,
- You can log on to your Facebook account.
This syllogism and the previous one about John's habits have the same form, but of course, logic is not concerned about one's password or John's habits. When logic is using mathematical techniques or when formal logic is employed in mathematical reasoning, then it may be called mathematical logic.
In logic, we can combine statements or sentences, as they are usually called, in various ways to form more complicated sentences. Negation is the simplest logical operation and if ![]() is a sentence, then its negation will be written as
is a sentence, then its negation will be written as ![]() . The truth table for negation (i.e. its “multiplication table”) follows:
. The truth table for negation (i.e. its “multiplication table”) follows:

Thus, if ![]() is true, then
is true, then ![]() is false, and when
is false, and when ![]() is false, then
is false, then ![]() is true. Recall that the symbols
is true. Recall that the symbols ![]() and
and ![]() denote the truth values true and false, respectively.
denote the truth values true and false, respectively.
Given two sentences, ![]() and
and ![]() , their conjunction is the sentence
, their conjunction is the sentence ![]() , which is written as
, which is written as ![]() . The truth table of this operation follows:
. The truth table of this operation follows:

Thus, ![]() is true if and only if both
is true if and only if both ![]() and
and ![]() are true.
are true.
The disjunction of two sentences ![]() and
and ![]() is the expression
is the expression ![]() , which means “
, which means “![]() .” The disjunction of two sentences is written as
.” The disjunction of two sentences is written as ![]() and its truth table follows:
and its truth table follows:

Thus, ![]() is false if and only if both
is false if and only if both ![]() and
and ![]() are false.
are false.
The conditional or implication is an expression of the form “if ![]() , then
, then ![]() ,” written as
,” written as ![]() . Typically, if
. Typically, if ![]() , the antecedent, is true and
, the antecedent, is true and ![]() , the consequent, is false, then the whole expression is false. However, in all other cases, it is really not clear what is the truth value of the whole expression. For instance, the following sentences, borrowed from [217], should clearly demonstrate this point:
, the consequent, is false, then the whole expression is false. However, in all other cases, it is really not clear what is the truth value of the whole expression. For instance, the following sentences, borrowed from [217], should clearly demonstrate this point:
- If
 , then Paris is the capital of France.
, then Paris is the capital of France. - If
 , then Paris is the capital of France.
, then Paris is the capital of France. - If
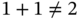 , then Rome is the capital of France.
, then Rome is the capital of France.
Since we have agreed that ![]() is false only when
is false only when ![]() and
and ![]() , we have made the convention that in all other cases, the expression shall be true:
, we have made the convention that in all other cases, the expression shall be true:

The expressions ![]() and
and ![]() are logically equivalent since they receive the same truth value under every assignment of truth values to their statement letters, as the following truth table shows:
are logically equivalent since they receive the same truth value under every assignment of truth values to their statement letters, as the following truth table shows:

The expression ![]() means that
means that ![]() and
and ![]() are logically equivalent.
are logically equivalent.
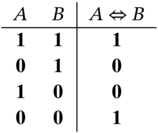
The linguistic expression “![]() if and only if
if and only if ![]() ” is denoted by the mathematical expression
” is denoted by the mathematical expression ![]() . This expression is called a biconditional, and it is true only when
. This expression is called a biconditional, and it is true only when ![]() and
and ![]() have the same truth value:
have the same truth value:
The operators ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() will be called propositional connectives. The letters
will be called propositional connectives. The letters ![]() ,
, ![]() ,
, ![]() ,…will be called statement letters. A statement form will be formed by following these rules:
,…will be called statement letters. A statement form will be formed by following these rules:
- All statement letters with or without numerical subscripts are statement forms.
- If
 and
and  are statement forms, then so are
are statement forms, then so are  ,
,  ,
,  ,
,  , and
, and  .
.  is a statement form if and only if there is a finite sequence
is a statement form if and only if there is a finite sequence  ,
,  , such that
, such that 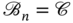 and, if
and, if  , then
, then  is either a statement letter or a negation, conjunction, disjunction, conditional, or biconditional constructed from previous expressions in the sequence.
is either a statement letter or a negation, conjunction, disjunction, conditional, or biconditional constructed from previous expressions in the sequence.
To simplify things, we may omit the outer pair of parentheses of a statement form. Also, we assume the following decreasing order of operator precedence: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Thus,
. Thus, ![]() can be written as
can be written as ![]() . What we presented so far is called propositional logic.
. What we presented so far is called propositional logic.
Consider a discrete set ![]() of
of ![]() elements
elements ![]() . Also, consider the powerset of
. Also, consider the powerset of ![]() . Then, the subsets
. Then, the subsets ![]() can also be considered as logical statements. Thus, set operations can be viewed as logical connectives. In particular,
can also be considered as logical statements. Thus, set operations can be viewed as logical connectives. In particular,
| Set operation | Logical connective |
| Union ( |
Disjunction ( |
| Intersection ( |
Conjunction ( |
| Complement ( |
Negation ( |
Based on this “equivalence,” we can reformulate De Morgan's laws as follows:

Similarly, the law of the excluded middle and the law of contradiction can be expressed as follows:

The law of the excluded middle is a tautology (i.e. a statement form that is always true, no matter what the truth values of its statement letters may be), while the law of contradiction is contradictory (i.e. a statement form that is always false, no matter what the truth values of its statement letters may be).
Propositional logic, in particular, and any logic, in general, can be used to answer questions about specific statement forms (e.g. whether it is a tautology or a contradiction). However, more complex things are not possible using truth tables. More specifically, we need to define a formal theory ![]() that consists of
that consists of
- A countable set of symbols that are the symbols of
 . A finite sequence of symbols is called an expression of
. A finite sequence of symbols is called an expression of  .
. - A subset of the set of expressions of
 called the well‐formed formulas of
called the well‐formed formulas of  .
. - A set of well‐formed formulas called the set of axioms of
 . When we can decide whether a well‐formed formula is an axiom, then
. When we can decide whether a well‐formed formula is an axiom, then  is an axiomatic theory.
is an axiomatic theory. - There is a finite set
 of relations among well‐formed formulas called rules of inference. The important thing is that we can effectively decide whether a set of well‐formed formulas are in relation
of relations among well‐formed formulas called rules of inference. The important thing is that we can effectively decide whether a set of well‐formed formulas are in relation  to a well‐formed formula
to a well‐formed formula  . If this is true, then we say that
. If this is true, then we say that 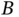 is a direct consequence of the given well‐formed formulas.
is a direct consequence of the given well‐formed formulas.
Informally, this methodology was introduced by Euclid (Eὐκλɛίδης). For the propositional logic, the following tautologies are the axioms of the formal theory:
When a sentence ![]() is provable, we write
is provable, we write ![]() . In propositional logic, we use modus ponens as the inference rule. This rule specifies that if
. In propositional logic, we use modus ponens as the inference rule. This rule specifies that if ![]() and
and ![]() , then infer
, then infer ![]() . Another common proof rule is the adjunction rule: if
. Another common proof rule is the adjunction rule: if ![]() and
and ![]() , then infer
, then infer ![]() . The opposite of this rule is the simplification rule. This rule has two forms: if
. The opposite of this rule is the simplification rule. This rule has two forms: if ![]() , then
, then ![]() or if
or if ![]() , then
, then ![]() . Instead of writing the steps of proof as a list, one can write a proof tree. For instance, the following is an example of a trivial proof tree:
. Instead of writing the steps of proof as a list, one can write a proof tree. For instance, the following is an example of a trivial proof tree:
More formally, we can say that a proof is a sequence ![]() of sentences such that each
of sentences such that each ![]() is either an axiom of propositional logic or it follows from some preceding
is either an axiom of propositional logic or it follows from some preceding ![]() ,
, ![]() ,
, ![]() , by modus ponens. Such systems are known as Hilbert systems. A more advanced way to prove theorems in a logic is to use Gentzen systems. However, we will not discuss these systems, and the interested reader should consult a more specialized text (e.g. see Ref. [218]).
, by modus ponens. Such systems are known as Hilbert systems. A more advanced way to prove theorems in a logic is to use Gentzen systems. However, we will not discuss these systems, and the interested reader should consult a more specialized text (e.g. see Ref. [218]).
Propositional logic cannot be used to express certain kinds of deductions. For example, consider the following deduction:
All human beings are rational.
Some animals are human beings.
Therefore, some animals are rational.
The correctness of this deduction depends on the meaning of various connectives and on the meaning of expressions such as “any,” “all,” “some.” To allow the expression of such statements, we introduce predicates that express attributes, properties, etc., and quantifiers. Thus, ![]() is a predicate that asserts that
is a predicate that asserts that ![]() has the property
has the property ![]() , while
, while ![]() is a predicate that asserts that
is a predicate that asserts that ![]() and
and ![]() have a property in common (e.g. it may express the fact that
have a property in common (e.g. it may express the fact that ![]() and
and ![]() are brothers). The number of terms (i.e. the symbols in a predicate) equals to the arity of the predicate. Moreover, the sentence “there is an
are brothers). The number of terms (i.e. the symbols in a predicate) equals to the arity of the predicate. Moreover, the sentence “there is an ![]() with the property
with the property ![]() ” is written as
” is written as ![]() , whereas the sentence “all
, whereas the sentence “all ![]() have the property
have the property ![]() ” is written as
” is written as ![]() . The symbols “
. The symbols “![]() ” and “
” and “![]() ” are called a universal quantifier and an existential quantifier, respectively. For instance, the previous deduction becomes
” are called a universal quantifier and an existential quantifier, respectively. For instance, the previous deduction becomes

Here ![]() ,
, ![]() , and
, and ![]() designate the properties of being human, rational, and an animal, respectively. Also, to simplify expressions, we drop the parentheses whenever this is possible.
designate the properties of being human, rational, and an animal, respectively. Also, to simplify expressions, we drop the parentheses whenever this is possible.
One interesting question is whether there are other quantifiers. Andrzej Mostowski [225] gave an affirmative answer to this question by introducing a generalization of quantifiers. Here is an outline of what he meant by this. Assume that ![]() is an arbitrary set and
is an arbitrary set and ![]() is its infinite Cartesian product. A mapping
is its infinite Cartesian product. A mapping ![]() is called a propositional function on
is called a propositional function on ![]() provided that it satisfies the following condition: there is a finite set
provided that it satisfies the following condition: there is a finite set ![]() of integers such that if
of integers such that if
then ![]() . Clearly, the value of
. Clearly, the value of ![]() depends on a finite number of arguments. Assume that
depends on a finite number of arguments. Assume that ![]() is an injective mapping, where
is an injective mapping, where ![]() is not necessarily different from
is not necessarily different from ![]() . Then,
. Then, ![]() , where
, where ![]() , is the tuple
, is the tuple ![]() . Also, if
. Also, if ![]() is a propositional function on
is a propositional function on ![]() , then
, then ![]() is the propositional function on
is the propositional function on ![]() such that
such that ![]() . A quantifier limited to
. A quantifier limited to ![]() is a function
is a function ![]() that assigns one of the elements
that assigns one of the elements ![]() and
and ![]() to each propositional function
to each propositional function ![]() on
on ![]() that takes one argument only and satisfies the invariance condition
that takes one argument only and satisfies the invariance condition
for each ![]() and each permutation
and each permutation ![]() of
of ![]() .
.
Suppose that ![]() is the finite or transfinite sequence of all pairs of cardinal numbers that satisfy the equation
is the finite or transfinite sequence of all pairs of cardinal numbers that satisfy the equation ![]() . For every function
. For every function ![]() that assigns one of the truth values to each pair
that assigns one of the truth values to each pair ![]() , we write:
, we write:
It can be shown that for each ![]() , which is a quantifier limited to
, which is a quantifier limited to ![]() , there is a
, there is a ![]() such that
such that ![]() . The quantifier determined by
. The quantifier determined by ![]() is the dual of
is the dual of ![]() and is denoted by
and is denoted by ![]() . Finally, an unlimited quantifier or just quantifier is a function that assigns a quantifier
. Finally, an unlimited quantifier or just quantifier is a function that assigns a quantifier ![]() limited to
limited to ![]() to each set
to each set ![]() and satisfies the equation
and satisfies the equation ![]() for each propositional function
for each propositional function ![]() on
on ![]() with one argument and for each 1–1 mapping from
with one argument and for each 1–1 mapping from ![]() to
to ![]() .
.
7.2 Many‐Valued Logics
It seems that Aristotle not only invented logic but also he invented multivalued logics, as he was the first who recognized that there are propositions that cannot be classified as either true or false. In particular, in chapter IX of his treatise De Interpretatione (![]() On Interpretation), which is part of his Organon, he ponders about future contingents and their truth values. He concludes that [12]:
On Interpretation), which is part of his Organon, he ponders about future contingents and their truth values. He concludes that [12]:
Unfortunately, the idea that there are more than two truth values was not particularly appealing until the 1920s when Jan Łukasiewicz introduced a three‐valued logic [198]. Besides ![]() and
and ![]() , this logic includes the truth value
, this logic includes the truth value ![]() (later he used the symbol
(later he used the symbol ![]() to denote this value), which may be interpreted as “possibility.” Later on, in his Philosophical Remarks on Many‐Valued Systems of Propositional Logic [199], he presented the truth tables for negation and implication for the three‐valued logic:
to denote this value), which may be interpreted as “possibility.” Later on, in his Philosophical Remarks on Many‐Valued Systems of Propositional Logic [199], he presented the truth tables for negation and implication for the three‐valued logic:

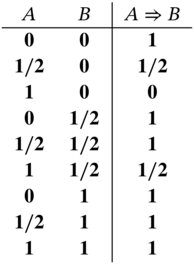
In the same paper, he discussed what happens when the truth values are “certain numbers of the interval ![]() ”:
”:

Emil Leon Post [242] described another logic with ![]() truth values
truth values ![]() . The following are the truth tables for negation and disjunction:
. The following are the truth tables for negation and disjunction:


The generalized negation permutes the truth values cyclically, while the generalized disjunction yields from the two truth values the one with smaller subscript. Note that Post did not provide the truth table for conjunction, mainly because he was not really interested in many‐valued logics.
Stephen Cole Kleene [175] presented yet another logic with three truth values: true, false, and undefined. In the case of negation: ![]() ,
, ![]() , and
, and ![]() . The truth tables for the other logical operations are given as follows:
. The truth tables for the other logical operations are given as follows:

In a very short note, Gödel [155] introduced a many‐valued logic to show that intuitionistic propositional logic cannot be viewed as a many‐valued logic. In this logic, the truth values are elements of the set ![]() , where
, where ![]() is a designated element. The various logical connectives are defined as follows:
is a designated element. The various logical connectives are defined as follows:

Dmitri Anotolevich Bochvar [32] introduced a three‐valued logic, where every statement is either meaningless (denoted by ![]() ), true, or false. In this logic, if some statement
), true, or false. In this logic, if some statement ![]() is meaningless, then the statements “
is meaningless, then the statements “![]() is false” and “
is false” and “![]() is true” are meaningful and false, respectively. In addition, he considered two kinds of statements: internal and external. The following table shows the difference between the two kinds.
is true” are meaningful and false, respectively. In addition, he considered two kinds of statements: internal and external. The following table shows the difference between the two kinds.
| Internal statements | External statements |
| “ |
“ |
| “not‐ |
“ |
| “ |
“ |
| “ |
“ |
| “if |
“if |
| “ |
In order to see the difference between the two kinds of statements, assume that ![]() is a meaningless statement (i.e. its truth value is
is a meaningless statement (i.e. its truth value is ![]() ). Then, the statement “not‐
). Then, the statement “not‐![]() ” is also meaningless, but the statement “
” is also meaningless, but the statement “![]() is false” is not meaningless but false. Also, if
is false” is not meaningless but false. Also, if ![]() is a meaningless statement, then any possible combination of
is a meaningless statement, then any possible combination of ![]() with any statement
with any statement ![]() , regardless of its truth value, by means of the various internal connectives, will yield another meaningless statement. However, no combination of external connectives will yield a meaningless statement. The following tables are the truth tables for internal denial (“not‐
, regardless of its truth value, by means of the various internal connectives, will yield another meaningless statement. However, no combination of external connectives will yield a meaningless statement. The following tables are the truth tables for internal denial (“not‐![]() ,” denoted by
,” denoted by ![]() ) and internal conjunction (denoted by
) and internal conjunction (denoted by ![]() ):
):


The statements “![]() is true” and “
is true” and “![]() is false” are denoted by
is false” are denoted by ![]() and
and ![]() , respectively. Their truth tables follow:
, respectively. Their truth tables follow:

The operations “![]() or
or ![]() ” (denoted by
” (denoted by ![]() ), “if
), “if ![]() , then
, then ![]() ” (denoted by
” (denoted by ![]() ), and the internal equivalence operation (denoted by
), and the internal equivalence operation (denoted by ![]() ) are defined as follows:
) are defined as follows:

The various external logical connectives are defined as follows:

The expression ![]() is read as “
is read as “![]() is true and
is true and ![]() is true”; the expression
is true”; the expression ![]() is read as “
is read as “![]() is true or
is true or ![]() is true”; the expression
is true”; the expression ![]() is read as “if
is read as “if ![]() is true, then
is true, then ![]() is true”; the expression
is true”; the expression ![]() is read as “
is read as “![]() is of the same strength as
is of the same strength as ![]() ”; and the expression
”; and the expression ![]() is read as “
is read as “![]() is equivalent to
is equivalent to ![]() .” The truth tables for the remaining two connectives follow:
.” The truth tables for the remaining two connectives follow:

So far we have described logics that have three different truth values. However, there are logics with more truth values, and there are logics with an infinite number of truth values. Łukasiewicz and Alfred Tarski [200] discussed these ideas in detail. In particular, they described many‐valued logics that are now known as Łukasiewicz logics. Each of these finite logics is denoted by ![]() , where
, where ![]() is the number of truth values. For a logic
is the number of truth values. For a logic ![]() , its truth values follow:
, its truth values follow:
Thus, when ![]() , the truth values are 0,
, the truth values are 0, ![]() , and 1. When the set of truth values is infinite (i.e. when its cardinality is equal to
, and 1. When the set of truth values is infinite (i.e. when its cardinality is equal to ![]() , where
, where ![]() denotes the cardinality of
denotes the cardinality of ![]() , that is, the set of positive integers including zero), then the logic is denoted by
, that is, the set of positive integers including zero), then the logic is denoted by ![]() and its truth values are all fractions
and its truth values are all fractions ![]() , for
, for ![]() , and the truth‐value 1. For all these logics, given two truth values
, and the truth‐value 1. For all these logics, given two truth values ![]() and
and ![]() , negation and implication are defined as follows:
, negation and implication are defined as follows:
In the case of the infinite‐valued logic, it was proposed that the following sentences
- (Ł1)

- (Ł2)

- (Ł3)
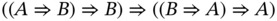
- (Ł4)

- (Ł5)

form a set of axioms for ![]() . Later on, it was shown that axiom (Ł4) is deducible from the remaining axioms.
. Later on, it was shown that axiom (Ł4) is deducible from the remaining axioms.
In the 1950s Robert McNaughton [213] described an infinite‐valued logic whose truth values belong to the unit interval, that is, any truth value ![]() . In this logic 1 denotes complete truth and 0 denotes complete falsity. The logic has two basic logical connectives: negation and implication. Conjunction and disjunction are defined in terms of negation and implication. These basic logic connectives are defined as follows:
. In this logic 1 denotes complete truth and 0 denotes complete falsity. The logic has two basic logical connectives: negation and implication. Conjunction and disjunction are defined in terms of negation and implication. These basic logic connectives are defined as follows:
The other two operations are defined as follows:
Let us see how these two connectives are defined in terms of the basic connectives:

7.3 On Fuzzy Logics
When Zadeh introduced fuzzy sets by extending the notion of sets, he also introduced fuzzy logic. However, it was Goguen [143] who actually introduced a fuzzy logic, in the sense of a logical system. Zadeh himself was more interested in applications of fuzzy sets and not so much in the logical aspect of fuzzy set theory. After all, Zadeh was an engineer and not a mathematician or a computer scientist. Since the term “fuzzy logic” was used for different things, Zadeh proposed the use of the term fuzzy logic in the narrow sense to mean fuzzy logic, and the term fuzzy logic in the wide sense to mean the application of fuzzy sets to everything else. Zadeh himself explained the difference between the two terms as follows2:
Many of the misconceptions about fuzzy logic stem from differing interpretations of what “fuzzy logic” means. In the narrow sense, fuzzy logic is a logical system that focuses on modes of reasoning that are approximate rather than exact. In this sense, fuzzy logic, or FLn for short, is an extension of classical multivalued logical systems, but with an agenda that is quite different in spirit and in substance.
In the wide sense, which is in predominant use today, fuzzy logic, or FLw for short, is almost synonymous with the theory of fuzzy sets. The agenda of FLw is much broader than that of FLn, and logical reasoning–in its traditional sense–is an important but not a major part of FLw. In this perspective, FLn may be viewed as one of the branches of FLw. What is important to note is that, today, most of the practical applications of fuzzy logic involve FLw and not FLn.
The use of the word “wide” was not a good idea. So, many authors proposed the replacement of this word with the word “broad”, mainly because it is more natural in this case (see Ref. [26]). Thus, this chapter is about fuzzy logic in the narrow sense and the rest of the book about fuzzy logic in the broad sense. And of course, fuzzy logic in the broad sense is not really logic…
In fuzzy logic, the truth values are the elements of the set ![]() . Thus, one can say that fuzzy logic is an infinite‐valued logic since the cardinality of the unit interval is
. Thus, one can say that fuzzy logic is an infinite‐valued logic since the cardinality of the unit interval is ![]() , which is clearly greater than
, which is clearly greater than ![]() . It is not difficult to convince one about the need to have more than two truth values, nevertheless, one can easily abolish the idea of an infinite number of truth values as absurd. Petr Hájek [157] proposes the use of simple questions like Do you like Haydn? to demonstrate the usefulness of infinite‐valued logics. To answer such a question, one is offered a number of possible answers like: absolutely yes, more or less, rather not, absolutely not. But there is no reason to restrict the number of answers to 4 or 20 as one might not be happy with any of these answers. A better approach is to allow one to choose the required values by using a slider that can go from 0 (absolutely no) to 1 (absolutely yes). Since we cannot have such a slider at our disposal, we should be free to just choose an element of
. It is not difficult to convince one about the need to have more than two truth values, nevertheless, one can easily abolish the idea of an infinite number of truth values as absurd. Petr Hájek [157] proposes the use of simple questions like Do you like Haydn? to demonstrate the usefulness of infinite‐valued logics. To answer such a question, one is offered a number of possible answers like: absolutely yes, more or less, rather not, absolutely not. But there is no reason to restrict the number of answers to 4 or 20 as one might not be happy with any of these answers. A better approach is to allow one to choose the required values by using a slider that can go from 0 (absolutely no) to 1 (absolutely yes). Since we cannot have such a slider at our disposal, we should be free to just choose an element of ![]() as our truth value.
as our truth value.
We have talked about fuzzy logics and not fuzzy logic because one can use any ![]() ‐norm together with an implication connective to define all logical connectives. But how can we define such a logical connective? A good idea is to use the exponential element and use it to define the new logical connective. Indeed, the following result shows how this can be done.
‐norm together with an implication connective to define all logical connectives. But how can we define such a logical connective? A good idea is to use the exponential element and use it to define the new logical connective. Indeed, the following result shows how this can be done.
The operation ![]() is called the residuum of the
is called the residuum of the ![]() ‐norm. The next step is to give a concrete definition of this operation for specific
‐norm. The next step is to give a concrete definition of this operation for specific ![]() ‐norms. The result that follows answers the question: What are the residua of the Gödel, Łukasiewicz, and the product
‐norms. The result that follows answers the question: What are the residua of the Gödel, Łukasiewicz, and the product ![]() ‐norms?
‐norms?
7.4 Hájek's Basic Many‐Valued Logic
We can use any ![]() ‐norm and its residuum to define a propositional logic. First, the
‐norm and its residuum to define a propositional logic. First, the ![]() ‐norm will be used as a (strong) conjunction
‐norm will be used as a (strong) conjunction ![]() , its residuum
, its residuum ![]() as the truth function of the implication
as the truth function of the implication ![]() , and the truth constant
, and the truth constant ![]() for 0 (false). The table that follows shows the basic logical connectives and how they are defined:
for 0 (false). The table that follows shows the basic logical connectives and how they are defined:

These operations specify a propositional calculus that we call ![]() , where
, where ![]() is a
is a ![]() ‐norm.
‐norm.
Each statement letter ![]() is assigned a numerical value
is assigned a numerical value ![]() that is interpreted as its truth degree. Also, this extends to the evaluation of all statement forms as follows:
that is interpreted as its truth degree. Also, this extends to the evaluation of all statement forms as follows:

The evaluation rule for implication was exactly the reason why we had to introduce a new symbol for implication. In order to present the evaluation rules for conjunction and disjunction, we need the following result:
The following result is a direct consequence of the previous lemma:
Naturally, the set of 1‐tautologies depends on the choice of the ![]() ‐norm, and clearly, different
‐norm, and clearly, different ![]() ‐norms may have different sets of 1‐tautologies. We have presented the basic ingredients of the logic, and we can proceed with the presentation of the axioms of basic logic, BL.
‐norms may have different sets of 1‐tautologies. We have presented the basic ingredients of the logic, and we can proceed with the presentation of the axioms of basic logic, BL.
Note that the only inference rule is modus ponens. Also, all axioms of BL are 1‐tautologies in each ![]() .
.
7.5 Łukasiewicz Fuzzy Logic
Łukasiewicz fuzzy logic is actually the ![]() logic. If we start with axioms of basic logic and then add the following statement form as axiom:
logic. If we start with axioms of basic logic and then add the following statement form as axiom:
then we get a system that we will call Ł. It can be shown that this system is equivalent to ![]() . This equivalence is based on the following lemmas:
. This equivalence is based on the following lemmas:
We omit the proofs since they are based on many intermediate results that we have not presented here.
In the systems we have briefly described so far, the proofs are about sentences whose truth value is ![]() . However, this is particularly strange since we are interested in partial truth. Thus, is it reasonable to ask if it is possible to prove partially true conclusions from partially true premises? If we extend the language
. However, this is particularly strange since we are interested in partial truth. Thus, is it reasonable to ask if it is possible to prove partially true conclusions from partially true premises? If we extend the language ![]() by adding truth constants
by adding truth constants ![]() for each
for each ![]() , then this means that our calculus will have symbols like
, then this means that our calculus will have symbols like ![]() and
and ![]() as truth constants in addition to
as truth constants in addition to ![]() and
and ![]() .3 The result is a new language that is called Rational Pavelka Logic, RPL. This new language has the two connectives
.3 The result is a new language that is called Rational Pavelka Logic, RPL. This new language has the two connectives ![]() and
and ![]() . Negation and conjunction are defined as follows:
. Negation and conjunction are defined as follows:

In addition, the language has the connectives ![]() ,
, ![]() , and
, and ![]() . The following equations summarize the evaluation rules of all sentences of RPL:
. The following equations summarize the evaluation rules of all sentences of RPL:

The axioms of RPL are the axioms of ![]() plus the axioms that follow, whereas the deduction rule is modus ponens:
plus the axioms that follow, whereas the deduction rule is modus ponens:

A graded sentence is a pair ![]() , where
, where ![]() is a sentence and
is a sentence and ![]() . Alternatively, one can write
. Alternatively, one can write ![]() .
.
7.6 Product Fuzzy Logic
We will now briefly present the propositional calculus ![]() , where
, where ![]() is the product
is the product ![]() ‐norm, and the corresponding product logic (Π). The implication used in the calculus is the Goguen implication (see Theorem 7.3.1), while the negation is the Gödel negation:
‐norm, and the corresponding product logic (Π). The implication used in the calculus is the Goguen implication (see Theorem 7.3.1), while the negation is the Gödel negation:

The direct analog of RPL over product logic is not possible, and this happens because of the discontinuity of Goguen implication. It is possible to overcome this difficulty, but we will not discuss the technicalities involved, so we will not present how this can be done.
7.7 Gödel Fuzzy Logic
Gödel logic, G, is another logic generated by a continuous ![]() ‐norm. In this case, the strong conjunction operator is the
‐norm. In this case, the strong conjunction operator is the ![]() operator. The set of axioms of G includes all axioms of BL plus the following one:
operator. The set of axioms of G includes all axioms of BL plus the following one:
This axiom together with ![]() , which is a special case of (A2), prove that
, which is a special case of (A2), prove that ![]() (i.e. the connective
(i.e. the connective ![]() is idempotent).
is idempotent).
In other words, this lemma shows that one of the two conjunction connectives is redundant. Therefore, we should simplify G by having only one conjunction connective. Let us call this new simplified system ![]() . This new logical system has the connectives
. This new logical system has the connectives ![]() ,
, ![]() , and
, and ![]() (nullary connective) and its set of axioms includes (A1)–(A3), (A5)–(A7) of BL, where
(nullary connective) and its set of axioms includes (A1)–(A3), (A5)–(A7) of BL, where ![]() is replaced by
is replaced by ![]() , and the axiom
, and the axiom
In addition, there are three more connectives that are defined as follows:

It is necessary to show that the introduction of ![]() brings nothing new and the following result states exactly this.
brings nothing new and the following result states exactly this.
Thus, G and ![]() are indistinguishable!
are indistinguishable!
Gödel logic is related to intuitionist logic. The connection between the two logical systems will be outlined in what follows.
One can prove the converse by extending I with (A6). Note that in I, the connective ![]() cannot be defined from the other connectives.
cannot be defined from the other connectives.
7.8 First‐Order Fuzzy Logics
For all three fuzzy logics presented so far (i.e. Łukasiewicz, Product, and Gödel logic), there is a corresponding first‐order language (i.e. a corresponding predicate calculus). Beneath each of these logics lies a predicate language that consists of a nonempty set of predicates and a (possibly empty) set of object constants (i.e. something that we presume or hypothesize to exist in the world). Predicates like ![]() are atomic sentences or formulas. If
are atomic sentences or formulas. If ![]() and
and ![]() are formulas, then
are formulas, then ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are formulas. The following are logical axioms on quantifiers:
are formulas. The following are logical axioms on quantifiers:
 (
(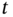 is substitutable for
is substitutable for 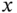 in
in  );
); (
( is substitutable for x in
is substitutable for x in  );
); (
( not free in
not free in  );
); (
( not free in
not free in  ); and
); and (
( not free in
not free in  ).
).
In the rest of this section, we discuss some logical calculi ![]() that are derived from C by adding the logical axioms on quantifiers to its axioms.
that are derived from C by adding the logical axioms on quantifiers to its axioms.
Let us start our very brief discussion with the Gödel predicate logic ![]() [18]. A Gödel set is a closed set
[18]. A Gödel set is a closed set ![]() that contains 0 and 1. Given a Gödel set
that contains 0 and 1. Given a Gödel set ![]() , then an interpretation
, then an interpretation ![]() into
into ![]() for
for ![]() consists of
consists of
- a nonempty domain
 ;
; - for each
 ‐ary predicate symbol, a function that maps elements of
‐ary predicate symbol, a function that maps elements of  to
to  ;
; - for each
 ‐ary function symbol, a function that maps elements of
‐ary function symbol, a function that maps elements of  to
to  ;
; - for each variable, an element of
 .
.
For atomic formulas:
For a variable ![]() ,
, ![]() , where
, where ![]() . For all formulas:
. For all formulas:

If ![]() , we say that
, we say that ![]() satisfies
satisfies ![]() , and write
, and write ![]() . Also, if
. Also, if ![]() for every
for every ![]() ‐interpretation
‐interpretation ![]() , we say
, we say ![]() is valid in
is valid in ![]() and write
and write ![]() . If
. If ![]() is a set of sentences, we define
is a set of sentences, we define
Given a possibly infinite set of formulas ![]() , we say that
, we say that ![]() entails
entails ![]() ,
, ![]() , if and only if for all
, if and only if for all ![]() into
into ![]() ,
, ![]() .
.
Similar things can be said about the Łukasiewicz predicate logic ![]() [17]. Thus, we will not repeat what has been already discussed. Instead, we just present the valuations in what follows:
[17]. Thus, we will not repeat what has been already discussed. Instead, we just present the valuations in what follows:

In general, one uses modus ponens and the adjunction rule
plus the axioms in order to deliver a proof.
7.9 Fuzzy Quantifiers
Zadeh [315] was the first who introduced fuzzy quantifiers. Naturally, many people worked on this subject, but it was Helmut Thiele who introduced ![]() ‐norm and
‐norm and ![]() ‐conorm fuzzy quantifiers (e.g. see Ref. [285]). This section is based on Ingo Glöckner's monograph [141].
‐conorm fuzzy quantifiers (e.g. see Ref. [285]). This section is based on Ingo Glöckner's monograph [141].
The definition given in Section 7.1 is not very “useful.” A better formulation follows:
The definition of Boolean quantifiers is used as a basis to define fuzzy quantifiers:
From this definition, it should be clear that ![]() assigns to an
assigns to an ![]() ‐tuple of fuzzy sets
‐tuple of fuzzy sets ![]() an interpretation
an interpretation ![]() .
.
for all ![]() .
.
7.10 Approximate Reasoning
Without trying to exaggerate, we could say that pure mathematics is the only field where we reason in precise terms. In all other areas, we reason in approximate terms. Since fuzzy set theory is about vagueness, one could use it to reason in all these cases where we reason in approximate terms. Zadeh [310] used his fuzzy restrictions to propose concrete tools that would allow one to mechanically reason approximately. However, we have presented a number of fuzzy logics and, obviously, it would be better to reformulate these tools in these new languages. Thus, we first present Zadeh's original ideas and then we will present their reformulation in these languages of logic.
We introduced fuzzy restrictions in Section 5.1. The following is a summary of what is a fuzzy restriction. Assume that ![]() is a collection of universes and that
is a collection of universes and that ![]() . Then, by a fuzzy restriction on
. Then, by a fuzzy restriction on ![]() , written as
, written as ![]() , we mean a fuzzy relation in
, we mean a fuzzy relation in ![]() that defines the compatibility with
that defines the compatibility with ![]() of values that are assigned to
of values that are assigned to ![]() . If
. If ![]() is a proposition of the form
is a proposition of the form
where ![]() is a fuzzy relation in
is a fuzzy relation in ![]() , then the previous “equation” may be interpreted as the assignment equation
, then the previous “equation” may be interpreted as the assignment equation
Thus, for the propositions
the relational assignment equations are
Given these two propositions/equations, what can be said about ![]() ? To answer this question, we use the compositional rule of inference:
? To answer this question, we use the compositional rule of inference:

Now assume that

We need to compute the composition ![]() . This can be expressed as the max–min composition of the relation matrices of small and approximately equal. Thus,
. This can be expressed as the max–min composition of the relation matrices of small and approximately equal. Thus,

Therefore, the fuzzy restriction on ![]() is given by
is given by
A rough linguistic approximation of this fuzzy restriction is
where LA is the operation of linguistic approximation and

If you attempt to calculate the values, you will notice that you do not get the expected value, but something close to it. This is why Zadeh called it approximate reasoning! From the premises ![]() and
and ![]() , we conclude that
, we conclude that
Along those lines, Zadeh defined a compositional modus ponens as follows:

where ![]() .
.
The previous inference rules can be reformulated so as to make it possible to have them as ingredients of predicate calculus. In order to achieve this, first we need to introduce variates. A variate consists of a symbol ![]() , which is its name, and a nonempty set
, which is its name, and a nonempty set ![]() , which is its domain. For instance, height (in centimeters) with domain the set of integers
, which is its domain. For instance, height (in centimeters) with domain the set of integers ![]() is a variate. Roughly, we can take the domains to be collections of different things (e.g. plants and animals) that will allow us to interpret a predicate language. In addition, fixed fuzzy subsets of a domain will interpret some unary predicates. Furthermore, the name of a variate will play the role of an object constant, which is interpreted as the actual value of the variate. Thus, the expression “
is a variate. Roughly, we can take the domains to be collections of different things (e.g. plants and animals) that will allow us to interpret a predicate language. In addition, fixed fuzzy subsets of a domain will interpret some unary predicates. Furthermore, the name of a variate will play the role of an object constant, which is interpreted as the actual value of the variate. Thus, the expression “![]() is
is ![]() ” is a formula
” is a formula ![]() . For example, the typical rule “IF
. For example, the typical rule “IF ![]() is
is ![]() THEN
THEN ![]() is
is ![]() ” may be interpreted as
” may be interpreted as ![]() . The compositional rule of inference is expressed as follows:
. The compositional rule of inference is expressed as follows:
From “
is
” and “
is
” infer “
is
” if for all
,
Here ![]() is a continuous
is a continuous ![]() ‐norm, and
‐norm, and ![]() ,
, ![]() , and
, and ![]() are fuzzy relations corresponding to the predicates
are fuzzy relations corresponding to the predicates ![]() ,
, ![]() , and
, and ![]() . This condition means that the formula
. This condition means that the formula
is 1‐true in any structure ![]() of domains of variates (i.e. the valuation of this formula is equal to 1).
of domains of variates (i.e. the valuation of this formula is equal to 1).
It can be shown that compositional modus ponens is actually a special case of the compositional inference rule.
This can be visualized as follows:
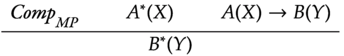
In what follows, we will suppose that the predicates ![]() and
and ![]() are of the same sort (i.e. they are of the same type in programming languages parlance, that is, they are of the same kind) and
are of the same sort (i.e. they are of the same type in programming languages parlance, that is, they are of the same kind) and ![]() and
and ![]() are also of the same sort. The following result holds of the generalized simplification rule:
are also of the same sort. The following result holds of the generalized simplification rule:
As in the previous case, this can be visualized as follows:

These rules are primarily used in fuzzy expert systems.
7.11 Application: Fuzzy Expert Systems
Generally speaking, an expert system is a computer program that uses tools and methods employed in artificial intelligence to solve problems that typically require human expertise, hence the term “expert system.” The definition that follows, borrowed from [234], describes the functionality of an expert system.
An expert system is a program that relies on a body of knowledge to perform a somewhat difficult task usually performed only by a human expert. The principal power of an expert system is derived from the knowledge the system embodies rather than from search algorithms and specific reasoning methods. An expert system successfully deals with problems for which clear algorithmic solutions do not exist.
In expert systems, knowledge is represented with IF–THEN rules. For example, these are two simplified rules that describe what should be done when a car encounters traffic lights.
| IF | the “traffic light” is “green” |
| THEN | push pedal and go |
| IF | the “traffic light” is “red” |
| THEN | push brake and stop |
Fuzzy expert systems [150, 261] represent knowledge with fuzzy IF–THEN rules. Typically, fuzzy rules contain linguistic variables, and the following rules are a typical example of fuzzy rules:
| IF | player is a very good passer and ball handler and not primarily a shooter |
| THEN | player is a point guard |
| IF | player is not a great ball handler and a good perimeter shooter |
| THEN | player is a shooting guard |
In this example, we have used linguistic hedges (i.e. words that are used to soften what we say or write). Obviously, terms such as “good” and “great” are modeled with fuzzy sets. But what is the effect of hedges? Zadeh [308] gave an interpretation of hedges in the framework of fuzzy set theory. In particular, in this interpretation, hedges behave like operators that are applied to fuzzy sets and modify them. If ![]() is a hedge and
is a hedge and ![]() is a membership function, then
is a membership function, then ![]() will denote
will denote ![]() after applying
after applying ![]() to it. Here are some hedges, and how they modify a fuzzy set:
to it. Here are some hedges, and how they modify a fuzzy set:
- very
 .
. - more or less (morl)
 .
. - slightly
 .
. - extremely
 .
. - somewhat
 .
.
The modifier ![]() , where
, where ![]() , could correspond to exactly, since all membership degrees become equal to 1.
, could correspond to exactly, since all membership degrees become equal to 1.
The fuzzy inference engine is the core of a fuzzy expert system. This module performs fuzzy deductions using fuzzy logic. Traditionally, fuzzy inference engines use approximate deductions (i.e. deductions using the inference rules presented in the previous section). Fuzzy inference is a multistep process. Given some input, the output is produced by the following steps:
- Step 1. Define fuzzy sets
- Step 2. Relate observations to fuzzy sets
- Step 3. Define fuzzy rules
- Step 4. Evaluate each case for all fuzzy rules
- Step 5. Combine information from rules
- Step 6. Defuzzify results
The most interesting steps of this process are the fuzzification step, the rule evaluation step, and the defuzzification step. In what follows, we will briefly explain these steps.
7.11.1 Fuzzification
A process that makes a crisp quantity fuzzy is called fuzzification. In reality, many of the quantities that we think to be crisp are not actually crisp because they carry considerable uncertainty. And if this uncertainty has its roots to imprecision, ambiguity, or vagueness, then the quantity is possibly fuzzy and can be represented by a membership function.
In Section 1.3, we noted that hardware is actually vague since it operates within a specific range of accuracy. Thus, we can assume that the readings on a digital voltmeter are actually vague readings (after all, there are no infinitely accurate devices). Figure 7.1 shows the reading of such a device and, assuming a ![]() “error” range, how one can create a fuzzy set from such readings.
“error” range, how one can create a fuzzy set from such readings.
7.11.2 Evaluation of Rules
Evaluation rules are actually fuzzy implications. Thus, the rule IF ![]() THEN
THEN ![]() is actually a verbose way to say
is actually a verbose way to say ![]() . The most important problem as regards the evaluation of rules is how to choose the proper implication. In our opinion this is a bit silly since implication operators are used to build logics and logics have many properties (e.g., completeness results, truth values, etc.). Thus, the real question is not which implication the operator chooses but which logic to choose. Naturally, our choice should depend on the properties of a specific logic. These properties have been discussed thoroughly by Hájek [157].
. The most important problem as regards the evaluation of rules is how to choose the proper implication. In our opinion this is a bit silly since implication operators are used to build logics and logics have many properties (e.g., completeness results, truth values, etc.). Thus, the real question is not which implication the operator chooses but which logic to choose. Naturally, our choice should depend on the properties of a specific logic. These properties have been discussed thoroughly by Hájek [157].

Figure 7.1 Membership function of readings of a digital voltmeter.
7.11.3 Defuzzification
The term “defuzzification” refers to a process that makes crisp a fuzzy set. The most obvious method to transform a fuzzy set into a crisp one is to get an ![]() ‐cut of it. Another method that is very frequently used, is the center of gravity or centroid of area method. In the discrete case, we have a fuzzy set
‐cut of it. Another method that is very frequently used, is the center of gravity or centroid of area method. In the discrete case, we have a fuzzy set ![]() and
and ![]() elements
elements ![]() and from these, we compute the defuzzified value
and from these, we compute the defuzzified value ![]() :
:

For continuous membership functions, ![]() is computed by the following formula:
is computed by the following formula:

A very important usage of fuzzy expert systems is in medical diagnosis. Since exactness is something one encounters only in abstract worlds, a medical professional is typically forced to use vague, imprecise, and ambiguous information in his/her practice. Naturally, a medical expert system should be able to handle such kind of information as well. In other words, medical information is incomplete, inaccurate, and inconsistent [2]. In particular, typically, medical data are divided into four categories. Below we present these categories and give an outline of what may make data inaccurate, vague, etc.
- Medical history. Typically, a patient gives his/her own medical history. Of course, what the patient says is subjective and may say things that are not important, while he/she may forget to mention things that are important (e.g. diseases he/she or members of their family got).
- Physical examination. It is possible that a physician in a physical examination of a patient may overlook important indications, fail to carry out a complete examination, or may make some mistakes. Thus, a physical examination may not produce valid medical data.
- Results of laboratory tests. Although the results of laboratory tests are objective data, however, measurement errors, organizational problems (e.g. mislabeling samples), or improper patient behavior (e.g. eating fruits late at night may affect an examination of blood glucose level the next morning) may introduce some sort of inaccuracy in medical data.
- Results of histological, ultrasonic, PET scans, MRI scans, etc. These results depend on correct interpretation by medical or other staff. In many cases, uncertainty is part of the evaluation process.
The medical expert system CADIAG‐2 [2] was an attempt to create a fuzzy expert system to assist physicians in medical diagnosis. The symptom ![]() takes values in
takes values in ![]() . The value indicates the degree to which a patient exhibits symptom
. The value indicates the degree to which a patient exhibits symptom ![]() . If the value of
. If the value of ![]() is equal to
is equal to ![]() , this means the symptom has not yet been examined. The system built a fuzzy relation
, this means the symptom has not yet been examined. The system built a fuzzy relation ![]() , where
, where ![]() is a set of patients and
is a set of patients and ![]() a set of symptoms. In order to deliver results, the fuzzy logical operations have been extended. The value
a set of symptoms. In order to deliver results, the fuzzy logical operations have been extended. The value ![]() is assumed to be less than zero, so the
is assumed to be less than zero, so the ![]() and
and ![]() operations are adjusted accordingly. The fuzzy expert system used rules of the following form
operations are adjusted accordingly. The fuzzy expert system used rules of the following form
IF (antecedent) THEN (consequent) WITH (o, c)
where o is the frequency of occurrence and c the strength of confirmation.
A different approach to fuzzy medical diagnosis is based on intermediate diagnostic units [162] (IDU). This approach considers a universe of diseases ![]() and a universe of symptoms
and a universe of symptoms ![]() . Each patient corresponds to a fuzzy subset of
. Each patient corresponds to a fuzzy subset of ![]() and each symptom
and each symptom ![]() belongs to this fuzzy subset to a degree that corresponds to the degree the patient has this symptom. A model of a disease consists of a lattice structure composed of IDUs that are ordered by symptoms. The IDUs are formed from accumulated medical knowledge. There are many levels of IDUs. First‐level IDUs consist of symptoms that have common characteristics or criteria of diagnostic interest, whereas IDUs of higher levels consist of symptoms from IDUs from lower levels. Also, there are three types of IDUs and each type is associated with a formula that can be used to compute its membership degree. The associative IDUs consist of symptoms that must be present in order to make a diagnosis. For the nonassociative IDUs only one symptom, the most significant, is enough to make a diagnosis. Finally, the excluding IDUs include symptoms that can reduce the feasibility of a diagnosis when their intensity increases.
belongs to this fuzzy subset to a degree that corresponds to the degree the patient has this symptom. A model of a disease consists of a lattice structure composed of IDUs that are ordered by symptoms. The IDUs are formed from accumulated medical knowledge. There are many levels of IDUs. First‐level IDUs consist of symptoms that have common characteristics or criteria of diagnostic interest, whereas IDUs of higher levels consist of symptoms from IDUs from lower levels. Also, there are three types of IDUs and each type is associated with a formula that can be used to compute its membership degree. The associative IDUs consist of symptoms that must be present in order to make a diagnosis. For the nonassociative IDUs only one symptom, the most significant, is enough to make a diagnosis. Finally, the excluding IDUs include symptoms that can reduce the feasibility of a diagnosis when their intensity increases.
In order to derive a diagnosis using this model, one has to calculate the membership degree of each IDU from the symptoms of each patient. The estimated membership degree depends on a parameter ![]() whose value is initially set by an expert. This parameter may be adjusted later on. For an associative IDU, the membership degree is computed by the following formula:
whose value is initially set by an expert. This parameter may be adjusted later on. For an associative IDU, the membership degree is computed by the following formula:

where ![]() is a fuzzy relation on
is a fuzzy relation on ![]() and
and ![]() is the degree to which the specific IDU is related to the
is the degree to which the specific IDU is related to the ![]() th symptom,
th symptom, ![]() is again a fuzzy relation on
is again a fuzzy relation on ![]() and
and ![]() is the symptom intensity for symptom
is the symptom intensity for symptom ![]() for a specific patient, while
for a specific patient, while ![]() if
if ![]() and
and ![]() otherwise.
otherwise.
Nowadays, most people do not use standalone applications. Instead, it is customary to use some Web interface to some application or a real Web application. This is particularly useful in rural areas of underdeveloped countries that lack good medical facilities. A Web application that employs an alternative approach to computer‐aided medical diagnosis has been described in [84]. This application employs generalized fuzzy numbers, because it is extremely useful to be able to model the personal confidence level to a physician. Thus, the system has rules whose antecedent part uses generalized fuzzy numbers to quantify linguistic variables. On the other hand, the variables in the consequent part are quantified by “intuitionistic” fuzzy sets. The membership degree describes the degree of association of the disease to the patient, while the nonmembership degree describes the degree of nonassociation of the disease to the patient. To understand how all these things mix together, consider the following fuzzy decision rule:
If temperature is high with confidence level (CL) 0.7, headache is medium with CL 0.8, stomach pain is very low with CL 0.8, cough is very high with CL 0.5, and chest pain is low with CL 0.9, then the possibility of viral fever is
, for malaria is
, for typhoid is
, for stomach problem is
, for chest problem is
.
7.12 A Logic of Vagueness
Fuzzy set theory, in general, and fuzzy logic, in particular, are not universally accepted. Today, more than 50 years since Zadeh published his ideas on fuzzy sets and logic, there are scholars who do not think that fuzzy logic is a logic! In addition, many others do not buy the idea that vagueness is a property of our world. In fact, as it was already mentioned, some confuse fuzzy sets with probability theory and the first author [275] has presented a number of arguments that refute this wrong idea. As far as it regards fuzzy logic, the French logician Jean‐Yves Girard has put fuzzy logic under the “umbrella” of Broccoli logics [138] (i.e. new logics that are based on classical logic but have new connectives, new rules, etc.). However, Girard [140, p. 506] did not stop there and had to offer the following critique on fuzzy logic:
[s]peaking of fuzzy “logic”, what is wrong is not the idea of going beyond the boolean truth values
, it is the fact of confining one to the static, dead, domain of truth.
Clearly, this statement is a critique against all many‐valued logics. But why is it problematic to confine a logic to a “static, dead, domain of truth” and what does this really mean?
Girard [136] is the inventor of linear logic, a logic that has found many applications in computer science. In linear logic, propositions are not static as they are in classical logic. Obviously, since fuzzy logic is actually an extension of classical logic, propositions are static too. Thus, once a proposition gets a truth value, it will never change. And this is exactly what static means. But why is this bad? Let us give a simple example to make this clear. Assume that a certain moment a summit definitely belongs to a cloud. As it is natural, a few minutes later, the same summit may not definitely belong to the cloud. Of course, one could say that the point here is that time is not taken into account, nevertheless, we are not really interested in time, but instead, we want to emphasize that truth values are dynamic entities. In linear logic, a proposition is viewed as some kind of resource that can obviously be exhausted. The following example borrowed from Girard [137] should make things clear. Think of modus ponens:
if
and
, then
.
When applying this rule, ![]() is still valid. It is like saying that
is still valid. It is like saying that ![]() stands for “to spend €5” and
stands for “to spend €5” and ![]() stands for “to get a pack of cigarettes.” Then if
stands for “to get a pack of cigarettes.” Then if ![]() means that one spends €5 to get a pack of cigarettes, then an application of modus ponens if
means that one spends €5 to get a pack of cigarettes, then an application of modus ponens if ![]() holds means that one will spend €5, he/she will get the pack of cigarettes, and in the end, he/she will still have €5. Of course, it does not really matter if
holds means that one will spend €5, he/she will get the pack of cigarettes, and in the end, he/she will still have €5. Of course, it does not really matter if ![]() and
and ![]() are fuzzy predicates since this problem is still there. Of course, there are mechanisms that allow one to repeatedly use a proposition in proofs, but this is not the norm. The next question is how can one modify fuzzy logic to accommodate these ideas? Of course, this is not an easy task, but we can get inspiration from computer science.
are fuzzy predicates since this problem is still there. Of course, there are mechanisms that allow one to repeatedly use a proposition in proofs, but this is not the norm. The next question is how can one modify fuzzy logic to accommodate these ideas? Of course, this is not an easy task, but we can get inspiration from computer science.
The proofs‐as‐processes slogan by Samson Abramsky [1] was about the description of proofs in linear logic as expressions in some process calculus like Robin Milner's π‐calculus. In the framework of theoretical computer science, processes are perfect entities that either stop or work ad infinitum. However, in reality, processes may be similar to some degree, perform tasks to a certain degree, etc. This simply means that one could use processes and their interaction as a starting point and, by going back to logic, one could possibly define some vague logic that would have dynamic truth values. After all, as Girard [139] has pointed out: “Instead of teaching logic to nature, it is more reasonable to learn from her.” Thus, it is possible to take all these under consideration and produce a logic of vagueness.
Exercises
- 7.1 Write down the truth tables of the following expressions:
 ,
,  , and
, and  .
. - 7.2 Show that
 is logically equivalent to
is logically equivalent to  .
. - 7.3 Prove in BL the following:
 ;
; ; and
; and .
.
- 7.4 Show that
 is equivalent to
is equivalent to  in BL.
in BL. - 7.5 Assume that
 ,
,  ,
,  . Compute
. Compute  .
. - 7.6 If
 is a fuzzy set, explain how the hedge “very very” will modify it.
is a fuzzy set, explain how the hedge “very very” will modify it.
Notes
- 1 Translation: It is clear then that it is not necessary for every affirmation or negation taken from among opposite propositions that the one be true, the other false. For what is nonexistent but has the potentiality of being or not being does not behave after the fashion of what is existent, but in the manner just explained.
- 2 Since we did not have access to Zadeh's original paper, we present the quotation as it appeared in [26, p. 43].
- 3 Note that we write
 and
and  instead of
instead of  and
and  to avoid changing the notation used so far.
to avoid changing the notation used so far.

