Chapter 5
Understanding Probability Basics
IN THIS CHAPTER
![]() Warming up to probability rules and concepts
Warming up to probability rules and concepts
![]() Steering clear of probability misconceptions
Steering clear of probability misconceptions
![]() Forecasting the future with probabilities
Forecasting the future with probabilities
In this chapter, you practice using and applying the rules and ideas of probability. The rules and laws of probability often go against our intuition. For example, a combination like 1, 2, 3, 4, 5, 6 seems a very unlikely winner in the lottery, when, in fact, it has just the same chance as any other combination (which shows how unlikely they all really are). And it might seem that a couple that has three girls in a row should have a much higher chance of having a boy this time, but barring any genetic predisposition to girls, the chance is still 50-50 each time. The practice in interpreting probability that this chapter provides helps ease your statistical state of mind and allows you to avoid making some of the more common misconceptions about the subject.
Grasping the Rules of Probability
The definition of the probability of an outcome is the long-run percentage (or relative frequency) of times that you expect the outcome to occur. Probabilities follow certain rules. Here they are in a nutshell:
- Every probability is a percentage between 0 and 100. In terms of decimals, a probability (proportion) is a number between 0 and 1. A probability of 1 means the outcome is certain, and a probability of 0 means the outcome is impossible.
- The set containing all possible outcomes is called the sample space. The sum of the probabilities of all possible outcomes in the sample space is equal to 1.
- The probability of an event or set of outcomes that are disjoint (sharing no outcomes in common) is equal to the sum of the individual probabilities for each disjoint outcome.
- The complement of an event is all the possible outcomes except those that make up the event. The probability of the complement of an event is 1 minus the probability of the event.
The way to understand probability and how it works is to start with a small example, such as the following, and work from there.
 Q. Suppose that you flip a fair coin three times.
Q. Suppose that you flip a fair coin three times.
- How many outcomes are possible?
- What’s the probability of each outcome?
- What are the possible values for the total number of heads out of three tosses, and what are their probabilities?
A. Before you start flipping your coins, it’s good to know exactly what the possibilities and their probabilities are. The table at the end of this example shows you the possibilities and probabilities at a glance for this coin-flipping scenario.
- The sample space contains eight outcomes: HHH, HHT, HTH, THH, HTT, THT, TTH, TTT. Notice that each flip has two possible outcomes, so three flips has
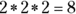 possible outcomes.
possible outcomes. - Each outcome has a probability of 1 in 8 (because the total number of outcomes is eight, and because you assume the coin to be two-sided and fair).
- The total number of heads can be 3, 2, 1, or 0. Three heads happens only one way, HHH, so its probability is 1 in 8. Two heads happens three ways, HHT, HTH, THH, so its probability is 3 in 8. One head happens three ways, HTT, THT, TTH, so its probability is 3 in 8. Zero heads happens in only one way, TTT, so its probability is 1 in 8. All these probabilities sum to 1.
|
Number of Heads |
Possible Outcomes |
Probability |
|
3 |
HHH |
1 in 8 |
|
2 |
HHT, HTH, THH |
3 in 8 |
|
1 |
HTT, THT, TTH |
3 in 8 |
|
0 |
TTT |
1 in 8 |
1 M&Ms colors come in the following percentages: 13 percent brown, 14 percent yellow, 13 percent red, 24 percent blue, 20 percent orange, and 16 percent green. Reach into a bag of M&Ms without looking.
- What’s the chance that you pull out a brown or yellow M&M?
- What’s the chance that you won’t pull out a blue?
2 Suppose that you flip a coin four times, and it comes up heads each time. Does this outcome give you reason to believe that the coin isn’t legitimate?
3 Consider tossing a fair coin 10 times and recording the number of heads that occur.
- How many possible outcomes would occur?
- What would be the probability of each of the outcomes?
- How many of the outcomes would have 1 head? What is the probability of 1 head in 10 flips?
- How many of the outcomes would have 0 heads? What is the probability of 0 heads in 10 flips?
- What’s the probability of getting 1 head or less on 10 flips of a fair coin?
4 What’s the probability of getting more than 1 head on 10 flips of a fair coin?
Avoiding Probability Misconceptions
Probability often goes against our intuition or our desires; we often ignore it or are unaware of its impact. For example, thinking that every situation with two possible outcomes is a 50-50 situation can get you into trouble (yet it seems tempting). And the biggest misconceptions are in the gambling arena, with people thinking they’ll hit it big any minute now. The casinos are counting on you having that attitude (and are literally counting your money).
- Believing that outcomes that appear to be “more random” have a higher chance of occurring than outcomes that don’t
- Thinking probability works well for predicting short-run behavior
- Claiming you can be “on a roll” or “due for a hit” by the law of averages
- Treating any situation with only two possible outcomes as a “50-50” situation
- Misinterpreting a rare event
The problem with these misconceptions is that they appear to make sense, and you may want them to be true, but they just aren’t. With probability practice, you can begin to see through the misconceptions and find out how to avoid them. (In the solutions at the end of this chapter, I elaborate more on these misconceptions as they come up in the practice problems. You can also find more discussion on probability misconceptions in Statistics For Dummies, 2nd Edition [Wiley], if you happen to have a copy.)
5 Suppose that an NBA player’s free throw shooting percentage is 70 percent.
- Explain what this means as a probability.
- What’s wrong with thinking that his chances of making his next free throw are 50-50 (because he either makes it or he doesn’t)?
6 Suppose that you buy a lottery ticket, and you have to pick six numbers from 1 through 50 (repetitions allowed). Which combination is more likely to win: 13, 48, 17, 22, 6, 39 or 1, 2, 3, 4, 5, 6?
7 You feel lucky again and buy a handful of instant lottery tickets. The last three tickets you open each win a dollar. Should you buy another ticket because you’re “on a roll”?
8 Suppose that a small town has five people with a rare form of cancer. Does this automatically mean a huge problem exists that needs to be addressed?
Making Predictions Using Probability
One of the most important functions of probability used by researchers and the media is its usefulness in making predictions. Forecasts can be very useful, but you have to temper them with the understanding that probability is a long-term predictor, not a short-term fix. You also need to realize that building a model to make a prediction can be a very complicated business.
See the following example for a problem dealing with probability and predictions.
 Q. Suppose you know that the chance of winning your money back on an instant lottery ticket is 1 in 10. Does that mean if you buy 10 lottery tickets, you know one of them will be an instant winner?
Q. Suppose you know that the chance of winning your money back on an instant lottery ticket is 1 in 10. Does that mean if you buy 10 lottery tickets, you know one of them will be an instant winner?
A. No. This misconception of probability is a popular one. Probability is the long-term percentage of instant winners, and it doesn’t apply to a sample as small as 10. Results will vary from sample to sample.
9 A couple has conceived three girls so far with a fourth baby on the way. Do you predict the newborn will be a girl or a boy? Why?
10 Meteorologists use computer models to predict when and where a hurricane will hit shore. Suppose they predict that hurricane Stat has a 20 percent chance of hitting the East Coast.
- On what info are the meteorologists basing this prediction?
- Why is this prediction harder to make than your chance of getting a head on your next coin toss?
11 Bob has glued himself to a certain slot machine for four hours in a row now with his bucket of coins and a bad attitude. He doesn’t want to leave because he feels the longer he plays, the better chance he has to win eventually. Is poor Bob right?
12 Which situation is more likely to produce exactly 50 percent heads: flipping a coin 10 times or flipping a coin 10,000 times?
Answers to Problems in Probability
1 Probabilities apply to individual selections as well as to long-term frequencies.
- Because 13 percent of all plain M&Ms are brown, the chance that the one M&M you pick is brown is 13 percent. For yellow, the chance is 14 percent. For brown or yellow, add the probabilities to get 27 percent.
- Because 24 percent of plain M&Ms are blue,
 aren’t blue, by the complement rule.
aren’t blue, by the complement rule.
2 You don’t have enough data to determine the probability until you look at the long-run percentage of heads, and four flips isn’t a long run of data collecting. But another way to look at this question is to find the probability of flipping four heads on four flips of a coin. Flipping a coin four times gives you ![]() possibilities. You can get four heads one way, so the chance of flipping four heads on four flips is
possibilities. You can get four heads one way, so the chance of flipping four heads on four flips is ![]() or 6%. It doesn’t happen very often, but it does happen. You may be skeptical of the coin, but you should collect more data before you decide.
or 6%. It doesn’t happen very often, but it does happen. You may be skeptical of the coin, but you should collect more data before you decide.
3 This problem seems daunting until you realize you have an easy way and a hard way to do this problem (and your professor is banking on you realizing the same thing!).
- Flipping a coin 10 times results in
 or
or  possible outcomes. (Don’t try to list them all out!)
possible outcomes. (Don’t try to list them all out!) - Because the coin is fair, each outcome is equally likely and has a probability of 1 in 1,024.
- You have 10 ways to get a single head on 10 flips. One way is to have HTTTTTTTTT. But the head can come on the second toss, the third toss, or anywhere up to the tenth toss. The probability is, therefore, 10 in
 .
. - To flip no heads, you have to get all tails, and that happens only one way out of 1,024, which equals 0.001.
- Add the two probabilities from Question 3c and 3d to get 11 in
 for the probability of less than or equal to 1 head on 10 flips of a coin.
for the probability of less than or equal to 1 head on 10 flips of a coin.
4 Solving this problem is much easier if you look at the complement. The complement of flipping more than one head is flipping less than or equal to one head (a number line can help show you this as well). In Question 3, you find the probability of less than or equal to one head to be 11 in 1,024. The probability of flipping greater than one head is, therefore, ![]() .
.
5 The misconception that random situations having only two possible outcomes are 50-50 situations is a very common one.
- The 70 percent shooting clip means that in the long term, over many free throws, this player makes his shots 70 percent of the time, on average.
- The 50-50 argument breaks down because the two outcomes aren’t equally likely. According to past data, this player hits 70 percent of his free throws and misses only 30 percent of the time. Using these numbers is similar to flipping an unfair coin. You have two sides, yes, but the two outcomes aren’t equally likely. If the 50-50 argument worked, we should all buy lottery tickets, because either you win or you don’t with a 50-50 chance, right? (In our dreams!)
 Just because you have two possible outcomes doesn’t mean they each have a 50 percent chance of happening. You have to look at past data and determine what the weight is for each outcome, just like in every other situation.
Just because you have two possible outcomes doesn’t mean they each have a 50 percent chance of happening. You have to look at past data and determine what the weight is for each outcome, just like in every other situation.
6 Both outcomes are equally likely. Assuming that the lottery process is fair, every single combination of six numbers has an equally likely chance of being selected. The combo 1, 2, 3, 4, 5, 6 seems like it could never happen, but the probability shows you how unlikely any combination is to win. After all, with 50 numbers to choose from and 6 numbers to pick, you have millions of possibilities. But here’s a tip: Go ahead and pick 1, 2, 3, 4, 5, 6. If you do win, you won’t have to split the money with anyone, because no one else is picking that combination! (Until they read this, at least …)
7 No. Probability is a long-term percentage. What recently happened has no impact on what happens in the future. Suppose that 5 percent of all instant lottery tickets are winners. This figure tells you nothing about when those winners will come up.
 Probability predicts long-term behavior only; it can’t guarantee any kind of short-term outcomes. Numbers may take a long time to “average out,” and there’s no such thing as being “on a roll” or “due for a hit.” The law of averages idea applies only to the long term.
Probability predicts long-term behavior only; it can’t guarantee any kind of short-term outcomes. Numbers may take a long time to “average out,” and there’s no such thing as being “on a roll” or “due for a hit.” The law of averages idea applies only to the long term.
8 Not necessarily. The chances of this happening are quite small, but even if the probability is one in a million, you should expect it to happen, on average, once out of every million times. Over a period of years, in a very large country, a situation like this is bound to happen just by chance. The outbreak may point to something else, and the town should investigate, but it doesn’t automatically mean that a problem exists.
9 The chance of having a boy this time is the same as it was with the previous births, 1 in 2. Probability has no memory of recent happenings and can’t predict short-term behavior.
10 Computer models use a process called simulation. You put all your data in, make a mathematical model out of it, and repeatedly run the computer through the scenario to see what happens.
- The 20 percent comes from the fact that 20 percent of the times the computers repeated the scenario the results pointed to the hurricane hitting the coast, and 80 percent of the times had it veering off into sea.
- Computer models are based on a great deal of information, but many assumptions fill in the blanks. Some of these assumptions can be wrong, thus throwing the percentage predictions right out the window.
11 Not really. In the long run, Bob should expect to lose a small amount with a very high probability every time he pulls the handle on the machine. Yes, he may win big on one pull, but the chance is so tiny that, on average, he doesn’t have enough time in his life to sit on that stool and wait to win. Who makes all the money? The person who owns the slot machine, that’s who.
12 Flipping a coin 10,000 times has a higher chance of landing 50 percent heads (exactly), because when you flip it only 10 times, the results still vary so much that you can get results like three, four, five, six, or seven heads with a fairly high probability. But when you increase the sample size to 10,000, the relative frequency (percentage of heads observed) becomes closer and closer to the true probability you expect (in this case, 50 percent). This shows the real law of averages at work.
 The law of averages says that, in the long run, the percentage of occurrences of an event gets closer and closer to the true probability of the event.
The law of averages says that, in the long run, the percentage of occurrences of an event gets closer and closer to the true probability of the event.

 Here are some common misconceptions about probability that you want to avoid:
Here are some common misconceptions about probability that you want to avoid: